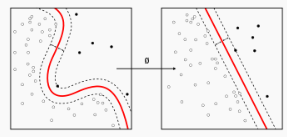
가우시안 분포와 분별 함수 (선형 분별 분석(LDA), 2차 분별 분석(QDA))

2020, Feb 01    

머신러닝 글 목록

• 참조 : 패턴인식 (오일석)
• 이번 글에서는 가우시안 분포를 이용한 분별 함수에 대하여 알아보도록 하겠습니다.

목차

• gaussian distribution과 discriminant function

• Linear Discriminant Analysis

• LDA 예제

• Quadratic Discriminant Analysis

• QDA 예제

• 정리

• 일반적으로 패턴 x개가 입력되면 M개 부류에 대해 사후 확률 \(P(w_{i} \vert x)\)를 계산하고 그들 중 가장 큰 값을 갖는 부류로 분류하면 됩니다.
• 하지만 사후 확률을 직접 계산하는 것은 현실적으로 매우 어렵습니다.
• 따라서 베이스 정리에 따라 상대적으로 계산이 쉬운 사전 확률 \(P(w_{i})\)와 가능도 \(p(x \vert w_{i})\)의 곱으로 대치하여 계산합니다.
• 그렇다고 하더라도 사전 확률을 구하는 것은 비교적 쉽지만 가능도의 추정은 경우에 따라 어려울 수도 있습니다.
• 이번 글에서는 training set이 가우시안 분포(정규 분포)와 유사한 형태로 나타났다는 가정하에서 전개해 보려고 합니다. 즉, 가우시안 분포에 베이지안 분류기를 접목하는 것이 이 글의 목적입니다.
  • 따라서 가능도 \(p(x \vert w_{i})\)가 정규 분포를 따르는 특수한 경우에 대하여 분류기가 가지는 성질을 분석해보려고 합니다.
  • 특히, 두 클래스의 영역을 나누는 decision boundary가 어떤 모양을 갖는지에 대한 분석이 주를 이룹니다.
• 특히 가우시안 분포에 대한 가정이 의미가 있는 것은 현실 세계의 많은 분포가 가우시안 분포를 따르기 때문입니다.
  • 이와 관련된 내용으로 중심 극한 이론이 있으니 링크를 참조하시기 바랍니다.
• 또한 평균과 분산이라는 단 2개의 매개 변수 만으로 확률 분포를 컨트롤 하기 때문에 다루기가 쉽습니다.
• 그리고 가우시안 분포는 수학적인 특성이나 계산할 때 편한 장점들이 많습니다.

• 먼저 가우시안 분포는 간단한 1차원 형태와 d차원인 경우를 구분하여 식으로 나타냅니다.
• 익히 알고있는 것처럼 가우시안 분포 또는 정규(Normal) 분포는 \(N(\mu, \sigma^{2})\) 또는 \(N(\mu, \Sigma)\) 형태로 표현 가능합니다.
• 먼저 잘 아시겠지만 1차원 가우시안 분포는 다음 분포와 식을 따릅니다.
• 1차원에서의 \(\mu\)와 \(\sigma^{2}\)은 각각 평균과 분산입니다.

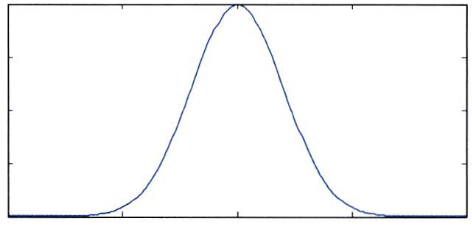
• \[N(\mu, \sigma^{2}) = \frac{1}{(2\pi)^{1/2}\sigma} exp(-\frac{(x - \mu)^{2}}{2\sigma^{2}})\]

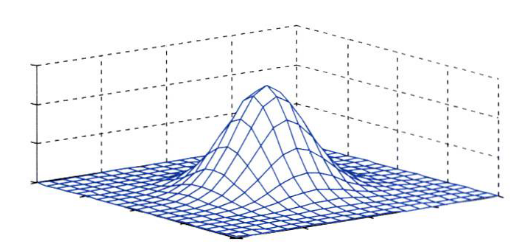
• d차원에서의 \(\mu\)는 평균 벡터이고 \(\Sigma\)는 d x d크기의 공분산 행렬입니다.
• 그리고 \(\vert \Sigma \vert\)와 \(\Sigma^{-1}\)은 각각 행렬 \(\Sigma\)의 행렬식(determinant)과 역행렬입니다.

• \[N(\mu, \Sigma) = \frac{1}{(2\pi)^{d/2}\vert \Sigma \vert^{1/2}} \text{exp}(-\frac{1}{2}(x - \mu)^{T}\Sigma^{-1}(x - \mu) )\]

• 클래스 \(w_{i}\)가 평균 벡터 \(\mu_{i}\)와 공분산 행렬 \(\Sigma_{i}\)를 갖는 가우시안 분포라고 가정해 보겠습니다.
• 그러면 가능도(likelihood)는 다음 식과 같이 나타낼 수 있습니다.

• \[p(x \vert w_{i}) = N(\mu_{i}, \Sigma_{i}) = \frac{1}{(2\pi)^{d/2} \vert \Sigma_{i} \vert ^{1/2}} \text{exp} (-\frac{1}{2}(x - \mu_{i})^{T} \Sigma_{i}^{-1}(x - \mu_{i}))\]

• 위에서 선언한 가능도(\(p(x \vert w_{i})\))와 사전 확률(\(P(w_{i})\))을 이용하여 사후 확률 \(p(x \vert w_{i}) P(w_{i})\)를 구할 때, 단조 증가 함수 성질을 이용하여 log를 취해 식을 간단하게 해보도록 하겠습니다. 여기서 가능도에 있는 지수를 없애기 위해 ln을 적용해 보겠습니다.

• \[g_{i}(x) = \text{ln}(f(x)) = \text{ln}(p(x \vert w_{i})P(w_{i}))\]
• \[= \text{ln}(N(\mu_{i}, \Sigma_{i})) + \text{ln}(P(w_{i}))\]
• \[= -\frac{1}{2}(x - \mu_{i})^{T}\Sigma_{i}^{-1}(x - \mu_{i}) - \frac{d}{2}\text{ln}(2\pi) - \frac{1}{2}\text{ln}(\vert \Sigma_{i} \vert) + \text{ln}(P(w_{i}))\]
• \[= -\frac{1}{2}(x^{T}\Sigma_{i}^{-1}x -x^{T}\Sigma_{i}^{-1}\mu_{i} - \mu_{i}^{T}\Sigma_{i}^{-1}x + \mu_{i}^{T}\Sigma_{i}^{-1}\mu_{i}) - \frac{d}{2}\text{ln}(2\pi) - \frac{1}{2}\text{ln}(\vert \Sigma_{i} \vert) + \text{ln}(P(w_{i}))\]

• 여기서 \(\Sigma^{-1}\)이 대칭행렬이므로 다음과 같이 정리할 수 있습니다.
• 대칭 행렬 양 옆으로 곱해진 행렬의 곱은 교환 법칙이 성립합니다. (\(B\) 가 대칭행렬일 때, \(A \cdot B \cdot C == C \cdot B \cdot A\))

• \[= -\frac{1}{2}(x^{T}\Sigma_{i}^{-1}x - 2\mu_{i}^{T}\Sigma_{i}^{-1}x + \mu_{i}^{T}\Sigma_{i}^{-1}\mu_{i}) - \frac{d}{2}\text{ln}(2\pi) - \frac{1}{2}\text{ln}(\vert \Sigma_{i} \vert) + \text{ln}(P(w_{i}))\]

• 식이 다소 복잡해 보이긴 하지만 의미를 살펴보면 간단합니다.
  • 입력 : 벡터 \(x\)
  • 클래스 별 평균과 벡터 : 클래스 \(i\) 별 \(\mu_{i}, \Sigma_{i}\)

• 앞에서 전개한 식을 이해하기 위해서 2차원 실수 공간에 정의된 \(x = (x_{1}, x_{2})^{T}\) 에 대하여 다루어 보겠습니다.
• 이 때 클래스 \(w_{i}\)는 다음 성질을 따른다고 가정하겠습니다.

• \[\mu_{i} = (3, 1)^{T}\]
• \[\Sigma_{i} = \begin{pmatrix} 2 & 0 \\ 0 & 2 \\ \end{pmatrix}\]

• 위 값을 앞에서 전개한 식에 대입해 보도록 하겠습니다.

• \[g_{i}(x) = -\frac{1}{2} \Biggl( \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \end{pmatrix} \Biggr)^{T} \begin{pmatrix} 2 & 0 \\ 0 & 2 \\ \end{pmatrix}^{-1} \Biggl( \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} - \begin{pmatrix} 3 \\ 1 \end{pmatrix} \Biggr) - \frac{2}{2} \text{ln}(2\pi) -\frac{1}{2} \text{ln}( \vert \begin{pmatrix} 2 & 0 \\ 0 & 2 \\ \end{pmatrix} \vert) + \text{ln}(P(w_{i}))\]

• \[= -\frac{1}{2} \begin{pmatrix} x_{1} -3 & x_{2} - 1 \end{pmatrix} \begin{pmatrix} 1/2 & 0 \\ 0 & 1/2 \\ \end{pmatrix}^{-1} \begin{pmatrix} x_{1} - 3 \\ x_{2} -1 \end{pmatrix} \text{ln}(2\pi) -\frac{1}{2} \text{ln}(4) + \text{ln}(P(w_{i}))\]

• \[= -\frac{1}{4}(x_{1}^{2} + x_{1}^{2}) + \frac{1}{2}(3x_{1} + x_{2}) -\frac{1}{2}(5 + 2\text{ln}(2\pi) + \text{ln}(4) - 2\text{ln}(P(w_{i})))\]

• 위 식의 term을 보면 처음에는 2차식, 두번째는 1차식 그리고 마지막은 상수항으로 정리됨을 알 수 있습니다.
• 즉, 특징 벡터의 차원에 따라 같은 차원으로 정리 됩니다.
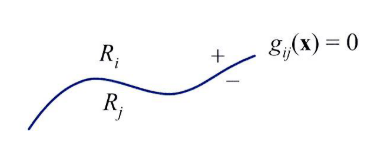
• 위 식은 \(w_{i}\)의 클래스에 속하는 어떤 값에 대한 사후 확률을 뜻합니다. 그러면 이 값을 좀 더 해석해 보겠습니다.
• 두 클래스 \(w_{i}, w_{j}\)의 decision boundary에 대하여 알아보면 어떤 데이터 \(x\)가 decision boundary에 존재한다면 \(g_{i}(x) = g_{j}(x)\)가 되어야 합니다.
• 이 식을 다음과 같이 정리할 수 있습니다.

• \[g_{ij} = g_{i}(x) - g_{j}(x)\]

• 두 클래스의 decision boundary를 나타내면 다음과 같습니다.

• 다음으로 알아볼 것은 각 클래스 별로 같은 공분산을 가지는 경우와 그렇지 않은 경우에 따라서 해석 방법이 다릅니다. 그것에 대하여 알아보겠습니다.

Linear Discriminant Analysis

• 먼저 클래스 별로 같은 공분산을 가지는 경우에 대하여 다루어 보도록 하겠습니다.
• 이 상황에서는 각 클래스의 \(\Sigma_{i}\)가 모두 같으므로 \(\Sigma\)라고 적어도 되니 편의상 통일하여 적겠습니다.

• \[= -\frac{1}{2}(x^{T}\Sigma^{-1}x - 2\mu_{i}^{T}\Sigma^{-1}x + \mu_{i}^{T}\Sigma^{-1}\mu_{i}) - \frac{d}{2}\text{ln}(2\pi) - \frac{1}{2}\text{ln}(\vert \Sigma \vert) + \text{ln}(P(w_{i}))\]

• 여기서 \(i\) 항과 관련된 것과 관련되지 않은 것을 분리해서 정리해보겠습니다.

• \[\frac{1}{2}(-2\mu_{i}^{T}\Sigma^{-1}x -\mu_{i}^{T}\Sigma^{-1}\mu_{i} + 2\text{ln}(P(w_{i}))) -\frac{1}{2}(x^{T}\Sigma^{-1}x + d\text{ln}(2\pi)) + \text{ln}\vert \Sigma \vert)\]

• 위 식에서 첫번째 항은 \(i\)와 관련이 있는 항들이고 두번째 항은 \(i\)와 무관합니다.
• 이렇게 나눈 이유는 \(i\)항과 무관한 항은 \(g_{i}(x)\)에서 어떤 \(i\)가 들어가더라도 똑같은 값을 가지므로 \(g_{ij}(x) = g_{i}(x) - g_{j}(x)\) 에서는 소거되므로 생략해도 됩니다. (물론 위 식은 단일 클래스에 대한 식이지만 미리 목적에 맞게 필요없는 항은 사전에 삭제한다는 뜻입니다.)
  • 즉, 우리과 관심을 가져야 하는 것은 함수 값 자체라기보다는 두 함수값을 비교하였을 때의 결과이기 때문에 식을 간단하게 만들 수 있습니다.
• 이렇게 식을 정리하였을 때, 유일한 2차항인 \(x^{T} \Sigma^{-1} x\)가 소거됩니다.
• 결국 클래스 별로 동일한 공분산을 가질 때, 분별 함수는 1차식이 됩니다.
• 이 식을 선형 방정식의 형태로 다시 정리해 보도록 하겠습니다.

• \[g_{i}(x) = (\Sigma^{-1} \mu_{i})^{T}x + (\text{ln}(P(w_{i})) -\frac{1}{2}\mu_{i}^{T}\Sigma^{-1}\mu_{i}) = w_{i}^{T}x + b_{i}\]

• 그러면 위 식을 이용하여 비교 식 \(g_{ij}(x)\)에 대하여 다루어 보겠습니다.

• \[g_{ij}(x) = g_{i}(x) - g_{j}(x) = (\Sigma^{-1}(\mu_{i} - \mu_{j}))^{T}x + (\text{ln}(P(w_{i})) -\text{ln}(P(w_{j})) -\frac{1}{2} \mu_{i}^{T}\Sigma^{-1}\mu_{i} + \frac{1}{2}\mu_{j}^{T}\Sigma^{-1}\mu_{j} )\]

• \[= (\Sigma^{-1}(\mu_{i} - \mu_{j}))^{T}\Biggl(x - \Biggl( \frac{1}{2}(\mu_{i} + \mu_{j}) - \frac{\mu_{i} - \mu_{j}}{(\mu_{i} - \mu_{j})^{T}\Sigma^{-1}(\mu_{i} - \mu_{j})} \text{ln}\frac{P(w_{i})}{P(w_{j})} \Biggr)\Biggr) = w^{T}(x - x_{0})\]
• 여기에서 \((\Sigma^{-1}(\mu_{i} - \mu_{j}))^{T}\) 를 \(w\)라고 하고 \(\Biggl( \frac{1}{2}(\mu_{i} + \mu_{j}) - \frac{\mu_{i} - \mu_{j}}{(\mu_{i} - \mu_{j})^{T}\Sigma^{-1}(\mu_{i} - \mu_{j})} \text{ln}\frac{P(w_{i})}{P(w_{j})} \Biggr)\)를 \(x_{0}\) 라고 정의하면 위와 같이 정리할 수 있습니다.

• 위 식을 기하학적으로 살펴보면 \(g_{ij}(x)\) 가 1차식 형태를 따르므로 decision boundary가 직선의 형태가 뜀을 알 수 있습니다.

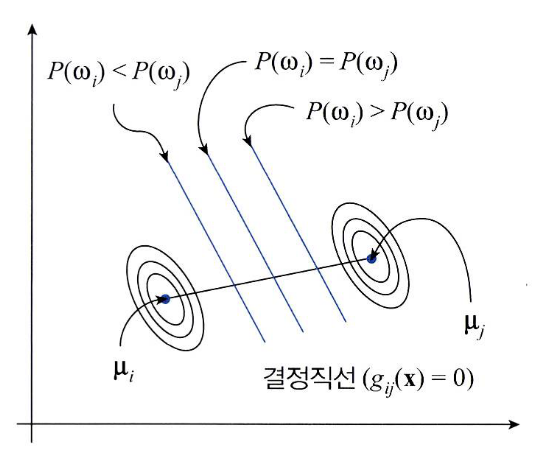
• 위 그림은 두 클래스 \(w_{i}, w_{j}\)의 가우시안 분포를 등고선 형태로 표현한 그림입니다.
• 두 클래스의 공분산이 같기 때문에 같은 모양의 타원을 띔을 알 수 있습니다.

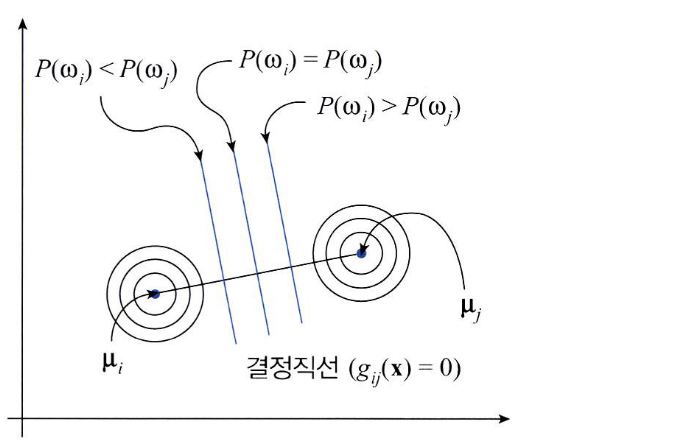
• 만약 공분산의 형태가 \(\sigma^{2}I\) (I는 Identity)라면 위 그림과 같이 타원이 아닌 원의 형태를 띕니다.
• decision boundary를 구하려면 위 식에서 \(x_{0} = 0\)을 만족하여 \(g_{ij}(x) = 0\)이 되는 경계입니다.
• 따라서 \(g_{ij}(x)\)가 1차식임을 이용하면 decision boundary는 \(x_{0}\)를 지나면서 \(w = \Sigma^{-1}(\mu_{i} - \mu_{j})\)와 직교하는 직선을 찾으면 됩니다. 그 직선이 decision boundary가 되고 그 지점에서는 \(g_{ij}(x) = 0\)을 만족합니다.
• 만약 비교하는 두 클래스의 사전 확률이 같으면 \(\text{ln}(P(w_{i}) / P(w_{j}) ) = 0\)이 됩니다.
• 즉, \(x_{0} = 1/2(\mu_{i} + \mu_{j})\)인 지점이 decision boundary가 되는데 이 지점은 \(\mu_{i}\)와 \(\mu_{j}\)의 중점입니다.
• 추가적으로 식을 살펴보면 \(P(w_{i}) > P(w_{j})\)이면 decision boundary는 \(\mu_{j}\)에 가까워집니다.
  • 즉, \(mu_{i}\)를 중심으로 하는 분포에 속할 영역이 더 넓어진다고 해설할 수도 있습니다.

• 지금까지 한것을 정리하면 클래스의 공분산이 같은 가우시안 분포에서는 decision boundary로 linear classifier를 얻었습니다.
• 이런 과정을 통하여 linear classifier를 만드는 방법을 LDA(Linear Discriminant Analysis) 라고 합니다.

LDA 예제

• 1번 클래스(\(w_{1}\))와 2번 클래스(\(w_{2}\))가 있고 현재 각각 4개씩의 샘플을 가지고 있다고 가정해 보곘습니다.

• \[w_{1} = \{ (1, 2)^{T}, (3, 1)^{T}, (5, 2)^{T}, (3, 3)^{T} \}\]
• \[w_{2} = \{ (6, 6)^{T}, (8, 5)^{T}, (10, 6)^{T}, (8, 7)^{T} \}\]

• 그러면 위 데이터를 기준으로 평균과 공분산을 구해보도록 하겠습니다.
• 먼저 평균입니다.

• \[\mu_{1} = \frac{1}{4} \Biggl( \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix} + \begin{pmatrix} 5 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} \Biggr) = \begin{pmatrix} 3 \\ 2 \end{pmatrix}\]
• \[\mu_{2} = \frac{1}{4} \Biggl( \begin{pmatrix} 6 \\ 6 \end{pmatrix} + \begin{pmatrix} 8 \\ 5 \end{pmatrix} + \begin{pmatrix} 10 \\ 6 \end{pmatrix} + \begin{pmatrix} 8 \\ 7 \end{pmatrix} \Biggr) = \begin{pmatrix} 8 \\ 6 \end{pmatrix}\]

• 그 다음으로 공분산을 구해보도록 하겠습니다.
• 공분산의 각 원소는 다음 식을 이용하여 구할 수 있습니다.

• \[\sigma(x, x) = \frac{ \sum_{i=1}^{n}(x_{i} - \mu_{x})^{2} }{n-1} = E[ (X - E(X))(X - E(X)) ]\]
• \[\sigma(x, y) = \frac{ \sum_{i=1}^{n}(x_{i} - \mu_{x})(y_{i} - \mu_{y}) }{n-1} = E[ (X - E(X))(Y - E(Y)) ]\]
• \[\sigma(y, x) = \frac{ \sum_{i=1}^{n}(y_{i} - \mu_{y})(x_{i} - \mu_{x}) }{n-1} = E[ (Y - E(Y))(X - E(X)) ]\]
• \[\sigma(y, y) = \frac{ \sum_{i=1}^{n}(y_{i} - \mu_{y})^{2} }{n-1} = E[ (Y - E(Y))(Y - E(Y)) ]\]

• 여기서 공분산을 구할 때, n-1로 나누는 이유는 표본분산을 구하기 때문이고 표본분산의 평균이 모분산과 같아지게 하기 위해서 입니다.

• \[\Sigma_{1} = \begin{pmatrix} ((1 - 3)^{2} + (3 - 3)^{2} + (5 - 3)^{2} + (3 - 3)^{2})/(4-1) & ((1 - 3)(2 - 2) + (3 - 3)(1 - 2) + (5 - 3)(2 - 2) + (3 - 3)(3 - 2))/(4-1) \\ ((2 - 2)(1 - 3) + (1 - 2)(3 - 3) + (2 - 2)(5 - 3) + (3 - 2)(3 - 3))/(4-1) & ((2 -2)^{2} + (1 - 2)^{2} + (2 - 2)^{2} + (3 - 2)^{2})/(4-1) \end{pmatrix}\]
• \[\Sigma_{2} = \begin{pmatrix} ((6 - 8)^{2} + (8 - 8)^{2} + (10 - 8)^{2} + (8 - 8)^{2}) / (4-1) & ((6 - 8)(6 - 6) + (8 - 8)(5 - 6) + (10 - 8)(6 - 6) + (8 - 8)(7 - 6))/(4-1) \\ ((6 - 6)(6 - 8) + (5 - 6)(8 - 8) + (6 - 6)(10 - 8) + (7 - 6)(8 - 8))/(4-1) & ( (6 -6)^{2} + (5 - 6)^{2} + (6 - 6)^{2} + (7 - 6)^{2})/(4-1) \end{pmatrix}\]

• 현재 구하는 LDA의 전제 조건이 각 클래스 별 가우시안 분포의 공분산은 같다 이기 때문에 실제 계산하면 동일한 값을 가집니다.

• \[\Sigma = \begin{pmatrix} 8/3 & 0 \\ 0 & 2/3 \end{pmatrix}\]

• 공분산이 \(\sigma^{2} I\) 형태가 아니므로 기하학적으로는 타원형의 분포를 띄는 가우시안 분포에 해당합니다.
• 그러면 앞에서 다룬 \(g_{ij}(x)\)와 \(\mu_{1}, \mu_{2}, \Sigma_{1}, \Sigma_{2}\)를 이용해서 식을 전개해 보겠습니다.

• \[g_{12}(x) = \Biggl(\begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} 3 - 8 \\ 2 - 6 \end{pmatrix} \Biggr)^{T} x + \Biggl(\text{ln}(P(w_{1})) - \text{ln}(P(w_{2})) - \frac{1}{2}\begin{pmatrix} 3 & 2 \end{pmatrix} \begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} + \frac{1}{2} \begin{pmatrix} 8 \ 6 \end{pmatrix} \begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} 8 \\ 6 \end{pmatrix} \Biggr)\]
• \[= \begin{pmatrix} -15/8 & -6 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} + (\text{ln}P(w_{1}) - \text{ln}P(w_{2}) + 34.3125)\]
• \[= \frac{-15}{8}x_{1} -6x_{2} + (\text{ln}(P(w_{1})) - \text{ln}(P(w_{2})) + 34.3125)\]

• 그러면 \(g_{12}(x) = 0\)으로 두고 아직 정해지지 않은 사전 확률인 \(P(w_{1}), P(w_{2})\)을 바꾸어가면서 사전 확률에 따라 decision boundary가 어떻게 바뀌는 지 살펴보겠습니다.
• 1) \(P(w_{1}) = 0.5, P(w_{2}) = 0.5\)인 경우 : \(5x_{1} + 16x_{2} - 91.5 = 0\)
• 2) \(P(w_{1}) = 0.8, P(w_{2}) = 0.2\)인 경우 : \(5x_{1} + 16x_{2} - 95.157 = 0\)
• 3) \(P(w_{1}) = 0.2, P(w_{2}) = 0.8\)인 경우 : \(5x_{1} + 16x_{2} - 87.803 = 0\)

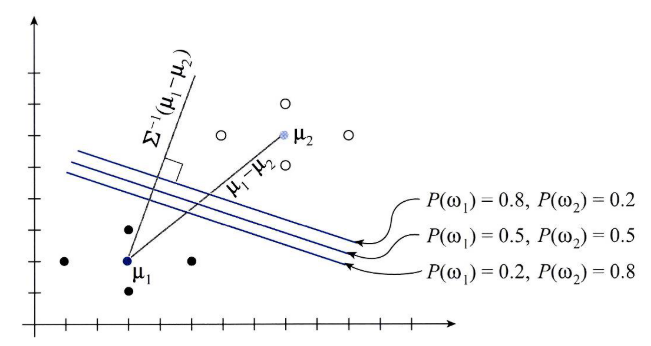
• 기하학적으로 decision boundary는 두 평균 벡터를 이은 벡터 \(\mu_{1} - \mu_{2}\)를 선형 변환한 \(\Sigma^{-1}(\mu_{1} - \mu_{2})\)와 직교한 것을 알 수 있습니다.

Quadratic Discriminant Analysis

• 앞에서 다룬 Linear Discriminant Analysis는 각 클래스 별로 공분산이 모두 같다는 가정으로 인하여 \(\Sigma_{i}\)에서 인덱스 \(i\)를 빼고 \(\Sigma\)로 표현하였습니다. 가정 그대로 공분산이 모두 같이 때문입니다.
• 즉, Linear Discriminant Analysis에서는 각 클래스 별 평균은 다를 수 있으나 공분산은 모두 같다는 전제 조건이 있습니다.
• 반면 이번에 알아볼 Quadratic Discriminant Analysis에서는 각 클래스 별 평균과 공분산 모두 다를 수 있다는 전제 조건을 적용합니다.
• 앞에서 정리한 식 \(g(x)\)를 다시 사용해 보도록 하겠습니다.

• \[g_{i}(x) = -\frac{1}{2}(x^{T}\Sigma_{i}^{-1}x - 2\mu_{i}^{T}\Sigma_{i}^{-1}x + \mu_{i}^{T}\Sigma_{i}^{-1}\mu_{i}) - \frac{d}{2}\text{ln}(2\pi) - \frac{1}{2}\text{ln}(\vert \Sigma_{i} \vert) + \text{ln}(P(w_{i}))\]

• QDA에서는 공분산이 각 클래스 별로 다르므로 공분산에도 인덱스 \(i\)가 모두 적용 되어 있습니다. 따라서 상수항 처럼 취급되는 것은 \(\frac{d}{2}\text{ln}2\pi\) 뿐입니다.
• decision boundary를 구할 때 \(g_{ij}(x) = g_{i}(x) - g_{j}(x)\)를 이용하므로 상수항은 소거해서 생각해도 상관없습니다.
• 그러면 위에서 정리한 식 \(g_{i}(x)\)를 다시 정리하면 다음과 같습니다.

• \[g_{i}(x) = -\frac{1}{2}x^{T}\Sigma_{i}^{-1}x + \mu_{i}^{T}\Sigma_{i}^{-1}x + \Biggl( -\frac{1}{2}\mu_{i}^{T}\Sigma_{i}^{-1}\mu_{i} -\frac{1}{2}\text{ln}\vert \Sigma_{i} \vert + \text{ln}(P(w_{i})) \Biggr)\]

• 위 식의 우변에서 첫번째 항은 2차식이고 두번째 항은 1차식 그리고 세번째 항은 상수항 입니다.
• 따라서 구해야 할 \(g_{ij}(x) = g_{i}(x) - g_{j}(x)\) 또한 2차식을 띄게 됩니다.
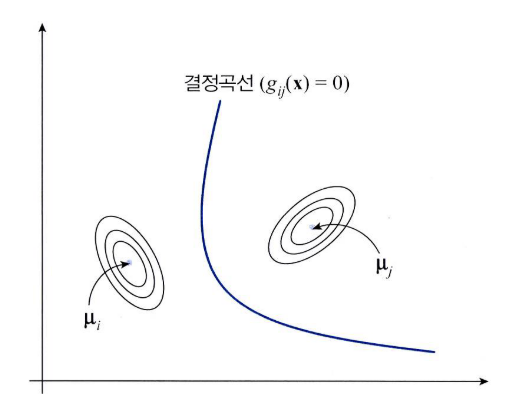
• decision boundary는 \(g_{ij}(x) = 0\)을 만족하는 식이고 2차식을 따르므로 2차원 형태의 포물선 / 쌍곡선 / 타원 등의 형태로 나타날 수 있습니다.

QDA 예제

• QDA를 적용한 예제에 대하여 한번 살펴보도록 하겠습니다.
• 먼저 QDA에 적용하려면 앞에서 다룬 \(g_{i}(x)\) 식에 클래스 별 데이터의 평균과 공분산을 구하여 모델식에서 평균과 공분산에 해당하는 부분을 세팅해 주면 됩니다.
• 만약 다음과 같은 데이터 셋이 있다고 가정해 보겠습니다.

• \[w_{1} = (1, 2)^{T}, (3, 1)^{T}, (5, 2)^{T}, (3, 3)^{T}\]
• \[w_{2} = (7, 6)^{T}, (8, 4)^{T}, (9, 6)^{T}, (8, 8)^{T}\]

• 이 데이터를 가지고 클래스 1과 2의 평균과 공분산을 구하면 다음과 같습니다.

• \[\mu_{1} = \begin{pmatrix} 3 \\ 2 \end{pmatrix}, \Sigma_{1} = \begin{pmatrix} 8/3 & 0 \\ 0 & 2/3 \end{pmatrix}\]
• \[\mu_{2} = \begin{pmatrix} 8 \\ 6 \end{pmatrix}, \Sigma_{2} = \begin{pmatrix} 2/3 & 0 \\ 0 & 8/3 \end{pmatrix}\]

• 방금 구한 평균과 공분산을 \(g_{i}(x)\)에 대입하여 \(g_{1}(x)\)와 \(g_{2}(x)\)를 구해보도록 하겠습니다.

• \[g_{1}(x) = -\frac{1}{2} \begin{pmatrix} x_{1} & x_{2} \end{pmatrix} \begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} + \begin{pmatrix} 3 & 2 \end{pmatrix} \begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} -\frac{1}{2} \begin{pmatrix}3 & 2 \end{pmatrix} \begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} -\frac{1}{2}\text{ln} \begin{vmatrix} \begin{pmatrix} 3/8 & 0 \\ 0 & 3/2 \end{pmatrix} \end{vmatrix} + \text{ln}P(w_{1})\]
• \[= -\frac{3}{16}x_{1}^{2} -\frac{3}{4}x_{2}^{2} + \frac{9}{8}x_{1} + 3x_{2} - \frac{75}{16} -\frac{1}{2}\text{ln}\frac{16}{9} + \text{ln}P(w_{1})\]

• \[g_{2}(x) = -\frac{1}{2} \begin{pmatrix} x_{1} & x_{2} \end{pmatrix} \begin{pmatrix} 3/2 & 0 \\ 0 & 3/8 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} + \begin{pmatrix} 8 & 6 \end{pmatrix} \begin{pmatrix} 3/2 & 0 \\ 0 & 3/8 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} -\frac{1}{2} \begin{pmatrix}8 & 6 \end{pmatrix} \begin{pmatrix} 3/2 & 0 \\ 0 & 3/8 \end{pmatrix} \begin{pmatrix} 8 \\ 6 \end{pmatrix} -\frac{1}{2}\text{ln} \begin{vmatrix} \begin{pmatrix} 3/2 & 0 \\ 0 & 3/8 \end{pmatrix} \end{vmatrix} + \text{ln}P(w_{2})\]
• \[= -\frac{3}{4}x_{1}^{2} -\frac{3}{16}x_{2}^{2} + 12x_{1} + \frac{18}{8}x_{2} - \frac{219}{4} -\frac{1}{2}\text{ln}\frac{16}{9} + \text{ln}P(w_{2})\]

• \[g_{12}(x) = g_{1}(x) - g_{2}(x) = \frac{9}{16}x_{1}^{2} - \frac{9}{16}x_{2}^{2} -\frac{87}{8}x_{1} + \frac{3}{4}x_{2} + \frac{801}{16} + \text{ln}P(w_{1}) - \text{ln}P(w_{2})\]

• 위와 같이 decision boundary를 \(g_{12}(x) = 0\)으로 두고 사전 확률을 바꾸어 보면 decision boundary가 어떻게 움직이는 지 알 수 있습니다.

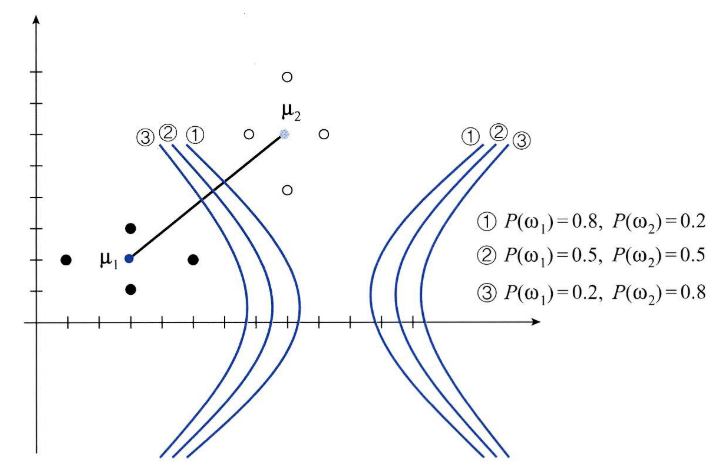
• 위 그림과 같이 \(P(w_{1}) > P(w_{2})\)일 때, decision boundary는 \(\mu_{2}\)에 가까워집니다. 즉, 클래스 1번의 영역이 넓어지므로 확률적으로 클래스 1로 분류될 가능성이 커지게 됩니다.

정리

• Linear Discriminant Analysis과 Quadratic Discriminant Analysis 모두 사후 확률 분포 (posterior) 입니다.
• 사후 확률 분포를 바로 구하는 것은 매우 어려운 일이기 때문에 베이즈 정리를 이용하여 가능도(likelihood)와 사전 확률(prior)를 이용하여 사후 확률을 구하는 문제로 바꾸었습니다.
• 하지만 likelihood를 구한 것 또한 꽤 어려운 일일 수 있으므로 likelihood를 가우시안으로 가정을 하고 문제를 단순화 시킵니다.
• likelihood가 가우시안이 되었으므로 다루어야 할 변수는 평균과 분산 두가지가 되었습니다.
• 이 때, 각 클래스 별로 평균은 다를 수 있지만 분산은 같다고 가정하게 되면 LDA(Linear Discriminant Analysis)라는 식을 도출할 수 있고 이 식은 1차식이 됩니다.
• 반면 각 클래스 별로 평균도 다를 수 있고 분산도 다를 수 있다고 가정하면 QDA(Quadratic Discriminant Analysis)라는 식을 도출할 수 있고 이 식은 2차식이 됩니다.
• LDA와 QDA 모두 각 클래스 별로 데이터들을 사전에 준비해 놓으면 LDA는 클래스 별 평균과 클래스 전체에 적용되는 공분산을 구할 수 있고 QDA는 클래스 별 평균과 공분산을 구할 수 있습니다.
• 각 클래스별 평균과 공분산을 구하였다면 그 값을 이용하여 각 클래스 \(i\) 별로 적용할 수 있습니다.

LDA

• \[g_{i}(x) = (\Sigma^{-1} \mu_{i})^{T}x + (\text{ln}(P(w_{i})) -\frac{1}{2}\mu_{i}^{T}\Sigma^{-1}\mu_{i})\]

QDA

• \[g_{i}(x) = -\frac{1}{2}x^{T}\Sigma_{i}^{-1}x + \mu_{i}^{T}\Sigma_{i}^{-1}x + \Biggl( -\frac{1}{2}\mu_{i}^{T}\Sigma_{i}^{-1}\mu_{i} -\frac{1}{2}\text{ln}\vert \Sigma_{i} \vert + \text{ln}(P(w_{i})) \Biggr)\]

• 각 클래스 별 평균과 공분산을 구하였으므로 각 클래스 \(i\)에 해당하는 평균과 공분산 그리고 사전 확률(prior) 까지 대입하여 계산을 하면 classifier가 완성이 됩니다.
• 이후에 어떤 인풋값 \(x\)가 들어왔을 때 사후 확률(posterior)가 최대가 되는 \(argmax_{i} g_{i}(x)\)를 선택하면 됩니다.

머신러닝 글 목록