가우시안 프로세스 (Gaussian Process) 내용 정리

머신러닝 관련 글 목차

참조 : https://www.edwith.org/bayesiandeeplearning/
참조 : https://students.brown.edu/seeing-theory/
참조 : https://youtu.be/9NeDYW9BfpQ

이 글은 edwith의 베이지안 딥러닝 강의를 요약한 내용입니다.
이 글의 학습 목적은 베이지안 딥러닝과 딥러닝에서의 Uncertainty를 이해하기 위하여 배경 지식을 쌓기 위함입니다.

Gaussian Process 퀵하게 알아보기

classification이나 regression과 같은 supervised learning은 parametric 모델을 통해 해결되고 있습니다. 여기서 말하는 parametric 모델은 모델 학습 동안 training data의 정보를 모델과 그 모델의 파라미터를 통해 표현하는 방법을 의미합니다.
이러한 모델들은 설명 가능하다는 장점을 가지나 복잡한 데이터 셋에서는 제대로 작동하기 힘든 단점이 있습니다. 이러한 단점을 개선하기 위하여 SVM (Support Vector Machine)이나 GP (Gaussian Process)와 같은 kernel 기반 모델이 등장하게 되었습니다.

먼저 GP에 대하여 알아보면 임의의 집합 \(S\) 가 있을 떄, GP는 \(S\) 에 대하여 jointly gaussian distribution을 따르는 random variable의 set을 의미합니다. 식으로 표현하면 다음과 같습니다.

\[f \sim GP(m, k)\]
\[m \text{ : mean function}, k \text{ : covariance function}\]

일반적인 가우시안 분포의 꼴은 다음과 같습니다.

\[X \sim N(\mu, \sigma^{2})\]

가우시안 프로세스와 가우시안 분포의 차이를 보면 가이시안 프로세스는 평균과 분산에 function형태가 들어간 반면 가우시안 분포는 평균과 분산에 특정 값이 들어간다는 차이가 있습니다.

아래 내용은 예시를 들어 GP에 사용되는 파라미터 함수 \(m, k\) 사용하는 방법에 대하여 다루어 보겠습니다.

\[f \sim GP(m, k)\]
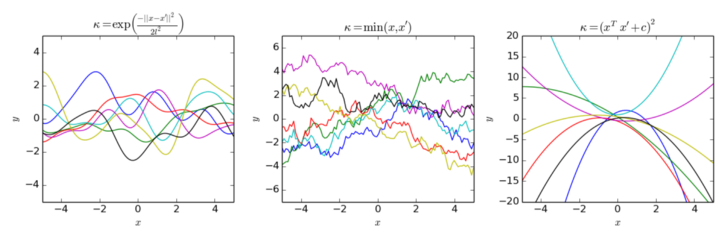
\[m(x) = \frac{1}{2} x^{2}\]
\[k(x, x') = \exp{( -\frac{1}{2} (x - x')^{2} )}\]

이러한 경우 가우시안 분포 처럼 아래와 같이 표현할 수 있습니다.

\[\mu_{i} = m(x_{i}) = \frac{1}{2} x_{i}^{2}, \ \ i = 1, 2, \cdots n\]
\[\sigma_{ij} = k(x_{i}, x_{j}) = \exp{(-\frac{1}{2}(x_{i} - x_{j})^{2} )}, \ \ i,j = 1, 2, \cdots n\]

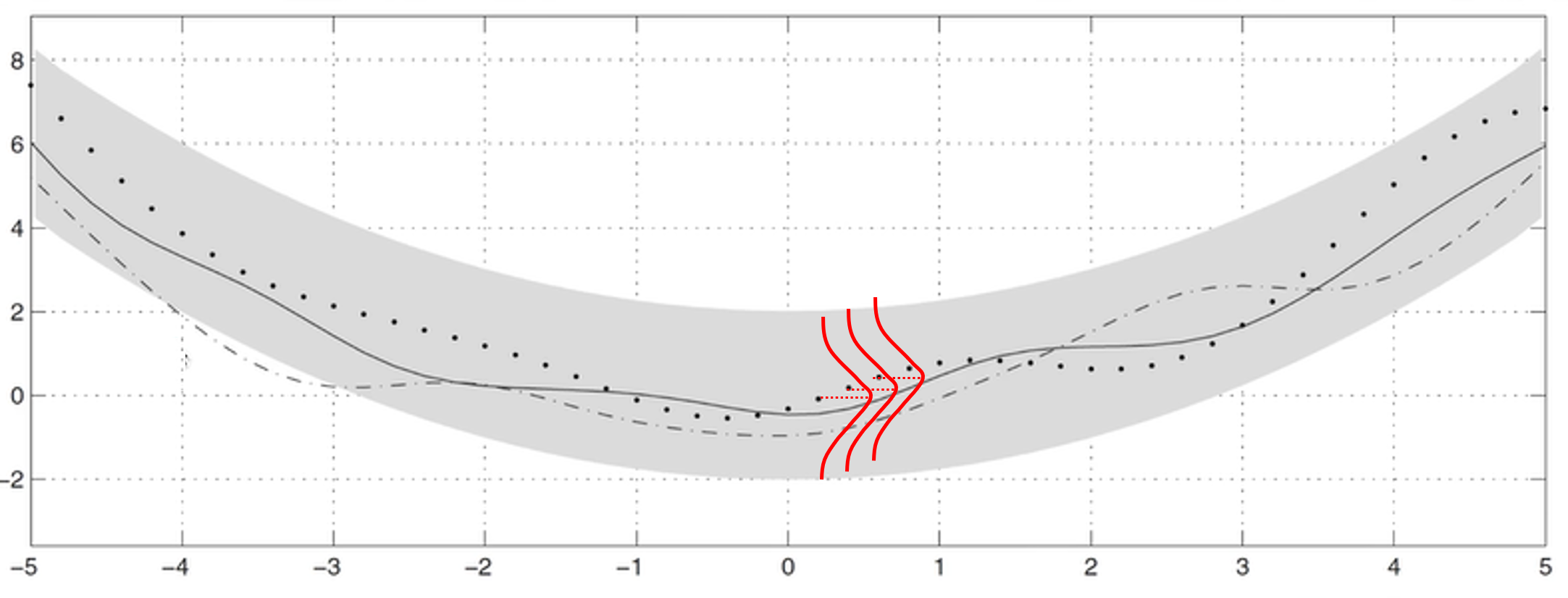
위 그림과 같이 함수 \(m, k\) 에 의해 각 점에서 가우시안 분포를 가지게 되면 음영으로 표시된 것과 같이 영역을 가지게 됩니다. 즉, 단순히 특정 데이터 하나가 아닌 확률 분포를 가지게됨을 알 수 있습니다.

이와 같은 가우시안 프로세스 과정은 베이지안 인퍼런스 과정에서 사용될 수 있습니다. 먼저 베이즈 이론을 다시 간략하게 살펴보면 다음과 같습니다.

\[\color{red}{P(\theta \vert x)} = \frac{\color{green}{P(x \vert \theta)} \color{blue}{P(\theta)}{P(x)}\]

위 식에서 빨간색이 베이즈 이론에서 구하고자 하는 posterior에 해당하고 초록색은 likelihood 그리고 파란색은 prior에 해당합니다. prior가 \(\theta\) 라는 모수를 가지는 확률 분포라 하고 최종적으로 구하고자 하는 posterior는 데이터 \(x\) 가 주어졌을 때, \(\theta\) 모수에 대한 확률 분포를 의미합니다. 반면 likelihood는 \(\theta\) 모수가 주어졌을 때, 주어진 데이터 \(x\) 를 얼만큼 잘 표현하는 지 나타내는 수치를 의미합니다.
베이지안 인퍼런스 과정에서는 앞에서 구한 GP를 prior로 사용하고 likelihood는 데이터 \(x\) 가 있으면 구할 수 있기 때문에 최종 목적인 posterior를 구할 수 있다는 컨셉입니다.

Gaussian Process

Weight Space View

Function Space View

Gaussian process latent variable model (GPLVM)

Gaussian process Application

Appendix : 배경지식 설명

아래는 이 글에서 설명할 Gaussian Process를 이해하기 위한 배경지식으로 스킵하셔도 됩니다.
먼저 gaussian process에 대한 개념을 알아보기 이전에 random variable, random process등과 관련한 내용에 대하여 알아보도록 하겠습니다.

random variable

먼저 random variable에 대하여 알아보겠습니다. 많은 분들이 기존 통계학을 공부하실 때 이미 학습하신 내용입니다.

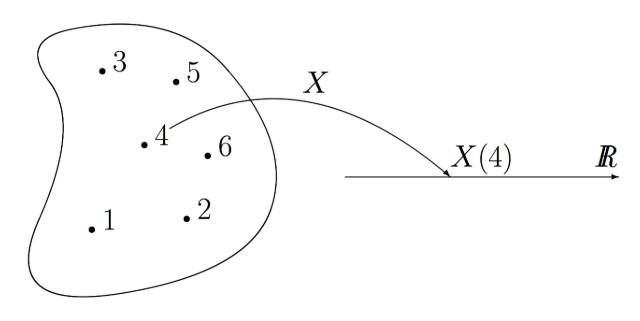
먼저 Random의 의미를 살펴보면 sample space에서 한 개의 원소를 뽑는 것을 의미합니다.
이 때, random variable은 임의의 프로그래밍 언어에서 랜덤값을 추출할 때, 그 랜덤 값이 어떤 방식으로 추출되는 지 모델링 되는 것을 random variable이라고 말할 수 있습니다.
위 그림에 빗대어 보면 sample space로 부터 실제 관측한 값을 뽑아 내는 함수가 random variable 입니다. 확률과 비교해 보면 확률은 sample space에서 영역(면적)을 만들어 낼 수 있는 subset인 반면에 random variable은 sample space에서 어떻게 원소를 추출할 지 또는 어떤 subset으로 원소를 배정할 지 정의되어 있는 함수라고 이해하면 됩니다.
추가적으로 Random Experiment라는 용어는 random variable을 이용하여 어떤 값을 추출하였을 때, 그 값을 실제 확인한 결과를 뜻합니다.
이와 같이 가상의 sample space에서 random variable을 통하여 원소를 뽑고 확인하는 이 전체 과정을 realization 또는 sampling 이라고 합니다.

\[\sum P(X = x_{i}) = 1 (x_{i} : i = 1, 2, ...)\]

위 식과 같은 discrete random variable을 해석하면 \(X\) 라는 random variable이 있는데 그 결과 값이 \(x_{i}\)가 나올 면적의 크기라고 말할 수 있습니다.

\[E[X] = \begin{cases} \sum_{x} x p(x) \ \ \ \ \text{discrete} X \\ \int_{-\infty}^{\infty} x f(x) dx \ \ \ \ \text{continuous} X \end{cases}\]

random variable \(X\) 를 이용하여 위 식과 같이 정의하였을 때, 잘 알려진 바와 같이 expectation 이라고 합니다.
위 식의 직관적인 의미는 random variable \(X\) 를 여러번 sampling 하였을 때, 평균적인 기댓값 (expectation)을 뜻합니다. random variable의 의미와 연관지어 생각하면 의미를 다시 느껴볼 수 있습니다.

또 다른 식으로 \(E(X \vert Y)\) 즉, conditional expectaion에 대하여 간단히 알아보겠습니다.
이 식에서 전제 조건은 random variable \(X\) 의 expectation인 \(E(X)\) 가 \(E(X) = \int x f(x) dx\) 로 정의되고 이 값이 특정 분포(ex. 가우시안 분포)로 정해져 있다고 하면 \(X\)는 deterministic variable 이 된다라는 것입니다.
이 때, \(Y\) 가 random variable이라고 하면 \(E(X \vert Y )\) 또한 random variable이 된다는 점입니다.

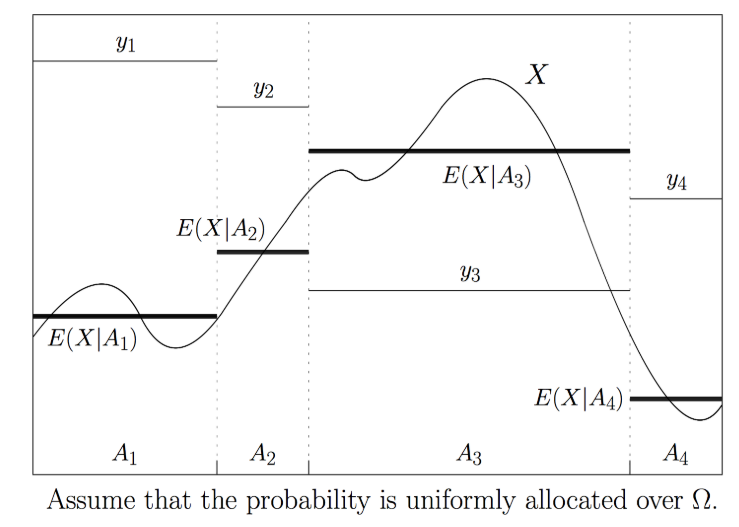
위 그래프에서 \(X\)는 위 그림과 같은 고정된 분포를 가지므로 deterministic variable이 됩니다.
이 때, random variable \(Y\) 는 4개의 값 \(y_{1}, y_{2}, y_{3}, y_{4}\) 로 추출될 수 있습니다. 즉, 확률 관점으로 보았을 때, sample space에 4개의 subset에 있고 4개의 subset의 확률 값을 모두 합하면 1이 됩니다.
이 각각의 \(Y\) 의 subset 내부에서 \(X\) 가 가지는 exectation을 계산하는 것이 conditional expectation이 됩니다. \(X\) 는 continuous 하여 많은 값을 가지게 되지만 \(Y\) 라는 random variable이 sample space를 굉장히 크게 나누어서 subset을 가졌기 때문에 \(X\) 도 영향을 받게 됩니다. (즉, conditional 하게 됩니다.)

moment

어떤 확률 분포를 나타낼 때 대표적인 값으로 기댓값 즉 평균값을 많이 사용합니다. 물론 평균값에 의해 왜곡되는 것이 많다는 것을 알고 있음에도 불구하고 대표적으로 사용하고 있습니다.

평균이라는 값은 n-th moment 중 1차에 해당하며 2-th moment는 흔히 아는 variance 이며 3차는 skewness, 4차는 kurtosis 라고 합니다.
어떤 두 분포가 비슷한 지 확인 할 때, 쉽게 비교할 수 있는 방법으로 두 분포의 n-th moment가 같은 지 확인하는 방법을 사용하곤 합니다. 이와 같은 방법을 이용하면 단순히 평균값을 통해 왜곡되는 문제를 보정하여 비교할 수 있습니다.

머신러닝 관련 글 목차