Huber Loss와 Berhu (Reverse Huber) Loss (A robust hybrid of lasso and ridge regression)

Huber Loss와 Berhu (Reverse Huber) Loss (A robust hybrid of lasso and ridge regression)

2021, Feb 17    


deep learning 관련 글 목차


  • 참조 : https://artowen.su.domains/reports/hhu.pdf
  • 참조 : https://github.com/abduallahmohamed/reversehuberloss/blob/master/rhuloss.py


  • 이번 글에서는 L1 Loss와 L2 Loss의 단점을 개선하고자 두 Loss를 조합하여 사용하는 Huber Loss와 Berhu (Reverse Huber) Loss를 간단히 다루어 보도록 하겠습니다.


목차



L1 Loss와 L2 Loss의 단점


  • 일반적으로 사용하는 L1 Loss와 L2 Loss는 간단 명료하면서 Error의 정도를 잘 계산할 수 있는 좋은 방법입니다.
  • 하지만 다음과 같은 단점이 있다는 것이 널리 알려져 있습니다.


L1 Loss의 단점


  • ① Sensitivity to Outliers : L1 Loss는 L2 Loss에 비하여 outlier에 덜 취약한 것으로 알려져 있긴 합니다. 하지만 근본적으로 outlier에 취약한 구조를 가집니다.
  • ② Non-Smoothness : L1 Loss는 구조상 gradient가 정의되지 않는 지점이 존재합니다. gradient 기반의 최적화 알고리즘을 사용하여 학습을 할 때, L1 Loss를 사용한다면 이런 점에서 취약함이 발생합니다.


L2 Loss의 단점


  • ① High Sensitivity to Outliers : L2 Loss는 error가 클수록 L1 Loss에 비해 Loss가 급격히 커지게 됩니다. 이 점이 학습에 유리할 수도 있지만 근본적으로 outlier에 매우 취약해 집니다. 어떤 경우에는 Loss가 outlier에 의해 계산된 error가 Loss 전체를 차지할 수도 있습니다.
  • ② slow to converge : L2 Loss는 2차 형식의 곡선 형태를 가집니다. 따라서 error가 작을 때에는 gradient가 매우 작아지므로 학습 결과가 수렴하는 데 오래걸린다는 단점이 있습니다.


Huber Loss와 BerHu Loss의 정의와 장점


  • 따라서 L1 Loss와 L2 Loss를 섞어서 사용하는 방법이 제안되었고 이 방법이 Huber Loss와 BerHu Loss 입니다. BerHu Loss는 Reverse Huber Loss라고도 합니다. 말그대로 Huber를 거꾸로 적어 BerHu로 표기하여 사용합니다.


  • L1 Loss와 L2 Loss를 섞어서 사용하여 다음과 같은 장점을 취합니다.
  • ① 데이터의 outlier가 있다고 하더라도 L2 Loss와 같이 취약해지지 않습니다. (기존 L2 Loss의 단점)
  • ② 모든 학습 단계에서 gradient가 존재하여 학습 관점에서 취약한 점이 개선됩니다. (기존 L1 Loss의 단점)
  • ③ 데이터 셋에 따라서 L1 Loss 또는 L2 Loss 각각 더 유리한 Loss가 있을 수 있는데 두가지를 모두 사용함으로써 좀 더 강건한 Loss를 적용할 수 있습니다.


Huber Loss의 정의


  • \[L_{\delta}(a) = \begin{cases} \frac{1}{2}(a)^{2} & \text{for } \vert a \vert \le \delta \\ \delta (\vert a \vert - \frac{1}{2}\delta) & \text{otherwise} \end{cases}\]
  • \[a = y_{\text{true}} - y_{\text{pred}}\]
  • \[\delta : \text{ hyperparameter}\]


  • 위 식과 같이 L1, L2 Loss를 조합하여 사용하였습니다. 따라서 모든 부분이 미분 가능해져서 gradient 기반의 최적화 알고리즘을 사용할 수 있고 outlier에 강건해 졌습니다.


BerHu Loss의 정의


  • \[L_{c}(a) = \begin{cases} \vert a \vert & \text{for } \vert a \vert \le c \\ \frac{a^{2} + c^{2}}{2c} & \text{otherwise} \end{cases}\]
  • \[a = y_{\text{true}} - y_{\text{pred}}\]
  • \[c = \delta \cdot \text{max}(a)\]
  • \[\delta : \text{ hyperparameter. default is 0.2}\]


  • BerHu Loss는 위 식에서 사용된 \(c\) 값은 하이퍼파라미터 \(\delta\) 와 \(a\) 의 최댓값에 의해 결정됩니다. 특히 \(a\) 는 데이터에 따라서 결정되기 때문에 데이터에 맞춰서 Loss가 사용될 수 있다는 장점이 있습니다. 이러한 장점을 Dynamic Transition이라고도 합니다.
  • BerHu Loss는 outlier가 많은 regression 태스크나 데이터마다 스케일이 다른 경우에 사용하기 좋습니다. 바로 Dynamic Transition으로 인하여 데이터에 따라 적합하게 Loss를 적용할 수 있기 때문입니다.
  • 마지막으로 regression 출력 시 smoothness가 적용된 것 처럼 출력값의 variation이 작아지도록 출력하는 효과가 있습니다. 왜냐하면 L2 Loss의 이차 형식으로 인하여 error가 적을 때에는 Loss값이 작아지게 되어 유사한 출력값이 도출되어야 하는 부분에서는 출력값 간에 급격한 변화없이 smooth하게 출력되도록 하는 경향이 생기게 됩니다.


  • BerHu Loss의 대표적인 3가지 특성인 ① Dynamic Transition을 통하여 데이터 노이즈에 강건함, ② Dynamic Transition을 통하여 데이터 스케일이 달라도 Loss에서 처리할 수 있다는 것, ③ smoothness 효과로 출력의 variation을 감소하는 것. 을 통하여 컴퓨터 비전의 대표적인 태스크인 Depth Estimation에서 BerHu Loss를 사용 시 꽤 좋은 학습 효과를 얻을 수 있는 것으로 알려져 있습니다.
  • Depth Estimation에서는 데이터에 노이즈가 많을 뿐 아니라 (ex. 라이다 포인트 클라우드) 이미지마다 학습에 사용되는 값들의 최소, 최대값의 범위가 달라질 수 있습니다. 예를 들어 카메라 앞이 텅 빈 상황과 카메라 앞에 장애물이 있는 경우 데이터의 스케일이 달라지게 됩니다. 그리고 Depth Estimation 시, 같은 평면의 Depth는 같도록 출력이 되어야 하는데 이 때, smoothness 효과를 통하여 같은 평면의 Depth의 variation이 작아져서 급격한 변화로 인한 오인식을 개선하는 효과도 가질 수 있습니다.


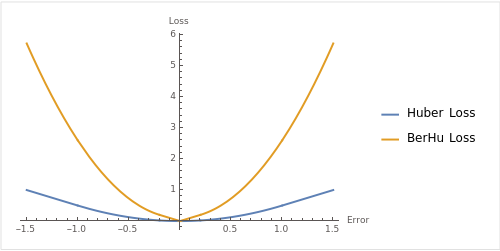
Drawing


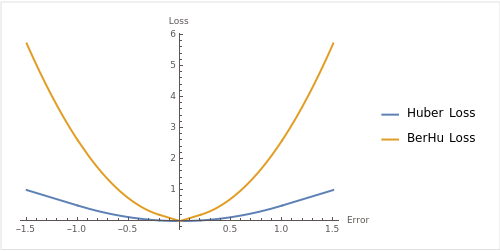
  • 위 이미지는 Huber Loss의 \(\delta = 1\) 을 적용하고 BerHu Loss의 \(c = 0.2\) 로 적용하여 그래프로 나타낸 것입니다. L1, L2 Loss가 어떻게 혼합되었는 지 참조하시면 됩니다.


Huber Loss와 BerHu Loss의 Pytorch Code


  • Pytorch에 Huber Loss는 구현이 되어 있으며 아래 식의 \(\delta = 1\) 로 적용되어 있습니다.


  • \[L_{\delta}(a) = \begin{cases} \frac{1}{2}(a)^{2} & \text{for } \vert a \vert \le \delta \\ \delta (\vert a \vert - \frac{1}{2}\delta) & \text{otherwise} \end{cases}\]
  • \[a = y_{\text{true}} - y_{\text{pred}}\]
  • \[\delta : \text{ hyperparameter}\]


  • 아래 코드는 custom하게 만든 Huber Loss와 Pytorch에서 구현한 nn.SmoothL1Loss를 비교한 코드입니다.


import torch
import torch.nn as nn

def huber_loss_custom(y_pred, y_true, delta=1.0):
    # Calculate the absolute error
    abs_error = torch.abs(y_true - y_pred)
    
    # Calculate the Huber loss based on the absolute error
    loss = torch.where(abs_error <= delta,
                       0.5 * abs_error ** 2,
                       delta * (abs_error - 0.5 * delta))
    
    # Return the mean loss
    return torch.mean(loss)

huber_loss = nn.SmoothL1Loss()

# Example usage
y_pred = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y_true = torch.tensor([1.5, 2.5, 3.5])

loss_custom = huber_loss_custom(y_pred, y_true)
loss = huber_loss(y_pred, y_true)

print("Huber Loss Custom :", loss_custom.item())
# Huber Loss Custom : 0.125
print("Huber Loss :", loss.item())
# Huber Loss : 0.125


  • BerHu Loss는 별도 구현된 함수가 없어 아래 수식을 직접 작성하여 사용해야 합니다.


  • \[L_{c}(a) = \begin{cases} \vert a \vert & \text{for } \vert a \vert \le c \\ \frac{a^{2} + c^{2}}{2c} & \text{otherwise} \end{cases}\]
  • \[a = y_{\text{true}} - y_{\text{pred}}\]
  • \[c = \delta \cdot \text{max}(a)\]
  • \[\delta : \text{ hyperparameter. default is 0.2}\] 


import torch
def berhu_loss(y_pred, y_true):
    abs_error = torch.abs(y_true - y_pred)
    c = 0.2 * torch.max(abs_error).detach()
    return torch.mean(torch.where(abs_error <= c, abs_error, (abs_error**2 + c**2) / (2*c)))

huber_loss = nn.SmoothL1Loss()

# Example usage
y_pred = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y_true = torch.tensor([1.5, 2.5, 3.5])

loss_huber = huber_loss(y_pred, y_true)
loss_berhu = berhu_loss(y_pred, y_true)

print("Huber Loss :", loss_huber.item())
# Huber Loss : 0.125
print("BerHu Loss :", loss_berhu.item())
# BerHu Loss : 1.2999999523162842


deep learning 관련 글 목차


Twitter Facebook Google+
# huber loss # berhu loss # l1 loss # l2 loss