머신러닝에서 사용되는 평가지표

• 출처 : 다크프로그래머
• 출처 : https://youtu.be/z5qA9qZMyw0

목차

• Confusion Matrix (혼합 행렬)

• Accuracy

• Precision

• Recall

• Precision-Recall 그래프

• Average Precision (AP)

• F1 Score

• ROC와 AUC

이번 글에서는 머신러닝에서 사용되는 대표적인 평가 지표에 대하여 알아보도록 하겠습니다.

• 먼저 아래 다룰 내용을 테이블 하나로 요약해 보겠습니다.

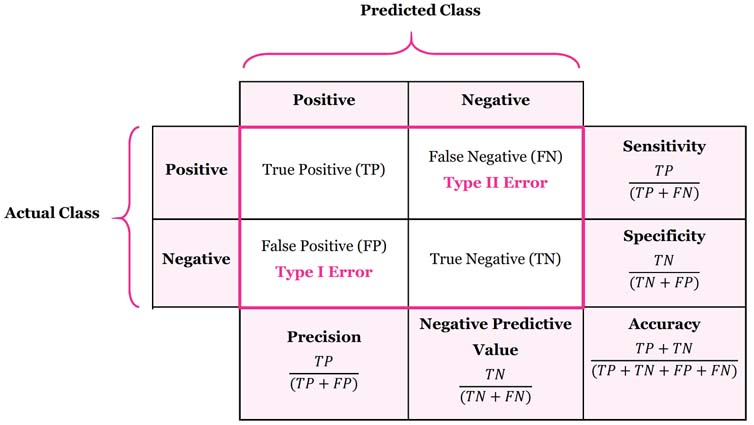
Confusion Matrix (혼합 행렬)

• 실제 라벨과 예측 라벨의 일치 갯수를 matrix로 표현하는 기법

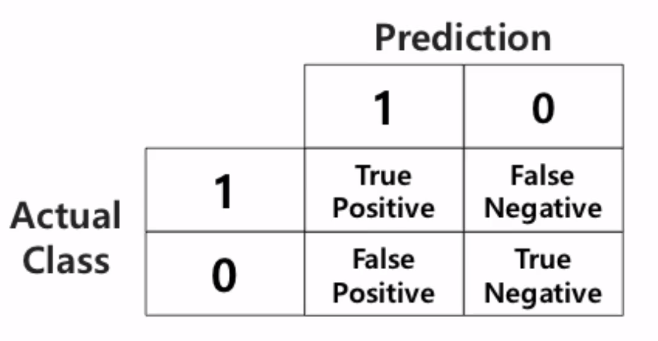
• 맞음여부 & 예측한값의 조합으로 표현
• TP(True Positive) : Positive로 예측해서 True임
  • True : 예측이 맞음
  • Positive : 예측값이 Positive(1)
• FP(False Positive) : Positive로 예측해서 False임
  • False : 예측이 틀림
  • Positive : 예측값이 Positive(1)인 경우 (즉, 실제값은 거짓(0)입니다.)
• FN(False Negative) : Negative로 예측해서 False임
  • False : 예측이 틀림
  • Nagative : 예측값이 Negative(0)인 경우 (즉, 실제값은 참(1)입니다.)
• TF(True Negative) : Negative로 예측해서 True임
  • True : 예측이 맞음
  • Negative : 예측값이 Negative(0)인 경우

from sklearn.metrics import confusion_matrix
y_true = [1, 0, 1, 1, 0, 1]
y_pred = [0, 0, 1, 1, 0, 1]
confusion_matrix(y_true, y_pred)

tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
>> (tn, fp, fn, tp)

(2, 0, 1, 3)

Accuracy

• 전체 대비 정확하게 예측한 개수의 비율
• 　\(ACC = \frac{TP + TN}{TP + TN + FP + FN}\)
• 　\(ACC = 1 - ERR\)

from sklearn.metrics import accuracy_score

y_true = np.array([0, 1, 0, 0])
y_pred = np.array([0, 1, 1, 0])

>> accuracy_score(y_true, y_pred)
0.75

• 불균형한 데이터셋에서 Accuracy를 사용한다면 그 결과는 상당회 왜곡되게 됩니다.
• 예를 들어 시험 합격률이 2%일 때, 모든 수험자가 불합격 한다고 하면 98%의 정확도를 가지게 되어 정확도는 높지만 쓸모없는 모델이 만들어 집니다.
• 이 때, Accuracy 대신 사용할 수 있는 지표가 Precision과 Recall입니다.

Precision

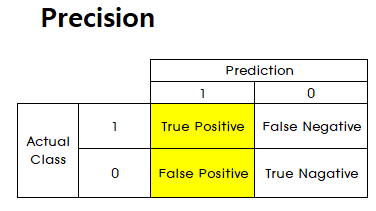
• Presicion은 ositive라고 예측한 비율 중 진짜 Positive의 비율을 나타냅니다. 즉, Positive라고 얼마나 잘 예측하였는지를 뜻합니다. (Positive라고 예측한 것 중에서 얼마나 잘 맞았는지 비율)

• \[Precision = \frac{TP}{TP + FP}\]

from sklearn.metrics import accuracy_score

y_true = np.array([0, 1, 0, 0])
y_pred = np.array([0, 1, 1, 0])

>> precision_score(y_true, y_pred)
0.50

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
>> confusion_matrix(y_true, y_pred)

array([ [2, 0, 0],
        [1, 0, 1],
        [0, 2, 0]])

• 위 confusion_matrix 예제에서 행은 실제값에 해당하고 열은 예측값에 해당합니다.
• precision_score에서는 average 옵션으로 micro와 macro를 둘 수 있습니다.
  • None : 라벨 별 각 평균을 그대로 구합니다.
  • micro : 전체 평균
  • macro : 라벨 별 각 합의 평균

>> precision_score(y_true, y_pred, average=None)
array([0.66666667, 0.        , 0.        ])

        
>> precision_score(y_true, y_pred, average='macro')
0.2222222222222222


>> precision_score(y_true, y_pred, average='mㅑcro')
0.3333333333333333

• average를 macro로 두면 각 열에 대한 precision 값을 모두 더한 다음 열의 갯수로 나눈 것입니다.
• 즉 average를 None으로 두었을 때 구한 각 열의 Precision들을 산술 평균한 값이 macro가 됩니다.
• average를 micro로 두면 전체 평균으로 모든 열에서 맞은 것 즉, 대각선 성분의 총 합을 총 갯수로 나눈 것입니다.

Recall

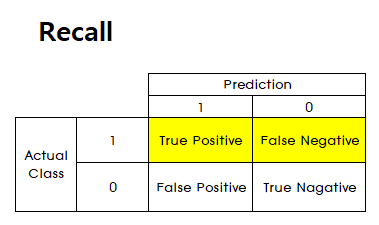
• 실제 Positive 데이터 중 Positive라고 예측한 비율을 뜻합니다.
• Presicion의 기준은 모델이 예측한 것인 반면 Recall의 기준은 데이터입니다.
• 따라서 실제 Positive한 것 중에서 얼마나 잘 예측하였는지 비율을 Recall이라고 해석하면 됩니다.

• \[Recall(True\ Positive\ Rate) = \frac{TP}{TP + FN}\]

• Precision과 Recall은 어느정도 Trade off가 발생합니다. 왜냐하면 Recall을 높이려면 FN을 줄여야 하고 Precision을 높이려면 FP를 줄여야 하기 때문입니다.

from sklearn.metrics import recall_score

y_true = np.array([0, 1, 0, 0])
y_pred = np.array([0, 1, 0, 0])

>> recall_score(y_true, y_pred)
1.0

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]

>> recall_score(y_true, y_pred, average=None)
array([1., 0., 0.])

>> recall_score(y_true, y_pred, average='macro')
0.3333333333333333

>> recall_score(y_true, y_pred, average='micro')
0.3333333333333333

• 앞에서와 마찬가지로 micro는 전체 평균, macro는 각 열의 산술 평균 입니다.

• 지금까지 Precision과 Recall에 대하여 알아보았습니다. 대부분의 시스템을 모델링 할 때에는 이 두 지표 중 하나를 선택하는 것이 아니라 두 지표 모두를 사용해야 하는 경우가 많습니다. 다시 두 지표를 정리해 보겠습니다.
• 이번에는 예시로 이미지 처리에서의 Precison, Recall에 대하여 살펴보겠습니다.

• A와 B라는 기술이 있습니다. A라는 기술은 이미지에 있는 사람을 99.99% 잡아내지만 이미지 1장 당 평균 10건 정도의 오검출이 발생합니다. 즉, 사람이 아닌 부분도 사람이라고 검출하는 경우가 발생하는 것입니다.
• 반면에 B라는 기술은 이미지에 있는 사람들 중 50%밖에 못 잡아내지만 오검출은 발생하지 않습니다.
• 그러면 A라는 기술과 B라는 기술 중 어느 기술이 뛰어난 기술일까요?
• 사용 용도에 따라 어느 기술이 좋은지 차이가 나겠지만, 중요한 것은 검출율 만으로 기술을 평가하는 것은 바람직 하지 않다는 것입니다. 예를 들어 모든 입력에 대하여 물체가 검출된 것으로 반환하면 검출률 100%의 물체인식 기술이 됩니다.
• Recall은 실제 대상 물체들을 빠뜨리지 않고 얼마나 잘 잡아내는지를 나타내는 지표입니다.
• Precision은 검출된 결과가 얼마나 정확한지 즉, 검출 결과들 중 실제 물체가 얼마나 포함되어 있는지를 나타냅니다.
• 어떤 알고리즘의 Recall과 Precision은 알고리즘의 파라미터 조절에 따라 유동적으로 변하는 값이기 때문에 어느 한 값으로는 알고리즘 전체의 성능을 제대로 표현할 수 없습니다.
• 일반적으로 알고리즘의 Recall과 Precision은 서로 반비례 관계를 가집니다. 알고리즘의 파라미터를 조절해 recall을 높이면 precision이 감소하고 반대로 precision을 높이려고하면 recall이 떨어집니다.
• 따라서 알고리즘의 성능을 제대로 비교하고 평가하기 위해서는 precision과 recall의 성능 변화 전체를 살펴봐야 합니다. 대표적인 방법으로 precision-recall 그래프를 이용하는 것입니다.

Precision-Recall 그래프

• 그러면 Precision과 Recall의 상관관계를 타나내는 Precision-Recall 그래프에 대하여 알아보겠습니다.

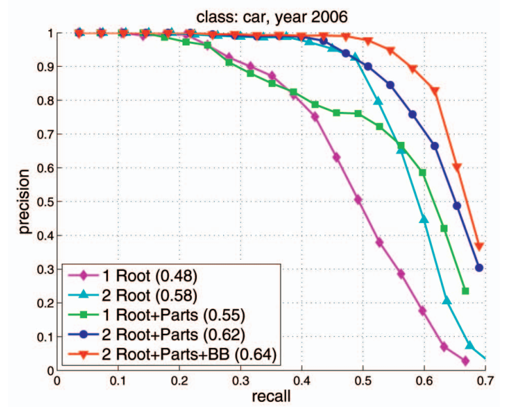
• 알고리즘의 파라미터 조절에 따른 precision과 recall의 값의 변화를 그래프로 표현하면 위와 같습니다.
• 상황에 따라, recall 대신 miss rate = 1- recall을 사용할 수 있고, precision 대신에 false alarm = 1 - precision을 사용할 수 있습니다.

Average Precision (AP)

• precision-recall 그래프는 어떤 알고리즘의 성능을 전반적으로 파악하기에는 좋으나 서로 다른 두 알고리즘의 성능을 정량적으로 비교하기에는 불편한 점이 있습니다.
• 따라서 Average precision을 이용하면 비교하기 용이합니다.
• Precision-recall 그래프에서 그래프 선 아래쪽의 면적을 계산하는 방식입니다. 면적의 값, 즉, AP가 클수록 성능이 좋은 알고리즘이라고 할 수 있습니다.

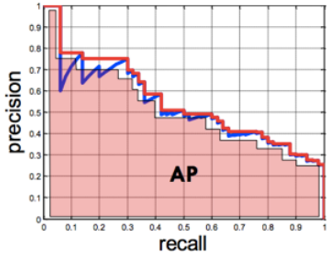
• 위 그래프의 아랫 면적의 총 합이 AP가 됩니다.

• 위 그래프의 legend에서 괄호 안의 숫자가 AP가 됩니다.
• 그러면 이 AP 값을 이용하여 다른 모델과의 정량적 비교가 가능해 집니다.

F1 Score

• Precision과 Recall은 서로 Trade-off 관계를 가지면서 접근하는 방식도 Precision은 모델의 예측, Recall은 정답 데이터 기준이므로 서로 상이합니다.
• 하지만 두 지표 모두 모델의 성능을 확인하는 데 중요하므로 둘 다 사용되어야 합니다. 따라서 두 지표를 평균값을 통해 하나의 값으로 나타내는 방법을 F1 score라고합니다.
• 이 때, 사용되는 방법은 조화 평균입니다. 조화 평균을 사용하는 이유는 평균이 Precision과 Recall 중 낮은 값에 가깝도록 만들기 위함입니다. 조화 평균의 경우 평균 계산에 사용된 값이 불균형할수록 페널티가 가해져서 작은 값에 가깝도록 평균이 계산됩니다.
  • 링크 참조 : https://gaussian37.github.io/math-pb-averages/

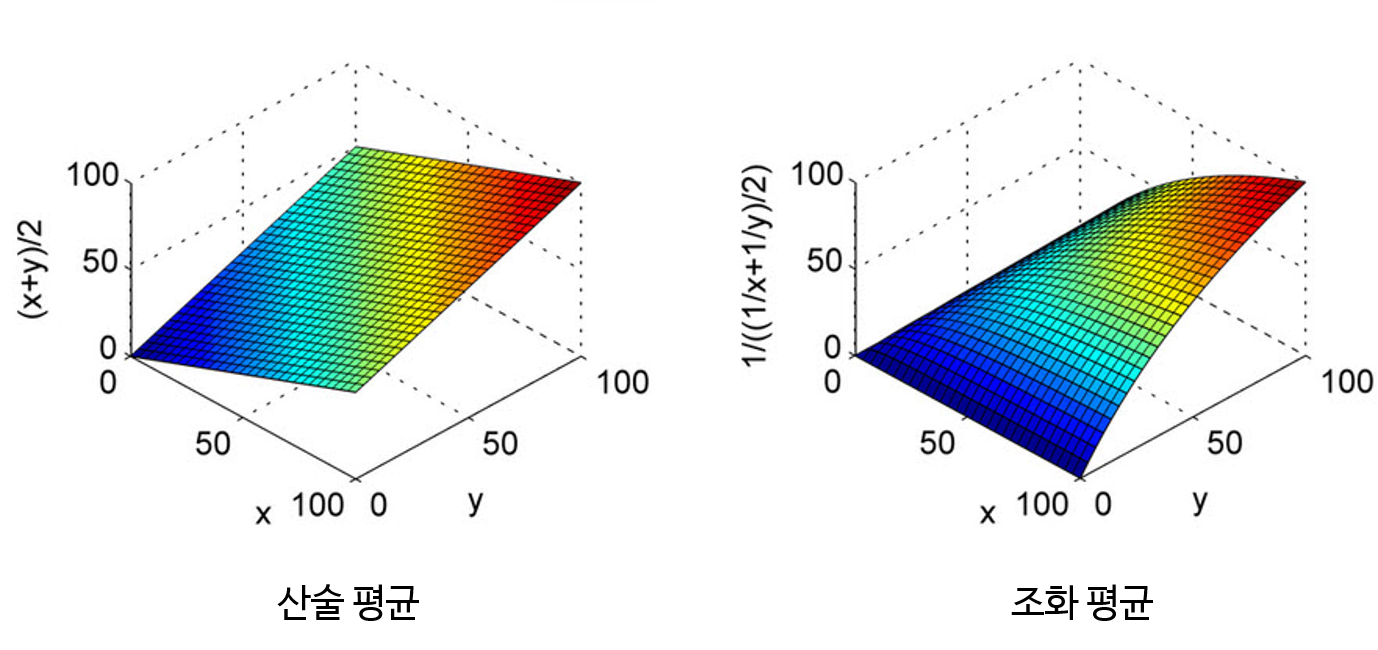
• 위 그래프 분포를 살펴보면 조화 평균의 경우 \(X, Y\)값의 차이가 크면 \(Z\) 축의 값이 작은 것을 볼 수 있습니다.
• 따라서 극단적으로 Precision과 Recall 중 한쪽이 1에 가깝고 한쪽이 0에 가까운 경우 산술 평균과 같이 0.5가 아니라 0에 가깝도록 만들어줍니다. 따라서 F1 score를 높이게 하려면 Precision과 Recall이 균일한 값이 필요하기 때문에 두 지표 성능 모두를 높일 수 있도록 해야 합니다.

• \[F_{1} = 2\frac{precision \ \times \ recall}{precision \ + \ recall}\]

• 물론 데이터셋 마다 특성이 다르므로, precision, recall, F1 score를 비교하며 가장 적합한 것을 사용해야 합니다.

ROC와 AUC