Probability Model (확률 모형) 및 likelihood 개념 학습

2020, Aug 08    

머신 러닝 관련 글 목록

• 이번 글에서는 Probability Model이란 개념을 Gaussian Distribution을 통해 이해해 보도록 하겠습니다.

목차

• 확률 모형 (Probability Model) 이란?

• 모수 추정의 의미

• MLE(Maximum Likelihood Estimation)

• Log likelihood function

• MLE with Gaussian

• Summary

확률 모형 (Probability Model) 이란?

• 확률 모형이란 수집 및 관측된 데이터의 발생 확률 (또는 분포)을 잘 근사하는 모형으로 일반적으로 \(p(x \vert \theta)\) 로 표기합니다. 확률 모형 (Probability Model), 통계 모형 (Statistical Model), 확률 분포 (Probability Distribution) 모두 같은 뜻으로 사용됩니다.
• 이때, \(\theta\) 는 확률 모형을 정의하는 데 중요한 역할을 하는 값으로 모수 parameter 또는 요약 통계량 (Descriptive measure)라고 부릅니다.
• 확률 모형은 상황에 따라 \(p(x; \theta), p_{\theta}(x)\) 와 같이 쓰이며 경우에 따라서 \(p(x)\) 와 같이 parameter \(\theta\) 를 생략하고 표기하기도 합니다.

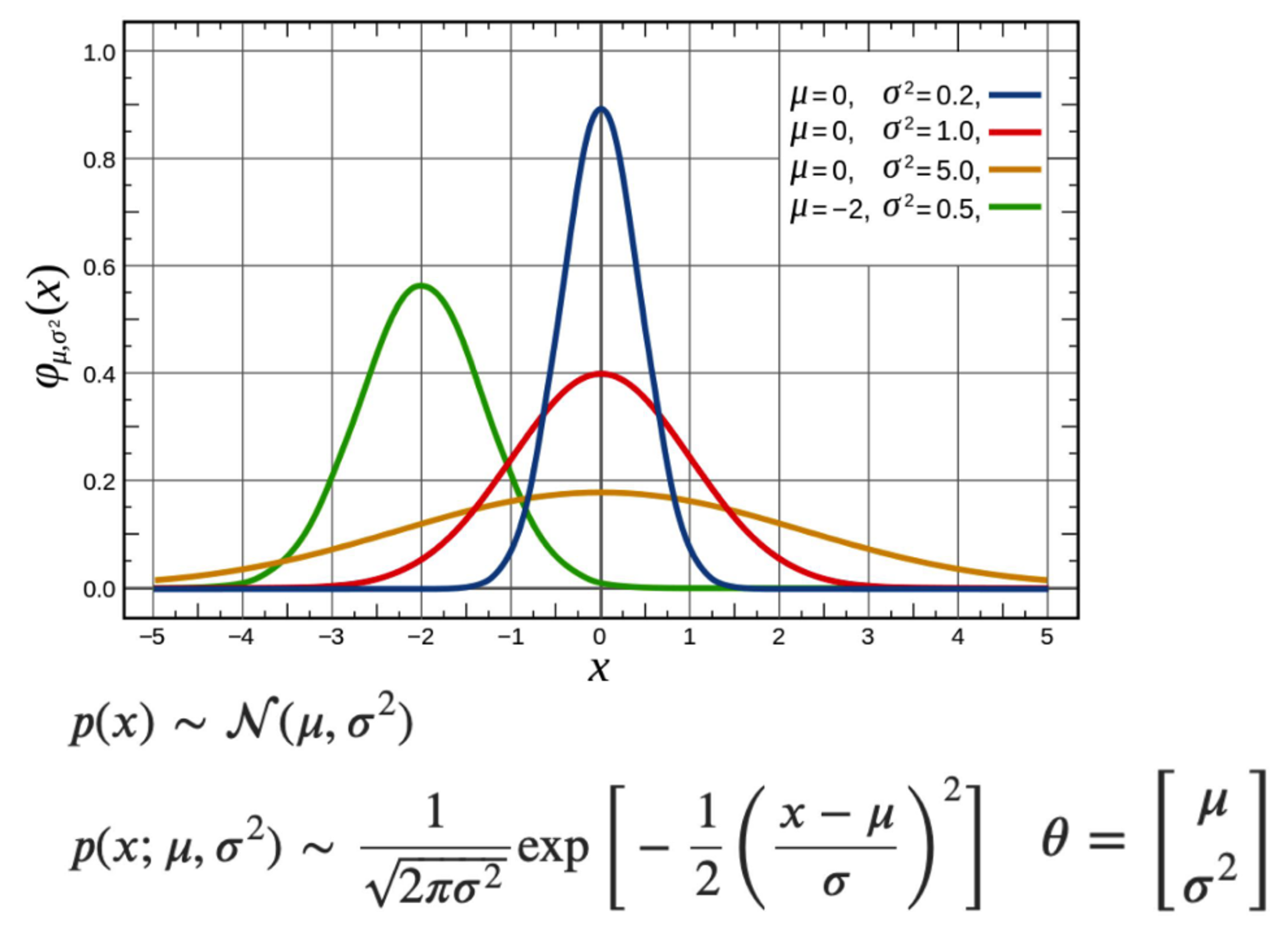
• 가우시안 분포와 관련된 상세 설명은 아래 링크를 참조하시기 바랍니다.
  • 링크 : 가우시안 분포 공식 유도
  • 링크 : 정규 분포

• 가우시안 분포를 확률 모형을 설명하는 데 사용하는 이유는 기초적인 확률 모형 (또는 확률 분포)로 관찰된 전체 데이터 집합이 평균을 중심으로 하여 뭉쳐져 있는 형태를 표현하는 데 가장 적합하기 때문입니다.

모수 추정의 의미

• 데이터들이 어떤 확률 분포 \(p(x \vert \theta^{*})\) 에 따라 샘플링 되어 구해졌다고 생각해 보도록 하겠습니다.

• \[X = (x_{1}, x_{2}, \cdots , x_{n}), \ \ x_{i} \sim p(x \vert \theta^{*}) \tag{1}\]

• 위 식에서 \(p(x \vert \theta^{*})\) 이 의미하는 바는 이상적인 실제 확률 분포를 뜻합니다. 이러한 이상적인 확률 분포에서 \(X\) 를 수집한다고 이해하면 됩니다.
• 일반적으로 모수 \(\theta\) 추정의 목적은 관측된 데이터의 실제 확률 분포 \(p(X \vert \theta^{*})\) 를 최대한 잘 근사 하는 수학적 모형을 찾는 것입니다. 이와 같이 근사화한 모델을 사용하는 이유는 실제 데이터 확률 분포 또는 실제 파라미터 \(\theta^{*}\) 를 정확히 할 수 없기 때문입니다.
• 따라서 임의의 확률 모형 \(p(x \vert \cdot)\) 을 가정한 뒤, 적어도 그 모형이 데이터를 가장 잘 설명하는 파라미터 \(\theta (\approx \theta^{*})\) 를 찾는 과정을 모수 추정이라고 합니다. 예를 들어 \(p(x \vert \theta) = N(x \vert \mu, \sigma^{2}), \theta = [\mu, \sigma]\) 와 같은 식에서 구체적인 값 \(\theta\) 를 찾는 과정이라고 말할 수 있습니다.

MLE(Maximum Likelihood Estimation)

• 관측된 데이터 \(X = (x_{1}, x_{2}, x_{3}, \cdots , x_{n})\) 를 토대로 우리가 상정한 확률 모형이 데이터를 잘 설명하도록 \(\theta\) 를 찾는 방법을 MLE (Maximum Likelihood Estimation) 이라 부릅니다. 바꾸어 말하면 \(n\) 개의 관측된 데이터의 발생 확률이 전체적으로 최대가 되도록 하는 \(\theta\) 를 찾는 것이 MLE가 되겠습니다. 수식은 다음과 같습니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta L(\theta) = \operatorname*{argmax}_\theta p(X \vert \theta) \tag{2}\]

• 이 때, \(L(\theta)\) 는 \(\theta\) 에 대한 함수로서 가능도(우도) 함수 (likelihood function) 라고 부르며 확률 모형을 나타내는 함수입니다.
• 여기서 주의할 점은 상황에 따라 \(L(\theta \vert X)\) 와 같이 표기하기도 하지만, 가능도 함수는 관측된 데이터 \(X = (x_{1}, x_{2}, x_{3}, \cdots , x_{n})\) 을 토대로 정의된 것으로 데이터에 관한 함수가 아니라는 점입니다. 즉, 데이터는 고정이고 \(\theta\) 가 변수로 움직이면서 likelihood가 변하게 됩니다. 이 때, \(\operatorname*{argmax}_\theta p(X \vert \theta)\) 를 통해 \(p(X \vert \theta)\) 확률값이 최대화가 되도록 하는 것이 위 식 MLE의 목적입니다.

• MLE 식을 좀 더 자세히 써보면 다음과 같습니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta L(\theta) \tag{3}\]
• \[= \operatorname*{argmax}_\theta p(X \vert \theta) \tag{4}\]
• \[= \operatorname*{argmax}_\theta \prod_{i=1}^{n} p(x_{i} \vert \theta) \tag{5}\]

• 식 (4) → (5) 로 전개할 때, iid(Independent and identically distributed random variables) 조건 즉, 데이터들의 발생 사건들이 독립적으로 발생한다고 가정하여 전개하였습니다.
• 지금까지 전개한 식을 다시 정리해보면 likelihood function의 값을 최대화 하는 \(\theta\) 를 찾는 작업과 \(X\) 데이터 셋 전체에 대하여 확률값이 최대가 되도록 하는 \(\theta\) 를 찾는 것은 같은 작업을 뜻하며 우리의 관심사는 \(\theta\) 라는 것입니다.

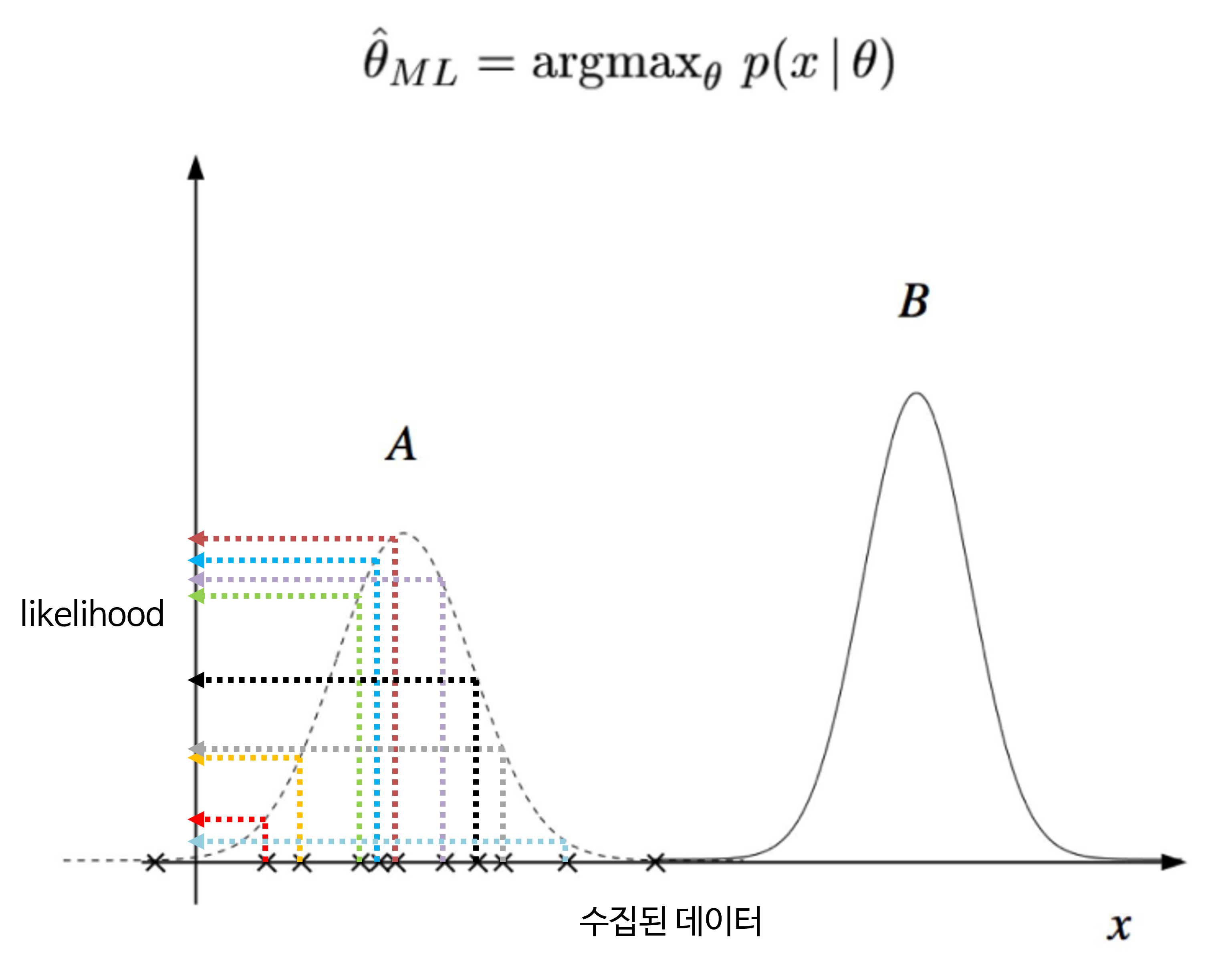
• 위 그래프 예제를 통하여 MLE를 좀 더 직관적으로 알아보도록 하겠습니다. 위 그래프에는 가우시안 분포 A, B가 있고 \(x\) 축을 보면 x로 표시된 수집된 데이터가 있습니다.
• 두 가우시안 분포 중에서 어떤 모델이 더 수집된 데이터를 잘 표현한다고 말할 수 있을까요? 바꿔 말하면 두 가우시안 분포 중에서 어떤 분포가 데이터 셋 전체에 대하여 확률 값이 최대가 되도록 만든다고 말할 수 있을까요?
• 정답은 A 입니다. 위 그림과 같이 색깔로 표시된 각각의 데이터의 likelihood를 살펴보면 (각 분포의 \(y\) 값) A의 경우 값이 존재하지만 B의 경우 가우시안 분포의 꼬리 부분에 위치하여 값이 0에 수렴합니다. A의 전체 likelihood를 계산하려면 iid 조건에 따라 위 그림에서 \(y\) 값에 대응되는 값을 모두 곱하면 됩니다. B의 경우 0에 수렴하기 때문에 A의 likelihood가 더 크다고 말할 수 있습니다.
• 즉, A 가우시안 확률 분포가 좀 더 데이터를 잘 표현하는 분포라고 말할 수 있는데, 이 때 A, B를 결정하는 값은 무엇일까요? 바로 \(\theta = (\mu, \sigma^{2})\) 입니다. 앞에서 설명한 바와 같이 likelihood의 곱을 최대로 만들어 주는 \(\hat{\theta}_{ML}\) 을 찾는 문제가 MLE입니다.

Log likelihood function

• 머신러닝 및 딥러닝에서 많이 다루는 방법이 단순히 likelihood를 최대화 하는 것이 아니라 log likelihood를 최대화 하는 방법을 많이 사용하곤 합니다. 왜냐하면 MLE를 추정할 때, likelihood를 모두 곱하였는데, 이 결과가 기하급수적으로 작아지므로 합으로 바꾸어서 표현하기 위함입니다.
• MLE 방식으로 모수 추정을 하기 위해서 실제 likelihood ( \(L(\theta)\) )에 log를 붙인 log likelihood \(l(\theta)\) 를 아래 식과 같이 표현할 수 있습니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta L(\theta) = \operatorname*{argmax}_\theta l(\theta) \tag{6}\]
• \[= \operatorname*{argmax}_\theta \log{\prod_{i=1}^{n}} p(x_{i} \vert \theta) \tag{7}\]
• \[= \operatorname*{argmax}_\theta \sum_{i=1}^{n} \log{p(x_{i} \vert \theta)} \tag{8}\]
• \[= \operatorname*{argmax}_\theta \frac{1}{n} \sum_{i=1}^{n} \log{p(x_{i} \vert \theta)} \tag{9}\]

• 식 (6) → 식 (7)로 변경해도 등식이 성립하는 것은 log 함수가 단조 증가 함수이기 때문입니다. 따라서 log 함수를 적용하여도 최솟값, 최댓값에 해당하는 모수를 추정할 때에는 전혀 영향을 끼치지 않습니다.
• 그리고 식 (8) → 식 (9)로 변경하면서 평균을 구하는 의미를 부여합니다. 물론 이 과정에서도 MLE에 해당하는 \(\theta\)를 찾는 것에는 영향을 미치지 않습니다.
• 데이터 셋 \((x_{i})_{i=1}^{n}\) 으로 부터 정의된 식 (9)를 흔히 empirical expectation 이라고 부르며 다음과 같이 표현합니다.

• \[E_{x \sim p(x \vert \theta^{*})} \log{p(x_{i} \vert \theta)} \approx \frac{1}{n} \sum_{i=1}^{n} \log{p(x_{i} \vert \theta)} \tag{10}\]

MLE with Gaussian

• 구체적으로 확률 분포를 가우시안이라고 가정하고 모수를 추정해 보겠습니다. 가우시안으로 추정하면 확률 분포는 다음과 같습니다.

• \[p(x \vert \theta) = N(x \vert \mu, \sigma^{2}), \ \ \theta = (\mu, \sigma)\]

• 앞에서 사용한 MLE 방법을 이용하여 모수 추정을 해보겠습니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta l(\theta) \tag{11}\]
• \[l(\mu, \sigma) = \sum_{i=1}^{n} \log{N(x_{i} \vert \mu, \sigma^{2})} \tag{12}\]
• \[= \sum_{i=1}^{n} \log{\frac{1}{\sigma \sqrt{2\pi}} \exp{ (-\frac{(x_{i} - \mu)^{2}}{2\sigma^{2}})}} \tag{13}\]
• \[-\frac{n}{2} \log{2\pi \sigma^{2}} - \frac{1}{2\sigma^{2}} \sum_{i=1}^{n} (x_{i} - \mu)^{2} \tag{14}\]

• 위 식 (14) 에서 \(l(\mu, \sigma)\) 를 최대로 만드는 \(\mu, \sigma\) 를 구하기 위하여 \(\mu\) 와 \(\sigma\) 각각에 대하여 미분을 취하여 구해보겠습니다. 식 (14)가 위로 볼록한 포물선 형태이기 때문에 미분을 구하여 변곡점을 찾으면 최댓값을 구할 수 있기 때문입니다.
• 먼저 \(\mu\) 에 대하여 미분을 취해보겠습니다.

• \[\frac{d l(\mu, \sigma)}{d \mu} = \frac{d}{d\mu} \biggl(-\frac{n}{2} \log{(2\pi \sigma^{2})} -\frac{1}{2\sigma^{2}} \sum_{i=1}^{n} (x_{i} - \mu)^{2} \biggr) \tag{15}\]
• \[= 0 -\frac{1}{2\sigma^{2}} \sum_{i=1}^{n} (-2x_{i} + 2\mu) \tag{16}\]
• \[= \frac{1}{\sigma^{2}}(\sum_{i=1}^{n} (x_{i}) - n\mu) \tag{17}\]
• \[\therefore \ \ \mu = \frac{1}{n}\sum_{i=1}^{n} x_{i} \tag{18}\]

• 식 (18)을 통하여 확인할 수 있는 점은 가우시안 분포에서 MLE를 하기 위하여 모수 중 하나인 \(\mu\) 를 기준으로 MLE를 하면 흔히 사용하는 평균값이 된다는 점입니다.

• 마찬가지로 \(l(\mu, \sigma)\) 를 최대로 만드는 \(\sigma\)를 구하기 위해 \(\sigma\)로 미분을 취해보겠습니다.
• 식 (19) → 식 (20) 전개 시 식 전개 과정은 글 마지막 이미지를 참조해 주시기 바랍니다.

• \[\frac{d l(\mu, \sigma)}{d \sigma} = \frac{d}{d\sigma} \biggl(-\frac{n}{2} \log{(2\pi \sigma^{2})} -\frac{1}{2\sigma^{2}} \sum_{i=1}^{n} (x_{i} - \mu)^{2} \biggr) \tag{19}\]
• \[= -\frac{n}{\sigma} -\frac{1}{2}\sum_{i=1}^{n} (x_{i} - \mu)^{2} \frac{d}{d\sigma}(\frac{1}{\sigma^{2}}) \tag{20}\]
• \[= -\frac{n}{\sigma} -\frac{1}{2}\sum_{i=1}^{n} (x_{i} - \mu)^{2} \times 2\frac{1}{\sigma}(-\frac{1}{\sigma^{2}}) \tag{21}\]
• \[= -\frac{n}{\sigma} + \frac{1}{\sigma^{3}}\sum_{i=1}^{n} (x_{i} - \mu)^{2} = 0 \tag{22}\]
• \[\therefore \ \ \sigma^{2} = \frac{1}{n} \sum_{i=1}^{n} (x_{i} - \mu)^{2}\]

• 이와 같이 \(\sigma\) 를 이용하여 MLE를 하였을 때, 흔히 말하는 분산의 정의대로 식이 도출된 것을 알 수 있습니다.

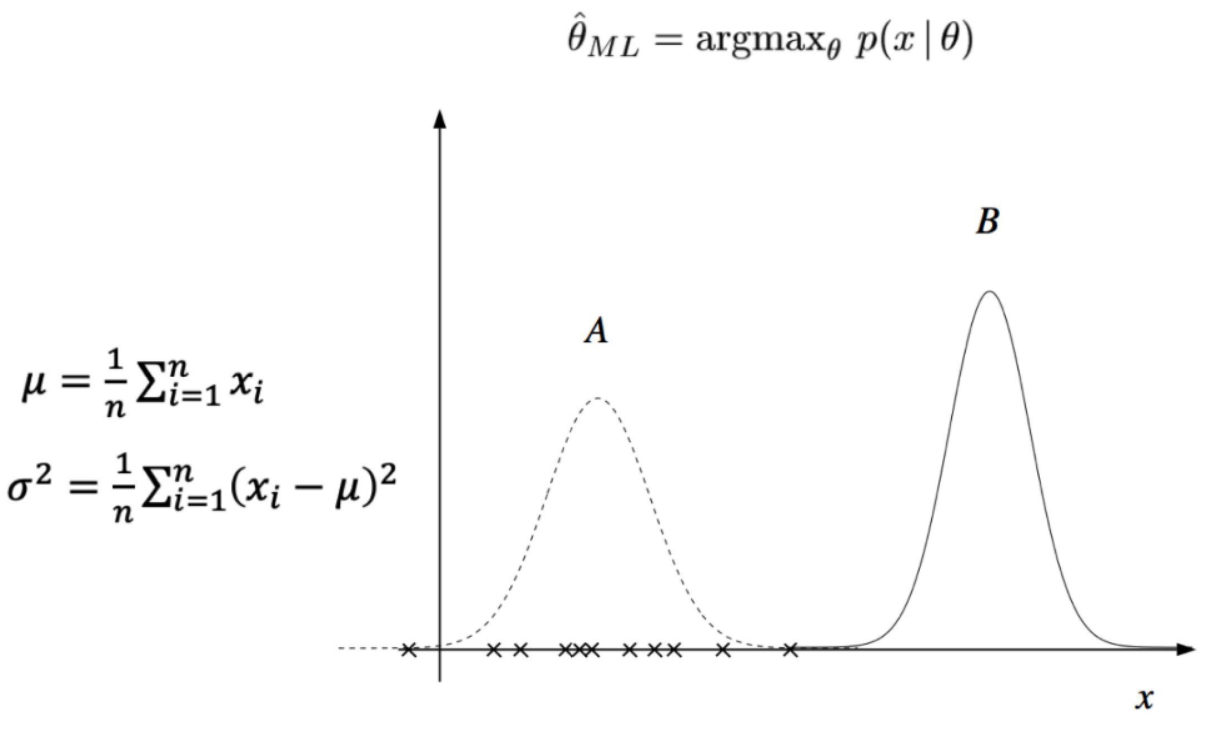
• 만약 A 분포가 주어진 데이터 셋을 가장 잘 표현하는 가우시안 분포라고 한다면 주어진 데이터 셋으로 부터 확인할 수 있습니다. 앞에서 살펴본 MLE를 하기 위한 모수 추정을 하면 됩니다.
• 주어진 데이터 셋에서 평균 \(\mu\) 와 분산 \(\sigma^{2}\) 을 구한 다음에 실제 A 분포에 적합한 지 비교하면 됩니다. 실제로 데이터셋의 평균 및 분산과 가우시안 분포 A가 일치한다면 MLE를 성공적으로 하였다고 말할 수 있습니다.

• 이와 같이 미분을 이용하여 MLE를 하는 방법을 analytic solution 이라고 하며 직접적으로 해를 찾을 수 있는 방법이다.
• 확률 모델이 점점 복잡해질 수록 직접적으로 해를 찾기 어려운 경우가 많아지므로 최근의 딥러닝 모델과 같은 경우들은 직접적으로 해를 찾는 방법이 아닌 점직적 (iterative)하게 찾는 방법을 많이 사용하기도 합니다. 하지만 근본적인 목적은 같으니 이해하시는 데 참조하시면 됩니다.

Summary

• 확률 모형 (Probability Model) 이란 수집 및 관측된 데이터의 발생 확률 (또는 분포)를 잘 근사하는 모형으로 일반적으로 \(p(x \vert \theta)\) 로 표기합니다.
• MLE (Maximum Likelihood Estimation)는 관측된 데이터 \(X = (x_{1}, x_{2}, \cdots , x_{n})\) 을 토대로 상정한 확률 모형이 데이터를 가장 잘 설명하도록 \(\theta\) 를 찾는 방법입니다.
• MLE에서 \(L(\theta) = p(X \vert \theta)\) 는 \(\theta\) 에 대한 함수로 해석하고 likelihood function 이라고 부릅니다.
• MLE 방식으로 모수 추정을 하기 위해서는 수식에 log를 붙인 lig-likelihood function인 \(l(\theta)\) 의 형태로 사용합니다.

• ※ 식 (20) 전개 시 \(\frac{d}{d\sigma} (-\frac{n}{2} \log{(2\pi \sigma^{2})}) \to -\frac{n}{\sigma}\) 로 유도하는 과정은 아래에서 참조하시기 바랍니다.

머신 러닝 관련 글 목록