Luis Serrano의 HMM(Hidden Markov Model) 강의
2020, Mar 15
- 참조1 : https://youtu.be/Ws63I3F7Moc
- 참조2 : https://youtu.be/kqSzLo9fenk
- 이번 글에서는 Markov chain에 대하여 알아보고 Hidden Markov Model에 대하서도 다루어 보도록 하겠습니다.
Markov Chain
- Markov Chain이 나오게 된 배경은 마코프가 파벨 네크로소프의 주장을 반박하려는 과정 속에서 나오게 되었다고 알려져 있습니다. 정확히는 큰 수의 법칙을 해석하는 관점의 차이에서 마코프가 Markov Chain을 도입하였습니다.
- 네크로소프의 주장은 신학생이었는데 운명이 결정되어 있다는 것이 아닌 종교적 자유의지를 중요하게 생각하였었습니다. 즉 사건의
독립성에 대하여 상당히 중요하게 생각하였다고 합니다. - 큰 수의 법칙을 해석하는 네크로소프의 주장은
큰 수의 법칙에서 독립성은 꼭 필요한 조건이라고 주장하였습니다. 예를 들어 주사위 던지기 같은 사건의 결과가 현재와 미래의 주사위를 던지는 사건의 확률을 변화시키지 않는데 이러한 예시들이 독립성을 통하여 설명할 수 있기 때문입니다. - 이 관점을 좀 더 확대시켜 보면 세상의 수많은 분포가 가우시안 분포로 되어있고 그 이론적 배경에는 중심 극한 이론이 있습니다.
- 수많은 시행을 거치게 되면(즉,
큰 수의 법칙을 거치게 되면) 대부분의 분포들이 가우시안 분포를 따르게 되는데 이 시행들은 독립이어야 한다 라고 확장하고 싶었던 것입니다. (그것이 자유의지에 해당하는 종교적 신념 이었기 때문입니다.)
- 하지만 세상의 많은 일들은 독립적이라기 보다
종속적입니다. 대부분의 사건, 날씨 등을 보면 어느 하나 독립적인 것이 잘 없습니다. - 즉, 현실 세계의 많은 경우와 같이 어떤 사건이 다른 사건에 영향을 주게 되는 사건을
종속 사건이라고 합니다. - 그래서 마코프는
Markov Chain을 이용하여 종속 사건 또한 큰수의 법칙을 따른다는 것을 보여주었습니다.
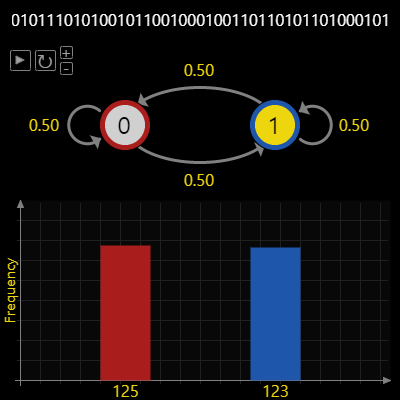
- 위 그림을 살펴보겠습니다. 두 가지의 상태 0, 1이 있고 각 상태에 머무르는 확률과 다른 상태로 천이하는 확률이 나뉘어져 있습니다.
- 즉, 현재 상태가 0일 확률이 이전 상태에 영향을 받게 되는 구조입니다. 단순히 주사위 던지기 문제와는 다른
종속 사건이 됩니다. - 위 경우의 예에서는 모든 사건이 0.5로 설정하였기 때문에 큰 수의 법칙을 적용하였을 때에 동일하게 각 상태에 머무를 확률이 0.5가 됩니다.
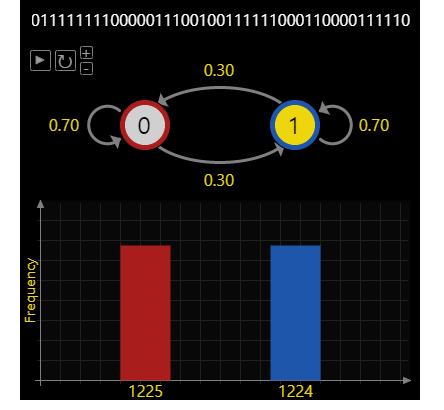
- 이번에는 확률의 비율을 다르게 가져갔으나 각 상태 0, 1이 천이하거나 머무르는 확률을 동일하게 설정하였습니다. (천이 = 0.3, 머무르는 경우 = 0.7)
- 이 경우에도 큰 수의 법칙을 적용하였을 때, 각 상태에 머무를 확률은 0.5와 0.5가 되었습니다.
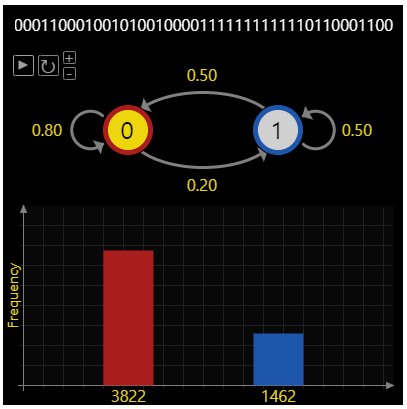
- 반대로 위와 같은 경우에는 0번 상태에 머무르는 확률이 0.72로 수렴하였습니다. 계속 돌려봤을 때에도 0.72로 수렴한 것으로 보아서 큰 수의 법칙이 적용된 것으로 볼 수 있습니다.
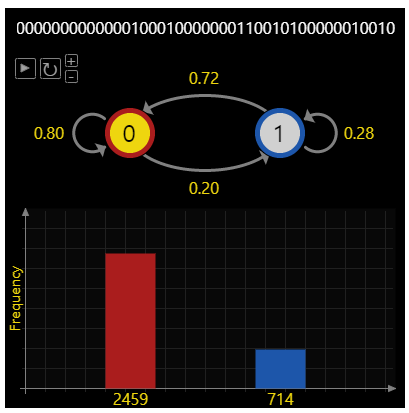
- 이번에는 양쪽의 확률을 완전 다르게 잡아보았습니다. 이 때에는 0번 상태에 머무르는 확률이 0.77로 수렴하였습니다. 즉 큰 수의 법칙이 적용되었습니다.
- 여기서 살펴보면 n번째에 0번 상태일 확률과 1번 상태일 확률은 이전 상태에 영향을 받기 때문에 독립적이지 않습니다.
- 하지만 상태의 모든 확률을 아는 상태에서 (위 처럼 천이할 때와 머무를 때의 확률을 아는 경우) 계속 반복하게 되면 어떤 특정한 확률로 수렴하게 됩니다.
- 즉, 이 방법은 독립성이 있는 사건들만 예측 가능한 분포에 수렴하게 된다는 네크로소프의 주장을 반박하게 됩니다. 즉 종속 사건들에서도
상태의 모든 확률을 아는 경우에예측 가능한 분포로 수렴하게 된다는 것입니다. - 이 때, 위 상태 천이를 모델링 한 것을
Markov Chain이라고 하며 모델링 행렬을 다음과 같이 나타낼 수 있습니다.
- \[\text{trasition matrix} = \begin{pmatrix} 0.8 & 0.2 \\ 0.72 & 0.28 \end{pmatrix}\]
- 위와 같은 형태로 다양한 Markov Chain을 모델링 할 수 있고 다음과 같이 조금 더 복잡하게 만들 수도 있습니다.
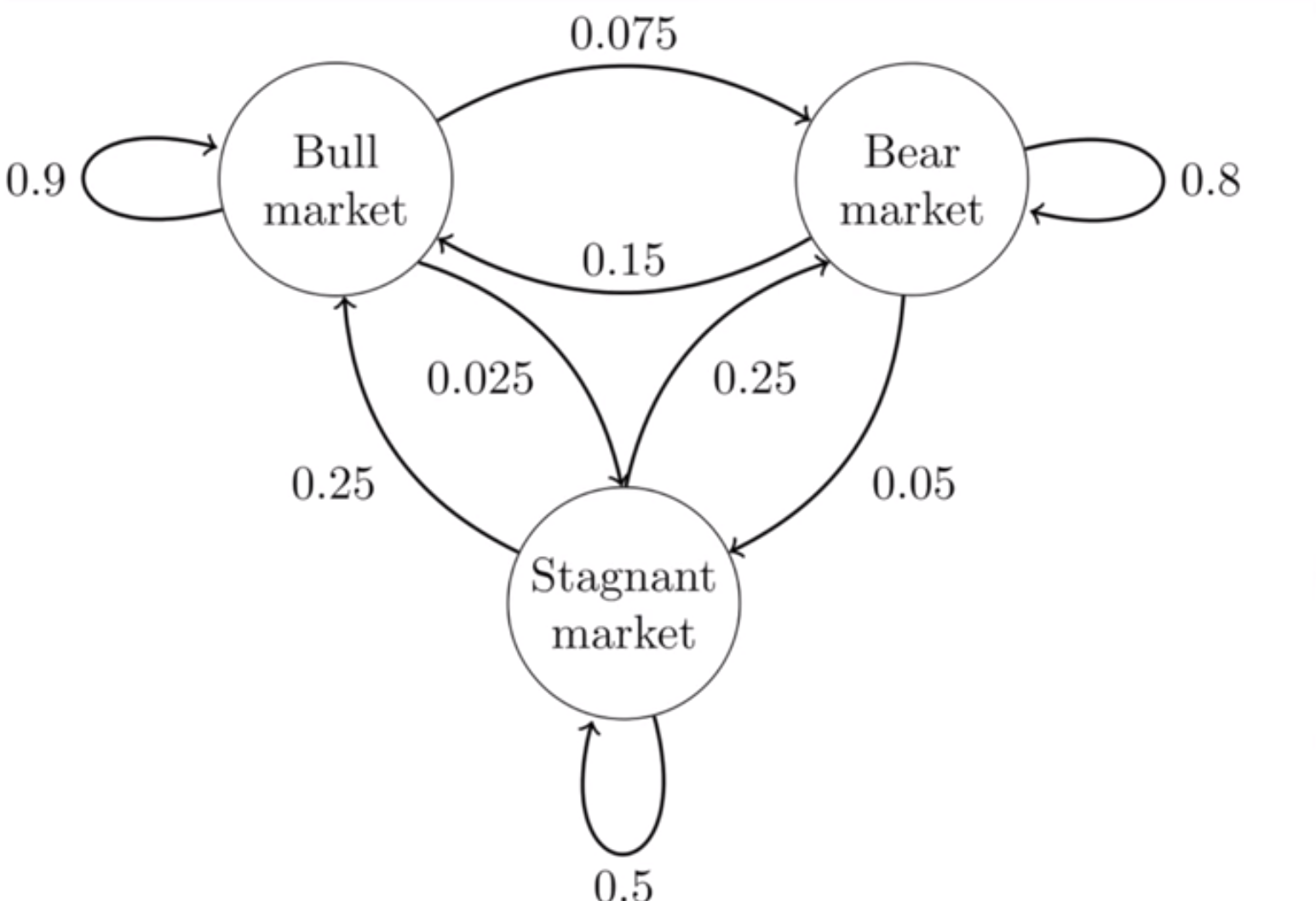
- 다음 링크를 클릭하면 마코프 체인에 대한 시뮬레이션을 해볼 수 있습니다.
마코프 체인
Hidden markov model
- 앞에서 배운 Markov Chain을 이용하여
HMM(Hidden Markov Model)에 대하여 다루어 보도록 하겠습니다.
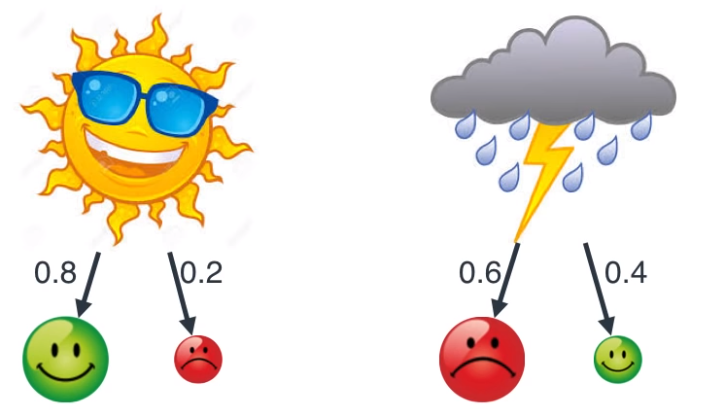
- 위 그림처럼 어떤 사람A는 해가 떳을 때에는 80%의 확률로 기분이 좋고 20%의 확률로 기분이 나쁘다고 가정해보겠습니다. 반면 날씨가 안좋을 때에는 40% 확률로 기분이 좋고 60% 확률로 기분이 나쁘다고 가정해보겠습니다.
- 이 때 멀리 떨어진 다른 사람B가 A에게 전화를 해서 A의 기분을 파악하고 A가 있는 날씨를 추정한다고 해보겠습니다.

- 이 때, 각각의 요일을 독립적으로 본다고 하면 기분이 좋은 날은 해가 떴을 가능성이 높고 기분이 안좋은 날은 날씨가 안좋을 가능성이 높으므로 위 처럼 판단할 수 있습니다.
- 하지만 위와 같은 상황이 현실적으로 발생할 수 있을까요? 날씨가 좋았다 비왔다 번갈아 계속 일어날 가능성은 매우 낮습니다.
- 특히 날씨와 같은 경우는 독립적이지 않습니다. 어제의 날씨가 오늘의 날씨에 영향을 줄 수도 있기 때문입니다.
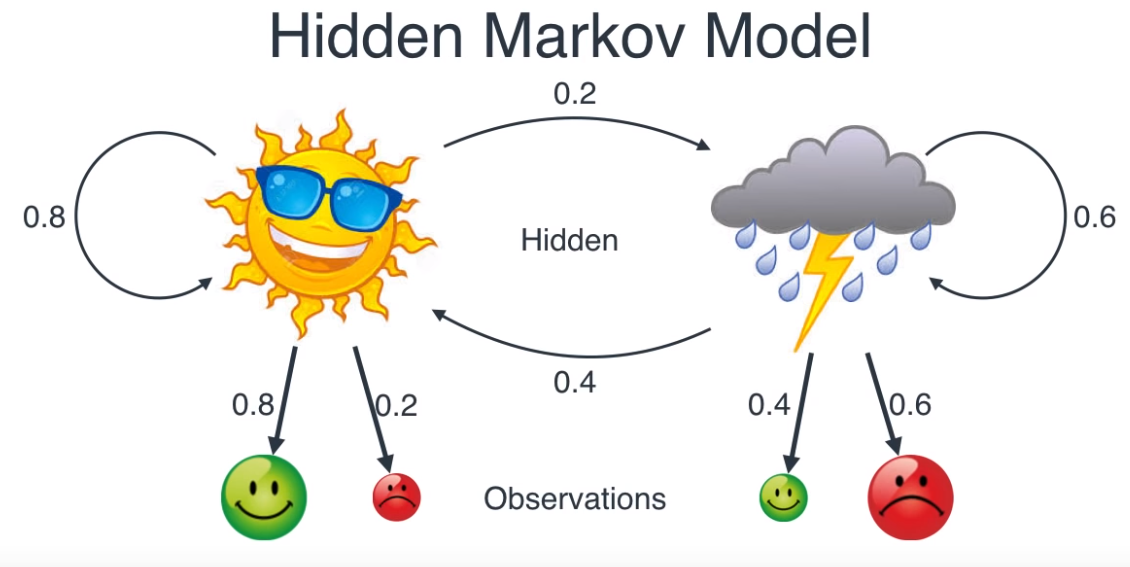
- 위와 같이 날씨가 변경되는 확률까지 도입된다면 상황은 조금 달라집니다.
- 보통 날씨는 연속되는 경향이 있으니 위와 같이 날씨의 상태 변화를 확률로 나타낼 수 있습니다.
- 그러면 위 모델에서는 2개 타입의 상태 (날씨, 기분)이 존재하고 기분이란 것은 직접 관측할 수 있는 것이므로
observation이라 하고 날씨는 기분을 통해 추정하는 것으로hidden이라고 하곘습니다.
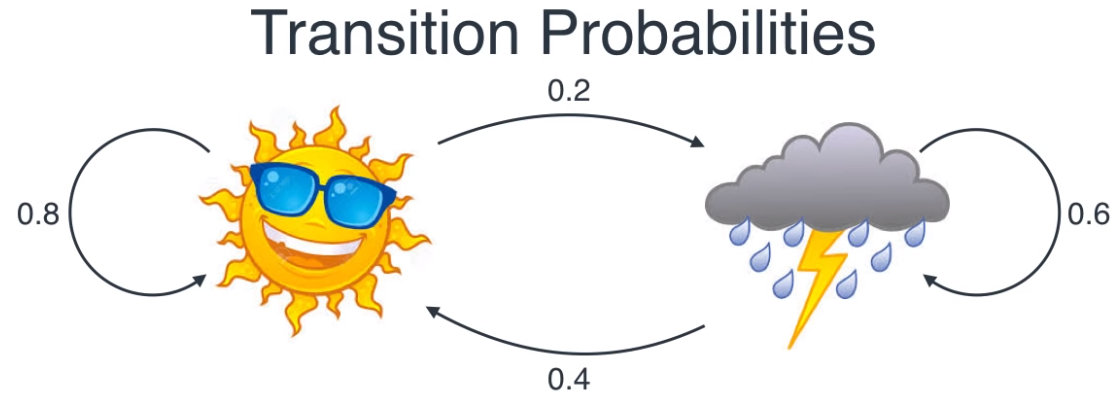
- 여기서
hidden state간의 확률을transition probability라고 합니다. 말 그대로 hidden state가 천이되는 확률을 나타내기 때문입니다.

- 반면
hidden state에서 뻗어나온 확률을emission probability라고 합니다.
- 그러면 위와 같은 Hidden Markov Model을 완성시키기 위해서는 몇가지 확인해야 할 사항들이 있습니다. 예를 들면 다음과 같은 것들을 해결해야 합니다.
- ① Hidden Markov Model들의 확률들은 어떻게 찾을 것인가?
- ② (어떤 정보도 주어지지 않은) 어떤 임의의 날이 해가 뜨는 지 비가 오는 지 어떻게 알 것인가?
- ③ (어떤 정보가 주어짐 ) A가 오늘 기분이 좋다면, 해가 뜬 확률과 비가 올 확률은 어떻게 구할 것인가?
- ④ 만약 A의 기분이 3일 동안 좋음, 나쁨, 좋음이면 날씨는 어떠하였을까?
- 그러면 첫번째, ① Hidden Markov Model들의 확률들은 어떻게 찾을 것인가? 부터 해결해 보겠습니다.
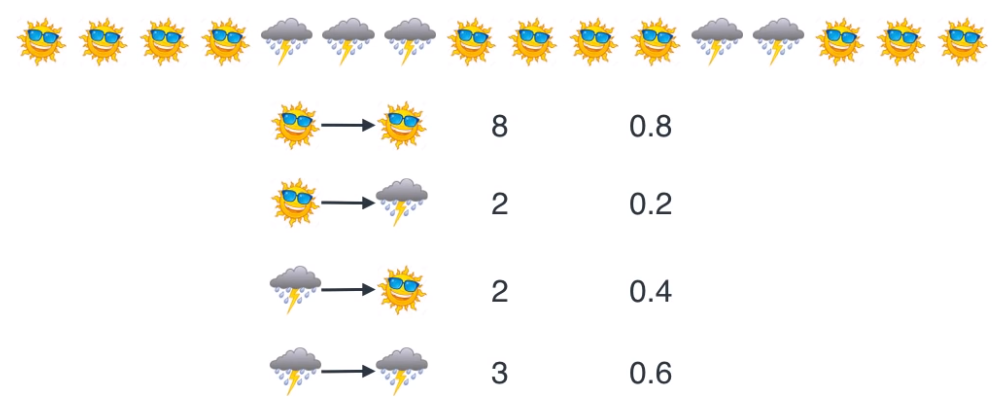
- 먼저 transition probability는 실제 데이터를 수집하여 구해야 합니다. 날씨와 같은 경우 일기 예보등을 구해서 맑음과 비옴에 대한 상관 관계가 어떤지 위 처럼 알 수 있습니다.

- 그 다음 emission probability 또한 실제 데이터를 기반으로 구할 수 있습니다.
- 위 그림처럼 날씨의 상태에 따라 A의 기분을 기록해 놓고 날씨에 따른 기분의 확률을 계산해 놓아야 합니다.
- ② (어떤 정보도 주어지지 않은) 어떤 임의의 날이 해가 뜨는 지 비가 오는 지 어떻게 알 것인가?
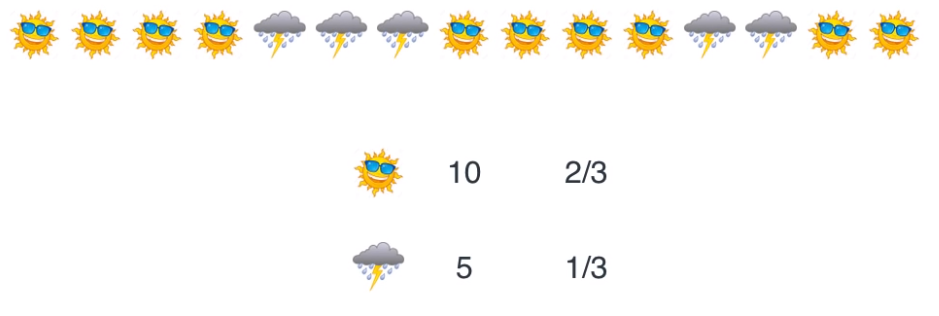
- 앞에서 살펴본 데이터 기준으로 해가 뜬 날의 날 수가 2배 더 많은 것을 사전에 확인할 수 있습니다.
- 그리고 다음과 같이 transition probability를 통해 식을 만들어 보겠습니다.
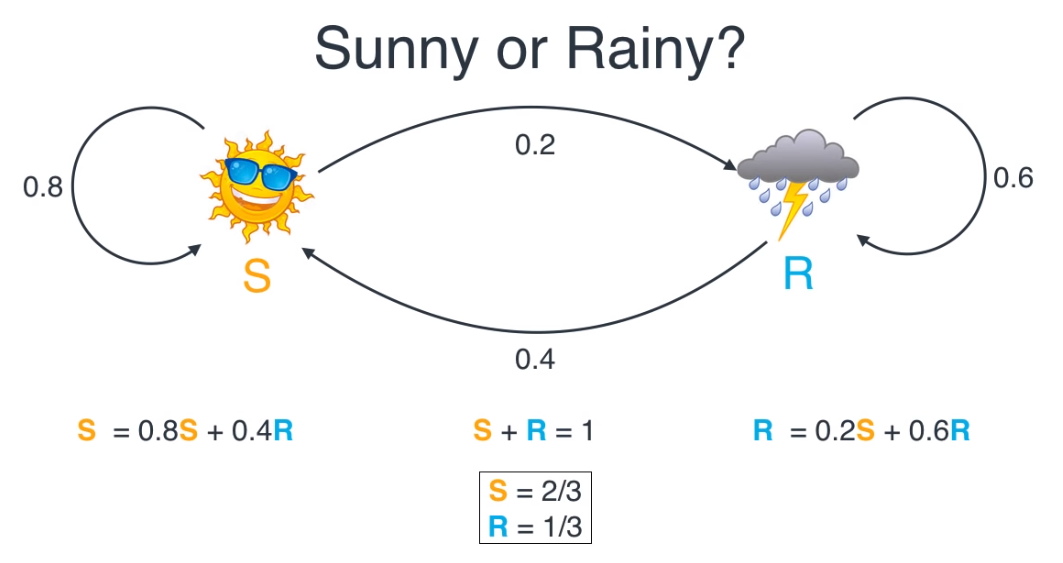
- 각각의 상태
S와R은 각 상태로 유입되는 상태의 확률만 모아서 식을 정의할 수 있습니다. - 이 때
S에 있을 확률과R에 있을 확률의 합은 1이 되어야 하고 앞에서 확인한 바와 같이 전체 사건을 기준으로S에 있을 확률이 2배 높습니다. - 따라서 어떤 정보가 없다면 높은 확률의 상태를 초깃값으로 가져가는 것이 합당합니다.
- ③ (어떤 정보가 주어짐 ) A가 오늘 기분이 좋다면, 해가 뜬 확률과 비가 올 확률은 어떻게 구할 것인가?
- 이 문제를 해결하기 위해서는
Beyes theorem을 이용해야 합니다. 왜냐하면 A가 오늘 기분이 좋다면 이란 observation 조건이 있기 때문입니다. - 오늘 기분이 좋다고 단순히 오늘이 날씨가 좋다고 판단하였을 때의 문제는 앞에서 다룬 것 처럼 날씨가 오락가락 할 수 있습니다.
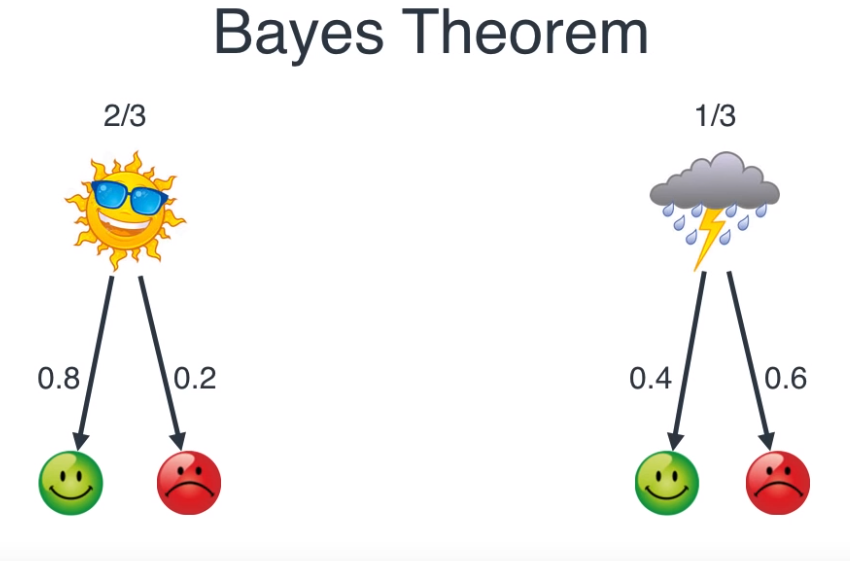
- Bayes theorem에는
prior,likelihood,posterior가 있습니다. 위 예제를 통해 prior와 posterior에 대한 정의를 해보면 다음과 같습니다.posterior: 최종적으로 구하고 싶은 기분이 주어졌을 때, 날씨를 추측하는 것으로 \(P(\text{날씨의 상태} \vert \text{기분의 상태})\) 가 됩니다. 가장 알고 싶은 것이지만 현재 바로 추정할 수는 없습니다.likelihood: ① 과정에서 살펴보았습니다. 실제 날씨를 통해 그날의 기분을 기록해서 나타내었습니다. 즉 날씨가 주어졌을 때, 기분을 나타내므로 \(P(\text{기분의 상태} \vert \text{날씨의 상태})\) 가 됩니다.prior: likelihood의 condition에 해당합니다. 즉, likelihood의 조건인 날씨의 상태가 되어 \(P(\text{날씨의 상태})\)가 됩니다.
- 구해야 할 posterior는 \(P(\text{날씨의 상태} \vert \text{기분의 상태})\)입니다. 예를 들어 \(P(\text{해} \vert \text{기분좋음})\) 같은 것입니다.
- posterior는 prior와 likelihood를 통해 구할 수 있으므로 다음과 같이 구해보겠습니다.
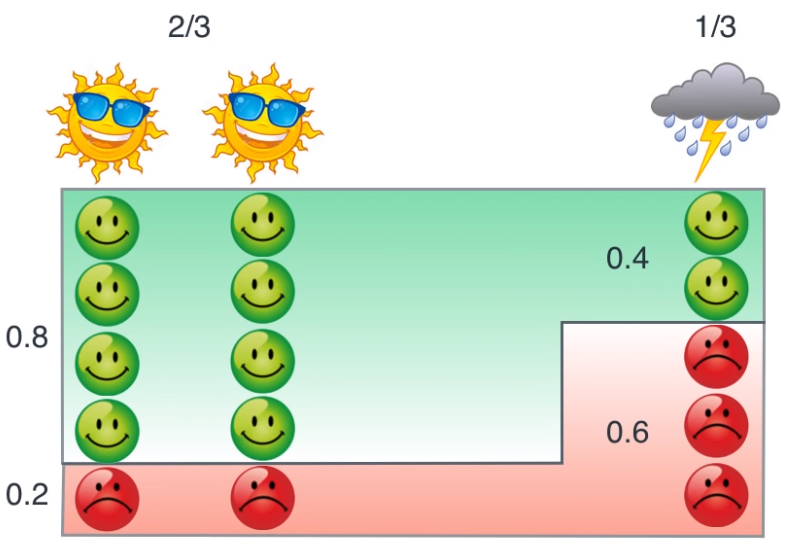
- 먼저
prior를 반영하여 날씨가 맑은 날이 2/3, 비가 오는 날이 1/3임과 앞에서 계산한likelihood를 반영하여 위와 같이 구성할 수 있습니다. - 즉 기분이 좋을 때, 날씨의 상태와 기분이 나쁠 때의 날씨의 상태를 구분해서 확률로 나타내었기 때문에
posterior를 구할 수 있습니다.
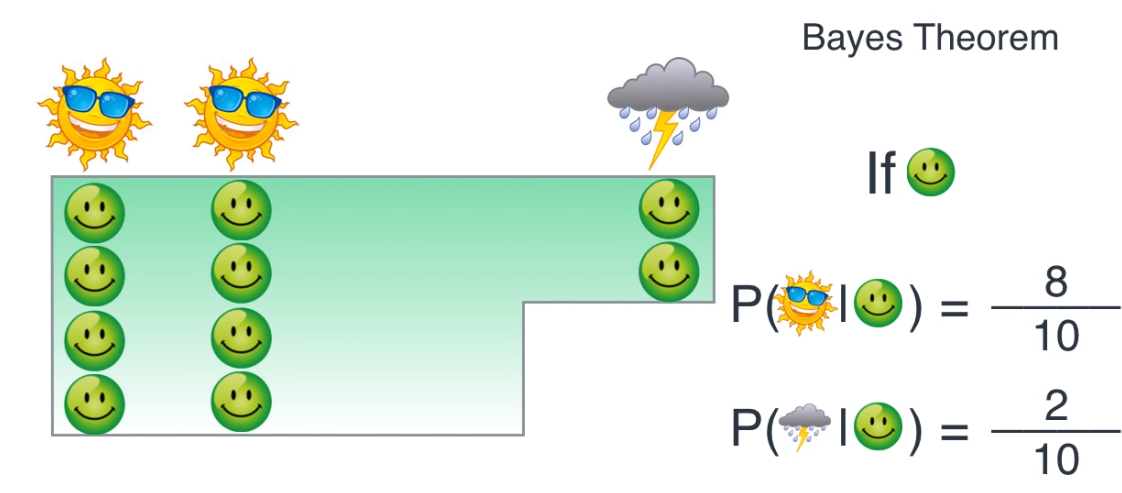
- 예를 들어 위와 같은 경우에는 기분이 좋은 상태일 때의 날씨의 확률을 나타냅니다.
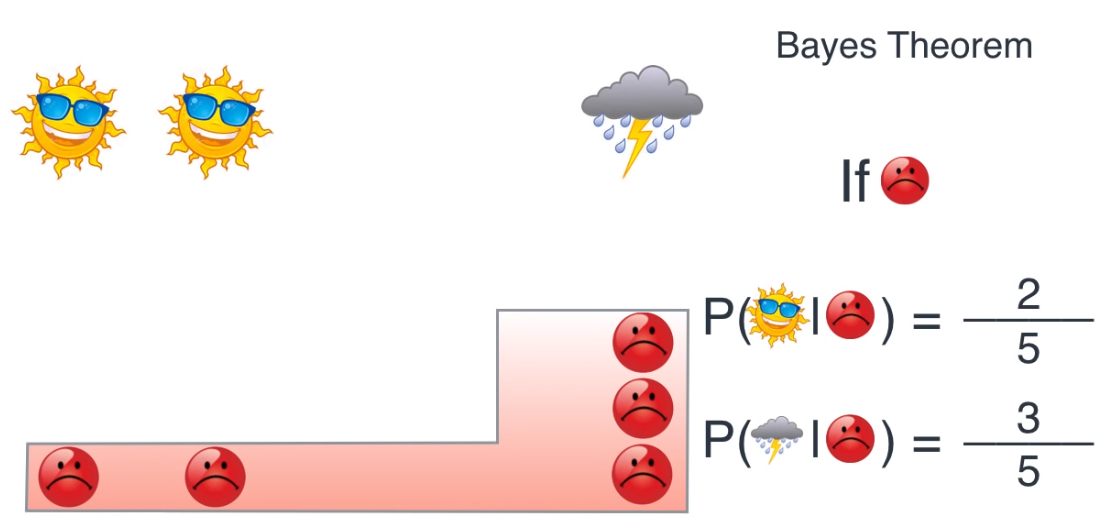
- 반면 위 같은 경우는 기분이 좋지 않은 상태일 때의 날씨의 확률을 나타냅니다.
- 이렇게 beyes theorem을 사용하면 ③ (어떤 정보가 주어짐 ) A가 오늘 기분이 좋다면, 해가 뜬 확률과 비가 올 확률은 어떻게 구할 것인가? 문제를 해결할 수 있습니다.
- ④ 만약 A의 기분이 3일 동안 좋음, 나쁨, 좋음이면 날씨는 어떠하였을까? 를 해결해 보도록 하겠습니다.
- 앞에서 다루었듯이 단순히 기분히 좋음 → 나쁨 → 좋음 이었다고 날씨가 해 → 비 → 해 라고 단정지을 수 없습니다.
- 먼저 가장 단순한 케이스 부터 살펴보겠습니다.
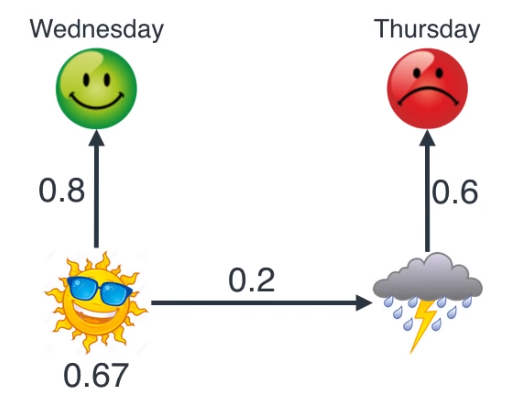
- 위 케이스 같은 경우가 발생할 확률은 임의의 날에 해가 뜰 확률 0.67, 해가 떳을 때 기분이 좋을 확률 0.8, 해가 뜬 다음날 비가올 확률 0.2 그리고 비가 왔을 때 기분이 나쁠 확률 0.6을 모두 곱하여 0.06432가 됩니다.
- 기분의 경우 좋음 → 나쁨으로 변경되어야 하는 것이 정해져 있기 때문에 변수는 날씨가 됩니다. 날씨의 경우 해가뜸, 비가옴 2가지의 경우가 있으므로 2일의 경우의 수는 다음과 같이 총 4가지가 됩니다.
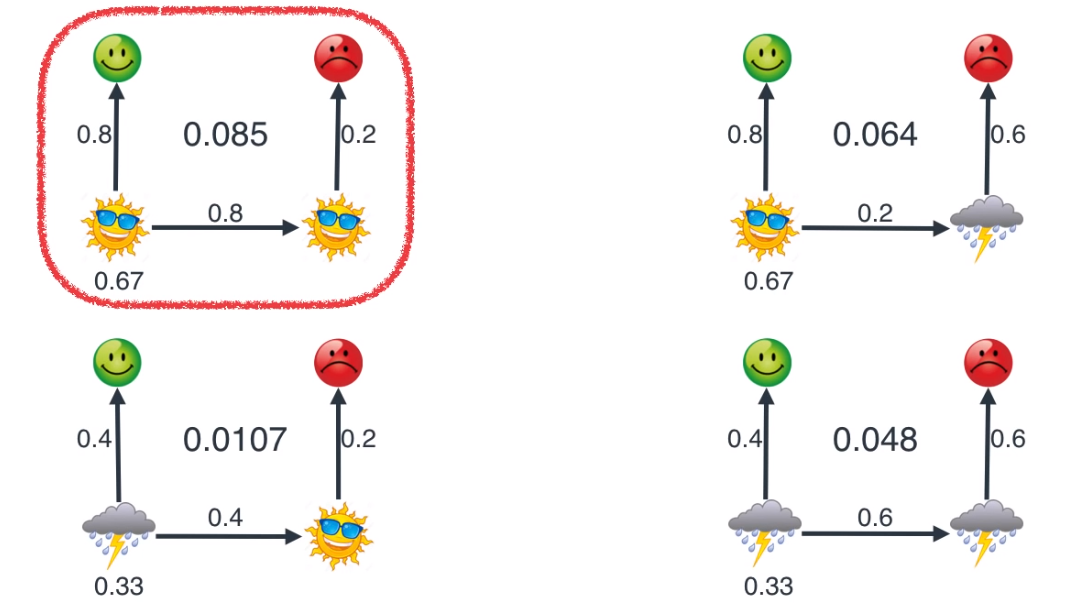
- 2일 동안의 날씨는 (해 → 해), (해 → 비), (비 → 해), (비 → 비)로 총 4가지 경우가 있고 그 경우에 따라 확률을 표현하면 위와 같습니다.
- 이 때 가장 확률 값이 높은 것이 실제로 발생할 확률이 높다는 것입니다. 이것이 바로
Maximum likelihood입니다. 가능도가 가장 높은 경우를 선택하는 것입니다.
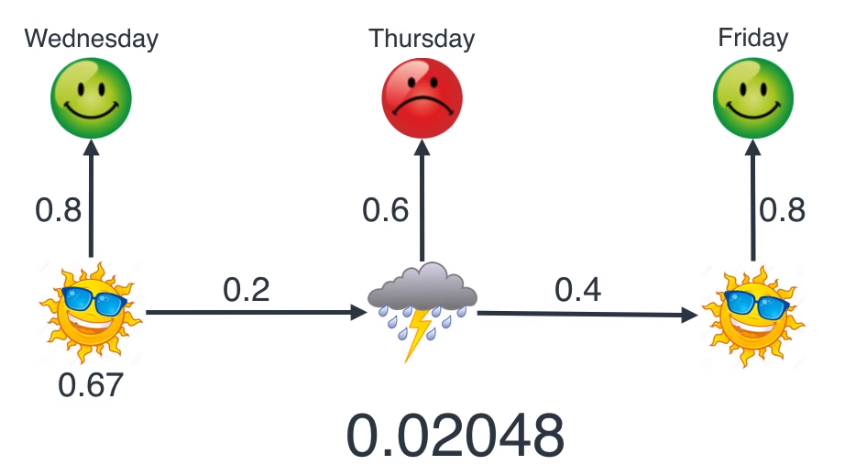
- 3일 동안의 날씨의 경우에 대해서도 살펴보겠습니다. 한가지 예로 (해 → 비 → 해) 의 경우를 살펴보면 위와 같습니다.
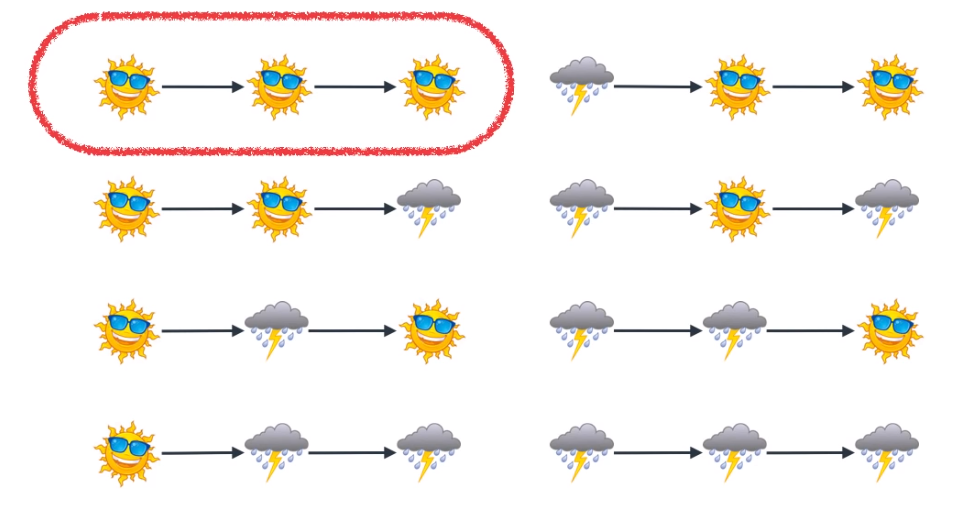
- 이 경우에도 계산을 해보면 (해 → 해 → 해)인 경우가
Maximum likelihood가 됩니다. - 그런데 매번 이렇게 계산을 하게 되면 경우의 수가 너무 기하급수적으로 많아지게 됩니다.
- 매번 모든 경우의 수를 다 확인해보고
Maximum likelihood를 선택해야 한다면 상당히 비효율적이고 계산량이 지수적으로 증가하게 됩니다.
- 따라서 이 과정을 좀 더 효율적으로 하는 방법이
Viterbi Algorithm으로 dynamic programming 기법을 이용하여 문제를 해결한 방법입니다. dynamic programming을 하려면 2가지 전제 조건이 필요합니다.optimal subprolbem: 문제들이 서로 겹쳐야 한다.optimal substructure: 각 문제들이 최적인 상태가 되어야 한다.
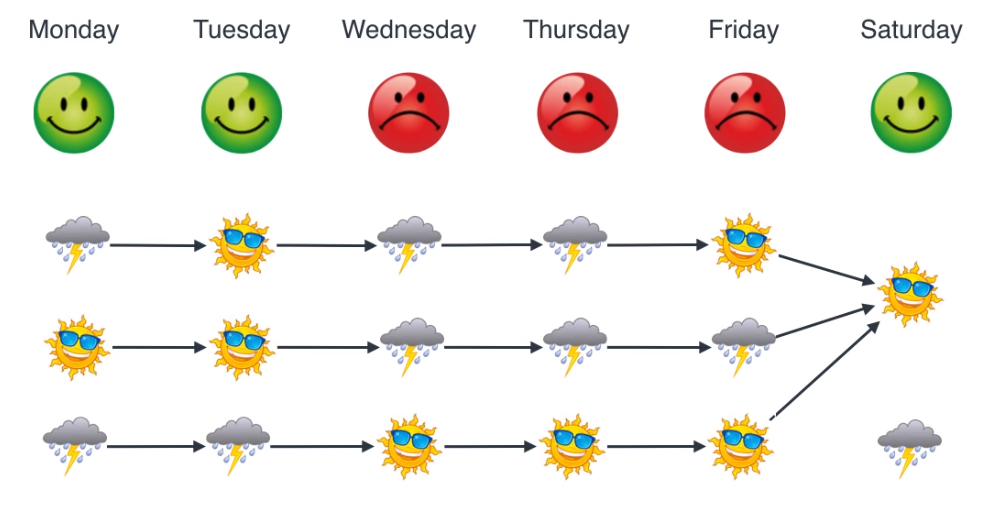
- 만약에 월요일 부터 토요일 까지의 기분의 상태가 있을 때,
Maximum likelihood에 해당하는 날씨의 상태를 찾는 방법에 대하여 알아보도록 하겠습니다. 일단 위 경우에서는 64개의 경우의 수가 있습니다.

dynamic programming의optimal substructure의 성질을 이용하면 월요일 부터 토요일 까지의 Maximum likelihood는 더 작은 문제로 쪼갤 수 있고 월요일에서 금요일 까지의 Maximum likelihood를 기준으로 토요일을 추가하면 된다는 생각을 가지면 됩니다.- 그러면 토요일날 해가 떳다는 상태를 고정 시킨 채 월요일 ~ 금요일 까지의
Maximum likelihood를 살펴보겠습니다.

- 먼저 금요일 까지의 상태만 살펴보면 위와 같이 금요일에 해가 뜬 상태에서 기분이 안좋은 경우가 Maximum likelihood 일 수 있습니다. 이 경우를 ① 이라고 하겠습니다.

- 또한 금요일 까지의 상태가 비가 온 상태에서 기분이 안좋은 경우가 Maximum likelihood 일 수 있습니다. 이 경우를 ② 라고 하겠습니다.
- 그러면 이 두가지 경우를 기준으로 토요일에 해가 뜨고 & 기분이 좋은 상태로 천이 되었을 때의 Maximum likelihood를 계산해 볼 수 있습니다. 즉, ① 상태에서 토요일에 해가 뜬 상태로 천이 하였을 때의 Maximum likelihood를 구할 수 있고 (이것을 ①’ 라고 하겠습니다.) ② 상태에서 토요일에 해가 뜬 상태로 천이하였을 때의 Maximum likelihood를 구할 수 있습니다. (이것을 ②’ 라고 하겠습니다.)
- 그러면 토요일날 해가 뜬 상태의 Maximum likelihood는 ①’과 ②’ 중의 더 큰 값이 되겠습니다.
- 즉, 더 작은 문제에서의 최적(Maximum likelihood)을 이용하여 더 큰 문제의 최적(Maximum lilkelihood)를 구하는 dynamic programming 방법입니다.
- 예시를 통해 살펴보겠습니다.
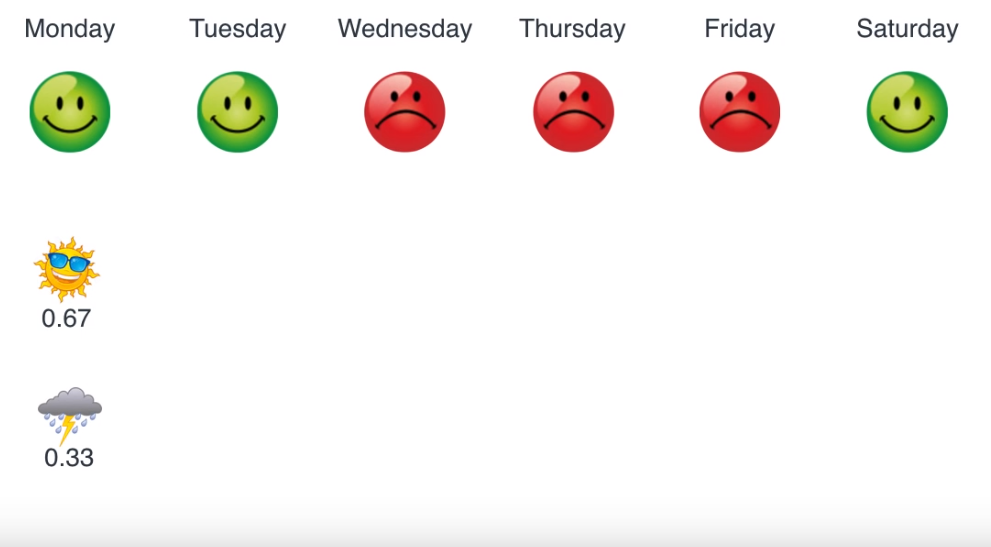
- 먼저 시작은 prior의 확률대로 시작하겠습니다.
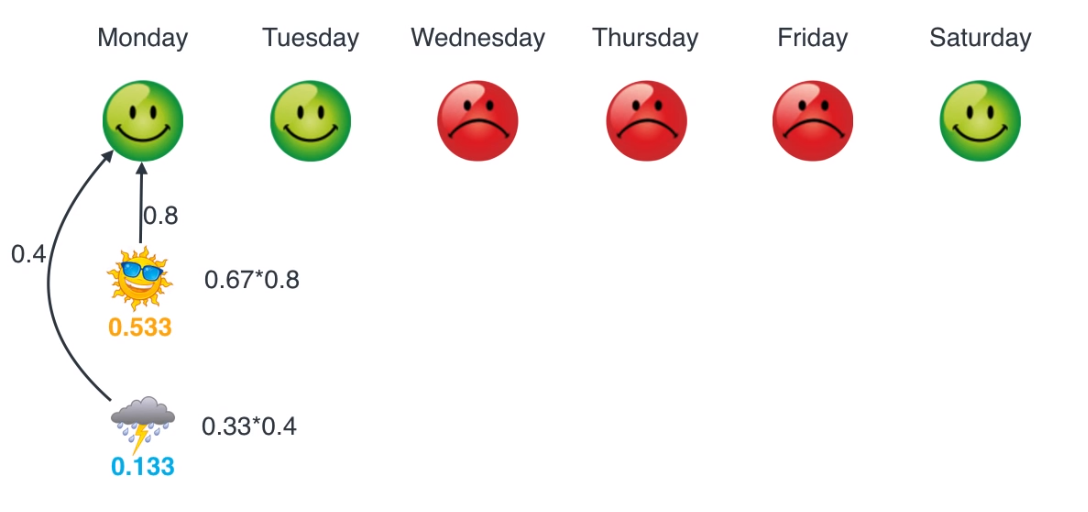
- 월요일에서의 Maximum likelihood를 살펴보면 위와 같습니다. 구한 결과를 업데이트 합니다.
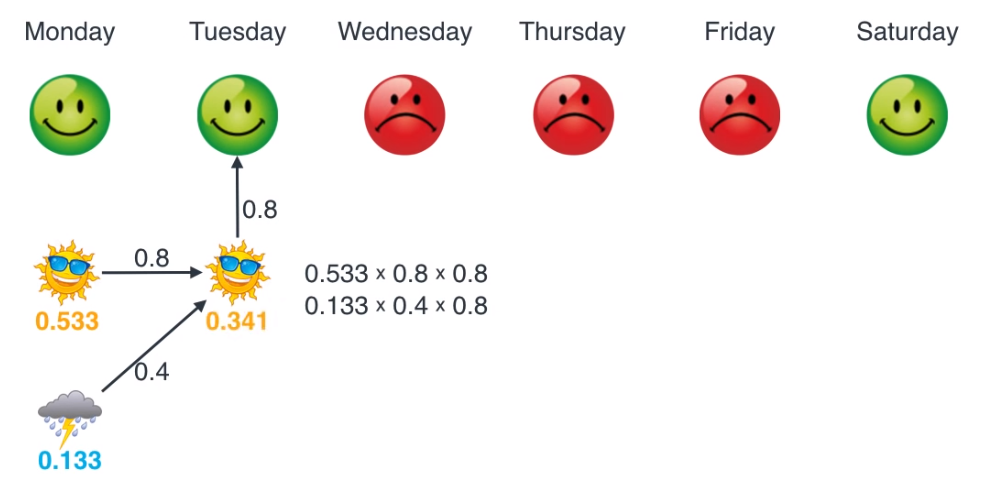
- 그 다음 화요일에서의 Maximum likelihood를 살펴보겠습니다. 먼저 화요일에 해가 떳을 상태에 대한 업데이트 입니다. 두 가지 경우 중 0.533 * 0.8 * 0.8의 경우가 더 크므로 이 계산 결과 (0.341)로 업데이트합니다.
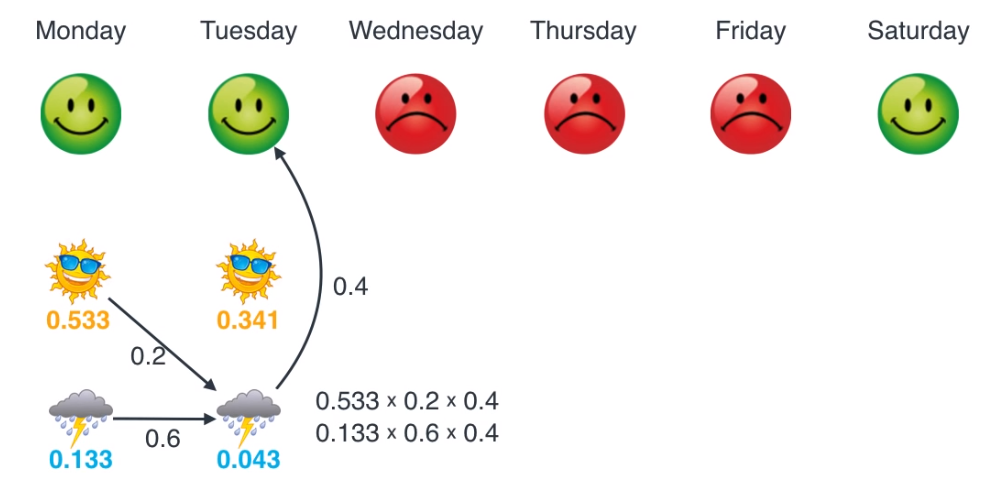
- 동일한 방법으로 화요일에서 비가 왔을 때의 상태에 대한 업데이트를 합니다.
- 그럼 수요일 ~ 토요일 까지 차례대로 업데이트 해보겠습니다.
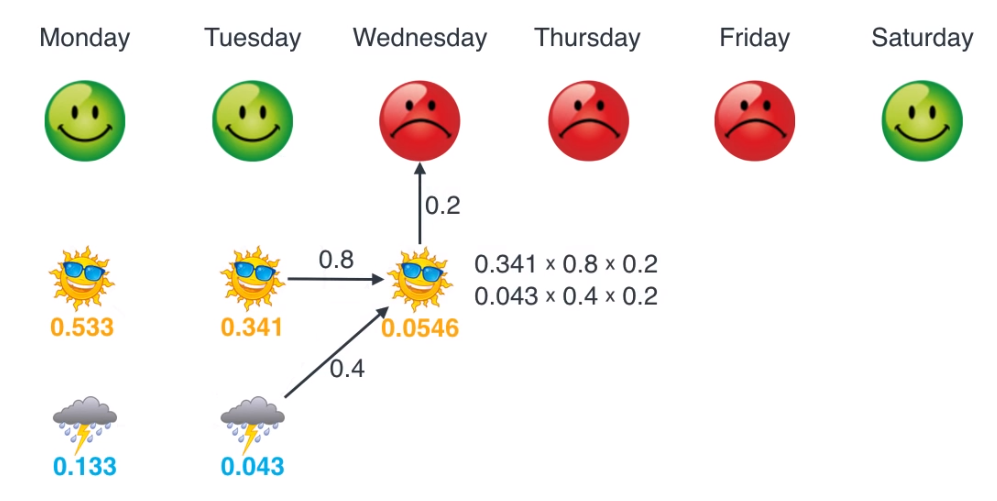
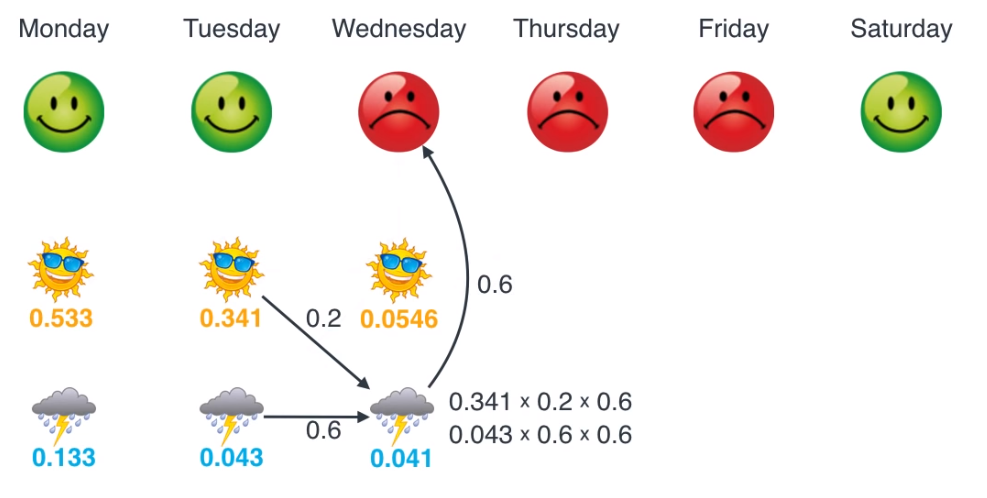
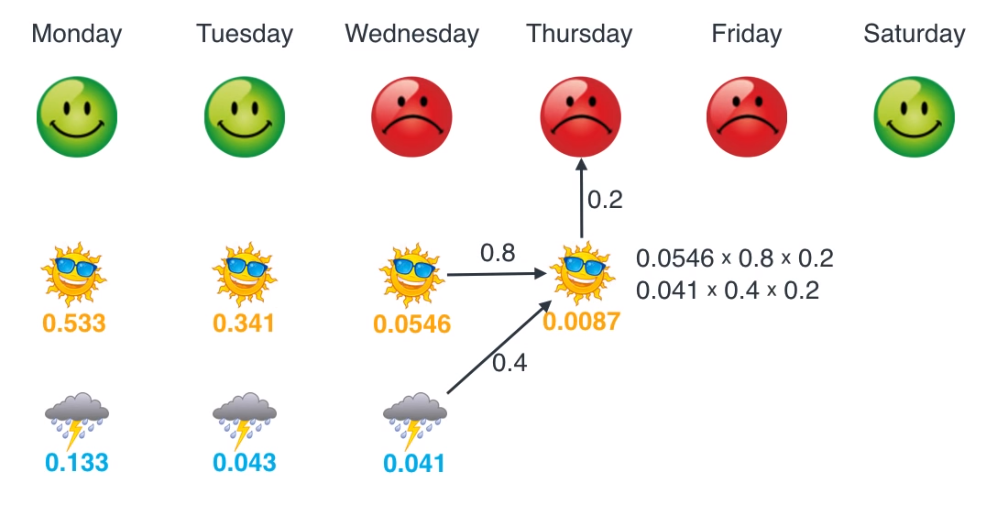
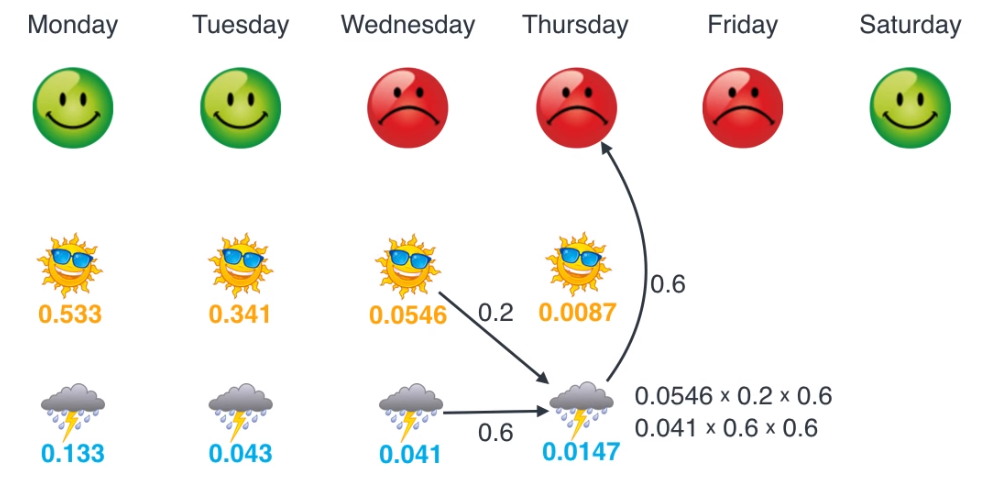
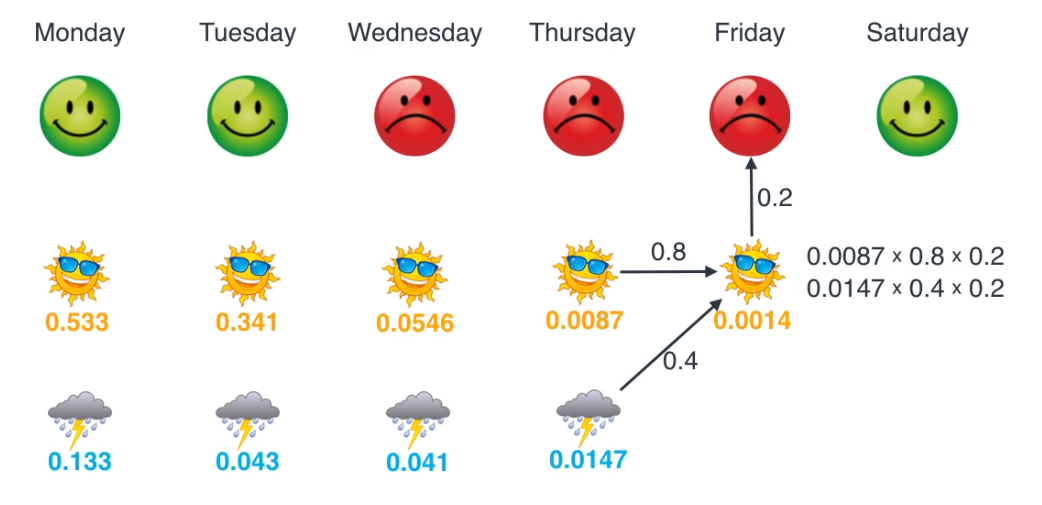
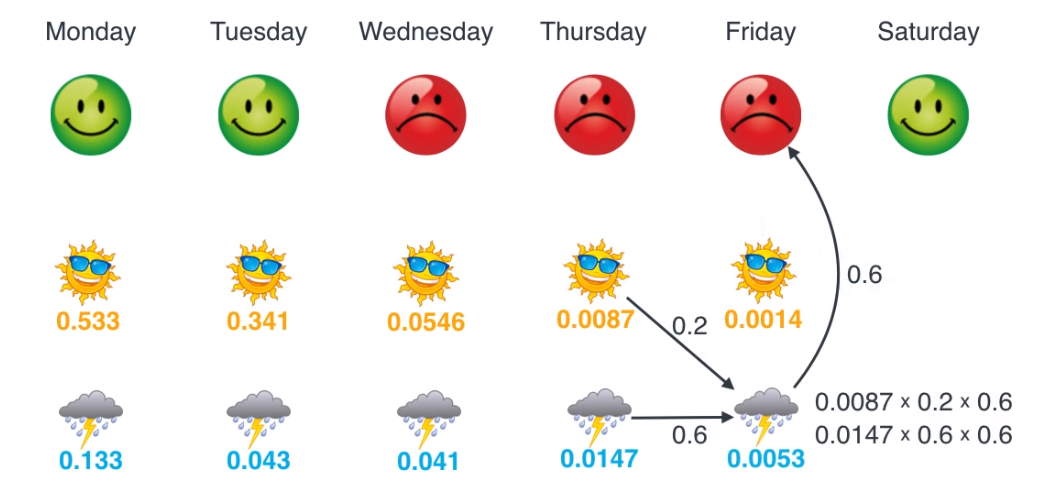
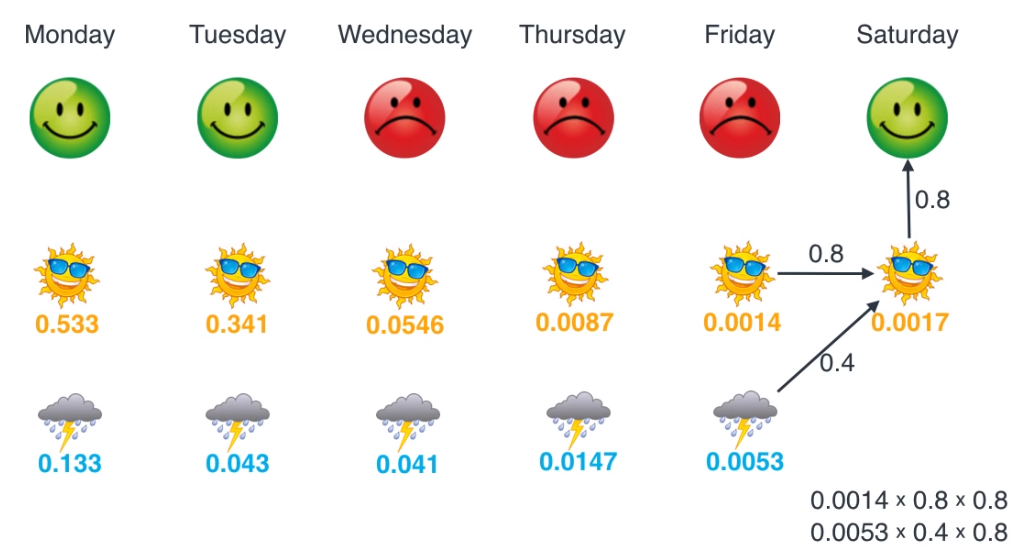
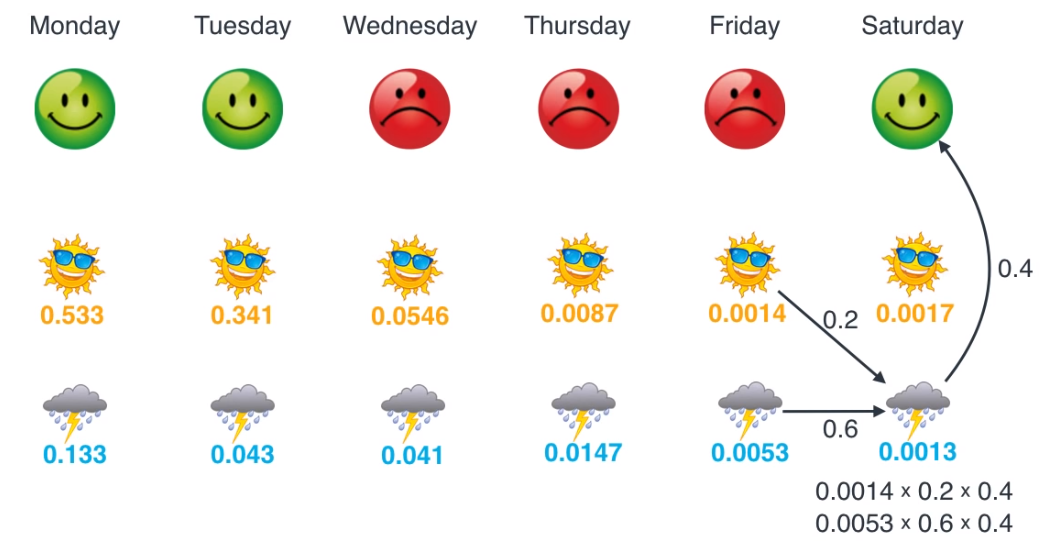
- 이렇게 모든 작업을 마쳤으면 마지막으로 각 요일별로
Maximum likelihood가 되는 상태를 선택하면 됩니다.
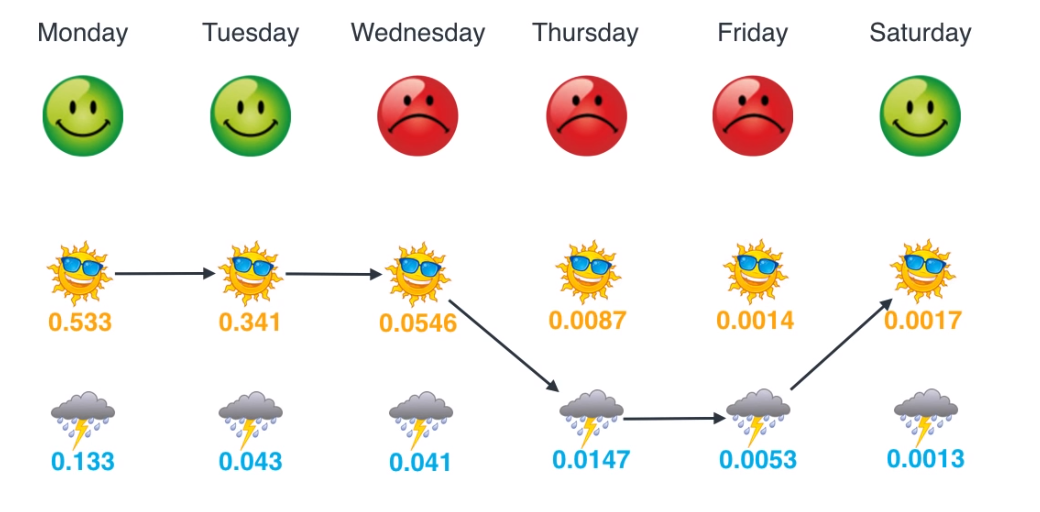
- 월,화,수,토요일에는 해가 떳을 떄의 likelihood가 더 크고 목,금요일에는 비가 올 때의 likelihood가 더 크기 때문에 위와 같이 상태가 선택되어야 가장 합당합니다.