Luis Serrano의 PCA(Principal Component Analysis) 강의

머신러닝 글 목록

참조 : https://youtu.be/g-Hb26agBFg?list=WL
참조 : http://www.stat.cmu.edu/~cshalizi/350/lectures/10/lecture-10.pdf
이번 글에서는 주성분 분석 (Principal Component Analysis)에 대하여 다루어 보도록 하겠습니다. Luis Serrano 강의를 주 내용으로 하며 중간 중간에 설명이 필요한 부분은 제 블로그를 참조하여 보충하였습니다.
제 블로그에 PCA와 관련된 글들이 더 있으니 아래 링크를 참조하셔도 됩니다.
- Andrew Ng PCA lecture : https://gaussian37.github.io/ml-concept-andrewng-pca/
- Mathematics for Machine Learning : https://gaussian37.github.io/math-mfml-table/

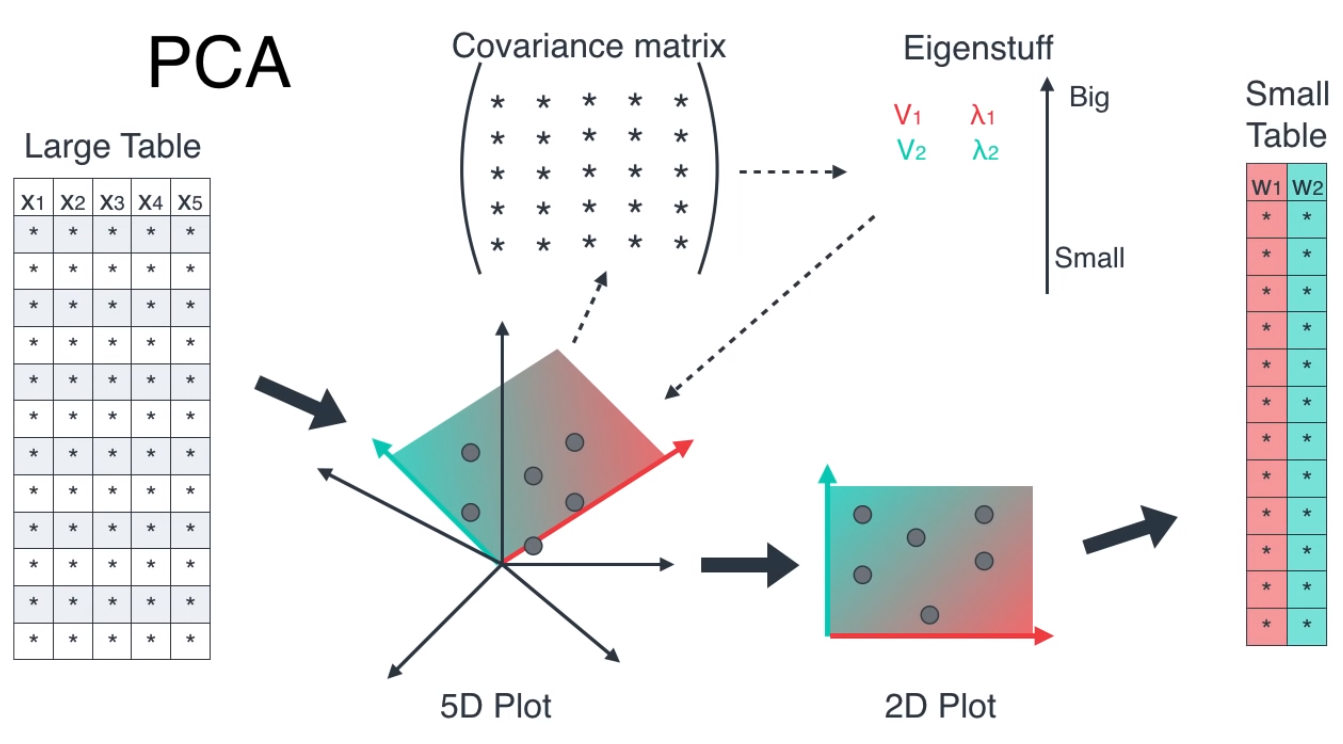
PCA의 전체 프로세스는 위 그림과 같습니다.
① 기존의 데이터에 사용된 feature들을 이용하여 공분산 행렬을 만듭니다.
② 공분산 행렬을 이용하여 고유값과 고유벡터를 구한다.
③ 고유값이 큰 고유벡터 \(N\)개를 선택하여 \(N\) 개의 feature로 전체 feature의 갯수를 줄인다.

Dimensionality Reduction

PCA의 목적인 Dimensionality Reduction이란 현재 데이터를 feature의 갯수를 줄여서 나타내는 방법입니다.
feature의 갯수가 많으면 시각화 해서 보기 어려운 문제가 있으므로 임시로 2, 3 개의 feature만 선택하여 시각화 하는 방법을 사용하거나 feature가 너무 많아서 차원의 저주에 빠진 경우 일부로 feature의 갯수를 줄일 수 있습니다.
그러면 PCA의 목적인 Dimensionality Reduction에 대하여 알아보도록 하겠습니다.

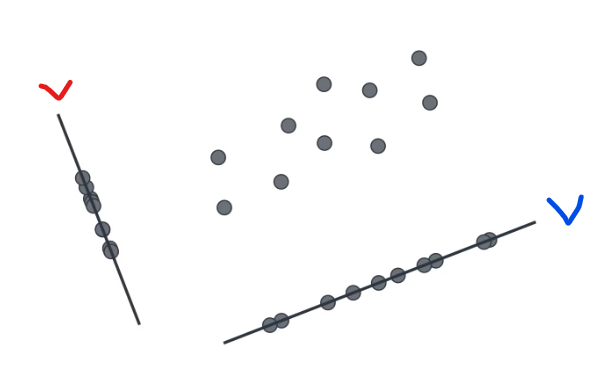
위 그림의 가운데에 있는 점들을 빨간색, 파란색 체크한 두 선에 정사영(projection) 하려고 합니다.
그러면 각 선에 정사영 된 점들이 위 그림 처럼 배치됩니다. 어떤 선에 정사영 한 것이 더 좋을까요?
느낌적으로 생각하였을 때, 파란색 체크한 선에 정사영 한 것이 더 나아 보입니다. 왜냐하면 점들이 기존 데이터 성향에 맞게 잘 분포되어 있기 때문입니다.
두 선분에 따라 정사영한 결과에 차이가 발생하는 이유는 각 선이 실제 데이터를 얼마나 잘 나타내는 정도가 다르기 때문입니다.
위 예시에서는 파란색 선이 실제 데이터를 더 잘 표현하기 때문에 원본 데이터에서 나타난 분포의 차이가 파란색 선에 정사영하였을 때에도 잘 나타나 집니다.
먼저 예제를 살펴보도록 하겠습니다.

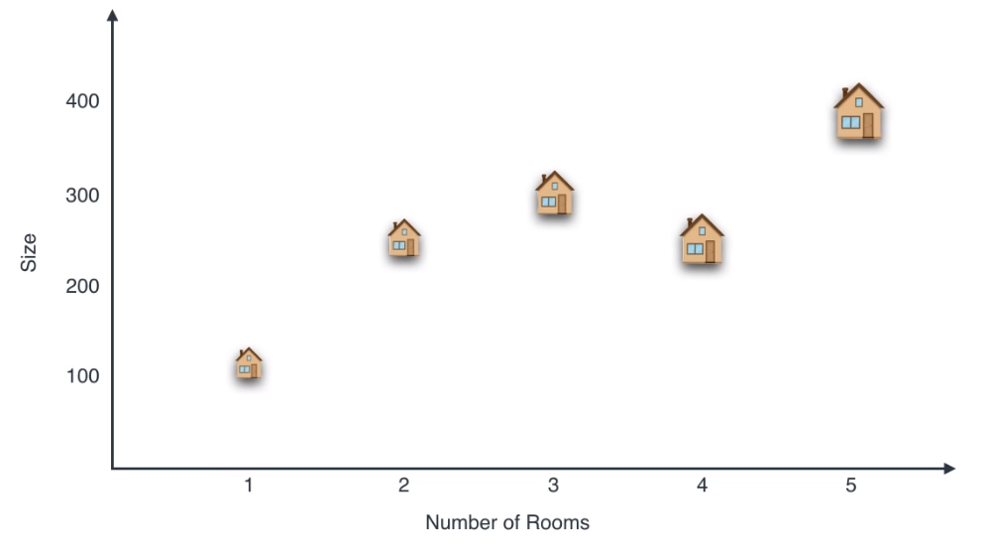
위 그림과 같이 2 축인 방의 갯수와 사이즈를 기준으로 2차원 평면위에 5개의 집 데이터를 표시해 보겠습니다. 그러면 위 그림처럼 나타나집니다.

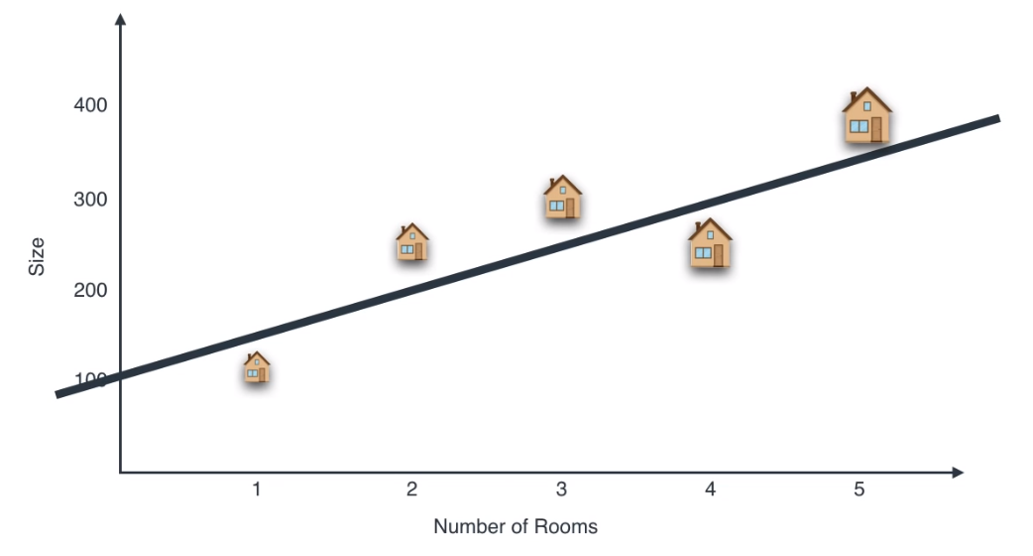
이 때, 위 그림의 검은 선과 같이 데이터를 잘 표현할 수 있을 것 같은 기준을 정해야 합니다. 위 검은 선은 상당히 데이터 들을 잘 반영하도록 정해져 있습니다.

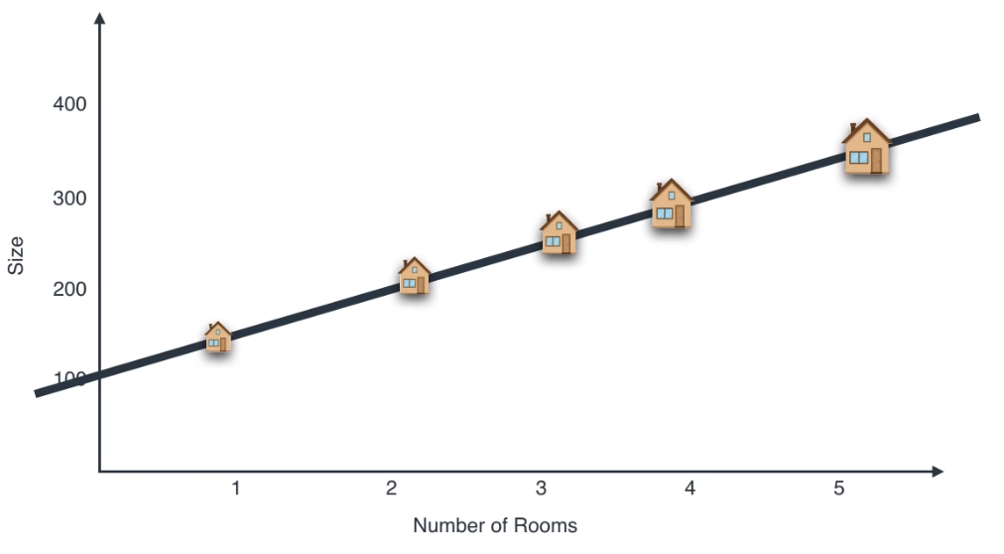
이 때, 검은 선에 데이터 들을 정사영 하면 위 그림 처럼 나타낼 수 있습니다.

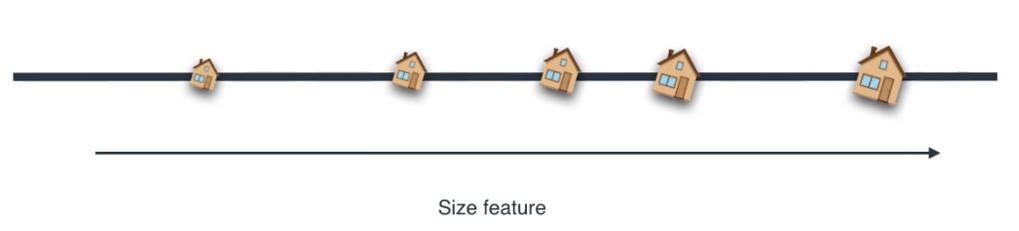
앞에서는 사이즈와 방의 갯수 즉, 2가지 feature를 이용하여 데이터를 표현하였습니다.
사실 집의 사이즈나 방의 갯수는 상관 관계가 있습니다. 넓은 집이 많은 방을 가질 수 있기 때문입니다.
위 그림에서도 2개의 차원을 1개의 차원으로 줄이고 이 때 사용된 1개의 차원을 size feature 라고 하겠습니다.

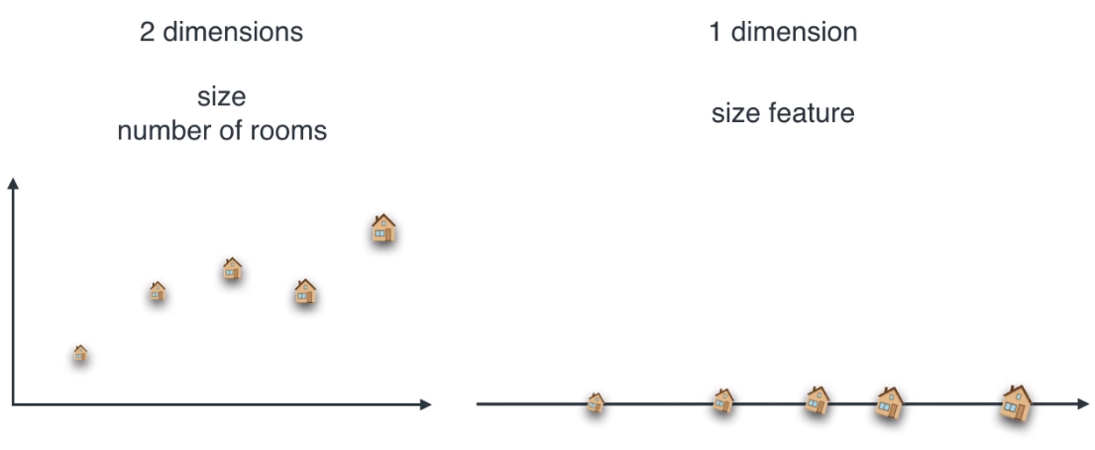
위와 같이 기존의 데이터를 어떤 feature에 정사영 시키면 차원을 줄일 수 있고 이 때 사용된 feature가 원래 데이터를 잘 나타내는 좋은 feature라면 정사영 하였을 때에도 데이터가 기존의 데이터를 잘 나타낼 수 있습니다. 이 예시를 위 그림의 size feature를 통해 확인 하실 수 있습니다.

특히 , 위 예와 같이 feature 중에서 유사 성격의 feature가 있으면 줄일 수 있습니다. 위 예제에서는 5개의 feature 중 3개는 size와 관련이 있고 2개는 위치와 관련되어 있습니다. 따라서 size, localization으로 feature를 2개로 줄일 수 있고 이 때, PCA와 같은 차원 축소 기법을 사용할 수 있습니다.

Covariance

차원 축소를 하기 위한 첫번째 단계는 각 feature들의 데이터들을 이용하여 공분산을 만드는 것입니다.
공분산의 개념을 알면 이 부분은 넘어가도 상관없습니다.
공분산의 개념에 대하여 알기 위하여 간단한 1차원 데이터의 분산에 대해서 먼저 다루겠습니다.

위 그림에서는 1차원 데이터의 평균, 분산을 나타냅니다. 분산은 평균에서 부터 얼만큼 떨어져 있는지를 나타내는 개념입니다. 위 그림을 통해 확인하시기 바랍니다.
그러면 2차원 데이터의 분산에 대하여 알아보겠습니다.

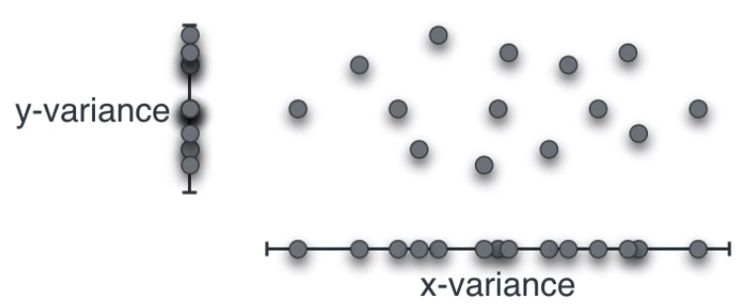
위 그림과 같이 2차원 데이터의 경우 \(X, Y\) 두 축을 기준으로 2가지의 분산을 구할 수 있습니다.

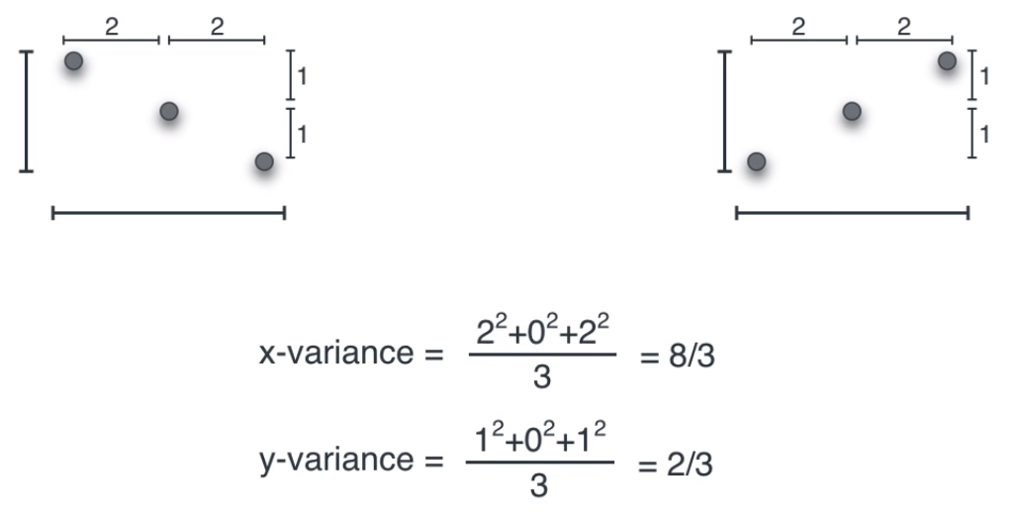
하지만 1차원 데이터에서 구한 방식으로 2차원 데이터에 그대로 적용하면 문제가 발생할 수 있습니다.
위 그림을 보면 두 분포가 다름에도 불구하고 X축과 Y축의 분산이 같습니다.

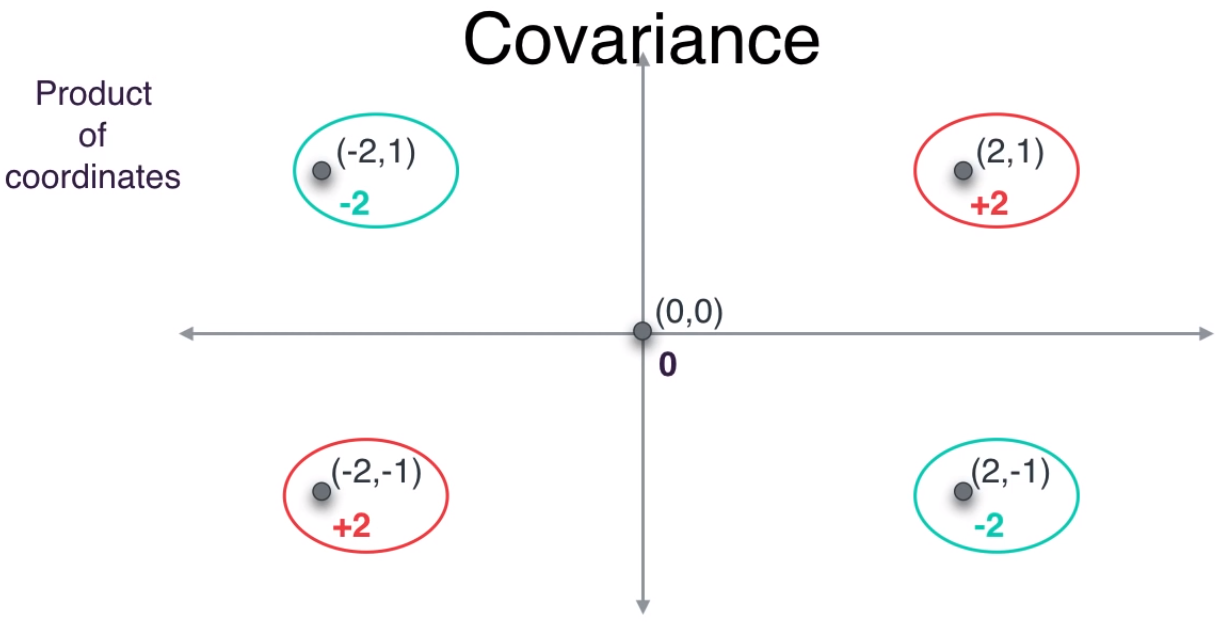
이번에는 방법을 바꿔서 두 좌표를 곱해보도록 하겠습니다. 그러면 빨간색으로 표시한 부분은 곱의 결과가 양수이고 초록색으로 표시한 부분은 곱의 결과가 음수인 것을 확인할 수 있습니다. 즉, 두 분포의 결과가 구분이 됩니다.

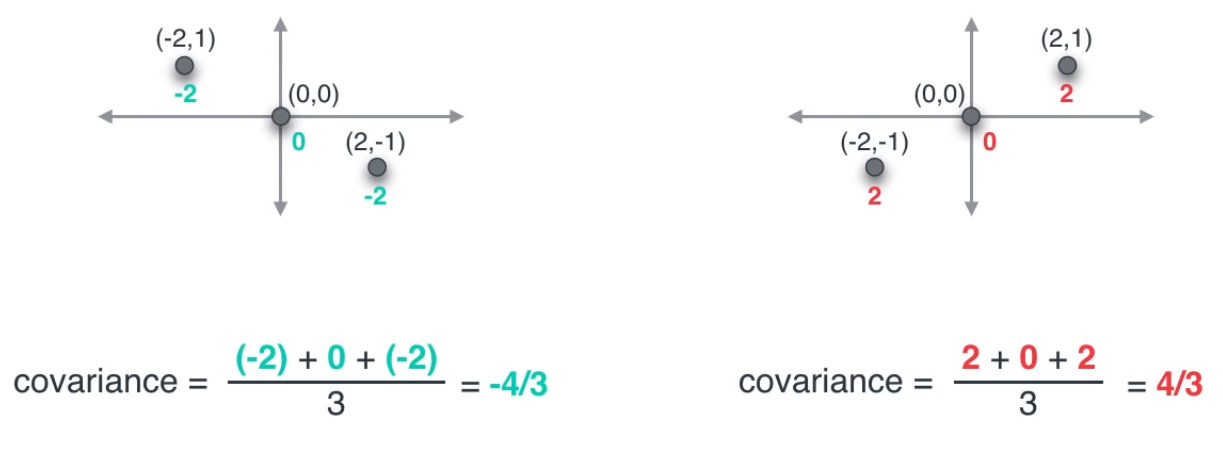
앞에서 설명한 방법과 같이 두 좌표의 곱을 통하여 분산을 구하면 위 그림과 같이 구할 수 있습니다.
공분산은 위 계산법과 같이 각 축 (feature)에 해당하는 두 값 (위에서는 X 좌표값, Y 좌표값)들을 곱한 뒤, 곱한 값들을 모두 더한 후 데이터의 갯수만큼 나누는 방법을 취합니다.
특히 각 축 (feature)에 대한 평균을 구한 다음에 모든 데이터에 평균값을 빼주면 위 그림 처럼 평균이 0인 상태로 만들 수 있습니다.
따라서 모든 데이터를 위 그림 처럼 평균은 원점이고 두 축에 의해 좌표 평면으로 나타낼 수 있습니다.

위 그림과 같은 분포를 앞에서 다룬 방식으로 분산을 구해보면 위 그림의 식과 같이 구할 수 있습니다.
앞에서 설명한 것과 같이 분산은 데이터들이 평균으로 부터 얼만큼 떨어져 있는지를 나타냅니다. 하지만 공분산의 의미는 조금 다릅니다. 공분산에서 계산한 값은 두 축의 상관관계를 나타냅니다. 위 그림을 보면 데이터 전체의 평균이 0인 데이터 셋이 공분산 또한 0으로 계산되어 있습니다. 공분산이 0이면 두 축의 상관관계가 없다는 뜻입니다.
한 축의 값이 증가하더라도 다른 축이 같이 증가하거나 감소하는 경향이 없이 마치 원 처럼 균등하게 퍼져있습니다. 이런 경향에서는 데이터의 상관관계가 없다고 합니다.

위 그림과 같이 어떤 두 feature를 이용하여 데이터를 표현하였을 때, 음의 기울기를 가지는 형태의 분포를 가지면 두 feature의 공분산은 음수값을 가집니다. 반면 양의 기울기를 가지는 형태의 분포를 가지면 두 feature의 공분산은 양수값을 가집니다.
앞선 예제 처럼 공분산이 0이라면 어떤 상관관계를 가지지 않는 극단적인 상태입니다.
따라서 두 feature의 공분산의 절대값이 0에 가까울수록 두 feature는 상관관계가 없다는 뜻이고 0에서 멀어질수록 양의 방향 또는 음의 방향으로 상관관계를 가진다는 뜻입니다.

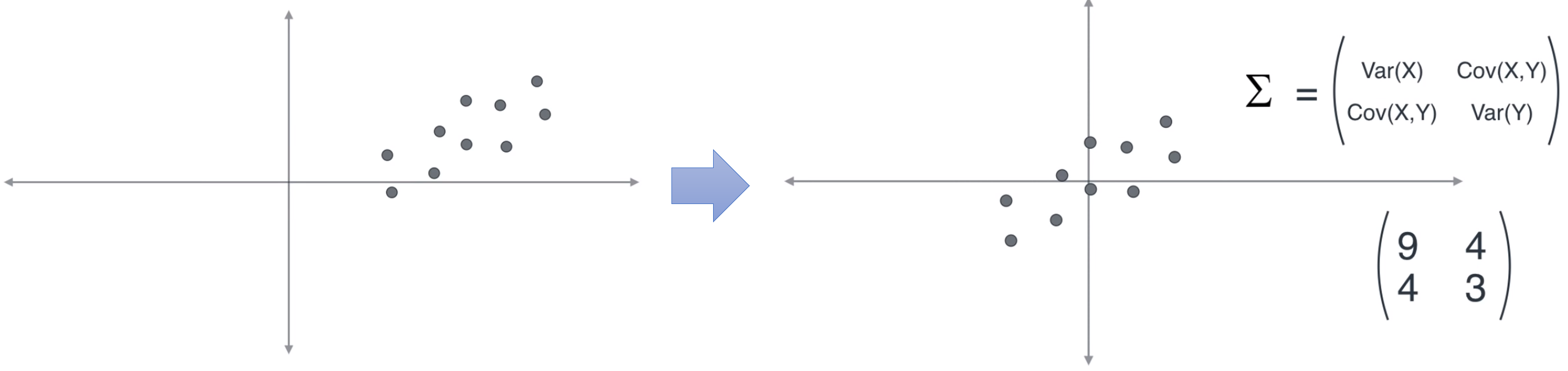
따라서 어떤 데이터가 있을 때, 그 데이터를 2개의 feature를 이용하여 표현하면 (현재 다루는 차원이 2차원 데이터 입니다.)위 그림과 같이 좌표 평면에 표시할 수 있습니다.
그러면 각 feature의 평균을 구해서 모든 데이터에 평균을 빼면 데이터 들을 원점 주변으로 모을 수 있습니다.
두 feature의 이름을 \(X, Y\) 라고 하면 총 4가지 경우의 feature 쌍을 만들 수 있습니다. \((X, X), (X, Y), (Y, X), (Y, Y)\) 4가지 쌍에 대하여 앞에서 설명한 방법으로 공분산을 구하면 다음과 같이 행렬 형태로 나타낼 수 있습니다.

\[\Sigma = \begin{pmatrix} \text{Cov}(X, X) & \text{Cov}(X, Y) \\ \text{Cov}(Y, X) & \text{Cov}(Y, Y) \end{pmatrix} = \begin{pmatrix} \text{Var}(X) & \text{Cov}(X, Y) \\ \text{Cov}(Y, X) & \text{Var}(Y) \end{pmatrix}\]

특히 \((X, X), (Y, Y)\) 같이 같은 차원의 공분산을 구하는 경우 분산을 구하는 것과 같습니다. 왜냐하면 같은 feature의 좌표를 두번 곱하기 때문에 제곱한 것과 같기 때문입니다. 즉, 실제 분산과 같기 때문에 위 식과 같이 정리됩니다.
따라서 공분산 행렬의 \((i, j)\) 성분은 \(i\) 번째 feature와 \(j\) 번째 feature의 상관관계를 나타내고 대각 성분은 같은 feature의 상관관계를 나타내기 때문에 양의 상관관계를 가집니다.
또한 공분산 행렬을 대칭 행렬입니다. \((i, j)\) 관계와 \((j, i)\) 관계가 서로 같기 때문입니다.
정리하면 공분산 행렬은 \(i, j\) 두 feature에 대한 데이터 상관관계를 수치적으로 나타내는 대칭 행렬 이며 각 항의 값이 0에 가까울수록 상관관계가 없으며 양의 값을 가지면 비례 관계, 음의 값을 가지면 반비례 관계를 가집니다.
그러면 위 데이터의 공분산이 \((9, 4; 4, 3)\)이라고 가정하고 설명을 계속 진행해 보겠습니다.

Linear Transformation

먼저 행렬의 주요한 성질인 고유 벡터와 고유 값의 뜻을 확인해보겠습니다. 먼저 행렬의 선형 변환 (Linear Transformation)의 주축을 고유 벡터 라고 합니다. 고유 벡터는 선형 변환을 하였을 때, 크기만 바뀌고 방향은 바뀌지 않는 벡터를 뜻합니다. 반면 행렬의 고유 값은 고유벡터의 방향으로 얼마 만큼 늘어뜨려줄 것인가를 의미합니다.
먼저 앞에서 공분산 개념을 도입한 이유는 공분산 행렬의 고유 벡터가 데이터 분포의 분산 방향이 되고 고유 값이 그 분산의 크기가 되기 때문입니다. 즉, 공분산의 고유벡터, 고유값을 이용하면 데이터가 어떤 방향으로 얼만큼 퍼져있는 지 알 수 있습니다. (이 글에서는 내용이 길어지니 직관적으로만 설명드리겠습니다. 공분산의 고유벡터를 구하는 이유는 제 블로그의 다른 글에서 자세히 다루겠습니다.)

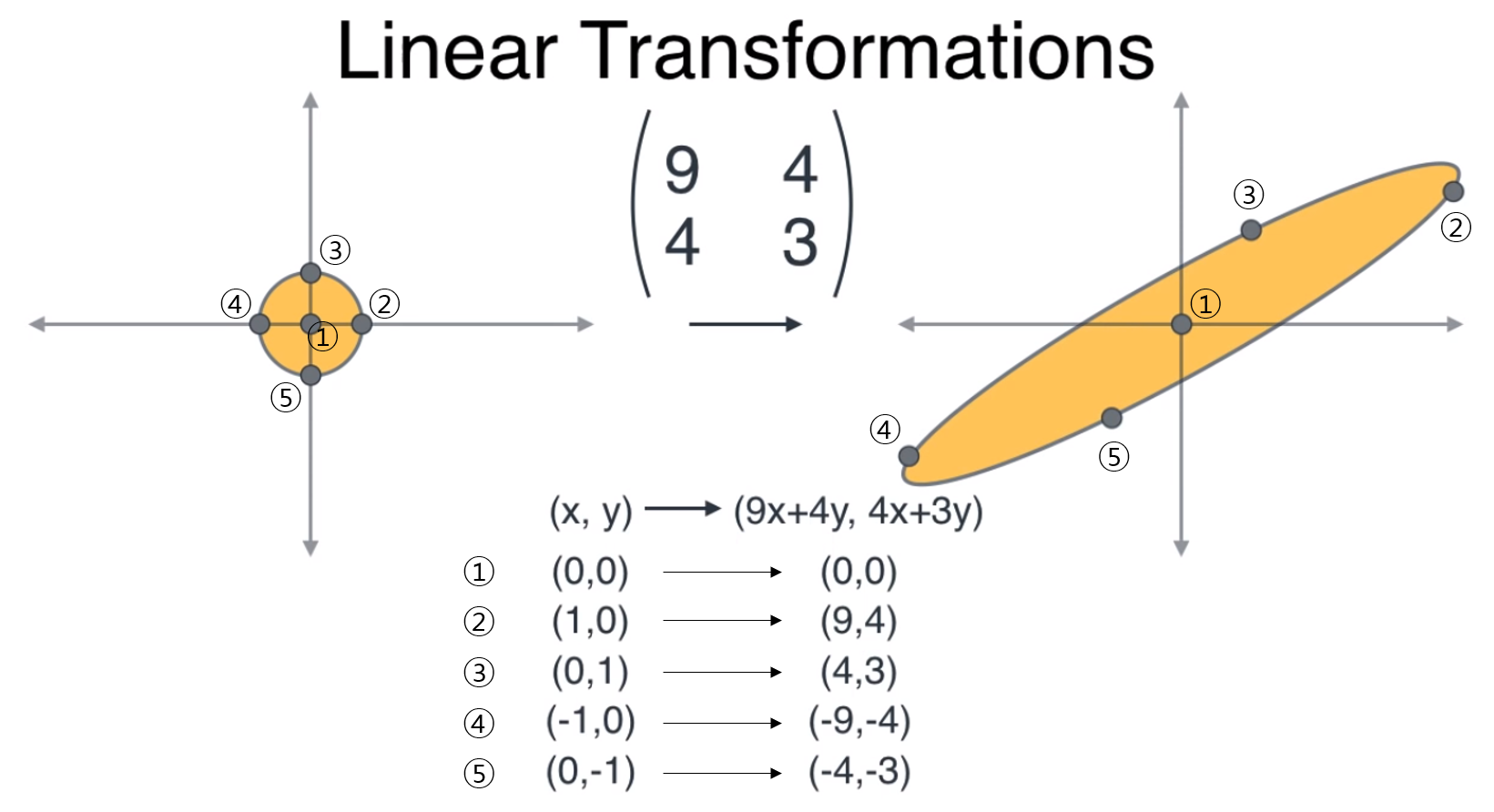
그러면 선형 변화의 개념 부터 간단하게 알아보도록 하겠습니다. 선형 변환은 간단하게 설명하면 한 좌표 평면에서 다른 좌표 평면으로 매핑 시키는 작업입니다.

\[\begin{pmatrix} 9 & 4 \\ 4 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 9x + 4y \\ 4x + 3y \end{pmatrix}\]

위 식에서 (9, 4; 4, 3) 행렬이 선형 변환 행렬입니다. 왜냐하면 \((x, y)\) 좌표를 \((9x + 4y, 4x + 3y)\)로 변환해 주고 그 변환 방식이 선형적이기 때문입니다.
왼쪽 좌표 평면의 원 안에 있는 모든 좌표는 오른쪽 좌표 평면의 타원안에 매핑됩니다. 마치 쭉 늘어뜨린 모양같습니다.

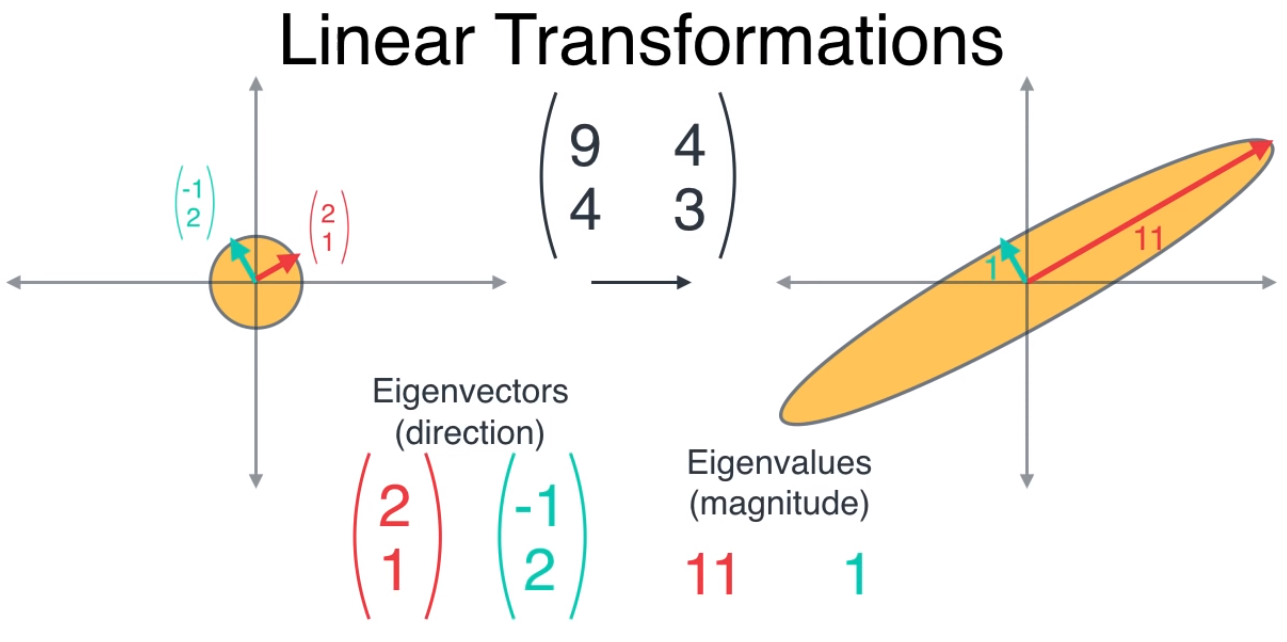
앞에서 설명한 바와 같이 고유벡터(eigenvector)는 선형 변환을 하더라도 그 방향성에는 변함이 없는 벡터를 말합니다.
위 그림을 보면 빨간색, 초록색 벡터는 그 크기는 다르더라도 벡터의 방향은 변함이 없습니다. 그리고 고유값은 고유 벡터의 방향으로 얼만큼 고유 벡터를 늘려줄 지에 대한 크기값입니다.

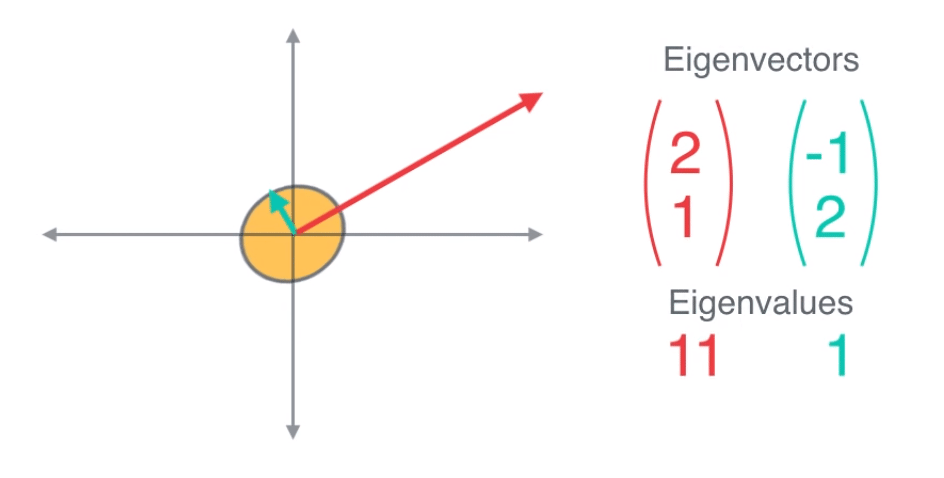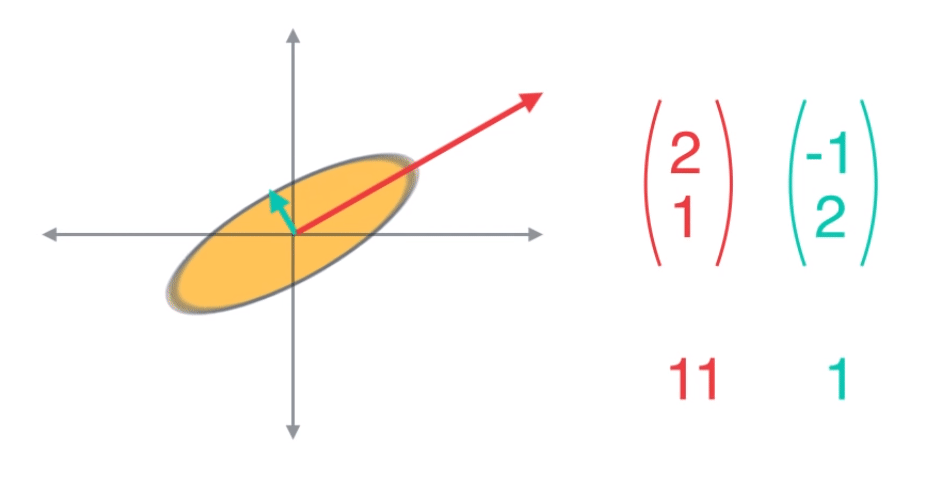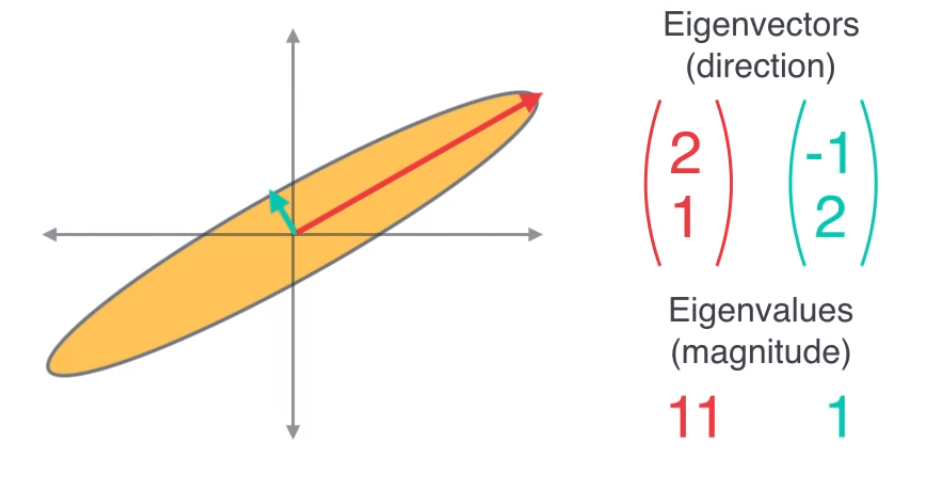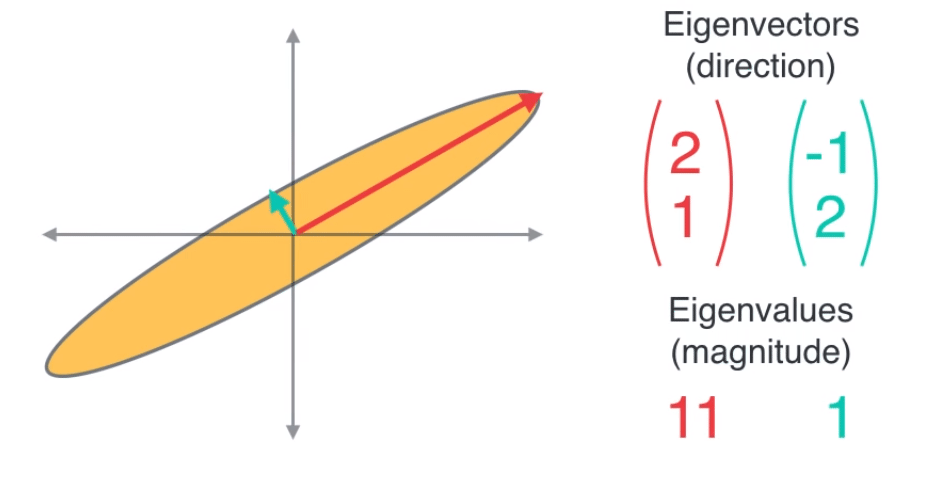
따라서 고유 벡터의 방향에 고유 값을 곱해주면 선형 변환된 축의 방향과 크기를 알 수 있습니다.

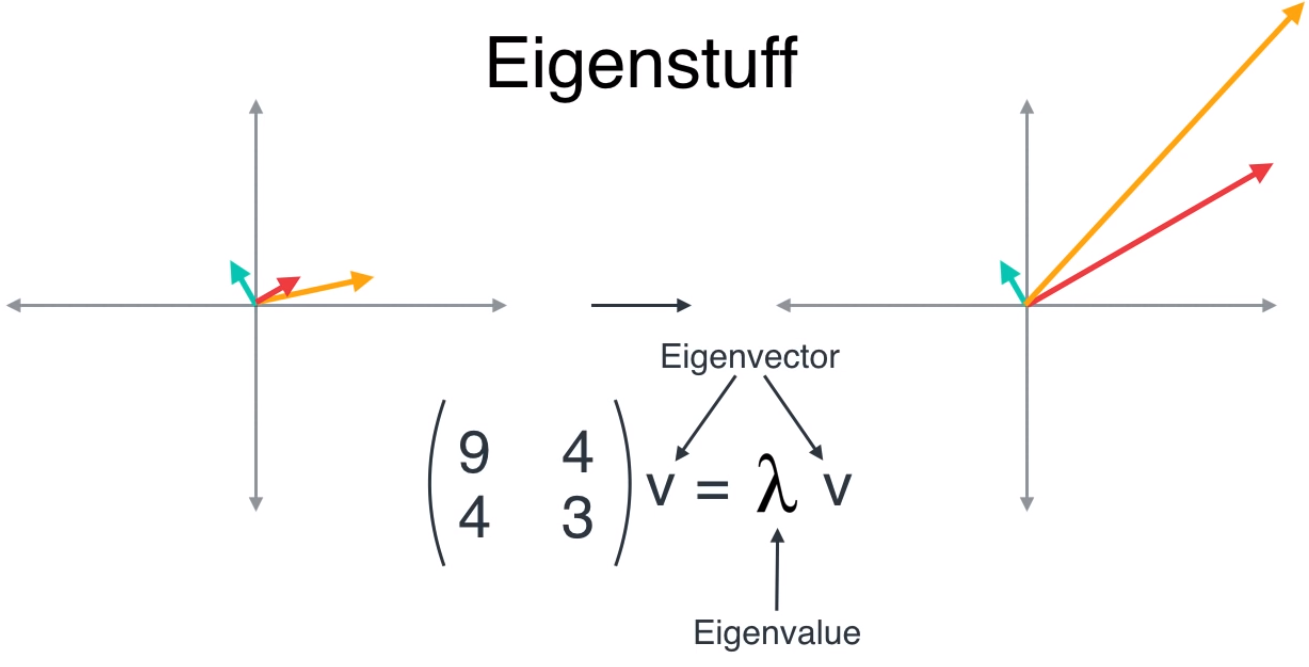
고유값과 고유벡터의 정의를 식을 통해 살펴보면 위 그림과 같습니다.
어떤 벡터 \(v\)를 선형 변환을 하면, 스칼라 값 \(\lambda\)를 이용하여 \(\lambda v\)로 나타낼 수 있을 때, \(v\)를 고유 벡터라고 하고 \(\lambda\)를 고유값이라고 합니다.
고유 벡터를 norm으로 나누어 정규화 하면 그 크기가 사라지므로 고유 벡터 \(v\)는 선형 변환 전 후가 완전히 동일해 집니다. 그리고 선형 변환 전 후의 크기 차이는 \(\lambda\)로 나타내 집니다.

고유 벡터를 구할 때, 일반적으로 사용하는 방식은 특성 방정식 입니다.

특성 방정식은 앞에서 다룬 고유 벡터와 고유값의 정의인 \(Av = \lambda v\)의 식을 풀어서 나타낸 것이고 위 예제처럼 풀 수 있습니다.
먼저 위 그림의 식을 보면 특성 방정식을 통하여 고유값을 구할 수 있습니다.

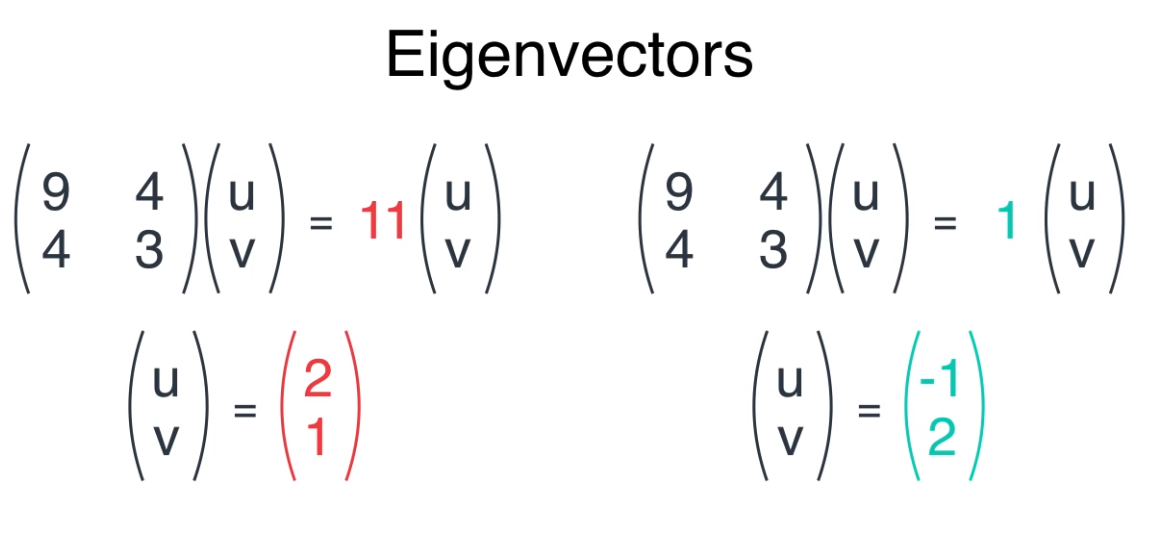
특성 방정식을 통해 구한 2개의 고유값을 이용하여 2개의 고유벡터를 구할 수 있습니다.

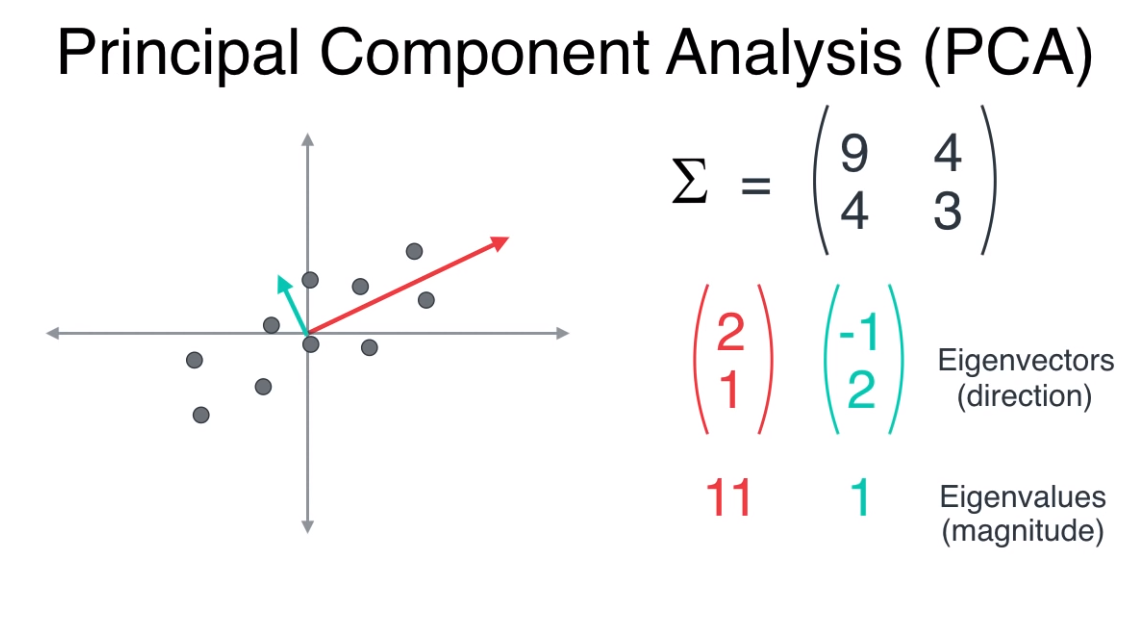
기존의 데이터에 고유 값을 반영한 고유벡터를 표시하면 위 그림의 빨간색, 초록색 벡터처럼 나타낼 수 있습니다.
빨간색 벡터의 고유값이 11배 정도 큽니다. 앞에서 설명한 바와 같이 고유값이 큰 고유벡터를 이용하여 새로운 차원을 만들면 넓은 분산의 축에 데이터를 표현하는 효과가 있어 데이터를 잘 나타낼 수 있음을 배웠습니다.
위 그림의 빨간색 벡터의 고유값이 더 크기 때문에 기존 데이터를 좀 더 잘 나타낼 수 있습니다. 따라서 고유값이 큰 빨간색 벡터를 새로운 축으로 정하게 됩니다.

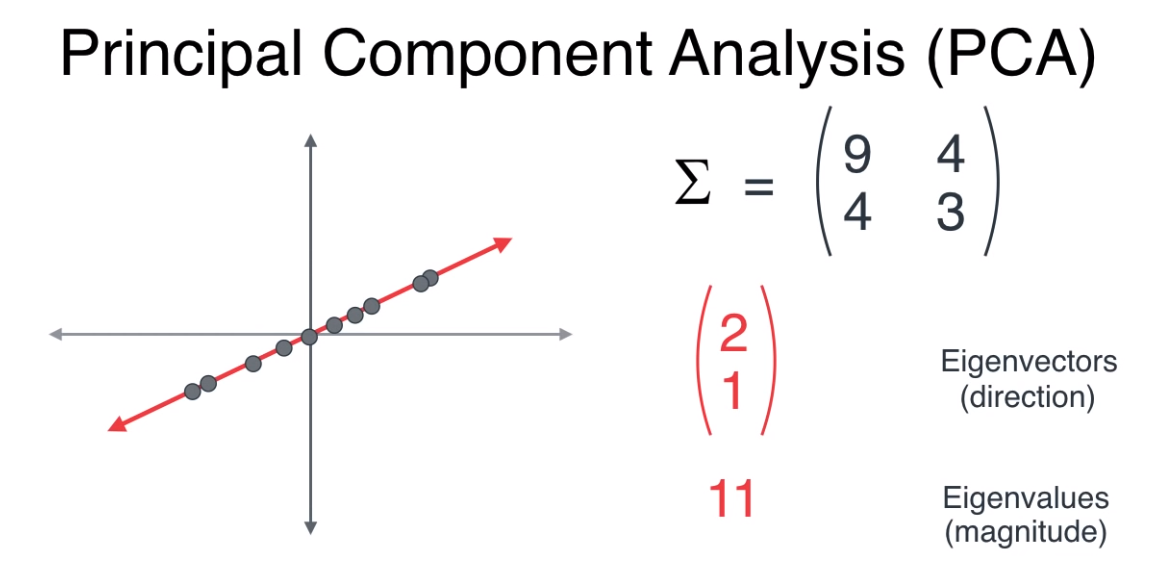
따라서 위 그림과 같이 빨간색 벡터가 고유벡터로 선정됩니다.
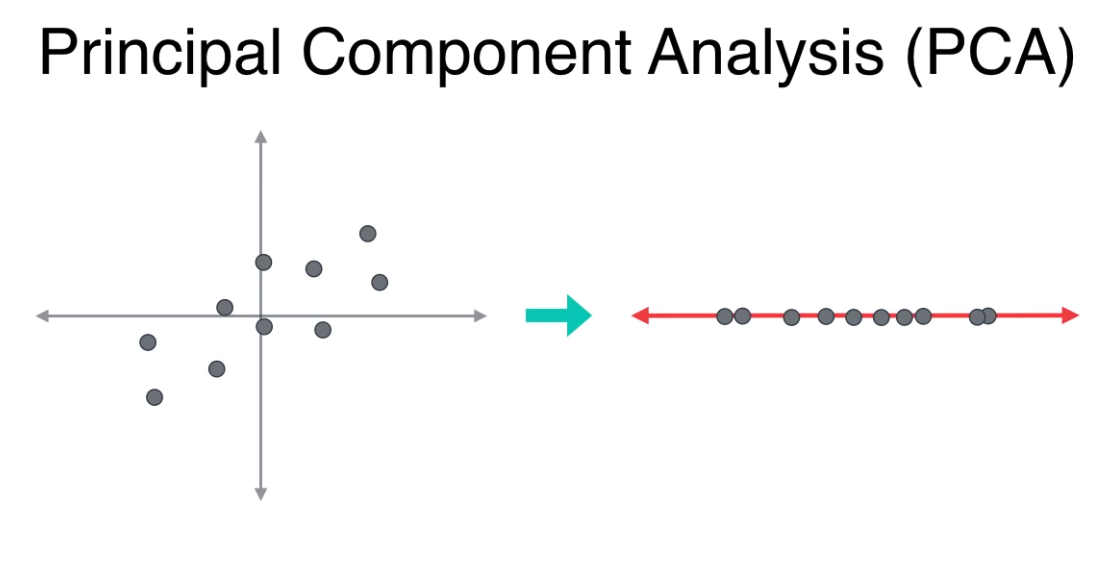
기존 데이터를 고유벡터인 빨간색 벡터로 정사영(projection) 한다면 위 그림과 같이 기존의 2 축 (x, y)를 한 개의 축으로 차원을 축소해서 나타낼 수 있습니다.

PCA process

그러면 앞에서 다룬 모든 절차를 정리하여 PCA의 과정을 다시 한번 설명해 보겠습니다.
① 위 그림의 Large Table과 같이 준비된 데이터가 있다고 가정해 보겠습니다. 위 데이터는 차원이 5개 (\(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\))이며 데이터의 갯수는 12개인 데이터셋 세입니다.
② \(n\) 개의 차원을 가진 데이터는 \(n \times n\) 크기의 공분산을 가집니다. 따라서 위 데이터는 5 x 5 크기의 공분산을 가집니다.
③ \(n\) 차원의 데이터는 최대 \(n\) 개의 고유값과 고유벡터를 가집니다. 모든 고유값과 고유벡터를 구한 다음에 고유값이 큰 순서로 정렬합니다.
④ \(n\) 차원의 데이터를 더 작은 차원인 \(k\) 차원으로 줄이기 위하여 \(k\)를 선정합니다. 만약 시각화를 위한 목적이라면 2차원이나 3차원으로 줄여서 사람이 보고 이해할 수 있는 차원으로 줄여야 합니다. 위 예제에서는 2차원으로 줄였습니다. 그러면 기존의 데이터를 선택된 2차원인 고유값과 고유벡터로 정사영 시킵니다.
⑤ 선택된 고유값, 고유벡터가 새로운 축이 되며 새로운 축을 기준으로 데이터를 정렬할 수 있습니다.

머신러닝 글 목록

목차

Dimensionality Reduction

Covariance

Linear Transformation

PCA process

Dimensionality Reduction

Covariance

Linear Transformation

PCA process