t-SNE 개념과 사용법

• 참조 : https://www.datacamp.com/community/tutorials/introduction-t-sne
• 참조 : https://www.youtube.com/watch?v=zpJwm7f7EXs&t=58s
• 참조 : https://blog.naver.com/PostView.nhn?blogId=yunjh7024&logNo=220832689977&proxyReferer=http:%2F%2Fm.blog.naver.com%2F
• 참조 : http://www.ktword.co.kr/abbr_view.php?m_temp1=1134
• 참조 : https://youtu.be/zCYKD3YfcSM
• 참조 : https://youtu.be/NEaUSP4YerM
• 참조 : https://youtu.be/MNfcUxmnRkQ
• 참조 : https://youtu.be/INHwh8k4XhM
• 참조 : 머신러닝 도감
• 참조 : https://learnopencv.com/t-sne-for-feature-visualization/
• 참조 : https://nextjournal.com/ml4a/image-t-sne

목차

• Dimensionality Reduction의 의미

• t-분포의 의미

• t-SNE의 의미와 기본적인 활용 방법

• t-SNE에 대한 수식적 의미

• Principal Component Analysis (PCA)와 파이썬에서의 사용법

• t-Distributed Stochastic Neighbor Embedding (t-SNE)와 파이썬에서의 사용법

• PCA와 t-SNE 의 visualization 차이점

• PCA와 t-SNE의 차이점 비교

Dimensionality Reduction의 의미

• 수많은 feature들을 가지고 있는 데이터셋을 이용하여 작업을 해보았다면, feature들 간의 관계를 파악하기가 어려운 것을 느꼈을 것입니다.
• 예를 들어 feature의 수가 너무 많으면 머신 러닝 모델의 성능을 저하시키곤 하고 feature의 갯수가 너무 많으면 overfit이 될 가능성이 있습니다.
• 머신 러닝에서 dimensionality reduction(차원 축소)는 중요한 feature의 갯수는 남기고 불필요한 feature의 갯수를 줄이는 데 사용되곤 합니다.
• 불필요한 feature의 갯수를 줄이는 방법으로 복잡한 feature들 간의 관계를 줄일 수 있고 2D, 3D로 시각화 할 수도 있습니다. 뿐만 아니라 앞에서 언급한 문제인 overfit을 방지할 수도 있습니다.
• Dimensionality Reduction은 다음과 같은 방법으로 사용 할 수 있습니다.
• ① Feature Elimination
  • Feature를 단순히 삭제하는 방법입니다. 이 방법은 간단하나 삭제된 feature들로 부터 어떠한 정보를 얻지는 못합니다.
• ② Feature Selection
  • 통계적인 방법을 이용하여 feature들의 중요도에 rank를 정합니다.
  • 이 방법 또한 information loss가 발생할 수 있으며 동일한 문제를 푸는 다른 데이터셋에서는 다른 rank를 매길 수 있다는 문제가 있을 수 있습니다.
• ③ Feature Extraction
  • 새로운 독립적인 feature를 만드는 방법이 있습니다.
  • 새로 만들어진 feature는 기존에 존재하였던 독립적인 feature들의 결합으로 만들어 집니다.
  • 이 방법에는 linear한 방법과 non-linear한 방법들로 나뉘어 집니다.

t-분포의 의미

• t-분포의 정확한 수식적 유도를 확인하려면 다음 글에서 확인 하시면 알 수 있습니다.
  • 링크 : https://gaussian37.github.io/math-pb-distribution_of_sampling_variance_and_t_distribution/
• 너무 상세한 내용이 아닌 대략적인 t-분포의 의미에 대해서는 이 글에서 설명해 보겠습니다.
• t-분포는 소 표본 (n < 30)으로 모 평균 추정하고 모집단이 정규분포와 유사함을 알고 있으나 모 표준편차를 모를 때 주로 사용합니다.
• t 분포의 이름은 Student 라는 가명을 사용한 이름의 학자가 발표한 Student t-분포에서 이름을 따왔습니다.

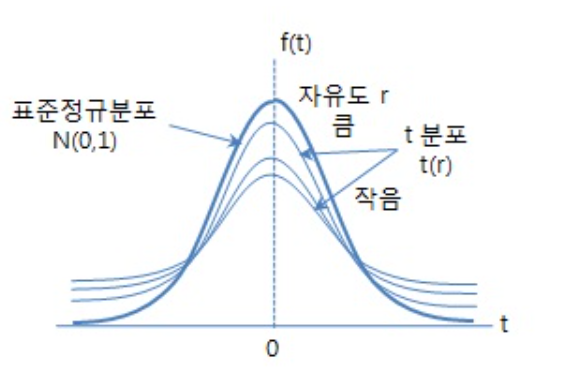
• t-분포는 표준 정규분포와 유사하게 0을 중심으로 좌우 대칭 형태를 이루며 표준 정규분포보다 평평하고 기다른 꼬리 형태를 가집니다. 즉, 양쪽 꼬리 형태가 두터운 형태를 가집니다. 이와 같은 형태를 가지는 이유는 표준 정규분포보다 분산이 크기 때문입니다.
• 정규분포는 평균과 분산을 통하여 그 형태가 달라지게 됩니다. 반면 t-분포는 자유도에 따라 다른 모양을 나타냅니다. 이 점은 카이 제곱 분포와 유사하다고 말할 수 있습니다. 자유도 = 표본의 수 -1로 정의되며 자세한 의미는 위에서 언급한 상세 내용 링크에서 확인할 수 있습니다. 이 자유도가 점점 더 커질수록 표준 정규분포에 가까워지고 대개 자유도가 30이 넘으면 표준 정규분포와 가까워지기 때문에 표본이 30이 넘어가게 되면 정규 분포를 사용하고 표본이 30 보다 작으면 t-분포를 사용하는 것이 일반적인 사용법입니다.

• t-분포에서 확률 변수를 \(T\)로 표현하면 \(T\)는 모평균 \(\mu\)의 추정에 사용되는 추정 통계량을 의미합니다. 이는 표준정규분포에서 표준화 변량인 \(Z\)와 같이 표본 평균 \(\bar{X}\)를 변환한 것과 같은 의미입니다.

• \[T = \frac{\bar{X} - \mu}{s / \sqrt{n}}\]

• 　\(n\) : 표본 수
• 　\(n - 1\) : 자유도
• 　\(\bar{X}\) : 표본 평균
• 　\(\mu\) : 모 평균
• 　\(s\) : 표본의 표준편차

• 정리하면 t-분포는 자유도 = 표본 수 - 1라는 모수에 따라 그 분포가 달라지며, 자유도가 30 이하이면 표준정규분포 보다 분산이 커져서 평평한 모양이 되고, 30이 넘으면 표준 정규분포와 비슷해지며 120 이상이 되면 표준정규분포와 완전히 같아집니다.

t-SNE의 의미와 기본적인 활용 방법

• t-distributed stochastic neighbor embedding 소위 t-SNE라고 불리는 방법은 높은 차원의 복잡한 데이터를 2차원에 차원 축소하는 방법입니다. 낮은 차원 공간의 시각화에 주로 사용하며 차원 축소할 때는 비슷한 구조끼리 데이터를 정리한 상태이므로 데이터 구조를 이해하는 데 도움을 줍니다.

• t-SNE는 매니폴드 학습의 하나로 복잡한 데이터의 시각화가 목적입니다. 높은 차원의 데이터를 2차원 또는 3차원으로 축소시켜 시각화 합니다.
• t-SNE를 사용하면 높은 차원 공간에서 비슷한 데이터 구조는 낮은 차원 공간에서 가깝게 대응하며, 비슷하지 않은 데이터 구조는 멀리 떨어져 대응됩니다.

• 위 그림을 보면 왼쪽의 스위스 롤과 같은 3차원 데이터를 오른쪽과 같이 2차원 데이터로 차원을 축소해 볼 수 있습니다. 이 떄 사용되는 방법이 t-SNE입니다.
• t-SNE가 동작되는 전체적인 흐름은 다음과 같습니다.

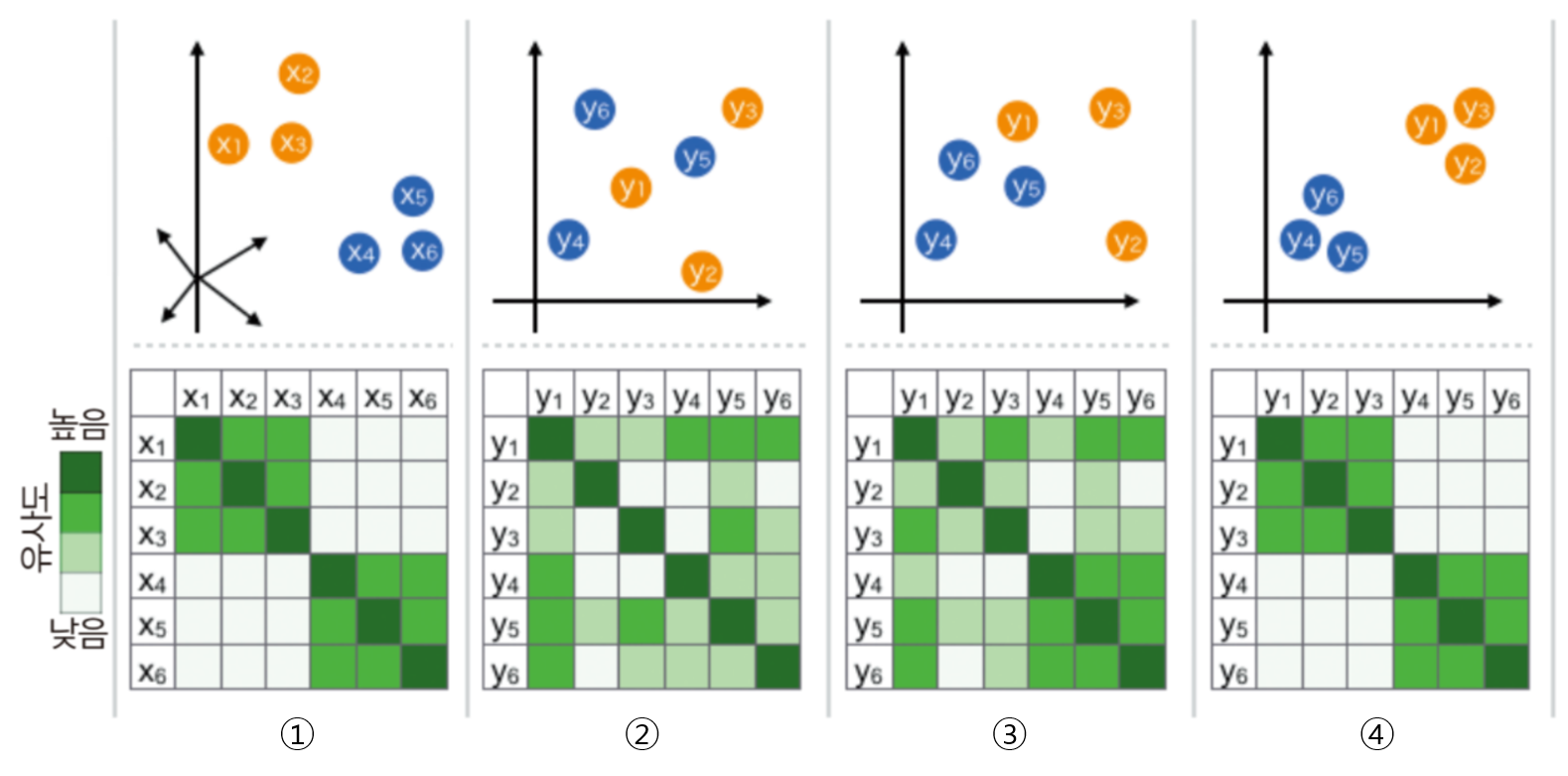
• 위 그림에서 \(x_{i}\)는 기존 데이터에 해당하며 고차원에 분포되어 있고 \(y_{i}\)는 t-SNE를 통하여 저차원으로 매핑된 데이터로 볼 수 있습니다. 위 예시에서 기존 데이터는 3차원이고 저차원은 2차원으로 사용되었습니다.
• ① 모든 \(i, j\) 쌍에 대하여 \(x_{i}, x_{j}\)의 유사도를 가우시안 분포를 이용하여 나타냅니다.
• ② \(x_{i}\)와 같은 개수의 점 \(y_{i}\)를 낮은 차원 공간에 무작위로 배치하고, 모든 \(i, j\) 쌍에 관하여 \(y_{i}, y_{j}\)의 유사도를 t-SNE를 이용하여 나타냅니다.
• ③ 앞의 ①, ②에서 정의한 유사도 분포가 가능하면 같아지도록 데이터 포인트 \(y_{i}\)를 갱신합니다.
• ④ 수렴 조건까지 과정 ③을 반복합니다.

• 위 알고리즘에서 ①, ②의 유사도는 데이터 포인트들이 얼마나 비슷한지 나타냅니다. 단순히 데이터 사이의 거리를 이용하는 것이 아니라 확률 분포를 이용합니다.

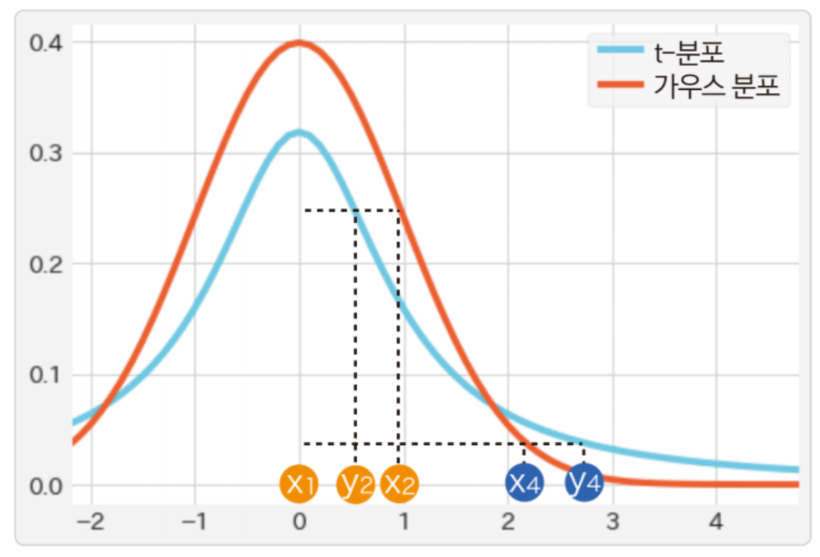
• 위 그래프는 가로축으로 거리, 세로축으로 유사도를 설정하여 t-분포와 가우시안 분포를 비교한 것입니다.
• 데이터 사이의 거리가 가까울수록 유사도가 크고, 멀수록 유사도가 작아집니다. 먼저 원본의 높은 차원 공간에서 정규 분포로 유사도를 계산하고 \(p_{ij}\)라는 분포로 나타냅니다. \(p_{ij}\)는 데이터 포인트 \(x_{i}, x_{j}\)의 유사도를 나타냅니다.
• 다음으로 \(x_{i}\)에 대응하는 데이터 포인트 \(y_{i}\)를 낮은 차원 공간에 무작위로 배치합니다. \(y_{i}\)에 관해서도 t-분포로 유사도를 나타내는 \(q_{ij}\)를 계산합니다.
• 여기서 \(p_{ij}\)와 \(q_{ij}\)를 계산하면 \(q_{ij}\)를 \(p_{ij}\)와 같은 분포가 되도록 데이터 포인트 \(y_{i}\)를 갱신합니다. 이는 높은 차원 공간의 \(x_{i}\) 유사도 각각의 관계를 낮은 차원 공간의 \(y_{i}\)에서 재현하는 것입니다. 이 때, 낮은 차원 공간에서 t-분포를 이용하므로, 유사도가 큰 상태의 관계를 재현할 때는 낮은 차원 공간에서 데이터 포인트를 더 가까이 배치합니다. 반대로 유사도가 작은 상태의 관계를 재현할 때에는 낮은 차원 공간에서 데이터 포인트를 더 멀리 배치합니다.

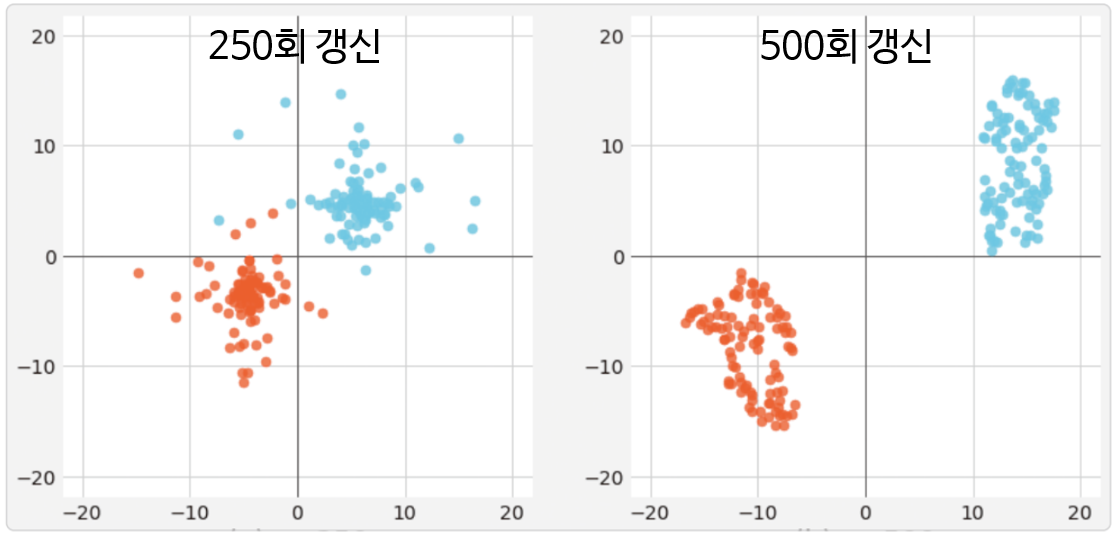
• 위 그림은 앞의 스위스 롤 데이터셋에서 t-sne를 적용하였을 때, 데이터 포인트 \(y_{i}\)를 갱신하는 모습입니다.
• 왼쪽 그래프는 갱신 횟수가 250회이고 오른쪽 그래프는 갱신 횟수가 500회 입니다. 갱신 횟수가 늘수록 데이터 포인트의 차이를 명확하게 나타냅니다.

• t-SNE에서 낮은 차원에 임베딩 할 때, 정규 분포를 사용하지 않고 t-분포를 사용합니다. 그 이유는 앞에서 다루었듯이 t-분포가 heavy-tailed distribution임을 이용하기 위해서 입니다. 즉, t-분포는 일반적인 정규분포보다 끝단의 값이 두터운 분포를 가집니다.
• t-SNE가 전제하는 확률 분포는 정규 분포이지만 정규 분포는 꼬리가 두텁지 않아서 i번째 개체에서 적당히 떨어져 있는 이웃 j와 아주 많이 떨어져 있는 이웃 k가 선택될 확률이 크게 차이가 나지 않게 됩니다. 또한 높은 차원 공간에서는 분포의 중심에서 먼 부분의 데이터 비중이 높기 때문에 데이터 일부분의 정보를 고차원에서 유지하기가 어렵습니다.
• 이러한 문제로 인하여 구분을 좀 더 잘하기 위해 정규 분포보다 꼬리가 두터운 t분포를 쓰게 되며 꼬리가 부분이 상대적으로 더 두텁게 degree of freedom = 1로 적용하여 사용합니다.
• 또한 앞에서 설명드린 바와 같이 t-분포도 마찬가지로 표본 평균, 표본 분산으로 정의되는 확률변수이기 때문에 표본의 수가 많아질수록 중심 극한 정리에 의해 결국에는 정규 분포로 수렴하게 됩니다. 이것은 t-SNE가 전제하는 확률 분포가 정규 분포인 점과 일맥상통 합니다.

t-SNE에 대한 수식적 의미

Principal Component Analysis (PCA)

• PCA는 Feature Extraction의 방법이고 linear한 방법을 사용합니다.
• PCA는 원본 데이터를 저차원으로 linear mapping 합니다. 이 방법으로 저차원에 표현되는 데이터의 variance가 최대화 됩니다.
• 기본적인 방법은 공분산 행렬에서 고유벡터를 계산하는 것 입니다.
• 가장 큰 고유값을 가지는 고유벡터를 principal component로 생각하고 새로운 feature를 생성하는 데 사용합니다.
• 위 방법을 이용하여 PCA는 입력 받은 데이터 들의 feature를 결합합니다.
  • feature들을 결합할 때, 가장 중요하지 않은 feature들은 제거해가고 가장 중요한 feature들은 남깁니다.
  • 새로 생성된 feature들은 기존의 feature들과 독립적입니다. 즉 기존 feature들의 단순 선형 결합으로 만들어진 것은 아닙니다.
• PCA에 대한 자세한 방법은 선형대수학 관련 기본 내용 또는 PCA 개념 설명 글을 참조하시기 바랍니다.

t-Distributed Stochastic Neighbor Embedding (t-SNE)

• t-SNE는 비선형적인 방법의 차원 축소 방법이고 특히 고차원의 데이터 셋을 시각화하는 것에 성능이 좋습니다.
• t-SNE는 다양한 분야에서 시각화 하는 데 사용되고 있습니다.
• t-SNE 알고리즘은 고차원 공간에서의 점들의 유사성과 그에 해당하는 저차원 공간에서의 점들의 유사성을 계산합니다.
  • 점들의 유사도는 A를 중심으로 한 정규 분포에서 확률 밀도에 비례하여 이웃을 선택하면 포인트 A가 포인트 B를 이웃으로 선택한다는 조건부 확률로 계산됩니다.
• 그리고 저 차원 공간에서 데이터 요소를 완벽하게 표현하기 위해 고차원 및 저 차원 공간에서 이러한 조건부 확률 (또는 유사점) 간의 차이를 최소화하려고 시도합니다.
• 조건부 확률의 차이의 합을 최소화하기 위해 t-SNE는 gradient descent 방식을 사용하여 전체 데이터 포인트의 KL-divergence 합계를 최소화합니다.
  • Kullback-Leibler divergence 또는 KL divergence는 한 확률 분포가 두 번째 예상 확률 분포와 어떻게 다른지 측정하는 척도입니다.
• 정리하면 t-SNE는 두가지 분포의 KL divergence를 최소화 합니다.
  • 입력 객체(고차원)들의 쌍으로 이루어진 유사성을 측정하는 분포
  • 저차원 점들의 쌍으로 유사성을 측정하는 분포
• 이러한 방식으로, t-SNE는 다차원 데이터를보다 낮은 차원 공간으로 매핑하고, 다수의 특징을 갖는 데이터 포인트의 유사성을 기반으로 점들의 클러스터를 식별함으로써 데이터에서 패턴을 발견합니다.
• 하지만 t-SNE 과정이 끝나면 input feature를 확인하기가 어렵습니다. 그리고 t-SNE 결과만 가지고 무언가를 추론 하기는 어려움도 있습니다.
  • 따라서 t-SNE는 주로 시각화 툴로 사용 됩니다.

파이썬을 이용한 t-SNE 구현 방법

• T-SNE를 사용하기 위해서 대표적으로 sklearn에 구현된 T-SNE를 많이 사용합니다.
• 매뉴얼 : https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html
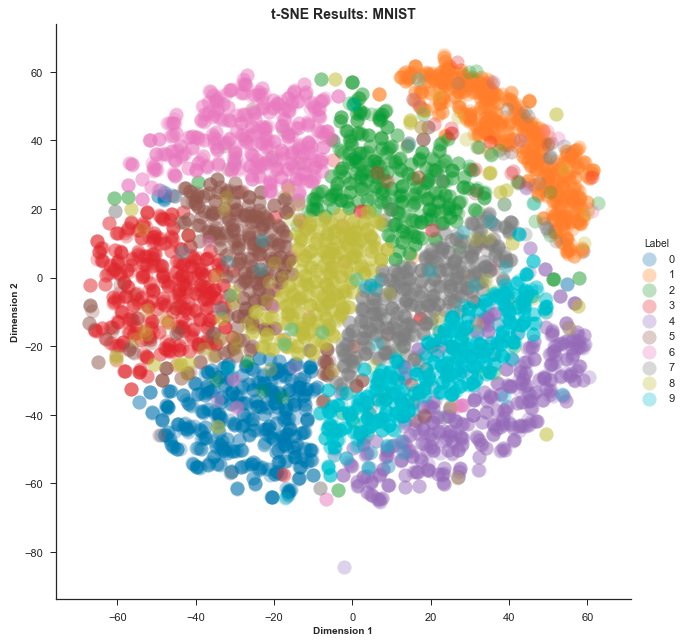
• 먼저 MNIST 데이터를 이용하여 시각화 하는 방법에 대하여 살펴보도록 하겠습니다. sklearn을 통하여 TSNE를 사용합니다.

from sklearn.manifold import TSNE
from sklearn.datasets import load_digits

# MNIST 데이터 불러오기
data = load_digits()

# 2차원으로 차원 축소
n_components = 2

# t-sne 모델 생성
model = TSNE(n_components=n_components)

# 학습한 결과 2차원 공간 값 출력
print(model.fit_transform(data.data))
# [
#     [67.38322, -1.9517338],
#     [-11.936052, -8.906425],
#     ...
#     [-10.278599, 8.832907],
#     [25.714725, 11.745557],
# ]

• 위 코드에서는 MNIST 이미지를 받아서 2차원으로 차원 축소하므로 그 결과 2차원 좌표계에서 각 데이터의 좌표값이 출력됩니다.

• 위 시각화 결과는 왼쪽부터 차례로 PCA, Local Linear Embedding, T-SNE 결과를 나타냅니다. PCA와 Local Linear Embedding은 차원 축소 방법을 선형적으로 접근하지만 T-SNE는 비선형적으로 접근하기 때문에 표현력이 증가됩니다. 따라서 위 시각화 결과와 같이 T-SNE는 클래스 간 분별력이 있게 시각화 할 수 있습니다.

• 위 예제 코드에서 입력된 n_components는 축소할 차원을 정하는 것이기 때문에 반드시 필요합니다. 반면 다른 파라미터는 차원 축소를 좀 더 잘 하기 위한 파라미터로 반드시 필요한 것은 아니나 사용 방법은 반드시 숙지해 놓는 것이 알고리즘을 이해하는 데에도 도움이 됩니다.
• T-SNE 함수에 사용되는 대표적인 옵션은 다음과 같습니다. 일부 생략된 옵션은 공식 문서를 참조하시기 바랍니다.
  • 링크 : https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html

• n_components
• 데이터 타입 : int
• 기본값 : 2
• 의미 : 차원 축소 결과 임베딩되는 차원

• perplexity
• 데이터 타입 : float
• 기본값 : 30.0
• 의미 : 다른 manifold learning의 nearest neighbors 갯수에 사용되는 값을 뜻합니다. 일반적으로 더 큰 데이터 셋은 보통 더 큰 perplexity 값을 필요로 합니다. 이 값을 정할 때, 5 ~ 50 사이의 값을 선택해 보고 더 좋은 결과를 얻기 위해서 값을 변경해 가면서 조정할 필요가 있습니다.

• early_exaggerattion
• 데이터 타입 : float
• 기본값 : 12.0
• 의미 : 기존 공간에서 데이터의 클러스터 간 거리가 타겟 공간에서 얼만큼 조밀하거나 먼 지 나타내는 파라미터 입니다. 이 값을 큰 값으로 설정할 경우 기존 공간의 클러스터 사이의 공간이 타겟 공간에서 더 커지도록 학습됩니다. 이 매개 변수의 선택은 크게 중요하지는 않으나 학습 초기에 비용 함수가 증가하면 early_exaggeration 또는 initial learning rate가 너무 높을 수 있으니 이 경우 살펴 보면 됩니다.

• learning_rate
• 데이터 타입 : float
• 기본값 : 200.0
• 의미 : 학습을 할 때 사용하는 learning rate 이며 일반적으로 10 ~ 1000 사이의 값을 가집니다. learning rate가 너무 높으면 데이터가 가장 가까운 이웃과 거의 같은 거리에있는 ‘공’처럼 보일 수 있습니다. 반면 learning rate가 너무 낮으면 대부분의 포인트가 특이치가 거의 없는 조밀 한 클라우드에서 압축 된 것처럼 보일 수 있습니다.

• n_iter
• 데이터 타입 : int
• 기본값 : 1000
• 의미 : 최적화를 위한 최대 반복 횟수입니다. 이 값은 최소 250 이상이어야 학습하는 데 지장이 없습니다.

• n_iter_without_progress
• 데이터 타입 : int
• 기본값 : 300
• 의미 : 성능 개선 없이 학습이 지속되면 학습을 중지하는 옵션이며 카운트는 50의 배수 단위로 카운트 됩니다.