1.1. 다항식 곡선 피팅 예시
2019, Jan 10
본 글의 내용 및 이미지는 Pattern Recognition and Machine Learning (Christopher M. Bishop)의 책의 내용을 사용하였습니다.
머신 러닝(패턴 인식)에 대한 소개
- Rule 기반 : 사람이 직접 규칙성을 만드는 방법
- 수 많은 규칙 및 예외 사항 발생 할 수 있습니다.
- 머신 러닝(패턴 인식) : 데이터의
규칙성을 자동적으로 찾아내고 이 규칙성을 이용하여 데이터를 각각의카테고리로 분류하는 일을 뜻합니다.- 데이터들을
훈련 집합(training set)으로 활용하여 변경 가능한 모델의매개변수들을 조절하는 방법 입니다. - 분류 해야 할 정답 값을
표적 벡터(target vector)라고 합니다.
- 데이터들을
- 머신러닝 알고리즘
- y(x)라는 함수 형태로 정의 할 수 있고 이 때, x는 입력되는 데이터 입니다.
- 학습 단계(learning, training, …)에서는
training set을 이용하여 y(x) 함수의 형태가 결정 됩니다. - 시험 단계에서는
test set이라는training set에서는 전혀 사용되지 않았던 데이터를 이용하여 성능을 테스트 합니다.- 시험 단계에서 좋은 성능을 얻었다면 모델은
일반화(generalization)에 성공하였다고 볼 수 있습니다. - 머신러닝에서 가장 중요한 것인
일반화성능 입니다.
- 시험 단계에서 좋은 성능을 얻었다면 모델은
- 입력 변수에 대한
전처리(preprocessing)을 하면 좀 더 간단한 변수 공간으로 전환할 수 있어 문제를 쉽게 풀 수 있습니다. - 변수 공간의 가변성을 줄이기 위해
특징 추출(feature extration)이 필요합니다.특징 추출을 하여 변수 공간을 간단하게 만드는 방법으로차원 감소(dimensionality reduction)이 있습니다.차원 감소를 통하여 계산 과정의 속도 또한 빨라질 수 있습니다.차원 감소를 잘못하게 되면 중요한 정보가 소실 될 수 있는 문제도 있습니다.
- 전처리는
training set에 적용을 하였으면test set에도 그대로 적용해야 합니다.
머신러닝의 분류
- 지도 학습
- 훈련 데이터가
Input vector와 그에 해당하는target vector가 있는 경우에 해당합니다. classification:target의 값이 discrete 한 문제에 해당합니다.- 예시 : 숫자 분류
regression:target의 값이 continuous 한 문제에 해당합니다.- 예시 : 온도, 농도, 압력 예측
- 훈련 데이터가
- 비지도 학습
- 훈련 데이터가 오직
input vector로만 이루어진 경우에 해당합니다. clustering: 데이터 내에서 비슷한 예시들의 집단을 찾는 문제입니다.density estimation: 입력 공간에서 데이터의 분포를 찾습니다.visualization: 높은 차원의 데이터를 저차원(2,3 차원)에 투영하여 이해하기 쉽게 보여주는 방법입니다.
- 훈련 데이터가 오직
강화 학습은 이 책에서 다루지 않을 계획입니다.
다항식 곡선 피팅 예시
- 실수값의 Input variable인 x를 관찰한 후 실수 값의 Target variable인 t를 예측하려고 합니다.
- 이 때, \(sin(2\pi x)\) 함수를 이용하여 Target variable을 구성하였고, Target variable t에는 약간의 노이즈를 첨가하였습니다.
- N개의 데이터 셋이 있다면 Training set과 Target set은 다음과 같습니다.
- Training set : \(\mathbf x = (x_{1}, ..., x_{N})^{T}\)
- Target set : \(\mathbf t = (t_{1}, ..., t_{N})^{T}\)
- = sin(2\(\pi\) * Training set) + gaussian noise
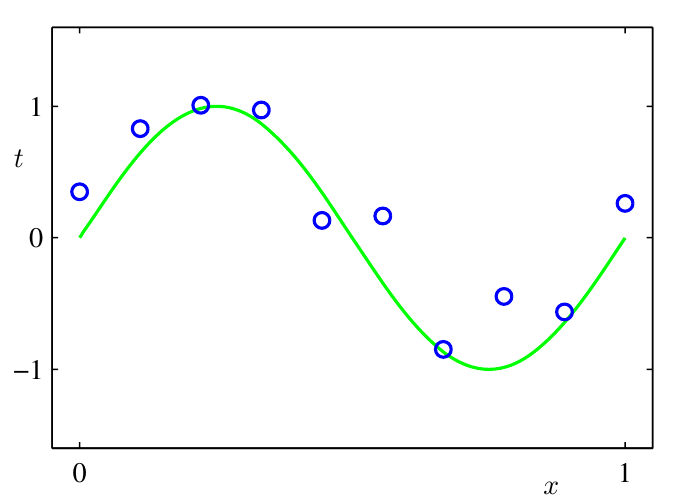
- 위 그림은 N = 10인 경우에 훈련 데이터 집합 예시 입니다.
- 녹색 곡선이 \(sin(2 \pi x)\) 에 해당합니다.
- 녹색 커브에 대한 지식이 없는 상태에서 파란색 점인 target을 예측해야 합니다.
- 모델링의 어려운 점
- 제한된 데이터를 이용하여 일반화 할 수 있는 모델을 만드는 것이 어려운 문제 입니다.
- 관측 값들이 노이즈로 인해 변질 되어 있을 수가 있습니다.
- 문제점들의 대책
확률론을 통해 불확실성을 정량화- ` 의사 결정 이론`을 통해 최적의 예측
- 위의 곡선을 fitting 하기 위해 다항식을 만들어 보겠습니다.
[y(x, w) = w_{0} + w_{1}x + w_{2}x^{2} + … + w_{M}x^{M} = \sum_{j=0}^{M}w_{j}x^{j}]
- 다항 함수 y(x, w)은 x에 대해서는
비선형이지만 계숙 w에 대해서는선형입니다.- 다항 함수와 같이 알려지지 않은 변수에 대해 선형인 함수들을
선형 모델이라고 합니다.
- 다항 함수와 같이 알려지지 않은 변수에 대해 선형인 함수들을
- 다항식을 훈련 집합 데이터에 피팅해서
계수의 값들을 정할 수 있고, 이 때 target 값과 y(x, w) 값의 차이를 줄이기 위해error function을 사용할 수 있습니다.- 예시 : \(E(w) = \frac{1}{2} \sum_{n=1}^{N} \{y(x_{n}, w) - t_{n} \}^{2}\)
- 이 함수의 값은 항상 0보다 크거나 같으며 정확히 \(y(x_{n}, w) - t_{n}\) 인 경우만 0이 됩니다.
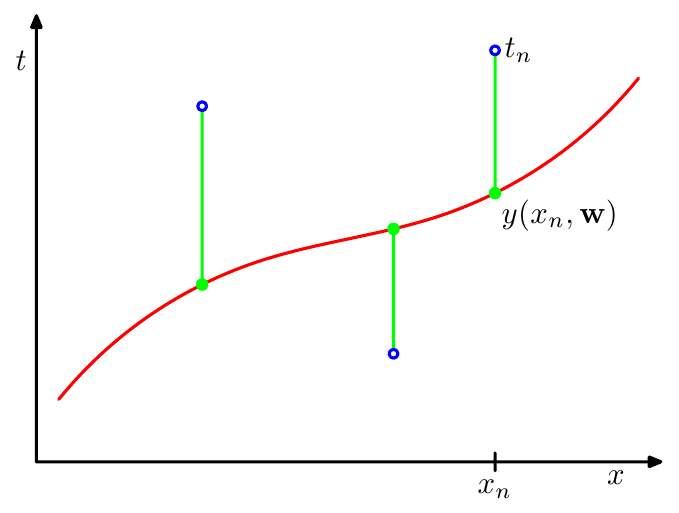
- E(w) 식의 오차는 각각의 데이터 포인트와 y(x, w)간의 간격 (녹색 선)의 제곱값에 해당합니다.
- E(w)가 이차 다항식이므로 미분을 하여 최소값을 찾을 수 있습니다.
- 이 방법으로 구한 \(w^{*}\) 가 E(w)를 최소화하므로 일반화에 적합한 다항식의 계수임을 알 수 있습니다.
- 예시 : \(E(w) = \frac{1}{2} \sum_{n=1}^{N} \{y(x_{n}, w) - t_{n} \}^{2}\)
-
y(x, w) 다항식을 정의할 때 몇 차수 까지 정의해야 할까요? 즉, 다항식의 차수 M을 결정해야 하는 문제가 있습니다.
-
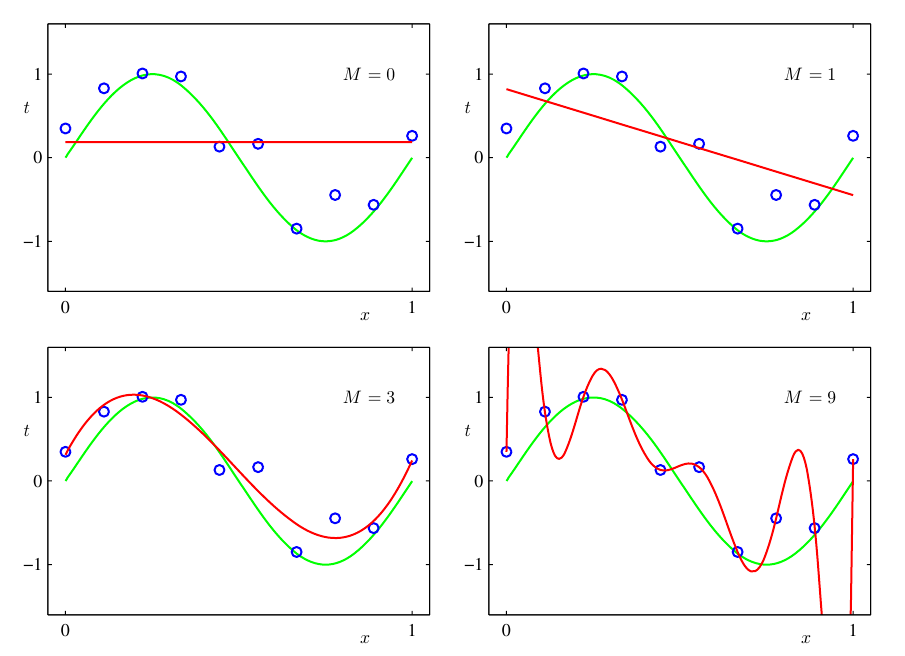
- M = 0, 1 일 때에는 \(sin(2\pi x)\) 함수를 잘 표현하지 못하였습니다.
- M = 3 일 때에는 \(sin(2\pi x)\) 함수와 가장 비슷하게 표현되어 있습니다.
- M = 9 일 때에는 모든 Training set에 대하여 정확하게 fitting 하여 \(E(w^{*}) = 0\) 이지만 이 때를
overfitting이라고 합니다.- fitting의 목표는
일반화인데, 일반화에 실패한 케이스 입니다.
- fitting의 목표는