2.1. 이산확률분포

밀도 추정(density estimation) : 관찰 집합 \(x_{1}, x_{2}, ... , x_{N}\)이 주어졌을 때, 확률 변수 x의 확률 분포 p(x)를 모델링 하는것
밀도 추정 문제를 풀기 위하여 데이터 포인트들은 독립적이며 동일하게 분포되어 있다고 가정합니다.
제한된 수의 관찰 데이터 집합으로부터 적절한 분포를 선택하는 것은 모 확률 분포의 가짓수가 무한대이므로 추정하는 것이 사실상 어렵습니다.
- 모델 선택의 문제와 연관되어 있습니다.
2.1과 2.2에서 살펴볼 확률 분포는 이산확률변수의 분포와 연속확률변수의 분포 입니다.
- 이산확률변수의 분포
  - 이항 분포
  - 다항 분포
- 연속확률변수의 분포
  - 가우시안 분포
- 이산확률변수의 분포와 연속확률변수의 분포 모두 매개변수적 분포입니다.
  - 분포가 매개변수에 의해 결정됩니다.
  - 매개변수는 어떻게 결정 될까요?
    - 빈도적 관점 : 가능도함수 최적화 방법 이용
    - 베이지안 관점 : 사전분포 기준으로 사후분포를 계산
켤레 사전 확률 : 사후 확률이 사전 확률과 같은 함수적 형태
- 사전 확률 : 디리클레 분포 → 사후 확률 : 다항 분포
- 사전 확률 : 가우시안 분포 → 사후 확률 : 가우시안 분포
- 켤레 사전 확률을 가지는 분포들은 지수족(exponential family)에 속합니다.
매개변수적인 접근법의 한계점
- 분포가 특정한 함수의 형태를 띠고 있다고 가정한다는 것
매개변수적인 접근법의 대안으로 비매개변수적 밀도 추정을 하기도 합니다.
- 비매개변수적 밀도 추정은 분포가 특정한 함수의 형태를 띄지 않습니다.
- 분포의 형태가 데이터 집합의 크기에 종속적 입니다.
- 매개변수가 분포의 형태를 결정 짓는것이 아니라 모델의 복잡도에 영향을 미칩니다.

2.1 이산 확률 변수

특수한 동전의 동전 던지기를 할 때, 앞면이 나올 확률과 뒷면이 나올 확률이 동일하지 않을 수 있습니다.
x = 1일 확률을 매개변수 \(\mu\) 를 통해 다음과 같이 표현할 수 있습니다.
- ·\(p(x=1 \vert \mu) = \mu, (0 \ge \mu \le 1)\)
- ·\(p(x=0 \vert \mu) = 1 - \mu\)’
위의 이산형 분포는 다음과 같이 베르누이 분포로 정의할 수 있습니다.
- ·\(Bern(x \vert \mu) = \mu^{x}(1-\mu)^{1-x}\)
- 베르누이 분포는 정규화되어 있으며, 그 평균과 분산이 다음과 같이 주어집니다.
  - ·\(\mathbb E[x] = \mu\)
  - ·\(var[x] = \mu(1 - \mu)\)
- x의 관측값 데이터 집합 \(D = {x_{1}, x_{2}, ..., x_{N}}\) 에서
- 관측값들이 \(p(x \vert \mu)\) 에서 독립적으로 추출되었다면 \(\mu\)의 함수로써 가능도 함수를 구할 수 있습니다.
- ·\(p(D \vert \mu) = \prod_{n=1}^{N} p(x_{n} \vert \mu) = \prod_{n=1}^{N} \mu^{x_{n}}(1-\mu)^{1 - x_{n}}\)
- 빈도적 관점에서는 가능도 함수를 최대화하는 \(\mu\)를 찾아서 \(\mu\)의 값을 추정할 수 있습니다.
  - 베르누이 분포의 경우 로그 가능도 함수로 표현할 수 있습니다.
  - ·\(ln p(D \vert \mu) = \sum_{n=1}^{N} ln p(x_{n} \vert \mu) = \sum_{n=1}^{N}\{x_{n}ln\mu + (1 - x_{n})ln(1-\mu)\}\)
    - 로그 가능도 함수는 오직 관측값들의 합인 \(\sum x_{n}\)을 통해서만 N개의 관측값과 연관됩니다.
  - ·\(ln p(D \vert \mu)\)를 \(\mu\)에 대해 미분하고 이를 0과 같다고 놓으면 다음과 같습니다.
    - 상세 연산은 울프람 알파를 이용해 보세요.
    - ·\(\mu_{ML} = \frac{1}{N} \sum_{n=1}^{N} x_{n}\)
      - 이 식을 표본 평균 이라고 합니다.
    - 데이터 x = 1(이산 확률 0, 1)인 관찰값의 수를 m이라고 하면 \(\mu_{ML} = \frac{m}{N}\) 으로 정의할 수 있습니다.
      - 최대 가능도 체계하에서는 동전의 앞면이 나올 확률을 데이터 집합에서 앞면이 나온 비율로 주어지게 됩니다.
    - 만약 3번 던져서 3변 앞면이 나온 것으로 최대 가능도 추정을 하면 \(\mu_{ML} = 1\) 이 됩니다.
      - 이 문제를 최대 가능도를 사용하였을 떄 발생하는 과적합 입니다.
- 크기 N인 데이터가 주어졌을 때, x = 1인 관측값의 수 m에 대해서 분포를 이항 분포(binomial distriution) 이라고 합니다.
  - ·\(\mu^{m}(1 - \mu)^{N-m}\) 에 비례
  - 정규화 계수를 구하기 위하여 동전 던지기를 N번 했을 때 앞면이 m번 나올 수 있는 모든 가짓수를 구해야 합니다.
  - ·\(Bin(m \vert N, \mu) = \begin{pmatrix} N \\ m \\ \end{pmatrix} \mu^{m}(1-\mu)^{N-m}\)
    - ·\(\begin{pmatrix} N \\ m \\ \end{pmatrix} = \frac{N!}{(N-m)!m!}\)
      - N개의 물체들 중 m개의 물체를 선별하는 가짓수
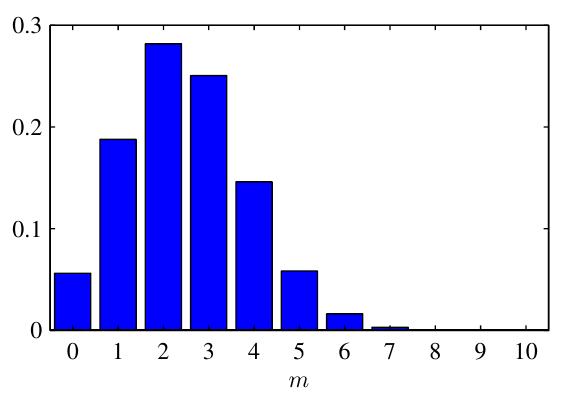
  - 다음은 N = 10, \(\mu\) = 0.25 일 떄의 이항분포의 히스토그램 입니다.
- 이항 분포의 평균과 분산의 경우 사건들이 서로 독립적일 경우
  - 평균 = \(mathbb E[x]\), 분산 = \(var[x]\) 일 때,
  - 사건들의 합의 평균값 = 평균값들의 합
    - ·\(\mathbb E[m] = \sum_{m=0}^{N}mBin(m \vert N, \mu) = N_{\mu}\)
  - 사건들의 합의 분산 = 분산들의 합
    - ·\(var[m] = \sum_{m=0}^{N}(m - \mathbb E[m])^{2}Bin(m \vert N. \mu) = N_{\mu(1-\mu)}\)
  - 연습문제 1.10 참조