
Numpy 및 Cupy 관련 Snippets
2019, Jan 06
- 이번 글에서는 Numpy에서 종종 사용하는 기능들을 정리해 보려고 합니다.
목차
-
np.c_[]
-
np.meshgrid()
-
ravel(), flatten()
-
np.polyfit으로 fitting
-
np.swapaxes
-
복원/비복원 랜덤 넘버 추출
-
차원 순서 변경 방법
-
차원 확장 방법
-
결측값 제거하기
-
np.einsum
-
np.where로 필요한 값 인덱스 찾기
-
np.delete를 이용한 값 제거
-
np.testing을 이용한 두 값의 차이값 확인
-
np.cov를 이용한 공분산 구하기
-
np.savetxt 관련 기능 정리
np.c_[]
np.c_[]를 이용하면 행으로 입력한 것이 열로 입력이 됩니다. 정확하게는 첫번째 축이 두번째 축이 되는 것입니다. 예제를 보면 쉽게 이해하실 수 있습니다.
>>> np.c_[np.array([1,2,3]), np.array([4,5,6])]
array([[1, 4],
[2, 5],
[3, 6]])
>>> np.c_[np.array([[1,2,3]]), 0, 0, np.array([[4,5,6]])]
array([[1, 2, 3, 0, 0, 4, 5, 6]])
첫 번째 예제를 보면 행으로 입력한 것이 열 단뒤로 들어간 것을 볼 수 있습니다.
np.meshgrid()
2차원 평면에서 grid를 만들어 주려면 x, y 축에 대하여 겹치는 좌표의 경우를 다 만들어 주어야합니다.
이 때, grid에 해당하는 격자를 쉽게 만들어 주는 함수가 np.meshgrid() 함수 입니다.
예를 들면 x = {0, 1, 2} 이고 y = {0, 1, 2, 3} 이라면 좌표로 총 12개의 경우의 수가 나옵니다. 이것을 간단하게 만들어 보겠습니다.
x = np.arange(3)
y = np.arange(4)
xx, yy = np.meshgrid(x, y)
>> xx
array([[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]])
>> yy
array([[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3]])
이 때, (0, 0) ~ (4, 3)까지의 조합을 만들 수 있습니다.
ravel(), flatten()
다차원 배열을 1차원으로 펼치기 위해서는 np.flatten() 또는 np.ravel() 메서드를 사용합니다.
>> xx
array([[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]])
>> xx.flatten() # 또는 xx.ravel()
array([0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2])
np.polyfit으로 fitting
np.polyfit으로least square방법으로 fitting하는 방법을 간략하게 정리하겠습니다.- 자세한 내용은 링크를 참조하시면 됩니다.
- 전체적인 방법은
least square를 이용하여 1차, 2차, n차 다항식을 fitting 합니다. - 파라미터는 첫번째로 입력할
x 값, 두번째로 입력할y 값, 그리고 fitting할degree를 입력하면 됩니다.
x = [1,2,3,4,5]
y = [2,4,6,8,10]
one_d_fit = np.polyfit(x, y, 1)
print(one_d_fit)
two_d_fit = np.polyfit(x, y, 2)
print(two_d_fit)
p1 = np.poly1d(one_d_fit)
p2 = np.poly1d(two_d_fit)
p1(1)
p2(1)
- 먼저
np.polyfit(x, y, degree)순으로 입력하면 됩니다. - 그러면 출력되는 값은 파라미터 값이 차례대로 출력되는데 1차로 fitting한 경우 \(ax + b\)에서 (a, b) 순서대로 출력됩니다.
- 2차로 fitting한 경우 \(ax^{2} + bx + c\)에서 (a, b, c) 순서로 출력됩니다.
- prediction할 때에 파라미터와 값을 대응시키기 불편할 수 있습니다. 이 때,
np.poly1d함수를 이용하여 함수를 생성할 수 있습니다. - 위 코드와 같이
p1 = np.poly1d(onw_d_fit)을 선언하고y예측값 = p1(x값)과 같이 이용할 수 있습니다. 즉,np.poly1d에 입력된 파라미터와 파라미터 갯수에 따라서 degree와 계수가 정해지게 되고 입력값만 넣으면 예측값이 나오는 함수가 만들어진 셈입니다.
np.swapaxes
- 넘파이에서 두 축을 교환합니다.
reshape과 유사하지만 역할이 조금 다른 것이 여기서는 두 축만 교환하는 것이기 때문입니다. - 예를 들어 (10, 150, 2) 라는 사이즈의 배열 a가 있을 때,
a.swapzxes(0, 1)라고 하면 0번 축과 1번축의 위치를 교환하는 것이므로 결과는 (150, 10, 2)가 됩니다. - 아래와 같은 예제로도 사용할 수 있습니다.
x = np.array([[1,2,3]])
np.swapaxes(x,0,1)
: array([[1],
[2],
[3]])
복원/비복원 랜덤 넘버 추출
- 아래 코드는 랜덤 숫자를 추출하는 방법으로
rng.choice의replace인자에 따라서 복원 또는 비복원으로 랜덤 넘버를 추출할 수 있습니다. replace가 False 이면 중복없이 추출하고 True이면 중복을 허용합니다. 중복없이 추출할 때에는 size의 최댓값은rng.choice의 첫번째 인자 값을 넘을 수 없습니다.- 랜덤 넘버의 범위는 0 이상 최댓값 미만입니다.
from numpy.random import default_rng
rng = default_rng()
numbers = rng.choice(20, size=10, replace=False)
차원 순서 변경 방법
- 어떤 numpy array의 크기를 변경하지 않고 차원의 순서만 변경해야 하는 경우가 있습니다. 예를 들어 opencv에서 이미지를 읽었을 때, (height, width, channel) 순서로 읽어오는데 반면 Pytorch와 같은 경우는 (channel, height, width) 순서이기 때문입니다.
- 이와 같이 array의 크기는 변경하지 않고 순서만 바꾸는 방법에 대하여 알아보겠습니다.
- 먼저
.transpose()방법을 이용하여 차원의 순서를 변경하는 방법입니다. 이 방법이 가장 직관적인데, 기존 채널의 순서를 바꿀 채널의 순서대로 입력하면 됩니다.
import numpy as np
A = np.ones((5, 6, 7))
print(A.shape)
# (5, 6, 7)
B = A.transpose(2, 1, 0)
print(B.shape)
# (7, 6, 5)
- 위 예제에서
.transpose()함수의 인자로 2, 1, 0을 차례대로 입력하였습니다. 즉, 2번째 차원 → 0번째 차원으로 변경하라는 뜻입니다. - 이와 같은 방법으로 앞에서 예를 든 (height, width, channel)을 (channel, height, width) 순으로 변경할 수 있습니다.
np.moveaxis()또한 방법은 유사합니다. 아래 코드를 살펴보겠습니다.
A = np.ones((5, 6, 7))
print(A.shape)
# (5, 6, 7)
B = np.moveaxis(A, 2, 0)
print(B.shape)
# (7, 5, 6)
np.moveaxis(array, 대상 채널, 이동할 위치)순서로 받게 됩니다. 위 예제에서는 2번째 채널을 0번째 채널로 이동하게됩니다.
차원 확장 방법
- 배열의 크기는 변경하지 않으나 차원을 늘릴 필요가 있을 때가 있습니다. 예를 들어 이미지를 학습할 때, (batch, channel, height, width)와 같은 형태로 입력이 들어가는데 기존에 (channel, height, width)이면 맨 앞에 차원을 추가해야 합니다.
- 예를 들어 (3, 100, 100) → (1, 3, 100, 100)으로 변경해야 할 경우입니다. 이와 같이 사이즈는 변경하지 않되 차원만 확장하려면 다음 함수를 사용합니다.
x = np.ones((2, 3))
y1 = np.expand_dims(x, axis=0)
print(y1.shape)
# (1, 2, 3)
y2 = np.expand_dims(y1, axis=0)
print(y2.shape)
# (1, 1, 2, 3)
결측값 제거하기
- numpy로 임의의 행렬을 만들어 보겠습니다.
- 이 때,
np.nan이 결측값 입니다. 엑셀 시트에서 값이 아무것도 없는 셀에 속합니다.
X = np.array([[1.1, 11.1],
[2.2, 22.2],
[3.3, 33.3],
[4.4, 44.4],
[np.nan, 55]])
- 결측값을 처리하는 방법에는 다양한 방법이 있습니다.
- 먼저 결측값이 있는 행을 제거해 주는 방법이 있습니다. 일반적으로 행을 기준으로 새로운 데이터가 추가 되므로 행을 제거합니다.
X[~np.isnan(X).any(axis=1)]
# array([[ 1.1, 11.1],
# [ 2.2, 22.2],
# [ 3.3, 33.3],
# [ 4.4, 44.4]])
- 반면 결측값에 특정값을 넣는 방법이 있습니다. 예를 들어 0을 입력해 보겠습니다.
X[np.isnan(X)] = 0
# array([[ 1.1, 11.1],
# [ 2.2, 22.2],
# [ 3.3, 33.3],
# [ 4.4, 44.4],
# [ 0. , 55. ]])
np.einsum
- 넘파이에서 행렬 연산을 할 때,
.einsum함수를 사용하면 유연하게 연산을 할 수 있습니다. einsum은 einstein notation을 이용하여 행렬 연산을 할 수 있도록 지원하는 함수 입니다.- 따라서 einsum 방식을 이용하면 matrix multiplication, batch matrix multiplication, element-wise multiplication, permutation, dot product, outer product, specific summation등과 같이 기본적으로 많이 사용하는 행렬 연산을
einsum함수 하나로 적용할 수 있습니다. - 특히 여기서 사용하는 문법은 numpy 뿐만 아니라 pytorch와 tensorflow에서도 사용하기 때문에 한번 익혀 두면 상당히 유용하게 사용할 수 있습니다.
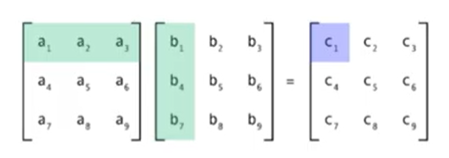
- 위 행렬 연산을 기준으로
einsum의 사용 방법에 대하여 알아보겠습니다. einsum을 사용하려면 먼저 수식으로 나타낼 수 있어야 합니다.
- \[M_{ij} = \sum_{k}A_{ik}B_{kj} \to A_{ik}B_{kj}\]
- 이 식에서 \(\sum\)을 빼고 \(A_{ik}B_{kj}\)으로만 나타낸 형태가 바로 einstein notation 방식 입니다.
- 위 식을 기본적인 코드, matmul 함수 그리고 einsum을 이용하여 나타내 보겠습니다.
A = np.random.rand(3, 5)
B = np.random.rand(5, 2)
# 기본적인 matrix multiplication 방식
M1 = np.empty((3, 2))
for i in range(3):
for j in range(2):
total = 0
# k index is used in sum loop
for k in range(5):
total += A[i, k] * B[k, j]
M1[i, j] = total
print(M1)
# [[0.90647435 2.04230236]
# [0.60864101 1.74284471]
# [0.52098582 1.18645873]]
# matmul 함수를 통한 matrix multiplication
M2 = np.matmul(A, B)
print(M2)
# [[0.90647435 2.04230236]
# [0.60864101 1.74284471]
# [0.52098582 1.18645873]]
# einsum을 이용한 matrix multiplication
M3 = np.einsum('ik,kj->ij', A, B)
print(M3)
# [[0.90647435 2.04230236]
# [0.60864101 1.74284471]
# [0.52098582 1.18645873]]
- 위 코드를 보면 모두 같은 연산 결과가 나타나는 것을 볼 수 있습니다.
- einsum 부분을 먼저 살펴 보면
np.einsum('ik,kj->ij', A, B)에서 첫 인자로 문자열을 받습니다. 문자열은->를 기준으로 좌변과 우변으로 나뉘게 됩니다, 좌변은,를 구분자로 행렬이 입력되게 되고 이는 두번째, 세번째 인자에 대응됩니다. 우변은 출력 결과의 포맷을 나타냅니다. - 첫번째 인자의 식을 보면 반복되는
k부분에서 곱셈 연산이 발생하는 것을 유추해 볼 수 있습니다. 즉 좌변에서 나타난 인덱스 중 우변에 나타나지 않으면 이 인덱스를 기준으로 연산이 되었다는 것을 알 수 있습니다. - 또한 위 예제에서는
i,k,j라는 인덱스를 사용하였지만 인덱스를 사용하는 것에는 제한이 없습니다. 자유롭게 어느 인덱스 알파벳이든지 사용하시면 됩니다. - 따라서
np.einsum('ik,kj->ij', A, B)에서i,j는 free index라고 지칭하고k는 summation index라고 지칭하겠습니다. 이는 위 코드의 파이썬 기본 버전과 대응 됩니다.
for i in range(3):
for j in range(2):
total = 0
for k in range(5):
total += A[i, k] * B[k, j]
M1[i, j] = total
- 위 코드를 보면 알 수 있듯이 행렬 A와 B의 k 인덱스에 해당하는 길이는 같아야 행렬 연산이 가능해집니다. 이를 유의하여 사용하시면 도움이 됩니다.
- 다른 예제를 한번 살펴 보겠습니다.
a = np.random.rand(5) # (5, )
b = np.random.rand(3) # (3, )
outer = np.einsum('i, j -> ij', a, b) # (5, 3)
- 이 경우 free index로 i, j가 사용되었고 summation index는 사용되지 않았습니다. 즉, 좌변에 있는 모든 인덱스가 우변에서도 사용되었습니다.
- 위 einsum을 파이썬 기본 코드로 옮기면 다음과 같습니다.
for i in range(5):
for j in range(3):
total = 0
# no sum loop index
total += a[i] * b[j]
outer[i, j] = total
- 따라서 einsum 사용 방법을 정리하면 다음과 같습니다.
- ① 서로 다른 입력 값에서 반복적으로 사용되는 index를 기준으로 곱셈을 통한 합이 발생하게 됩니다.
M = np.einsum('ik,kj -> ij', A, B)
- ② 생략되는 인덱스는 그 축을 기준으로 합이 발생하게 됩니다. 아래와 같은 경우 벡터의 합을 구하게 됩니다.
x = np.ones(3); sum_x = np.einsum('i -> ', x)
- ③ 우변에서 결과를 생성할 때, 축의 순서를 원하는 순서로 만들 수 있습니다. 아래와 같은 경우 0, 1, 2 축을 2, 1, 0 순서로 바꿉니다.
x = np.ones((5, 4, 3)); np.einsum('ijk -> kji', x)
- 아래 예제에서는 numpy에서 주로 사용할 수 있는 einsum 예제를 나열해 보겠습니다.
import numpy as np
x = np.random.random((2, 3))
# array([[0.11689396, 0.51696615, 0.66606396],
# [0.74145923, 0.4904741 , 0.18798271]])
# permutation of tensor
np.einsum("ij->ji", x)
# array([[0.11689396, 0.74145923],
# [0.51696615, 0.4904741 ],
# [0.66606396, 0.18798271]])
# summation
np.einsum("ij->", x)
# 2.7198400974055774
# column sum
np.einsum("ij->j", x)
# array([0.85835318, 1.00744025, 0.85404666])
# row sum
np.einsum("ij->i", x)
# array([1.29992407, 1.41991603])
x = np.random.random((2, 3)) # matrix
v = np.random.random((1, 3)) # row vector
np.einsum("ij,kj->ik",x, v)
# array([[0.91583178],
# [0.89804757]])
# matrix multiplication
np.einsum("ij,kj -> ik", x, x) # (2, 3) x (3, 2) = (2, 2)
# array([[0.70325902, 0.46933496],
# [0.46933496, 0.88504483]])
# Dot product first row with first row of matrix
np.einsum("i,i->", x[0], x[0])
# 0.703259019471991
# Dot product with matrix
np.einsum("ij, ij ->", x, x)
# 1.5883038495134512
# Elementi-wise multiplication
np.einsum("ij,ij->ij", x, x)
# array([[1.73036585e-02, 2.22586769e-01, 4.63368592e-01],
# [1.51640646e-02, 8.69504488e-01, 3.76277064e-04]])
# Outer product
a = np.random.random((3))
b = np.random.random((5))
np.einsum("i,j->ij", a, b)
# array([[0.19387425, 0.18228663, 0.35972633, 0.06095902, 0.30084629],
# [0.08433169, 0.07929129, 0.15647426, 0.02651604, 0.13086253],
# [0.45217691, 0.42515087, 0.83899715, 0.14217597, 0.70167001]])
# Batch matrix multiplication
a = np.random.random((3, 2, 5))
b = np.random.random((3, 5, 3))
np.einsum("ijk, ikl -> ijl", a, b) # (3, 2, 3)
# array([[[1.12661976, 2.24143829, 1.73480083],
# [0.93774707, 2.06820069, 1.93695202]],
# [[1.73253468, 0.62380984, 1.34472972],
# [1.58940717, 0.65081129, 0.91891999]],
# [[0.7734934 , 0.79936733, 0.55098931],
# [1.35982801, 1.58176646, 0.76229892]]])
# Matrix diagonal
x = np.random.random((3, 3))
np.einsum("ii->i", x)
# array([0.98143151, 0.4845303 , 0.61908454])
# Matrix trace
np.einsum("ii->", x)
# 2.0850463488460376
np.where로 필요한 값 인덱스 찾기
- numpy array에서 필요한 값을 찾을 때, 인덱싱을 이용하여 찾으면 쉽게 찾을 수 있습니다. 간단하게 다음과 같습니다.
import numpy as np
arr = np.arange(5, 30, 2)
boolArr = arr < 10
print(boolArr)
# [ True True True False False False False False False False False False False]
newArr = arr[boolArr] # newArr = arr[arr < 10]
print(newArr)
# [5 7 9]
- 위 구조를 보면 조건문을 통하여 각 인덱스 별 True, False를 확인하고 True값에 해당하는 값만 선택하도록 되어있습니다. 이 방법이 numpy array에서 가장 일반적으로 값을 조회하여 선택하는 방법입니다.
- 이와는 조금 다르게 조건에 해당하는 인덱스만 먼저 찾은 다음에 인덱스로 값을 선택하는 방법이 있습니다. 이 방법 또한 많이 사용되며
np.where를 이용하여 사용 가능합니다.
import numpy as np
arr = np.array([11, 12, 13, 14, 15, 16, 17, 15, 11, 12, 14, 15, 16, 17])
result = np.where(arr == 15)
print(result)
# (array([ 4, 7, 11], dtype=int64),)
print(arr[result])
# [15 15 15]
# Create a 2D Numpy array from list of lists
arr = np.array([[11, 12, 13],
[14, 15, 16],
[17, 15, 11],
[12, 14, 15]])
# Get the index of elements with value 15
result = np.where(arr == 15)
print(result)
# (array([1, 2, 3], dtype=int64), array([1, 1, 2], dtype=int64))
print(arr[result])
# [15 15 15]
- 위 예제를 보면 1차원 뿐만 아니라 2차원 이상의 다차원에서도 적용 가능한 것을 확인할 수 있습니다.
np.where(condition)을 통하여 condition을 만족하는 인덱스를 차원에 맞게 출력하는 것을 확인할 수 있습니다.
np.delete를 이용한 값 제거
- numpy에서 특정 값 또는 행, 열 등을 삭제할 때
np.delete를 이용하면 쉽게 삭제할 수 있습니다. delete 결과는 원본 array에 영향을 주지 않으며 따로 저장해야 합니다. 아래 예제를 살펴보겠습니다. - 사용 방법은
np.delete(array, 삭제할 인덱스, 차원)입니다.
import numpy as np
arr = np.array([[11, 12, 13],
[14, 15, 16],
[17, 15, 11],
[12, 14, 15]])
# 1 번째 인덱스 (12)만 삭제되어 행렬 shape이 깨져서 벡터로 변경됨
print(np.delete(arr, 1))
# [11 13 14 15 16 17 15 11 12 14 15]
# axis = 0은 행을 의미하며 1번째 행인 [14, 15, 16]이 삭제됨
print(np.delete(arr, 1, axis=0))
# [[11 12 13]
# [17 15 11]
# [12 14 15]]
# axis = 1은 열을 의미하며 1번째 행인 [13, 16, 11, 15]' 열이 삭제됨
print(np.delete(arr, 1, axis=1))
# [[11 13]
# [14 16]
# [17 11]
# [12 15]]
np.testing을 이용한 두 값의 차이값 확인
- numpy 두 배열이 얼만큼 차이나는 지 알고 싶을 때, 많이 사용하는 함수로
np.testing.assert_allclose가 있습니다. - 아래 코드를 통하여 actual 값이 desired 값과 오차 범위 이내에 있는 지 확인이 가능하며 오차 범위 밖에 있으면 다른 값으로 간주하고 그 결과를 출력합니다.
- 오차 범위는
rtol (relative tolerance)와atol (absolute tolerance)를 이용하여 나타내며 actual 값이rtol * abs(desired) + atol의 범위를 넘어가면 에러를 발생시킵니다. - 간단하게
atol = 0으로 두었을 때,rtol의 값 만큼의 허용 오차를 가진다고 생각해도 됩니다. 예를 들어 아래 기본 코드와 같이rtol=1e-7, atol=0으로 두었다면 허용 오차는 1e-7 미만이며 1e-7이상의 차이가 나면 다른 값으로 인식합니다.
def compare_two_array(actual, desired, rtol=1e-7, atol=0):
# actual * ato
try :
np.testing.assert_allclose(actual, desired, rtol=rtol, atol=atol)
print("allwable difference.")
except AssertionError as msg:
print(msg)
desired = np.array([0.1, 0.1, 0.1])
actual = np.array([0.1, 0.1000001, 0.1])
# 1e-7의 오차 범위로는 다른 값으로 인식함
compare_two_array(actual, desired)
# Not equal to tolerance rtol=1e-07, atol=0
# Mismatched elements: 1 / 3 (33.3%)
# Max absolute difference: 1.e-07
# Max relative difference: 1.e-06
# x: array([0.1, 0.1, 0.1])
# y: array([0.1, 0.1, 0.1])
# 1e-6의 오차 범위로는 같은 값으로 인식함
compare_two_array(actual, desired, rtol=1e-6)
# allwable difference.
np.cov를 이용한 공분산 구하기
- 참조 : https://numpy.org/doc/stable/reference/generated/numpy.cov.html
- 넘파이를 이용하여 확률 및 통계 관련 개념을 구현할 때, 공분산 (covariance)는 항상 쓰이게 됩니다.
- N 차원의 데이터 \(X = [ x_{1}, x_{2}, \cdots , x_{n} ]^{T}\) 를 입력 받았을 때, 공분산 행렬 \(C\) 의 각 원소값인 \(C_{ij}\) 는 \(x_{i}\) 와 \(x_{j}\) 를 통해 구해집니다.
- 대각성분인 \(C_{ii}\) 는 \(x_{i}\) 와 \(x_{i}\) 를 통해 구해집니다.
x = np.array([[0, 2], [1, 1], [2, 0]]).T
# array([[0, 1, 2],
# [2, 1, 0]])
np.cov(x)
# array([[ 1., -1.],
# [-1., 1.]])
np.savetxt 관련 기능 정리
- numpy의 배열 값을 txt나 csv 형태로 저장하려고 할 때,
np.savetxt함수를 사용하면 됩니다. - 아래는 (N, 6)의 값을 가지는 배열을 소수와 정수가 섞인 포맷의 csv 파일로 저장하는 예시 입니다.
np.savetxt("np_test.csv", C, fmt="%.2f,%.2f,%.2f,%d", header="x,y,z,r,g,b", comments='')
- 위 예시에서
fmt를 통해 저장할 파일의 형식을 하나의 형식이 아닌 여러 형식으로 정의할 수 있습니다. header를 통하여 1행에 열의 이름을 지정할 수 있습니다. header를 사용하면 가장 첫번째 요소에 #이 붙게 되는데 이 문제를 없애기 위하여comments=''을 사용하였습니다.
cupy의 필요성
numpy는 매우 쉽게 연산을 할 수 있는 라이브러리이지만 연산량이 커지면 계산하는 데 시간이 많이 소요됩니다. 왜냐하면numpy의 모든 연산은cpu에서 동작하기 때문입니다.- 이러한 연산 속도 문제를 개선하기 위하여
cupy라는 라이브러리가 개발되었습니다.cupy는numpy연산을cuda로 할 수 있도록 하는 라이브러리 입니다. cupy의 연산 효율성을 다음 예제를 통해 살펴 보도록 하겠습니다. 참고로cupy를 처음 실행할 때에는 초기화 때문에 numpy 보다 다소 오래 걸릴 수 있지만 초기화가 끝나면 연산속도는 다음과 같이 매우 빨라집니다. 아래는 제 PC에서 속도를 측정한 결과입니다.
import numpy as np
import cupy as cp
start = time.time()
x_cpu = np.random.rand(500, 200, 400)
y_cpu = np.random.rand(500, 400, 200)
print(time.time() - start)
# 0.6273207664489746
start = time.time()
x_cpu @ y_cpu
print(time.time() - start)
# 0.19546985626220703
start = time.time()
for _ in range(100):
x_cpu @ y_cpu
print(time.time() - start)
# 19.48985266685486
start = time.time()
x2_gpu = cp.random.rand(500, 200, 400)
y2_gpu = cp.random.rand(500, 400, 200)
print(time.time() - start)
# 0.0009970664978027344
start = time.time()
x2_gpu @ y2_gpu
print(time.time() - start)
# 0.0009732246398925781
start = time.time()
for _ in range(100):
x2_gpu @ y2_gpu
print(time.time() - start)
# 0.006982564926147461
- 위 결과를 살펴보면 1개의 행렬곱 연산을 하였을 때, (0.19546985626220703 / 0.0009732246398925781) = 약 200배의 연산 속도 차이가 났으며 100개의 행렬곱 연산을 하였을 때, (19.48985266685486 / 0.006982564926147461) = 약 2800 배의 연산 속도가 차이가 났습니다.
cuda를 이용하여 GPU로 병렬 연산을 하면 이와 같이 빠르게 연산할 수 있습니다.
numpy, torch와 cupy의 비교
- 이번에는
numpy와torch그리고cupy의 연산 시간에 대하여 비교해 보도록 하겠습니다. - 먼저
numpy를 이용하여 랜덤 변수를 만들고tensor (cuda)로 변환하였을 때 소요되는 시간을 확인해 보겠습니다. 시간 측정을 위해 1,000번 반복하였습니다.
start_time = time.time()
for _ in range(1000):
np_mat = np.random.rand(1000, 1000)
tensor_mat = torch.as_tensor(np_mat).cuda()
print(time.time() - start_time)
# 8.527007102966309
start_time = time.time()
for _ in range(1000):
cp_mat = cp.random.rand(1000, 1000)
tensor_mat = torch.as_tensor(a, device="cuda")
print(time.time() - start_time)
# 0.28897643089294434
cupy를 이용하였을 때, 수십배 빨라진 것을 볼 수 있습니다.cupy로 배열을 생성하면cuda메모리에 변수를 생성하고 같은 메모리의 값을 사용하여tensor (cuda)를 생성합니다. 이러한 이유로numpy로 생성하여cpu → gpu로 메모리 복사가 발생하는 시간을 줄일 수 있기 때문에cupy를 이용하여 바로 변수를 생성하는 것이 빠릅니다.
- 이번에는 앞에서 생성한
numpy행렬,cupy행렬,tensor를 이용하여 간단한 행렬 연산을 한 뒤 시간 측정을 해보도록 하겠습니다.
start_time = time.time()
for _ in range(1000):
np_mat2 = np_mat @ np_mat
print(time.time() - start_time)
# 12.938754320144653
start_time = time.time()
for _ in range(1000):
cp_mat2 = cp_mat @ cp_mat
print(time.time() - start_time)
# 0.03754234313964844
start_time = time.time()
for _ in range(1000):
tensor_mat2 = tensor_mat @ tensor_mat
print(time.time() - start_time)
# 7.614563703536987
cupy를 사용하였을 때, 가장 빠르고 그 다음tensor (cuda), 마지막이numpy입니다.cupy가 가벼우면서cuda를 이용하기 때문에 위 코드와 같이 간단한 연산은 가장 빠르게 동작할 수 있는 것으로 추정됩니다.
cupy 설치 방법
- 먼저
cupy를 사용하려면 GPU 연산을 위해cuda를 사용할 수 있는 환경이 되어야 합니다. 따라서 다음과 같이cuda버전을 확인함으로써cuda가 설치 되어있는 지 확인을 먼저 해야 합니다.
nvcc --version
- 제 컴퓨터 환경에서는 아래와 같이 확인할 수 있었습니다.
nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2020 NVIDIA Corporation
Built on Tue_Sep_15_19:12:04_Pacific_Daylight_Time_2020
Cuda compilation tools, release 11.1, V11.1.74
Build cuda_11.1.relgpu_drvr455TC455_06.29069683_0
- cuda 설치가 확인되었으면 아래와 같은 설치합니다.
pip install cupy-cuda111
cuda111은 제 PC의 환경 cuda 버전이 11.1이기 때문이며 다른 버전의 경우 다른 버전을 사용해서 설치하시면 됩니다.- 참고로 아래
pip install cupy-cuda11x에서 명령어x는 실제로 알파벳x를 입력하시면 됩니다.
# For CUDA 10.2
pip install cupy-cuda102
# For CUDA 11.0
pip install cupy-cuda110
# For CUDA 11.1
pip install cupy-cuda111
# For CUDA 11.2 ~ 11.x
pip install cupy-cuda11x
# For CUDA 12.x
pip install cupy-cuda12x
# For AMD ROCm 4.3
pip install cupy-rocm-4-3
# For AMD ROCm 5.0
pip install cupy-rocm-5-0
- 상세 설치 가이드는 다음 페이지를 참조하시기 바랍니다.
- 링크 : https://cupy.dev/
cupy 기본 사용법
cupy는 cuda를 backend로 사용하며 구현 방식은 numpy와 같습니다. 다만 모든 numpy의 기능이 구현되어 있지는 않으므로 numpy 기능의 부분집합 정도로 생각하시면 됩니다.- 아래 코드에서
cupy.ndarrary클래스는 numpy의numpy.ndarrary의 역할과 동일합니다. cupy의 사용방법은numpy와 동일하며 결과 또한 같습니다.
import numpy as np
import cupy as cp
x_gpu = cp.array([1, 2, 3])
l2_gpu = cp.linalg.norm(x_gpu)
print(l2_gpu)
# 3.7416573867739413
x_cpu = np.array([1,2,3])
l2_cpu = np.linalg.norm(x_cpu)
print(l2_cpu)
# 3.7416573867739413
- 위 코드와 같이
cupy와numpy의 연산 결과가 같은 것을 확인할 수 있습니다.
- 만약 컴퓨터가 멀티 GPU라면 원하는 GPU에 cupy 연산을 할당할 수 있습니다. pytorch에서도 동일한 기능을 제공하는데 cupy에서도 동일하게 제공하며 이와 같은 방법으로 메모리가 상대적으로 작은 GPU에서 작업을 여러 GPU로 분할할 수 있습니다.
# device : 0
x_on_gpu = cp.array([1,2,3,4,5])
with cp.cuda.Device(0):
x_on_gpu = cp.array([1,2,3,4,5])
with cp.cuda.Device(1):
x_on_gpu = cp.array([1,2,3,4,5])
- 기본값은
cuda의 device 아이디는 0입니다. 만약 멀티 GPU라면 사용가능한 갯수 까지 0 ~ N 까지 할당 가능합니다.
cupy와numpy간의 데이터 이동 또한 자유롭게 할 수 있습니다.cupy에서 복잡한 연산을 한 뒤 마지막에numpy로 변환하여 다른 라이브러리와 연계해서 사용할 때 유용합니다.- 먼저
numpy → cupy부터 알아보도록 하겠습니다.
x_cpu = np.array([1, 2, 3])
x_gpu = cp.asarray(x_cpu) # move the data to the current gpu device
- GPU 간 데이터 이동도 아래와 같이 가능합니다.
with cp.cuda.Device(0):
x_gpu_0 = cp.ndarray([1, 2, 3])
with cp.cuda.Device(1):
x_gpu_1 = cp.asarray(x_gpu_0)
- 다음으로
cupy → numpy방법은 다음과 같습니다.
x_gpu = cp.array([1, 2, 3])
x_cpu = cp.asnumpy(x_gpu)
# or
x_cpu = x_gpu.get()
cupy와numpy는 다른 클래스이고 데이터가 저장된 위치 또한 다릅니다.cupy의 데이터는 gpu의 RAM에 있고numpy의 데이터는 cpu의 RAM에 있습니다. 따라서 두 연산은 동일한 위치에 사용하지 않으면 연산되지 않습니다.
x_gpu = cp.array([1, 2, 3])
x_cpu = cp.asnumpy(x_gpu)
# x_gpu + x_cpu : error
x_cpu + cp.asnumpy(x_gpu)
# array([2, 4, 6])
cp.asarray(x_cpu) + x_gpu
# array([2, 4, 6], dtype=int32)
- 위 코드와 같이 같은 타입으로 변경하여 연산해야 사용 가능합니다.
- 다음은
Numpy,Tensor,Cupy간의 변환 방법 및 변환 시 소요되는 시간 테스트를 기록한 것입니다. - 결과적으로
Cupy와Tensor는 같은cuda메모리에 변수가 있으므로 변환 시간이 상대적으로 짧습니다. 따라서 가능하면Tensor와Cupy를 비교하여 사용해 보는 것을 권장드립니다. - 테스트 방법은 다음과 같습니다.
src_data = np.random.rand(1000, 1000) # numpy → cupy/tensor
src_data = cp.random.rand(1000, 1000) # cupy → numpy/tensor
src_data = torch.randn(1000, 1000, device="cuda") # tensor → numpy/cupy
total_time = 0
for i in range(10):
start_time = time.time()
for _ in range(1000):
# dest_data = cp.array(src_data)
# dest_data = src_data.get()
# dest_data = torch.as_tensor(src_data, device="cuda")
# dest_data = src_data.cpu().numpy()
total_time += (time.time() - start_time)
print(total_time / 10)
