위도, 경도를 이용하여 거리 구하기

이번 글에서는 위도, 경도를 이용하여 거리를 구하는 방법에 대하여 알려드리겠습니다.

지도 서비스에서 특정 위치를 검색하면 위도 경도가 나오게 됩니다. 위도 경도를 나타낼 때 일반적으로 3가지 방법을 볼 수 있습니다.

• 도, 분 및 초(DMS): 41°24’12.2”N 2°10’26.5”E
• 도 및 십진수 분(DMM): 41 24.2028, 2 10.4418
• 십진수 도(DD): 41.40338, 2.17403

지도 서비스에서 주로 나타나는 것은 3번째 십진수 도 입니다. 왜냐하면 숫자 만으로 되어 있으니, 처리하기가 쉽기 때문입니다. 마치 X, Y 좌표 같지 않나요?

두 점과의 거리를 구할 때 잘 알고 있는 공식이 있습니다. 예를 들어 유클리디안 거리가 있습니다. 점과 점 사이의 직선 거리를 구해줍니다. 또는 맨하탄 거리 같은 것도 있습니다. 예를 들어 유클리다안 거리를 위치를 구하는 데 사용하면 문제가 있습니다. 바로 지구는 둥근 구 형태이기 때문에 점과 점사이의 직선 거리를 구하는 것은 이치에 맞지 않습니다.

이 때 사용할 거리는 Haversine formula 입니다. 간단하게 설명하면 위도/경도가 주어졌을 때, 구 형태에서의 두 점사이의 거리를 구하는 방식 입니다.

• 설명 참조 : https://en.wikipedia.org/wiki/Haversine_formula

저희는 이제 어떻게 사용할 것인가에 좀 더 초점을 맞추겠습니다. 파이썬에서 pip를 이용하여 추가적으로 패키지를 설치하면 금방 해결할 수 있습니다.

• 참조 : https://pypi.org/project/haversine/

아래와 같이 명령어를 입력하여 패키지를 설치합니다.

pip install haversine

공식 예제를 보면 다음과 같습니다.

from haversine import haversine

lyon = (45.7597, 4.8422) # (lat, lon)
paris = (48.8567, 2.3508)

haversine(lyon, paris)
>> 392.2172595594006  # in kilometers

haversine(lyon, paris, unit='mi')
>> 243.71201856934454  # in miles

haversine(lyon, paris, unit='nmi')
>> 211.78037755311516  # in nautical miles

위와 같이 위도/경도 순으로 2개의 점을 튜플/리스트 형태로 넣으면 km 단위로 반환 됩니다. 만약 mile로 구하고 싶으면, 옵션을 추가해 주면 됩니다.

예를 들어 한국의 예를 적용해 보겠습니다.

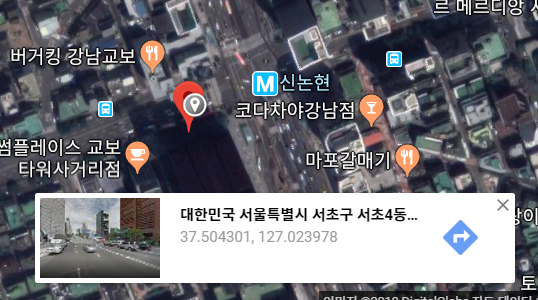
강남 교보문고의 좌표 입니다. 위도/경도를 확인할 수 있습니다. 이제 haversine 함수를 적용해 보겠습니다.

kyobo = (37.504030, 127.024099) # 교보 문고 위도/경도
gangnam = (37.497175,127.027926) # 강남역 위도 경도

>> haversine(kyobo, gangnam) * 1000

833.6603247358311

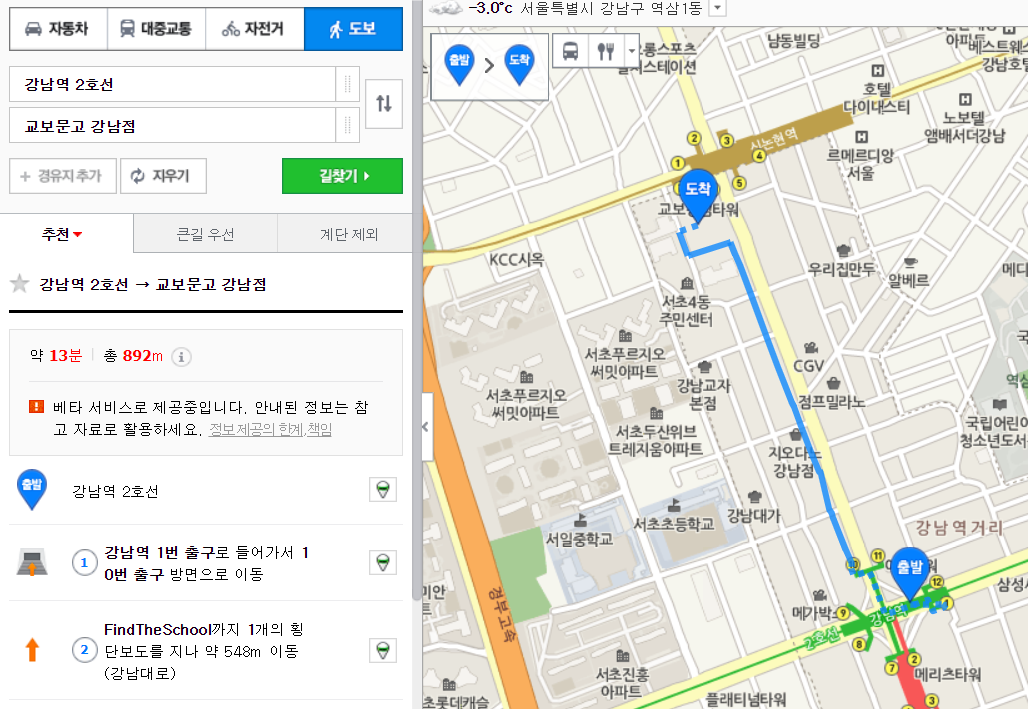
결과는 약 833m 입니다. 실제 지도에서 한번 찍어볼까요?

892m 입니다. 약간 차이가 있습니다. 왜냐하면 보통 지도 서비스에서 제공하는 것은 도보/운전/대중 교통 상황을 이용한 거리가 나오기 때문입니다. 반면 저희는 물리적인 거리를 구한 것이지요. 그래도 뭔가 절대적인 거리가 필요한 땐 도움이 되겠지요?