
실좌표공간
출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)
Video

고등학교 수학을 공부할 때 다음과 같이 R 왼쪽에 선을 하나 더 그은 것을 보았을 것입니다. 이것을 \(R^{2}\) 라고 합니다. 교재에 따라 굵은 글씨로 \(R^{2}\)라고 적기도 합니다. 이것이 2차원 실수 좌표 공간을 의미합니다. 2차원 실수 좌표 공간이라니 굉장히 멋지지 않나요? 이렇게 생각해 봅시다. 이것은 단순히 좌표평면을 통해서 이미 다루어왔던 2차원 공간입니다. 꼭 필요한 것은 아니지만 추상적으로 설명해 보자면 이렇습니다. 시각적으로 표현하는 것은 실수 좌표공간을 이해하는 하나의 방법입니다. 조금 더 추상적으로 생각해본다면 2차원 실수 좌표공간에서 \(R^{2}\) 는 다음과 같이 분리시켜 생각해볼 수 있습니다. 2는 다루는 차원을 의미하고 R은 실수 좌표공간을 의미합니다. 2차원 실수 좌표공간은 실수값을 가진 모든 2-튜플을 말합니다. 실수값을 가지는 모든 2-튜플 뭘까요? 튜플은 순서가 정해진 숫자들의 리스트입니다. 실수에 대해서 배우기 때문에 실수들의 순서 리스트라고 말해야겠죠. 그럼 2-튜플은 숫자 2개의 순서 리스트이자 실수 2개의 순서 리스트가 됩니다. 바로 여기 이것을 가지고 2차원 벡터에 대해 생각할 수 있습니다. 바로 여기 2-튜플이 있네요.
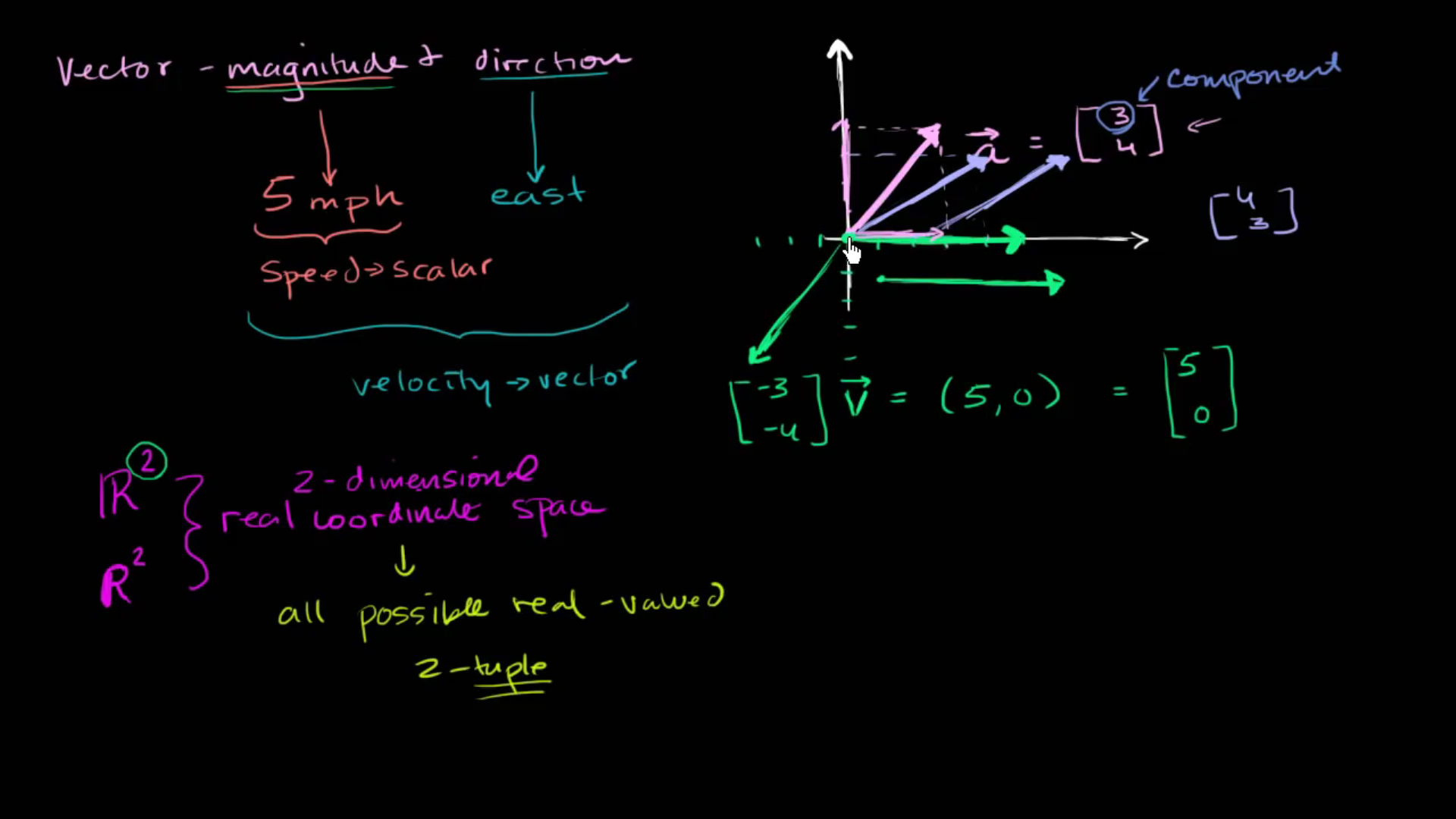
이것은 실수값을 가지는 2-튜플입니다. 둘 중 어느것도 허수가 아니면서 순서대로 3과 4를 가지고 있어요. 만일 순서가 바뀌면 다른 2-튜플이 됩니다. 그러면 4와 3이 됩니다. 이 벡터를 좌표축에 표현해 보겠습니다. 벡터 (4, 3)을 표현한다면 가로축으로 4만큼 세로축으로 3만큼 이동할 것입니다. 크기와 방향만 같으면 같은 벡터입니다. 그러므로 \(R^{2}\) 를 다룬다는 것은 모든 가능한 실수값을 가지는 2-튜플을 다루는 것입니다. 따라서 이 공간위의 모든 벡터들이 어디에 있는지 알 수 있으며 그리고 그 벡터의 각 성분들은 실수로 이루어져 있습니다. 3과 4가 성분이 될 수도 있고 -3과 -4가 성분이 될 수도 있습니다. 성분 -3과 성분 -4 벡터 (-3, -4)는 이렇게 표현되겠죠. 벡터 (-3, -4) 크기는 없고 방향은 정해지지 않은 영벡터를 포함한 모든 2-튜플에 대해서 이 벡터들을 조합하여 2차원 실수좌표공간도 만들어낼 수 있습니다. 그럼 이것은 \(R^{2}\) 일 것입니다 여기에 2라고 적었지만 더 나아가 생각해봅시다. 3이라고 적으면 안될까요?

그럼 전 이렇게 말합니다 물론 3이라고 적을 수 있습니다. \(R^{3}\)는 3차원 실수 좌표공간입니다. 실수값을 가지는 3-튜플입니다. 예를 들어 열 벡터 [0 0 0]은 \(R^{3}\) 상의 벡터입니다. 이 벡터를 부를만한 적당한 이름을 붙여보면 이것은 x벡터라고 부르겠습니다. b벡터는 열 벡터 [-1 5 3]과 같은 형태가 될 수 있겠네요. x벡터와 b벡터는 둘 다 \(R^{3}\) 상의 벡터입니다. 조금 더 덧붙이자면 x벡터와 b벡터는 \(R^{3}\)이라는 집합의 원소라고 할 수 있죠. 그리고 이것은 실수값을 가지는 3-튜플입니다. 이제 \(R^{3}\)에 속하지 않는 것들은 뭐가 있는지 알아볼까요? 이것은 실수값을 가지는 3-튜플이 아니고 \(R^{2}\)에 속하는 벡터입니다. 0을 더하거나 해서 이 벡터를 확장시킬 순 있겠지만 원래 이 벡터는 3-튜플이 아닙니다. 또 \(R^{3}\) 상의 벡터가 아닌 것으로는 허수 성분을 가진 벡터가 있다고 해봅시다. 그 벡터를 열 벡터 [i 0 1] 이라고 하겠습니다. 이것은 더 이상 실수가 아닌 허수입니다. i는 허수입니다. 그러므로 더 이상 실수값을 가지는 3-튜플이 있을 수 없습니다. \(R^{3}\)를 시각화 하였고 이를 좌표로도 그러보았습니다. 3차원을 시각화하는 일은 홀로그램이나 여러가지 경험을 통해 이미 해봐서 그렇게 어렵지는 않습니다. 하지만 우리는 3차원을 넘어서서 계속해서 차원을 확장할 수 있습니다. 4차원, 5차원, 6차원, 7차원 20차원, 100차원 까지도요. 물론 이것은 명백하게 점점 더 어려워지겠지만요. 시각화하는것은 불가능하더라도 우리는 적어도 그것을 n-튜플 벡터라고 수학적으로 표현할 수 있습니다. 일반적으로 실수좌표공간에 대해 이야기할 때 종종 \(R^{n}\)이라는 표현을 볼 수 있을겁니다. \(R^{n}\)은 n차원을 의미합니다. n차원 실수 좌표공간 입니다.
