벡터와 스칼라의 곱셈
출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)
Video
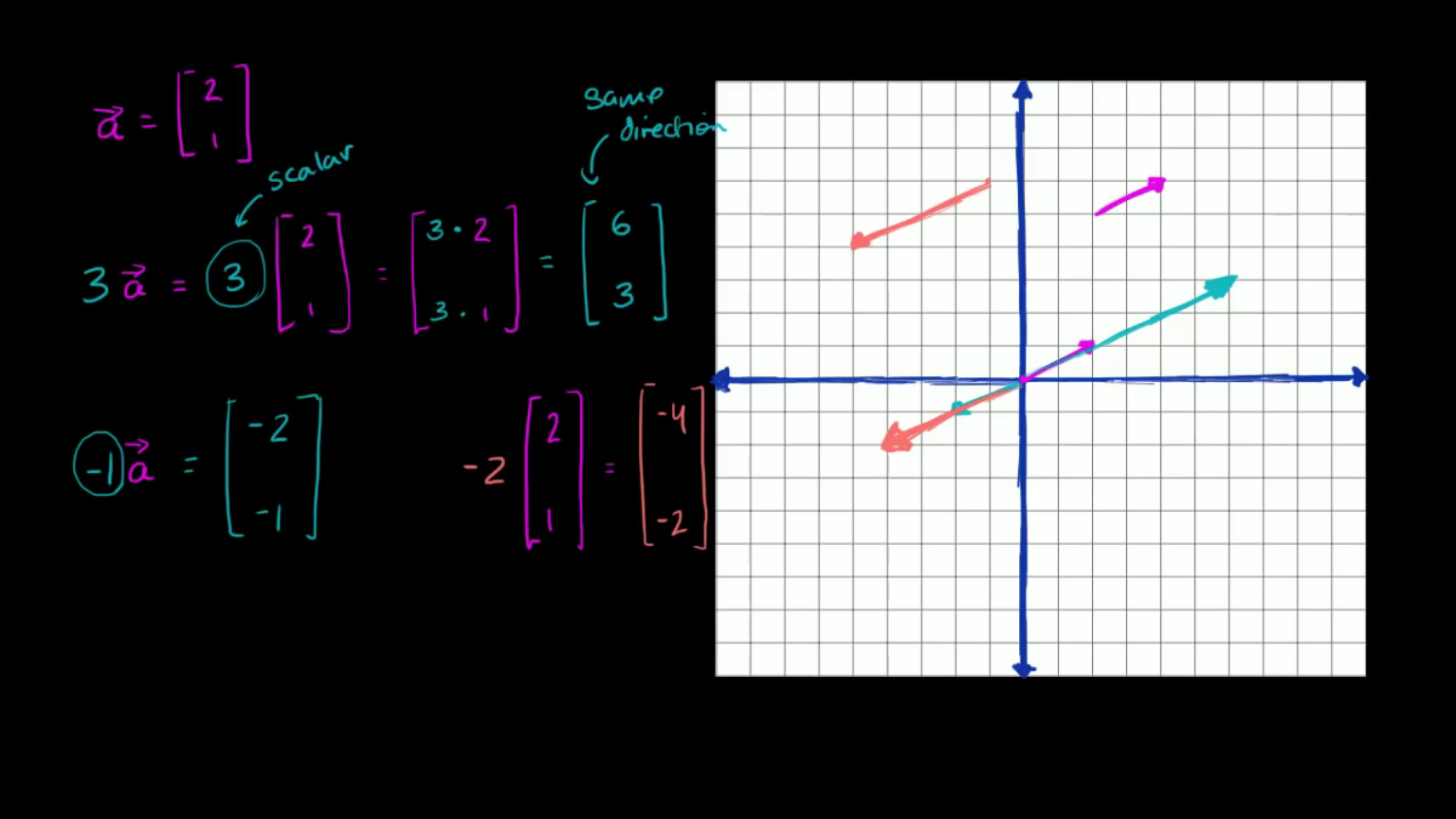
(2,1)인 벡터 a가 있습니다. 여기에 한번 그려볼까요? (2,1)을 원점에서 시작한다면 수평 방향으로 2만큼 수직 방향으로 1만큼 움직일 것입니다. 벡터의 스칼라 곱을 어떻게 정의할 수 있을지 한번 생각해봅시다. 예를 들어 벡터 a에 3을 곱한다고 하면 3 x (2,1)과 같습니다. 3은 그저 숫자입니다. 스칼라가 어떤 의미인지 벡터와 비교해보죠. 3은 단지 숫자인 데 비해 벡터는 얼마만큼 어느 방향으로 움직여야 하는지 크기와 방향, 둘 다 알려줍니다. 여기 있는 것은 평범한 숫자입니다. 이 벡터에 3을 곱하는 것을 어떻게 정의할 수 있을까요? 머릿속에 떠오르는 합리적인 생각은 각각의 성분에 3을 곱하는 것일 겁니다. 2와 1이 벡터의 각 성분이니 이들을 3으로 곱할 것입니다. \(3 \times 2\)와 \(3 \times 1\)이 됩니다. 스칼라를 곱한 벡터는 여전히 2차원 벡터일 겁니다. 2차원 벡터 (6,3)이 됩니다.
벡터 (6,3)은 원점에서 시작하면 수평으로 6만큼 움직입니다.
수직으로는 3만큼 움직입니다.
이 벡터에 무슨 일이 일어났습니까?
이 벡터에서 무엇이 바뀌었고 무엇이 바뀌지 않았는지 살펴보세요.
바뀌지 않은 점은 여전히 같은 방향을 가리키고 있다는 겁니다.
여기 이 벡터는 방향이 바뀌지 않았습니다.
벡터의 스칼라 곱은 적어도 우리가 정의한 바에 의하면 벡터의 방향은 변하지 않았습니다.
최소한 이 경우에서는 방향이 안 변했죠. 하지만 크기는 바뀌었습니다.
이 벡터의 크기는 3배로 늘어났습니다.
3을 곱했기 때문에 당연합니다.
벡터를 3배 확대했다고 생각하시면 됩니다.
스칼라가 확대해줬다고 생각하면 이해가 될 겁니다.
스칼라(scalar)와 확대하다(scale up)의 어원이 같음을 눈치채셨을 겁니다. 스칼라의 곱은 벡터를 확대합니다. 방향 변화 없이 크기는 3배 증가하게 되었습니다.
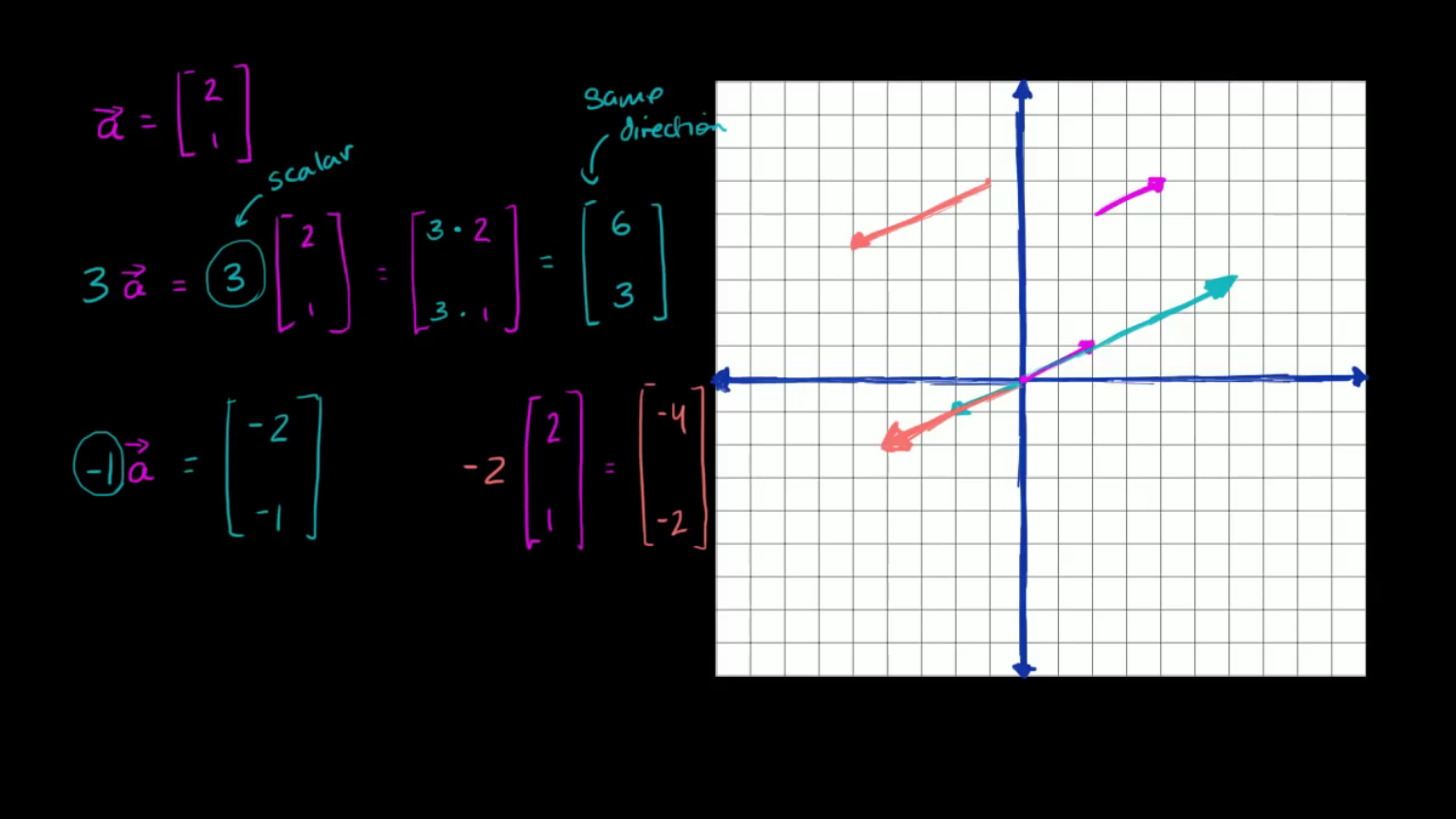
벡터 a에 음수를 곱해보도록 합시다. 간단하게 -1을 곱해보죠. -1을 a에 곱해보겠습니다.
a에 3을 곱했던 때와 마찬가지로 각각의 성분에 -1을 곱합니다.
\(2 \times -1\)은 -2, \(1 \times -1\) 은 -1입니다.
-1을 벡터 a에 곱하면 (-2,-1)이 됩니다.
우리가 원점에서 시작한다면 수평으로 -2만큼 수직으로 -1만큼 움직여야 합니다.
-1을 곱했을 때 벡터에 무슨 일이 일어났나요?
방향을 완전히 뒤집어 버렸습니다.
-1을 곱하니 방향이 완전히 뒤집혔습니다.
벡터의 크기는 변하지 않았습니다.
그러나 방향은 완전히 반대가 되었습니다.
음수를 곱했을 때 방향은 바뀌게 됩니다.
수직선을 다뤘을 때도 마찬가지였습니다.
\(5 \times -1\) 을 하면 반대방향으로 가게 됩니다.
0의 왼쪽으로 다섯 칸 즉, -5에 있게 됩니다.
그러므로 음수를 곱하면 방향이 바뀌는 것입니다.
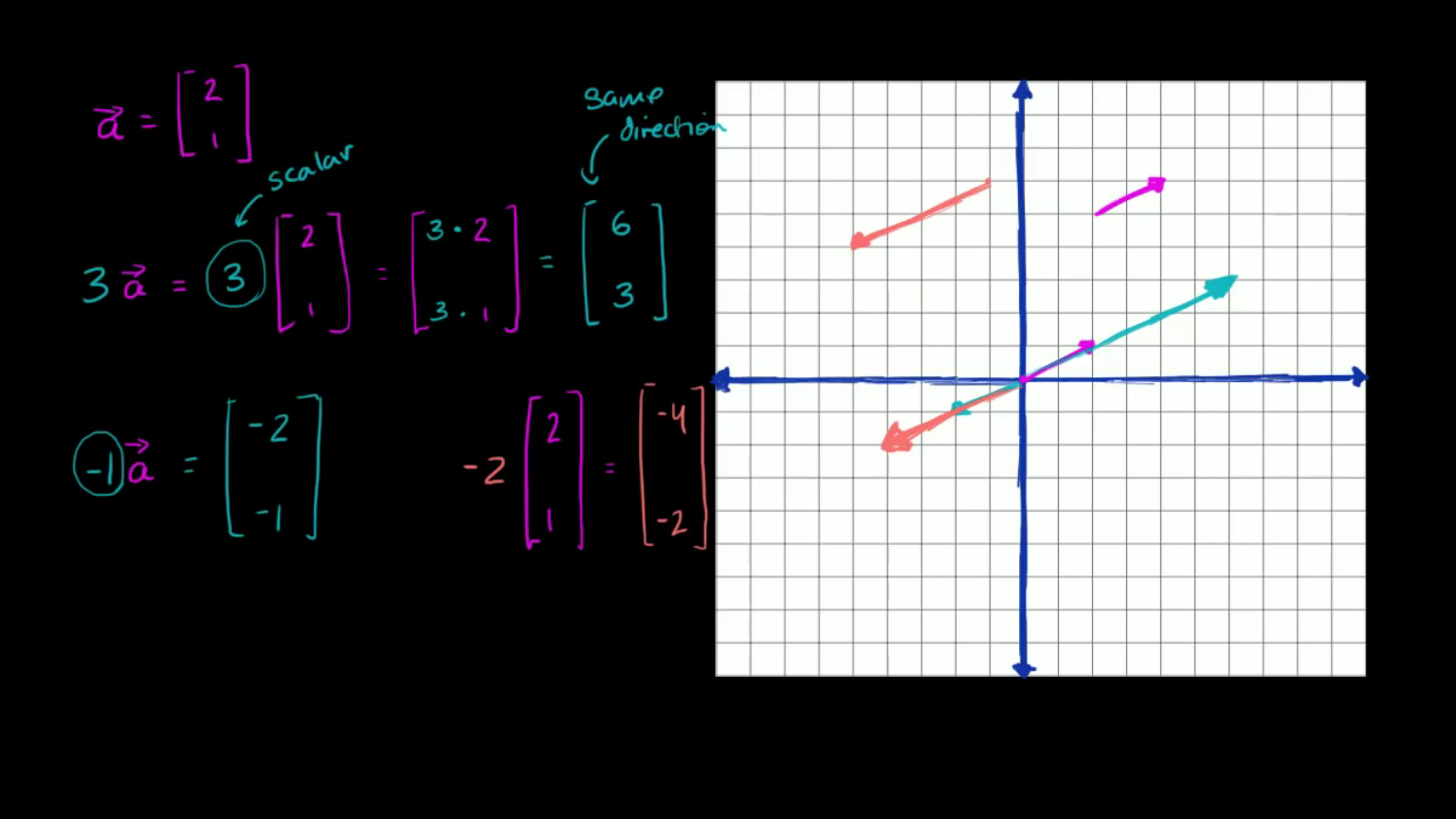
이번에는 -2를 벡터 a에 곱해 봅시다. 이 벡터의 스칼라 곱은 무엇인가요? 그래프에 어떻게 표현할 수 있나요? 이 벡터의 스칼라 곱은 \(-2 \times 2\) 는 -4이고 \(-2 \times 1\)은 -2 입니다. 우리가 처음 다뤘던 벡터 a는 이렇게 생겼었습니다. (2,1)은 이렇게 생겼습니다. 거기에 -2를 곱하면 이러한 형태의 벡터가 됩니다.
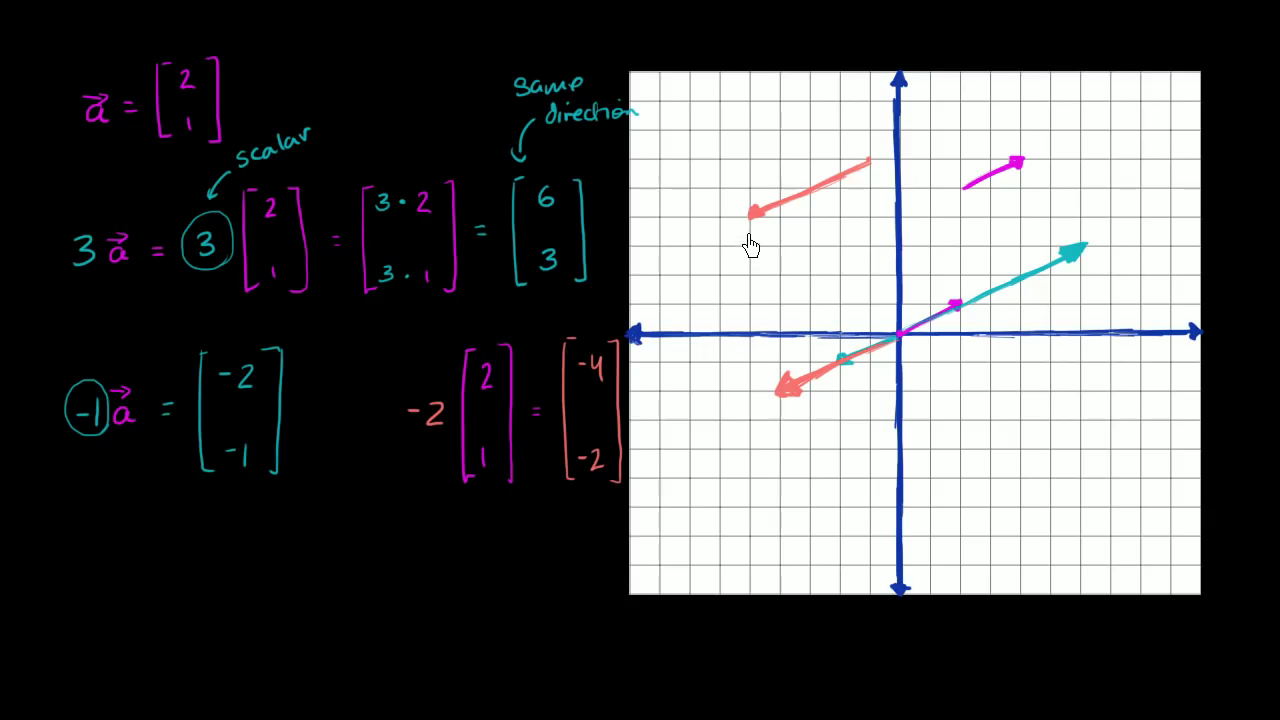
이번에는 의도적으로 원점에서 시작하지 않았습니다. 왜냐하면 원점에서 시작할 필요가 없기 때문입니다. 그렇다면 벡터 a와 -2의 곱은 어떻게 다르나요? 마이너스 부호가 벡터의 방향을 뒤집고 2가 벡터의 크기를 2배로 키웁니다. 벡터의 크기는 2배가 되었고 마이너스 부호로 인해 방향은 반대가 됐습니다.