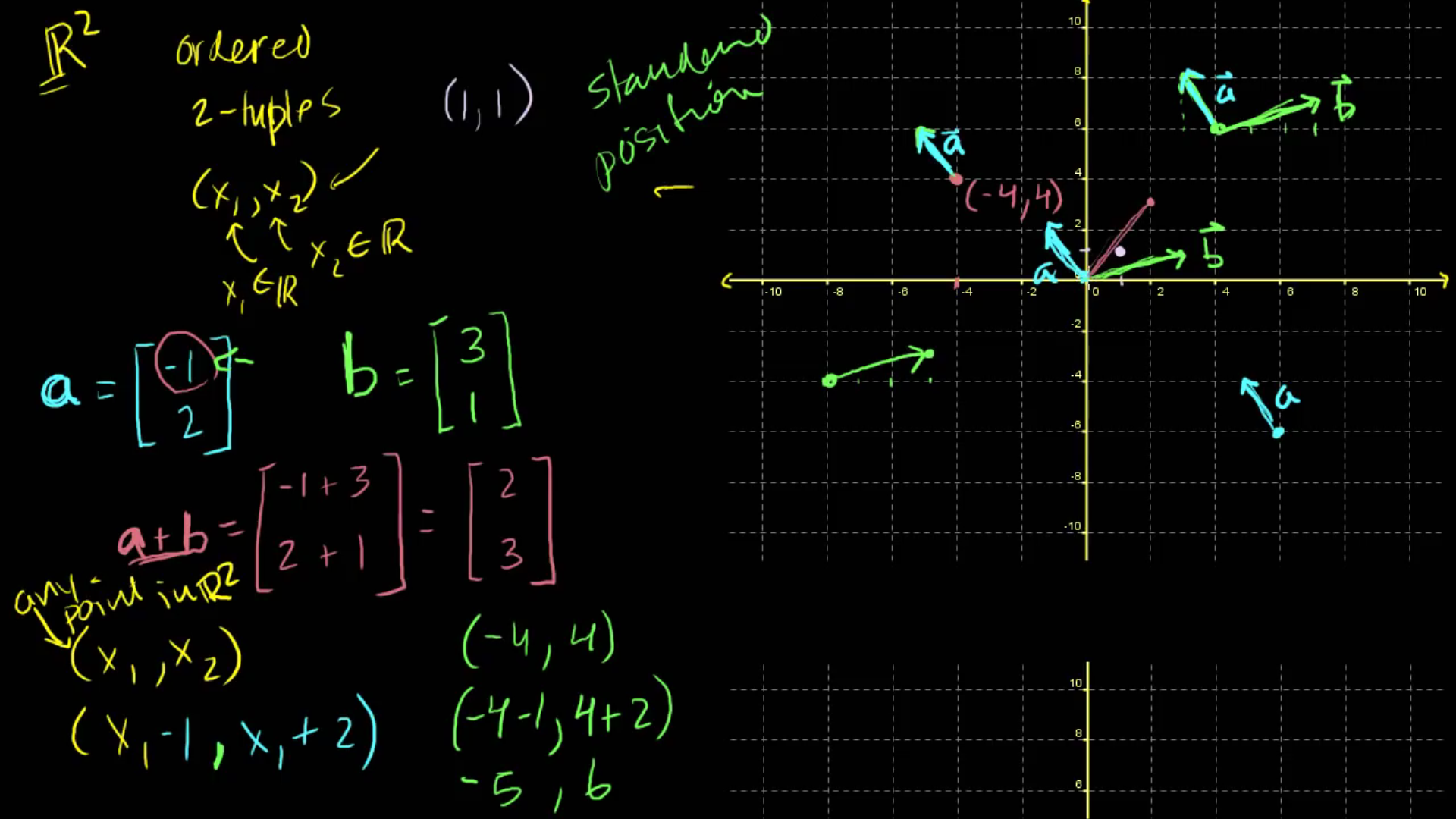벡터 예제

출처 : 칸 아카데미 선형대수학 (https://ko.khanacademy.org/math/linear-algebra/vectors-and-spaces)

Video

$1$

지난 글에서 $R_^{n}$ , 벡터, 덧셈, 스칼라곱 등을 정의하였습니다. 그래서 이번 영상에서는 기초로 돌아가서 예시를 많이 보여드리려고 해요. 벡터가 뭔지 어떻게 다루는지에 대해 좀 더 구체적인 직관을 가질 수 있도록 말이죠. 그럼 몇 가지 벡터를 정의해 봅시다.

이 영상에서 쓰이는 대부분의 벡터는 $R_^{2}$ 상에 있습니다. 편의를 위해서죠. $R_^{n}$ 는 모든 2-튜플의 집합이라는 것을 기억하죠? 순서가 주어진 2-튜플로써 먼저 x1이 있고 x2가 있습니다. 두 수 모두 실수입니다. 그러므로 x1이 실수 집합의 원소이고 x2도 마찬가지입니다.

여기에 좌표평면이 있고 x1, x2를 찍어보도록 하죠. 아시다시피 이걸 x 좌표로 생각할 수 있겠죠. 이게 x 축이라고 생각하면 돼요. 두 번째 좌표는 세로축에 찍으면 되고요. 보통 y 축이라고 많이 하는데 그냥 두 번째 축으로 부르도록 하죠. 이제 $R_^{2}$ 위의 모든 벡터는 말 그대로 무한대로 뻗어나간다면 이 평면 위의 각 점으로 모두 나타낼 수 있습니다. 무한대로 뻗어나간다면 이 평면 위의 각 점으로 모두 나타낼 수 있습니다. 그게 $R_^{2}$죠. $R_^{1}$은 그저 한 수직선상의 모든 점이에요. 즉 $R_^{2}$가 $R_^{1}$보다 더 큰 공간이라는 것을 금방 확인할 수 있습니다.

$2$

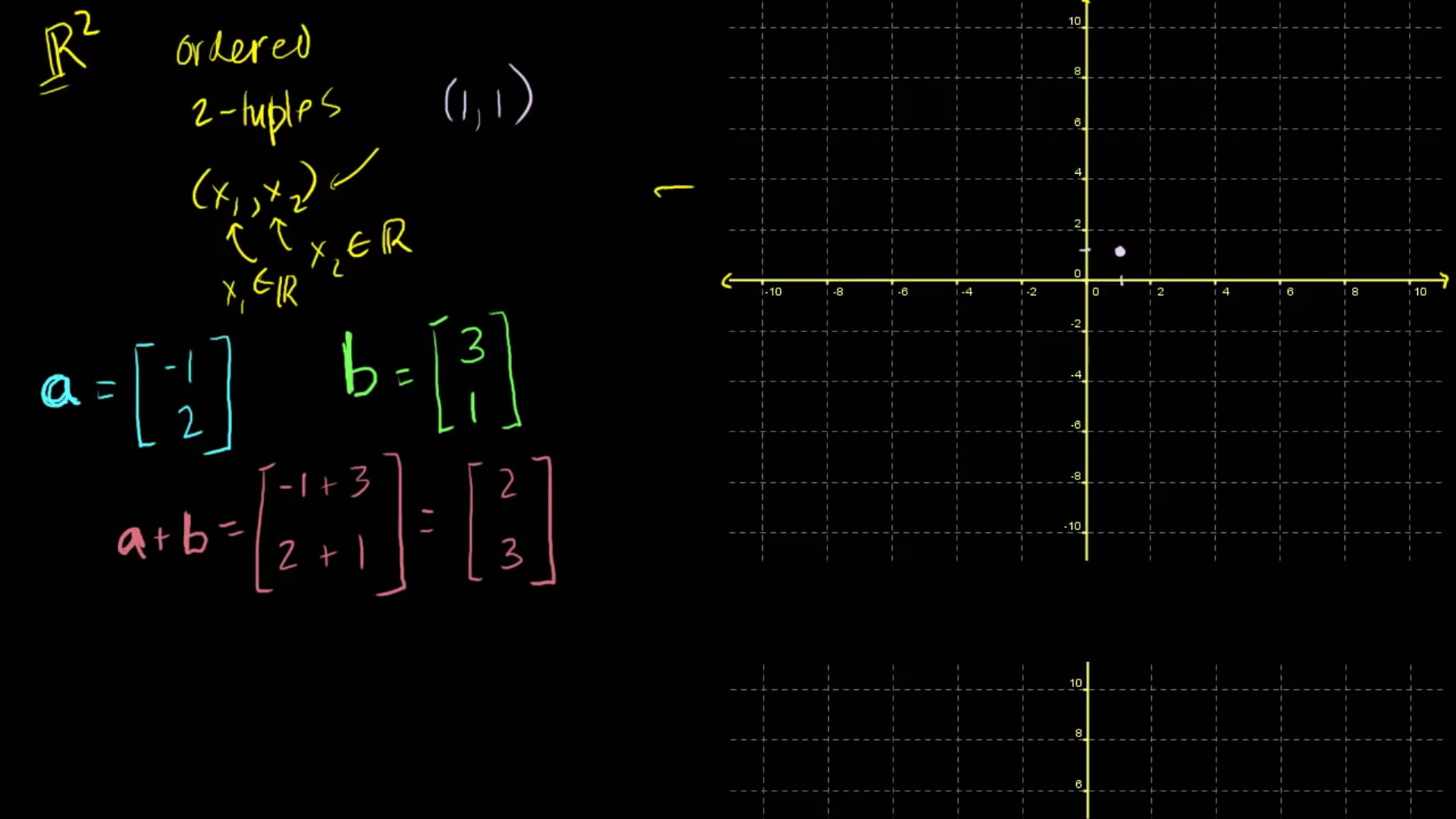
몇 가지 예를 들어볼게요. $R_^{2}$ 위의 벡터 몇 가지를 생각해 봅시다. 먼저 벡터 a를 정의할게요. a를 (-1, 2)라고 해봅시다. a를 (-1, 2)라고 해봅시다. b를 (3, 1)이라고 하죠. 이렇게 두 벡터가 있습니다. 이제 a와 b를 더해요. 성분별로 더합시다 -1 + 3 하고 2 + 1이네요.

만약 (1, 1)을 나타내려 한다면 그럼 좌표평면에 x축이라고 부르는 축에서 가로선에서 그 방향으로 1만큼 가죠. 두 번째 점은 위쪽으로 1만큼 가고요. 따라서 여기가 (1, 1)이죠. 이것이 관례적인 방식입니다. 벡터를 나타낼 때는 보통 그냥 점 (-1, 2)로 나타낼 수도 있겠죠. 어느 정도까지는 이렇게 해도 됩니다. 하지만 벡터는 어떤 점에서든 시작할 수 있어요. 2차원 벡터를 생각해 봅시다. $R_^{2}$ 위의 어떤 점에서든 시작할 수 있어요. (x1, x2)에서 시작한다고 해봅시다. $R_^{2}$ 위의 어떤 점이든 상관 없어요. 벡터를 나타내기 위해 그 점에서 점 x1로 선을 긋습니다.

$3$

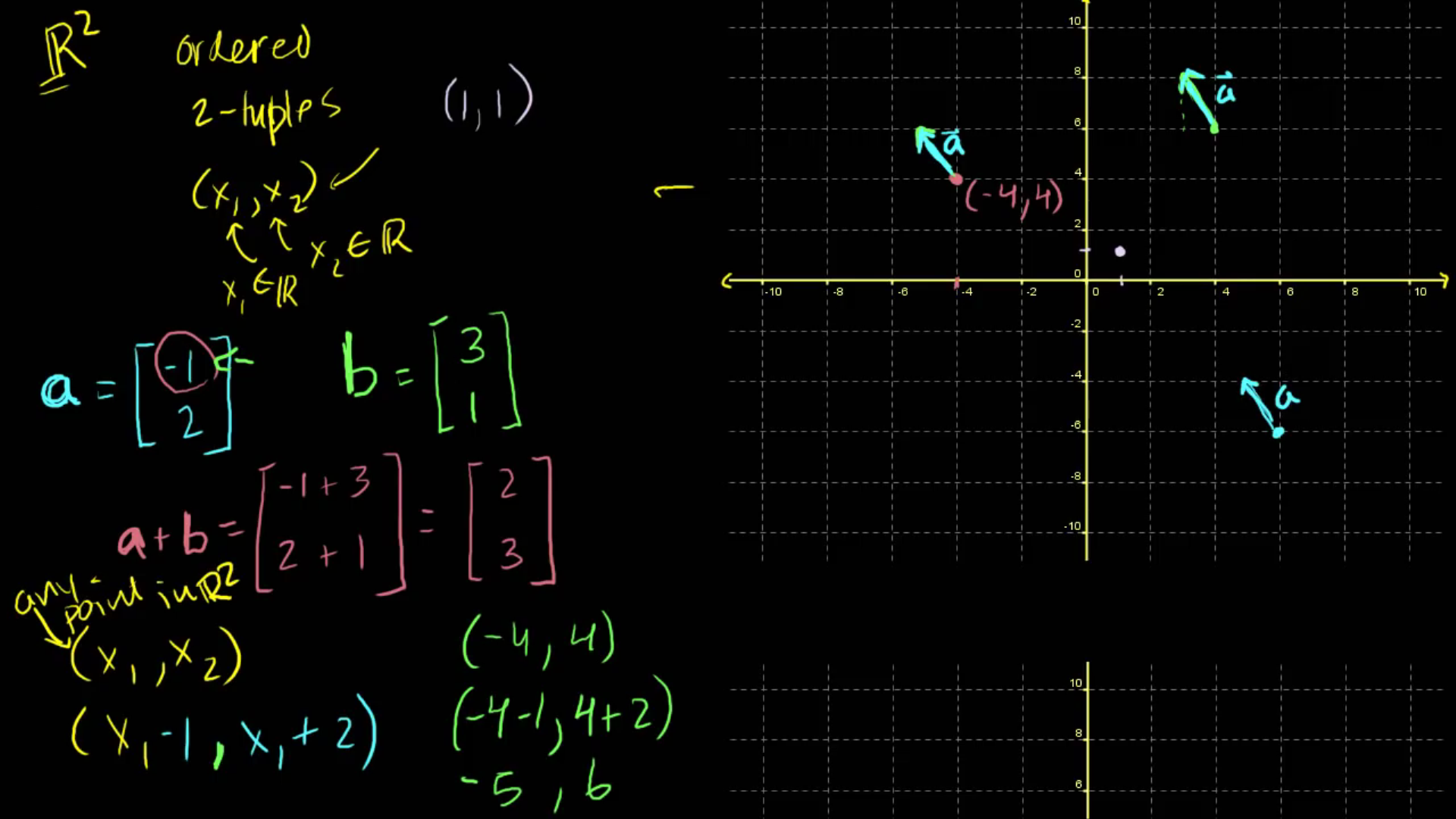
벡터 a를 나타내는 과정입니다. x1 -1, x1 +2 입니다. 어디서 시작할까요? 별다른 이유 없이 여기서 아무 점이나 찍겠습니다. 점 하나를 고릅니다. 여기로 잡죠 여기가 시작점이에요. (-4, 4) 입니다 (-4, 4) 입니다. 만약 벡터 a를 나타내고 싶다면 벡터 a의 첫 번째 성분을 첫 번째 좌표에 더합니다. 따라서 x1 + (-1) = x1 -1 입니다. 지금 여기서는 x1이 -4죠. 그러므로 시작점은 바로 (-4, 4)가 됩니다. 벡터 a를 나타내고자 한다면 -4에서 첫 성분 -1을 더한 점까지 화살표를 그립니다. 그 다음 4에 두번째 성분을 더하죠 4 + 2입니다.

그럼 여기는 어떻게 되나요? (-5, 6)이 됩니다. 이 점에서 선을 하나 긋습니다. 벡터는 이렇게 생겼겠죠. 여기서 저기까지 선을 긋습니다. 끝에는 화살표를 표시해주고요. 이것이 벡터 (-1, 2)를 나타내는 하나의 방법이에요. (-5, 6)이 바로 여기니까 벡터를 이렇게 그리죠. (-4, 4)는 아무렇게나 고른 점이었다는 걸 기억하세요.

여기서 시작했을 수도 있어요. (4, 6)에서 시작하고 똑같이 할 수도 있었죠. (4, 6)에서 시작하고 똑같이 할 수도 있었죠 수평 방향으로 -1만큼 가고 수직 방향으로 +2만큼 가는 거죠. 수평 방향으로 -1, 수직 방향으로 2만큼 가서 여기로 가서 나타낼 수도 있었어요. 저기서 그려도 똑같았겠죠. 같은 벡터 a를 나타낸 거예요.

$4$

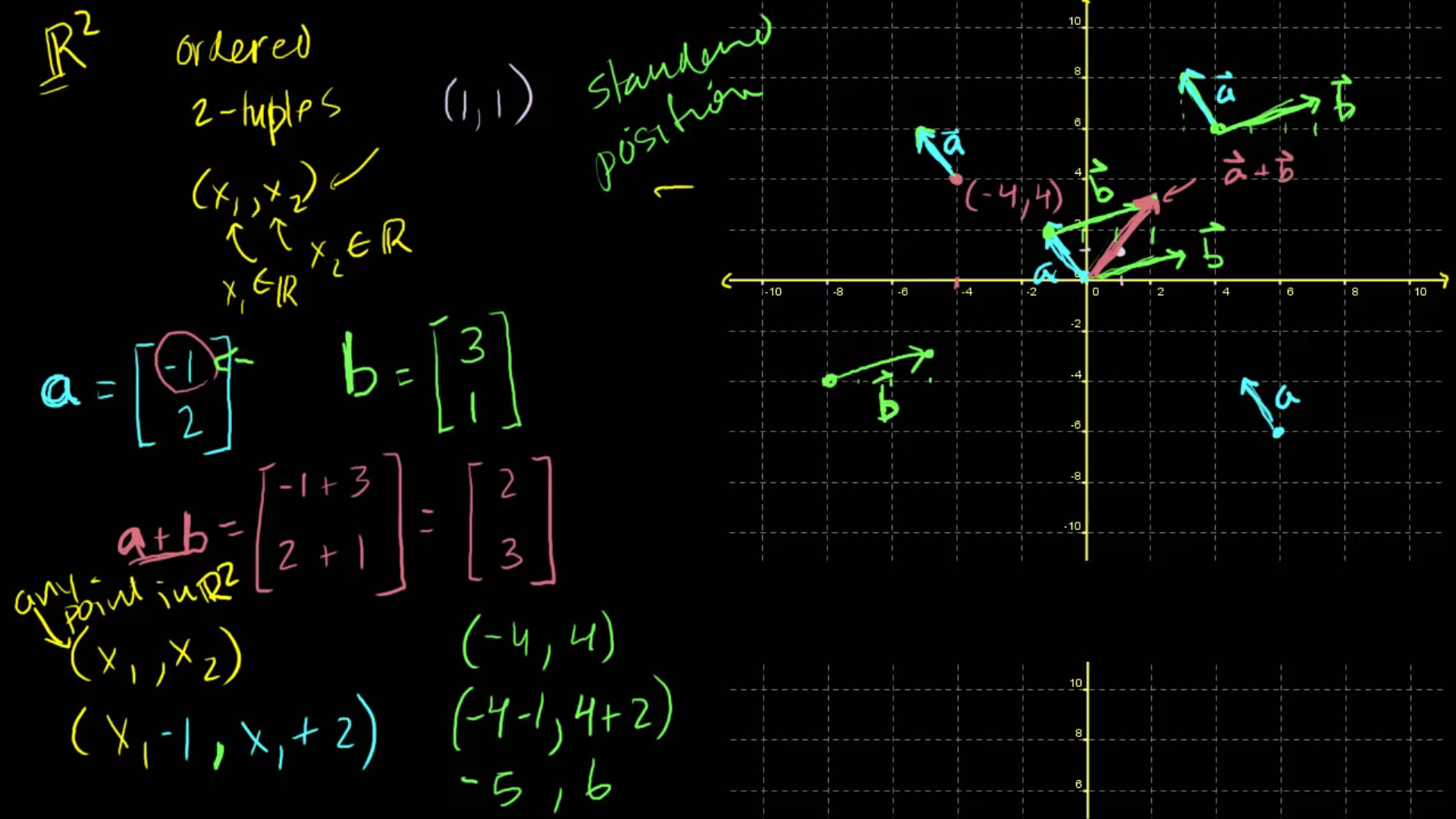
b도 똑같아요 b는 어떤가요? b를 시작할 점을 임의로 정할 수 있어요. 오른쪽으로 세 칸이므로 하나, 둘, 셋 그리고 위로 한 칸 올라갑니다. 벡터 b를 나타내면 이렇게 되겠죠. 나타내는 방법은 무한합니다.

하지만 일반적으로는 표준점이라는 곳에 놓습니다. (0, 0)에서 시작하는 거죠. 그러므로 시작점은 직접 써보도록 하겠습니다. 시작점을 (0, 0)으로 하는 벡터를 그립니다. 따라서 벡터 a는 (0, 0)에서 시작하여 왼쪽으로 한 칸, 위로 두 칸 가는 거죠. 이게 표준점에서 나타낸 벡터 a입니다. 벡터 b도 표준점에서 나타내보죠. 이게 표준점에서 나타낸 벡터들인데 다른 위치에서 시작해도 모두 동일합니다. 그럼 a+b를 나타내면 뭘 얻는지 한 번 확인해봅시다. a+b 만약에 이걸 표준점에서 그렸다면 계산 다 했죠 (2, 3)입니다. 2만큼 오른쪽으로 가고 위로 3만큼 가요. 표준점에서 그리면 이렇게 생겼겠죠 이 벡터입니다. 여기 그린 이 벡터가 표준점에서 그린 벡터 a+b인데요. a와 b를 더했을 때 그 관계가 명확하지는 않아요. 이 관계를 확실히 하려면 a와 b를 연결해야 합니다.

b의 꼬리를 a의 머리에 연결하라는 뜻입니다. 그러니까 b를 나타내는 다른 방법은 표준점에서 시작한 a의 끝점에서 b를 시작하는 것입니다. 그곳을 시작점으로 잡은 뒤에 b를 그리는 거죠.

b를 표준점에서 나타낸 건 아니지만 여기서 나타내도 상관은 없었어요 지금 무엇이 보이나요? 여기 있는 a와 b를 더하면 a의 시작점이랑 b의 끝점이랑 이으면 어떻게 되나요? 바로 벡터의 합이 됩니다. 두 벡터를 더한 거죠. 어디서 시작했든 상관은 없었어요. 여기서 a를 시작할 수도 있었겠죠.

그렇게 끝점을 찍고요. 여기서 b를 시작해서 오른쪽으로 하나, 둘, 세칸 만큼 가고 위로 1만큼 가서 여기다 b를 그려도 됩니다 a+b를 그린다고 하면 a의 시작점에서 b의 끝점까지 이으면 됩니다 그게 a+b를 시각적으로 나타낸 것입니다 그게 a+b를 시각적으로 나타낸 것입니다 여기서 뭘 한 건지 정확하게 얘기하자면 오른쪽으로 2만큼 가고 하나, 둘, 셋 위로 3만큼 간 거죠 하나, 둘, 셋 a+b를 얻었어요 이제 벡터의 스칼라곱을 취하면 어떻게 되는지 생각해봅시다 어떤 스칼라만큼 곱합니다 새 벡터를 골라볼게요 이제 얘들은 좀 지겹잖아요 벡터 v를 정의하겠습니다 vector의 첫 글자를 따서 말이죠 v = (1, 2)로 정해봅시다 표준점에서 v를 그린다고 하면 오른쪽으로 1만큼 위로 2만큼 가면 되겠죠 좋아요 이게 표준점에서 잡은 벡터입니다 표준점 말고 다른 데서 하고 싶으면 여기서 해도 되고요 오른쪽으로 1만큼, 위로 2만큼 말이죠 v를 이렇게 그려도 상관 없어요 동일한 벡터입니다 이제 v에 스칼라를 곱하면 어떻게 되는지 봅시다 2v는 어떻게 되죠? 2v는 v의 각 성분을 2배한 것입니다 2 × 1 = 2 이고 2 × 2 = 4 입니다 2v는 그럼 어떻게 생겼을까요? 임의의 지점에서 시작해보죠 여기서 시작할게요 여기서 하나, 두 칸 만큼 오른쪽으로 위로 4만큼 움직입니다 1, 2, 3, 4 2v는 이렇게 생겼습니다 v에 2만큼 곱한 거죠 v와 방향은 똑같은데 길이만 2배가 됐죠 크기만 2배로 늘렸으므로 성립하는 것입니다 따라서 스칼라곱을 하면 방향은 변하지 않아요 방향은 곱하기 전이랑 똑같고요 크기만 이 값만큼 늘리는 거죠 아무데서나 시작해도 됩니다 여기서 시작할 수도 있었죠 2v를 v 바로 위에 그려도 돼요 어떻게 되는지 보일겁니다 하지만 가리고 싶지는 않습니다 만약 표준점에 그렸다면 동일선상에 놓이는 걸 확인할 수 있습니다 같은 선 위에 있고 크기만 두 배인 경우죠 길이는 두 배인데 방향은 똑같고요 그럼 v에 -4를 곱한다면 어떻게 되었을까요? 그럼 v에 -4를 곱한다면 어떻게 되었을까요? 그럼 v에 -4를 곱한다면 어떻게 되었을까요? -4 × 1 = -4 입니다 -4 × 1 = -4 이고 -4 × 2 = -8 입니다 바로 이 벡터입니다 (-4, -8) 입니다 이것이 바로 -4v 인거죠 임의로 시작점을 잡아볼게요 일단 표준점에서 해볼까요 오른쪽으로 -4만큼 가고 또는 왼쪽으로 4만큼 왼쪽으로 하나, 둘, 셋, 네칸 만큼 가고요 아래로 8만큼 가는 거죠 이렇게 생겼네요 벡터는 이렇게 생겼습니다 직선처럼 똑바로 그려볼게요 좋습니다 이게 -4v입니다 화살표 표시를 해서 확실히 벡터처럼 보이게 할게요 어떻게 됐나요? 같은 방향에 있다고도 할 수 있지만 실제로는 정반대 방향에 있네요 하지만 같은 직선 상에 있죠? 방향만 반대인 거고요 여기 이 - 부호가 방향을 반대로 바꾸었습니다 만약에 -1을 곱했다면 방향만 바뀌고 끝났겠죠? 하지만 -4를 곱했잖아요 따라서 4만큼 곱했으므로 길이를 4배한 다음에 마이너스니까 반대방향으로 가는 거죠 방향이 거꾸로 되는 것입니다 이것을 이해했으므로 벡터의 차에 대해서도 이해할 수 있습니다 벡터 2개를 떠올려 봅시다 굵은 글씨의 이 벡터 x는 물론 R²의 원소입니다 영상에서 후반부에 R³이나 R⁴에 대한 예시를 몇 가지 알아볼 예정입니다 x = (2, 4) 라고 해 봅시다 다른 벡터 y를 설정합니다 굵은 글씨로 하죠 (-1, -2)라고 할게요 이제 x - y가 무엇인지 구하고자 합니다 이제 x - y가 무엇인지 구하고자 합니다 이제 x - y가 무엇인지 구하고자 합니다 이렇게 생각할 수 있어요 x + (-1) × y 로 말이죠 그렇죠? x + (-1) × y 입니다 이제 기존의 정의를 사용합니다 스칼라곱을 어떻게 하는지 알고 있죠 계산하면 다음과 같습니다 색을 바꿔볼게요 이 색이 마음에 안 드네요 x 벡터는 (2, 4)이고 그럼 (-1) × y는 무엇일까요? (-1) × y는 먼저 (-1) × (-1) = 1 이고 -1에 -2를 곱하면 2가 됩니다 x - y는 그냥 이 두 벡터를 더한 거죠 그렇죠? -y를 더하는 거예요 -y를 말이죠 x - y를 계산하면 (3, 6) 입니다 그럼 시각적으로 나타냈을 때 어떻게 생겼는지 한번 봅시다 x는 (2, 4)였고요 표준점에서 그린 (2, 4)는 이렇게 생겼고요 이게 x 벡터죠 그 다음에 벡터 y를 표준점에서 그리는데 다른 색으로 해 볼게요 녹색으로요 y는 (-1, -2) 입니다 y는 (-1, -2) 입니다 이렇게 생겼습니다 이렇게 생겼습니다 의도치 않게 같은 직선 위의 벡터를 잡았는데 이것도 나름대로 흥미로운 부분입니다 이게 벡터 y죠 그럼 두 벡터의 차는 뭔가요? (3, 6)이죠 이게 벡터 (3, 6)이에요 차가 이 벡터인데요 다른 곳에 그려볼게요 여기서 시작해서 1, 2, 3만큼 가고 위로 6만큼 가는 거죠 위로 6만큼 가면 이렇게 생긴 벡터를 얻지요 이게 두 벡터의 차입니다 x - y라고 할 수 있어요 어떻게 이 값이 차가 되는거죠? 이 벡터를 겹친다고 생각해 보세요 이 벡터를 평행이동시키고 여기를 시작으로 쭉 올라가면 됩니다 그러면 사실 끝점끼리의 차라는 걸 확인할 수 있을 것입니다 끝점끼리 잇고 있는 거죠 사실 같은 직선 위에 있는 벡터를 잡고 싶진 않았어요 다른 예시를 들어볼게요 저것도 충분히 흥미롭긴 한데요 보통 책에서는 안나오니까요 벡터 x를 (2, 3)으로 잡고 벡터 y는 (-4, -2)로 하겠습니다 x를 표준점을 기준으로 하면 어디에 위치하게 되나요? (2, 3) 입니다 이렇게 되겠죠 원점에서 시작하여 그린 벡터 x 입니다 이게 x고요 y는 어떻게 생겼나요? y는 주황색으로 해볼게요 (-4, -2) 이므로 y는 이렇게 생겼습니다 y는 이렇게 생겼습니다 그러면 x - y는 무엇일까요? 그러면 x - y는 무엇일까요? 알다시피 2에 -1을 곱한 것을 더하는 거죠 2 - (-4)라고 할 수 있겠죠 슬슬 감이 오지 않나요? 처음부터 이렇게 안 한 이유는 스칼라곱의 기초적인 정의를 이용하여 보여주고 싶었기 때문입니다 x - y는 2 + (-1)(-4)니까 2 - (-4)이고 2 + 4랑 같으므로 6이고요 3 - (-2)니까 5죠 맞죠? 즉, 두 벡터의 차는 (6, 5)가 되는 거죠 여기에도 그릴 수 있어요 4에 6을 더하고, 위로 5만큼 올라가고 이런 식으로 말이죠 그러면 이렇게 생겼겠죠 사실 이렇게 휘어지면 안 되는데 어쨌든 x - y입니다 저번 예시처럼 이 벡터를 끝점끼리 잇는 것으로 나타낼 수도 있습니다 여기서 그리면 어떻게 될까요? 이 점에서 시작하여 오른쪽으로 6만큼 위로 5만큼 가면 여기에 도달하죠 따라서 두 벡터의 차는 다시 정확히 그리면 이렇게 생긴 겁니다 딱 이렇게요 직관적으로 이해가 되죠 x - y 이게 두 벡터의 차입니다 이 차를 한 벡터에서 다른 벡터로 어떻게 가느냐로 해석할 수도 있겠죠? 예컨대, 초등학교 2학년 시절에 스칼라밖에 없던 시절을 생각해보면요 7-5가 뭐냐고 물어보면 여러분은 2라고 답했을 것이고 그건 5+2가 7이라는 얘기잖아요 또는 5와 7의 차가 2라고 할 수도 있고요 여기서 말하고자 하는 건 두 벡터 x와 y의 차가 바로 이 벡터라는 겁니다 여기 이 벡터와 같다는 거죠 5에 2를 더하면 7이 되잖아요 벡터 y에 벡터 x-y를 더하면 벡터 x를 얻는다고 할 수 있죠 이제 또 다른 재밌는 걸 하나 살펴보죠 y - x는 무엇인지 알아봅시다 y - x 그 값은 무엇일까요? 다른 색깔로 해볼게요 -4 - 2 = -6이고 -2 - 3 은 -5가 됩니다 그렇다면 y-x는 여기서 시작하면 6만큼 아래로 가고 1, 2, 3, 4, 5, 6 왼쪽으로 5만큼 갑니다 2, 4, 5 따라서 y - x는 이렇게 생겼습니다 따라서 y - x는 이렇게 생겼습니다 사실상 본질적으로 같은 벡터죠 어디서 시작하는지는 상관 없고요 방향만 반대죠 만약에 여기로 평행이동을 시켰다면 정확히 위에 겹치게 될 것입니다 x-y랑 똑같은데 방향만 반대겠죠 이는 일반적으로 쓰이는 알아두면 좋은 사실입니다 서로의 덧셈 역으로 생각할 수 있다는 거죠 한 번 더 설명해드릴게요 y를 그린다고 하면요 아니, x를 그릴게요 x를 (2, 3)으로 그릴 수 있죠 오른쪽으로 2, 위로 3 여러 번 했어요 표준점 아닌 곳에서 x를 나타낸 거죠 이것도 x죠 -x는 무엇인가요? -x는 (-2, -3)입니다 여기서 시작했으면 -2만큼 가고 -3만큼 가는 거죠 -x는 이렇게 생겼습니다 -x x랑 똑같잖아요 평행하고요 크기도 똑같고요 방향만 정반대죠 기억하고 있으면 직관적으로 이해하는데 꽤 도움이 됩니다 이제 이 덧셈 뺄셈을 정리합시다 이제 이 덧셈 뺄셈을 정리합시다 지금까지는 전부 R²에서만 했습니다 이를 일반화하고자 합니다 어디까지 일반화할 수 있냐면 직관적으로 시각적으로 나타내기 어려운 벡터공간에까지 일반화할 수 있습니다 몇 가지 벡터를 정의해볼게요 벡터 a를 (0, -1, 2, 3)으로 정하고 벡터 b는 (4, -2, 0, 5)로 정하겠습니다 이 벡터들에 대해서도 똑같이 덧셈과 뺄셈을 할 수 있습니다 단지 시각적으로 나타내기 어려울 뿐이죠 그냥 벡터 형태로 두면 됩니다 4차원에도 적용할 수 있어요 먼저 4a를 보면 먼저 4a를 보면 4a - 2b를 봅시다 이 값은 무엇일까요? 벡터가 되겠죠 무엇과 같을까요? 먼저 4를 벡터 (0, -1, 2, 3)에 곱합니다 먼저 4를 벡터 (0, -1, 2, 3)에 곱합니다 여기에 -2b를 계산합니다 -2에 (4, -2, 0, 5)를 곱하죠 그 결과는 어떻게 될까요? 이 항에 4를 곱하면 태블릿이 오류가 나서 여기서 다시 하겠습니다 태블릿이 오류가 나서 여기서 다시 하겠습니다 4를 곱하는 거니까 먼저 4 × 0 = 0, -4, 8 4 × 2 = 8이죠 4 × 3 = 12고요 노란색으로 해봅시다 빼기 2 × 4 = 8이고 2 × (-2) = -4 2 × 0 = 0 2 × 5 = 10 입니다 여기는 좀 별로네요 여기에선 잘 안 써지는군요 왜 그런지는 모르겠지만 하여튼 여기다 쓴다고 하면 답은 뭐죠? 0 - 8은? -8 입니다 -4 - 4, 아니 -4를 빼는 거죠 -4 + 4니까 0이고요 8 - 0 = 8이고 12 - 여기 값이 뭐죠? 뭔지 보이지도 않네요 아, 10이군요 다시 보이네요 지금 뭔가 굉장히 이상하네요 2 × 5 = 10이니까 12 - 10 = 2가 나오겠네요 즉, 이 벡터를 4배하고 이 벡터를 2배한 뒤 빼면 이 벡터를 얻는 겁니다 이 결과를 시각적으로 나타내기는 어렵지만 이 결과를 시각적으로 나타내기는 어렵지만 여전히 유용한 개념이지요 나중에는 이 벡터들을 좀더 다차원에 적용하는 경우를 알아보겠습니다 좀더 다차원에 적용하는 경우를 알아보겠습니다