Direct Linear Transformation

참조 : http://www.cs.cmu.edu/~16385/s17/Slides/10.2_2D_Alignment__DLT.pdf
참조 : https://gaussian37.github.io/vision-concept-image_transformation/

사전 지식 : 특이값 분해 (Singular Value Decomposition)

DLT (Direct Linear Transformation) 개념

이번 글에서는 Homography 적용 시 4개의 점을 이용하여 3 X 3 Homography 행렬을 만드는 방법에 대하여 다루어 보도록 하겠습니다.

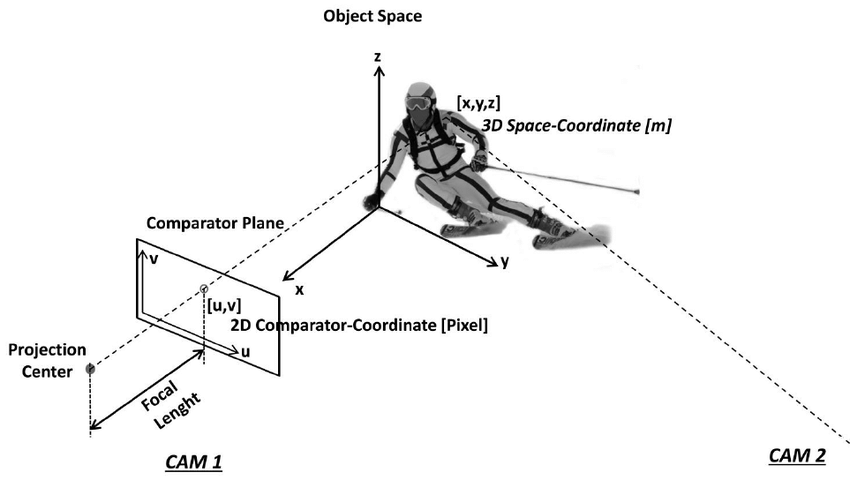
이미지 변환을 할 때, 위 그림과 같이 왼쪽의 이미지를 오른쪽 이미지와 같이 기하학적 변환을 적용하곤 합니다.
이 때, 동일 평면 (coplanar) 상의 점들을 3차원 변환을 하기 위하여 Homography(또는 Perspective Transformation, Projective Transformation) 방법을 사용합니다.
이번 글에서는 Homography에 대한 자세한 개념 보다는 두 이미지에서 대응되는 4개의 점을 이용하여 3 X 3 Homography를 구하는 방법에 대하여 다루어 보겠습니다.
Homography에 대한 개념은 아래 링크에서 확인하시기 바랍니다.
- 링크 : https://gaussian37.github.io/vision-concept-geometric_transformation/
- 링크 : https://gaussian37.github.io/vision-concept-camera_and_geometry/

\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \alpha H \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\]

\[H = \begin{bmatrix} h_{1} & h_{2} & h_{3} \\ h_{4} & h_{5} & h_{6} \\ h_{7} & h_{8} & h_{9} \end{bmatrix}\]

먼저 행렬 H를 Homography 행렬이라고 합니다. 위 식의 좌변과 우변의 \(x, y\) 쌍을 대응해 주기 때문입니다.
H에서 \(h _{9}\)는 스케일과 관련된 값으로 1 또는 사용할 스케일 값을 사용합니다. 즉, \(h_{i}\)해를 구할 때, 크게 고려하지 않아도 됩니다.
따라서 8개의 파라미터 \(h_{1}, h_{2}, \cdots h_{8}\)을 구하기 위하여 8개의 식이 필요합니다. 즉, \((x, y)\)로 이루어진 4개 점을 통하여 8개의 식을 얻고 8개의 식을 이용하여 파라미터 8개를 연립방정식을 통하여 구할 수 있습니다.

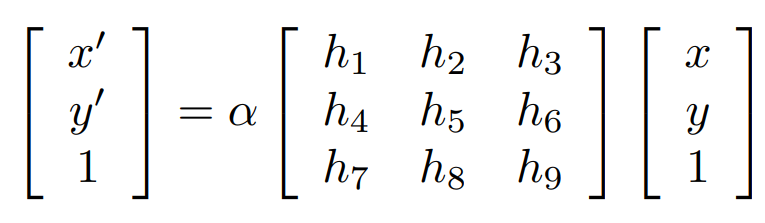
먼저 Homography의 파라미터를 구하기 위하여 위 식을 homogeneous linear equation 형태로 변형한 뒤 해를 구하는 방법을 사용하도록 하겠습니다.

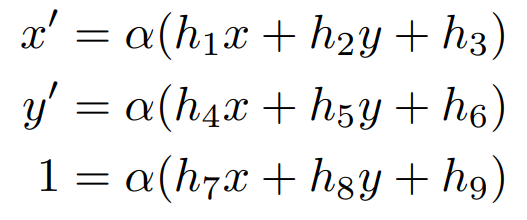
우변의 행렬을 전개하여 위 식과 같이 3개의 식으로 풀어 보겠습니다. 그 다음, 좌변이 1인 세번째 식을 첫번째, 두번째 식에 나누어 보겠습니다.

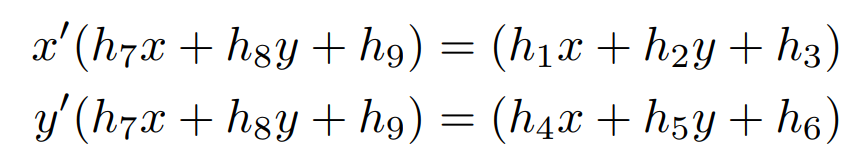
세번째 식으로 나눈 식에서 분모가 없도록 정리를 하면 위 식과 같이 2개의 식으로 정리할 수 있습니다.

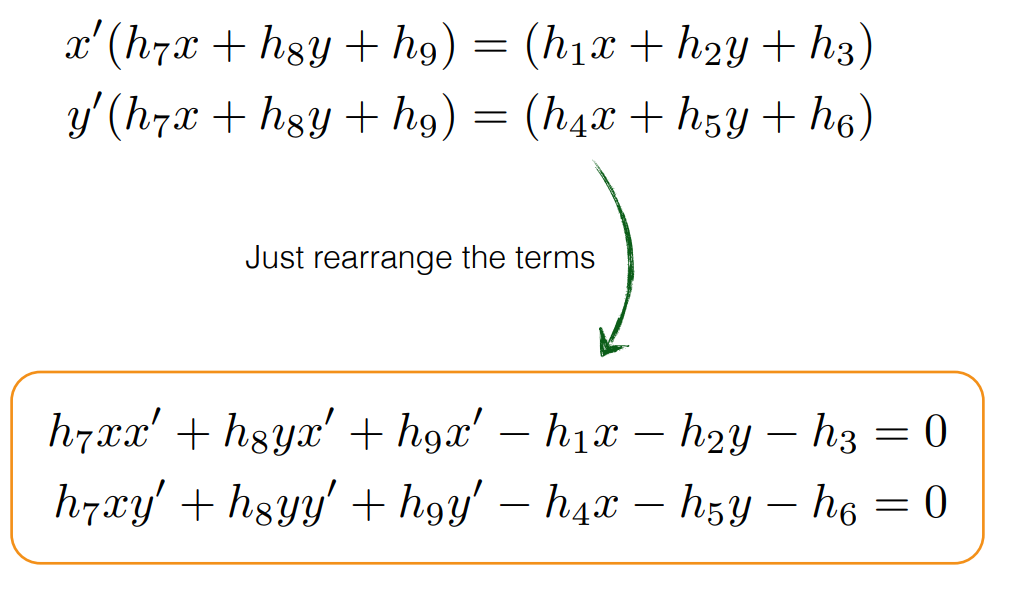
이 때, 우변이 0이 되도록 좌변과 우변을 정리하면 위 식과 같이 정리할 수 있습니다. 이제 우변을 0으로 만들었으므로 homogeneous 형태의 식을 만들 수 있습니다.

위 식에서 \(A_{i}\)는 (2 X 9) 크기의 행렬이고 \(h\)는 (9 X 1) 크기의 행렬이므로 연산 결과 (2 X 1) 크기의 영행렬을 얻을 수 있습니다.
이를 확장하여 4개의 좌표 쌍을 사용한다면 \(A_{1}, A_{2}, A_{3}, A_{4}\)를 사용하여 (8 X 9) 크기의 행렬 \(A\)를 만들 수 있고 \(h\)는 (9 X 1) 크기의 행렬이므로 우변은 (8 X 1) 크기의 행렬을 만들 수 있습니다.

\[Ah = 0\]

\[\begin{bmatrix} -x_{1} & -y_{1} & -1 & 0 & 0 & 0 & x_{1}x_{1}' & y_{1}x_{1}' & x_{1}' \\ 0 & 0 & 0 & -x_{1} & -y_{1} & -1 & x_{1}y_{1}' & y_{1}y_{1}' & y_{1}' \\ -x_{2} & -y_{2} & -1 & 0 & 0 & 0 & x_{2}x_{2}' & y_{2}x_{2}' & x_{2}' \\ 0 & 0 & 0 & -x_{2} & -y_{2} & -1 & x_{2}y_{2}' & y_{2}y_{2}' & y_{2}' \\ -x_{3} & -y_{3} & -1 & 0 & 0 & 0 & x_{3}x_{3}' & y_{3}x_{3}' & x_{3}' \\ 0 & 0 & 0 & -x_{3} & -y_{3} & -1 & x_{3}y_{3}' & y_{3}y_{3}' & y_{3}' \\ -x_{4} & -y_{4} & -1 & 0 & 0 & 0 & x_{4}x_{4}' & y_{4}x_{4}' & x_{4}' \\ 0 & 0 & 0 & -x_{4} & -y_{4} & -1 & x_{4}y_{4}' & y_{4}y_{4}' & y_{4}' \end{bmatrix} \begin{bmatrix} h_{1} \\ h_{2} \\ h_{3} \\ h_{4} \\ h_{5} \\ h_{6} \\ h_{7} \\ h_{8} \\ h_{9}\end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\]

위 식에서 \((x_{i}, y_{i})\)와 \((x_{i}', y_{i}')\)는 변환 전, 변환 후에 대응되는 좌표값으로 실제 값이 입력됩니다.
즉, 구해야 하는 미지수는 \(h_{i}\) 값이 됩니다.
따라서 이 문제는 Homogeneous Linear Least Squares 문제가 되며 SVD(Singular Value Decomposition)을 이용하여 풀 수 있습니다.

\[A = U \Sigma V^{T}\]

행렬 A를 SVD를 이용하여 분해하였을 때, Singular Value가 최소가 되는 Right Singular Vector를 \(V\) 행렬에서 선택하면 \(Ah = 0\) 에 가장 근사하는 \(h\) 를 구할 수 있습니다.
SVD를 하였을 때, Singular Value 중 가장 작은 값이 0이면 \(Ah = 0\) 문제를 푸는 것이고 \(h\) 는 가장 작은 Singular Value에 해당하는 Right Singular Vector가 됩니다.
반면 Singular Value 중 가장 작은 값이 0이 아닌 양수이더라도 해는 가장 작은 Singular Value에 해당하는 Right Singular Vector가 되지만 \(Ah = 0 \to Ah = \delta \gt 0\) 의 문제로 바뀌게 되며 근사값을 찾게 됩니다. ( \(\delta\) 는 0에 가까운 작은 값입니다.)
이와 같은 방법은 아래 링크에 자세하게 설명 되어 있으니 참조하시면 됩니다.
- 링크 : SVD를 이용한 선형 연립 방정식 풀이

위 방법을 통하여 \(h\) 를 구하였으면 처음에 구하고자 한 형식에 맞게 \(H\) 행렬 (3 x 3) 으로 모양을 바꿔주면 homography를 최종적으로 구할 수 있습니다.

지금까지 살펴본 Direct Linear Transformation의 순서를 다시 정리하면 위 절차와 같습니다.

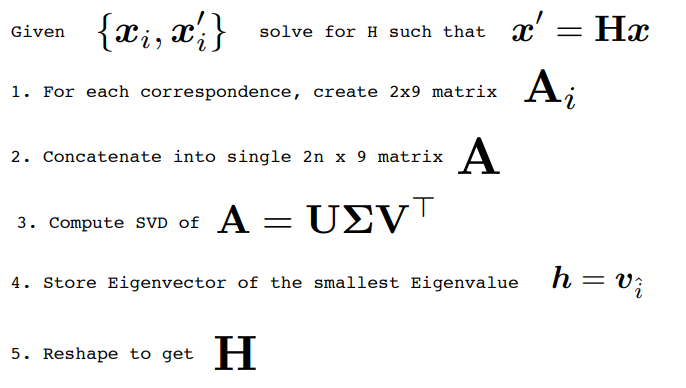
Python 실습

앞에서 살펴본 DLT 내용을 파이썬 코드로 실습해 보면 다음과 같습니다. 아래 코드에서 compute_homography 함수가 SVD를 이용하여 Homography를 구하는 연산이고 apply_homography 함수는 Transformation을 적용하는 함수입니다.

import numpy as np
from numpy.linalg import svd
np.set_printoptions(suppress=True)

def compute_homography(points1, points2):
    # Ensure the points are in homogeneous coordinates
    points1 = np.array(points1)
    points2 = np.array(points2)
    
    assert points1.shape == points2.shape
    assert points1.shape[0] >= 4  # Need at least 4 points
    
    # Construct matrix A
    A = []
    for i in range(len(points1)):
        x, y = points1[i][0], points1[i][1]
        x_prime, y_prime = points2[i][0], points2[i][1]
        
        A.append([-x, -y, -1, 0, 0, 0, x_prime * x, x_prime * y, x_prime])
        A.append([0, 0, 0, -x, -y, -1, y_prime * x, y_prime * y, y_prime])
    
    A = np.array(A)
    
    # Perform SVD
    U, S, Vt = svd(A)
    
    # The homography is the last row of V (or the last column of V transpose)
    H = Vt[-1].reshape(3, 3)
    
    # Normalize H
    H = H / H[2, 2]
    
    return H

def apply_homography(H, point):
    """Apply the homography matrix H to a point."""
    point_homogeneous = np.array([point[0], point[1], 1]).T
    transformed_point = H @ point_homogeneous
    # Convert from homogeneous to 2D coordinates
    transformed_point /= transformed_point[2]
    return transformed_point[:2]

src_points = [
    (100, 100), (150, 100), (200, 100), (250, 100), (300, 100), (350, 100), (400, 100),
    (100, 150), (150, 150), (200, 150), (250, 150), (300, 150), (350, 150), (400, 150),
    (100, 200), (150, 200), (200, 200), (250, 200), (300, 200), (350, 200), (400, 200)
]
dest_points = [
    (120, 110), (170, 110), (220, 110), (270, 110), (320, 110), (370, 110), (420, 110),
    (120, 160), (170, 160), (220, 160), (270, 160), (320, 160), (370, 160), (420, 160),
    (120, 210), (170, 210), (220, 210), (270, 210), (320, 210), (370, 210), (420, 210)
]

# Compute homography
H = compute_homography(src_points, dest_points)
print(f"Computed Homography Matrix: \n{H}\n")

# Apply homography to each point in points1
transformed_points = [apply_homography(H, pt) for pt in src_points]

# Compare the transformed points with the original points2
for i, (transformed_point, dest_point) in enumerate(zip(transformed_points, dest_points)):
    print(f"Point {i + 1}: Transformed Point = {transformed_point}, Destination Point = {dest_point}, Difference: {np.round(np.abs(transformed_point - dest_point), 4)}")

# Computed Homography Matrix: 
# [[ 1.  0. 20.]
#  [-0.  1. 10.]
#  [ 0. -0.  1.]]

# Point 1: Transformed Point = [120. 110.], Destination Point = (120, 110), Difference: [0. 0.]
# Point 2: Transformed Point = [170. 110.], Destination Point = (170, 110), Difference: [0. 0.]
# Point 3: Transformed Point = [220. 110.], Destination Point = (220, 110), Difference: [0. 0.]
# Point 4: Transformed Point = [270. 110.], Destination Point = (270, 110), Difference: [0. 0.]
# Point 5: Transformed Point = [320. 110.], Destination Point = (320, 110), Difference: [0. 0.]
# Point 6: Transformed Point = [370. 110.], Destination Point = (370, 110), Difference: [0. 0.]
# Point 7: Transformed Point = [420. 110.], Destination Point = (420, 110), Difference: [0. 0.]
# Point 8: Transformed Point = [120. 160.], Destination Point = (120, 160), Difference: [0. 0.]
# Point 9: Transformed Point = [170. 160.], Destination Point = (170, 160), Difference: [0. 0.]
# Point 10: Transformed Point = [220. 160.], Destination Point = (220, 160), Difference: [0. 0.]
# Point 11: Transformed Point = [270. 160.], Destination Point = (270, 160), Difference: [0. 0.]
# Point 12: Transformed Point = [320. 160.], Destination Point = (320, 160), Difference: [0. 0.]
# Point 13: Transformed Point = [370. 160.], Destination Point = (370, 160), Difference: [0. 0.]
# Point 14: Transformed Point = [420. 160.], Destination Point = (420, 160), Difference: [0. 0.]
# Point 15: Transformed Point = [120. 210.], Destination Point = (120, 210), Difference: [0. 0.]
# Point 16: Transformed Point = [170. 210.], Destination Point = (170, 210), Difference: [0. 0.]
# Point 17: Transformed Point = [220. 210.], Destination Point = (220, 210), Difference: [0. 0.]
# Point 18: Transformed Point = [270. 210.], Destination Point = (270, 210), Difference: [0. 0.]
# Point 19: Transformed Point = [320. 210.], Destination Point = (320, 210), Difference: [0. 0.]
# Point 20: Transformed Point = [370. 210.], Destination Point = (370, 210), Difference: [0. 0.]
# Point 21: Transformed Point = [420. 210.], Destination Point = (420, 210), Difference: [0. 0.]

위 결과와 같이 Transformed Points와 Dest Points가 같으므로 정상정으로 Homography를 구한 것을 알 수 있습니다. 위 예제는 매우 간단하고 노이즈가 없는 예제이므로 Transformed Points와 Dest Points의 차이가 없습니다.
아래 예제는 점들에 노이즈가 추가되어 조금 어렵게 형성된 예제입니다.

src_points = [
    (154.2, 247.8), (191.3, 110.5), (213.7, 313.9), (341.1, 134.2), (432.5, 275.7),
    (287.4, 189.2), (345.3, 248.8), (290.8, 379.4), (132.1, 354.6), (178.5, 298.2),
    (341.5, 210.7), (254.3, 245.9), (310.9, 157.4), (420.7, 193.5), (387.2, 245.3),
    (187.4, 184.5), (342.9, 300.3), (238.7, 172.5), (179.8, 349.4), (230.1, 300.2),
    (415.6, 129.4)
]
dest_points = [
    (162.7, 258.3), (198.1, 120.4), (220.8, 323.5), (352.1, 144.6), (441.2, 285.9),
    (295.3, 200.8), (356.9, 259.7), (300.2, 388.1), (140.4, 364.7), (189.2, 308.3),
    (352.7, 221.5), (264.1, 255.7), (320.3, 168.2), (431.6, 203.7), (398.5, 254.8),
    (197.3, 195.2), (354.6, 311.7), (249.2, 183.8), (190.6, 360.1), (240.3, 310.5),
    (426.8, 140.6)
]


# Compute homography
H = compute_homography(src_points, dest_points)
print(f"Computed Homography Matrix: \n{H}\n")

# Apply homography to each point in points1
transformed_points = [apply_homography(H, pt) for pt in src_points]

# Compare the transformed points with the original points2
for i, (transformed_point, dest_point) in enumerate(zip(transformed_points, dest_points)):
    print(f"Point {i + 1}: Transformed Point = {transformed_point}, Destination Point = {dest_point}, Difference: {np.round(np.abs(transformed_point - dest_point), 4)}")

# Computed Homography Matrix: 
# [[ 0.62948896 -0.13996937 77.26706373]
#  [-0.11301842  0.64689205 66.98207917]
#  [-0.00043868 -0.000458    1.        ]]

# Point 1: Transformed Point = [170.54145084 256.27588536], Destination Point = (162.7, 258.3), Difference: [7.8415 2.0241]
# Point 2: Transformed Point = [210.54638186 135.00544025], Destination Point = (198.1, 120.4), Difference: [12.4464 14.6054]
# Point 3: Transformed Point = [220.13844963 322.48393338], Destination Point = (220.8, 323.5), Difference: [0.6616 1.0161]
# Point 4: Transformed Point = [346.30683226 146.08219468], Destination Point = (352.1, 144.6), Difference: [5.7932 1.4822]
# Point 5: Transformed Point = [454.57957033 287.20811344], Destination Point = (441.2, 285.9), Difference: [13.3796  1.3081]
# Point 6: Transformed Point = [294.30884688 199.28732076], Destination Point = (295.3, 200.8), Difference: [0.9912 1.5127]
# Point 7: Transformed Point = [353.68274796 257.16161861], Destination Point = (356.9, 259.7), Difference: [3.2173 2.5384]
# Point 8: Transformed Point = [296.59180241 400.11663673], Destination Point = (300.2, 388.1), Difference: [ 3.6082 12.0166]
# Point 9: Transformed Point = [142.10299935 360.98670428], Destination Point = (140.4, 364.7), Difference: [1.703  3.7133]
# Point 10: Transformed Point = [188.36905383 305.31898979], Destination Point = (189.2, 308.3), Difference: [0.8309 2.981 ]
# Point 11: Transformed Point = [348.61359007 218.50735649], Destination Point = (352.7, 221.5), Difference: [4.0864 2.9926]
# Point 12: Transformed Point = [261.5654585  254.32745519], Destination Point = (264.1, 255.7), Difference: [2.5345 1.3725]
# Point 13: Transformed Point = [317.03916619 168.87108922], Destination Point = (320.3, 168.2), Difference: [3.2608 0.6711]
# Point 14: Transformed Point = [433.40576589 198.96037183], Destination Point = (431.6, 203.7), Difference: [1.8058 4.7396]
# Point 15: Transformed Point = [399.37763163 253.42100193], Destination Point = (398.5, 254.8), Difference: [0.8776 1.379 ]
# Point 16: Transformed Point = [203.30153802 198.19534621], Destination Point = (197.3, 195.2), Difference: [6.0015 2.9953]
# Point 17: Transformed Point = [352.63059622 312.4693712 ], Destination Point = (354.6, 311.7), Difference: [1.9694 0.7694]
# Point 18: Transformed Point = [249.15616129 185.71242178], Destination Point = (249.2, 183.8), Difference: [0.0438 1.9124]
# Point 19: Transformed Point = [185.97323943 358.27897753], Destination Point = (190.6, 360.1), Difference: [4.6268 1.821 ]
# Point 20: Transformed Point = [236.47802522 308.80249163], Destination Point = (240.3, 310.5), Difference: [3.822  1.6975]
# Point 21: Transformed Point = [422.9471876  136.75769408], Destination Point = (426.8, 140.6), Difference: [3.8528 3.8423]

위 예제와 같이 Homography를 이상적으로 구할 수 없는 상황이라면 Transformed Points와 Dest Points 간의 차이가 있지만, 차이를 최소화하는 방향으로 Homography를 구하게 됩니다.
가장 좋은 방법은 노이즈가 포함된 점들은 계산에 악영향을 끼치므로 제거하는 것이 좋습니다. 따라서 Homography를 구할 때, RANSAC과 같은 노이즈 제거 방법을 통하여 좀 더 강건한 Homography를 구할 수 있습니다. RANSAC의 내용은 아래 링크를 참조하시면 됩니다.
- RANSAC (RANdom SAmple Consensus) 개념 및 실습 : https://gaussian37.github.io/vision-concept-ransac/

목차

DLT (Direct Linear Transformation) 개념

Python 실습

DLT (Direct Linear Transformation) 개념

Python 실습