Fourier transform (푸리에 변환)

2021, Feb 17    

• 참조 : Introduction to Computer Vision
• 참조 : https://youtu.be/TB1A2-Db67s
• 참조 : https://www.youtube.com/watch?v=spUNpyF58BY
• 참조 : https://www.youtube.com/playlist?list=PL5yujGYFVt0DhDXdKkFeou8zSV-KjOlAG (공돌이의 수학정리노트)
• 참조 : https://youtu.be/c8Q2lZvvnJo
• 참조 : https://www.youtube.com/playlist?list=PLEGnaIwMq6ozCqLEM_rEGxvZqqDi63omB

• 이번 글에서는 기본적인 푸리에 변환 (Fourier transform)에 대하여 다루어 보도록 하겠습니다.
• 보다 자세한 내용의 푸리에 변환은 아래 링크를 참조해 주시기 바랍니다. 이 글은 신호와 시스템 전반적인 내용을 다루며 그 중 푸리에 변환에 대한 자세한 내용을 확인하실 수 있습니다.
  • 링크 : https://gaussian37.github.io/vision/signal/

목차

• 푸리에 급수를 배우는 이유

• 푸리에 급수의 의미와 주파수 분석에서의 활용

• 연속 시간 푸리에 급수 유도

• 이산 시간 푸리에 급수 유도

• 연속 시간 푸리에 변환 유도

• 이산 시간 푸리에 변환 유도

• MATLAB 및 Python에서의 Fast Fourier Transform

• 푸리에 변환에서 음의 주파수

• 라플라스 변환과 푸리에 변환

푸리에 급수를 배우는 이유

푸리에 급수의 의미와 주파수 분석에서의 활용

• 아래 두가지 식은 푸리에 급수에 관련된 동일한 식을 다른 관점으로 표현한 식입니다.

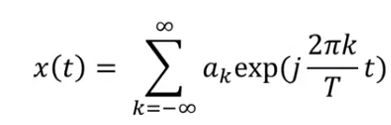
• 위 식의 관점은 연속 신호(함수)는 무한 차원 벡터이고, 이것은 기저 벡터의 선형 결합으로 재구성할 수 있음입니다.

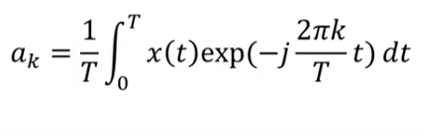
• 반면 위 식의 관점은 신호를 구성하는 각 기저 벡터는 얼마 만큼의 기여도를 가지고 있는지를 뜻하며 이는 주파수 분석에 활용 가능합니다.

• 푸리에 급수에 대하여 알아보기 이전에 벡터와 직교에 대하여 간략하게 알아보도록 하겠습니다.

• 벡터 \(\overrightarrow{i}, \overrightarrow{j}\)가 직교한다면 내적 \(\overrightarrow{i} \cdot \overrightarrow{j} = 0\)을 만족합니다.
• 두 벡터가 직교한다는 의미는 두 벡터의 내적이 0임을 뜻합니다. 벡터의 내적은 두 벡터가 얼마나 닮았는 지를 뜻하기 때문에 두 벡터의 내적이 0이되어 직교한다는 뜻은 두 백터가 전혀 닮지 않았다는 뜻이되고 바꿔 말하면 두 벡터가 서로 독립적이라는 말이 됩니다.

• \[\vec{a} \cdot \vec{b} = \vert \vec{a} \vert \vert \vec{b} \vert \cos{\theta}\]

• 이렇게 직교하는 벡터들을 이용하여 단위 벡터를 만들 수 있는데, 2차원에서 2개의 단위 벡터가 있으면 2차원 공간의 모든 벡터를 표현할 수 있습니다. 같은 개념으로 N차원 공간의 모든 벡터를 표현하기 위해서는 N개의 직교하는 벡터가 필요합니다.

• 앞으로 다룰 내용은 함수이기 때문에 벡터가 아닌 함수를 다루어야 합니다. 함수에서도 벡터의 직교와 같은 개념이 있을까요?
• 먼저 함수는 일반화된 벡터로 취급할 수 있습니다. N차원 벡터는 N개의 숫자 나열이듯이 실수 함수는 실수 값을 무한 개 나열한 것으로 본다면 실수 함수는 무한 차원 벡터라고 볼 수 있습니다. 따라서 앞으로는 실수 (혹은 복소수) 함수는 무한차원 벡터로 생각하도록 하곘습니다.
• 이러한 무한 차원의 벡터 공간을 표현하기 위해서 함수의 직교를 이용해야 합니다. 직교하는 함수를 무한 개 찾을 수 있다면 이 함수를 이용해서 어떤 실수 (혹은 복소수) 함수라도 그 구간 내의 함수를 표현할 수 있습니다.

• 함수의 내적은 위 식과 같이 나타낼 수 있습니다. 이는 벡터의 내적과 개념이 유사합니다.
• 벡터의 내적을 할 때 두 벡터 \((a, b), (c, d)\)를 내적하면 \(ac + bd\)가 됩니다. 이와 같이 함수의 내적을 할 때에도 두 함수를 특정 범위 내에서 함수값을 곱해주게 됩니다.
• 위 식을 보면 함수 \(f_{2}(x)\)에는 * 즉, 켤레복소수를 적용해 주도록 되어있습니다. 이는 함수값이 복소수(복소 벡터)일 때, 계산이 실수 공간에서 만족해야 하는 내적의 공리와 연관되어 있기 때문입니다. 따라서 계산을 실수화 하기 위함이라고 보시면 됩니다.

• \[z = a + jb\]
• \[\vert z \vert^{2} = a^{2} + b^{2} = (a + jb)(a - jb) = a^{2} + b^{2} = z \cdot \bar{z}\]

• 복소수의 크기(절대값)을 구할 때에도 켤레 복소수를 통하여 실수화 한 것과 동일한 방식입니다.

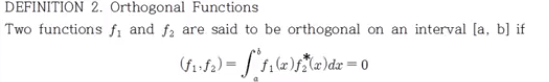
• 만약 두 함수가 직교한다는 것은 두 함수의 내적이 0임을 뜻합니다. 이는 벡터의 직교와 같은 의미입니다.

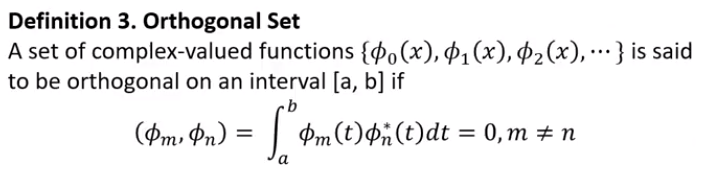
• 무한 차원의 공간을 표현하기 위해서는 무한 차원의 직교하는 함수들이 필요하다고 앞에서 언급하였습니다.
• 범위를 줄여서 (a, b) 구간을 표현하기 위해서는 이 범위에서 직교하는 함수들이 필요합니다. 이 때 사용 될 직교 함수들의 집합을 Orthogonal Set이라고 하며 그 표기법은 위 식과 같습니다. 위 식과 같이 직교하는 함수들의 집합을 통하여 (a, b) 구간 표현할 수 있습니다.
• 따라서 같은 구간에서 정의된 함수 \(f(x)\)는 이 직교 함수들의 대수 합으로 나타낼 수 있습니다.

• \[f(x) = c_{0}\phi_{0}(x) + c_{1}\phi_{1}(x) + c_{2}\phi_{2}(x) + \cdots + c_{n}\phi_{n}(x) + \cdots\]
• \[f(x) = \sum_{n=0}^{\infty}c_{n}\phi_{n}(x)\]

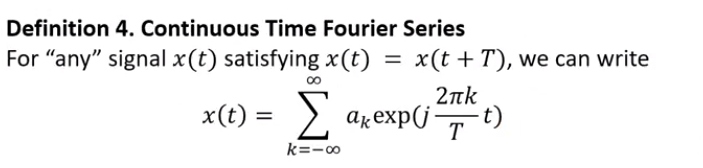
• 앞에서 살펴본 푸리에 급수의 식을 함수 직교와 연관하여 다시 살펴보도록 하겠습니다. 먼저 위 식에서 지수 함수부에 해당하는 식을 자세히 살펴보면

• \[\text{exp}(j \frac{2\pi k}{T} t)\]

• 이산 시간 푸리에 급수에서 위 지수부에 해당하는 식이 orthogonal set이 됩니다.
• 이 값은 오일러 공식 \(\text{exp}(j\theta) = \cos{\theta} + j\sin{\theta}\)을 이용하면 다음과 같이 변환되어 사용되어 집니다.
  • 오일러 공식 참조 : https://gaussian37.github.io/math-calculus-euler_formula/

• \[\text{exp}(j \frac{2\pi k}{T} t) = \cos{\frac{2\pi k}{T} t} + j\sin{\frac{2\pi k}{T} t}\]
• \[x(t) = \sum_{k=-\infty}^{\infty}a_{k}(\cos{\frac{2\pi k}{T} t} + j\sin{\frac{2\pi k}{T} t})\]

• 즉, 어떤 임의의 신호(함수값)은 cos, sin 함수의 합으로 표현할 수 있음을 알 수 있습니다.
• 이 식에서 가장 중요한 것은 지수부의 식 \(\text{exp}(j \frac{2\pi k}{T} t)\)가 Orthogonal set인 지 확인하는 것입니다. 따라서 다음 집합이 orthogonal set인 지 확인해 보겠습니다.

• \[\{\phi_{k}(t) \ \vert \ \phi_{k}(t) = \text{exp}(j \frac{2\pi k}{T}t), \ \ k = \text{integer on } [0, T] \}\]

• 위 집합의 임의의 두 원소인 함수 \(\phi_{\color{red}{k}(t) = \text{exp}(j \frac{2\pi \color{red}{k}}{T} t)\)와 \(\phi_{\color{blue}{p}}(t) = \text{exp}(j \frac{ 2\pi \color{blue}{p} }{T} t)\)가 있을 때, 두 함수의 내적을 해보겠습니다.

• \[\begin{align} \int_{0}^{T} \phi_{k}(t) \phi_{p}^{*}(t) dt &= \int_{0}^{T} \text{exp}(j \frac{2\pi k}{T} t) \text{exp}(-j \frac{2\pi p}{T} t)dt \\ &= \int_{0}^{T} \text{exp}(j \frac{2\pi (k-p)}{T} t)dt = \Biggl[ \frac{T}{j 2\pi (k-p)} \text{exp}(j \frac{2\pi (k-p)}{T} t) \Biggr]_{0}^{T} \\ &= \frac{T}{j 2\pi (k-p)} [ \text{exp}(j 2\pi(k-p)) - 1] \\ &= \frac{T}{j 2\pi (k-p)}[\cos{(2\pi(k-p))} + j\sin{(2\pi(k-0))}] = 0 \quad (\because \cos{(2n\pi)} = 0 \text{ and } \sin{(2n\pi)} = 1) \end{align}\]

• 따라서 서로 다른 \(k\)와 \(p\)에 대하여 두 함수가 내적이기 때문에 위 집합은 orthogonal set임을 확인할 수 있습니다.
• 처음 위 식을 설명할 때 다음과 같은 문구와 같이 설명하였었습니다.

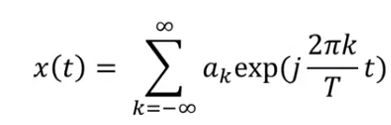
• 위 식의 관점은 연속 신호(함수)는 무한 차원 벡터이고, 이것은 기저 벡터의 선형 결합으로 재구성할 수 있음입니다.
• 이 때, 기저 벡터는 삼각 함수이므로 \([0, T]\) 구간 사이에 정의된 어떤 주기 신호는 삼각 함수의 선형 결합으로 재구성 할 수 있음을 확인하였습니다.

• 다음으로 아래 식과 뜻에 대하여 알아보도록 하겠습니다.

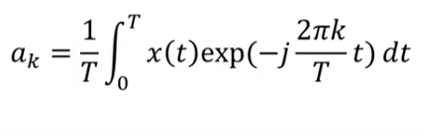
• 반면 위 식의 관점은 신호를 구성하는 각 기저 벡터는 얼마 만큼의 기여도를 가지고 있는지를 뜻하며 이는 주파수 분석에 활용 가능합니다.

• 위 \(a_{k}\) 식에 대하여 생각해 보기 위해 주기 \(T = 1\)인 임의의 신호 \(x(t)\)에 대해서, \(k=1\)일 때, \(a_{k}\)의 의미를 살펴보겠습니다.

• \[a_{1} = \int_{0}^{1} x(t) \text{exp}(-j 2\pi t) dt = \int_{0}^{1} x(t) \times \{\cos{2\pi t - j \sin{2\pi t}} \} dt\]

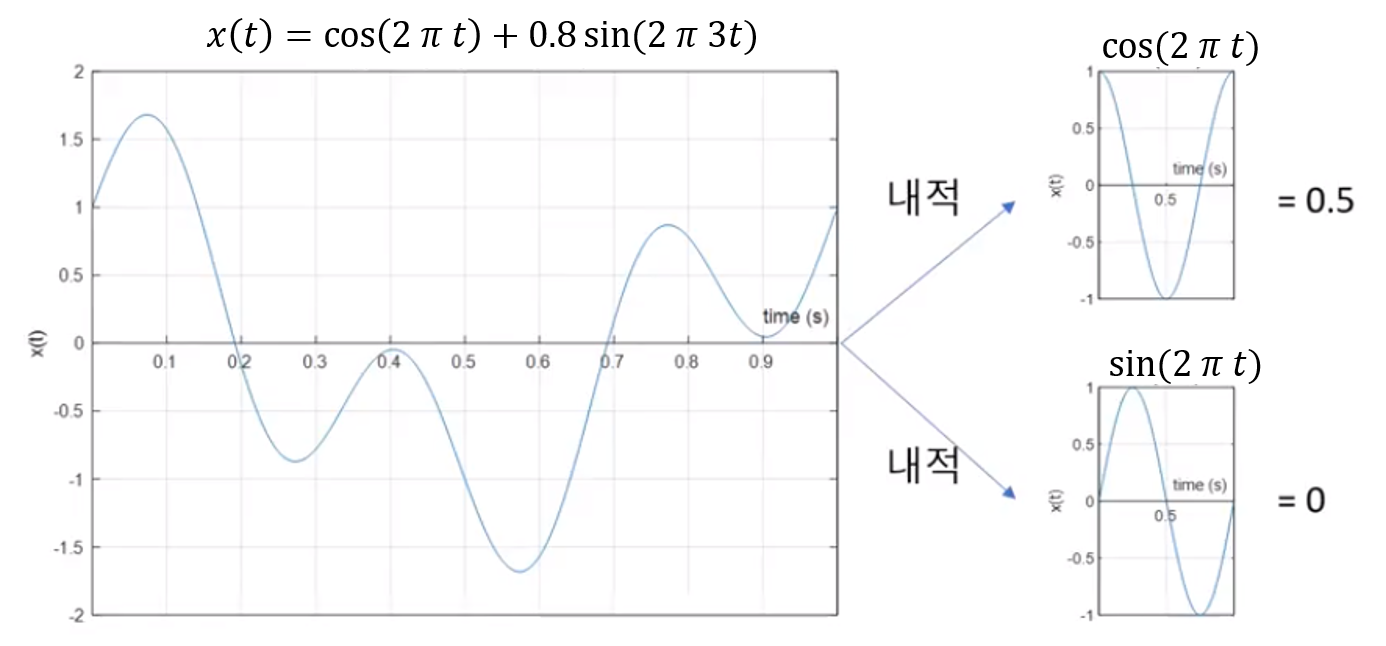
• 위 식에서 cos 함수는 1Hz를 가지고 sin 함수는 3Hz를 가진다고 가정을 하여 식을 정하면 위 그래프와 같이 나타낼 수 있습니다.
• 왼쪽의 큰 그래프는 함수 \(x(t)\)를 뜻하며 수식에 해당하는 그래프를 그리면 위 그래프와 같습니다.
• 이 \(x(t)\) 함수와 \(\cos{2 * \pi * 1 * t}, \sin{2 * \pi * 1 * t}\)를 각각 내적 후 적분을 취하면 각각 0.5, 0이 됨을 계산할 수 있습니다.

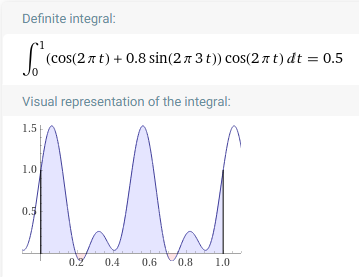
• 상세 계산 과정 : 링크

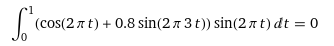
• 상세 계산 과정 : 링크

• 앞에서 설명하였듯이 내적은 두 벡터 또는 함수가 얼마나 닮았는 지 나타냅니다. 위 식에 이 개념을 대입하면 \(x(t)\)의 삼각함수 성분 중 kernel의 성분을 얼만큼 내포하고 있는 지 뜻하게 됩니다. 여기서 kernel은 \(x(t)\)에 곱해지는 \(\cos{2 \pi t}, \sin{2 \pi t}\)에 해당합니다.

• 위 계산은 \(a_{1}\)의 경우에 해당합니다. 계산해야 하는 전체 영역은 음의 무한대에서 양의 무한대이기 때문에 전 과정을 계산을 해야 푸리에 급수를 나타낼 수 있습니다. 따라서 몇 가지 \(a_{k}\)를 좀 더 다루어 보도록 하겠습니다.

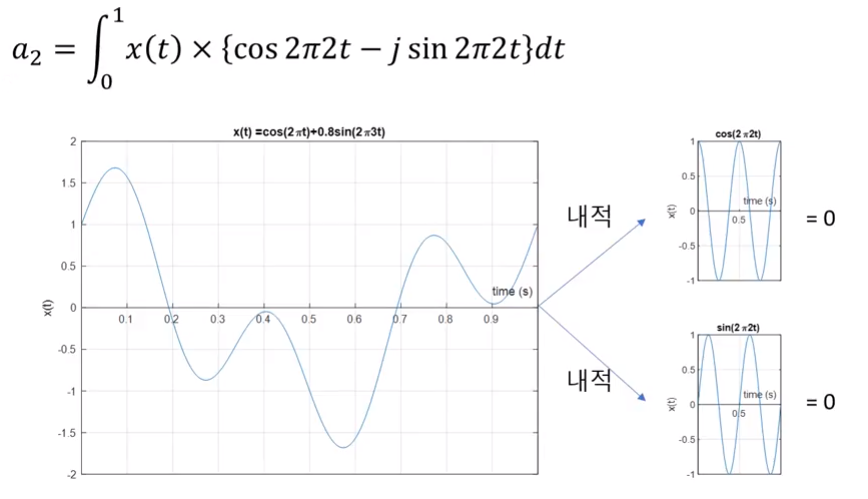
• 위 그래프는 \(a_{2}\)를 나타냅니다.

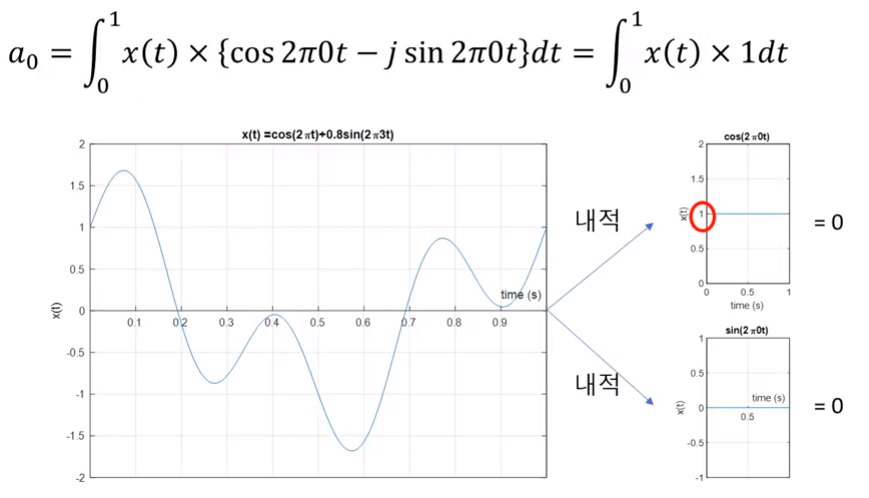
• 위 그래프는 \(a_{0}\)을 나타냅니다. cos, sin 함수가 상수로 수렴되기 때문에 계산이 쉽게 가능합니다.

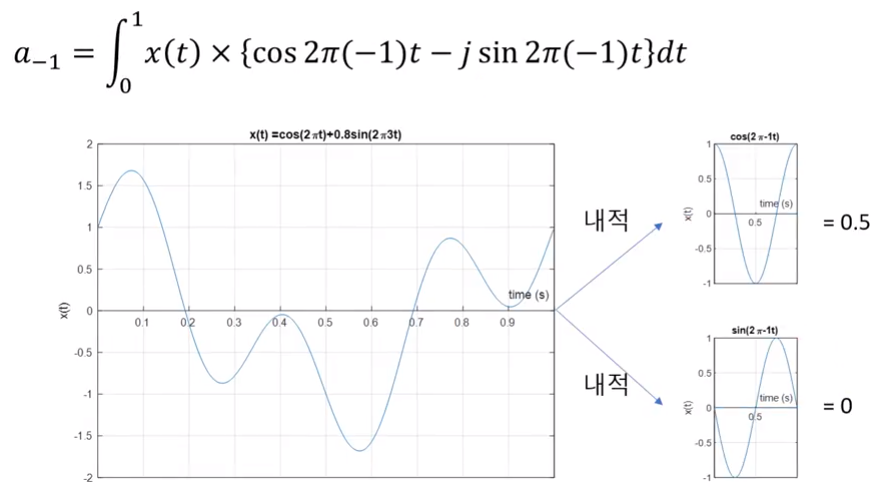
• 이번에는 음의 방향으로 계산을 해보겠습니다. 위 그래프는 \(a_{-1}\)을 나타냅니다.

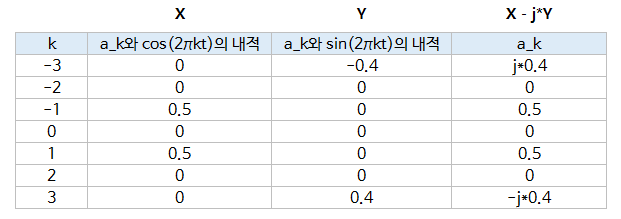
• 이와 같은 계산을 -3 ~ 3까지 적용하였을 때, 위 테이블과 같습니다.
• 위 테이블에서 \(a_{-3} = j * 0.4, a_{3} = -j * 0.4\)임을 확인할 수 있습니다. 여기서 \(j\)는 복소 평면의 Im 축을 나타내며 이와 관련된 자세한 내용은 아래 글을 통하여 복소 평면의 개념을 확인 하실 수 있습니다.
  • 링크 : https://gaussian37.github.io/math-calculus-phasor/
• 간단한 이해를 위하여 가로축은 실수축 Re로 생각하고 세로축은 허수축 Im로 생각하고 \(j\)가 붙은 숫자는 복소 평면에서 Im 축의 숫자로 이하해시면 됩니다.

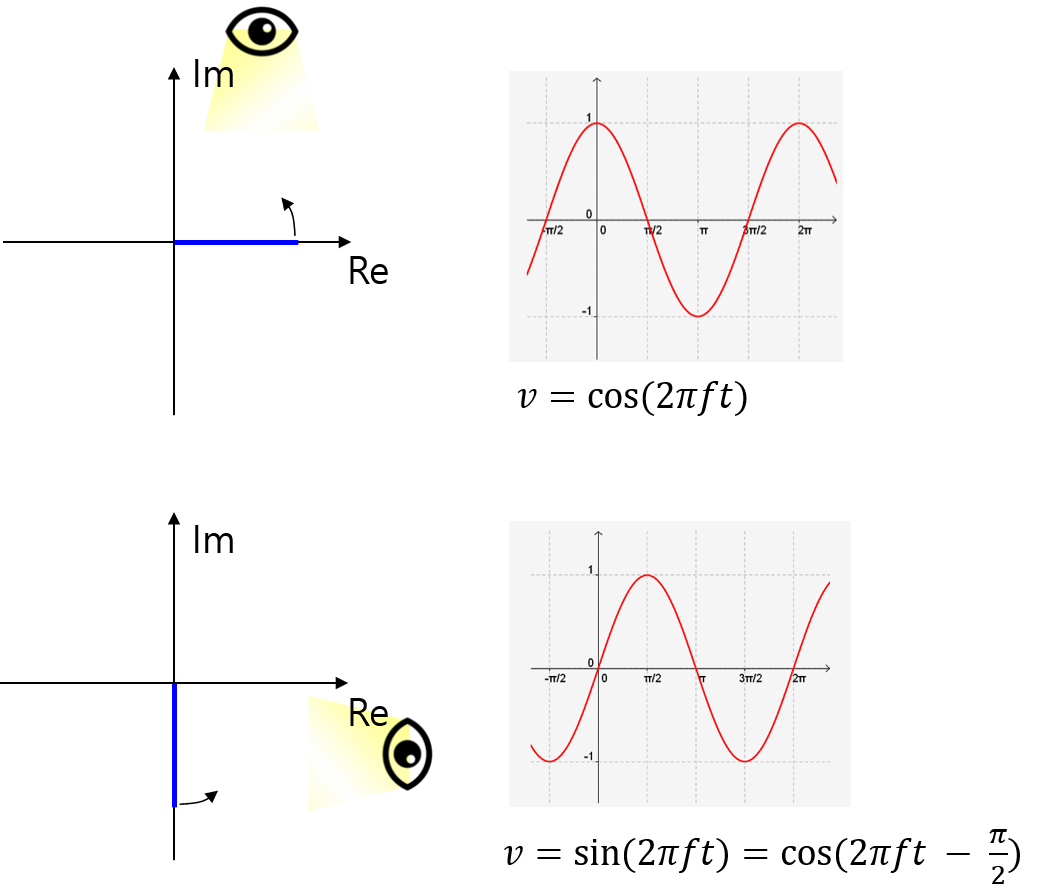
• cos 함수의 자취는 위에서 바라보았을 때, 막대의 길이 자취와 같고 sin 함수의 자취는 오른쪽에서 바라보았을 때, 막대의 길이와 같습니다.
• 가로축인 실수축 Re는 실수부에 해당하고 세로축인 허수축 Im는 허수부에 해당합니다. 따라서 앞의 테이블의 \(j\)는 허수부에 해당하고

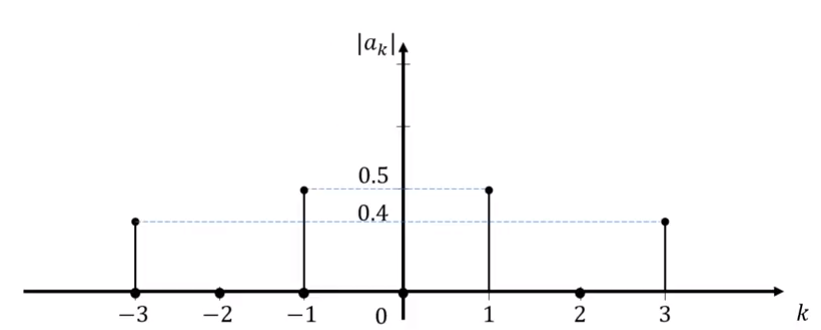
• 테이블의 \(a_{k}\)의 크기를 확인하기 위하여 \(a_{k}\)의 절대값을 취한 뒤 그래프로 나타나면 위 그래프와 같습니다.
• 여기서 주파수를 구해보겠습니다. 일반적으로 \(\cos{2 \pi \color{red}{f} t}\)에서 \(\color{red}{f}\)가 주파수를 뜻합니다.

• \[\text{exp}(-j \frac{2\pi k}{T} t) = \cos{\frac{2\pi \color{red}{k}}{\color{red}{T}} t } -j\sin{\frac{2\pi \color{red}{k}}{\color{red}{T}}t }\]

• 위 식과 같이 cos, sin 함수를 정의 할 수 있기 때문에 주파수는 \(k / T\)가 되고 \(T = 1\)로 가정을 하였기 때문에 주파수는 \(k / T = k\)가 되어 가로축이 주파수 Hz가 됨을 알 수 있습니다. 따라서 그래프를 조금 수정하면 다음과 같습니다.

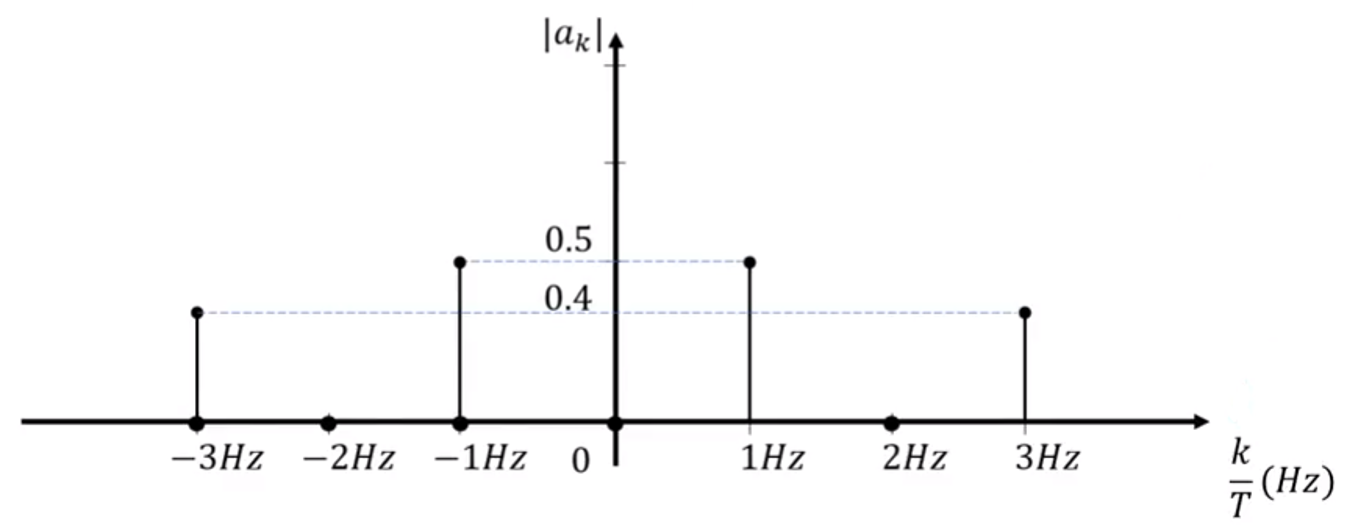
• 따라서 위 그래프와 같이 \(a_{k}\)를 이용하여 가로축이 주파수인 주파수 분석을 할 수 있음을 의미합니다.
• 위 그래프를 해석하면 1, -1 Hz 성분은 0.5씩 존재하고 3, -3 Hz 성분은 0.4씩 존재한다는 것을 확인할 수 있습니다. 여기서 음의 주파수의 의미는 이 글에 뒷부분에서 다루겠습니다.
• 이 값을 처음에 다룬 \(x(t) = \color{red}{1}*\cos{2 \pi \color{red}{t}} + \color{blue}{0.8}\sin{2 \pi \color{blue}{3t}}\)와 연계해서 보면 cos의 1Hz 성분 \(\color{red}{t}\)를 음의 주파수, 양의 주파수 반반씩 0.5로 나타내어 지고 (0.5 * 2 = \(\color{red}{1}\)), sin의 3Hz 성분 \(\color{blue}{3t}\)를 음의 주파수, 양의 주파수 반반씩 0.4로 나타내어 집니다. (0.4 * 2 = \(\color{blue}{0.8}\))

연속 시간 푸리에 급수 유도

• 앞에서 다룬 내용을 기반으로 연속 시간 푸리에 급수를 유도해 보도록 하겠습니다.
• 연속 시간 푸리에 급수는 주기 \(T\)를 가지는 연속 함수 \(x(t) = x(t + T)\)를 정현파의 합으로 표현할 수 있음을 의미합니다.

• \[x(t) = \sum_{k=\infty}^{\infty} a_{k} \exp{(j \frac{2\pi k}{T})t}\]
• \[\exp{j\theta} = \cos{\theta} + j \sin{\theta}\]

• 이 성질은 오일러 공식을 이용하였을 때, 지수 함수 부가 정현파의 합으로 표현되는 것을 이용하기 때문에 성립하는 것을 알 수 있습니다.
• 또한 푸리에 급수에서 \(a_{k}\)를 기준으로 식을 정리하면 다음과 같이 정리할 수 있습니다.

• \[a_{k} = \frac{1}{T} \int_{0}^{T} x(t) \exp{(-j \frac{2\pi k}{T}t)} dt\]

• 이번 글에서는 푸리에 급수로 나타내는 \(x(t)\) 식의 의미와 \(a_{k}\)로 식을 전개하는 방법에 대하여 다루어 보도록 하겠습니다.

• 푸리에 급수의 의미와 주파수 분석에서의 활용에서 자세히 다룬 것 처럼 푸리에 급수의 의미를 알기 위해서는 orthogonal function에 대한 의미를 알아야 합니다.
• 이 의미는 벡터의 내적을 통하여 확장할 수 있습니다. 두 벡터 \(\overrightarrow{i}, \overrightarrow{j}\) 가 내적한다면 \(\overrightarrow{i} \cdot \overrightarrow{j} = 0\) 관계를 가지고 이 때,직교함을 알 수 있었습니다. 그리고 직교하는 N개의 벡터를 이용하여 N차원의 모든 좌표를 표현할 수 있음을 확인하였습니다.
• 이 개념을 함수 영역으로 확장하겠습니다. 먼저 함수는 벡터의 개념이 확장된 것으로 이해할 수 있습니다. 함수 \(f(t)\)에서 \(t\)의 값에 따라 함수 값이 출력이 되는데 이를 벡터 형태로 나타낼 수 있고 함수값이 무한이 늘어나면 무한 차원의 벡터로 해석할 수 있습니다.
• 이러한 관점에서 두 함수 \(f_{1}(t), f_{2}(t)\)를 내적해 보도록 하겠습니다. 두 함수의 내적을 할 때, 범위는 \([a, b]\) 구간으로 두고 이 구간의 함수값에 대하여 내적을 하기 위해 정적분을 하도록 하겠습니다.

• \[\int_{a}^{b} f_{1}(t) f_{1}(t) f_{2}(t) dt = 0\]

• 위 식을 함수의 내적이라고 보았을 때 \(f_{1}(t), f_{2}(t)\)는 구간 \([a, b]\)에서 직교한다는 것을 알 수 있습니다. 여기까지는 벡터의 내적 개념과 큰 차이가 없습니다.
• 이 개념을 이용하면 구간 \([a, b]\)에서 직교하는 함수 \(f_{1}(t), f_{2}(t)\)를 이용하면 구간 \([a, b]\)의 모든 함수를 표현할 수 있다고 생각할 수 있습니다.
• 예를 들어 함수 \(f_{1}(t), f_{2}(t), f_{3}(t)\)가 구간 \([a, b]\)에서 직교한다고 가정해 보겠습니다. 임의의 함수 \(f_{n}(t)\)는 다음과 같이 표현할 수 있습니다.

• \[f_{n}(t) = a_{1}f_{1}(t) + a_{2}f_{2}(t) + a_{3}f_{3}(t) = \sum_{i=1}^{\infty} a_{i}f_{i}(t)\]

• 합으로 표현된 \(f_{i}(t)\)는 구간 \([a, b]\)에서 서로 직교하는 함수의 집합으로 표현할 수 있습니다. 이를 orthogonal set이라고 합니다.

• \[x(t) = \sum_{k=\infty}^{\infty} a_{k} \exp{(j \frac{2\pi k}{T})t}\]

• 그러면 위 식에서 \(\exp{(j \frac{2\pi k}{T})t}\)가 모든 정수 \(k\) 에 대하여 orthogonal set인지 증명을 하면 어떠한 연속 함수를 정현파의 합으로 표현할 수 있음을 확인할 수 있습니다.

이산 시간 푸리에 급수 유도