히스토그램

• 출처 : 컴퓨터 비전 (오일석)
• 이번글에서는 기본 영상처리 방법인 히스토그램에 대하여 알아보도록 하겠습니다.

히스토그램 계산

• 영상 f의 히스토그램은 명암값이 나타난 빈도수로 0 ~ L-1 사이의 명암값 각각이 영상에 몇 번 나타나는지를 표시합니다.
• 다음은 명암 영상 f의 히스토그램 h를 계산하는 알고리즘 입니다.
• 입력 : 명암 영상 \(f(j, i), \ \ \ 0 \le j \lt M-1, \ \ \ 0 \lt i \lt N-1\)
• 출력 : 히스토그램 \(h(l)\)과 정규 히스토그램 \(\hat{h}(l), \ \ \ 0 \le l \lt L-1\)

for(l = 0 to L-1)
    h(l) = 0; // 초기화
    
for(j = 0 to M-1)
    for(i = 0 to N-1) // f의 화소 (j,i) 각각에 대하여
        h(f(j,i))++ //명암값에 해당하는 히스토그램을 1 증가

for(l=0 to L-1)
    h^(l) = h(l) / (M*N)   // 정규화
    

• 먼저 모든 명암값의 히스토그램 h(.)을 0으로 초기화 합니다.
• 다음으로 모든 화소에 접근하여 명암값에 해당하는 히스토그램의 칸을 1 증가시킵니다.
• 마지막으로 히스토그램의 값을 모두 더하면 1이 되도록 정규화 합니다.

• 히스토그램 알고리즘을 수식으로 표현하면 다음과 같습니다.

• 아래 수식의 $$

  .

  $$은 집합의 크기를 나타냅니다.

• $$ h(l) =

  {(j,i)

  f(j,i) = l}

  $$

• 　\(\hat{h}(l) = \frac{h(l)}{M \times N}\)

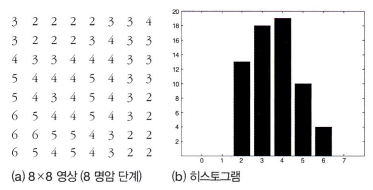
• 예를 들어 아래 그림을 참조하면 영상에서 얻을 수 있는 값을 통하여 어떤 히스토그램을 얻는지 알 수 있습니다.
• 아래 그림은 M과 N이 8이고 L=8인 아주 작은 영상입니다. 이 영상에서 명암값이 2인 화소는 13개이므로 \(h(2) = 13\)이 됩니다.
• 다른 명암값에 대해서도 화소의 갯수를 세어보면 h = (0, 0, 13, 18, 19, 10, 4, 0) 이고 h^ = (0, 0, 0.203, 0.281, 0.297, 0.156, 0.063) 입니다.

히스토그램 용도

• 영상의 특성 파악
  • 먼저 히스토그램을 사용하는 용도는 영상의 특성을 파악하는 것입니다.
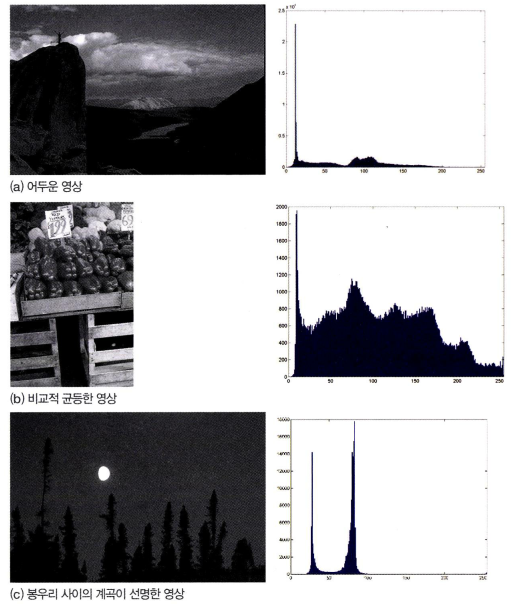
  • 아래 첫번째 그림은 히스토그램이 왼쪽으로 치우처져 있는 어두운 영상입니다.
  • 두번째 그림은 밝기 분포가 비교적 균일한 영상입니다.
  • 마지막 그림은 두 개의 봉우리가 선명하게 나타난 영상으로 이런 영상은 이진 영상으로 변환하기가 쉽습니다.

• 평활화를 통한 영상 품질 개선
  • 히스토그램의 또 다른 용도는 조작을 통한 영상 품질 개선입니다.
  • 가장 대표적인 연산은 히스토그램 평활화(histogram equalization) 입니다.
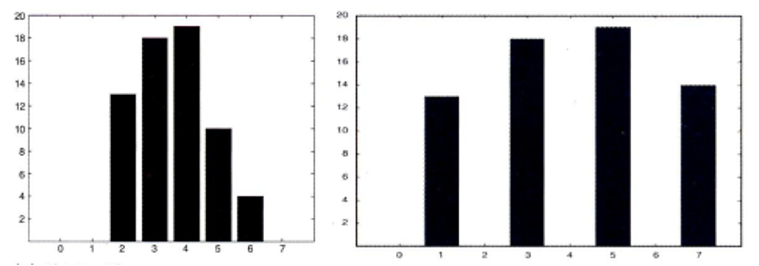
  • 이 연산은 아래 그림의 왼쪽과 같은 분포를 오른쪽 분포와 같이 평평하게 만듭니다.
  • 평활화 작업을 하면 영상이 사용하는 명암의 범위, 즉 동적 범위가 늘어나 영상이 이전보다 선명해집니다.

• 다음 식은 입력 영상 \(f\)를 평활화하여 출력 영상 \(g\)를 만드는 데 사용하는 변환식입니다.
• 여기에서 c(.)는 누적 히스토그램이고 round(.)는 반올림 연산입니다. T(.)는 입력 영상 f의 명암값 \(l_{in}\)을 출력 영상 g의 명암값 \(l_{out}\)으로 변환하믄 매핑함수입니다.
• 이 매핑함수는 누적 히스토그램에 (L-1)을 곱하고 결과를 반올림하면 됩니다.
• 　\(l_{out} = T(l_{in}) = round(c(l_{ln}) \times (L-1))\) 이고 이 때, \(c(l_{in}) = \sum_{l=0}^{l_{in}} \hat{h}(l)\) 입니다.

• 위 그림의 가장 왼쪽 매핑 표를 보면 매핑 함수 T(.)를 구하는 과정을 보여줍니다.
• 입력 영상의 명암값 0은 0으로 1은 2로 1은 3으로 … 7은 7로 매핑해 주게 됩니다.
• 그 결과 가운데 평활화된 영상을 얻을 수 있고 그 영상을 평활화된 영상의 히스토그램으로 나타낼 수 있습니다.
• 평활화 하기전에는 영상의 범위가 2 ~ 6인 반면에 새로운 영상은 1 ~ 7로 범위가 넓어졌음을 알 수 있습니다.

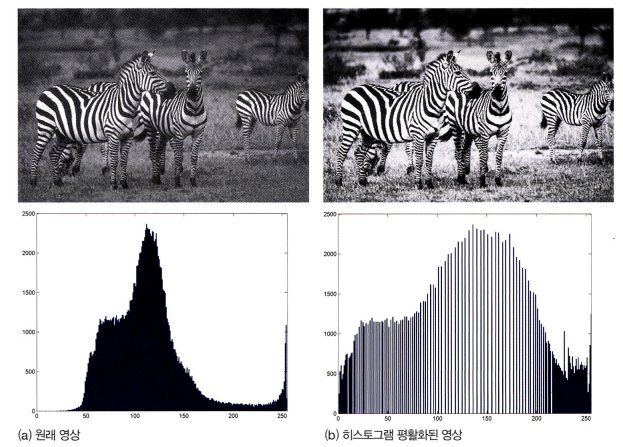
• 위 그림은 실제 영상에 히스토그램 평활화를 적용한 결과입니다. 얼룩말의 줄무늬가 훨씬 선명하고 숲에 있는 나무도 훨씬 잘 보입니다.
• 원래 영상의 명암은 50 ~ 150으로 분포되어 있지만 새로운 영상은 그 범위가 크게 넓어졌습니다.

• 위 그림은 오히려 히스토그램 평활화가 이미지 품질을 떨어뜨린 사례라고 할 수 있습니다.
• 전체적인 새의 사진은 조금 훼손되었지만 새에게 잡아먹히는 곤충은 영상이 선명해졌습니다.
• 즉, 히스토그램은 상황과 목적에 따라서 품질 개선을 할 수 있고 오히려 훼손할 수 있음을 알아야 합니다.

히스토그램 역투영과 얼굴 검출

• 마지막으로 다루어 볼 히스토그램 사용 방법은 히스토그램 역투영(histogram backprojection) 연산과 이를 활용한 물체 검출 방법입니다.