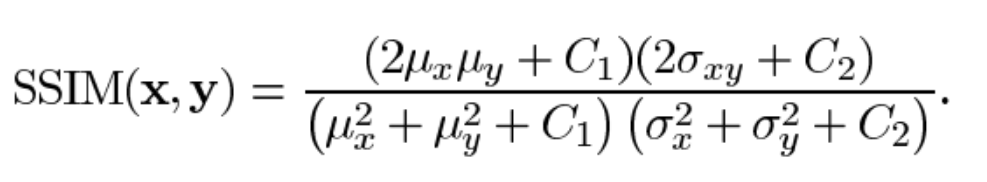
SSIM (Structural Similarity Index)

• 참조 : https://en.wikipedia.org/wiki/Structural_similarity
• 참조 : https://medium.com/srm-mic/all-about-structural-similarity-index-ssim-theory-code-in-pytorch-6551b455541e
• 참조 : https://bskyvision.com/878
• 참조 : https://walkaroundthedevelop.tistory.com/m/56
• 참조 : https://nate9389.tistory.com/2067
• 참조 : https://medium.com/@sanari85/image-reconstruction-%EC%97%90%EC%84%9C-ssim-index%EC%9D%98-%EC%9E%AC%EC%A1%B0%EB%AA%85-b3ca26434fb1

• 이번 글에서는 두 이미지를 비교하는 지표인 SSIM에 대하여 다루어 보도록 하겠습니다.
• SSIM은 Structural Similarity Index의 약어로 사용되며 주어진 2개의 이미지의 similarity(유사도)를 계산하는 측도로 사용됩니다.
• SSIM은 두 이미지의 단순 유사도를 측정하는데 사용하기도 하지만 풀고자 하는 문제가 두 이미지가 유사해지도록 만들어야 되는 문제일 때 SSIM을 Loss Function 형태로 사용하기도 합니다. 왜냐하면 SSIM이 gradient-based로 구현되어 있기 때문입니다.
• 딥러닝에서 두 이미지를 유사하게 만드는 문제나 depth estimation시 disparity를 구하기 위하여 이미지를 복원할 때, 두 이미지 또는 두 패치의 유사도를 측정하여 Loss Function을 사용하는 방법이 많이 사용됩니다.
• 따라서 이번 챕터에서는 SSIM의 원리에 대하여 먼저 알아보고 Pytorch의 구현 방법을 통하여 학습에 사용하는 방법과 skimage를 이용하여 단순히 이미지의 유사도를 측정하는 방법에 대하여 살펴보도록 하겠습니다.

목차

• SSIM의 정의

• SSIM의 Pytorch에서의 사용법 (globally)

• SSIM의 Pytorch에서의 사용법 (locally)

• SSIM의 skimage에서의 사용법

SSIM의 정의

• SSIM은 Structural Similarity Index Measure의 약어로 두 이미지의 유사도를 luminance, contrast, structure 3가지 요소를 이용하여 비교하는 방법을 의미합니다. 이와 같은 요소를 이용하여 이미지를 비교하는 이유는 실제 인간의 시각 기관도 이와 같은 방법으로 인식하기 때문입니다.
• SSIM의 최종 결과는 0 ~ 1 사이이며 1에 가까울수록 두 이미지가 유사함을 의미합니다. 그러면 luminance, contrast, structure가 각각 어떻게 계산되어서 하나로 합쳐지는 지 살펴보도록 하곘습니다. 입력값의 범위에 따라서 -1 ~ 1 사이의 값을 가질수도 있으며 1에 가까울수록 두 이미지가 유사한 것은 동일합니다.

Luminance

• luminance는 한글로 휘도라고 하며 빛의 밝기를 나타내는 양입니다. SSIM에서 계산할 때, 별도 빛의 밝기 성분을 추출해서 사용하지는 않고 이미지의 픽셀값을 이용합니다. (픽셀 값이 클수록 밝음을 이용함) grayscale 이미지에서는 각 픽셀의 값을 의미하며 RGB 이미지에서는 R, G, B 각 채널 별 픽셀 값을 의미합니다.

• \[\mu_{x} = \frac{1}{N}\sum_{i=1}^{N} x_{i}\]

• \(x_{i}\) : 각 픽셀의 값 (밝기 값을 의미함)

• \(N\) : 전체 픽셀의 갯수

• \(\mu_{x}\) : 이미지의 평균 luminance

• 두 이미지의 luminance가 얼마나 다른 지 비교하기 위해 \(\mu_{x}\) 값을 이용합니다. 두 이미지를 \(x, y\) 라고 할 때 두 이미지의 luminance를 비교하기 위한 식은 다음과 같습니다.

• \[l(x, y) = \frac{2\mu_{x}\mu_{y} + C_{1}}{\mu_{x}^{2}+ \mu_{y}^{2} + C_{1}} \tag{1}\]

• 식 (1)의 \(C_{1}\) 을 제외하고 살펴보면 \(\frac{2\mu_{x}\mu_{y}}{\mu_{x}^{2} + \mu_{y}^{2}}\) 가 되며 \(\mu_{x}, \mu_{y}\) 각 같으면 1이 되고 두 값이 차이가 많이 날수록 0에 가까워 집니다. 이와 같은 성질을 이용하여 두 값의 차이에 따른 값의 범위를 0 ~ 1로 계산될 수 있도록 합니다.
• 식 (1)에서 \(C_{1}\) 의 사용 용도는 분모에 0이 되는 것을 방지하기 위하여 안정성을 위해 추가하였고 값의 정의 방법은 아래 식을 따르는 것으로 알려져 있습니다. (하지만 크게 중요하지 않으니 적당한 상수값을 사용하여도 무관합니다.)

• \[C_{1} = (K_{1}L)^{2}\]

• 위 식에서 \(K_{1}\) 는 일반 상수이며 보통 0.01을 많이 사용합니다. \(L\) 은 픽셀값의 범위를 입력하며 일반적으로 8비트 값을 사용하여 0 ~ 255의 픽셀 값을 사용하므로 255를 \(L\) 로 사용합니다.
• 따라서 \(C_{1} = (0.01 \times 255)^{2} = 6.5025\) 를 사용합니다.

Contrast

• contrast는 한글로 대조라고 하며 이미지 내에서 빛의 밝기가 바뀌는 정도를 나타내는 양입니다. 이 값은 픽셀 간의 값이 얼마나 차이가 나는 지 통하여 정량화 할 수 있으므로 표준 편차를 사용합니다.

• \[\sigma_{x} = \left( \frac{1}{N-1} \sum_{i=1}^{N} (x_{i} - \mu_{x})^{2} \right)^{1/2}\]

• \(N - 1\) : 표본의 표준 편차를 구하기 때문에 표본의 표준편차가 모표준 편차가 될 수 있도록 하기 위해 \(N - 1\)을 사용합니다.

• \(\sigma_{x}\) : 이미지의 픽셀 간 표준편차로 contrast를 의미합니다.

• 두 이미지의 contrast 성분을 비교하기 위해서는 \(\sigma_{x}\) 를 사용합니다. 상세식은 luminance의 \(l(x, y)\) 와 동일합니다.

• \[c(x, y) = \frac{2\sigma_{x}\sigma_{y} + C_{2}}{\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2}} \tag{2}\]

• 위 식에서도 luminance의 경우와 동일하게 두 이미지의 contrast 성분이 같을 수록 1에 가깝고 다를수록 0에 가까워집니다.
• 식 (2)의 \(C_{2}\) 의 경우 \(C_{2} = (K_{2}L)^{2}\) 로 구하며 \(K_{2} = 0.03\) 을 주로 사용하여 다음과 같은 값을 가집니다.

• \[C_{2} = (K_{2}L)^{2} = (0.03 \times 255)^{2} = 58.5225\]

Structure

• 마지막으로 structure는 픽셀값의 구조적인 차이점을 나타내며 정성적으로 성분을 확인 시, edge를 나타냅니다. sturucture를 구하기 위하여 luminance을 평균, contrast를 표준 편차로 이용하여 Normalized된 픽셀 값의 분포에서 픽셀 값을 다시 정의합니다.

• \[(X - \mu_{x}) / \sigma_{x}\]
• \(X\) : 입력 이미지

• 두 이미지의 structure 성분의 유사성을 확인하는 것은 두 이미지의 correlation을 이용하것과 같은 의미를 지닙니다.

• \[\text{corr}(X, Y) = \frac{\sigma_{xy}}{\sigma_{x}\sigma_{y}} = \frac{E[(x - \mu_{x})(y - \mu_{y})]}{\sigma_{x}\sigma_{y}} = E \left[\frac{(x - \mu_{x})(y - \mu_{y})}{\sigma_{x}\sigma_{y}}\right]\]
• \[= E \left[\frac{(x - \mu_{x})}{\sigma_{x}} \frac{(y - \mu_{y})}{\sigma_{y}}\right]\]

• 따라서 두 이미지의 correlation을 구하는 것은 각 이미지의 structure 성분의 곱의 평균을 구하는 것과 같고 structure 성분이 같은 방향으로 커지면 1에 가까워지는 성질을 이용하여 앞선 luminance, contrast와 동일하게 이용할 수 있습니다.
• 따라서 두 이미지의 structure를 비교하는 함수를 다음과 같이 정의할 수 있습니다.

• \[s(x, y) = \frac{\sigma_{xy} + C_{3}}{\sigma_{x}\sigma_{y} + C_{3}} \tag{3}\]
• \[\sigma_{xy} = \frac{1}{N-1} \sum_{i=1}^{N}(x_{i} - \mu_{x})(y_{i} - \mu_{y})\]

• 이 때, \(C_{3}\) 는 식의 편의상 \(C_{2} / 2\) 로 사용합니다. 그 이유는 SSIM은 \(l(x, y), c(x, y), s(x, y)\) 의 곱으로 정의되는 데 \(C_{3} = C_{2} / 2\) 로 정의하면 식을 간편화 할 수 있습니다. 이는 이후 식을 전개하면서 보여드리겠습니다.

• 이와 같이 luminance, contrast, strucrue를 모두 반영한 이미지의 유사도를 결정하는 SSIM은 다음과 같이 정의됩니다.

• \[\text{SSIM}(x, y) = l(x, y)^{\alpha} \cdot c(x, y)^{\beta} \cdot s(x, y)^{\gamma} \tag{4}\]

• 식 (4)에서 \(\alpha, \beta, \gamma > 0\) 이면 luminance, contrast, structure 에 상대적인 중요도를 설정할 수 있습니다.
• 앞에서 설명한 대로 식을 간소화 하기 위하여 \(\alpha = \beta = \gamma = 1\) 로 두고 \(C_{3} = C_{2} / 2\) 로 하여 식을 전개해 보겠습니다.

• \[\text{SSIM}(x, y) = l(x, y) \cdot c(x, y) \cdot s(x, y) = \frac{2\mu_{x}\mu_{y} + C_{1}}{\mu_{x}^{2} + \mu_{y}^{2} + C_{1}} \frac{2\sigma_{x}\sigma_{y} + C_{2}}{\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2}} \frac{\sigma_{xy} + C_{2}/2}{\sigma_{x}\sigma_{y} + C_{2}/2} \tag{5}\]
• \[= \frac{(2\mu_{x}\mu_{y} + C_{1}) (2\sigma_{xy} + C_{2})}{(\mu_{x}^{2} + \mu_{y}^{2} + C_{1})(\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2})} \tag{6}\]

• SSIM은 symmetry 성질은 만족하여 x, y 이미지의 순서를 바꿔도 됩니다. 하지만 triangle inequality ( \(\vert a + b \vert \le \vert a \vert + \vert b \vert\) ) 를 만족하지 않아서 distance를 구하기 위한 함수로는 사용할 수 없습니다.
• SSIM을 좀 더 효과적으로 사용하기 위해서는 이미지 전체를 한번에 비교하기 보다는 N x N 윈도우를 이용하여 (ex. 8 X 8, 11 X 11) 지역적으로 비교하여 사용하는 것이 효과적입니다. 왜냐하면 이미지의 왜곡이나 통계적 특성이 이미지 전반에 걸쳐서 나타나는 경우보다 지역적으로 나타나는 경우가 많고 지역적으로 더 다양한 특성을 분석할 수 있기 때문입니다.
• 이와 같은 방법으로 지역적으로 SSIM을 구하려면 윈도우를 이용하여 슬라이딩 윈도우를 적용하여 각 부분의 값을 구해야 합니다. 이와 관련된 구현 내용으로 아래 SSIM의 Pytorch에서의 사용법 (locally)을 참조해 주시기 바랍니다.

• 만약 SSIM을 Loss로 사용하려면 아래와 같이 식을 변경해서 사용하면 됩니다.

• \[L_{\text{SSIM}} = 1 - \text{SSIM}(x, y) \tag{7}\]

• SSIM은 미분 가능하므로 Loss로 사용 가능하며 0 ~ 1 사이의 스코어 값을 1에서 빼주면 두 이미지의 유사도가 낮을수록 값이 커지기 때문에 Loss로 사용할 수 있습니다.

• 만약 RGB 이미지에서 SSIM을 적용해야 한다면 각 채널 별로 SSIM을 구한 후 모두 합해주면 됩니다. 식으로 나타내면 아래와 같습니다.

• \[\text{SSIM}_{\text{rgb}} = w_{r}\text{SSIM}_{r}(I_{1}, I_{2}) + w_{g}\text{SSIM}_{g}(I_{1}, I_{2}) + w_{b}\text{SSIM}_{b}(I_{1}, I_{2}) \tag{8}\]

• 특정 채널에 대하여 더 가중치를 줄 수도 있으며 일반적으로 RGB에 1/3 씩 균등하게 가중치를 주어서 사용합니다.
• YCrCb에서는 Y에 0.8, Cr, Cb에 각각 0.1을 주어서 사용하기도 합니다. (링크 참조)

SSIM의 Pytorch에서의 사용법 (globally)

• 먼저 이미지 전체에서 한번에 SSIM을 구하는 방법을 Pytorch을 이용해서 구해보도록 하곘습니다. 이와 같은 방법으로 SSIM을 구하면 간단하게 전체 이미지에 대하여 SSIM의 Score 또는 SSIM을 이용한 Loss를 구할 수 있습니다.

class SSIM(nn.Module):
    """Layer to compute the SSIM loss between a pair of images
    """
    def __init__(self):
        super(SSIM, self).__init__()
        self.mu_x_pool   = nn.AvgPool2d(3, 1)
        self.mu_y_pool   = nn.AvgPool2d(3, 1)
        self.sig_x_pool  = nn.AvgPool2d(3, 1)
        self.sig_y_pool  = nn.AvgPool2d(3, 1)
        self.sig_xy_pool = nn.AvgPool2d(3, 1)

        # 입력 경계의 반사를 사용하여 상/하/좌/우에 입력 텐서를 추가로 채웁니다.
        self.refl = nn.ReflectionPad2d(1)

        self.C1 = 0.01 ** 2
        self.C2 = 0.03 ** 2

    def forward(self, x, y):
        # shape : (xh, xw) -> (xh + 2, xw + 2)
        x = self.refl(x) 
        # shape : (yh, yw) -> (yh + 2, yw + 2)
        y = self.refl(y)

        mu_x = self.mu_x_pool(x)
        mu_y = self.mu_y_pool(y)

        sigma_x  = self.sig_x_pool(x ** 2) - mu_x ** 2
        sigma_y  = self.sig_y_pool(y ** 2) - mu_y ** 2
        sigma_xy = self.sig_xy_pool(x * y) - mu_x * mu_y

        SSIM_n = (2 * mu_x * mu_y + self.C1) * (2 * sigma_xy + self.C2)
        SSIM_d = (mu_x ** 2 + mu_y ** 2 + self.C1) * (sigma_x + sigma_y + self.C2)

        # SSIM score
        return torch.clamp((SSIM_n / SSIM_d) / 2, 0, 1)

        # Loss function
        # return torch.clamp((1 - SSIM_n / SSIM_d) / 2, 0, 1)

SSIM의 Pytorch에서의 사용법 (locally)

• 이번에는 convolution 연산을 이용하여 로컬한 영역에서 SSIM을 구하는 방법에 대하여 Pytorch 코드를 통해 알아보도록 하겠습니다.
• 앞에서 설명 드렸듯이, 이미지의 특성상 이미지 전체를 한번에 계산하는 것 보다 local한 영역을 기준으로 계산하는 것이 이미지의 각 부분 별 특성을 비교할 수 있습니다.

import torch  
import torch.nn.functional as F 
import numpy as np
import math
import cv2

def gaussian(window_size, sigma):
    """
    Generates a list of Tensor values drawn from a gaussian distribution with standard
    diviation = sigma and sum of all elements = 1.

    Length of list = window_size
    """    
    gauss =  torch.Tensor([math.exp(-(x - window_size//2)**2/float(2*sigma**2)) for x in range(window_size)])
    return gauss/gauss.sum()

def create_window(window_size, channel=1):

    # Generate an 1D tensor containing values sampled from a gaussian distribution
    # _1d_window : (window_size, 1)
    # sum of _1d_window = 1
    _1d_window = gaussian(window_size=window_size, sigma=1.5).unsqueeze(1)
    
    # Converting to 2D  : _1d_window (window_size, 1) @ _1d_window.T (1, window_size)
    # _2d_window : (window_size, window_size)
    # sum of _2d_window = 1
    _2d_window = _1d_window.mm(_1d_window.t()).float().unsqueeze(0).unsqueeze(0)
     
    # expand _2d_window to window size
    # window : (channel, 1, window_size, window_size)
    window = torch.Tensor(_2d_window.expand(channel, 1, window_size, window_size).contiguous())

    return window

def ssim(img1, img2, window_size=11, val_range=255, window=None, size_average=True, full=False):

    # L is the dynamic range of the pixel values (255 for 8-bit grayscale images),    
    L = val_range
    
    try:
        _, channels, height, width = img1.size()
    except:
        channels, height, width = img1.size()

    # if window is not provided, init one
    if window is None: 
        # window should be at least 11x11 
        real_size = min(window_size, height, width) 
        window = create_window(real_size, channel=channels).to(img1.device)
    
    # calculating the mu parameter (locally) for both images using a gaussian filter 
    # calculates the luminosity params
    pad = window_size//2
    mu1 = F.conv2d(img1, window, padding=pad, groups=channels)
    mu2 = F.conv2d(img2, window, padding=pad, groups=channels)
    
    mu1_sq = mu1 ** 2
    mu2_sq = mu2 ** 2 
    mu12 = mu1 * mu2

    # now we calculate the sigma square parameter
    # Sigma deals with the contrast component 
    sigma1_sq = F.conv2d(img1 * img1, window, padding=pad, groups=channels) - mu1_sq
    sigma2_sq = F.conv2d(img2 * img2, window, padding=pad, groups=channels) - mu2_sq
    sigma12 =  F.conv2d(img1 * img2, window, padding=pad, groups=channels) - mu12

    # Some constants for stability 
    C1 = (0.01 ) ** 2  # NOTE: Removed L from here (ref PT implementation)
    C2 = (0.03 ) ** 2 

    contrast_metric = (2.0 * sigma12 + C2) / (sigma1_sq + sigma2_sq + C2)
    contrast_metric = torch.mean(contrast_metric)

    numerator1 = 2 * mu12 + C1  
    numerator2 = 2 * sigma12 + C2
    denominator1 = mu1_sq + mu2_sq + C1 
    denominator2 = sigma1_sq + sigma2_sq + C2

    ssim_score = (numerator1 * numerator2) / (denominator1 * denominator2)

    if size_average:
        ret = ssim_score.mean() 
    else: 
        ret = ssim_score.mean(1).mean(1).mean(1)
    
    if full:
        return ret, contrast_metric
    
    return ret

• 위 코드에서 gaussian 함수는 가우시안 분포를 출력합니다. 다음과 같습니다.

gauss_dis = gaussian(11, 1.5)
print("Distribution: ", gauss_dis)
# Distribution:  tensor([0.0010, 0.0076, 0.0360, 0.1094, 0.2130, 0.2660, 0.2130, 0.1094, 0.0360, 0.0076, 0.0010])
print("Sum of Gauss Distribution:", torch.sum(gauss_dis))
# Sum of Gauss Distribution: tensor(1.)

• 위 가우시안 분포를 이용하여 이미지의 local 영역을 순회하는 window를 생성해야 합니다. 이 때, create_window 함수를 사용합니다.
• create_window 함수를 보면 동일한 값의 1D gaussian distribution (N) 을 cross product하여 (N, N) 크기의 2D로 window로 만들고 channel 수 만큼 복사하여 확장합니다.
• 아래 코드에서는 (11, 11) 크기의 window 를 channel 방향으로 3 만큼 복사합니다.

window = create_window(11, 3)
print(window.shape)
# torch.Size([3, 1, 11, 11])

• F.conv2d 연산을 보면 생성된 window를 순회하면서 local 영역의 평균과 표준편차를 구하도록 되어있습니다.
• F.conv2d의 첫번째 인자는 입력으로 (B, C, H, W)의 크기를 가지고 두번째 인자는 convolution 연산을 위한 weight로 (#num_filter, channel, H, W) 의 크기를 가집니다. window = create_window(11, 3)으로 window를 생성하면 사이즈가 torch.Size([3, 1, 11, 11])가 되므로 (channel=1, H=11, W=11) 크기의 필터가 3개 있다는 뜻입니다.
• 이와 같은 입력과 필터의 연산으로 평균과 표준편차를 local 영역 단위로 구하여 전체 SSIM을 구하게 됩니다.

• 위 이미지의 가장 왼쪽부터 첫번째 이미지가 원본이고 2 ~ 4번째 이미지는 원본 이미지에 노이즈를 추가한 케이스 입니다.
• 위 코드를 이용하여 (원본, 두번째 이미지), (원본, 세번째 이미지), (원본, 네번째 이미지) 간의 SSIM을 구하면 아래와 같습니다.

load_images = lambda path, h, w: cv2.resize(cv2.cvtColor(cv2.imread(path, cv2.IMREAD_UNCHANGED), cv2.COLOR_BGR2RGB), ((w, h)))
tensorify = lambda x: torch.Tensor(x.transpose((2, 0, 1))).unsqueeze(0).float().div(255.0)

img_tensor = tensorify(load_images("origin.png", 400, 300))
noise1_tensor = tensorify(load_images("noise1.png", 400, 300))
noise2_tensor = tensorify(load_images("noise2.png", 400, 300))
noise3_tensor = tensorify(load_images("noise3.png", 400, 300))

print(ssim(img_tensor, noise1_tensor), ssim(img_tensor, noise2_tensor), ssim(img_tensor, noise3_tensor))
# tensor(0.2894) tensor(0.7756) tensor(0.8177)

• 위 코드 결과 원본 이미지와 가장 마지막 이미지가 SSIM 기준으로 가장 유사한 것을 확인할 수 있습니다.

SSIM의 skimage에서의 사용법

• 참조 : https://scikit-image.org/docs/stable/api/skimage.metrics.html#skimage.metrics.structural_similarity

• 마지막으로 skimage를 이용하여 구하는 방법에 대하여 알아보도록 하겠습니다. 학습에 사용이 아니라 단순히 SSIM 스코어를 구하는 데 사용하려면 아래 코드와 같이 간단히 사용해도 무방합니다.

• 위 그림과 같이 4개의 이미지가 있고 가장 왼쪽이 원본 이미지인 origin, 그리고 그 다음 이미지 부터는 노이즈가 섞여있는 이미지로 각각 noise1, noise2, noise3 이라고 해보겠습니다.
• 아래 코드에서 ssim 함수에서 channel_axis는 RGB와 같이 채널이 여러개 존재할 때, 그 채널의 axis 인덱스를 명시하는 것이며 full은 SSIM 스코어 뿐 아니라 평균을 구하기 이전의 픽셀 단위의 계산 결과도 모두 포함하여 출력하도록 합니다. 이 중간 출력 결과를 통해 두 이미지에 어떤 차이가 있는 지 시각화 해서 볼 수 있습니다.
• win_size 옵션을 추가로 입력하면 로컬 영역에서 SSIM을 구하도록 할 수 있습니다.

import cv2
import matplotlib.pyplot as plt
from skimage.metrics import structural_similarity as ssim

origin = cv2.cvtColor(cv2.imread("origin.png"), cv2.COLOR_BGR2RGB)
noise1 = cv2.cvtColor(cv2.imread("noise1.png"), cv2.COLOR_BGR2RGB)
noise2 = cv2.cvtColor(cv2.imread("noise2.png"), cv2.COLOR_BGR2RGB)
noise3 = cv2.cvtColor(cv2.imread("noise3.png"), cv2.COLOR_BGR2RGB)

ssim_1, diff1 = ssim(origin, noise1, channel_axis=2, full=True)
diff1 = (diff1 * 255).astype("uint8")
# plt.imshow(diff1)
ssim_2, diff2 = ssim(origin, noise2, channel_axis=2, full=True)
diff2 = (diff2 * 255).astype("uint8")
ssim_3, diff3 = ssim(origin, noise3, channel_axis=2, full=True)
diff3 = (diff3 * 255).astype("uint8")

print(ssim_1, ssim_2, ssim_3)
# 0.21075336301148573 0.6888119020545118 0.7808179172891382

ssim_1, diff1 = ssim(origin, noise1, channel_axis=2, win_size=11, full=True)
diff1 = (diff1 * 255).astype("uint8")
ssim_2, diff2 = ssim(origin, noise2, channel_axis=2, win_size=11, full=True)
diff2 = (diff2 * 255).astype("uint8")
ssim_3, diff3 = ssim(origin, noise3, channel_axis=2, win_size=11, full=True)
diff3 = (diff3 * 255).astype("uint8")

print(ssim_1, ssim_2, ssim_3)
# 0.23226598957553168 0.7078116166774144 0.7831195478428952

• 위 SSIM의 결과를 보면 원본 이미지와 노이즈 추가 이미지3의 SSIM이 0.78로 가장 유사하며 원본 이미지와 노이즈 추가 이미지1의 SSIm이 0.21(0.23)으로 가장 차이가 있는 것을 확인할 수 있습니다.