11. Detection and Segmentation

이 때까지의 수업에서는 주로 Image Classification 문제를 다루었습니다.
입력 이미지가 들어오면 Deep ConvNet을 통과하고 네트워크를 통과하면 Feature Vector가 나옵니다. AlexNet이나 VGG의 경우에는 4096차원의 Feature Vector가 생성되었습니다.
그리고 최종 Fully Connected Layer에서는 1000개의 클래스 스코어를 나타냅니다. 이 예제에서 1000개의 클래스는 ImageNet의 클래스를 의미합니다.
즉, 전체 구조는 입력 이미지가 들어오면 전체 이미지가 속하는 카테고리의 출력입니다.
이번 강의에는 Deep Learning을 이용한 이미지 처리의 다양한 Task들에 대하여 알아보도록 하겠습니다.

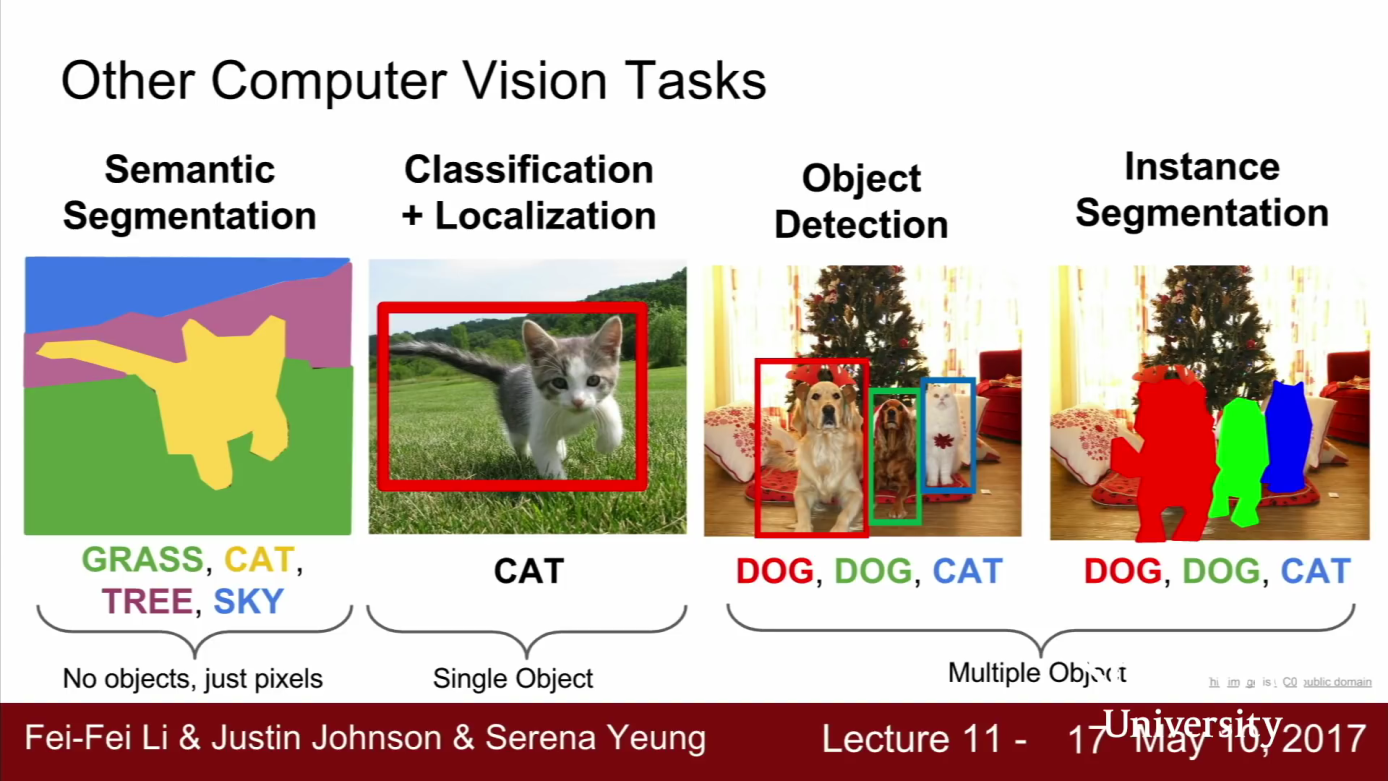
이번 강의에서 배울 내용은 크게 4가지 입니다.
- Semantic Segmentation
- Classification + Localization
- Object Dectection
- Instance Segmentation

Semantic Segmentation

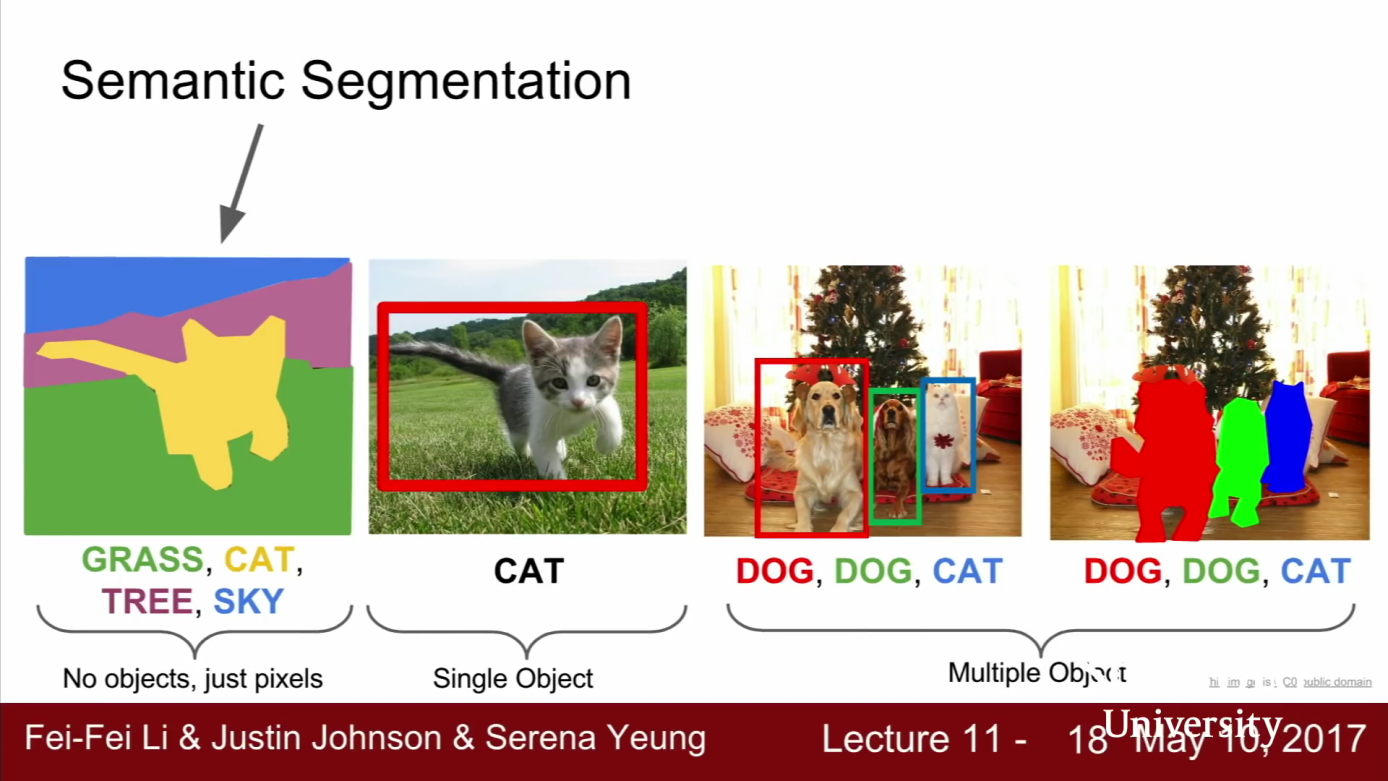
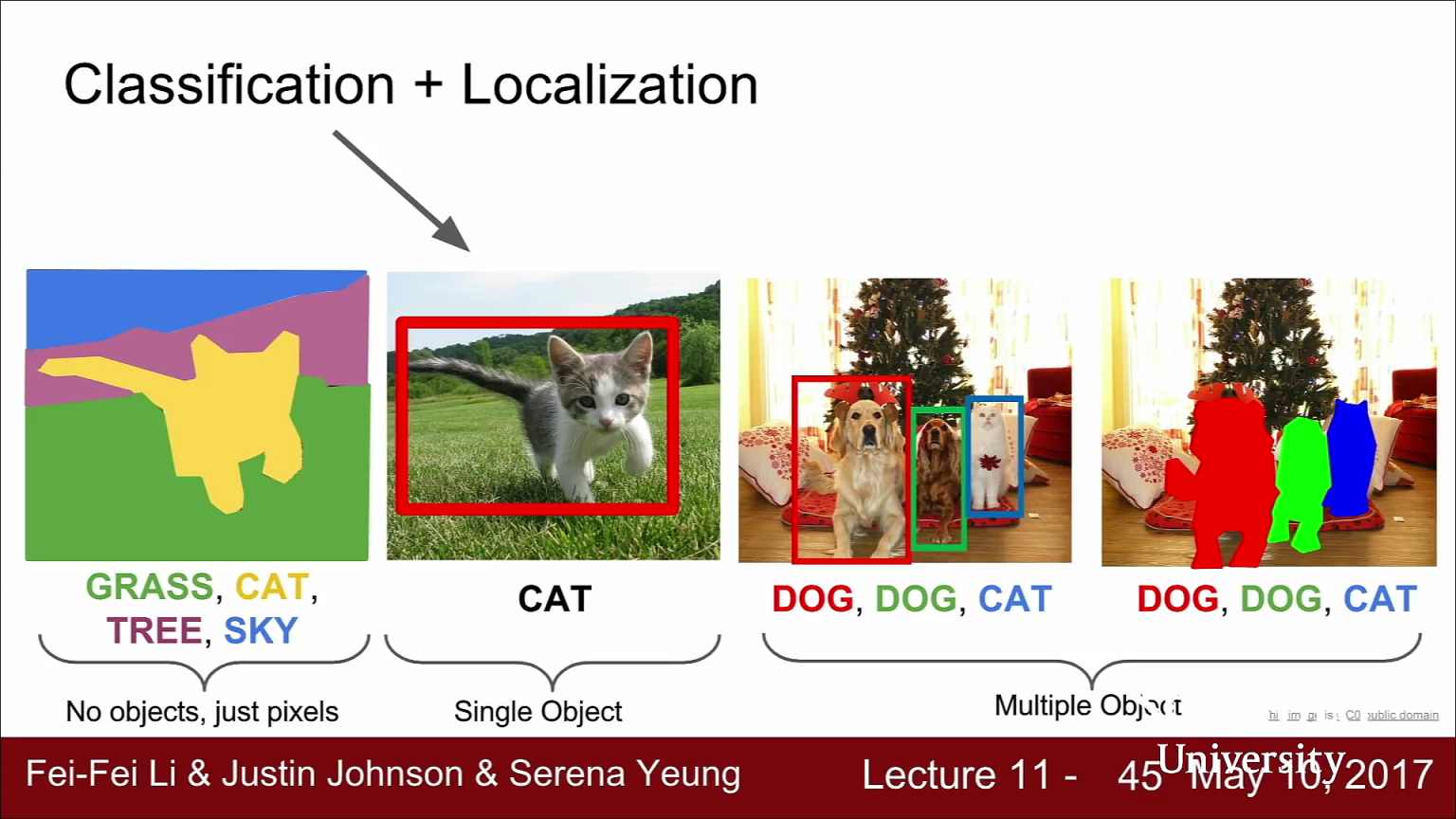
Semantic Segmentation 문제에서는 입력은 이미지이고 출력으로 이미지의 모든 픽셀에 카테고리를 정합니다.
- 예를 들어 위 슬라이드의 예제를 보면 입력은 고양이 입니다.
- 출력은 모든 픽셀에 대하여 그 픽셀이 고양이, 잔디, 하늘, 나무, 배경인지를 결정합니다.
Semantic Segmentation에서도 Classification 처럼 카테고리가 있습니다. 하지만 차이점은 Classification처럼 이미지 전체에 카테고리 하나가 아니라 모든 픽셀에 카테고리가 매겨집니다.

Semantic Segmentation은 개별 객체를 구별하지 않습니다.
위 슬라이드의 Semantic Segmentation 결과를 보면 픽셀의 카테고리만 구분해 줍니다. 즉, 오른쪽 슬라이드의 결과를 보면 소 2마리가 있는데 2마리 각각을 구분할 수는 없습니다. 이것은 Semantic Segmentation의 단점이고 나중에 배울 Instance Segmentation에서 이 문제를 해결할 수 있습니다.

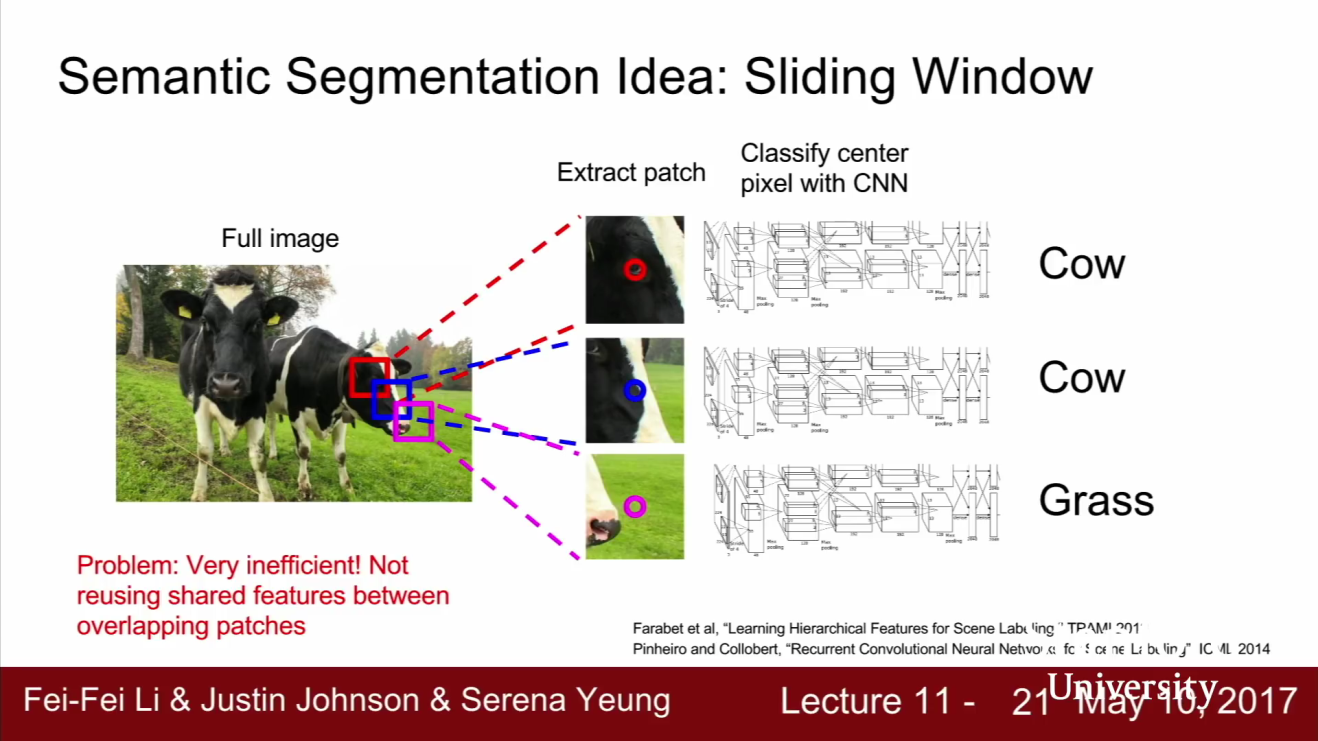
Semantic Segmentation 문제에 접근해 볼 수 있는 방법 중 하나는 Classification을 통한 접근 방법입니다. Semantic Segmentation을 위해서 Classification 모델을 Sliding Window를 이용하여 적용해 볼 수 있습니다.
먼저 입력 이미지를 아주 작은 단위로 쪼갭니다. 위 슬라이드의 예제에서는 소의 머리 주변에서 영역 세개를 추출하였습니다. 이 작은 영역만을 가지고 classification 문제를 푼다고 가정하여 해당 영역이 어떤 카테고리에 속하는지 알아볼 수 있습니다.
즉, 이미지 한장을 분류하기 위해서 만든 모델을 이용해서 이미지의 작은 영역을 분류하게 할 수 있습니다. 그러나 이 방법이 어느 정도는 동작할 지 모르겠지만 그렇게 좋은 방법은 아닙니다. 왜냐하면 계산 비용이 굉장히 많이 들기 때문입니다.
모든 픽셀에 대하여 작은 영역으로 쪼개고, 이 모든 영역을 forward/backward pass 하는 일은 상당히 비효율적입니다. 먼저 계산량 측면에서도 상당히 비효율적일 뿐 아니라 공간 상에서 공유하는 서로 다른 feature들을 공유해서 사용할 수도 없습니다.
그리고 서로 다른 영역이라도 인접해 있으면, 어느 정도 겹쳐져 있기 때문에 특징들을 공유할 수 있습니다. 이렇게 영역을 분할하는 경우에도 영역들끼리 공유할만한 특징들이 아주 많을 것입니다.
따라서 각 픽셀마다 개별적으로 classification을 적용하는 방법은 아주 나쁜 방법입니다. 하지만 semantic segmentation을 할 때 가장 쉽게 생각할 수 있는 아이디어 이기도 합니다.

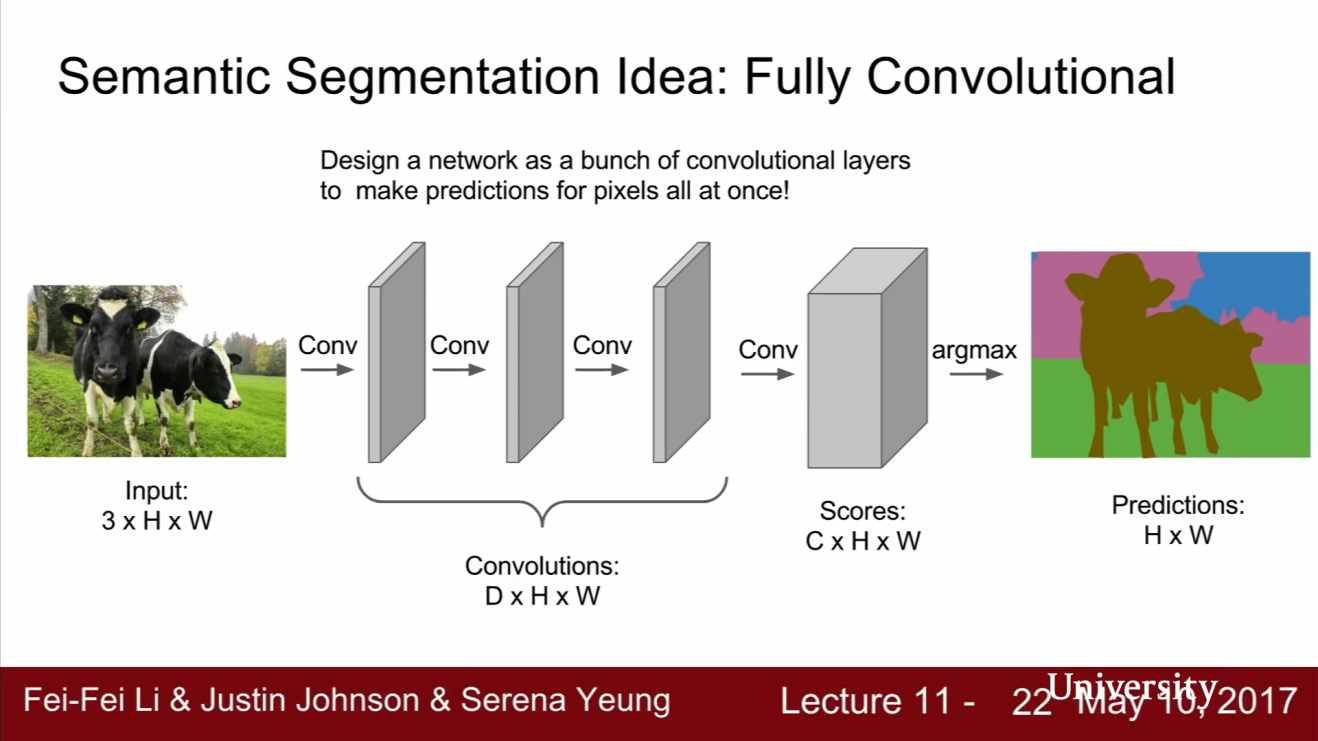
슬라이딩 윈도우 방법보다 조금 더 개선된 방법으로 Fully Convolutional Network가 있습니다.
이 방법은 이미지 영역을 패치 단위로 나누고 독립적으로 분류하는 방법과는 다릅니다. FC layer가 없고 Convolution layer로 구성된 네트워크크 형태입니다.
위 그림과 같이 3 x 3 zero padding을 수행하는 Convolution Layer들을 쌓아올리면 이미지의 공간 정보를 손실하지 않을 수 있습니다.
이 네트워크의 출력 Tensor는 C x H x W입니다. 여기서 C는 카테고리의 수 입니다.
이 출력 Tensor는 입력 이미지의 모든 픽셀 값에 대하여 classification score를 매긴 값입니다.
이 네트워크를 학습시키려면 먼저 모든 픽셀의 classification loss를 계산하고 평균 값을 취합니다. 그리고 기존처럼 back propagation을 수행하면 됩니다.

이러한 방법을 사용하려면 training data을 만들 때 각 픽셀마다 classification을 한 데이터가 있어야 합니다. 따라서 training data를 만들 때에도 상당히 큰 비용이 발생하게 됩니다. classification 문제는 한 장의 이미지에 1개의 label값이 필요하지만 segmentation 문제에서는 이미지의 해상도에 일치하는 label 값이 필요합니다. 예를 들어 100 x 100 크기의 이미지라면 10,000개의 label 값이 필요합니다.

segmentaion 문제에서는 각 픽셀 마다 classification을 해야하므로 모든 픽셀 출력값에 대하여 Cross Entropy를 적용해야 합니다.
따라서 출력의 모든 픽셀에는 Ground Truth가 반드시 존재합니다. 출력의 모든 픽셀과 Ground Truth 간의 Cross Entropy를 계산하며 이 때 계산한 값들을 모두 더하거나 평균화시켜서 Loss를 계산할 수 있습니다. 또는 Mini-batch 단위로 계산할 수도 있습니다.
따라서 모든 픽셀의 카테고리를 알고 있어야 데이터셋을 만들 수 있고 학습할 수도 있습니다.

이 모델은 하이퍼파라미터만 잘 조절해서 학습시켜주면 비교젹 잘 동작합니다.
하지만 위 그림과 같은 모델의 단점은 입력 이미지의 Spatial size를 계속 유지시켜주어야 합니다. 위 그림을 보면 입력의 height, width 사이즈와 중간 레이어의 height, width 사이즈 그리고 출력의 height, width 사이즈 까지 모두 같습니다.
만약 이 네트워크에 고해상도 이미지가 입력으로 들어오게 되면 계산량과 메모리가 상당히 커져서 감당하기 어려운 계산량이 될 수 있습니다.
왜냐하면 height, width의 크기도 큰 반면 중간 레이어 들의 채널 수가 늘어나는 구조이기 때문에 기하급수 적으로 계산량이 늘어나기 때문입니다.

따라서 spatial size를 유지해야 하는 구조 대신에 위 슬라이드와 같은 downsampling/upsampling 구조를 사용하는 것이 대부분입니다.
위 슬라이드를 보면 feature map을 downsampling/upsampling 을 합니다.
즉, spatial resolution 전체를 가지고 Convolution을 수행하기 보다는 original resolution에서는 conv layer는 소량만 사용합니다. 그리고 max pooling, stride convolution 등으로 feature map을 downsample 합니다.
위 구조는 classification network와 구조가 유사하게 보입니다. 하지만 차이점이 있습니다. classification에서는 FC layer가 있었습니다. 하지만 위 슬라이드 방법은 Spatial resolution을 다시 입력 이미지의 크기로 키우기 때문에 FC layer가 삭제되었습니다.
입력 - 중간 - 출력 레이어의 해상도를 유지하는 구조 대신에 위 그림과 같은 구조를 사용하면 출력의 해상도는 입력의 해상도와 같아지면서 기존 방식보다 계산 효율이 좋아지는 장점을 갖습니다. 계산 효율이 좋아진 덕분에 더 깊은 레이어 구조를 만드는 데에도 도움이 됩니다.

이전 강의에서 다루었던 내용을 살펴보면 Convolutional Networks에서의 Downsampling에 대해서 다루어 본 적이 있을 것입니다. 예를 들어 이미지의 Spatial Size를 줄이기 위한 stride conv 또는 다양한 pooling들을 다루어 본 적이 있을 것입니다.

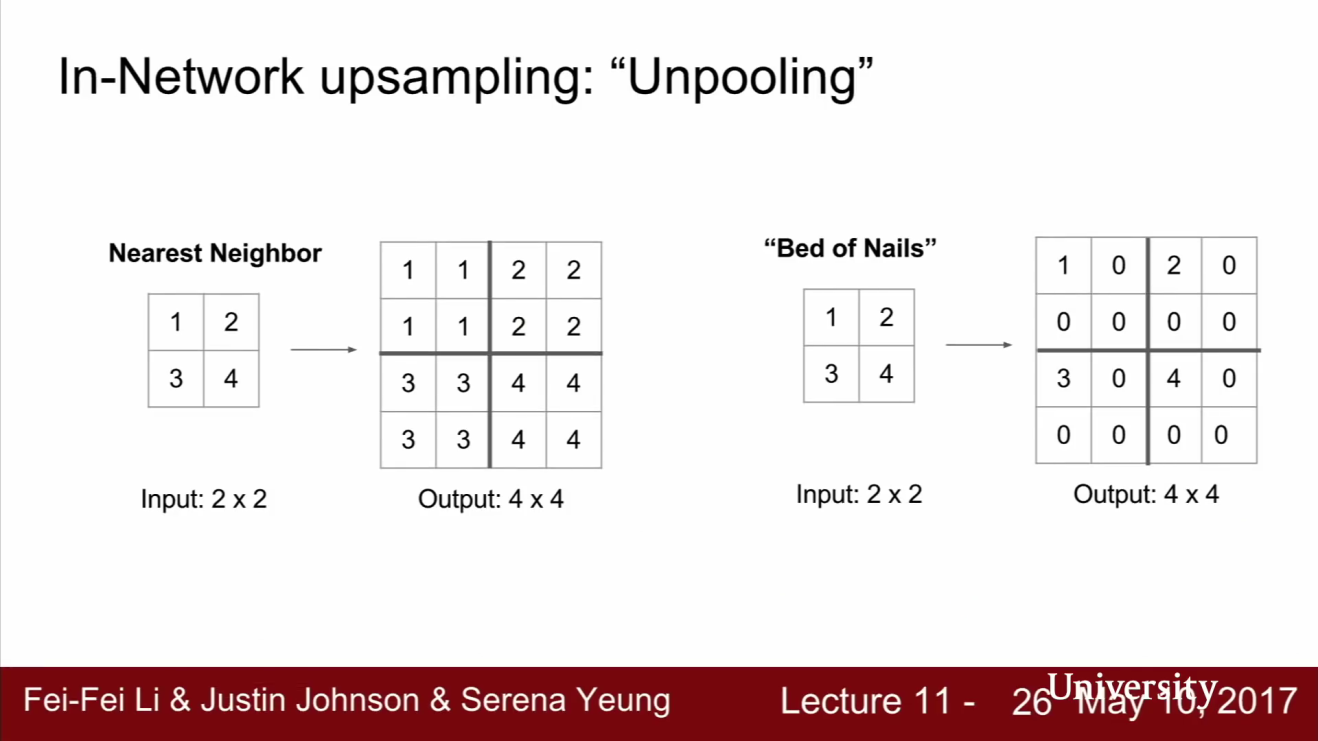
Upsampling의 방법 중 하나는 unpooling 입니다.
unpooling 방법 중에는 슬라이드 왼쪽과 같이 nearest neighbor unpooling 방법이 있습니다.
왼쪽의 nearest neighbor unpooling 예제를 보면 입력은 2 x 2 그리드이고 출력은 4 x 4 그리드입니다. 2x2 stride nearest neighbor unpooling은 해당하는 receptive field 값을 그냥 복사합니다.
또 다른 방법으로는 bed of nails unpooling 이라는 것이 있습니다. 이 방법은 unpooling region에만 값을 복사하고 다른 곳에는 모두 0을 채워넣습니다.
이 경우 하나의 요소를 제외하고 모두 0으로 만듭니다. 이 예제에서는 왼쪽 위에만 값이 있고 나머지는 0입니다. bed of nails 라는 표현의 유래는 zero region은 평평하고 non-zero region은 바늘처럼 뾰족하게 값이 튀기 때문입니다.

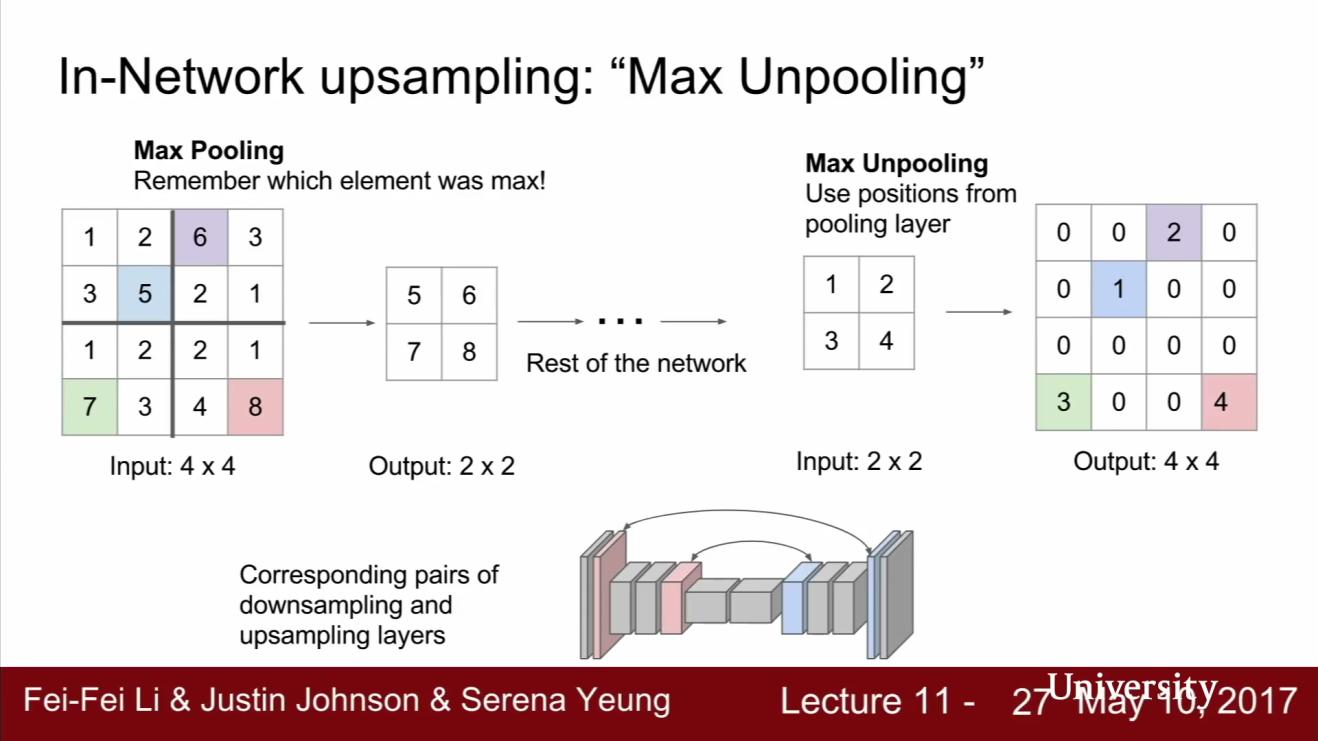
또 다른 Upsampling 방법에는 Max unpooling이 있습니다.
대부분의 네트워크는 대칭적인 경향이 있습니다. 예를 들어 Downsampling/Upsampling의 비율이 대칭적입니다. Max unpooling은 이런 대칭적인 구조에서 사용되는 upsampling 방법입니다.
먼저 downsampling 시에는 Max pooling에 사용했던 요소들을 잘 기억하고 있어야 합니다. 다음으로 upsampling 시에는 bed of nails upsampling과 유사하지만 같은 자리에 값들을 넣는게 아니라 이전 maxpooling에서 선택된 위치에 맞게 넣어줍니다. max unpooling을 하고 빈자리에는 0으로 채워줍니다.
정리하면 Low Resolution feature map을 High resolution feature map으로 만들어 주는 것인데, 이 때 Low resolution의 값들을 Max pooling에서 선택된 위치로 넣어주는 것입니다.
이 방법의 장점은 무엇일까요? semantic segmentation에서는 모든 픽셀들의 클래스를 모두 잘 분류해야 합니다.
따라서 예측한 segmentation 결과에서 객체들간의 디테일한 경계가 명확할수록 좋습니다.
하지만 Maxpooling을 하게 되면 feature map이 비균일해 집니다. 즉, 공간 정보를 잃게 되어 픽셀 값들이 어디서 부터 왔는지 알 수 없어 집니다.
즉, Maxpooling 후의 feature map만 봐서는 이 값들이 receptive field 중 어디에서 왔는 지 알 수 없습니다.
따라서 unpooling 시에 기존 max pooling 에서 뽑아온 자리로 값을 넣어주면, 공간 정보를 조금은 더 디테일하게 다룰 수 있습니다.

지금 까지 배운 unpooling의 방법인 bed of nails, nearest neighbor, max unpooling은 고정된 값을 사용하고 별도로 값을 학습하진 않습니다.
반면 uppooling 시 고정값이 아닌 학습가능한 값으로 upsampling 하는 방법이 있습니다. 그 방법이 Transpose convolution 입니다.
즉, feature map을 upsampling 할 때, 어떤 방식으로 할 지를 학습할 수 있습니다.

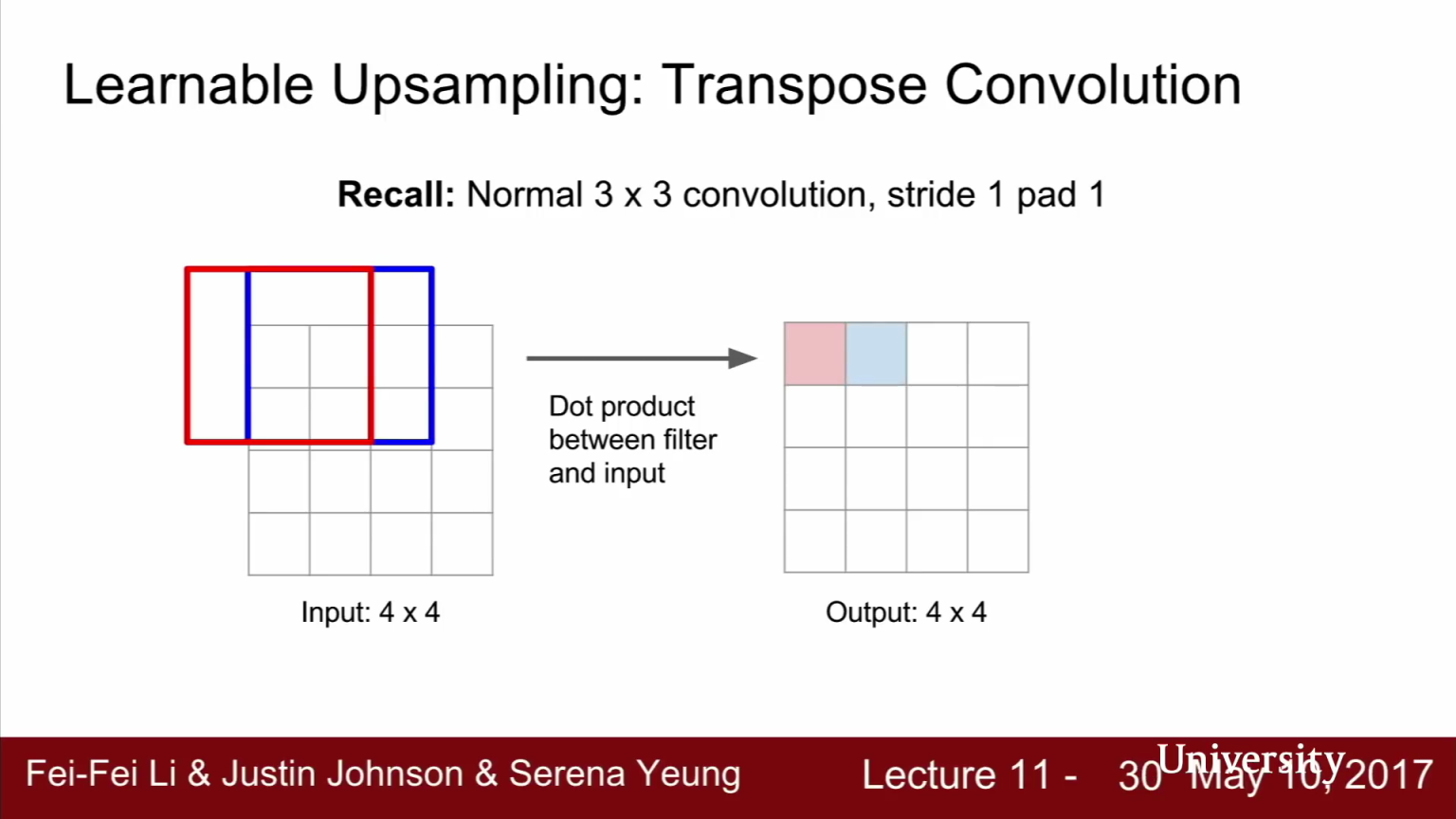
먼저 일반적인 3x3(stride = 1, padding = 1)의 convolution filter가 동작하는 방식을 다시 한번 살펴보겠습니다. 위 그림과 같이 입력이 4 x 4이고 출력 또한 4 x 4 인 경우로 예를 들어보겠습니다.
먼저 3x3 convolution 필터가 있고 이미지와 내적을 수행합니다. 우선 이미지의 좌 상단 구석부터 시작합니다.
현재 사용하는 필터가 3 x3 convolution에 stride = 1, padding = 1이므로 각 영역에 대하여 convolution한 결과는 그대로 4 x 4 의 크기를 가지게 됩니다.

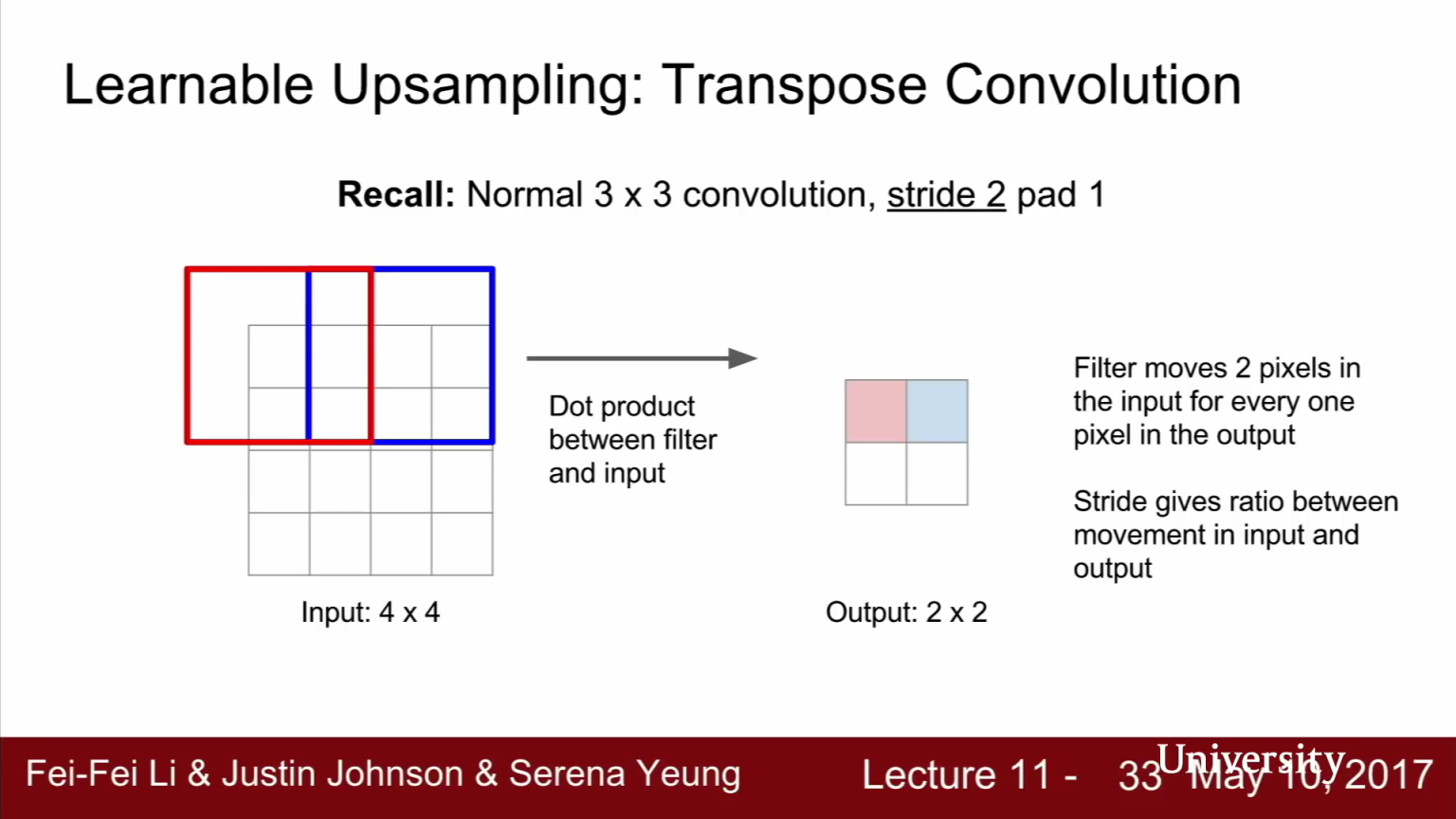
이번에는 strided convolution에 대하여 살펴보겠습니다.
strided convolution은 한 픽셀씩 이동하면서 계산하지 않습니다. 출력에서 한 픽셀 씩 움직이려면 입력에서는 두 픽셀 씩 움직여야 합니다. 즉, stdied는 입력/출력에서의 움직이는 거리 사이의 비율이라고 해석할 수 있습니다.
따라서 stride=2인 strided convolution은 학습 가능한 방법으로 2배 downsampling하는 것을 의미합니다.

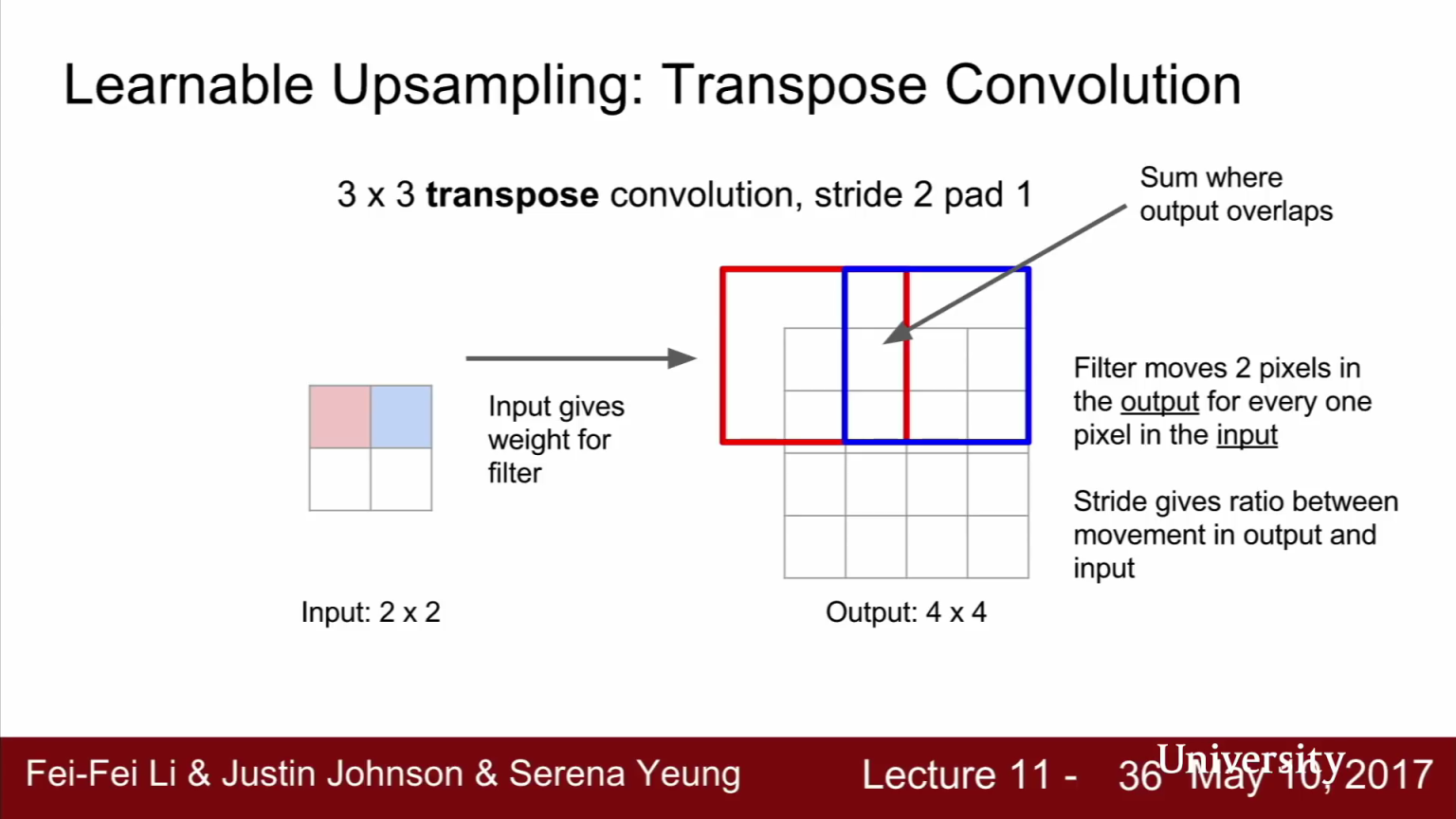
반면 Transpose convolution은 stride convolution과 반대의 경우입니다. 입력이 2x2이고 출력이 4x4 입니다. 출력의 크기가 더 커졌습니다. 그러면 과정을 한번 살펴보도록 하겠습니다.
먼저 입력 feature map에서 값을 하나 선택합니다.
선택된 스칼라 값을 3x3 필터와 곱합니다. 그리고 출력의 3x3 영역에 그 값을 넣습니다. (위 오른쪽 그림의 빨간색, 파란색의 3 x 3 영역에 해당합니다.)
즉, Transpose convolution에서는 필터와 입력의 내적을 계산하는 것이 아니라 입력 값이 필터에 곱해지는 가중치의 역할을 합니다. 따라서 출력 값은 필터 * 입력 (가중치) 입니다.
그리고 현재 적용한 Transpose convolution에 stride = 2가 적용 되었기 때문에 Upsampling 시에는 입력에서 한 칸씩 움직이는 동안 출력에서는 두 칸씩 움직입니다.
이렇게 가중치가 곱해진 필터 값을 출력 값에 넣어줍니다. 그러면 출력에서는 Transpose convolution 간에 Receptive field가 겹칠 수 있습니다.
이런 경우에는 간단하게 두 값을 더해줍니다. 이 과정을 반복해서 끝마치면 학습 가능한 upsampling을 수행한 것입니다.
앞에서 다룬 다른 방법과 비교하면 Transpose convolution은 Spatial size를 키워주기 위해서 학습된 필터 가중치를 이용한 것입니다.

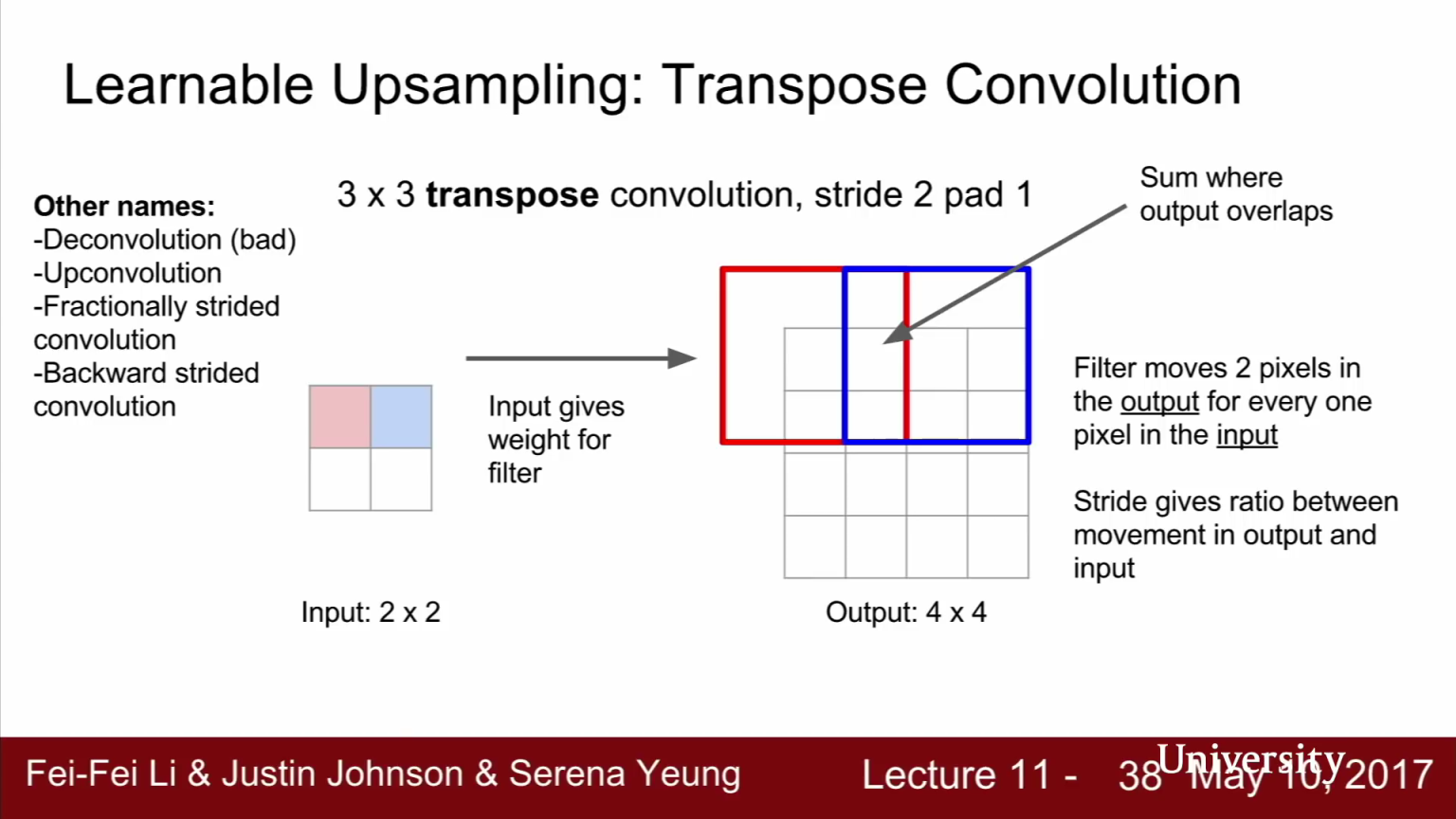
이 방법은(Transpose convolution)은 문헌에 따라서 부르는 이름이 다양합니다.
간혹 deconvolution이라고 하는데 이 용어는 신호처리 관점에서는 convolution의 역연산을 뜻하므로 혼돈을 주기에 적합하지 않습니다.
Upconvolution이라는 용어도 있고 Fractionally strided convolution 이라는 용어도 있습니다.
stride를 input/output 간의 크기의 비율로 생각하면 이 예제는 stride 1/2 convolution이라고 볼 수 있습니다. 왜냐하면 input : output = 1 : 2이기 때문입니다.
또는 Backward strided convolution 이라는 용어로도 불립니다. 왜냐하면 transpose conv의 forward pass를 수학적으로 계산해 보면 일반 Convolution의 backward pass와 수식이 동일하기 때문입니다.

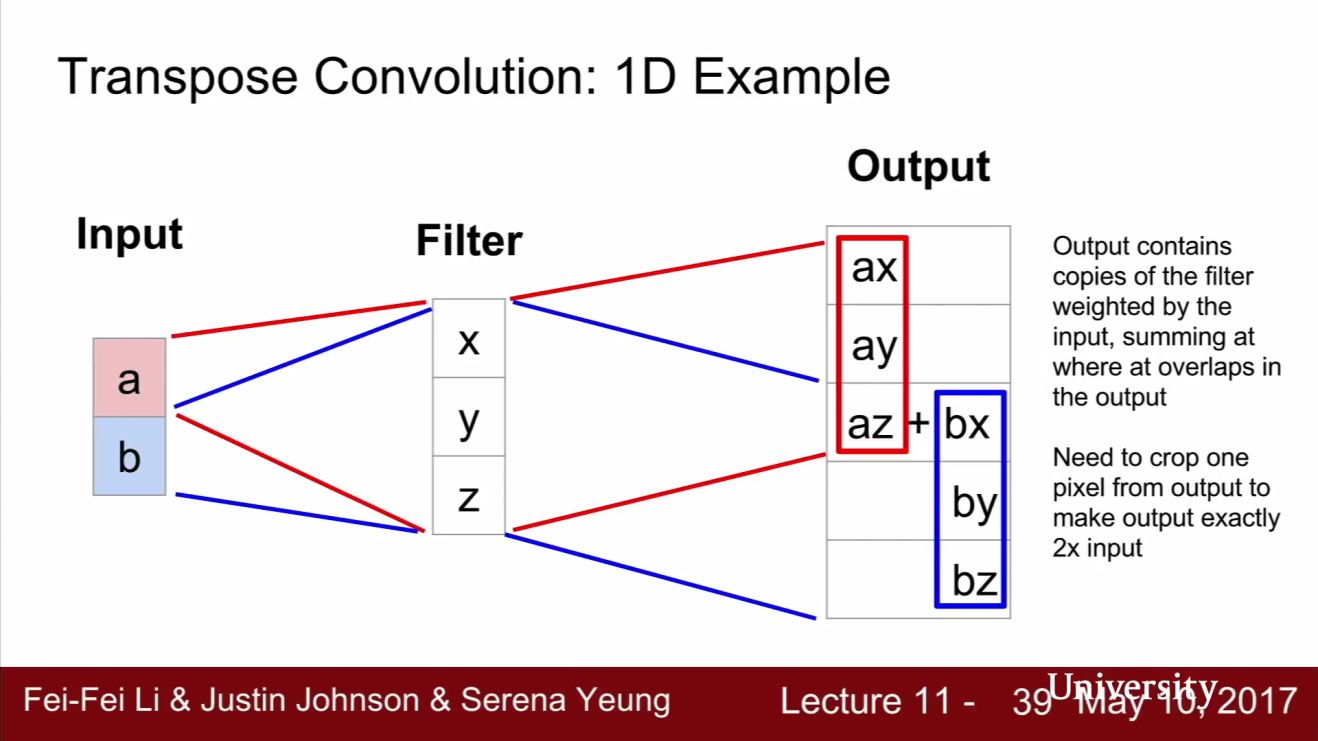
Transpose Convolution의 구체적인 예시를 살펴보겠습니다. 이해를 돕기 위해서 1D example에 대하여 살펴보겠습니다.
이 예제에서는 1차원에서 3x1 Transpose convolution을 수행합니다.
필터에는 세 개의 숫자가 있습니다 : x, y, z
입력은 두 개의 숫자가 있습니다 : a, b
출력값을 계산해 보면 입력이 가중치로 쓰이고 필터에 곱해집니다. 그리고 이 값을 출력에 넣습니다.
그리고 Receptive Field가 겹치는 부분은 그냥 더해줍니다.
이 연산을 하다 보면 왜 이 연산이 Transposed Conv 라는 이름이 붙었는지 궁금하실 수 있습니다.

Transposed 라는 이름의 유래는 Convolution 연산 자체를 해석해보면 알 수 있습니다.
Convolution 연산은 언제든지 행렬 곱 연산으로 나타낼 수 있습니다.
위 슬라이드의 왼쪽을 보면 간단한 1차원 예제를 볼 수 있습니다. 4 x 6 행렬을 보면 \((x, y, z)\) 벡터가 위치를 이동하면서 채워져 있는 것을 볼 수 있습니다.
- 슬라이드에서는 오타가 있는데 x, y, x가 아니라 x, y, z 입니다. x, y, z 이외의 자리에는 0으로 채워집니다.
위 예는 1D Conv이고 size=3, stride=1, padding=1 입니다.
convolution 필터인 \(\vec{x}\)는 3개의 원소(\(x, y, z\))를 가지고 있습니다. 그리고 입력 벡터인 \(\vec{a}\)는 4개의 원소(\(a, b, c, d\))를 가지고 있습니다.
여기서 3x1 filter & stride=1 convolution 연산을 수행한 행렬곱을 표현하면 위의 슬라이드와 같습니다.
convolution 계산할 벡터를 행렬식으로 표현한 뒤 \(X\) 라고 표현할 수 있습니다.
이렇게 만든 가중치 행렬 \(X\)를 가지고 \(X \cdot a\) 연산을 수행하면 convolution과 결과가 동일합니다.

이번에는 슬라이드의 오른쪽과 같이 \(X^{T}\)를 곱하는 형태를 만들어 보겠습니다.
- Transpose Convolution은 Convolution 때와 같은 행렬을 사용해서 행렬곱을 하되 곱할 행렬을 Transpose한 것입니다.
즉, 왼쪽의 행렬은 stride 1 convolution이고 오른쪽 행렬은 stride 1 transpose convolution 입니다.
stride=1일 때에는 convolution과 transpose convolution의 연산이 굉장히 비슷해 보입니다.

하지만 stride > 1인 경우에는 convolution과 transpose convolution의 연산 결과가 많이 달라지는 것을 알 수 있습니다.

기본적인 transpose convolution에서는 receptive field가 겹치는 부분은 덧셈을 해주고 있습니다. transpose convolution의 정의에 따라서 receptive filed의 겹치는 부분을 합칠 때 다른 연산이 없이 덧셈을 하였었습니다.
하지만 Receptive field가 겹치는 부분을 그냥 sum을 하는 것은 문제가 될 수 있습니다.
예를 들어 3x3 stride 2 transpose convolution을 사용하면 checkerboard artifacts가 발생하곤 합니다.
관련 논문에서는 4x4 stride 2 또는 2x2 stride 2 transpose convolution을 사용하면 조금 완화된다고는 합니다.

다시 Semantic segmentation 으로 돌아가 보겠습니다. 위에서 보이는 Semantic segmentation 구조는 상당히 일반적입니다.
네트워크 내부에 downsampling/upsampling을 하는 거대한 convolution network가 있습니다.
여기서 downsampling은 strided convolution 또는 pooling을 사용합니다.
그리고 upsampling은 transpose convolution 또는 다양한 종류의 unpooling/upsampling을 사용합니다. 간단하게 interpolation(bilinear) + convolution 하는 방법도 많이 사용됩니다.
이러한 네트워크 구조를 만든 다음에 모든 픽셀에 대하여 cross entropy를 계산하면 네트워크 전체를 end-to-end로 학습시킬 수 있습니다.
기본적인 segmentation 문제는 classification 문제를 확장시킨 문제와 유사한 것을 확인해 보았습니다.

Classification + Localization

그 다음 다루어 볼 Task는 Classification + Localization 입니다.
이미지 분석을 하다 보면 이미지가 어떤 카테고리에 속하는지 뿐만 아니라 실제 객체가 어디에 있는지를 알고 싶을 수 있습니다. 이 작업은 이미지를 “cat”에 분류하는 것 뿐만 아니라 이미지 내에 cat이 어디에 있는지 네모 박스를 그리는 것입니다.
Classification + Localization 문제는 Object Detection 문제와는 구분이 됩니다. 왜냐하면 Localization 문제에서는 이미지 내에서 관심있는 객체는 오직 하나라고 가정하기 때문입니다. 기본적으로 이미지 내에 객체 하나만 찾아서 레이블을 매기고 위치를 찾는 문제 입니다.

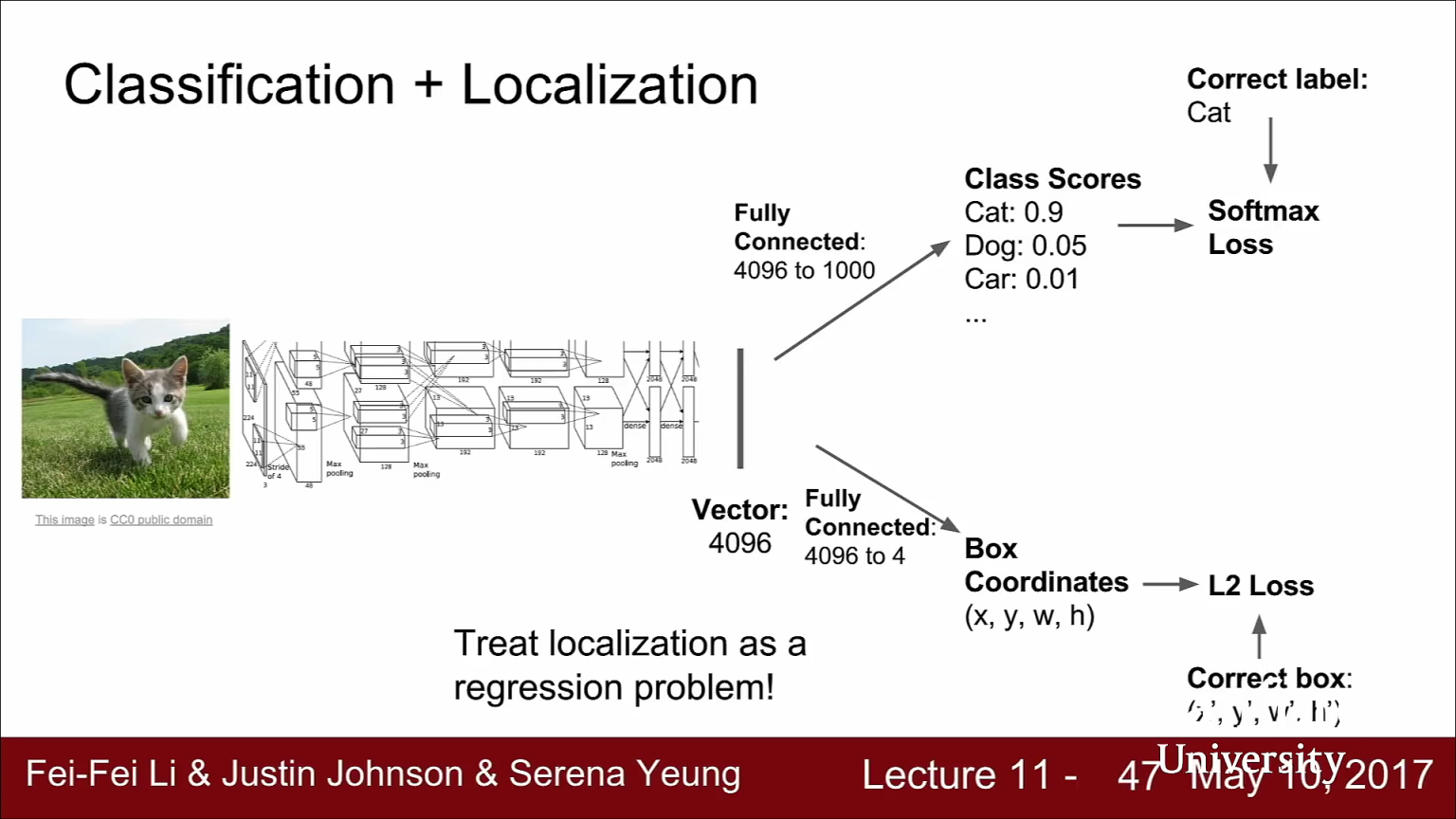
이 문제를 풀때에도 기존의 image classification에서 사용하던 기법들을 고스란히 녹일 수 있습니다.
아키텍쳐의 기본 구조는 위 슬라이드와 같습니다. 위 슬라이드에서는 예제로 AlexNet을 사용하였습니다.
네트워크는 입력 이미지를 받아서 출력을 내보내는 구조는 Classification과 같습니다. 출력 레이어 직전의 FC layer는 Class score로 연결되어서 카테고리를 결정합니다.
하지만 여기에서는 FC layer가 하나 더 있습니다. 이는 4개의 원소를 가진 vector와 연결되어 있습니다. 이 4개의 출력 값은 width/height/x/y로 bounding box의 위치를 나타냅니다.
이런 방법으로 네트워크는 2가지 출력값을 반환합니다. ① class socre 와 ② 입력 영상 내의 객체 위치의 bounding box 좌표입니다.
그리고 이 문제에서는 학습 방법이 fully supervised setting을 가정합니다. 즉, 학습 이미지에는 카테고리 레이블과 해당 객체의 bounding box의 Ground Truth를 동시에 가지고 있어야 합니다.
따라서 이 문제에는 두 가지의 Loss function이 있습니다.
① 먼저 Class score를 예측하기 위한 softmax loss가 있습니다.
② GT(Ground Truth) Bounding Box와 예측한 Bounding Box 좌표 사이의 차이를 측정하는 Loss도 있습니다. 이 Loss는 예측한 box의 좌표와 GT box 좌표간의 차이에 대한 regression loss 입니다.

Localization 문제를 풀면서 오분류한 케이스에 대하여 Bounding box를 학습하는 것에 대한 우려가 있을 수 있습니다.
일반적으로 이 문제 또한 학습하면서 정정되기 때문에 괜찮습니다. Classification과 Localization이 동시에 학습되기 때문입니다.
하지만 성능을 높이기 위하여 classification이 잘 된 경우에 한해서만 bounding box를 학습 하는 방법을 사용할 수도 있습니다.

또 생각할 수 있는 의문점은 Class score의 Loss와 Bounding box에 대한 Loss의 단위가 다를 수 있는데 gradient 시에 같이 계산된다면 문제가 되지 않을 까 입니다.
이렇게 두 개의 Loss를 합친 Loss를 Multi-task Loss 라고 합니다.
먼저 gradient를 구하려면 네트워크 가중치들의 각각의 미분값(scalar)을 계산해야 합니다.
이제는 Loss가 두 개이니 미분값도 두개이고 이 두개를 모두 최소화 시켜야 합니다.
학습을 설정할 때 두 Loss의 가중치를 조절하는 하이퍼파라미터가 있습니다. 두 Loss의 가중치 합이 최종 Loss 입니다. 이 때 사용하는 하이퍼파라미터는 사용자가 설정해 주어야 하는 값으로 적절한 값을 설정하기가 상당히 까다롭습니다.
그리고 이 두 Loss의 가중 합에 대한 gradient를 계산하는 것입니다.

물론 Localization 문제를 풀 때에도 Transfer Learning을 하는 것은 아주 좋은 방법입니다.
Transfer Learning의 관점에서 보면 fine tuning을 하면 항상 성능이 좋아지기 때문입니다.
ImageNet으로 학습시킨 모델을 가지고 데이터셋에 작용한다면 적절한 Fine tuning이 성능 향상에 도움이 될것입니다.
실제로 많은 사람들이 사용하는 방법 중 하나는 우선 네트워크를 Freeze하고 Class score와 Bounding box 관련된 두 FC layer를 학습시킵니다.
그리고 두 FC layer가 수렴하면 다시 합쳐서 전체 시스템을 Fine tuning 하는 것입니다.
지난 시간에는 ImageNet을 예로 들어서 Pre-Trained Network를 소개한 적이 있습니다.

Bounding Box와 같이 이미지 내의 어떤 위치를 예측한다는 아이디어는 Classification + Localization 문제 이외에도 아주 다양한 문제에도 적용할 수 있습니다.
그 중 하나는 위의 슬라이드와 같이 human pose estimation 입니다.
human pose estimation에서는 사람 이미지가 입력으로 들어갑니다. 출력은 이 사람의 각 관절의 위치입니다. 이 네트워크는 사람의 포즈를 예측합니다. 즉, 이 사람의 팔 다리가 어디에 있는지를 예측합니다.
보통 이런 문제를 풀 때에는 관절의 갯수를 14개로 간략화 하고 사람의 포즈를 정의합니다.

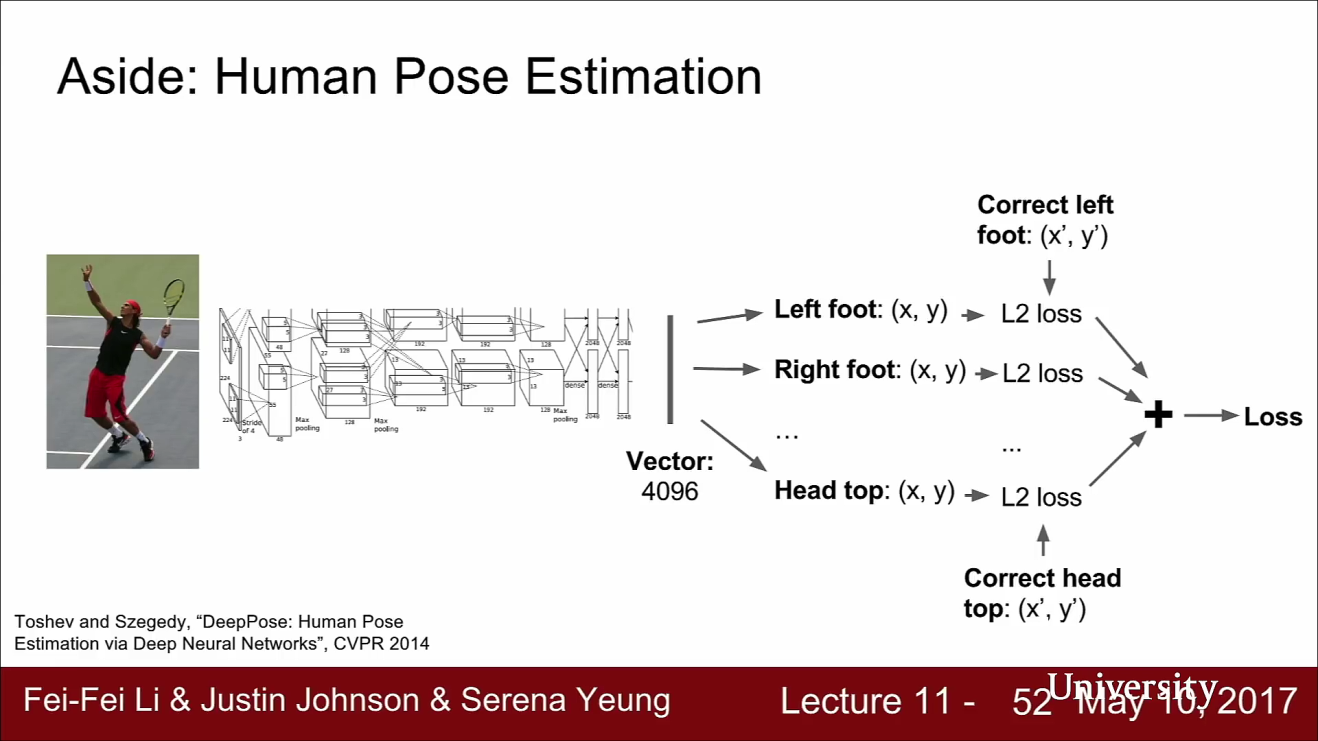
그리고 네트워크의 출력은 각 관절에 해당하는 14개의 좌표값입니다.
예측된 14개의 점에 대해서 regression으로 loss를 계산하고 backprop으로 학습시킵니다.
Pose estimation에서는 관절의 갯수와 관절의 순서를 미리 정하고 학습을 시켜야 합니다.
이와 유사하게 Regression output이 고정된 갯수라면 Pose estimation과 같은 다양한 문제를 풀 수 있습니다.

Object detection

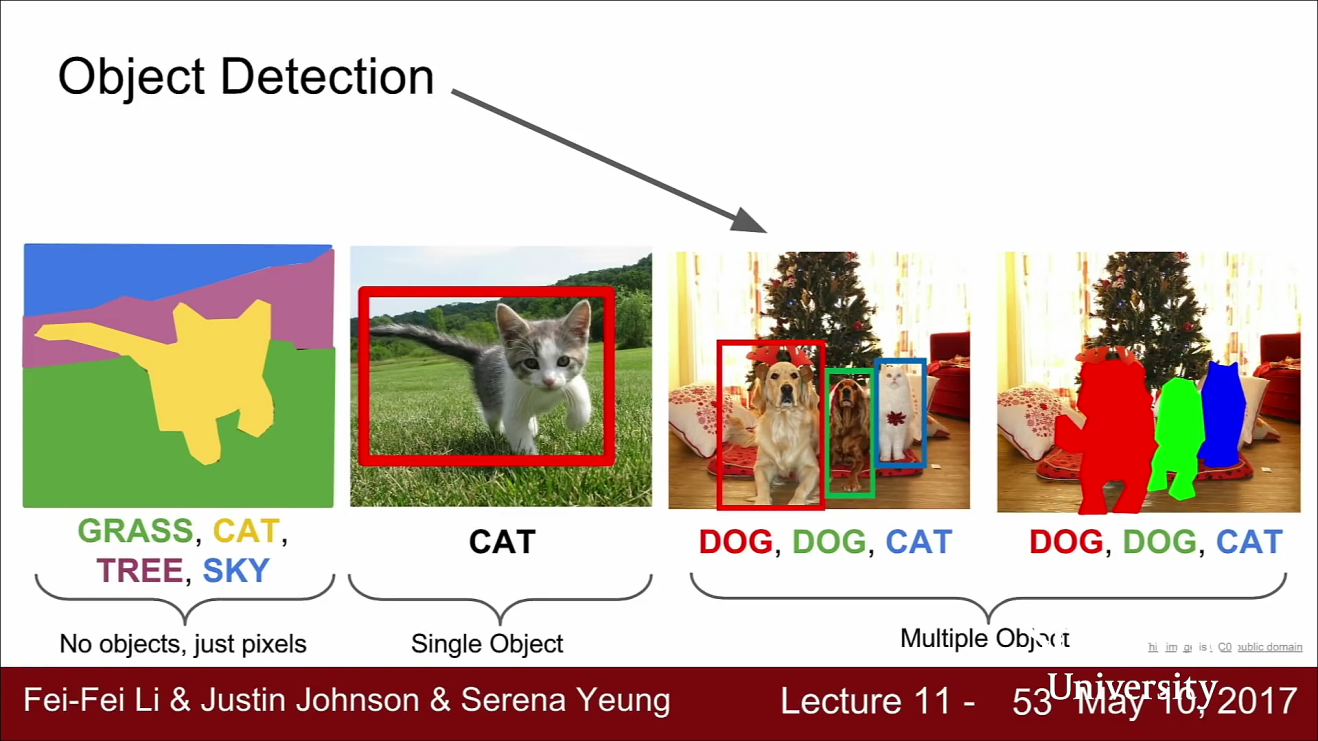
다음으로 다룰 문제는 object detection 입니다. object detection은 computer vision에서 중요한 문제 중 하나입니다.
object detection은 연구된 역사가 길어서 다룰 수 있는 내용은 상당히 많지만 이번 강의에서는 deep learning과 연관된 object detection의 내용만 살펴볼 예정입니다.
object detection의 task는 입력 이미지가 주어지면 이미지에 나타나는 객체들의 bounding box와 해당하는 카테고리를 예측합니다. 즉, 앞에서 다룬 classification + localization과는 조금 다릅니다.
이렇게 하는 이유는 예측하야 하는 Bbox의 수가 입력 이미지에 따라 달라지기 때문입니다. 각 이미지에 객체가 몇 개나 있을 지는 미지수입니다.

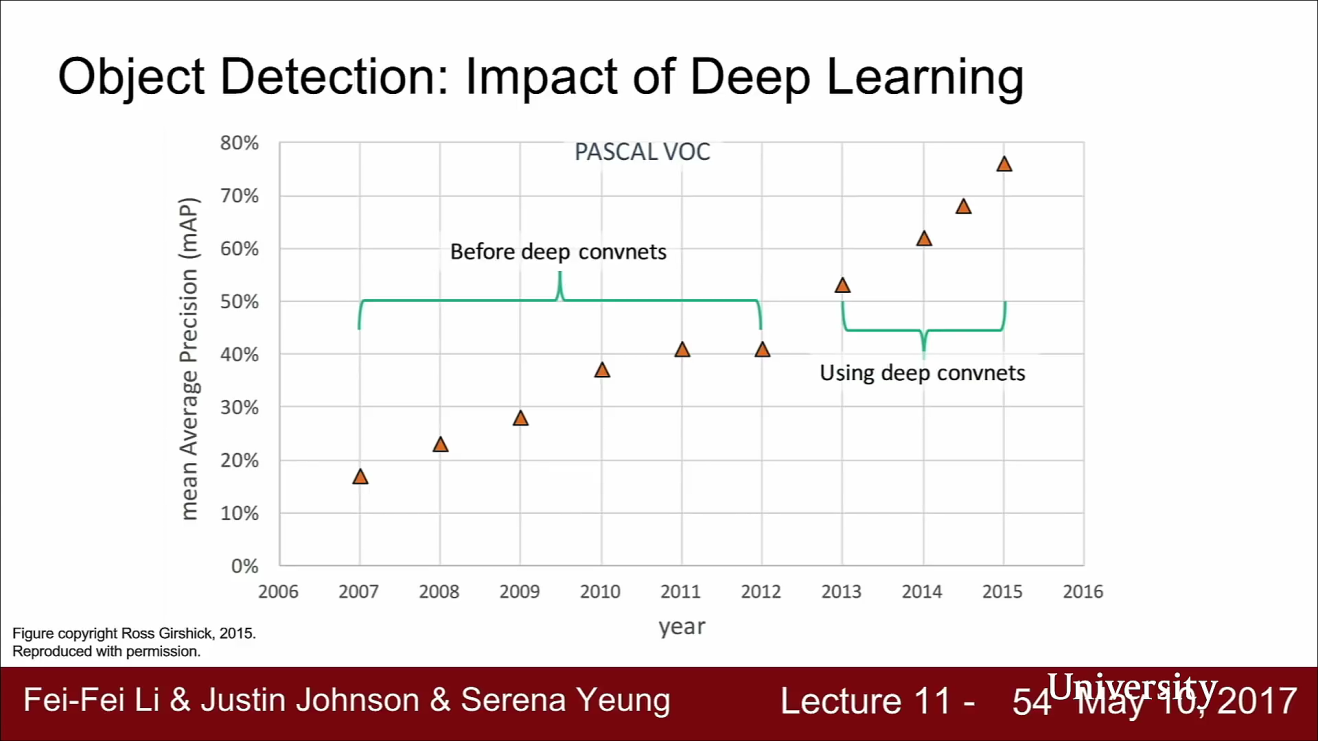
위 슬라이드는 PASCAL VOC Dataset을 이용한 모델들의 성능이 발전하는 과정을 보여줍니다. PASCAL VOC는 Detection에서 아주 오래전부터 사용되었습니다.
데이터를 보면 Deep learning이 도입된 이후 부터 성능이 아주 좋아진 것을 볼 수 있습니다.
그리고 2015년 이후의 데이터는 없는데요, 그 이유는 이미 성능이 너무 좋아져서 State of the art에 대한 논의가 무의미해 졌기 때문입니다.

위 슬라이드를 보면 첫 번째 사진에는 고양이 한마리에 대한 Bbox의 정보가 있어야 하고 두 번째 사진은 개 2마리, 고양이 1마리에 대한 Bbox 정보가 있어야 합니다.
마지막 사진에는 오리 여러 마리에 대한 Bbox가 있어야 합니다.

따라서 object detection을 하기 위해서는 새로운 아이디어가 필요합니다. 먼저 가장 간단한 sliding window 아이디어 부터 알아보겠습니다.
앞선 semantic segmentation에서 작은 영역으로 쪼갰던 아이디어와 비슷한 방법을 사용합니다.
Sliding Window를 이용하려면 입력 이미지로부터 다양한 영역을 나눠서 전처리 합니다.
CNN은 이 작은 영역에 대하여 classification을 수행합니다. 이 때 위 파란색 박스 영역에는 어떤 object도 없고 background 카테고리임을 인식할 것입니다.
- 즉 object가 없는 경우를 대비하여 background 카테고리를 입력해 주어야 합니다.
- 네트워크가 배경이라고 예측했다면, 이 곳은 어떤 카테고리에도 속하지 않는다는 것을 의미합니다.
이미지의 왼쪽 밑 영역에는 아무것도 없으므로 네트워크는 배경이라고 예측할 것이므로 아무것도 없다는 뜻입니다.

다른 영역을 추출해 보겠습니다. 여기에는 개는 있고, 고양이는 없고, 배경은 아닌 상태입니다.
이렇게 sliding window를 통하여 문제를 해결할 수 있지만, 이 방법에는 몇가지 문제가 있습니다.

먼저 어떻게 영역을 추출할 지가 문제가 될 수 있습니다.
이미지 안에서 어떤 크기의 object가 어디에 위치가 될 지 모르니 window의 사이즈 자체를 설정하는 것에 문제가 있습니다.
따라서 이런 brute force 방식의 sliding window를 하려면 너무나 많은 경우의 수가 존재합니다.
또한 계산량의 문제가 있습니다.
작은 영역 하나 하나마다 거대한 CNN을 통과시키려면 이 때의 계산량은 다를 수 없는 양입니다.
따라서 Object detection문제를 풀기 위하여 brute force sliding window를 하는 일은 절대 없습니다.

대신에 Regional Proposals 라는 방법이 있습니다. 이 방법은 Deep learning을 사용하는 방법은 아닙니다.
Regional Proposal Network는 전통적인 신호처리의 기법을 사용합니다. Regional Proposal Network는 Object가 있을 법한 Bbox를 제공해 줍니다. 예를 들어 1000 ~ 2000 개 정도의 region을 제공해 준다고 가정해 봅시다.
이미지 내에서 객체가 있을 법한 후보 region proposal을 찾아내는 다양한 방법이 있습니다. 예를 들어 Regional Proposal Network는 이미지 내의 뭉텅이가 진 곳(blobby)한 곳을 찾아냅니다.
이 지역들은 객체가 있을지도 모르는 후보 영역들입니다. 이런 알고리즘은 비교적 빨리 작동합니다.
Region Proposal의 방법 중 유명한 알고리즘에는 Selective Search가 있습니다.
이 방법은 노이즈가 심하여 대부분은 실제 객체가 아니지만 Recall은 아주 높습니다. 따라서 이미지내에 객체가 존재한다면 Selective Search의 Region Proposal 안에 속할 가능성이 높습니다.
따라서 Sliding window와 같이 굉장히 비효율적인 방법보다 Selective Search를 이용하여 가능성 있는 부분을 선택한 다음에 CNN의 입력으로 이용하면 좀 더 효율적입니다.

R-CNN

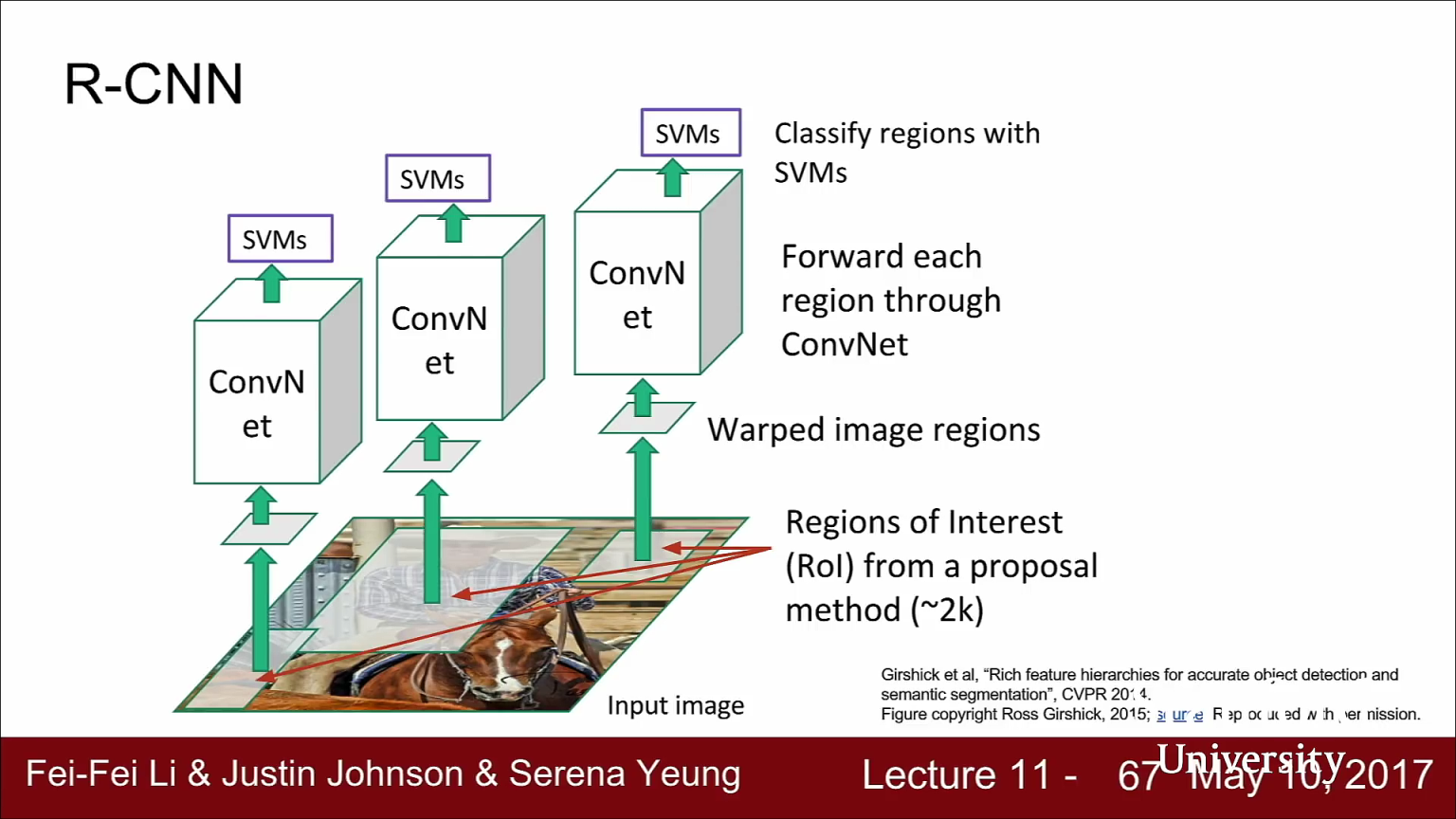
위에서 소개한 Selective Search의 개념이 R-CNN에서 소개됩니다. 위 그림의 과정이 R-CNN의 전체 과정입니다.

먼저 이미지가 주어지면 Region Proposals을 얻기 위해 Region Proposal Network를 수행합니다.
Region Proposal은 Region of Interest(ROI)라고도 합니다. Selective Search를 통하여 2000여개의 ROI를 얻어냅니다. 위 그림의 회색 영역을 Selective Search를 통하여
하지만 여기에서는 각 ROI의 사이즈가 각양각색이라는 문제가 생길 수 있습니다.

추출된 ROI로 CNN classification을 수행하려면 FC layer 등으로 같은 입력사이즈로 맞추어 줘야 하기 때문에 ROI의 크기가 같아야 합니다.
따라서 Region Proposal을 추출하면 CNN의 입력으로 사용하기 위하여 동일한 고정된 크기로 변형해야 합니다. 즉, Regional Propose를 추출하면 고정된 사이즈로 크기를 바꿉니다. 위 그림의 warped image region이 이 부분에 해당합니다.

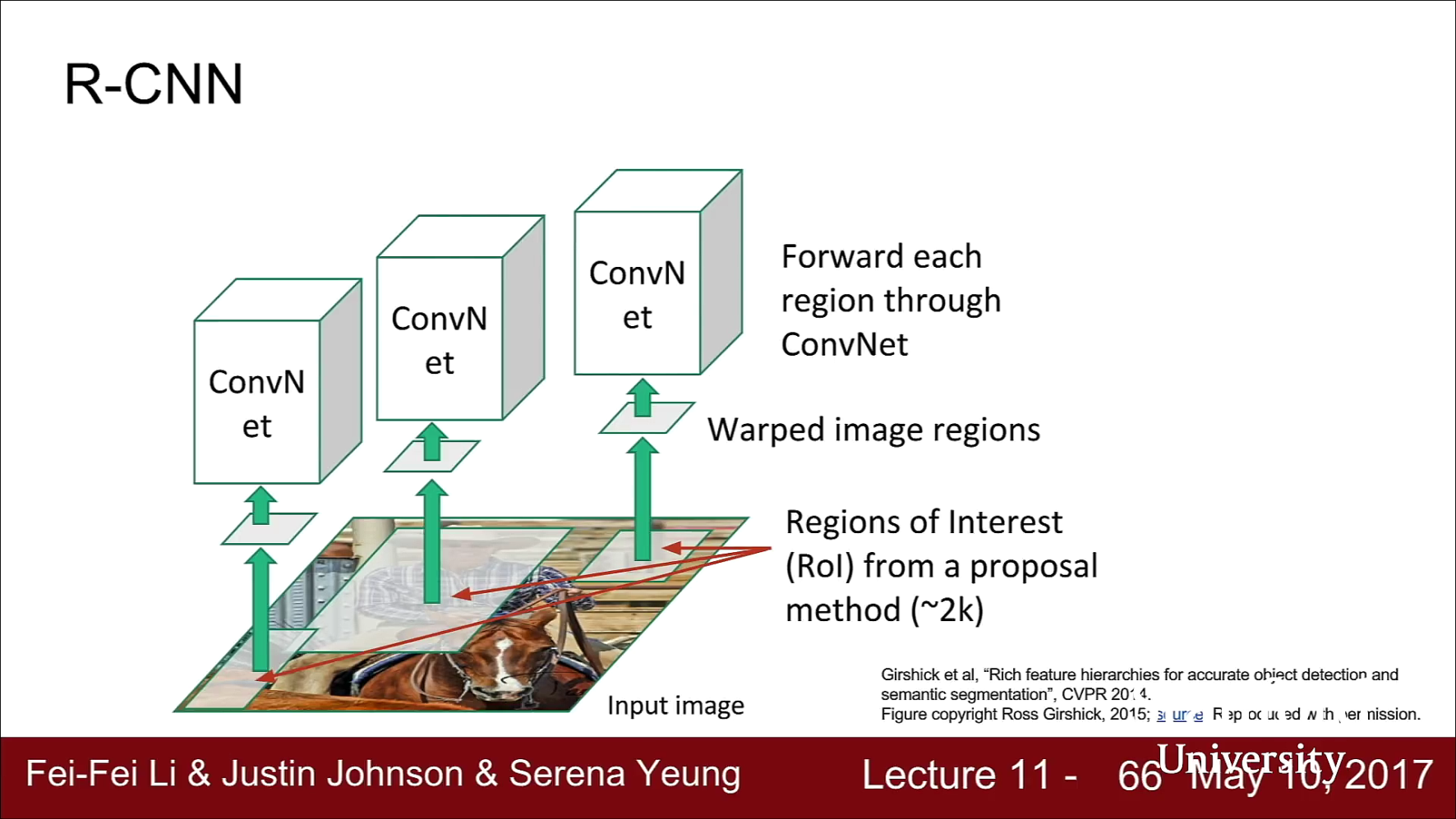
추출된 ROI의 크기를 고정된 사이즈로 바꾼 뒤 그 영역을 CNN에 통과시킵니다.

마지막으로 R-CNN의 경우에는 ROI들의 최종 classification에는 SVM을 사용하였습니다.
여기 슬라이드에는 빠져있지만 R-CNN은 Region Proposal을 보정하기 위한 regression 과정도 거칩니다. Selective Search의 Region Proposal이 대게는 정확하지만 그렇지 못한 경우도 있기 때문입니다.
RCNN은 BBox의 카테고리도 예측하지만 BBox를 보정해 줄 수 있는 offset값 4개도 예측합니다. 이를 Multi-task loss로 두고 한번에 학습합니다.
예를 들어 Region Proposal이 사람을 잡았는데 머리를 빼먹었다고 가정하면, 네트워크는 이 object가 사람인 것을 알고 사람은 머리가 있어야 함을 예측하여 offset은 Bbox를 조금 더 위로 올립니다.
RCNN은 정리하자면 Region Proposal(Selective Search)라는 전통적인 방식을 사용합니다. 즉, RCNN에서는 Region Proposal을 하기 위하여 학습을 하지 않습니다.
RCNN을 사용하려면 어떻게 학습 데이터를 마련해야 할까요? RCNN은 Fully Supervised 입니다. 따라서 학습 데이터에 대하여 이미지 내의 모든 객체에 대한 BBox가 있어야 합니다. 즉, 이미지에 대하여 BBox와 그 BBox의 class가 주어져야 합니다.
자세한 내용은 R-CNN 논문을 참조하시기 바랍니다.

RCNN에 대하여 살펴보면 알 수 있겠지만 RCNN에는 문제점 들이 있습니다. RCNN은 여전히 계산 비용이 큽니다.
RCNN은 2000개의 Region Proposal이 있고 각각이 독립적으로 CNN의 입력으로 들어갑니다. 너무 많은 양입니다.
RCNN의 구현을 살펴보면 CNN에서 나온 Feature를 디스크에 덤핑 하는데 이 용량 또한 어마어마 합니다.
그리고 RCNN은 학습과정 자체가 상당히 오래 걸립니다. 이미지당 2000개의 ROI를 Forward/Backward pass를 수행해야 합니다. 논문에는 81시간 정도 학습이 되어있다고 합니다.
Test time도 아주 느립니다. 이미지 한 장당 대략 30초가 걸립니다. 각 Region proposal 마다 CNN을 수행해야 하므로 수천 번의 forward pass가 요구됩니다. 아주 느린 과정입니다.
R-CNN은 결론적으로 모든 과정이 비효율적입니다. 학습, 추론 과정이 느리고 학습에 필요한 메모리량도 많이 필요하여 비효율적인 문제가 있습니다.

Fast R-CNN

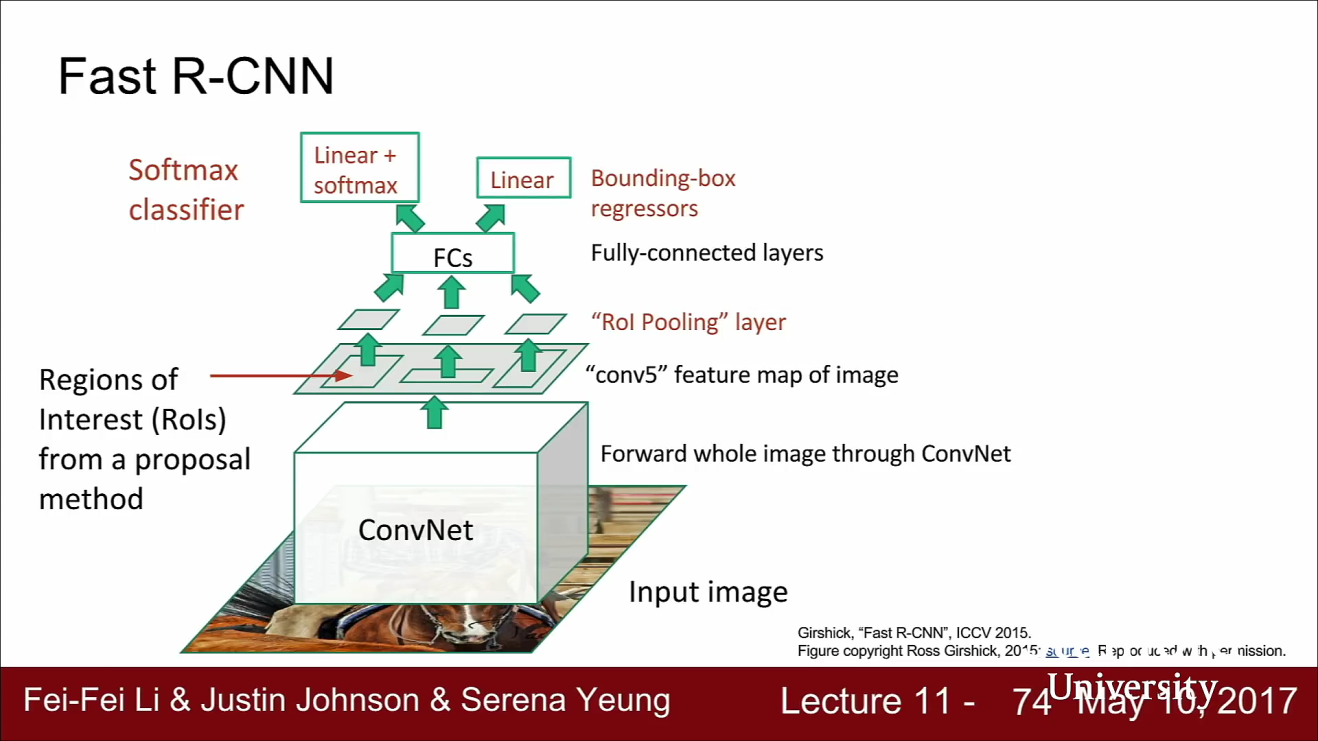
Fast RCNN은 RCNN의 계산 비용 문제를 다소 해결하였습니다.
Fast RCNN도 RCNN과 시작은 같습니다. 하지만 Fast RCNN에서는 각 ROI마다 각각 CNN을 수행하지는 않습니다. 대신 전체 이미지에 CNN을 수행합니다.
- 그 결과 전체 이미지에 대한 고해상도 Feature Map을 얻을 수 있습니다.
Fast RCNN에서도 여전히 Selective Search 같은 방법으로 Region proposal을 계산합니다.
- 하지만 여기서는 ROI를 각각을 가져오지는 않습니다.
CNN Feature map에 ROI를 Projection 시키고 전체 이미지가 아닌 Feature map에서 가져옵니다.
이제는 CNN의 Feature를 여러 ROI가 서로 공유할 수 있습니다.
그 다음 FC layer가 있습니다. FC layer는 고정된 크기의 입력을 받습니다. 따라서 CNN의 Feature map에서 가져온 ROI는 FC layer의 입력에 맞게 크기를 조정해 줘야 합니다.
- 학습이 가능하도록 미분가능한 방법을 사용해야 합니다. 이 방법이 ROI Pooling layer 입니다.
Feature map에서 가져온 ROI의 크기를 조정하고 나면 FC layer의 입력으로 넣어서 Classification Score와 Linear Regression offset을 계산할 수 있습니다.

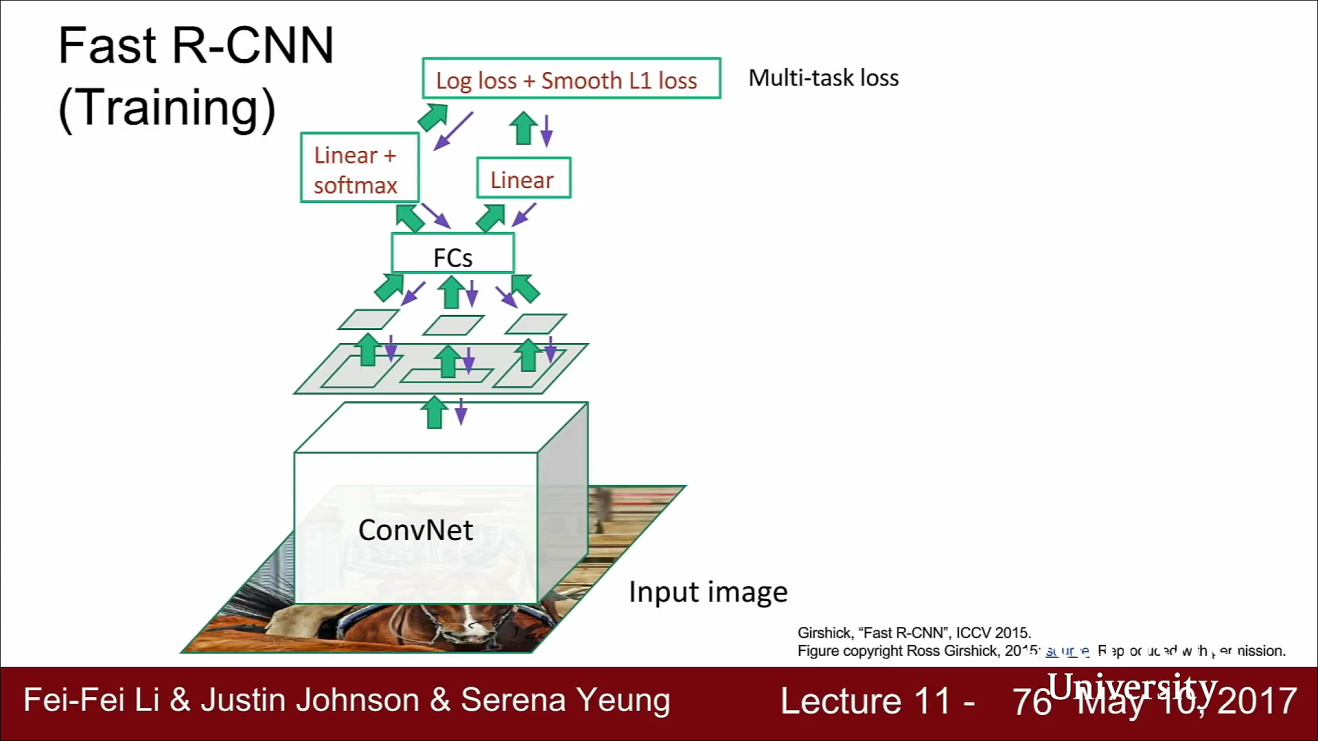
Fass RCNN을 학습할 때에는 두 Loss를 합쳐서 Multi-task Loss로 Backprop을 진행합니다.
이 방법을 통하여 전체 네트워크를 합쳐서(jointly) 동시에 학습시킬 수 있습니다.

위 방법은 ROI Pooling에 대한 방법입니다. 이 방법은 이번 코스에서 다루진 않겠습니다. 내용은 논문을 참조하시기 바랍니다.

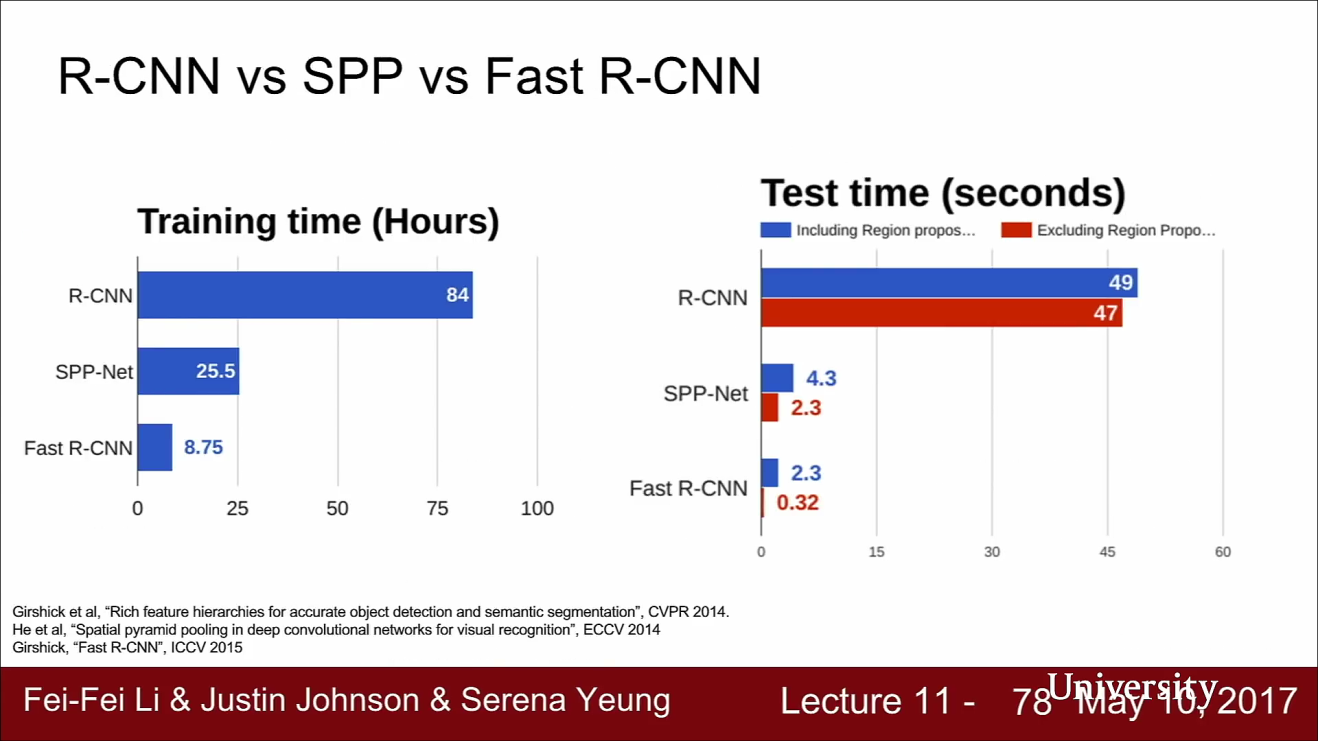
RCNN과 Fast RCNN에 대하여 비교해 보면 위 슬라이드의 결과와 같습니다.(비교를 위해 SPPNet이란 것도 포함시켰습니다.)
Train time을 살펴보면 Fast RCNN이 RCNN보다 10배 정도 빠릅니다.
- Faster RCNN의 속도가 더 빠른 이유는 Feature map을 공유하고 있기 때문입니다.
Test time을 살펴보아도 Fast RCNN의 Test time은 정말 빠릅니다.
- Test time을 보면 Regional Proposal 하는 시간이 대부분을 차지하고 있음을 알 수 있습니다.
- Fast RCNN을 보면 Region Proposal을 한 이후 CNN을 거치는 과정에서는 모든 Region Proposal을 공유하기 때문에 1초도 안걸리는 것을 알 수 있습니다.
- 따라서 Fast RCNN에서 Region Proposal은 계산과정 중의 병목임을 알 수 있습니다.

Faster R-CNN

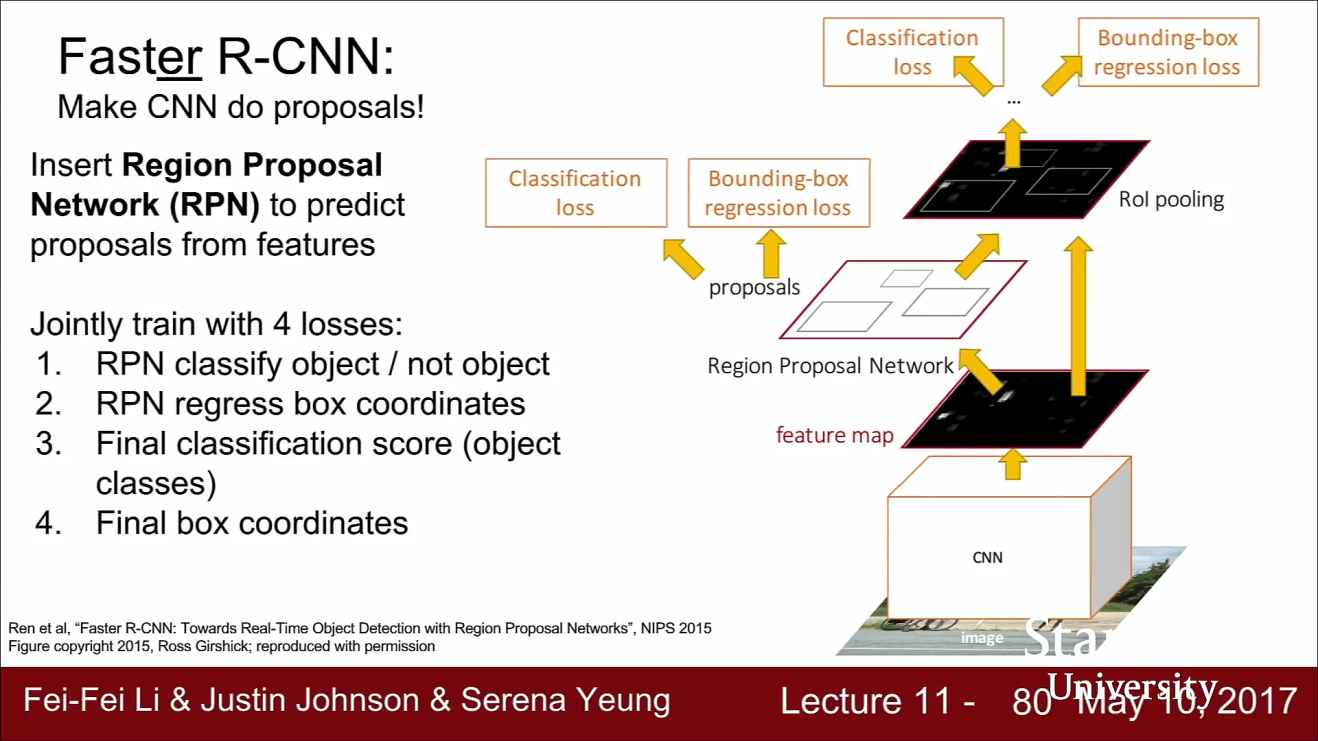
RCNN의 문제는 엄청난 계산량이 필요하다는 것이었고 Fast RCNN에서는 Feature map을 공유하는 방법을 통하여 계산 속도 문제를 일부 해결하였습니다.
Fast RCNN에서의 문제점 또한 여전히 계산 속도에 있었고 Fast RCNN의 계산 병목현상인 Regional Proposal 문제를 해결하는 것이 Faster RCNN입니다.
지금까지의 문제는 region proposal을 계산하는 과정이 병목이라는 점이었습니다.
Faster RCNN에서는 네트워크가 region proposal을 직접 만들 수 있습니다.
Faster RCNN에서는 입력 이미지가 있고 입력 이미지 전체가 네트워크로 들어가서 Feature map을 만듭니다.
Faster RCNN은 별도의 (RPN)Region Proposal Network가 있습니다. RPN은 네트워크가 Feature map을 가지고 Region Proposal을 계산하도록 합니다.
RPN을 거쳐서 Region Proposal을 예측하고 나면 나머지 동작은 Fast RCNN과 동일합니다.
Feature map에서 Region proposal을 가져오고 이들을 나머지 네트워크에 통과시킵니다.
그리고 multi-task loss를 이용해서 여러가지 Loss를 한번에 계산합니다. Faster RCNN은 4개의 Loss를 한 번에 학습합니다.
RPN에는 2가지 Loss가 있습니다.
- 먼저 한가지는 이곳에 객체가 있는지 없는지를 예측합니다.
- 나머지 Loss는 예측한 Bbox에 관한 것입니다.
Faster RCNN에서는 최종단에서도 두 개의 Loss가 있습니다.
- 하나는 Region Proposal의 Classification을 결정합니다.
- 나머지는 Bbox Regression 입니다. 앞서 만든 Regression Proposal을 보정해 주는 역할을 합니다.