3. Loss Functions and Optimization

① 현재 사용되는 분류기(classifier)가 얼마나 좋은지 나쁜지를 나타내는 지표. 즉, 모델의 예측 값(prediction)과 정답(ground-truth) 사이에 얼마나 차이가 있는지 나타내는 측도를 나타냅니다.
② 데이터 셋이 \((x_{i}, y_{i})_{i=1}^{N}\) 으로 주어졌을 때(여기서 \(x_{i}\)는 이미지, \(y_{i}\)는 라벨입니다.)
③ 데이터 셋 전체에 대한 손실(loss)는 아래와 같이 계산합니다.

\[L = \frac{1}{N}\sum_{i}L_{i}(f(x_{i}, W), y_{i})\]

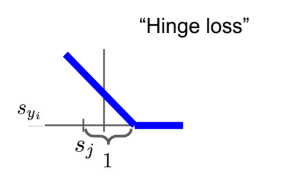
④ Multiclass SVM loss (Hinge Loss)

\[L_{i} = \sum_{j} \neq y_{i}} \text{max}(0, s_{j} - s_{y_{i}} + 1), \ \ \text{where, } s = f(x_{i}, W)\]

def L_i_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

Regularization

① Multiclass SVM loss를 0으로 하는 가중치(weight) W를 찾았을 때, W는 유일하다고 할 수 있을까요?
- 답은 NO입니다. 2W 또한 L을 0으로 만들 수 있기 때문입니다.
② Regularization은 model을 보다 심플하게 만들어서 test data에 대해서도 잘 작동하도록 만듭니다. 이를 오컴의 면도날이라고도 합니다.
③ 이러한 Regularization을 식으로 나타내면 다음과 같습니다.

\[L = \frac{1}{N} \sum_{i} L_{i} (f(x_{i}, W), y_{i}) + \lambda R(W)\]

위 식에서 \(\lambda\)는 regularization strength를 의미하는 하이퍼 파라미터입니다.
위 식에서 \(\frac{1}{N} \sum_{i} L_{i} (f(x_{i}, W), y_{i})\) 부분은 Data loss term이라고 부르고 \(\lambda R(W)\)는 Regularization term이라고 부릅니다.

④ 자주 쓰이는 Regularization term의 종류는 다음과 같습니다.
L2 Regularization : \(R(W) = \sum_{k}\sum_{l}W_{k,l}^{2}\)
L2 Regularization은 weight decay 라고도 불립니다. 왜냐하면 weight를 되도록이면 퍼뜨리면서 모든 input feature를 고려하기 원할 때 사용하기 때문입니다.
L1 Regularization : \(R(W) = \sum_{k}\sum_{l} \vert W_{k,l} \vert\)
ElasticNet (L1 + L2) : \(R(W) = \sum_{k}\sum_{l} \beta W_{k.l}^{2} + \vert W_{k,l} \vert\)
Max norm regularization (추후 강좌에서 설명)
Dropout (추후 강좌에서 설명)
최근 사용되는 기법: batch normalization, stochastic depth

소프트맥스 분류기(Softmax Classifier) : Multinomial Logistic Regression

① \(P(Y=k \vert X = x_{i}) = \frac{e^{s_{k}}}{\sum_{j} e^{s_{j} } }\) 여기서 scroe \(s = f(s_{i}; W)\)입니다.
② 소프트맥스에 대한 손실 함수(Loss function)는 다음과 같습니다.

\[L_{i} = -\log{P(Y=y_{i} \vert X = x_{i})} = -\log{ \frac{e^{s_{y_{i}}}}{\sum_{j}e^{s_{j}}} }\]

최적화(Optimization)

① 가중치(weight)를 최적화하여 손실(loss)을 줄이는 최적화 방법을 뜻합니다.
② 먼저 생각해 볼 수 있는 나쁜 솔루션 : 무작위 탐색(Random search)이 있습니다. 이는 Weight를 무작위로 선택하면서 가장 낮은 loss를 보이는 weight 를 사용하는 것을 뜻합니다.
③ 보다 나은 방법: 경사하강법(Gradient Descent)
Loss function에 대한 weight의 gradient를 계산하는 방법을 뜻합니다.
먼저 Numerical Gradient 방법은 다음과 같습니다.

\[frac{\partial L(W)}{\partial W} = \lim_{h \to 0} \frac{L(W + h) - L(W)}{h}\]

이 방법은 근사값을 계산하는 방식으로 사용하기는 쉬우나 연산 속도가 느리다는 단점이 있습니다. 따라서 실용성이 떨어지므로 Analytic gradient를 검증할 때에만 사용합니다.
그 다음 그래디언트를 계산하는 방법으로 Analytic gradient를 구하는 방법이 있습니다. 이 방법은 Loss가 W에 대한 수식이므로 미적분학을 사용하여 미분함수를 도출하여 사용합니다.
이 방식은 gradient를 구하는 데 Numerical한 방식보다 더 빠르게 gradient를 구할 수 있지만 오차가 발생할 수 있습니다. 그럼에도 불구하고 오차가 허용할 만한 수준이기에 좀 더 실용적인 이 방법을 사용합니다.
따라서 Analytic한 방식으로 gradient를 구하고 이를 통하여 weight를 업데이트 하는 방식을 gradient descent라고 하겠습니다.

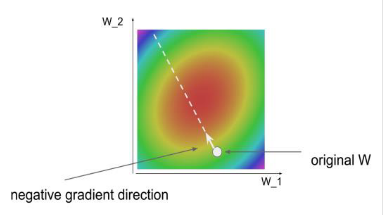
전체 데이터 셋에 대하여 gradient를 계산하면 위 그림과 같습니다. 빨간색 영역의 방향으로 Loss가 이동해야 하기 때문에 gradient가 negative 방향을 가리킵니다.

while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += -step_size * weights_grad # perform parameter update

SGD(Stochastic Gradient Descent)에 대하여 알아보도록 하겠습니다.
전체 데이터셋에 대하여 계산하는 것은 계산적 측면에서 굉장히 비용이 높은 연산입니다.
따라서 전체 데이터에 대하여 gradient를 계산하는 방식 보다는 Minibatch 만큼의 example에 대해서만 gradient를 계산하여 weight update 하는 방식을 사용합니다. mini batch 사이즈는 32 / 64 / 128과 같은 값을 사용하곤 합니다.
단순히 mini batch만을 사용한 SGD는 왼쪽 아래 그림과 같이 epoch에 따라 Loss가 위아래로 진동할 수 있습니다.
이러한 문제를 개선하기 위하여 오른쪽 아래 그래프의 빨간색 선과 같이 너무 높지도 낮지도 않는 적절한 learning rate를 설정하는 것이 중요합니다. 일반적으로 초기에 높은 learning rate를 설정하고 epoch이 진행될 때 이를 점차 감소시키는 방법을 사용합니다.
더 나아가 batch 단위의 normalization 하는 방식을 사용하는데 이 방법은 추후 강의에서 다루도록 하겠습니다.

퀴즈

Loss를 0으로 만드는 weight set은 항상 유일하다. (X)
Loss를 최소로 하는 weight set을 찾을 때, 일반적으로 random search를 먼저 시도한다. (X)
Loss function에 L2 Regularization term을 추가하면 Loss를 낮추면서도 가능한 한 작은 weight를 찾는 weight decay 효과가 있다. (O)

아래 그림과 같이 score들이 주어졌을 때, multiclass SVM에 대한 hinge loss의 평균값을 구해보겠습니다.

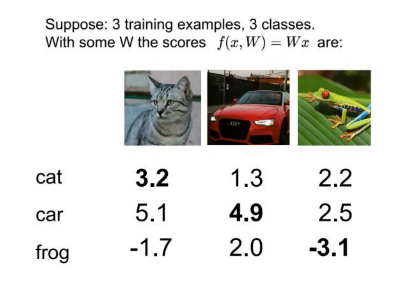
\[L_{i} = \sum_{j \neq y_{i}} \text{max}(0, s_{j} - s_{y_{i}} + 1), \ \ \text{where, } s = f(x_{i}, W)\]

첫번째 열 고양이의 경우 max(0, 5.1 - 3.2 + 1) + max(0, -1.7 - 3.2 + 1) = 2.9
두번째 열 자동차의 경우 max(0, 1.3 - 4.9 + 1) + max(0, 2.0 - 4.9 + 1) = 0
세번째 열 개구리의 경우 max(0, 2.2 - (-3.1) + 1) + max(0, 2.5 - (-3.1) + 1) = 12.9
따라서 Loss = (2.9 + 0 + 12.9) / 3 = 5.27이 됩니다.

Stochastic Gradient Descent (SGD) 에서는 아래 그림과 같이 epoch에 따른 loss가 왜 진동하며 감소할까요?

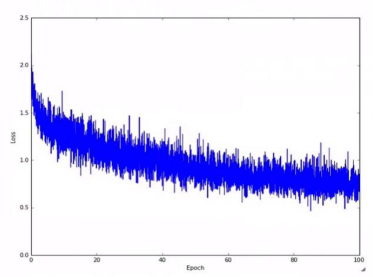
Minibatch size 만큼의 일부 샘플에 대해서만 gradient를 계산하고, 이를 weight 업데이트에 사용하기 때문에, 전체 데이터 셋에 대한 Loss는 일시적으로 증가하거나 감소할 수 있습니다. 대신 minibatch에 포함되는 샘플이 전체 데이터 셋에서 random sampling 하는 것을 가정한다면 minibatch에 대한 gradient의 기대값(expectation)이 전체 데이터셋에 대한 gradient와 같아지므로 SGD가 잘 동작할 것을 기대할 수 있습니다.

3. Loss Functions and Optimization

목차

Summary

Summary

손실 함수(Loss Function)

Regularization

소프트맥스 분류기(Softmax Classifier) : Multinomial Logistic Regression

최적화(Optimization)

퀴즈