Depth Estimation의 평가 지표 (Metric)

Depth Estimation 관련 글 목차

참조 : http://ylatif.github.io/papers/IROS2016_ccadena.pdf
참조 : https://medium.com/analytics-vidhya/mae-mse-rmse-coefficient-of-determination-adjusted-r-squared-which-metric-is-better-cd0326a5697e
참조 : https://towardsdatascience.com/ways-to-evaluate-regression-models-77a3ff45ba70
참조 : https://towardsdatascience.com/what-does-rmse-really-mean-806b65f2e48e
참조 : https://www.analyticsvidhya.com/blog/2021/10/evaluation-metric-for-regression-models/

Depth Estimation Metrics의 종류와 수식

이번 글에서는 Depth Estimation 논문에서 성능 지표로 사용하는 metric에 대하여 간략하게 알아보도록 하겠습니다.
주로 사용하는 metric은 Absolute Relative Error, Square Relative Error, Root Mean Square Error, log scale RMSE, Accuracy under a threshold 입니다.
위 metric은 Regression 모델을 평가하는 지표이며 각 지표의 의미는 아래와 같습니다.

아래 식에서 각 기호의 의미는 다음과 같습니다.
① \(p\) : 특정 픽셀을 의미합니다.
② \(\hat{d}_{p}\) : 특정 픽셀의 Depth Estimation한 예측값을 의미합니다.
③ \(d_{p}\) : 특정 픽셀의 Depth GT 값을 의미합니다.
④ \(T\) : 유효한 Depth GT와 Depth Estimation 출력이 모두 존재하는 픽셀의 총 갯수에 해당하며 이 지점에 한하여 metric을 계산합니다.

Absolute Relative Error

\[\frac{1}{T} \sum_{p} \frac{\vert d_{p} - \hat{d}_{p} \vert}{d_{p}} \tag{1}\]

Square Relative Error

\[\frac{1}{T} \sum_{p} \frac{(d_{p} - \hat{d}_{p})^{2}}{d_{p}} \tag{2}\]

Root Mean Square Error

\[\sqrt{\frac{1}{T}\sum_{p}(d_{p} - \hat{d}_{p})^{2}} \tag{3}\]

log scale RMSE

\[\sqrt{\frac{1}{T}\sum_{p}(\log{(d_{p})} - \log{( \hat{d}_{p} )})^{2}} \tag{4}\]

Accuracy under threshold

\[\text{max} \left(\frac{\hat{d}_{p}}{d_{p}}, \frac{d_{p}}{\hat{d}_{p}} \right) = \delta < \text{threshold} \tag{5}\]

Depth Estimation Metrics의 의미

Absolute Relative Error, Square Relative Error, Root Mean Square Error, log scale RMSE은 전통적으로 Regression 모델의 성능을 측정하기 위해 사용된 Metric이며 Accuracy under threshold는 Depth Estimation 모델의 Accuracy를 측정하기 위해 도입되었습니다.

Absolute Relative Error와 Square Relative Error

먼저 Absolute Relative Error와 Square Relative Error 부터 살펴보겠습니다. 두 metric은 계산 시, L1을 사용할 지 L2를 사용하는 지에 대한 차이가 있으며 나머지 형태는 같습니다.
먼저 L1 즉, 절대값을 사용하는 방식과 L2 즉, 제곱을 사용하는 방식의 가장 큰 차이점은 정답과 예측치의 차이인 에러에 대한 가중치를 할당하는 방법이 다릅니다.
L1의 경우 값에 상관 없이 절대값을 사용하여 차이만 보기 때문에 가중치 없이 모든 에러를 동등하게 바라봅니다. 반면 L2의 경우 더 큰 에러는 더 큰 가중치가 적용되도록 제곱을하여 에러를 계산한다는 차이점이 있습니다.
이러한 계산 방식의 차이로 인하여 L1의 경우에는 동일한 양의 에러는 동일한 에러 값으로 처리하기 때문에 이상치 (아웃라이어)에 의하여 에러의 총합이 크게 왜곡되지 않는 반면 L2의 경우 하나의 이상치가 예측값과 큰 차이가 나게되면 이상치에 의해 더 큰 가중치로 에러가 계산되어 다른 에러와 무관하게 에러가 크게 나타날 수 있다는 문제가 발생합니다.
경우에 따라서 L2와 같이 큰 에러에 가중치를 더 크게 적용하는 것이 좋을 수 있고 L1과 같이 동등하게 에러를 취급하는게 좋을 수 있습니다. 따라서 Depth Estimation의 성능을 확인할 때 2가지 모두 살펴보는 것이 일반적입니다. 부가 설명은 \(d_{p}\) 로 정규화 하는 것을 적용하는 이유를 살펴본 다음 첨언하겠습니다.

식(1), (2)를 살펴보면 Absolute Relative Error와 Square Relative Error 모두 계산 시 분모에 \(d_{p}\) 가 적용되어 있습니다.
Metric 계산 시 \(d_{p}\) 을 이용하여 정규화를 하는 이유는 Depth Estimation을 하는 scale의 범위에 따라서 값의 크기가 많이 달라질 수 있기 때문에 0 ~ 1 사이의 값으로 정규화 하는 것입니다. 예를 들어 어떤 Task에서는 0 ~ 50 m 까지 거리 값을 예측하는 반면 어떤 Task에서는 0 ~ 100 m 까지 거리 값을 예측해야 할 수 있습니다. Depth Estimation의 출력 특성 상 거리값이 커질수록 에러가 커지기 때문에 거리값의 범위가 달라지면 에러값의 크기가 완전히 달라지게 됩니다. 이와 같이 사용하고자 하는 값의 범위가 달라지면 단순 Error의 비교가 어렵기 때문에 상대적인 비율을 이용하여 나타내는 것이 regression 문제에서 많이 사용하는 방법입니다.
따라서 Absolute Relative Error와 Square Relative Error 모두 Error가 최대일 경우 1이되고 에러가 최소일 경우 0이 되도록 범위를 정규화한 다음에 에러 값을 계산합니다. 이와 같은 방식을 사용할 경우 L1, L2를 사용할 때 나타나는 값의 범위에 따른 에러 크기의 범위가 달라지는 문제를 개선할 수 있으며 나눗셈 시 발생하는 0으로 나누는 문제만 처리하면 문제 없이 사용할 수 있습니다.

지금까지 내용을 정리하면 Absolute Relative Error와 Square Relative Error의 차이점은 에러값의 크기에 따라 가중치를 적용하는 방법이 다르고 \(d_{p}\) 에 의해 정규화가 된 것으로 정리할 수 있습니다. 이 때 어떤 특성이 있는 지 살펴보겠습니다.

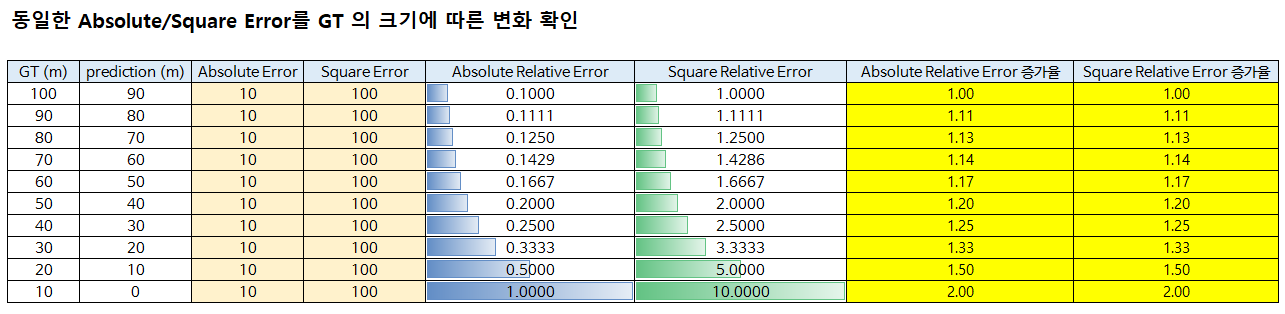
먼저 동일한 Absolute/Square Error를 GT 의 크기에 따른 변화 확인을 해보면 다음과 같습니다.

위 표에서 Absolute Error는 GT와 Prediction의 차이를 나타내고 Square Error는 GT와 Prediction의 차이의 제곱을 나타냅니다. Absolute Relative Error는 Absolute Error/GT 를 의미하고 Square Relative Error는 Square Error/GT를 의미합니다. Absolute/Square Relative Error의 증가율은
위 표를 살펴보면 동일한 Absolute (Square) Error를 GT 크기에 따라서 Abosolute Relative Error의 변화율과 Square Relative Error의 변화율을 살펴보았을 때, GT 값의 크기가 작을 수록 에러가 차지하는 비율이 커져서 각 Error값은 커지는 것을 알 수 있습니다.
동일한 Absolute (Square) Error가 유지될 때, Abosolute Relative Error의 변화율과 Square Relative Error의 값은 Square Relative Error가 더 크게 나타나지만 증가율은 동일함을 알 수 있습니다.

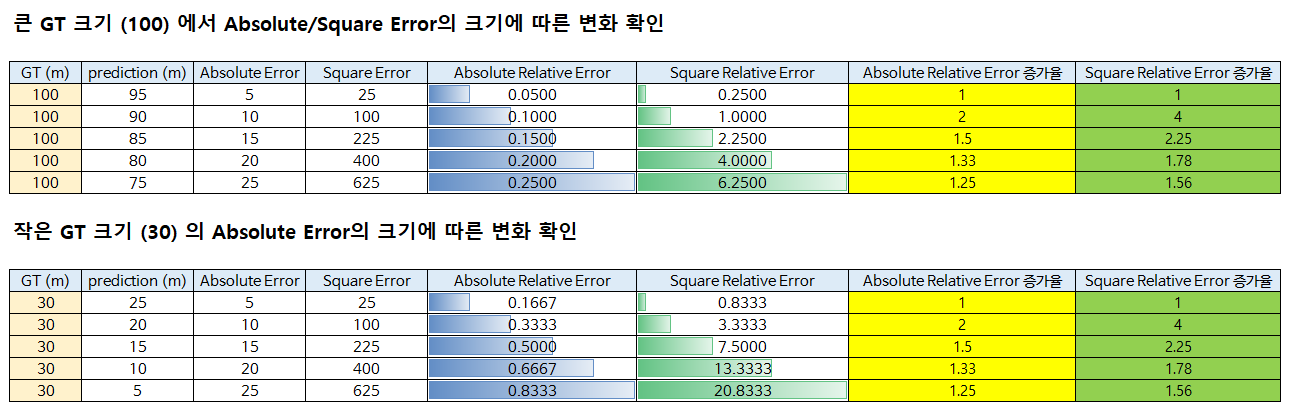
위 표에서는 GT 값이 100인 경우와 30인 경우를 비교하여 GT 값의 크기에 따른 Absolute Relative Error와 Square Relative Error의 증가율을 살펴보면 L1, L2의 계산 방식에 의하여 Square Relative Error가 커질 때 더 크게 증가하는 것을 확인할 수 있습니다.
GT 크기에 따른 Absolute/Square Relative Error의 크기를 살펴보면 같은 크기의 에러를 이용하여 비교하면 GT의 크기가 작을 때, 에러가 차지하는 비율이 더 커져서 더 큰 에러값을 가지게 됩니다. 물론 GT의 값이 커지는 경우 Depth Estimation에서는 에러 자체가 커져서 Absolute (Square) Error가 더 커질수도 있습니다.

지금까지 내용을 정리하면 Absolute/Square Relative Error 다음과 같습니다.
① Absolute/Square Relative Error는 GT 값에 대한 에러의 비율을 가지기 때문에 GT 값의 크기가 작으면 같은 에러에 비하여 Relative Error의 크기가 더 커질 수 있음을 확인하였습니다.
② Square Relative Error는 더 큰 에러에 페널티 (가중치)를 적용하는 방식이므로 Absolute Relative Error에 비하여 더 큰 에러값과 에러의 증가율을 가집니다.
③ Depth Estimation에서 두 metric을 사용할 때, Absolute Relative Error를 이용하여 모든 영역에 대한 전반적인 인식 성능을 확인할 수 있고 Square Relative Error를 이용하여 한계 상황에 대한 열악함 정도를 확인할 수 있습니다. 한계 상황에서 에러가 크게 발생하기 때문에 좀 더 큰 페널티가 적용한 상태로 계산되기 때문입니다. 한계 상황의 대표적인 예시는 원거리 영역과 객체와 배경의 경계 영역입니다.

따라서 Absolute/Square Relative Error 2가지 지표를 모두 이용하여 비교하고 경우의 수에 따라서 아래와 같이 해석할 수 있습니다.

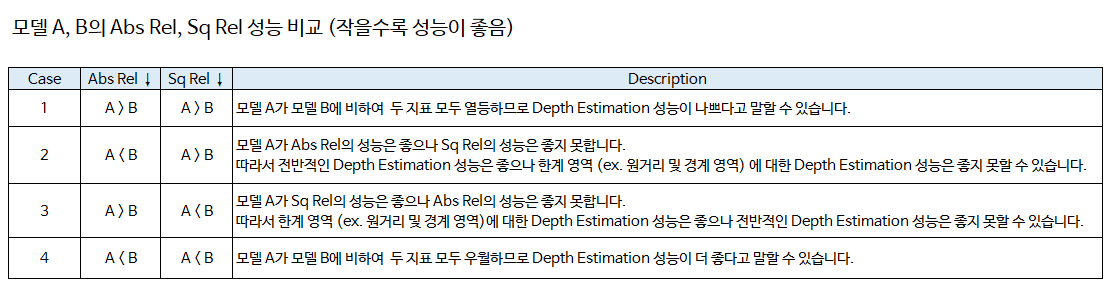
Root Mean Square Error와 log scale RMSE

Root Mean Squre Error (RMSE)와 log scale RMSE은 식 (3), (4)를 확인하면 식 (4)에서는 각 \(d_{p}, \hat{d_{p}}\) 에 log가 적용된 것 이외에는 차이가 없습니다.
앞에서 살펴본 Absolute Relative Error, Square Relative Error의 경우 두 모델을 비교할 때, 어떤 모델은 전자가 더 좋고 어떤 모델은 후자가 좋은 경우가 생깁니다. 상대적으로 우월한 모델의 경우 두 에러 모두 값이 작아집니다.
반면 RMSE와 log scale RMSE의 경우 연산 차이가 log가 적용된 차이점만 존재하고 log는 단조 증가 함수이기 때문에 두 모델을 비교할 때, 에러에 대한 비교가 교차되지 않지만 RMSE와 log scale RMSE를 같이 비교하는 것은 도움이 됩니다.
log scale RMSE는 Absolute Relative Error와 유사한 성향이 있고 RMSE는 Square Relative Error와 유사한 성향이 있기 때문입니다. 즉, log scale RMSE를 통해 전반적인 성능을 관측할 수 있고 RMSE를 통해 이상치 즉, Depth Estimation에서의 한계 상황에 대한 성능을 좀 더 명확하게 확인할 수 있습니다.

RMSE는 앞에서 다룬 Square Relative Error와 유사하지만 Relative 값이 아닌 값 그대로 에러값을 구하는 데 사용합니다. 이 경우 이상치에 민감한 문제가 발생하므로 그 문제를 일부 개선하기 위하여 Root를 적용합니다.
log scale RMSE는 원본 값에 log를 적용하여 값의 범위에 민감하지 않도록 만든 후 RMSE를 적용합니다. 이와 같은 방식을 이용하여 이상치에 강건해지고 기존 값의 범위가 아닌 log 값의 범위에서 에러를 계산함으로써 log 값의 범위에서 상대적인 비교를 할 수 있습니다. 따라서 모델 별 log scale RMSE의 값을 비교하면 값의 변동이 상대적으로 작은 것을 확인할 수 있습니다.

따라서 log scale RMSE과 RMSE는 Relative 값이 아닌 실제 값을 이용하여 에러를 계산하되 log scale RMSE는 Absolute Relative Error와 같이 이상치에 강건하며 전반적인 에러를 계산하게 되고 RMSE는 Square Relative Error와 같이 이상치에 좀 더 민감하므로 한계 상황에 대하여 에러를 계산하는 데 용이합니다.
앞에서 언급한 바와 같이 RMSE를 사용하는 이유는 Relative 값이 아닌 값 그 자체를 사용하는 데 의미가 있습니다.

Accuracy under threshold

Accuracy는 라이다 포인트 클라우드를 이용하여 만든 sparse depthmap GT와 Depth Estimation 모델을 통해 얻은 dense depthmap prediction 간의 Accuracy를 측정하는 것을 의미합니다.
Accruracy를 구하는 방법은 식 (5)와 같습니다. \(\hat{d}_{p}\) 와 \(d_{p}\) 중 큰 값을 분자, 작은 값을 분모에 두어 항상 1보다 큰값을 얻도록 합니다. 식 (5)에서는 편의를 위하여 max 값을 통해 1보다 큰 값을 얻도록 하였습니다. 즉, 예측값과 정답값 중 큰 값과 작은 값의 비율을 나타냅니다.
이 때, threshold 값인 \(\delta\) 를 이용하여 비율이 \(\delta\) 보다 작으면 True Positive로 간주합니다.
Depth Estimation에서는 전통적으로 \(\delta = 1.25\), \(\delta^{2} = 1.25^{2} = 1.5625\), \(\delta{3} = 1.25^{3} = 1.953125\) 을 threshold로 정의합니다.
이 값의 범위를 5(m) ~ 100 (m) 까지 이해하기 쉽게 표로 정리하면 다음과 같습니다.

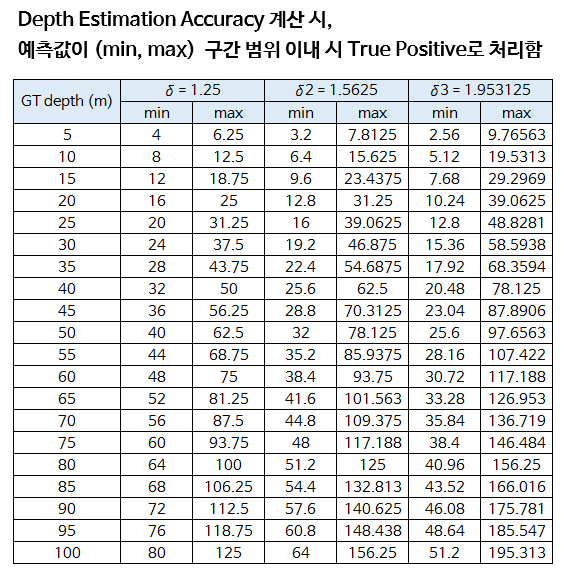
위 표를 보면 Depth의 크기가 커질수록 오차 범위도 커지는 것을 알 수 있습니다. 이것은 Depth Estimation의 Depth가 커질수록 정밀한 예측이 어렵다는 Task 자체의 한계를 반영한 것입니다.

위 식에서 \(\delta\) 의 값을 1.1, 1.15, 1.2로 변경하였을 때의 범위는 아래와 같습니다.

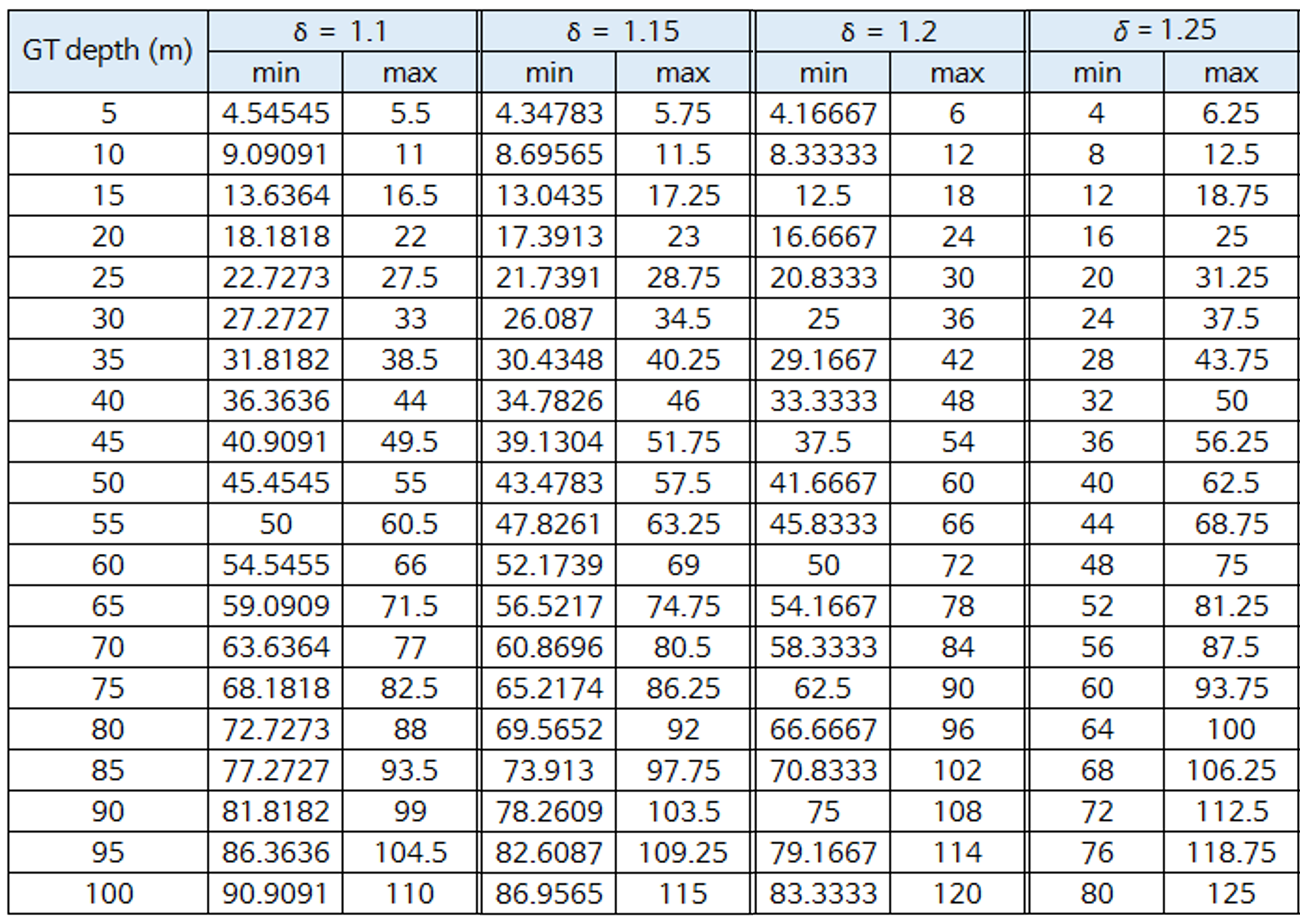
Pytorch Code

지금까지 설명한 7가지의 대표적인 Depth Estimation의 Metric의 계산 과정을 소개하면 아래 코드와 같습니다.
계산 과정은 매우 간단합니다. 아래 코드를 살펴보시기 바랍니다.

def compute_depth_errors(gt, pred):   

    abs_rel = torch.mean(torch.abs(gt - pred) / gt)

    sq_rel = torch.mean((gt - pred) ** 2 / gt)
    
    rmse = (gt - pred) ** 2
    rmse = torch.sqrt(rmse.mean())

    rmse_log = (torch.log(gt) - torch.log(pred)) ** 2
    rmse_log = torch.sqrt(rmse_log.mean())


    delta = torch.max((gt / pred), (pred / gt))
    a1 = (delta < 1.25     ).float().mean()
    a2 = (delta < 1.25 ** 2).float().mean()
    a3 = (delta < 1.25 ** 3).float().mean()

    return abs_rel, sq_rel, rmse, rmse_log, a1, a2, a3

Depth Estimation 관련 글 목차