FCOS (Fully Convolutional One-Stage Object Detection)
2022, Jan 28
- 논문 : https://arxiv.org/pdf/1904.01355.pdf
- 코드 : https://github.com/tianzhi0549/FCOS
- 코드 : https://github.com/rosinality/fcos-pytorch
- 이번 글에서는
Anchor Free기반의 Object Detection 모델인FCOS, Fully Convolutional One-Stage Object Detection 논문에 대하여 알아보도록 하겠습니다. - 전체적으로 논문의 내용을 리뷰한 뒤, Pytorch 코드를 확인하는 순서로 알아보겠습니다.
목차
Abstract

- FCOS는 one-stage detector의 한 종류이며 다른 one-stage detector와의 차이점은 semantic segmentation과 유사하게 픽셀 단위 (
per-pixel prediction)의 예측을 통해 Object Detection 문제를 해결하고자 합니다. 따라서 FCN(Fully Convolutional Network)에서 사용한 segmentation을 위한 다양한 기법들을 사용할 수 있습니다. - 특히 anchor box가 없다는 점에서 anchor free의 대표적인 방법으로 사용되고 있습니다. anchor box를 제거함으로써 FCOS는 복잡한 anchor box 관련 연산을 없앨 수 있었습니다. 또한 어떤 anchor box를 사용해야 하는 지 선택하는 것 또한 고민거리이지만 anchor box를 없앰으로써 고려하지 않아도 됩니다. 따라서 Anchor box와 관련된 다양한 하이퍼파라미터를 줄일 수 있고 이와 관련된 연산도 없앨 수 있습니다.
- 정리하면
FCOS는 semantic segmentation과 유사한 방법의 픽셀 단위의 prediction 방법을 이용하는 anchor free one-stage detector이며 이 방법은 간단하면서도 성능이 좋고 다른 instance-level task에도 사용될 수 있습니다.
Introduction
- Object Detection의 발전은 다양한 Anchor Box 기반의 모델과 함께 발전해 왔습니다. 즉, anchor box를 잘 사용하는 것이 detector의 성능을 높이는 중요한 역할이라고 믿어 왔습니다.
- 하지만 anchor box를 사용하는 모델에는 몇가지 단점이 있습니다. FCOS 논문에서는 크게 4가지 항목으로 문제를 지적하였습니다.

- ① Object Detection 모델의 성능이 anchor box에 민감하다는 것이 단점이 됩니다. 즉, anchor box의 크기, 비율 (aspect ratio), 갯수 등을 잘 선정해 주어야 좋은 성능을 기대할 수 있습니다. 하이퍼파라미터의 영역으로 anchor box가 남게 되어 사용하는 데 어려움이 있습니다. box scale과 aspect ratio가 고정이기 때문에 다양한 모양을 가지는 small object에는 비효율적일 수 있습니다.
- ② anchor box가 정해지면 학습할 때에는 보통 고정이 되는데, 어떤 물체의 크기의 변화가 크다면 anchor box가 효과적으로 사용되지 못할 수 있습니다. 즉, 물체의 변화가 커서 생각한 것과 많이 다른 크기의 형상을 가진다면 기존에 선정한 anchor box의 비율과 맞지 않게 되어 검출을 할 수 없습니다. 특히, 이러한 경향은 작은 물체에 대하여 종종 나타납니다.
- ③ 높은 recall 수치를 얻기 위해서는 다양한 갯수의 anchor box가 필요해 집니다. 어떤 경우에는 굉장히 dense한 형태로 anchor box의 경우의 수를 다양화하여 180,000 개 정도를 사용하기도 합니다. 이와 같은 경우의 문제점은 대부분의 경우가 negative sample로 분류되기 때문에 학습 시, positive와 negative간 갯수의 불균형이 심하게 발생할 수 있다는 점입니다.
- ④ anchor box를 이용한 GT와의 IoU (Intersection over union) 계산 비용이 별도로 필요해 집니다.
- 위 4가지의 anchor based 모델의 단점이 확인된 가운데 FCN (Fully Convolutional Network)과 같은 구조를 이용하여 semantic segmentation, depth estimation, keypoint estimation 등의 task에 좋은 성능을 보여 주어 object detection 또한 자연스럽게 이와 같은 방법 (per-pixel prediction)을 이용하고자 하는 시도가 FCOS를 통해 시도 되었습니다.

- FCN 구조를 이용하여 object detection을 할 때, semantic segmentation과 같이 단순히 픽셀 별 classification 만을 하는 것이 아니라 픽셀 별로 4개의 원소값을 가지는 4D vector를 추가적으로 가지게 됩니다.

- 위 그림의 왼쪽의 야구 이미지와 오른쪽의 테니스 이미지를 분리하여 살펴보겠습니다.
- 먼저 왼쪽의 야구 이미지를 보면 박스 내의 어떤 점을 기준으로 상/하/좌/우의 경계 부분까지의 거리를 추정하게 됩니다.
- 이와 같은 방법을 이용하여 박스를 추정하였을 때, 한가지 문제가 생기는데 바로 오른쪽 테니스 같은 이미지가 예입니다. 만약 어떤 하나의 위치를 기준으로 여러개의 상/하/좌/우의 경계를 추정하려면 어떻게 해야 할까요? 각 픽셀당 1개의 상/하/좌/우 위치를 추정하기 때문에 이와 같은 예시는 모호해질 수 있습니다.

- 오버랩이 되는 영역에서의 모호함을 개선하기 위하여
FPN (Feature Pyramid Network)구조를 사용합니다. Feature Pyramid 구조를 통하여 다양한 크기의 Feature를 사용할 수 있습니다. 이 내용은 이 글의 Approach 부분에서 살펴보도록 하겠습니다.

- FCOS에서는
center-ness라는 개념을 도입하여 실제 물체의 중심점으로 부터 멀리 떨어져 있게 바운딩 박스를 예측한 경우를 제한하도록 하였습니다. center-ness의 구체적인 개념은 Approach에서 알아볼 예정입니다. 이러한 center-ness의 도입으로 ancor 기반의 모델보다 더 좋은 성능을 가질 수 있을 수 있었습니다.

- Introduction에서 설명한 내용에 대하여 정리해 보도록 하겠습니다.
- ① semantic segmentation 문제를 푸는 FCN 구조를 이용하여 Detection에 접목할 수 있고 이러한 아이디어를 이용하여 다른 Task에도 접목할 수 있습니다.
- ② FCOS는 Region Proposal과 Anchor 모두가 free한 one-stage anchor free 모델입니다. 이러한 모델의 구조는 추가적인 하이퍼파라미터 튜닝 없이 구조가 간단하다는 장점이 있습니다.
- ③ Anchor의 제거는 Anchor box의 IoU 연산 제거와 Anchor box와 GT 간의 비교 연산을 없앨 수 있습니다.
- ④ FCOS는 one-stage detector 중에서 성능이 좋으며 FCOS의 결과는 two-stage detector의 Region Proposal로 사용할 수 있습니다.
- ⑤ 구조를 조금 수정하면 다른 task에 접목할 수 있고 특히 instance 단위의 prediction을 할 때 좋은 방법이 될 수 있습니다.
Related Work
Anchor-based Detector: Region Proposal의 반복적인 연산을 제거하기 위하여 Anchor Box 개념을 도입하여 Faster-RCNN, SSD, YOLOv2 등이 개발이 되어 왔습니다. 앞에서 언급한 바와 같이 Anchor를 잘 선정하기 위한 튜닝에 어려움이 있으며 수많은 Anchor들이 negative sample로 빠지게 되는 단점이 있습니다. Anchor 기반의 detector는 feature map의 각 픽셀 위치를 object center라고 가정하고 미리 정한 크기의 anchor box를 regression 합니다. 이중 IoU가 낮은 bounding box들은 negative sample이 되므로 실제 학습 과정에서 object의 위치를 추정하는데 사용되는 픽셀은 object center 근처에 있는 픽셀들이 전부입니다.Anchor-free Detector: 기존에 유명한 Anchor-free Detector는 YOLOv1이 있었습니다. 하지만 YOLOv1은 Recall 성능이 떨어진다는 단점이 있어서 YOLOv2에서 부터는 Anchor Box를 사용하게 되었습니다.FCOS는 YOLOv1과 같이 GT bounding box 이내의 모든 점들에 대하여 bounding box를 예측하도록 하고 low-quality를 가지는 점들에 대해서는center-ness개념을 도입하여 출력되지 않도록 억누르는 역할을 합니다. 이러한 방법으로 recall의 성능을 높일 수 있도록 하였습니다.

- 기존의 Anchor-freee Detector들은 Post Processing이 다소 복잡하거나 겹치는 bounding box를 처리하는 문제 또는 recall이 상대적으로 낮은 문제가 있었습니다. 하지만
multi-level FPN구조와center-ness를 통하여 이 문제를 개선하였고 더 간단한 구조로 구현할 수 있었습니다. - 또한 앞의 Anchor-based Detector에서 언급한 바와 같이 수많은 negative sample로 인하여 object의 위치 추정에 사용되는 픽셀 수가 작은 문제를 FCOS에서는 feature map의 모든 픽셀 위치에서 해당 픽셀이 특정 object에 속한 픽셀인 지 아닌 지 확인하고 object에 속한 픽셀이라면 해당 픽셀에서 예측한 bounding box는 무엇인지를 계산합니다.
Approach

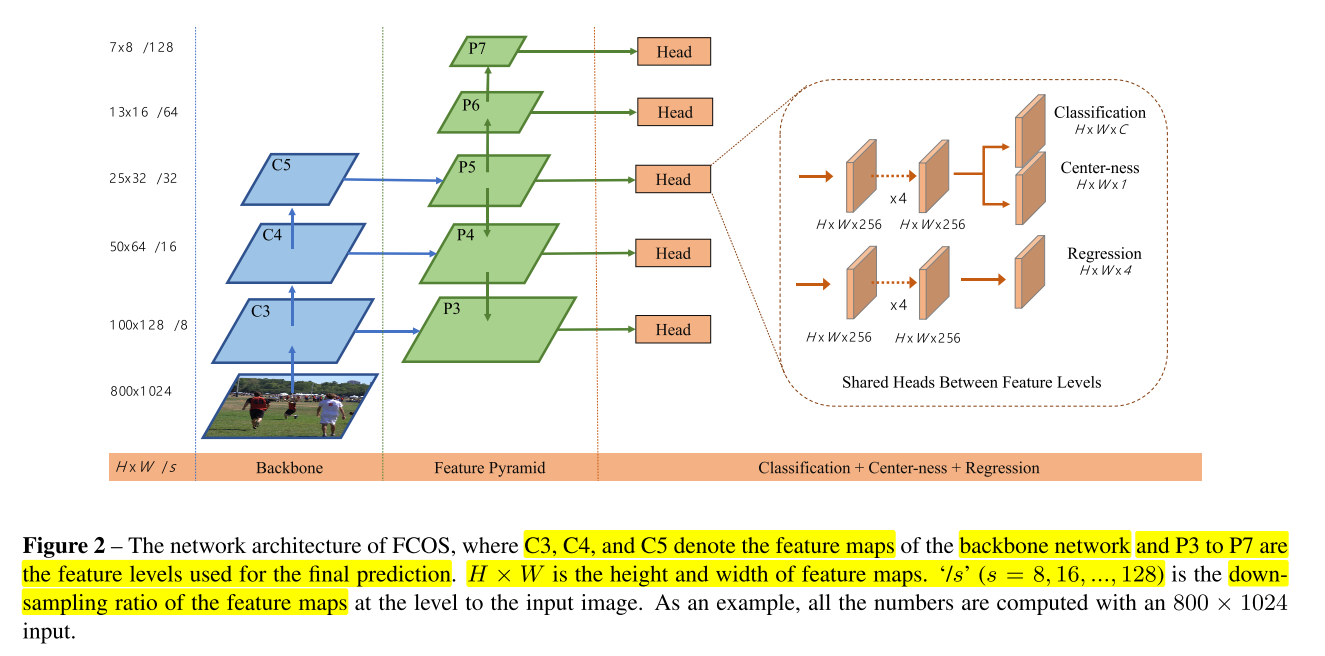
FCOS의 전체적인 architecture는 위 그림과 같습니다. Backbone 단계에서 3가지 크기의 feature를 추출하고 이 feature를 이용하여 5단계의 Feature Pyramid를 생성합니다. 이 Feature Pyramid를 통해 각 Head를 얻게되는데 Classification에 해당하는 부분이 FCN 기반의 세그멘테이션 구조와 유사합니다.- 나머지 Center-ness는 Object Detection 성능을 개선하기 위한 구조이며 마지막 Regression을 통하여 Bounding Box의 크기를 결정합니다.
- 자세한 내용은 차례대로 살펴보도록 하겠습니다.

- Approach에서는 FCOS의 컨셉에 대하여 본격적으로 알아보도록 하겠습니다.
- 먼저
Fully Convolutional One-Stage Object Detector에서는 Object Detection을 per-pixel prediction 방식으로 어떻게 하는 지 알아보겠습니다. - 그 다음으로
Multi-level Prediction with FPN for FCOS에서는 recall 성능 개선과 겹친 bounding box 처리 문제 개선을 위한 Multi-level Prediction 방법을 알아보겠습니다. - 마지막으로
center-nessbranch를 통하여 low-quality detected bounding box를 제거하는 방법에 대하여 다루어 보겠습니다.
Fully Convolutional One-Stage Object Detector

- 먼저 CNN의 backbone 중 layer \(i\) 에 해당하는
feature map을 \(F_{i}\) 라고 하고 \(s\) 는 각 layer에 사용된stride로 정의하겠습니다. - 각 이미지의 ground truth는 \(B_{i}\) 로 표시하며 \((x_{0}^{(i)}, y_{0}^{(i)}, x_{1}^{(i)}, y_{0}^{(i)}, c^{(i)}) \in \mathbb{R}^{4} \times \{1, 2, ... , C \}\) 의 형태를 가집니다. 즉, 임의의 픽셀에서 최대 클래스의 갯수 만큼의 물체의 위치를 가질 수 있다는 뜻이며 한 픽셀에서 2개 이상의 같은 클래스는 추정하지 않음을 나타냅니다. 그러면 최대 클래스의 갯수 C 만큼의 위치를 가진다면 각각의 클래스에 대하여 \(x_{0}^{(i)}, y_{0}^{(i)}, x_{1}^{(i)}, y_{0}^{(i)}\) 라는 bounding box 까지의 거리 정보를 가지게 됩니다.

- feature map \(F_{i}\) 의 (x, y) 위치의 좌표는 실제 이미지에서 다음 식을 따릅니다.
- \[( \lfloor{ \frac{s}{2} \rfloor} + xs, \lfloor{ \frac{s}{2} \rfloor} + ys )\]
- 예를 들어 어떤 layer에서의 좌표가 (23, 30) 이고 stride가 8이 었다면 실제 이미지에서는 (4 + 23 * 8, 4 + 30 * 8) = (188, 244)가 됩니다. 각 좌표에서 \(\lfloor{ \frac{s}{2} \rfloor}\) 는 stride 연산을 통해 발생하는 오차를 stride의 반 만큼만 더해줘서 보상을 해주는 역할을 합니다.
- 이러한 방법을 통하여 기존의 anchor box를 통하여 추정 하지 않고 직접적으로 각 위치를 추정하게 됩니다. 즉, 각각의 좌표 위치를 학습해야 할 대상으로 바라보게 됩니다. 이는 anchor 기반의 detector와는 차이점을 보입니다.

- 그러면 각 feature map에서의 (x, y)와 GT를 어떻게 비교하면 될까요? 컨셉은 간단합니다. (x, y)가 GT bounding box에 속하면 positive sample로 간주하고 클래스는 GT에 해당하는 클래스 \(c^{*}\) 에 대응합니다. 만약 (x, y)가 GT bounding box에 속하지 않는다면 negative sample로 간주하고 클래스는 0으로 ( \(c^{*} = 0\) ) 둡니다. 이는 background class 임을 뜻합니다.
- 이 때 bounding box의 크기를 예측하기 위하여 다음 식을 이용합니다.
- \[\boldsymbol{t^{*}} = (l^{*}, t^{*}, r^{*}, b^{*})\]
- \[l^{*} = x - x_{0}^{(i)}, t^{*} = y - y_{0}^{(i)}\]
- \[r^{*} = x_{1}^{(i)} - x, b^{*} = y_{1}^{(i)} - y\]
- 위 식을 이용하여 prediction과 target인 GT 간의 오차를 \(\boldsymbol{t^{*}}\) 벡터로 구할 수 있습니다. 벡터의 각 값은 차례대로 좌/상/우/하 방향으로 (x, y)와 bounding box 까지의 거리를 나타냅니다.

- 위 그림의 l, t, r, b 를 참조하시면 됩니다.
- 만약 한 점 (x, y)가 여러 개의 bounding box에 속하게 된다면 영역이 가장 작은 bounding box를 선택하는 방법을 이용합니다. 이와 같은 방식으로 bounding box를 선택하는 이유는 뒤에서 다룰 Multi-level prediction과 관련되어 있으며 Multi-level prediction을 이용하기 때문에 성능이 거의 영향을 주지 않습니다.

- FCOS 에서는 l, t, r, b를 추정하면서 가능한한 많이 foreground에 대하여 regressor를 학습하려고 합니다. anchor 기반의 모델에서는 GT bounding box와 anchor box의 IoU가 충분히 높은 경우에만 foreground인 positive sample로 학습하는 것과 차이점이 있습니다. 이 점이 FCOS가 anchor 기반의 모델에 비해 높은 성능을 내는 이유 중의 하나로 설명합니다.

- FCOS에서 사용하는 네트워크의 마지막 layer는 클래스 갯수 (MS COCO의 경우 80개)의 차원을 가지는 벡터와 4차원인 \(\boldsymbol{t^{*}} = (l^{*}, t^{*}, r^{*}, b^{*})\) 을 예측합니다. feature map의 모든 픽셀에 대하여 해당 픽셀이 속한 클래스 \(c^{i}\) 와 bounding box를 추측하기 위한 4개의 값 (\(l^{*}, t^{*}, t^{*}, b^{*}\))를 추정하도록 네트워크를 구성합니다. 따라서 **한 픽셀 당 (\(l, t, r, b, c\)) 5개의 값을 예측합니다.
- 이 때, feature map 상의 픽셀 (x, y)가 GT bounding box (클래스 = \(c^{*}\)) 내부에 있는 픽셀이라면 target의 클래스는 \(c^{*}\) 으로 정의하고 positive sample로 간주합니다. 반면 픽셀 (x, y)가 bounding box에 속하지 않는 픽셀이라면 \(c^{*} = 0\)으로 정의하여 nagetive sample로 간주합니다.
- 학습 시에는 multi-class classifier를 이용하여 학습하지 않고 클래스 갯수 \(C\) 개의
binary classifier를 사용합니다. - 실제 FCN과 같은 per-pixel prediction에서는 마지막 layer에서 채널 방향의 크기가 분류하려는 클래스의 갯수와 같으며 채널 방향으로 각 클래스가 선택될 확률이 나타날 수 있게
softmax를 적용합니다. 예를 들어 분류해야 할 클래스가 10개이면 채널의 사이즈가 10개이며 채널 방향으로 총합이 1이되도록 최종 layer에서 값이 출력됩니다. 이와 같은 방법을 이용하여 multi-class classification을 하는 것이 일반적인 per-pixel prediction (semantic segmentation)의 방법입니다.
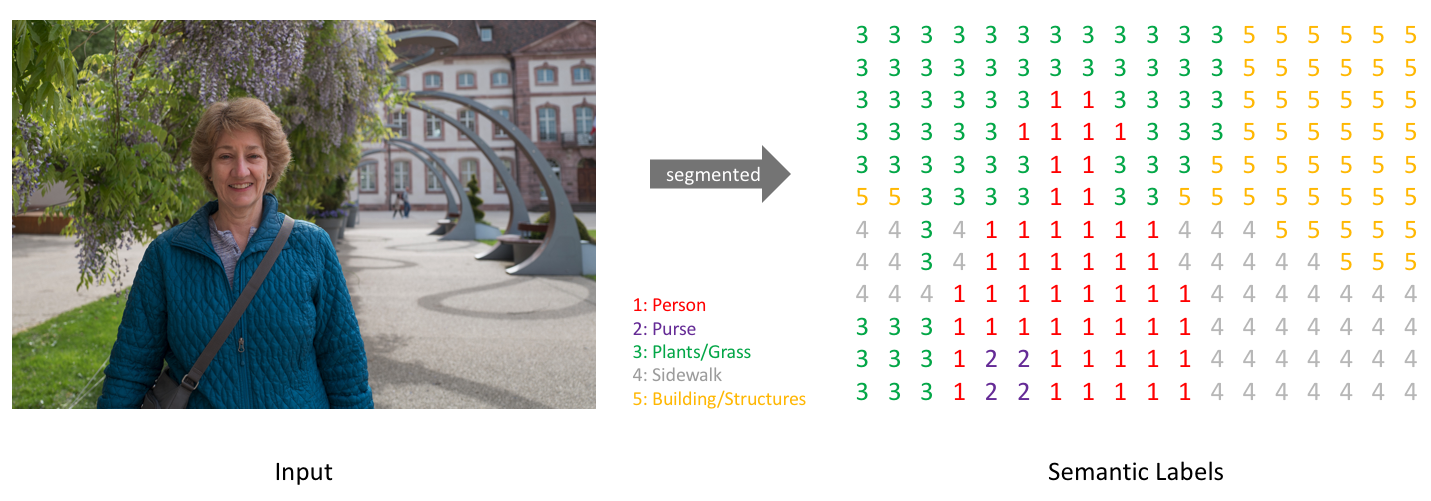
- 하지만 앞에서 설명한 바와 같이 각 채널 별로 binary classification을 적용하여 해당 픽셀 (x, y)가 각 클래스에 속하는 지 loss를 구함으로써 FCN에서 segmentation task와의 차이점을 두었습니다.
- 또한 4개의 convolutional layer를 backbone으로 부터 나온 feature map에 각각 추가하여 classification과 regression을 위한 branch로 만듭니다.
- regression을 할 때, regression의 target은 항상 positive로 분류되므로 regression branch에 exponential을 적용하여 0 ~ 양의 무한대 범위의 값으로 맵핑합니다.
- 이와 같은 방법을 통하여 FCOS는 anchor를 사용하지 않고 regression을 하며 anchor 기반의 네트워크에 비해 anchor의 갯수의 배수 만큼 더 적은 output variable을 가지게 됩니다.

- classification을 위한 Loss는
Focal Loss를 사용하였고 Regression을 위한 Loss는IoU Loss를 사용하였습니다. 각 Loss는 positive 샘플의 갯수 만큼 나누어서 normalization을 하였습니다. - regression 부분에서 \(\lambda\) 를 사용하여 loss의 weight를 조절할 수 있으나 기본적으로는 1을 사용하였습니다. 클래스 인덱스가 0보다 큰 경우 즉, positive sample일 때에는 모든 feature map에서 연산이 되는 반면 클래스 인덱스가 0인 경우에는 negative sample로 간주하여 연산이 무시됩니다.

- 인퍼런스를 할 때에는 이미지를 네트워크에 feedforward한 후에 각 feature map인 \(F_{i}\)의 각 (x, y) 위치에 대하여 classification score인 \(p_{x, y}\) 와 regression prediction 인 \(t_{x, y}\)를 얻습니다.
- 만약 \(p_{x, y} > 0.05\) 조건을 만족하면 positive sample로 간주하고 다음 식을 통하여 bounding box를 구할 수 있습니다.
- \[\hat{x_{l}} = x - l^{*}\]
- \[\hat{y_{l}} = y - t^{*}\]
- \[\hat{x_{r}} = x + r^{*}\]
- \[\hat{y_{r}} = y + b^{*}\]
Multi-level Prediction with FPN for FCOS

- 앞에서 설명한 내용 중에 FCOS의 문제점 2가지를
FPN 구조의 multi-level prediction을 통하여 해결한 내용을 설명하도록 하겠습니다. - 먼저 2가지 문제점은 ① stride가 크면 Recall이 낮아질 수 있는 문제점과 ② GT box가 겹칠 때, 모호함이 발생할 수 있는 것입니다.
- 먼저 첫번째 문제에 대하여 살펴보도록 하겠습니다. 예를 들어 stride가 누적된 결과 마지막 feature map에서의 stride가 16 정도가 되었다면 낮은
BPR(Best Possible Recall)을 얻을 수 있습니다. 큰 output stride를 가질 때, 작은 물체들은 해당 feature map에서 표현이 안될 수 있어서 찾기 어려우므로 recall을 낮게 만드는 원인이 됩니다. - 이 때, Anchor 기반의 디덱터에서는 recall 수치가 낮아지면 필요한 IoU 스코어를 낮추어서 Positive Sample의 갯수를 늘리면 Recall을 의도적으로 늘릴 수 있습니다. 반면 FCOS에서는 large stride로 인하여 마지막 feature map에서 해당 물체의 위치가 없어지게 되면 다른 방법으로 recall 성능을 높일 수 있습니다. 각 FPN에서 생성되는 feature map은 서로 다른 output stride를 가지므로 작은 output stride를 가지는 feature map에서 작은 물체를 찾고, 큰 output stride를 가지는 feature map 에서는 큰 물체를 찾도록 하면 됩니다. 상세 내용은 뒤에서 다룰 예정입니다.
- 이와 같은 방법을 이용하여 FCOS 모델을 이용하여 실험을 해보았을 때, Anchor 기반의 모델인 RetinaNet 보다 더 좋은 BPR 성능을 얻을 수 있음을 확인하였습니다. 또한
multi-level FPN prediction구조를 통하여 더 성능을 개선할 수 있음을 확인하였습니다.
- 다음의 두번째 문제인 GT 박스가 겹치는 상황의 모호성에 대해서도 multi-levl FPN prediction 구조가 개선책임 될 수 있음을 설명합니다. 이 문제는 overlap된 구간에 존재하는 pixel들이 어떤 겹쳐진 두 bounding box에 속하게 될 때, 어떤 bounding box와 class를 대상으로 학습을 해야하는 지에 대한 모호성 입니다.
- 이러한 문제 또한 FPN 구조를 이용하여 개선할 수 있음을 다룰 예정입니다. 개선되는 이유는 bounding box의 크기 차이가 발생하는 물체들 간에 모호성이 발생하게되는데 물체의 크기 차이가 발생하게 되면 서로 다른 feature map에서 찾게되므로 이 문제를 개선할 수 있습니다.
- 그러면 전반적인 Multi-level FPN 구조와 사용법에 대하여 살펴보도록 하겠습니다.

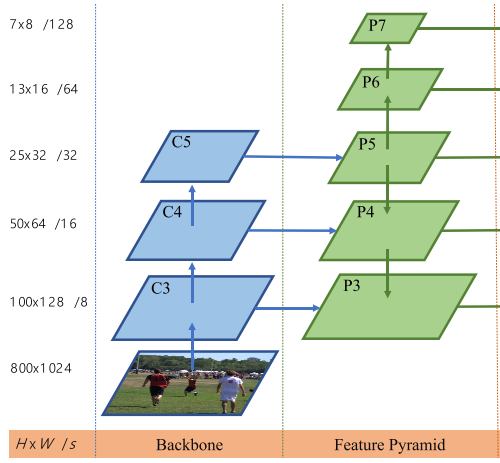
- 위 그림의 \(P_{3}\) ~ \(P_{7}\) 까지의 feature는 서로 다른 크기의 feature입니다. \(P_{3}, P_{4}, P_{5}\) 는 각각 \(C_{3}, C_{4}, C_{5}\) 에 1 x 1 convolution을 통해 feature를 얻고 \(P_{5} \to P_{4} \to P_{3}\) 의 top-down 방향으로 연결합니다.
- 그리고 \(P_{6}, P_{7}\) 은 \(P_{5}\) 부터 시작하여 stride 2를 차례대로 적용하여 \(P_{5} \to P_{6} \to P_{7}\) 순서로 만들어 냅니다.
- 그 결과 \(P_{3} = 8, P_{4} = 16, P_{5} = 32, P_{6} = 64, P_{7} = 128\) 에 해당하는 stride 크기를 가집니다.

- 기존의 anchor 기반의 detector와는 다르게 각 level의 feature에서 bounding box를 regression할 때, 범위를 제한합니다.
- 예를 들어 bounding box의 중심점에서 각 bounding box 까지의 좌/상/우/하 까지의 거리를 \(l^{*}, t^{*}, r^{*}, b^{*}\) 라고 하면 각 \(i\) 번째 feature 에서의 거리 범위는 아래와 같습니다.
- \[m_{i-1} \le \text{max}(l^{*}, t^{*}, r^{*}, b^{*}) \le m_{i}\]
- 위 식에서 \(m_{2}, ..., m_{6}\) 은 각각 0, 64, 128, 256, 512, \(\infty\) 가 되며 위 식의 범위를 벗어나면 negative sample로 인식합니다.
- 인덱스 \(i\) 가 작을 수록 stride가 작기 때문에 더 좁은 범위를 찾을 수 있고 \(i\) 가 클수록 stride가 더 크기 때문에 더 넓은 범위를 찾을 수 있습니다. 이 방식과 대응하여 \(i\) 가 작을수록 찾고자 하는 거리 범위의 제한도 작아 작은 물체를 찾도록 하고 \(i\) 가 클수록 찾고자 하는 거리 범위도 커져서 넓은 범위에서 큰 물체를 찾도록 합니다.
- 만약 이와 같은 multi-level FPN 구조를 사용하였음에도 불구하고 한 위치에 여러개의 gt 박스가 할당이 되면 면적이 가장 작은 gt box를 사용하는 것으로 기준을 정하여 모호함을 제거하였습니다.

- 예를 들어 위 그림과 같이 bounding box가 겹치는 경우 작은 박스는 \(p_{3}\)에서 검출되고 큰 박스는 \(p_{6}\) 에서 검출됩니다.

- 더 좋은 성능을 위하여 마지막 head 간에도 공유가 있는 것이 좋지만 앞에서 설명한 multi-level feature 간 서로 다른 사이즈의 범위로 regression 하는 것의 효과가 있기 때문에 서로 다른 level 에서의 head는 공유하지 않습니다.
- 추가적으로 regression brach의 exponential 함수에 trainable parameter를 적용하여 성능 개선을 하였습니다. 즉, bounding box를 추정할 때, 네트워크에서 추정한 값을 (\(l, t, r, b\))라 하고 최종 출력을 (\(l^{*}, t^{*}, r^{*}, b^{*}\))라고 하였을 때, exponential을 이용하여 \(l \to l^{*}\)로 변환합니다. 이렇게 사용하는 이유는 (\(l, t, r, b\))가 큰 값을 가지게 되면 원하는 만큼 학습이 잘 안될 수 있으므로 의도적으로 작은 값을 가지도록 하는 것이며 학습 가능한 파라미터 \(s_{i}\) 를 사용하여 \(\exp{(s_{i}l)}\)과 같이 사용하여 \(l \to l^{*}\) 을 추정하도록 하였습니다.
Center-ness for FCOS

- 앞에서 설명한 Multi-level Prediction을 사용하더라도 FCOS와 anchor 기반의 디텍터와의 성능 차이가 있었습니다.
- FCOS에서는 상대적으로 low-quality bounding box가 많이 예측이 되었기 때문인데 이러한 box들은 실제 물체의 중앙점에서 멀리 떨어진 상태로 추정되는 경향이 있습니다. low-quality bounding box의 정의는 IoU와 classification score 중에서 IoU의 스코어가 더 낮은 box를 의미합니다. 이와 같은 box는 위치는 부정확한 하지만 높은 확률을 가지므로 box를 오인식 할 수 있기 때문입니다.
- 간단히 말하면 물체의 중앙에서 멀리 떨어진 위치의 boundong box의 예측값의 품질이 좋지 않아 오인식 되는 경향이 있다는 뜻입니다.
- 여기서 소개하는
center-ness는 하이퍼파라미터 없이 실제 중앙에 가까운 점들을 예측할 수 있도록 돕는 역할을 합니다.center-ness는 중심점과의 거리를 정규화 하여 어떤 박스가 중심점과 가깝다면 1에 가까운 값을 배정하고, 중심정과 멀다면 0에 가까운 값을 갖도록 만듭니다. - 따라서 위 식에서 나타내는
center-ness를 classification score 출력에 곱해주게 되면 마지막 layer의NMS에서 객체의 중앙과 멀리 떨어져서 위치를 추정한 박스는 걸러지도록 만들 수 있습니다. 이와 같은 역할을 하기 위하여 single layer branch를 추가하여 어떤 위치에서의 center-ness를 예측합니다. center-ness식의 의미는 center 점에서 왼쪽(\(l^{*}\))/상단(\(t^{*}\))/오른쪽(\(r^{*}\))/하단(\(b^{*}\)) 끝 부분까지의 normalized distance를 의미합니다.
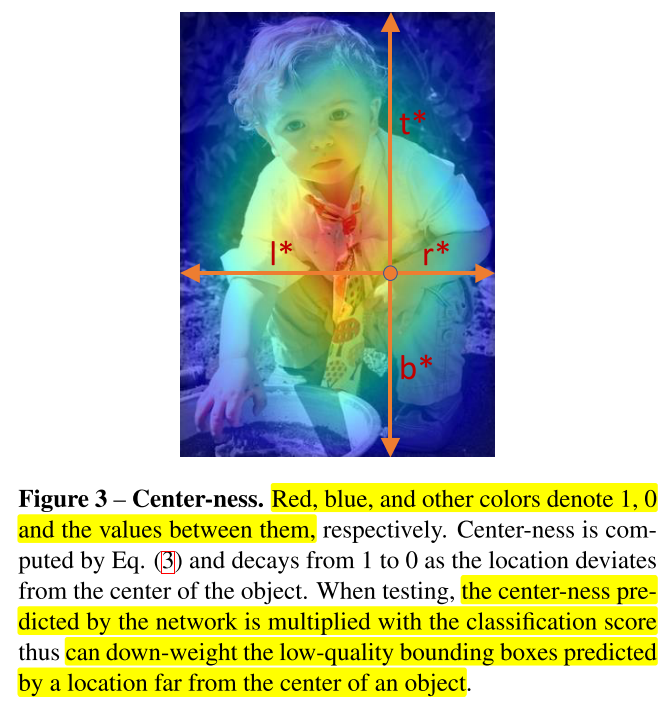
- 여기서
sqrt를 적용한 이유는 center-ness 값이 많이 줄어들지 않기 위함입니다. sqrt 내부의 값이 0 ~ 1 사이의 값이므로 sqrt를 적용하면 적용하지 않았을 때 보다 값이 더 커집니다. center-ness의 값의 범위는 0 ~ 1사이이며 Binary Cross Entropy Loss를 통하여 학습이 됩니다. - 이 때 사용된 Loss는 앞에서 정의한 전체 Loss에 추가적으로 더해집니다.
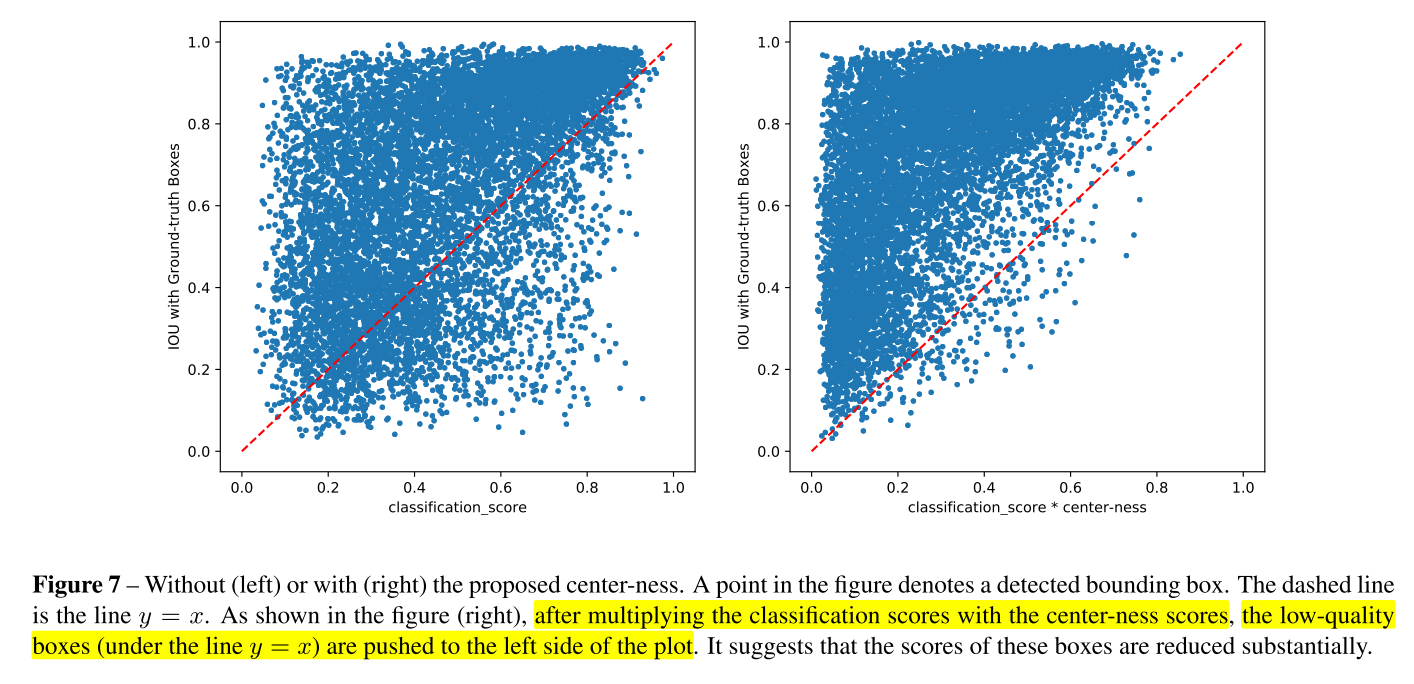
- 논문에서
center-ness를 사용하였을 때 효과를 위 그래프와 같이 나타내었습니다. 왼쪽 그래프의 가로축은 classification score를 나타내고 오른쪽 그래프의 가로축은 classification score에 center-ness를 곱한 값을 나타냅니다. 세로축은 Inference와 GT 간의 IoU를 나타내며 가로축, 세로축 값 모두 1에 가까울수록 좋습니다. - 왼쪽 그래프와 오른쪽 그래프를 비교하면 오른쪽 그래프는 y=x 선을 기준으로 왼쪽 상단에 대부분의 점들이 위치하는 것을 알 수 있습니다. 즉, IoU는 낮으나 classification score가 높은 샘플들을 IoU가 classification score (* center-ness) 보다 상대적으로 더 높도록 만들어지도록 하였습니다.
- 처음에 제기된 low-quality bounding box와 연결시켜 보면 왼쪽 그래프에서 y=x 선 아래에 있는 점들은 IoU가 Classification score보다 상대적으로 낮아서 오인식할 수 있는 가능성이 있는 집단을 표현하였습니다. 반면 오른쪽 그래프에서는 low-quality bounding box에 해당하는 집단의 수가 현저히 줄어들었습니다. 즉, Classification score가 상대적으로 높아서 출력 대상으로 뽑혔으나 IoU가 낮아서 잘못된 위치에 객체를 인식할 수 있는 대상들을 없앤 것입니다.

- test 시점에서는 앞에서 설명한 바와 같이 classification score와 center-ness를 곱한 결과를 이용하여 각 bounding box의 스코어를 계산하고 최종적으로는 NMS를 통하여 필터링이 되도록 하면 성능을 개선할 수 있습니다.
Experiments
- 지금까지 FCOS의 전체적인 아키텍쳐에 대하여 알아보았습니다.

- 위 내용은 Training와 Inference 시의 상세 내용을 기입한 것입니다. backbone은 ResNet-50을 사용하였고 상세 파라미터는 RetinaNet을 따른 것으로 설명합니다. Inference 또한 상세 내용은 RetinaNet을 따릅니다.
- FCOS 논문에서는 Anchor free 기반임에도 불구하고 Anchor 기반의 모델에 비해 좋은 성능을 낼 수 있는 이유로 ① Multi-level Prediction with FPN과 ② Center-ness를 제시하였습니다. 그러면 이 각각의 아이디어에 대한 실험 내용을 살펴보도록 하겠습니다.
Multi-level Prediction with FPN

- 먼저 Multi-level Prediction with FPN과 관련된 내용 됩니다. FCN 기반의 디텍터는 low recall에 대한 문제점과 출력 bounding box와 GT가 애매하게 겹치는 ambiguous samples에 대한 문제점이 나타나곤 합니다. 이 문제는
Multi-level Prediction with FPN을 통하여 크게 개선될 수 있음을 보여줍니다.

- 위 도표에서 RetinaNet은 Anchor 기반의 모델이고 FCOS는 Anchor free 기반의 모델입니다. 2번째 열인 w/FPN은 FPN이 사용된 구조에서 체크가 되어 있으며 3번째 열인 Low-quality matches는 Anchor 기반인 RetinaNet에서 사용되는 방법이며 Low-quality matche가 많이 사용될수록 Recall은 높아지게 됩니다. (반대로 Precision은 내려갈 수 있습니다.)

BPR은 Best Possible Recalls의 줄임말로 가능한 Recall의 최댓값을 의미합니다. BPR에서는 Precision은 고려하지 않고 Recall 수치만 고려하여 가능한 Recall의 최댓값은 얼마인지 확인을 통해 이 모델의 Recall 성능을 확인해 볼 수 있습니다.- 그 결과 FCOS를 사용하여도 Anchor 기반의 RetinaNet 보다 수치가 높거나 1% 미만으로 낮음을 알 수 있습니다. 특히 FPN을 사용하였을 때, 성능 개선이 있음을 통하여 Anchor free 모델의 recall 성능이 낮다는 문제는 개선할 수 있음을 확인하였습니다.
- 그 다음으로 다룰 문제는
Ambiguous Samples와 관련된 내용입니다.

Ambiguous Samples문제는 GT bounding box들이 겹치는 문제 때문에 발생하며 위 그림과 같은 문제가 있을 수 있습니다. 위 문제를 살펴보면 같은 위치의 센터점에서 사람과 테니스 라켓의 bounding box를 그리고 있습니다. 즉, 위 그림처럼 겹치는 문제로 인해 발생하는 문제가 Ambiguous Samples 라고 합니다.

- 먼저 FPN을 사용하지 않고 오직 \(P_{4}\) 의 feature만 사용 하여 ambiguous sample 을 확인하였을 때 약 23.16%의 샘플을 확인할 수 있었으나 FPN 구조를 사용하면 7.14 %로 줄어드는 것을 확인할 수 있었습니다. 즉, FPN 구조를 통하여 앞서 언급하였던 FCN 구조의 Detector에서 발생하는 2번째 문제인 Ambiguous Sample을 개선할 수 있었습니다.
With or Without Center-ness

- 위 테이블의 수치는 center-ness를 사용하였을 때, 얼마나 성능이 향상하는 지 나타냅니다. None은 center-ness를 사용하지 않은 것이고 십자가 모양의 center-ness는 center-ness에 필요한 수치를 regression vector를 사용한 것 그리고 마지막 행이 center-ness를 별도의 branch로 둔 다음에 (H X W X 1)의 형태로 예측하여 사용한 케이스 입니다.
- 결과적으로 논문의 아키텍쳐에서 제공한 형태로 branch를 별도로 사용하는 방식이 가장 성능이 좋으며 이렇게 사용할 때, Anchor 기반의 RetinaNet 보다 성능이 좋은 것을 확인하였습니다.
- 추가적으로 RetinaNet에는 Anchor box가 샘플을 Positive / Negative 로 구분하기 위한 2개의 하이퍼파라미터가 있는 단점이 있는데 FCOS의 구조에서는 이러한 하이퍼파라미터 없이 학습된 결과만으로도 더 좋은 성능을 얻었음을 제시합니다.
FCOS vs. Anchor-based Detectors

- FCOS 논문에서는 RetinaNet과의 동등 비교를 위하여 가능한한 하이퍼파라미터는 동일하게 사용하되 Group Normalization을 사용한 것과 전체 아키텍쳐 참조 시 \(C_{5}\) 대신 \(P_{5}\) feature를 이용하여 \(P_{6}, P_{7}\) 을 생성한 것에 차이를 확인할 수 있습니다.
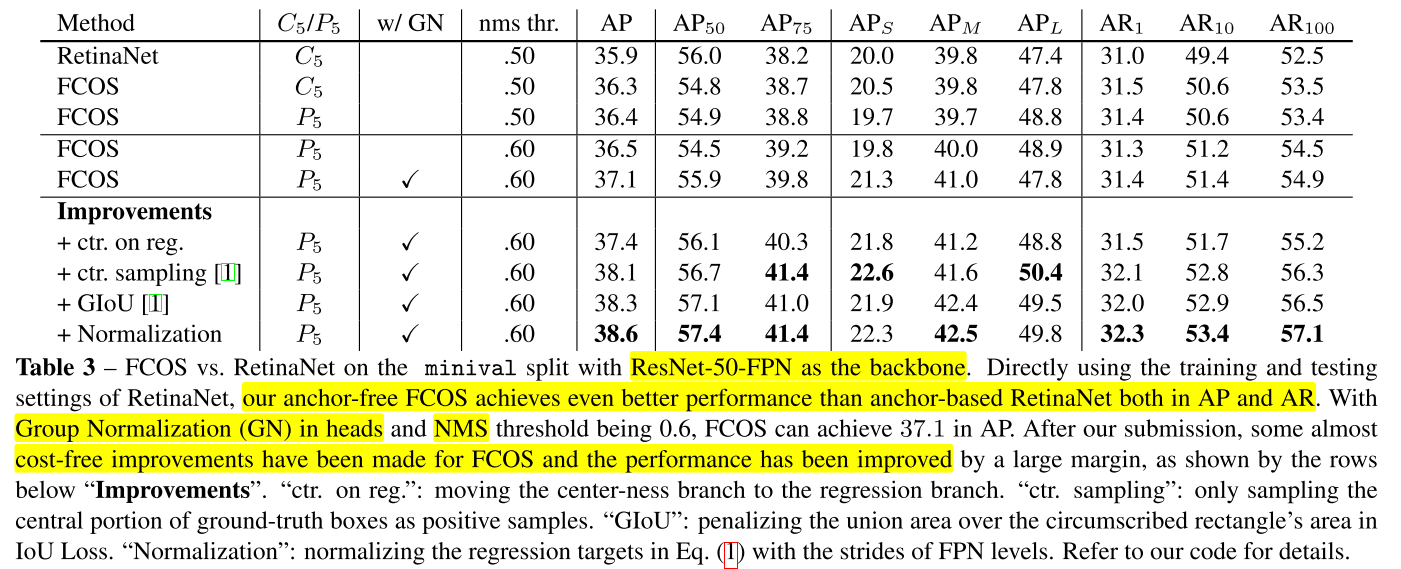
- 위 테이블 참조 시 RetinaNet과 FCOS, \(C_{5}, P_{5}\) 이용 유무, Group Normalization 사용 등이 주요 구분점으로 사용되었고 이 차이점을 이용하여 성능을 비교하였습니다.
- FCOS의 가장 기본이 되는 구조는 \(P_{5}\) 와 Group Normalization을 사용하는 것으로 위에서 5번째 성능을 참조하면 됩니다. 추가적인 Improvements 내용은 위 논문을 참조하시면 됩니다.
Comparison with State-of-the-art Detectors

- FCOS와 다른 Detector 모델을 비교한 결과를 살펴볼 수 있습니다. 결과적으로 FCOS가 Ancor 기반의 RetinaNet 보다 좋은 성능을 보였으며 Two-Stage 모델의 Faster R-CNN 보다 좋은 성능을 보인 것을 확인할 수 있습니다.
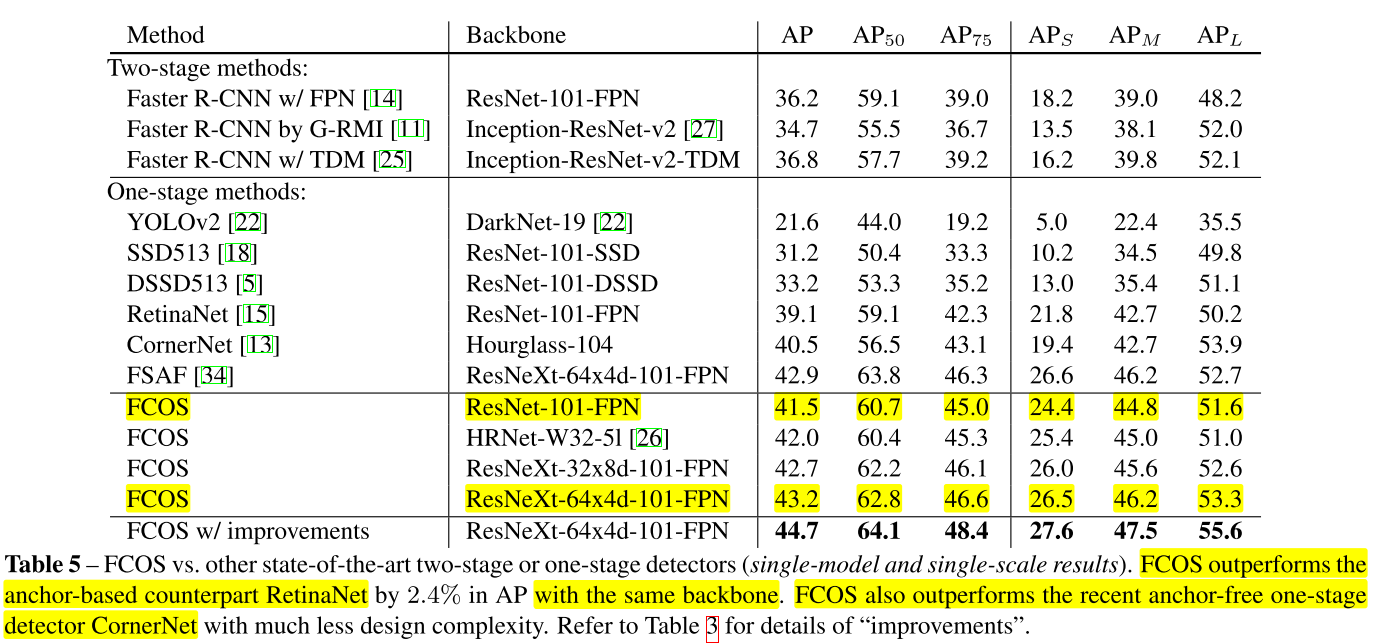
- 위 테이블에서
FCOS가 같은 backbone을 사용하였음에도 불구하고 높은 성능을 가진것을 확인할 수 있습니다.
Conclusion
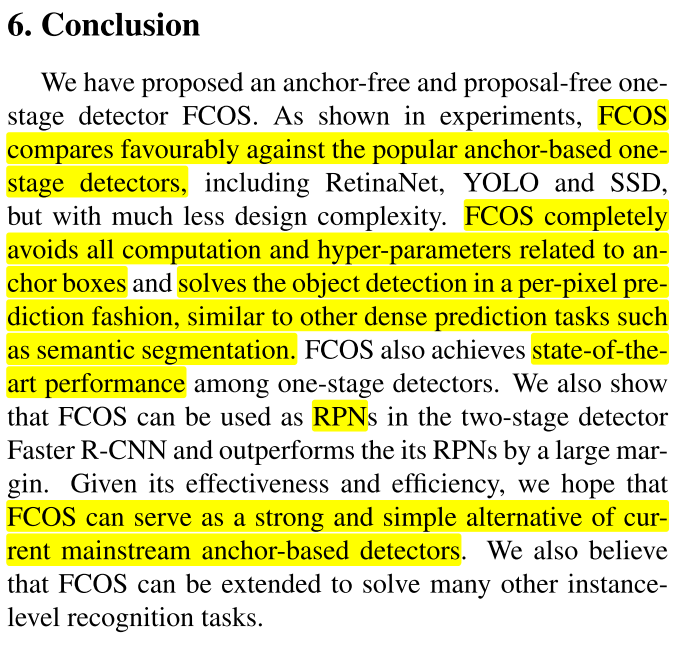
- 마지막으로 FCOS의 contribution을 정리하며 내용을 마치겠습니다.
- ① Anchor free 기반의 모델로 Anchor box와 관련된 내용과 관련 하이퍼파라미터는 모두 제외되었습니다.
- ② semantis segmentation을 구하는 방법과 유사하게 pixel 단위의 예측을 할 수 있는 구조를 사용하였습니다.
- ③
one-stage+anchor free+per-pixel prediction방법 (+multi-level FPN+center-ness)을 이용하여 SOTA를 기록하였습니다. - ④ two-stage detector로 응용하였을 때, 좋은 Resion Proposal Network로도 사용될 수 있습니다.
- ⑤ 전체 구조가 복잡하지 않고 간단하면서 성능이 좋기 때문에 다른 Task에 응용하기 쉽습니다.
Pytorch Code
- FCOS 구현과 관련된 Pytorch 코드에 대하여 살펴보도록 하겠습니다.