GIoU(Generalized Intersection over Union)
2020, Nov 08
- 참조 : https://giou.stanford.edu/
- 참조 : https://arxiv.org/abs/1902.09630v2
- 참조 : https://youtu.be/ENZBhDx0kqM
- IoU에 관한 상세 설명 : https://gaussian37.github.io/math-algorithm-iou/
- 이번 글에서는 object detection 문제에서 평가 지표로 많이 사용하는 IoU를 loss로 사용하기 위해 고안된
GIoU에 대하여 알아보도록 하겠습니다. - 이번 글에서는 위 영상 링크를 기준으로 작성되었습니다.
- 현재 바운딩 박스의 성능을 평가할 때 사용하는 평가 지표로 IoU (Jaccard Index 라고도 함)가 많이 사용되고 있습니다.
- 기본적인 IoU에 관한 설명은 아래 링크를 참조하시기 바랍니다.
- 링크 : https://gaussian37.github.io/math-algorithm-iou/
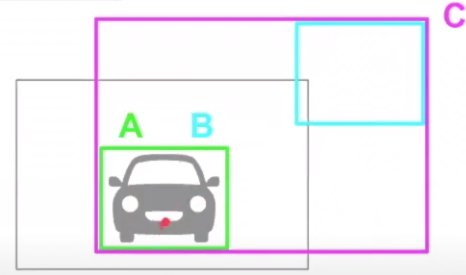
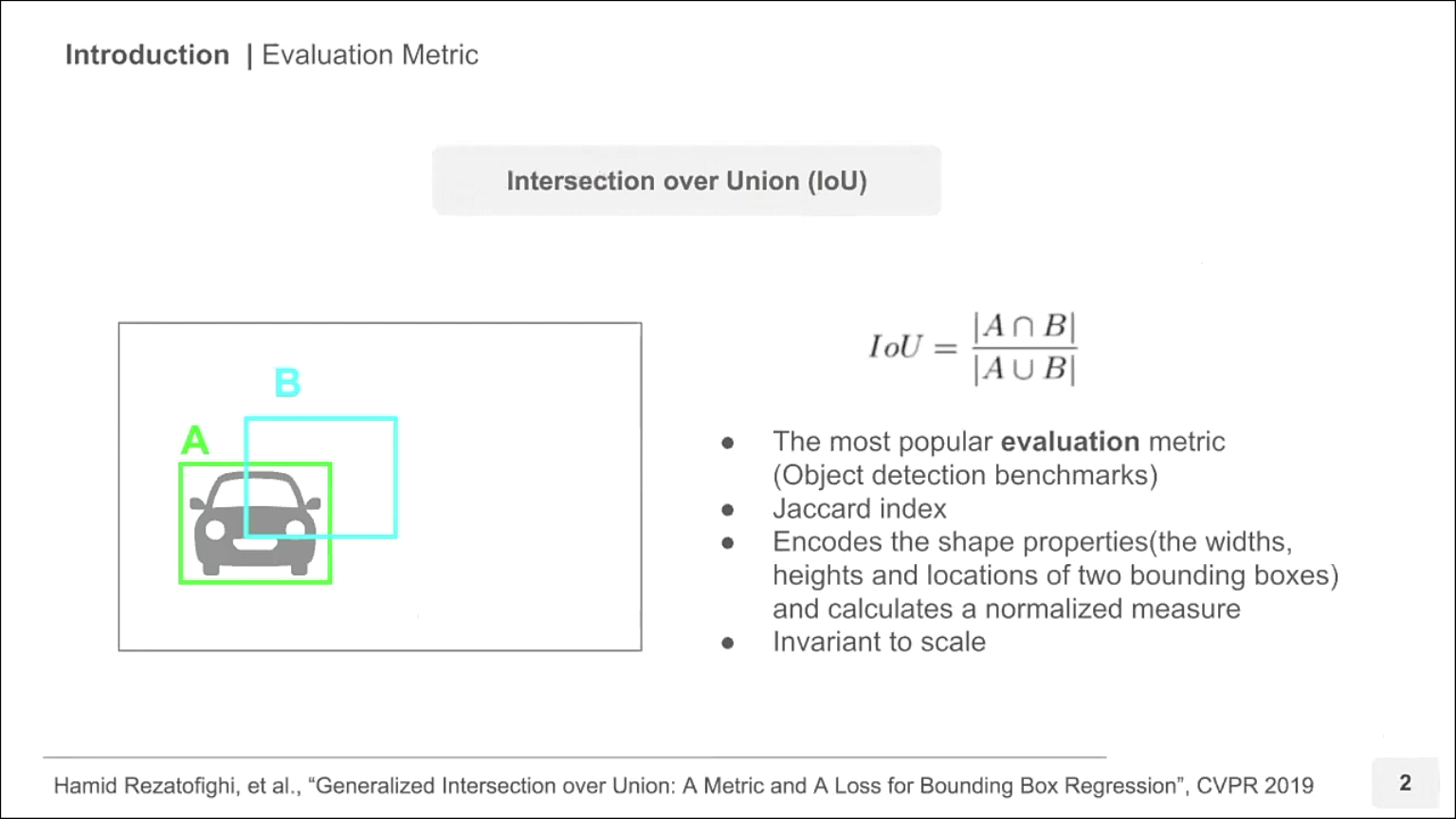
- 위 슬라이드를 기준으로 A 박스가 GT이고 B 박스가 Prediction이면 IoU에서 분모는 A 박스와 B 박스의 합집합 면적이고 분자는 A박스와 B박스의 교집합 면적입니다.
- IoU의 장점은 박스의 크기에 상관없이 마치 확률 값처럼 0 ~ 1 사이의 값을 가지게 되어 자동적으로 normalization이 됩니다. 확률과 같이 1에 가까울 수록 GT와 Prediction이 일치함을 나타냅니다.
- IoU는 GT와 Prediction의 박스가 얼만큼 잘 찾아졌는 지 확인할 수 있는 방법이고 잘 찾아진 경우에는 IoU는 1에 가까워지고 잘 못찾아진 경우에는 IoU가 0에 가까워지는 것을 이용하여 마치
Loss처럼 사용할 수 있습니다. - 그러면 IoU와 실제 Loss들을 비교하면서 IoU와 기존의 Loss의 차이점에 대하여 먼저 알아보도록 하겠습니다.
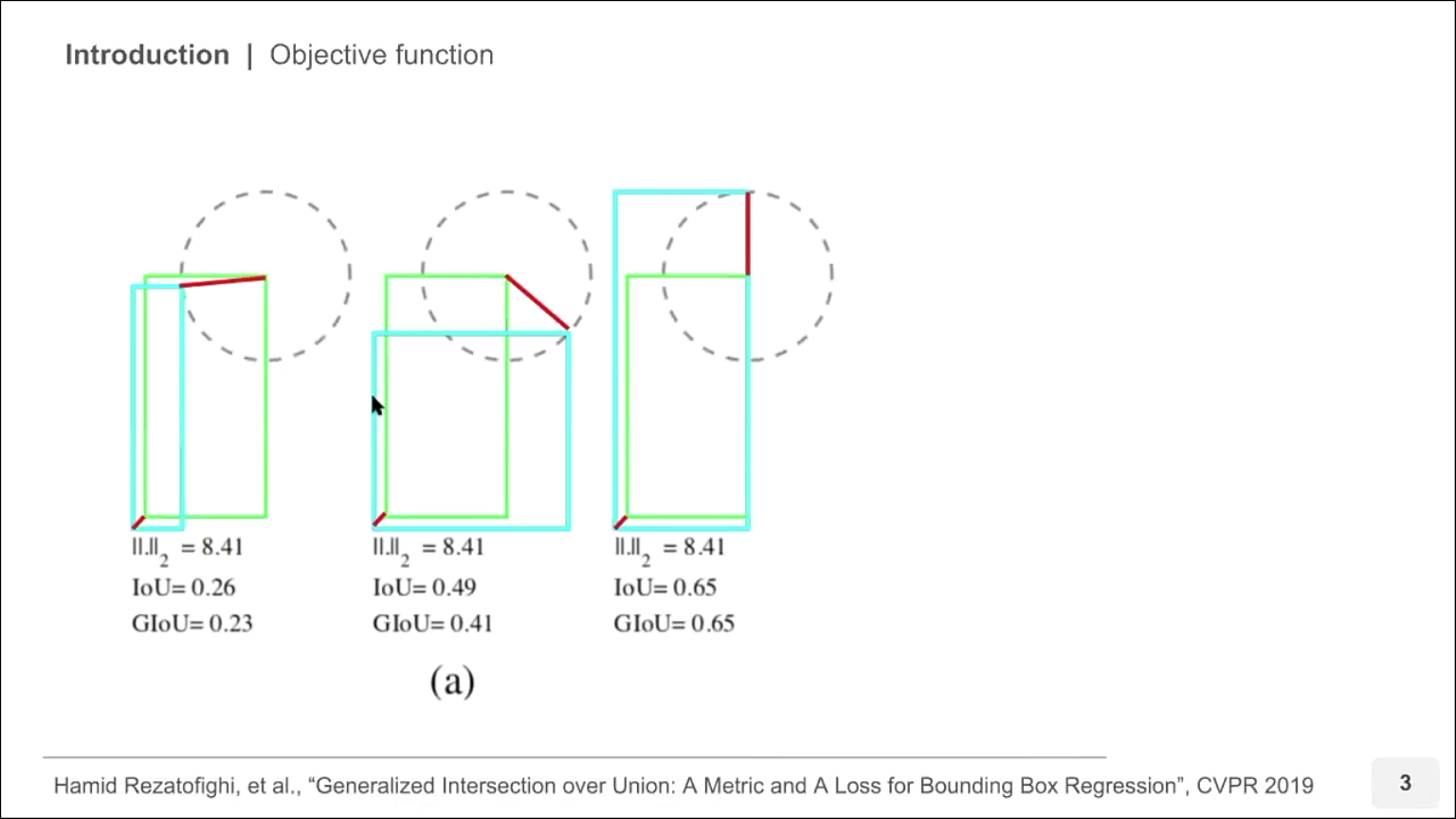
- 위 슬라이드는 박스의 위치를 regression 하는 문제에 대하여
MSE(Mean Squared Error)즉, L2 loss를 나타냅니다. - 위 3가지 경우에 대하여 비교해 보겠습니다. 예를 들어 3가지 경우 모두 두 박스의 왼쪽 하단 꼭지점 거리는 일정하다고 가정하였을 때, 단순히 MSE를 적용하면 오른쪽 상단 꼭지점의 거리 차이도 일정합니다. 왜냐하면 원의 반지름 형태만큼 차이가 나기 때문입니다.
- 3가지 경우 모두 MSE 기준의 Loss는 같으나 IoU를 비교하면 Loss가 같다는 것에 의문을 가질 수 있습니다.
- 직관적으로 봤을 때, 가장 왼쪽 경우가 IoU가 낮으므로 Loss도 커야하고 가장 오른쪽 경우가 IoU가 높으므로 Loss는 작아야 말이 됩니다.
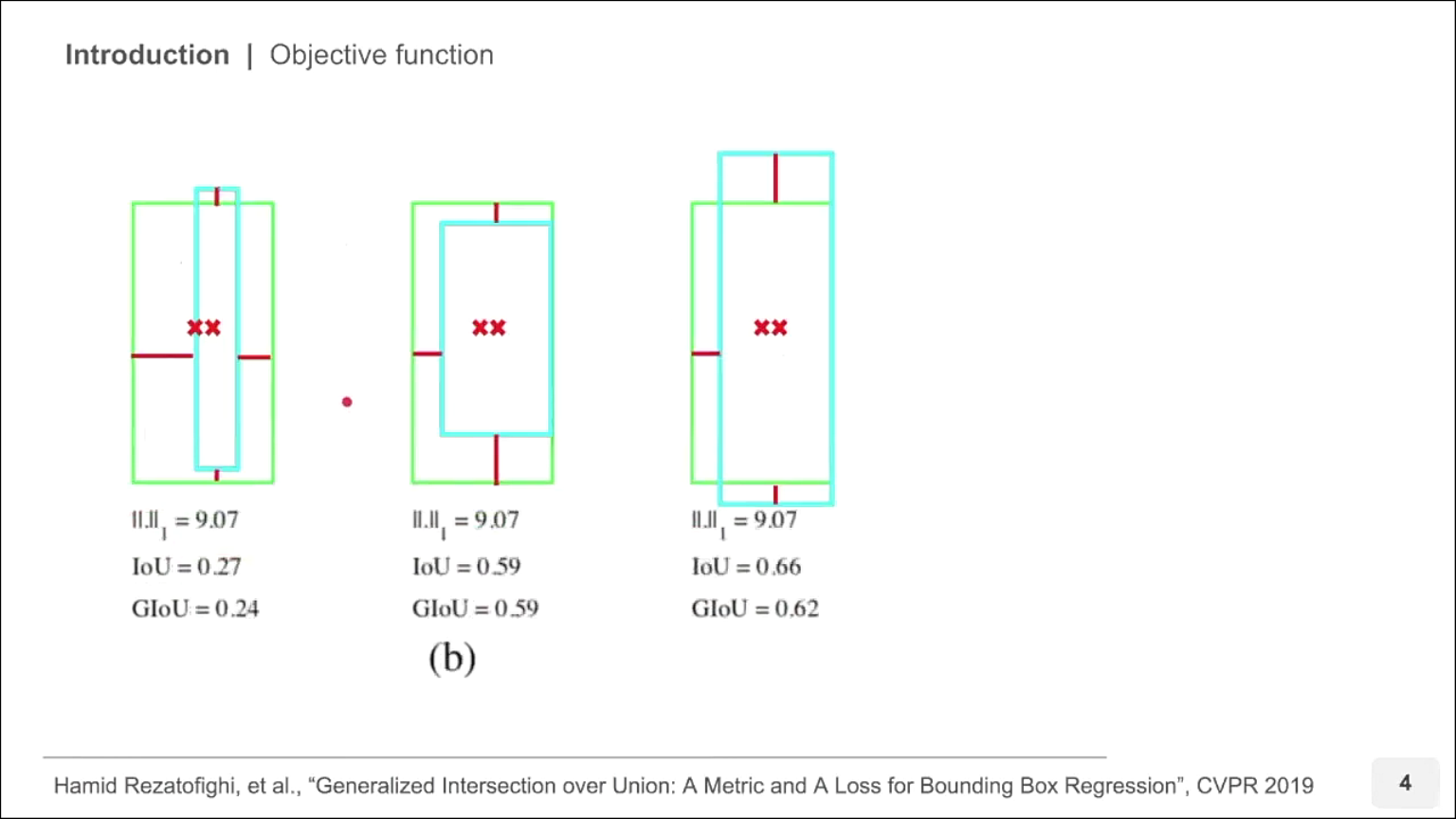
- 이번에는 중심 사이의 거리와 높이 너비의 차이를 L1 Loss를 이용하여 계산해 본 경우입니다.
- 이 경우에도 위 세가지 모두 같은 L1 Loss를 가집니다.
- 하지만 이 경우에도 IoU를 비교해 보았을 때, Loss가 두 박스의 겹침 정도를 정확하게 나타내지 못하는 것을 알 수 있습니다.
- 따라서 단순히 박스의 위치를 이용하여 두 박스의 유사성을 Loss로 나타내기보다는 IoU를 이용하여 Loss 처럼 사용하는 것이 regression loss에 더 적합할 수 있음을 시사합니다.
- 그러면 IoU를 이용하여 Loss를 사용해 보도록 하겠습니다.
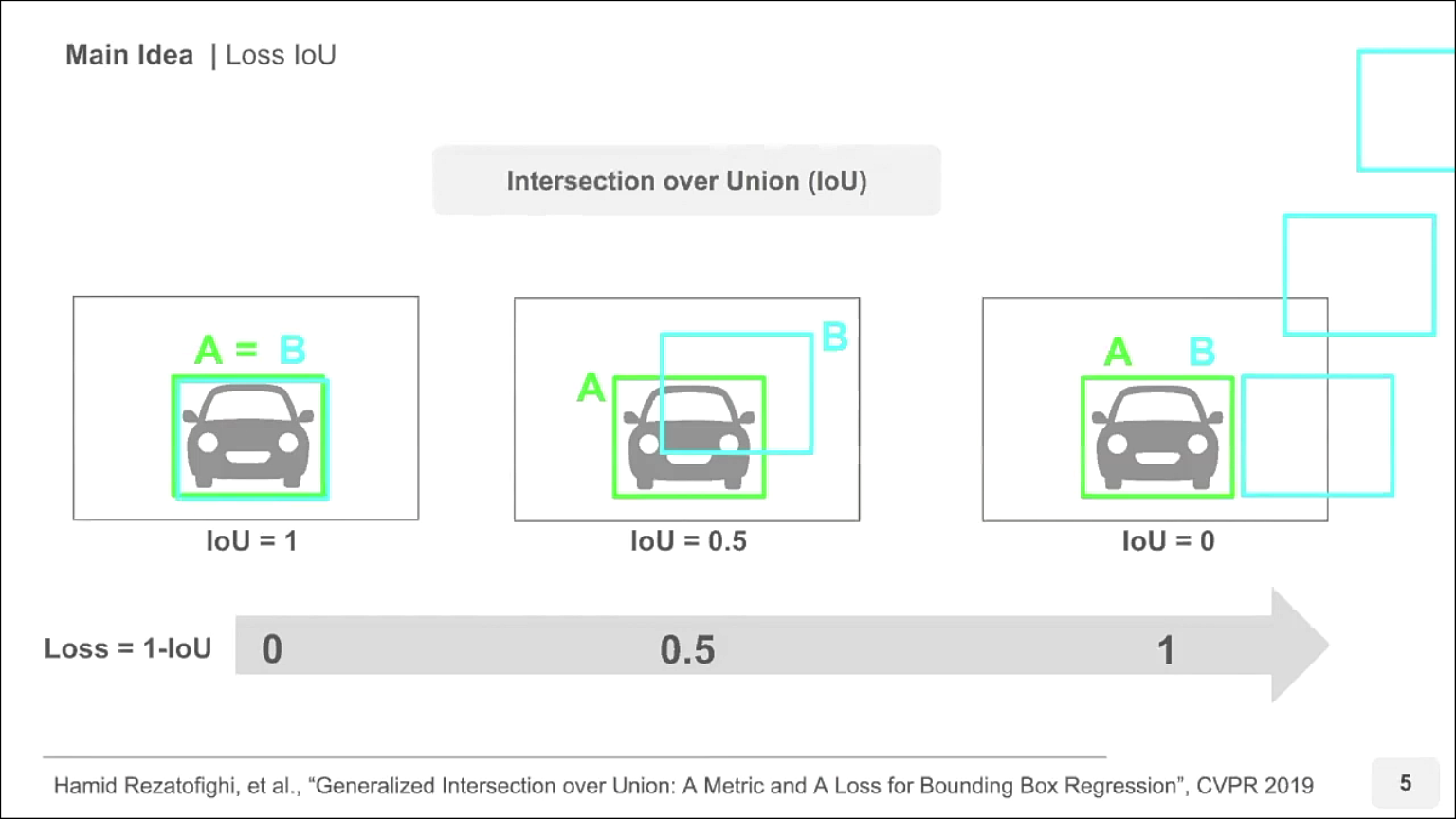
- IoU를 Loss로 사용하려면 1 - IoU를 사용하여 두 박스가 잘 겹칠수록 0에 가까워지도록 만들면 됩니다.
- 하지만 가장 오른쪽의 경우에서 문제가 발생합니다.
- 일반적으로 Loss는 Prediction이 잘 될수록 0에 가까워지고 Prediction이 잘못된 경우일수록 그에 비례하여 Loss가 커져야 합니다.
- 하지만 일반적인 IoU는 두 박스의 교집합이 없으면 0이 되므로 아깝게 교집합이 생기지 않았는 지, 굉장히 큰 오차로 교집합이 생기지 않았는 지 알 수 없습니다.
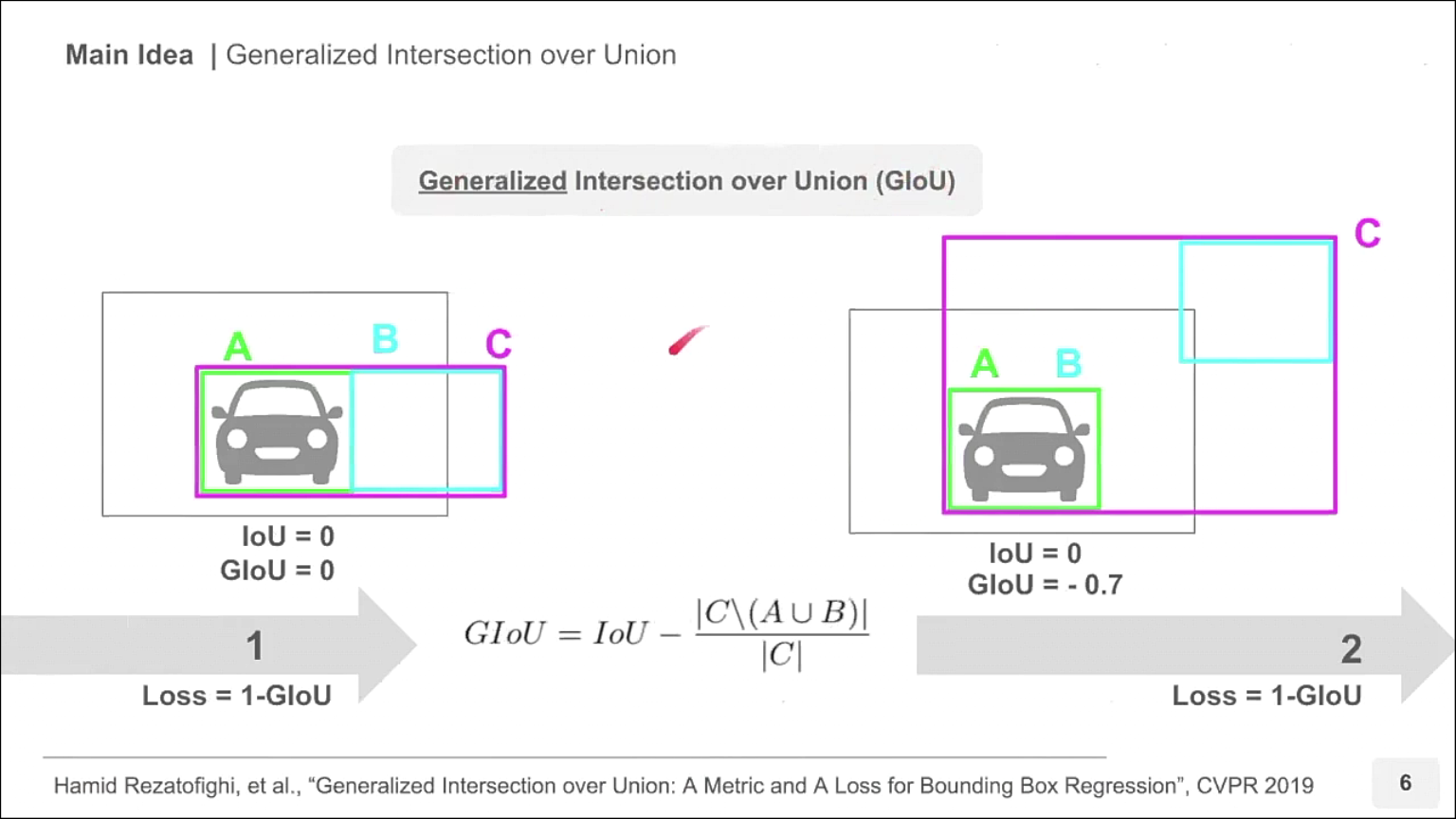
- 따라서 이번 글의 주제인 GIoU 방법을 이용하여 기존 IoU를 Loss로 사용하였을 때의 문제를 개선해 보겠습니다.
- GIoU에서는 위 슬라이드와 같이
C박스가 추가됩니다. C박스는 GT와 Prediction을 포괄하는 박스입니다. 간단하게 A, B 박스를 모두 포괄하는 가장 작은 박스라고 보시면 됩니다. - 따라서 A, B 박스가 많이 겹칠수록 C 박스의 크기가 작아지고 A, B 박스가 멀어질수록 C 박스의 크기가 커집니다.
- 위 슬라이드의 식에서
C \ (A ∪ B)는 C 박스의 영역에서 A와 B 박스의 합집합을 뺀 영역에 해당합니다. - 따라서 위 슬라이드의 2가지 경우를 계산해 보면 왼쪽과 오른쪽 모두 IoU는 0이지만 GIoU는 왼쪽의 경우 0인반면 오른쪽의 경우 -0.7로 음수의 값을 가집니다.
- A와 B의 박스가 무한히 멀어지게 되면
C \ (A ∪ B)의 값이C에 수렴하게 되므로(C \ (A ∪ B)) / C는 1에 수렴합니다. 따라서 GIoU는 -1까지 작아질 수 있습니다. - 따라서 GIoU를 Loss로 사용할 때에는
Loss = 1 - GIoU형태로 사용하며 Loss의 최대값은 2가 되고 최소값은 0이 되도록 설정할 수 있습니다.

- 수식으로 정리하면 위 슬라이드와 같습니다.

- 그러면 위 식들을 이용하여 GIoU를 실제 어떻게 적용하는 지 확인할 수 있습니다.
- 논문에서는 Yolo v3, Faster R-CNN, Mask R-CNN 등에 대하여 바운딩 박스 Regression을 위한 MSE, IoU, GIoU를 Loss를 사용하였을 때의 결과를 비교하였습니다. 결과적으로는 GIoU를 사용하는 것이 가장 성능을 높이는 데 좋았다고 설명합니다.
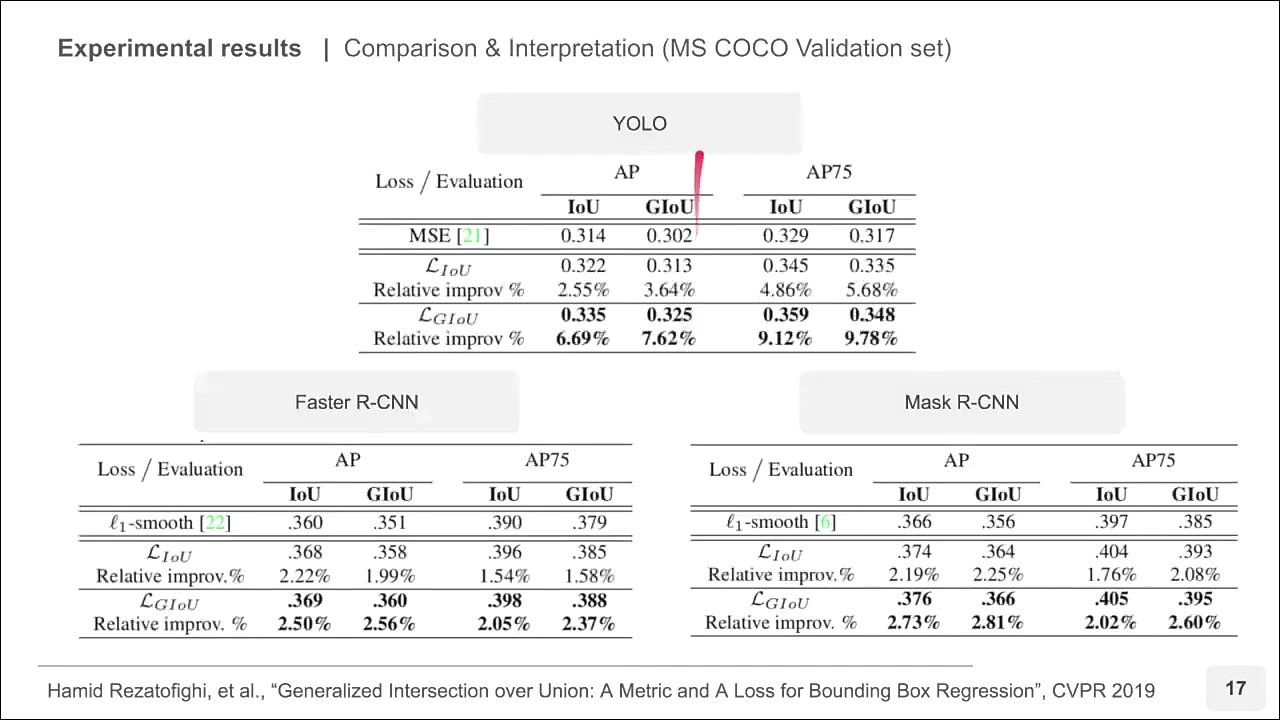
- 위 슬라이드와 같이 Yolo v3에서 GIoU를 사용하였을 때, 상대적으로 높은 AP 성능을 가질 수 있었습니다.
- Yolo의 경우가 Faster R-CNN 또는 Mask R-CNN에 비하여 성능이 더 높아진 것을 알 수 있습니다. 이는 Faster R-CNN, Mask R-CNN이 Yolo에 비하여 앵커 박스가 더 촘촘하게 나타나기 때문에 IoU와 큰 차이가 없다고 해석할 수 있습니다.
- 이 논문에서는 GIoU를 이용하여 기존 Loss를 대체하고 IoU가 0인 경우에 대해서도 얼만큼 두 박스가 더 멀리 있는 지 정량화 하는 방법에 대하여 소개하였습니다.
- 만약 두 박스가 얼만큼 떨어져 있는 지 정량화가 필요하면 GIoU를 사용해도 될 것으로 판된됩니다.