opencv를 이용한 선형 칼만 필터 구현 및 예제

opencv를 이용한 선형 칼만 필터 구현 및 예제

2019, Nov 19    


  • 참조 : Python으로 배우는 OpenCV
  • 이번 글에서는 opencv를 이용하여 칼만필터를 사용하는 방법에 대하여 알아보겠습니다.
  • 최종 목표는 2D 이미지에서 점을 선형 칼만 필터 알고리즘으로 tracking 할 예정입니다.
  • 선형 칼만 필터의 자세한 원리를 이해하고 싶으면 제 블로그의 이 링크를 참조하시기 바랍니다. 이 글에서는 간략하게만 이해하고 넘어갈 예정입니다.
  • 먼저 칼만 필터에 대한 간략한 이론을 다루고 opencv를 이용하여 어떻게 칼만 필터를 사용하는 지 관점으로 접근해 보도록 하겠습니다.


목차


  • 칼만 필터의 역할

  • (predict) State Transition Equation

  • (predict) Uncertainties 모델링

  • (predict) Control Input (optional)

  • (predict) Uncontrolled uncertainties

  • (update) Measurements

  • (update) Fusing information

  • opencv의 칼만 필터 함수 설명

  • opencv의 칼만 필터 함수 사용

  • 마우스 위치 추적 구현


칼만 필터의 역할


  • 칼만 필터는 2가지 전략을 따릅니다.
  • 1) predict : 시스템의 내부 상태에 대하여 예측을 합니다. (e.g. 드론의 위치와 속도) 이 예측은 이전 내부 상태와 센서 등으로 부터 입력된 값 (e.g. 드론의 프로펠러 force)을 기반으로 만들어집니다.
  • 2) update : 내부 상태에 관련된 새로운 계측값 (e.g. GPS 정보)이 들어오면 이 값을 사용하여 predict에 반영합니다.


(predict) State Transition Equation


  • 먼저 칼만 필터에서 predict에 관련된 과정부터 이해해 보도록 하겠습니다. 드론의 예를 들어서 한번 접근해 보도록 하겠습니다.
  • 드론이 비행을 할 때, 드론의 위치를 정확히 알아야 합니다. \(k\) 번째 스텝에서의 드론의 위치를 알고 싶으면 이전 스텝인 \(k - 1\) 스텝에서의 정보를 이용하여 predict 해야 합니다.
    • 먼저 \(k - 1\) 번째의 드론의 위치
    • 그리고 \(k - 1\) 번째의 드론의 속도
    • 그리고 \(k - 1\) 번째와 \(k\) 번째 사이의 시간 간격
  • 위 3가지 정보를 이용하여 설계를 해보겠습니다. 문제를 단순화 시키기 위하여 acceleration은 고려하지 않고 등속으로 간주하겠습니다.


[\begin{equation} p_{k} = p_{k-1} + v_{k-1} \Delta t \end{equation} \tag{1}]


[v_{k} = v_{k-1} \tag{2}]


  • 여기서 \(p\)는 3차원의 위치이고 \(v\)는 3D 속도벡터이고 \(\Delta t\)는 시간 간격 입니다.
  • 그리고 \(p_{k}\)와 \(v_{k}\)는 시스템의 state(상태)라고 하는데 \(p_{k}\)와 \(v_{k}\)는 벡터이고 각각의 원소가 무엇을 의미하는 지 알아보겠습니다.
  • 먼저 \(p = [x, y, z]^{T}\)는 각 \(x, y, z\) 축의 위치를 나타냅니다.
  • 그리고 \(v = [u, v, w]^{T}\)는 각 \(x, y, z\)축의 방향 속도를 나타냅니다.
  • 예를 들어 \(u\)는 \(x\) 방향으로의 속도를 뜻합니다.


  • 위의 (1), (2) 식을 결합해서 한 개의 state transition equation을 만들 수 있는데 다음 식과 같습니다.


[\begin{bmatrix} p_{k} \ v_{k} \end{bmatrix} = F_{k} \begin{bmatrix} p_{k-1} \ v_{k-1} \end{bmatrix} \tag{3}]


  • (3) 식의 의미를 보면 \(k-1\) 상태에서 \(F_{k}\)를 곱하면 \(k\) 상태가 된다라고 해석할 수 있습니다.
  • 그러면 \(F_{k}\)는 무슨 뜻일까요? \(F_{k}\)는 state transition matrix 라고 하고 그 의미는 아래 식을 통하여 확인할 수 있습니다.


[\begin{bmatrix} x_{k} \ y_{k} \ z_{k} \ u_{k} \ v_{k} \ w_{k} \ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & \Delta t & 0 & 0
0 & 1 & 0 & 0 & \Delta t & 0
0 & 0 & 1 & 0 & 0 & \Delta t
0 & 0 & 0 & 1 & 0 & 0
0 & 0 & 0 & 0 & 1 & 0
0 & 0 & 0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix} x_{k-1} \ y_{k-1} \ z_{k-1} \ u_{k-1} \ v_{k-1} \ w_{k-1} \ \end{bmatrix} \tag{4}]


  • 위 매트릭스를 보면 각 축의 이전 스텝의 위치에서 시간 간격 \(\Delta t\)에 그 축의 속도 만큼 곱하여 이동 거리를 구하면 현재 스텝의 위치를 예측 할 수 있다는 것으로 해석할 수 있습니다.
  • 그러면 식을 간단하게 표현하기 위하여 다음과 같이 정리하겠습니다.


[x_{k} = \begin{bmatrix} p_{k} \ v_{k} \end{bmatrix}]


[x_{k} = F_{k} x_{k-1} \tag{5}]


(predict) Uncertainties 모델링


  • 앞의 과정에서 위치와 속도를 predict 하였는데 그럼에도 이 예측은 다소 확률적입니다. 왜냐하면 우리의 예측에 다소 불확실적인 요소(Uncertainties, 불확실성))들이 있기 때문입니다. 바로 노이즈 들입니다.
  • 여기서 다룰 노이즈는 시스템 내부적으로 발생할 수 있는 노이즈들 입니다. 예제로 다루는 것이 드론이기 때문에 드론 시스템 내부적으로 처리할 때에도 노이즈가 발생할 수 있어서 그것을 고려하는 것이지요.
  • 이 글에서 이후에 시스템 외부적으로 발생할 수 있는 노이즈도 고려할 예정입니다. 그래서 여기서 다루는 노이즈는 시스템 내부적으로 발생하는 노이즈 임을 기억해야합니다.
  • 노이즈 같은 불확실성은 주로 가우시안 분포를 이용하여 모델링 됩니다. (가우시안 분포에는 평균 \(\mu\)와 분산 \(\Sigma\)가 있습니다.)
  • 먼저 드론의 예에서 상태 벡터는 6개의 요소를 가지고 있습니다. 세개는 속도였고 세개는 위치였습니다.
  • 이 경우에 (6 x 1)의 평균 벡터와 (6 x 6)의 공분산 행렬다변량 가우시안 분포를 이용하여 모델링 해야 합니다.
    • 여기서 (6 x 1) 의 분산 벡터를 사용하지 않고 (6 x 6) 크기의 공분산 행렬을 사용하는 이유는 correlation을 고려하기 위해서 입니다.
    • 예를 들어 \(x\)차원의 위치는 \(x\) 차원의 속도와 correlation이 있는데 공분산 행렬의 대각선 이외의 요소가 이런 correlation 관계를 캡쳐합니다.


  • 앞에서 다루었듯이 \(x_{k}\)를 predict 하는 방법은 확인하였는데 공분산 행렬 \(P_{k}\)는 어떻게 predict하면 될까요?
  • 공분산 행렬의 성질에 따라서 랜덤 확률 변수 \(y\)가 공분산 \(\Sigma\)를 가질 때, 랜덤 확률 변수 \(y\)에 임의의 행렬 \(A\)를 곱하여 \(Ay\)를 만든다면 공분산 행렬은 \(A\Sigma A^{T}\)가 됩니다. (이유는 링크에서 참조 하시기 바랍니다.)
  • 따라서 이 논리에 따라 \(P_{k} = F_{K} P_{k-1} F_{k}^{T} \tag{6}\)로 업데이트 될 수 있습니다.
  • 여기 까지 정리하면 predict하는 방법은 다음과 같습니다.


[x_{k} = F_{k} x_{k-1}]


[P_{k} = F_{K} P_{k-1} F_{k}^{T}]


(predict) Control Input (optional)


  • 여기 까지 식 (5), (6)의 이전 스텝의 상태를 이용하여 드론의 위치와 속도를 predict하는 방법 까지 다루었습니다.
  • 추가적으로 드론의 상태는 control input의 영향을 받을 수 있습니다. (이 내용은 앞으로 할 예제에서는 무시할 것이므로 스킵하셔도 됩니다.)
  • 예를 들어, 드론의 주행 코스를 수정하기 위해 수행된 몇 가지 내부 계산을 바탕으로 드론이 특정 방향으로 더 이동하려고 할 수 있습니다. 즉 특정 방향에 대한 가속도가 더 붙는 것이지요.
  • 이런 external control을 벡터 \(u_{k}\)로 나타내면 (5) 번 식에 다음과 같이 추가적으로 모델링 할 수 있습니다.


[x_{k} = F_{x}x_{k-1} + B_{k}u_{k} \tag{7}]


  • 위 식에서 \(B_{k}\)를 Control Matrix 라고 합니다. 이 행렬은 벡터 \(u_{k}\)와 연산되어 상태 \(x_{k}\)에 영향을 주게 됩니다.
  • 예를 들어 \(u_{k}\)가 3D 방향으로의 가속도라고 한다면 물리의 가속도 법칙에 의하여 Control Matrix는 다음과 같이 모델링할 수 있습니다.


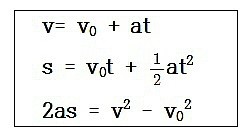
Drawing


[\begin{bmatrix}

\frac{ (\Delta t)^{2} }{2} & 0 & 0
0 & \frac{ (\Delta t)^{2} }{2} & 0
0 & 0 & \frac{ (\Delta t)^{2} }{2}
\Delta t & 0 & 0
0 & \Delta t & 0
0 & 0 & \Delta t

\end{bmatrix}]


(predict) Uncontrolled uncertainties


  • 여기 까지 과정을 보면 이전 스텝의 상태와 의도적인 control input에 의하여 \(x_{k}\)와 \(P_{k}\)를 모델링 할 수 있었습니다.
  • 여기서 한가지 더 추가해야 할 것은 시스템과 전혀 상관 없는 노이즈 입니다. 앞에서 살짝 언급하였지만 앞에서 연산한 \(P_{k}\)는 시스템 내부적인 노이즈 까지만 고려된 것입니다.
  • 예를 들어 드론이 운행중에 갑작스런 강풍을 만났다면, 그건 드론 시스템과는 전혀 무관하지만 외부적으로 노이즈가 발생한 것이라고 보아야 합니다.
  • 여기서도 노이즈는 가우시안 분포로 모델링 할 것입니다. 평균이 0인 가우시안 분포의 노이즈를 가지는 공분산 \(Q_{k}\)를 추가해 보겠습니다.


[\tag{9} x_{k} = F_{k} x_{k-1} + B_{k}u_{k}
P_{k} = F_{K} P_{k-1} F_{k}^{T} + Q_{k}\]


  • 여기까지가, predict 를 위한 과정이었습니다.



(update) Measurements


  • 앞의 predict 과정에서는 시스템의 이전 상태와 control input에 관하여 다루었습니다.
  • 이번에 다룰 것은 update 과정입니다. 간단하게 말하면 실제 센서를 통하여 계측한 값을 앞에서 predict한 값과 퓨젼하는 작업입니다.
  • 상식적으로 이 작업이 필요한 것이 predict 만을 이용하여 거리와 속도를 확정 짓는 것은 다소 위험이 있어 보이고 반면 오직 센서값만을 이용하는 것도 센서에 노이즈가 작용할 수 있기 때문에 어느 하나를 사용한다기 보다는 양쪽을 모두 반영한 값을 찾는것이 합당해 보입니다.
  • predict 과정에서 확인한 것이 위치 와 속도 였습니다.
  • GPS에서 확인할 수 있는 것은 위치입니다. GPS 즉, 센서값을 통하여 얻은 위치 벡터를 \(z_{k}\)라고 가정해 보겠습니다.
  • 이 위치 벡터 \(z_{k}\) 또한 불확실성을 가지고 있으므로 이것을 행렬 \(R_{k}\)로 반영해 보겠습니다.
  • 그러면 앞에서 말할 것과 같이 predict과정의 결과와 센서값의 결과를 잘 조합해야 하는데 센서값에는 속도 성분이 없습니다.
  • 따라서 predict에서 위치 성분만 관측이 필요하므로 위치 성분만 가져오도록 하겠습니다.
  • 이 때 사용되는 것이 Observation Matrix인 \(H_{k}\) 입니다. 즉, 말 그대로 관측할 대상만 가져오는 행렬입니다.


[H_{k} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0
0 & 1 & 0 & 0 & 0 & 0
0 & 0 & 1 & 0 & 0 & 0
\end{bmatrix}]


  • 이 행렬은 현재 상태(위치 + 속도) 공간을 관측 상태(위치) 공간으로 mapping 해주는 선형변환 역할을 하는 행렬입니다.
  • 따라서 \(H_{k}x_{k}\) 와 \(z_{k}\)는 비교할 수 있는 상태가 되었습니다.
  • 여기서 \(H_{k}x_{k}\)의 공분산을 계산하면 어떻게 될까요? 앞에서 \(x_{k}\)의 공분산을 \(P_{k}\)라고 정의하였고 앞에서도 다룬 행렬 연산 과정을 통하여 \(H_{k}P_{k}H_{k}^{T}\)가 됩니다. (위에서도 똑같은 것을 다루었죠?)


(update) Fusing information


  • 먼저 정보를 퓨전 하는 방법에 대하여 알아보도록 하겠습니다. 여기서 말하는 정보는 확률분포를 말한다고 생각하시면 됩니다.
  • 예를 2개의 온도 센서가 있다고 가정해 보겠습니다.


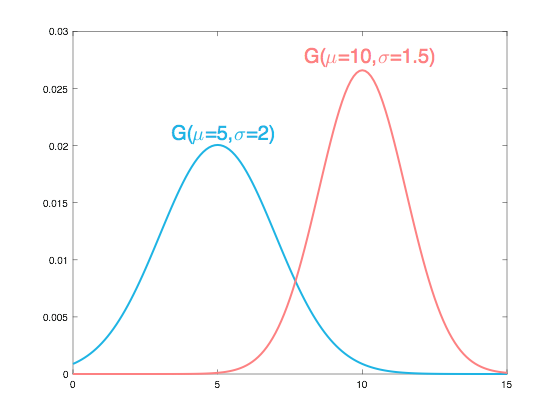
Drawing


  • 위 그림의 파란색 분포가 나타나는 센서보다 빨간색 분포가 나타나는 센서가 좀 더 신뢰도가 높다고 가정해 보겠습니다.
  • 수치적으로도 그렇게 나오는 것이 파란색 센서는 평균 5도에 표준 편차가 2입니다. 반면 빨간색 센서는 평균 10도에 표준 편차가 1.5 입니다.
  • 표준편차가 더 작은 빨간색 센서가 좀 더 신뢰도가 높다고 판단할 수 있죠.
  • 여기서 어떤 센서 하나를 따른다기 보다는 두 센서 모두를 참조해서 가장 합당한 결론을 내리는 것이 좋아보입니다.
  • 위 두 분포 모두 가우시안 분포이고 이와 같은 문제에서는 두 분포를 모두 만족시키는 가우시안 분포의 교집합을 찾으면 됩니다.
  • 이 때에는 가우시안 분포의 곱을 통하여 두 가우시안 분포의 교집합을 찾을 수 있습니다.
    • 참고로 가우시안 분포의 곱은 가우시안 분포로 도출됩니다.
    • 참조 : https://gaussian37.github.io/math-pb-product_convolution_gaussian_pdf/


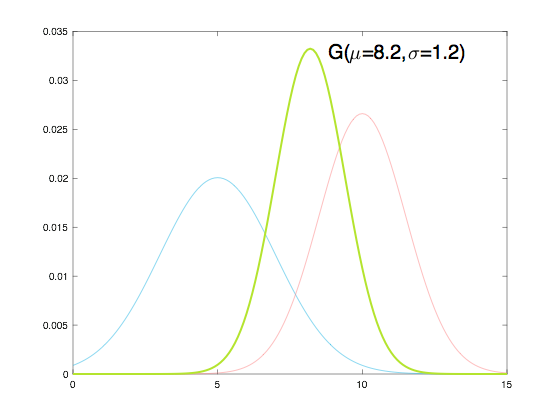
Drawing


  • 따라서 두 가우시안 분포의 곱을 통해서 얻은 결과는 위 그래프와 같이 초록색 가우시안 분포를 얻을 수 있습니다.
    • 초록색 가우시안 분포는 파란색과 빨간색 가우시안 분포를 곱한 다음에 정규화를 해주어 초록색 곡선 아래 영역 전체의 합이 1이 되도록 해준 결과입니다.


  • 그러면 다시 드론의 예로 다시 접목시켜 보겠습니다. 먼저 앞에서 거쳐온 과정을 보면 다음과 같습니다.
  • prediction \(H_{k}x_{k}\)와 공분산 행렬 \(H_{k}P_{k}H_{k}^{T}\)
  • measurement \(z_{k}\)와 공분산 \(R_{k}\)
  • 앞에서 온도 센서 2개를 가우시안 곱을 통하여 합친 것 처렴 prediction과 measurement를 합치는 과정을 update 라고합니다.
  • 자세한 update 과정은 링크를 참조하시기 바랍니다.
  • update 결과는 다음과 같습니다.


[\hat{x}{k} = x{k} + K(z_{k} - H_{k}x_{k}) \tag{10}]


[\hat{P}{k} = P{k} - KH_{k}P_{k}]


[K = P_{k}H_{k}^{T}(H_{k}P_{k}H_{k}^{T} + R_{k})^{-1} \tag{11}]


  • 지금까지 다룬 것을 모두 정리하면 칼만 필터는 1) 시스템 로직, 2) 컨트롤 인풋과 독립적인 센서값의 퓨젼을 통하여 시스템 내부를 tracking 하는 방법입니다.
  • Predict : Prediction은 시스템 로직 과 컨트롤 인풋을 통하여 만들어 집니다. (Equation 9번 참조)
  • Update : Update는 measurement값을 prediction에 반영하여 만들어 집니다. (Equation 10번 참조)


opencv의 칼만 필터 함수 설명


  • opencv에서 제공하는 칼만 필터 함수는 앞에서 설명한 선형 칼만 필터를 구현합니다.
  • 앞에서 쭉 설명한 것과 같이 이동 물체의 status 모델과 measurement에 의해 표현되었습니다.
  • 지금 부터 설명하는 내용은 opencv 문서 및 관련 책을 참조 하여 식의 기호가 조금 달라지는데 내용은 달라지는 게 없으니 참조하여 보시면 되겠습니다.


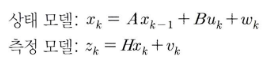
Drawing


  • 여기서 k는 이산 시간 (discrete-time)변수이면, k = 0, 1, 2, …이 됩니다.


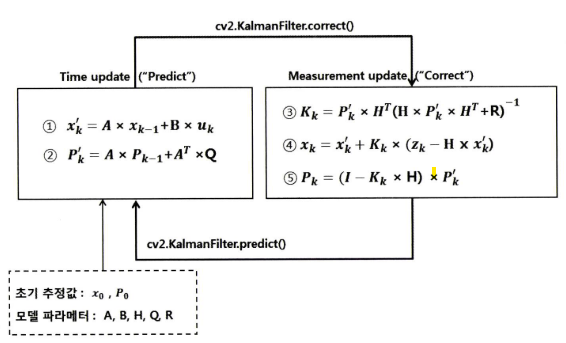
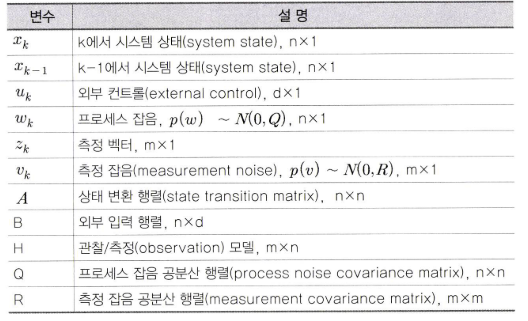
Drawing


Drawing


  • opencv의 칼만 필터 함수와 칼만 필터 과정을 연결해서 표현하면 위 state diagram과 같습니다.
  • 위 표를 보면 칼만 필터에서 사용하는 함수는 크게 2개인 predict와 correct가 있습니다.
  • 그러면 객체를 생성하는 함수, predict 그리고 correct에 대하여 살펴보면 선형 칼만 필터를 쉽게 사용할 수 있습니다.


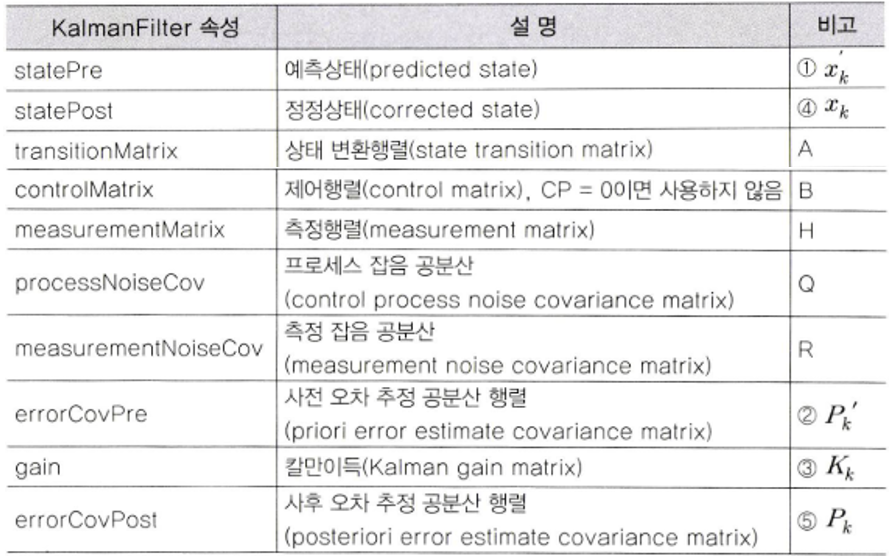
Drawing


  • 먼저 cv2.KalmanFilter 클래스를 설명하기 위해 위 테이블의 내용을 참조해서 설명해 보겠습니다.
  • cv2.KalmanFilter(state 벡터의 차원, measurement 벡터의 차원, control 벡터의 차원)
    • 칼만 필터 클래스 객체를 생성합니다.
    • 추가적으로 생성되는 행렬의 타입을 지정할 수 있습니다. cv2.cv_32F 또는 cv2.CV_64F 입니다.
  • retval = cv2.KalmanFilter.predict(control 벡터(옵션))
    • 칼만 필터의 예측 상태(predicted state)인 \(x'_{k}\) statePre를 반환합니다.
    • control은 외부 컨트롤 벡터인 \(u_{k}\)를 뜻합니다. 없으면 입력하지 않아도 됩니다.
  • retval = cv2.KalmanFilter.correct(measurement)
    • measurement를 사용하여 상태를 정정하고 \(x_{k}\) statePost를 반환합니다.


opencv의 칼만 필터 함수 사용


마우스 위치 추적 구현


Twitter Facebook Google+
# opencv # 칼만 필터 # kalman filter # tracking # 트래킹