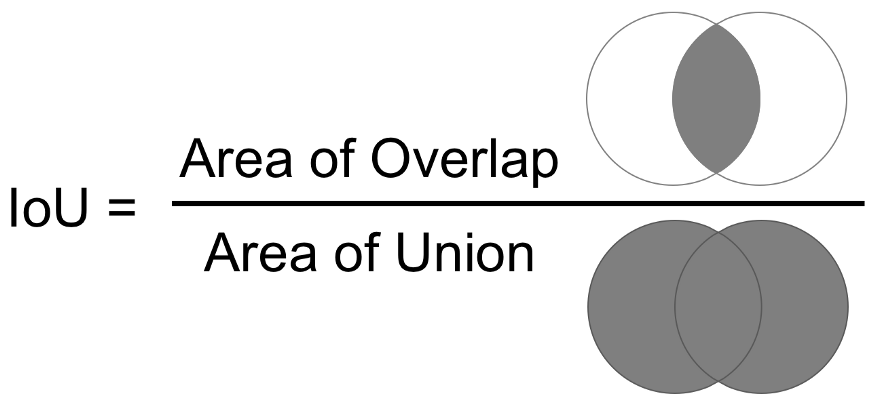
mIoU(Mean Intersection over Union) 계산

2020, Sep 07    

Segmentaion 관련 글 목록

• 참조 : https://medium.com/@cyborg.team.nitr/miou-calculation-4875f918f4cb

목차

• 세그멘테이션 데이터

• 1. 각 클래스 별 빈도수 카운트

• 2. 행렬을 벡터로 변환

• 3. 카테고리 행렬 생성

• 4. confusion matrix 생성

• 5. 클래스 별 IoU 계산

• 6. mIoU 계산

세그멘테이션 데이터

• 이번 글에서는 Semantic Segmentation에서 사용하는 대표적인 성능 측정 방법인 mIoU를 계산하는 방법에 대하여 다루어 보도록 하겠습니다.
• 특히 대부분의 문제에서 다루는 Multiple-class 기반의 Semantic Segmentation의 mIoU를 어떻게 계산하는 지 살펴보겠습니다.

• 먼저 mIoU를 계산하기 위해서는 2 종류의 매트릭스가 필요합니다. 첫번째는 GT(Ground Truth)에 해당하는 매트릭스이며 두번째는 segmentation을 거쳐서 나온 prediction 입니다.

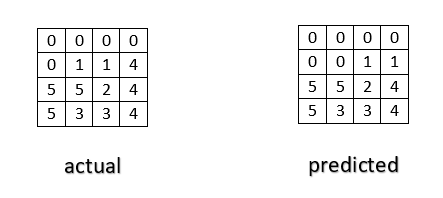
• 위 그림에서 actual이 Ground Truth에 해당하며 각 픽셀의 실제 클래스에 해당합니다.
• 반면 predicted는 위에서 설명한 prediction에 해당합니다.
• 위 데이터의 총 픽셀 수는 4 x 4 = 16개 이고 클래스의 갯수는 0 ~ 5 까지 총 6개 입니다.
• 그러면 아래 5단계 스텝을 따라서 mIoU를 계산해 보도록 하겠습니다.

1. 각 클래스 별 빈도수 카운트

• 먼저 actual 테이블과 predicted 테이블에 각 클래스 별 빈도수를 구합니다.
• numpy의 bincount 함수를 사용하면 쉽게 구현할 수 있습니다.

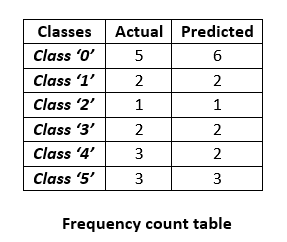
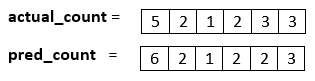
• 앞에서 보인 actual, predicted 테이블의 각 클래스 별 빈도수를 구하면 위와 같이 정리할 수 있습니다.

2. 행렬을 벡터로 변환

• 그 다음 actual, predicted 행렬을 1D 벡터로 변환합니다.

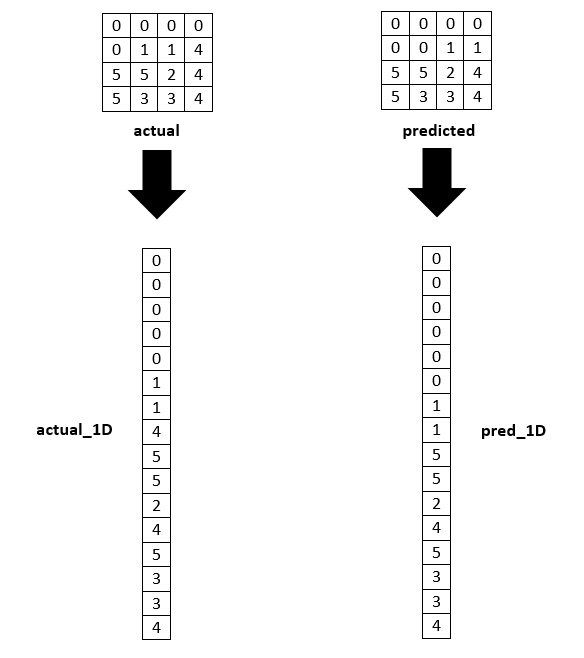
3. 카테고리 행렬 생성

• 이 때, 각 (actual 픽셀, predicted 픽셀) 쌍이 가질 수 있는 경우의 수는 36가지 입니다. 왜냐하면 현재 데이터에서 클래스의 갯수가 6개 이기 때문에 6 x 6 = 36 이기 때문입니다.
• 이 데이터를 카테고리로 분류하려고 합니다. 카테고리는 (actual 클래스 - predict 클래스)로 나뉘어 집니다. 따라서 위 예제에서는 36개의 카테고리로 나뉘어집니다.
• 가능한 카테고리는 (actual : 0, predict : 0) ~ (actual : 5, predict : 5)가 됩니다.
• 예를 들어 위 그림에서 6번째 픽셀은 actual 에서는 1이지만 predict 에서는 0입니다. 따라서 카테고리 ‘1-0’이 됩니다.
• 여기서 카테고리 (0, 0)을 0번 카테고리 (0, 1)을 1번 카테고리 마지막으로 (5, 5)를 36번 카테고리 라고 지칭하겠습니다.

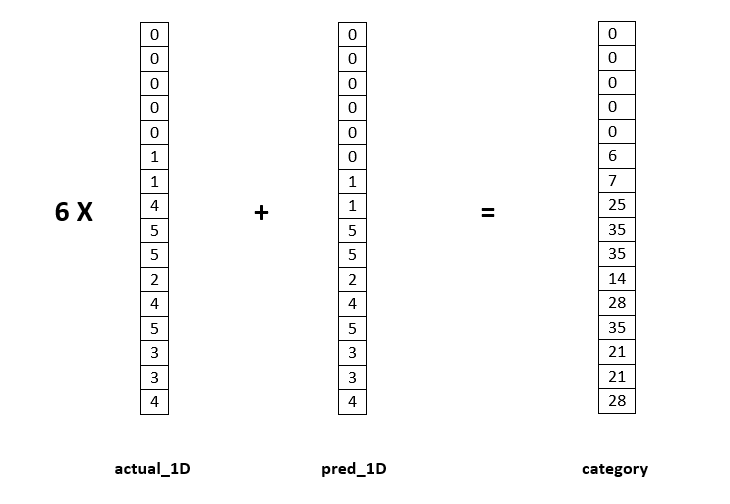
• actual 벡터와 predict 벡터를 이용하여 몇 번째 카테고리에 속하는 지 확인하는 방법은 위 그림과 같습니다. 식으로 나타내면 다음과 같습니다.

• \[\text{Category} = (\text{number of classes} \times \text{actual 1D vector}) + \text{pred 1D vector}\]

• ex1) actual이 0이고 pred가 0이면 카테고리는 1입니다. (1번 픽셀)
• ex2) actual이 1이고 pred가 1이면 카테고리는 6*1 + 1 = 7 입니다. (7번 픽셀)
• ex3) actual이 5이고 pred가 5이면 카테고리는 6*5 + 5 = 25 입니다. (9번 픽셀)

4. confusion matrix 생성

• confusion matrix는 정사각 행렬이며 각 행과 열의 크기는 클래스의 갯수와 같습니다. 즉, (class의 갯수, class의 갯수)의 크기를 가집니다.
• confusion matrix 각 원소의 값은 해당 카테고리의 갯수와 같습니다.

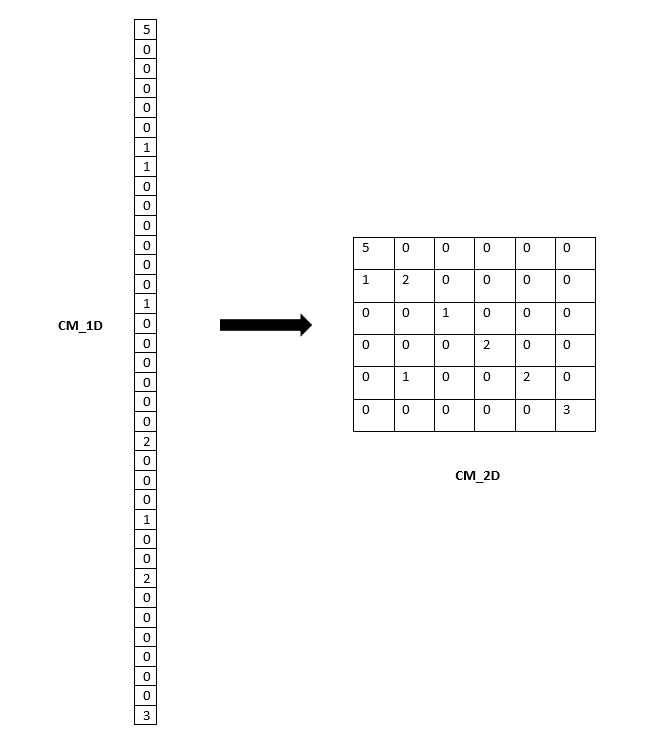
• 위 그림의 벡터의 첫번째 원소는 5 입니다. 즉, 0번째 카테고리인 (actual 0, pred 0)의 갯수가 5개라는 뜻입니다.
• 벡터의 마지막 원소는 3입니다. 이 경우는 (actual 5, pred 5)의 갯수가 3개라는 뜻입니다.
• 위와 같이 카테고리 별 벡터를 만든 다음에 class의 갯수 만큼 잘라서 행렬을 쌓아나가면 confusion matrix를 만들 수 있습니다.
• confusion matrix에서 대각 성분은 actual과 pred가 모두 일치하는 경우입니다. 대각 성분 이외의 성분은 actual과 pred가 불일치 하는 경우입니다.

5. 클래스 별 IoU 계산

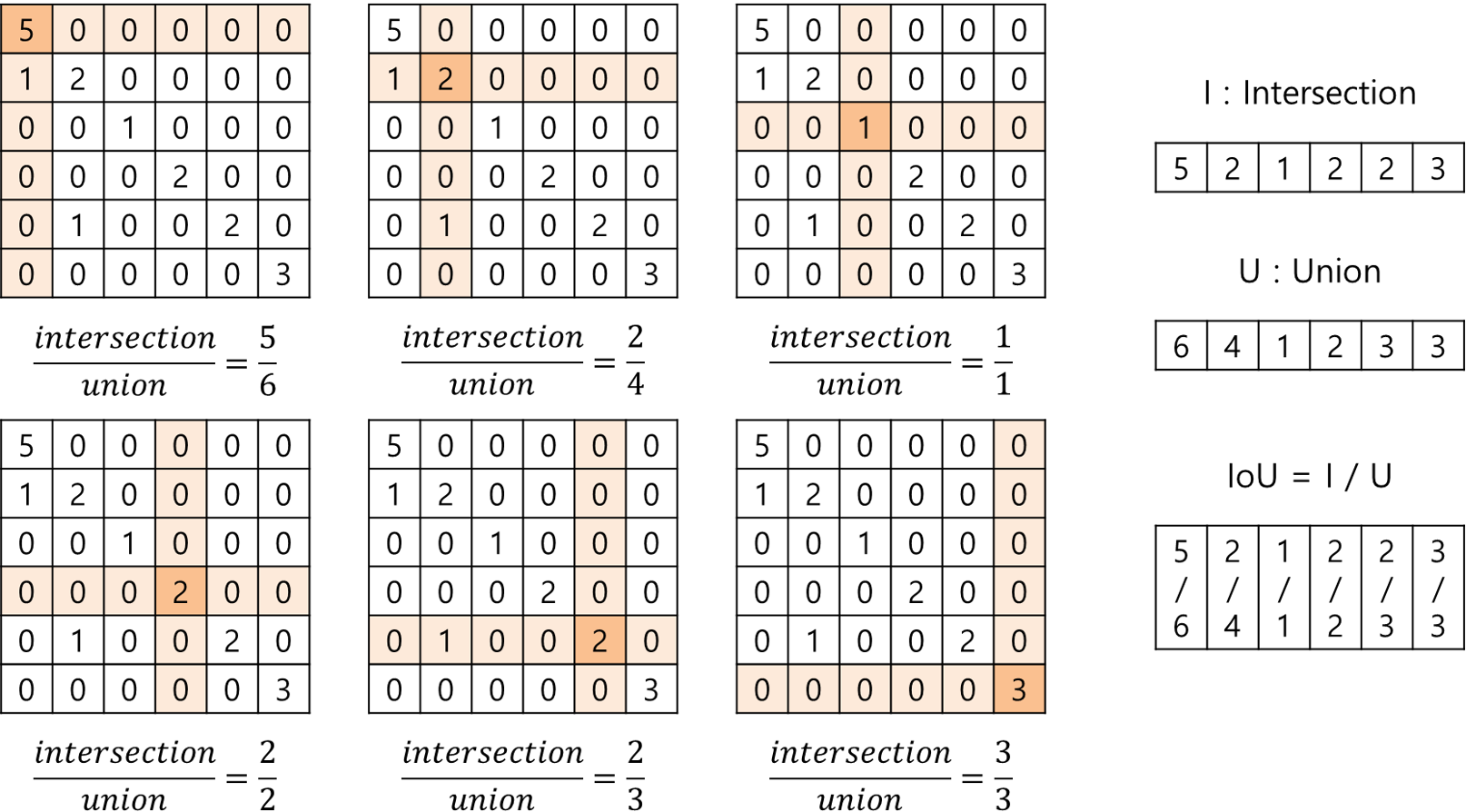
• 클래스 별 IoU를 계산하기 위해 confusion matrix를 위와 같이 만들어서 intersection과 union을 구할 수 있습니다.

6. mIoU 계산

• 클래스 별 IoU 계산 결과를 평균을 내면 mIoU를 구할 수 있습니다.
• 위 예제를 기준으로 mIoU는 \((0.8333 + 0.5 + 1 + 1 + 0.6667 + 1) / 6 = 0.8333\)이 됩니다.
• 계산을 할 때, 한번도 발생하지 않은 케이스는 Union이 0이기 때문에 무한대로 발산할 수 있습니다. 이 값을 Nan값으로 처리를 하고 Nan 값은 평균 계산 시 제외하도록 해야 합니다. 이 방법을 통해 안전하게 mIoU를 구할 수 있습니다.

Segmentaion 관련 글 목록