선형 칼만 필터의 원리 이해

2019, Nov 07    

• 선수 지식 : 베이즈 필터
• 칼만 필터의 뿌리는 베이즈 필터입니다. 즉, 칼만 필터 또한 베이지안 확률을 이용한 필터라고 말할 수 있습니다. 특히, 베이즈 필터의 문제점인 적분 계산을 개선하기 위해 칼만 필터가 도입된 만큼 시간적 여유가 있으시면 베이즈 필터를 먼저 숙지하시길 추천드립니다.

• 참조: https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/#mathybits

• 이번 글에서는 선형 칼만 필터를 통하여 칼만 필터의 기본 컨셉에 대하여 자세하게 알아보도록 하겠습니다.

목차

• 1. 칼만 필터란 무엇일까?

• 2. 칼만 필터로 무엇을 할 수 있을까?

• 3. 어떻게 칼만필터가 문제를 다루는 지 살펴보자

• 4. 행렬을 통하여 문제 다루어 보기

• 5. 측정값으로 추정치 조정

• 6. 가우시안 결합

• 7. 앞에서 다룬 내용 종합

• 8. 칼만 필터 Flow

1. 칼만 필터란 무엇일까?

• 칼만 필터는 일부 동적 시스템에 대한 정보가 확실하지 않은 곳에서 사용할 수 있으며 시스템이 다음에 수행 할 작업에 대한 정확한 추측을 할 수 있습니다.
• 칼만 필터는 센서를 통해 추측한 움직임에 노이즈가 들어오더라도 노이즈 제거에 좋은 역할을 합니다.
• 칼만 필터는 지속적으로 변화하는 시스템에 이상적입니다. 왜냐하면 어떤 연산 환경에서는 메모리가 부족할 수 있는데 칼만 필터에서는 이전 상태 이외의 기록을 유지할 필요가 없기 때문입니다.
• 또한 연산 과정 또한 빠르기 때문에 실시간 문제 및 임베디드 시스템에 적합합니다.
• 이 글에서 살펴볼 Linear 칼만 필터는 기본적인 확률과 행렬에 대한 지식만 있으면 이해 가능합니다. 여기까지 읽고 관심이 있으시면 아래 내용을 한번 살펴보시기 바랍니다.

2. 칼만 필터로 무엇을 할 수 있을까?

• 먼저 칼만 필터로 어떤것을 할 수 있는 지 한번 살펴보겠습니다.
• 만약 어떤 로봇이 있고 로봇이 이동하기 위해서는 어디에 있는지 정확히 알아야합니다.
• 그러면 로봇의 위치를 어떻게 나타낼 것인지 먼저 정해보겠습니다.
  • 로봇의 상태를 $\vec{x_{k}} = (\vec{p}, \vec{v})$ 이라고 정의하겠습니다.
  • 여기서 $\vec{p}$는 위치이고 $\vec{v}$는 속도입니다.
• 이 예에서는 위치와 속도이지만 탱크의 유체 양, 자동차 엔진의 온도, 터치 패드에서 사용자의 손가락 위치 또는 추적해야 할 여러 항목에 대한 데이터 일 수 있습니다.
• 만약 이 로봇의 GPS 센서의 정확도가 약 10m라고 가정해 보겠습니다. 만약 이 GPS 센서만을 이용하여 이동을 한다면 정확하게 움직일 수 있을까요? 아마도 절벽에 떨어질 수도 있을 것입니다.
• 따라서 GPS라는 센서만으로 위치를 파악하기에는 충분하지가 않습니다. 이것을 좀 더 개선을 해야하는데, 개선점을 칼만 필터를 통해서 찾아보겠습니다.

3. 어떻게 칼만필터가 문제를 다루는 지 살펴보자

• 먼저 어떤 로봇의 상태부터 정의해 보도록 하겠습니다.

• $$\vec{x} = \begin{bmatrix} p\\ v \end{bmatrix}$$

• 여기서 $p$는 위치를 나타내고 $v$는 속도를 나타냅니다.
• 이 때, 위치와 속도를 정확하게 알아내기는 어렵습니다. 대신 실제 속도와 위치가 어떤 범위안에 속할 것이라는 것 정도는 예측할 수 있습니다.

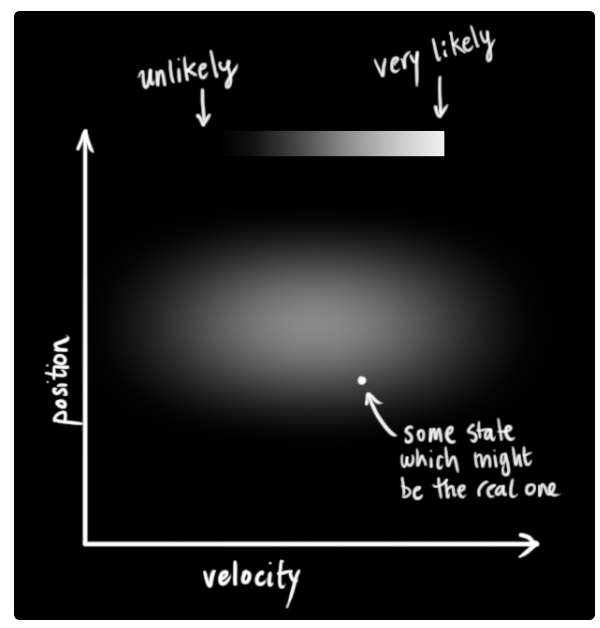
• 칼만 필터에서는 위치와 속도 두 변수를 랜덤 가우시안 분포로 가정합니다.
• 각 변수는 평균과 분산의 특성을 가지고 있습니다. 평균 $\mu$는 랜덤 분포의 중심이 되고 분산 $\sigma^{2}$은 불확실성(uncertainty)가 됩니다.

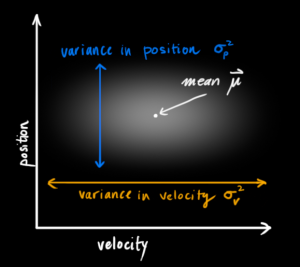
• 위 그래프를 보면 가로축은 속도이고 세로 축은 위치 입니다.
• 가로축과 세로축의 가운데에 하얀 점이 있는데 그것은 평균 $\mu$ 라고 하고 그 중심을 기준으로 분포가 되어 있음을 알 수 있습니다.
• 이 때, 가로축은 속도이므로 속도의 분산에 의해 분포가 되어 있고 세로축은 위치이므로 위치의 분산에 의해 분포가 되어 있습니다.
• 그런데 분포의 패턴을 보면 가로축으로만 넓게 분포되어 있고 세로축으로는 넓게 분포되어 있지 않습니다.
• 중요한 것은 가로축이 증가하면 세로축이 증가한는 등의 상관관계가 없다는 것에 있습니다.
  • 즉, uncorrelated 하다고 말할 수 있습니다.

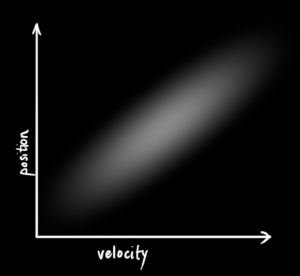
• 반면에 위 예시는 좀 더 재밌는데요, 위치와 속도가 서로 상관관계를 가지는 것으로 보입니다. 즉, correlated 합니다.

• 이런 경우에는 특정 위치를 관측하는 것이 특정 속도와 연관이 있다고 해석할 수도 있습니다.

• 사실 현실 세계에서도 위치와 속도의 관계를 보면 이와 유사한 관계를 가지고 있습니다.
  • 예를 들어 속도가 높으면 더 멀리까지 이동할 수 있고 속도가 느리면 그리 멀리 가지 못하는 것과 같습니다.
• 이러한 관계를 주목하는 것이 상당히 중요한데, 왜냐하면 이런 관계를 파악하게 되면 더 많은 정보를 얻을 수 있기 때문입니다.
  • 앞선 위치와 속도 관계와 같이 한 가지를 측정하게 되면 다른 값이 어떻게 나오게 되는 지 예측 할 수 있는 것과 같습니다.
• 이러한 관계를 파악하는 것이 칼만 필터의 한가지 목적이 됩니다.
• 불확실환 관측으로 부터 가능한한 더 많은 정보를 얻어내는 것이 우리의 목적입니다.

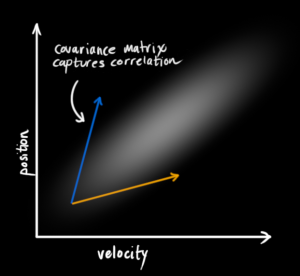
• 이러한 상관관계는 covariance matrix, 공분산을 통하여 정의될 수 있습니다.
• 공분산에서 각각의 원소 $\Sigma_{ij}$는 $i$번 째 상태 변수와 $j$ 번째 상태 변수의 상관관계를 나타냅니다.
  • 당연히 i,j 와의 관계와 j,i와의 관계는 같기 때문에 공분산 행렬은 대칭행렬이 됩니다.

4. 행렬을 통하여 문제 다루어 보기

• 앞에서 다룬 내용들을 이제 가우시안을 통하여 한번 모델링 해보려고 합니다.
• 먼저 $k$번째 타임에 필요한 정보는 2가지 입니다. 최적의 예측치라고 가정하는 $\hat{x_{k}}$ (앞에서 설명한 평균 $\mu$에 해당)과 공분산 행렬 $P_{k}$에 해당합니다.

• $$\begin{equation} \label{eq:statevars} \begin{aligned} \mathbf{\hat{x}}_k &= \begin{bmatrix} \text{position}\\ \text{velocity} \end{bmatrix}\\ \mathbf{P}_k &= \begin{bmatrix} \Sigma_{pp} & \Sigma_{pv} \\ \Sigma_{vp} & \Sigma_{vv} \\ \end{bmatrix} \end{aligned} \end{equation}$$

• 물론 여기에서는 간단하게 위치와 속도만 사용하고 있습니다. 하지만 어떤 상태를 모델링 하느냐에 따라서 어떤 변수가 추가될 지는 상황에 따라 다릅니다.

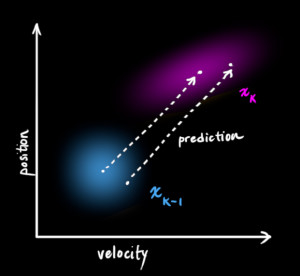
• 현재 상태가 (k - 1) 번째 상태라고 가정하고 그 다음 상태인 k번째 상태를 예측해보려고 합니다.
• 기억할 것은 우리는 어떤 상태가 진짜인지는 모르지만 예측 함수를 통하여 새로운 상태(k-1 → k)를 예측한다는 것입니다.

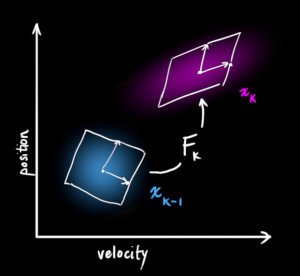
• 이렇게 상태 예측을 하는 것을 보면 공간 상에서 상태를 변환하는 것 처럼 볼 수 있습니다.

• 공간 상에서의 변환은 행렬을 통하여 나타낼 수 있습니다. 그러면 k-1 번째 상태에서 k 번째 상태로 변환하는 행렬을 $F_{k}$ 라고 두겠습니다.

• 다음 상태의 위치와 속도를 예측하기 위하여 행렬을 어떻게 사용하면 될까요?
• 이렇게 행렬을 만드는 모델링 작업을 할 때 필요한 것이 운동 방정식과 같은 기존의 알려진 물리 방정식들 입니다.

• $$\begin{split} \color{deeppink}{p_k} &= \color{royalblue}{p_{k-1}} + \Delta t &\color{royalblue}{v_{k-1}} \\ \color{deeppink}{v_k} &= &\color{royalblue}{v_{k-1}} \end{split}$$

• 다르게 표현하면 다음과 같습니다.

• $$\begin{align} \color{deeppink}{\mathbf{\hat{x}}_k} &= \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} \color{royalblue}{\mathbf{\hat{x}}_{k-1}} \\ &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} \label{statevars} \end{align}$$

• 여기서 적용된 식은 “거리 = 움직인 시간 x 속도” 입니다. 따라서 거리의 변화량을 표현할 때 이 식이 적용되었습니다.
• 현재 이 식에서 속도는 변화가 없는 등속 운동이라는 상황입니다.

• 여기 까지 살펴보면 운동 방정식을 통하여 prediction matrix인 $F_{k}$를 만들었습니다.
• 하지만 앞에서 살펴본 변수사이의 상관관계를 나타내는 공분산 행렬에 대해서는 아직 다루지 않았습니다.

• 만약 어떤 분포에 속하는 모든 점들을 행렬 $A$와 곱하게 하면 공분산 행렬 $\Sigma$는 어떻게 될까요?
• 이것을 살펴 보기에 앞서 다음 식을 한번 살펴보도록 하겠습니다.

• $$\begin{equation} \begin{split} Cov(x) &= \Sigma\\ Cov(\color{firebrick}{\mathbf{A}}x) &= \color{firebrick}{\mathbf{A}} \Sigma \color{firebrick}{\mathbf{A}}^T \end{split} \label{covident} \end{equation}$$

• 이 식에 대한 자세한 전개 내용은 다음과 같습니다. 단순히 계산적인 측면이니 스킵하셔도 무방합니다. 단 결과는 일단 숙지하고 적용해 보도록 하겠습니다.
• 그럼 여기서부터 식을 한번 전개해 보도록 하겠습니다.
• 일반적으로 ${\rm COV}[x]$은 $\mathbb{E}[(x - \mathbb{E}[x])(x - \mathbb{E}[x])^T]$으로 정의됩니다.
• 이 식을 이용하여 ${\rm COV}[A x]$을 전개하면 아래와 같습니다.

• $$\begin{align}{\rm COV}[A x] & = \mathbb{E}[(Ax - \mathbb{E}[Ax])(Ax - \mathbb{E}[Ax])^T] \\ & = \mathbb{E}[(Ax - A\mathbb{E}[x])(Ax - A\mathbb{E}[x])^T ]\\ & = \mathbb{E}[A(x - \mathbb{E}[x])(x - \mathbb{E}[x])^T A^T ] \\ & = A \mathbb{E}[(x - \mathbb{E}[x])(x - \mathbb{E}[x])^T ]A^T \\ & = A {\rm COV}[x] A^T \\ \end{align}$$

• 앞에서 설명한 다음 두 식을 조합해 보겠습니다.

• $$\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} \\ \color{deeppink}{\mathbf{P}_k} &= \mathbf{F_k} \color{royalblue}{\mathbf{P}_{k-1}} \mathbf{F}_k^T \end{split} \end{equation}$$

external influence

• 여기서 더 추가해야 할 것이 있습니다. 그것은 현재 시스템에 영향을 끼칠 수 있는 요소들 입니다.
• 예를 들어 자동차나 로봇 같은 경우에 이동 중에 가속도가 붙고 있기 때문에 단순히 (현재 속도 x 이동 시간)만큼만 더 이동하지 않고 가속도 만큼 더 반영 되어 이동하게 됩니다.
• 물론 속도 또한 가속도가 반영되어 변경되게 됩니다.
• 물리 시간에 많이 사용하였듯이 가속도를 $a$라고 한번 표현해 보겠습니다. 그러면 다음과 같이 표현할 수 있습니다.

• $$\begin{split} \color{deeppink}{p_k} &= \color{royalblue}{p_{k-1}} + {\Delta t} &\color{royalblue}{v_{k-1}} + &\frac{1}{2} \color{darkorange}{a} {\Delta t}^2 \\ \color{deeppink}{v_k} &= &\color{royalblue}{v_{k-1}} + & \color{darkorange}{a} {\Delta t} \end{split}$$

• 이것을 행렬 형태로 한번 나타내 보겠습니다.

• $$\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} + \begin{bmatrix} \frac{\Delta t^2}{2} \\ \Delta t \end{bmatrix} \color{darkorange}{a} \\ &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} + \mathbf{B}_k \color{darkorange}{\vec{\mathbf{u}_k}} \end{split} \end{equation}$$

• 여기서 $B_{k}$는 control matrix라고 하고 $\color{darkorange}{\vec{\mathbf{u}_k}}$ 은 control vector라고 합니다.
• 만약 다루고 있는 시스템이 간단하여 외부 영향이 없다면 이 부분을 생략해도 됩니다. 즉, 모델링에 따라 적용할 수 있고 적용 안할 수도 있습니다.

external uncertainty

• 만약 시스템이 모델링한 대로 움직이지 않으면 어떻게 될까요?
• 로봇의 경우에 갑자기 미끄러질수도 있고 드론의 경우 갑작스럽게 강한 바람에 맞닥뜨릴수도 있습니다.
• 이런 경우에 우리는 정확하게 상태 추적을 하기 어렵습니다. 왜냐하면 이런 예외적인 상황 또는 외력에 대한 고려를 하지 않고 모델링 하였기 떄문입니다.
• 정확하게 이런 예외적인 상태를 예측하기는 어렵더라도 이런 상황을 모델링에 접목해 보기 위하여 매번의 prediction 때 마다 새로운 uncertainty를 추가해 보도록 하겠습니다.

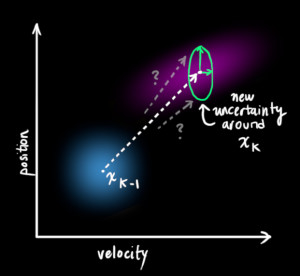
• 매 상태에서 기존의 estimate는 이제 특정 estimate가 아니라 범위를 가지는 estimate가 됩니다.
• 그러면 여기서 범위는 어떻게 될까요? uncertainty가 어떻게 발생할 지는 아무도 모릅니다. 이런 상황에서 우리는 가우시안 분포를 한번 사용해 보려고 합니다.
  • 왜냐하면 가우시안은 세상에서 발생하는 다양한 확률 분포에 대응될 수 있기 때문입니다. (중심 극한 이론)
  • 또한 가우시안은 계산 하기에도 상당히 용이한 측면이 있습니다.
• 그러면 $\color{royalblue}{\mathbf{\hat{x}}_{k}}$는 $\color{royalblue}{\mathbf{\hat{x}}_{k-1}}$ 에서 $\color{mediumaquamarine}{\mathbf{Q}_k}$ 공분산을 가지는 가우시안 분포의 범위를 가지는 영역으로 이동했다고 정의할 수 있습니다.
• 또는 공분산 $\color{mediumaquamarine}{\mathbf{Q}_k}$ 만큼의 노이즈가 있는 영역으로 $\color{royalblue}{\mathbf{\hat{x}}_{k-1}} \to \color{royalblue}{\mathbf{\hat{x}}_{k}}$가 이동했다고 보면 됩니다.

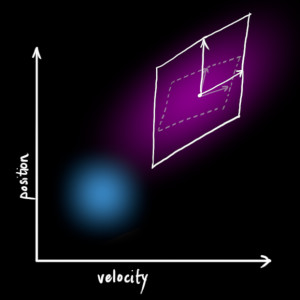
• 그러면 위 그림과 같이 noise가 추가된 prediction 영역을 구할 수 있습니다.
• 이것을 식으로 표현할 때에는 공분산을 기존의 식에서 더해주면 됩니다. 따라서 다음과 같이 식이 변형됩니다.

• $$\begin{equation} \begin{split} \color{deeppink}{\mathbf{\hat{x}}_k} &= \mathbf{F}_k \color{royalblue}{\mathbf{\hat{x}}_{k-1}} + \mathbf{B}_k \color{darkorange}{\vec{\mathbf{u}_k}} \\ \color{deeppink}{\mathbf{P}_k} &= \mathbf{F_k} \color{royalblue}{\mathbf{P}_{k-1}} \mathbf{F}_k^T + \color{mediumaquamarine}{\mathbf{Q}_k} \end{split} \label{kalpredictfull} \end{equation}$$

• 먼저 첫번째 식에 대해서 설명하겠습니다.
  • 여기서 $\color{deeppink}{\mathbf{\hat{x}}_k}$는 새로운 최고의 estimate이고 $\color{royalblue}{\mathbf{\hat{x}}_{k-1}}$는 이전의 최고의 estimate 입니다.
  • 여기에 $\color{darkorange}{\vec{\mathbf{u}_k}}$ 라는 알려져 있는 external influence 만큼 correction이 더해집니다.
• 그 다음으로 두번째 식에 대해서 설명하겠습니다.
  • 새로운 uncertainty인 $\color{deeppink}{\mathbf{P}_k}$는 이전의 uncertainty인 $\color{royalblue}{\mathbf{P}_{k-1}}$로 부터 도출되었고 거기에 외부로 부터의 uncertainty인 $\color{mediumaquamarine}{\mathbf{Q}_k}$ 가 추가된 형태입니다.
  • 즉, uncertainty가 시스템 내부에서도 존재하고 시스템 외부에서도 존재한다는 것을 기억해야 합니다.

5. 측정값(measurement)으로 추정치(estimate) 조정

• 시스템의 상태에 관하여 여러가지 정보를 주는 센서들이 여러개가 있습니다.
• 예를 들어 여러가지 센서 중 하나는 위치(position)을 읽을 것이고 또 다른 하나는 속도(velocity)를 읽을 것입니다.
• 각각의 센서는 시스템의 상태에 관하여 알려줄 때, 그 센서 또한 상태 상에서 동작한다는 것을 전제로 삼고 그 상태 상에서 읽은 것을 알려주게 됩니다.

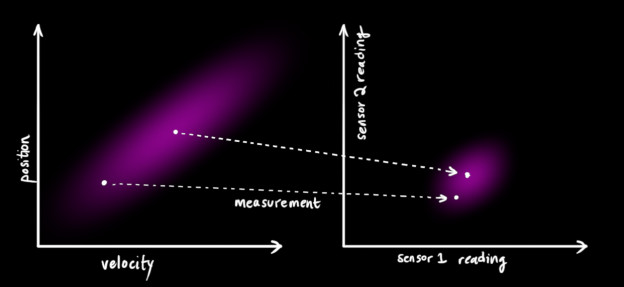
• 위 그래프의 왼쪽은 앞에서 계산한 속도와 위치 관계에 대한 prediction 입니다.
• 반면 오른쪽 그래프는 실제 센서를 통하여 읽어들인 속도와 위치 관계 입니다.
• prediction도 실제 정확한 값이라고 할 수 없지만 센서를 통해 읽어들인 값도 항상 정확한 값이라고 할 수 없습니다. 센서에도 노이즈가 있으니까요.
• 아무튼 여기에서 보면 prediction과 센서값 간의 unit이나 scale의 차이가 있을 수 있으니 이것을 변환해 주는 작업이 필요해 보입니다. prediction을 센서로 변환하기 위한 행렬로 $\mathbf{H}_k$를 사용해보겠습니다.

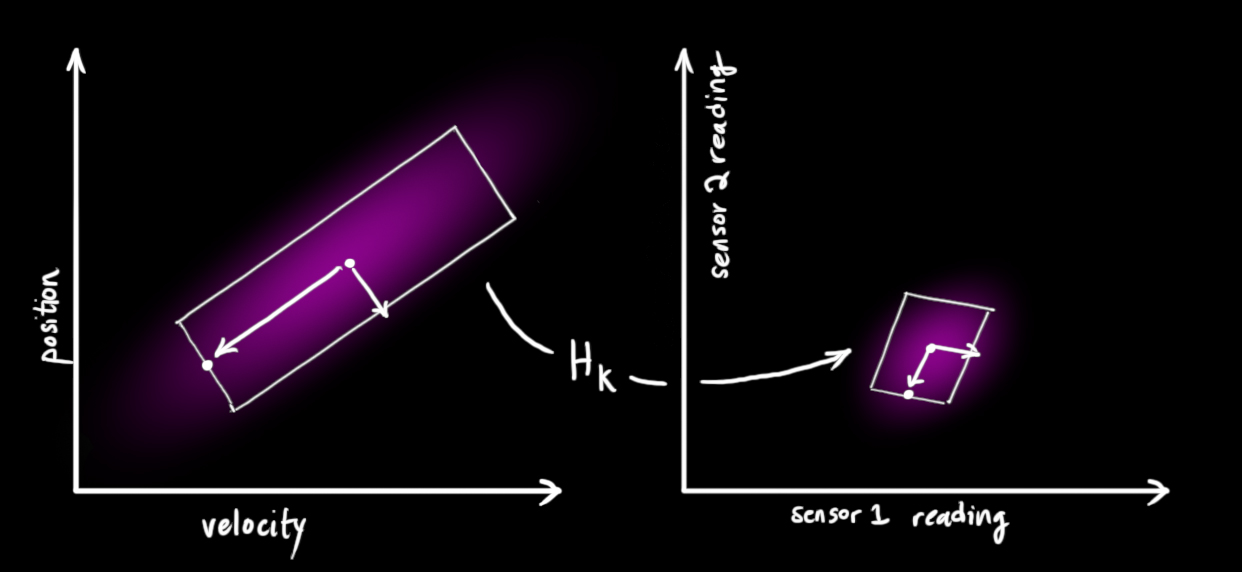
• 그러면 위 그림과 같이 $\mathbf{H}_k$을 통하여 변환을 하였습니다.

• $$\begin{equation} \begin{aligned} \vec{\mu}_{\text{expected}} &= \mathbf{H}_k \color{deeppink}{\mathbf{\hat{x}}_k} \\ \mathbf{\Sigma}_{\text{expected}} &= \mathbf{H}_k \color{deeppink}{\mathbf{P}_k} \mathbf{H}_k^T \end{aligned} \end{equation}$$

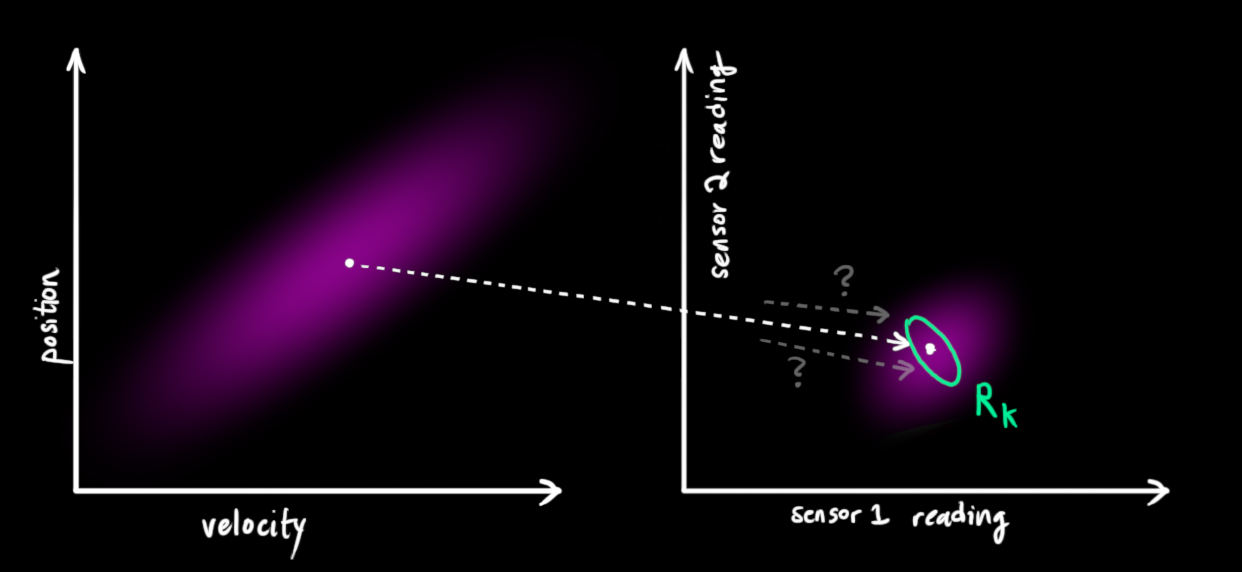
• 그리고 앞에서 부터 계속 고려해 왔던 것이 노이즈입니다. 센서를 통해서 읽은 것을 항상 신뢰할 수는 없기 때문이지요.
• 칼만 필터는 센서의 노이즈를 다루는 데 장점이 있습니다. 즉, 기존의 estimate를 특정 센서값으로 변환하는 것이 아닌 센서값의 범위로 변환하는 것입니다. 앞에서 계속 다루었던 내용의 연장입니다.

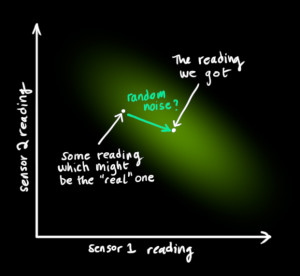
• 위 그림과 같이 실제 센서가 읽어야 할 값이 있는데, 노이즈로 인하여 센서가 읽은 값이 분포 형태로 나타날 수 있습니다.

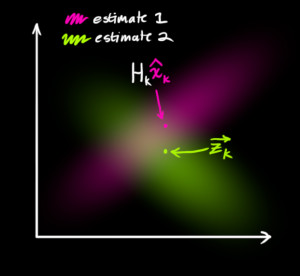
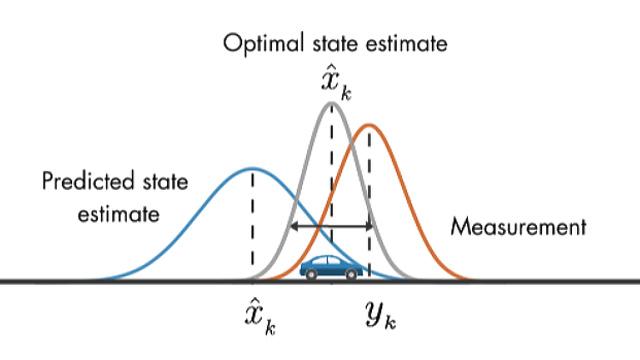
• 자 그러면 앞에서 다룬 것 까지 포함하여 2가지 분포를 가지게 됩니다.
• 첫번째는 transformed prediction 에 관련된 것 (평균이 $\vec{\mu}_{\text{expected}} = \mathbf{H}_k \color{deeppink}{\mathbf{\hat{x}}_k}$ 인 분포)으로 분홍색 분포에 해당합니다.
• 두번쨰는 센서값에 관련된 것 (평균이 $\color{yellowgreen}{\vec{\mathbf{z}_k}}$인 분포)으로 연두색 분포에 해당합니다.
• 여기서 어떤 분포를 따르는 것이 합당할까요? 두 분포 모두 타당성을 가지고 있기 때문에 두 분포 중 한개를 선택하기 보다는 두 분포를 조정하여 좋은 분포를 사용하는 것이 가장 합당해 보이므로 두 분포가 모두 True 라고 생각되는 교집합 영역의 분포를 따르도록 해보겠습니다.

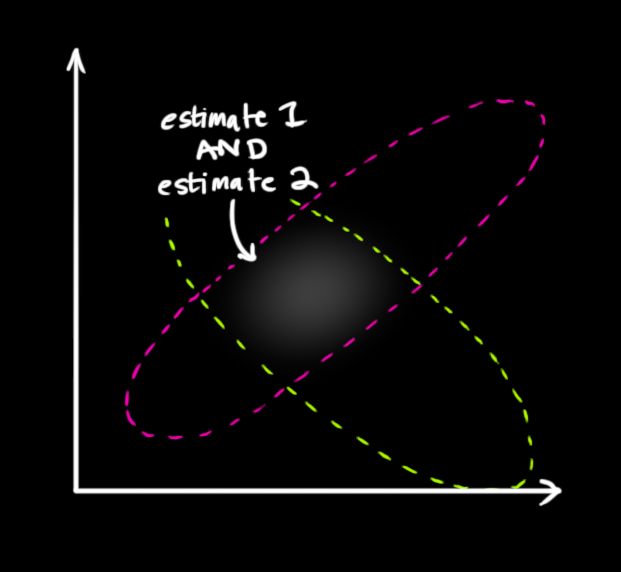
• 두 분포가 오버랩 된 영역이 각각의 분포에 대한 estimation 보다 더 정확한 분포이므로 이 오버랩 된 영역을 기준으로 평균과 분산을 구해보도록 하겠습니다.

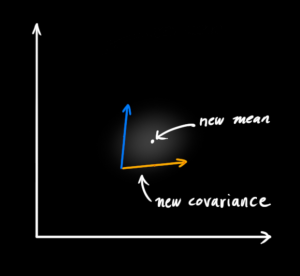
• 오버랩된 영역의 평균과 분산을 구하려면 각각의 가우시안 분포의 곱을 통하여 구할 수 있습니다.
• 그러면 오버랩된 영역의 가우시안 분포를 구해보도록 하겠습니다.

6. 가우시안 결합

• 먼저 가장 간단한 1차원 가우시안 분포에 대한 식을 살펴보도록 하겠습니다.

• $$\begin{equation} \label{gaussformula} \mathcal{N}(x, \mu,\sigma) = \frac{1}{ \sigma \sqrt{ 2\pi } } e^{ -\frac{ (x – \mu)^2 }{ 2\sigma^2 } } \end{equation}$$

• 여기서 우리가 알고 싶은 것은 두 개의 가우시안 분포를 곱하면 어떻게 되는지 입니다.

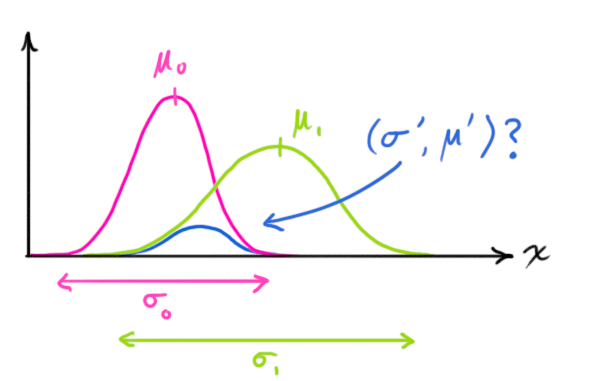
• 위 곡선 중에서 nomalize 되지 않은 파란색 곡선은 분홍색과 연두색 두 가우시안 분포의 교집합에 해당합니다.

• $$\begin{equation} \label{gaussequiv} \mathcal{N}(x, \color{fuchsia}{\mu_0}, \color{deeppink}{\sigma_0}) \cdot \mathcal{N}(x, \color{yellowgreen}{\mu_1}, \color{mediumaquamarine}{\sigma_1}) \stackrel{?}{=} \mathcal{N}(x, \color{royalblue}{\mu’}, \color{mediumblue}{\sigma’}) \end{equation}$$

• 그러면 위 등식이 만족하도록 식을 전개해 보도록 하겠습니다. 전개 방법은 간단합니다.

• $$\begin{equation} \mathcal{N}(x, \mu,\sigma) = \frac{1}{ \sigma \sqrt{ 2\pi } } e^{ -\frac{ (x – \mu)^2 }{ 2\sigma^2 } } \end{equation}$$

• 위 식을 각각의 분포에 대입하여 곱해주면 됩니다.
• 계산 과정은 다음 링크를 참조 하시기 바랍니다. 결과만 확인이 필요하시면 넘겨도 됩니다.
• 간단하게 설명하면 두 가우시안 PDF의 곱은 가우시안 PDF로 정리되기 때문에 곱의 가우시안 PDF를 확인해 보면 다음과 같습니다.

• $$\begin{equation} \label{fusionformula} \begin{aligned} \color{royalblue}{\mu’} &= \mu_0 + \frac{\sigma_0^2 (\mu_1 – \mu_0)} {\sigma_0^2 + \sigma_1^2}\\ \color{mediumblue}{\sigma’}^2 &= \sigma_0^2 – \frac{\sigma_0^4} {\sigma_0^2 + \sigma_1^2} \end{aligned} \end{equation}$$

• 여기서 $\color{royalblue}{\mu’}$와 $\color{mediumblue}{\sigma’}^2$의 식에 동시에 들어가 있는 부분을 따로 떼어 $k$ 라고 지칭해 보겠습니다.

• $$\begin{equation} \label{gainformula} \color{purple}{\mathbf{k}} = \frac{\sigma_0^2}{\sigma_0^2 + \sigma_1^2} \end{equation}$$

• 그러면 식을 다음과 같이 고쳐 쓸 수 있습니다.

• $$\begin{equation} \begin{split} \color{royalblue}{\mu’} &= \mu_0 + &\color{purple}{\mathbf{k}} (\mu_1 – \mu_0)\\ \color{mediumblue}{\sigma’}^2 &= \sigma_0^2 – &\color{purple}{\mathbf{k}} \sigma_0^2 \end{split} \label{update} \end{equation}$$

• 이 계산 결과가 1차원 가우시안 분포의 결합에 대한 식입니다. 그러면 2차원 matrix의 경우에는 어떻게 확장할 수 있을까요?
• 2차원 matrix에 적용 하기 전에 확실히 짚고 넘어가야 할 것은 가우시안의 곱은 가우시안이 된다는 것입니다.
• 앞선 예제에서 1차원 가우시안을 사용한 이유는 설명의 편리를 위함이었습니다. 즉, 간단한 1차원 가우시안의 곱을 통하여 두 가우시안의 분포를 만족하는 가우시안 교집합을 구할 수 있었습니다.
• 결과적으로는 2차원 가우시안의 곱 또한 가우시안이 됩니다. 즉 2차원에서도 가우시안 교집합을 찾을 수 있습니다. (링크 참조)
• 먼저 2차원 가우시안 분포에서 $\Sigma$는 공분산을 나타냅니다. 1차원에서는 $\sigma^{2}$이 분산이었었지요. 그리고 2차원 가우시안 분포에서의 평균은 $\vec{\mu}$로 표현되므로 다음과 같습니다.

• $$\begin{equation} \label{matrixgain} \color{purple}{\mathbf{K}} = \Sigma_0 (\Sigma_0 + \Sigma_1)^{-1} \end{equation}$$

• $$\begin{equation} \begin{split} \color{royalblue}{\vec{\mu}’} &= \vec{\mu_0} + &\color{purple}{\mathbf{K}} (\vec{\mu_1} – \vec{\mu_0})\\ \color{mediumblue}{\Sigma’} &= \Sigma_0 – &\color{purple}{\mathbf{K}} \Sigma_0 \end{split} \label{matrixupdate} \end{equation}$$

• 여기서 $\color{purple}{\mathbf{K}}$ 행렬은 Kalman gain에 해당합니다.

7. 앞에서 다룬 내용 종합

• 여기 까지 계산한 분포는 크게 2가지가 있었습니다.
• 먼저 prediction 또는 predicted measurement 입니다.

• $$(\color{fuchsia}{\mu_0}, \color{deeppink}{\Sigma_0}) = (\color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k}, \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T})$$

• 그 다음으로 센서값 또는 observed measurement입니다.

• $$(\color{yellowgreen}{\mu_1}, \color{mediumaquamarine}{\Sigma_1}) = (\color{yellowgreen}{\vec{\mathbf{z}_k}}, \color{mediumaquamarine}{\mathbf{R}_k})$$

• 그러면 앞에서 구한 두 가우시안 결합의 평균과 분산 식 (아래)에

• $$\color{royalblue}{\vec{\mu}’} = \vec{\mu_0} + \color{purple}{\mathbf{K}} (\vec{\mu_1} – \vec{\mu_0})$$

• $$\color{mediumblue}{\Sigma’} = \Sigma_0 – \color{purple}{\mathbf{K}} \Sigma_0$$

• predicted measurement와 observed measurement를 대입해 보겠습니다. 그러면 결과는 아래와 같습니다.

• $$\begin{equation} \begin{aligned} \mathbf{H}_k \color{royalblue}{\mathbf{\hat{x}}_k’} &= \color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k} & + & \color{purple}{\mathbf{K}} ( \color{yellowgreen}{\vec{\mathbf{z}_k}} – \color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k} ) \\ \mathbf{H}_k \color{royalblue}{\mathbf{P}_k’} \mathbf{H}_k^T &= \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T} & – & \color{purple}{\mathbf{K}} \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T} \end{aligned} \label {kalunsimplified} \end{equation}$$

• 앞에서 Kalman gain에 대한 정의를

• $$\color{purple}{\mathbf{K}} = \Sigma_0 (\Sigma_0 + \Sigma_1)^{-1}$$

• 위와 같이 하였기 때문에, 차례대로 predicted measurement의 공분산 값을 대입하면 다음과 같습니다.

• $$\begin{equation} \label{eq:kalgainunsimplified} \color{purple}{\mathbf{K}} = \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T} ( \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T} + \color{mediumaquamarine}{\mathbf{R}_k})^{-1} \end{equation}$$

• 여기서 도출한 식들($\mathbf{H}_k \color{royalblue}{\mathbf{\hat{x}}_k’}, \mathbf{H}_k \color{royalblue}{\mathbf{P}_k’} \mathbf{H}_k^T, \color{purple}{\mathbf{K}}$)을 보면 모두 양변에 $\mathbf{H}_k$가 앞쪽에 있습니다. 양변에서 소거해 보겠습니다.
• 그리고 소거하고 난 $\color{royalblue}{\mathbf{P}_k’} \mathbf{H}_k^T$식에서 양변을 보면 뒤쪽에 모두 $\mathbf{H}_k^T$가 있으니 양변에서 소거해 보겠습니다.

• $$\begin{equation} \begin{split} \color{royalblue}{\mathbf{\hat{x}}_k’} &= \color{fuchsia}{\mathbf{\hat{x}}_k} & + & \color{purple}{\mathbf{K}’} ( \color{yellowgreen}{\vec{\mathbf{z}_k}} – \color{fuchsia}{\mathbf{H}_k \mathbf{\hat{x}}_k} ) \\ \color{royalblue}{\mathbf{P}_k’} &= \color{deeppink}{\mathbf{P}_k} & – & \color{purple}{\mathbf{K}’} \color{deeppink}{\mathbf{H}_k \mathbf{P}_k} \end{split} \label{kalupdatefull} \end{equation}$$
• $$\begin{equation} \color{purple}{\mathbf{K}’} = \color{deeppink}{\mathbf{P}_k \mathbf{H}_k^T} ( \color{deeppink}{\mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T} + \color{mediumaquamarine}{\mathbf{R}_k})^{-1} \label{kalgainfull} \end{equation}$$

• 위 식이 바로 칼만 필터의 update step에 해당합니다.
• 여기서 $\color{royalblue}{\mathbf{\hat{x}}_k’}$가 새로운 최적의 estimate가 됩니다.
• 이 계산 과정에서 주의할 것은 역행렬 계산입니다. 역행렬이 없을 때에는 이 계산을 할 수 없으니 state estimation을 못할 수 있습니다.
• 따라서 역행렬이 없는 특이 행렬일 때도 구할 수 있는 Pseudo-Inverse를 적용하는 것이 좋습니다.
  • 일반적인 간단한 역행렬 계산(e.g. 가우스 조던 소거법)에서 역행렬을 구할 때 $O(n^{3})$ 의 연산량인 것과 같이 pseudo inverse를 구할 때에도 $O(mn^{2})$의 복잡도를 가지므로 연산량 측면에서도 유사합니다.

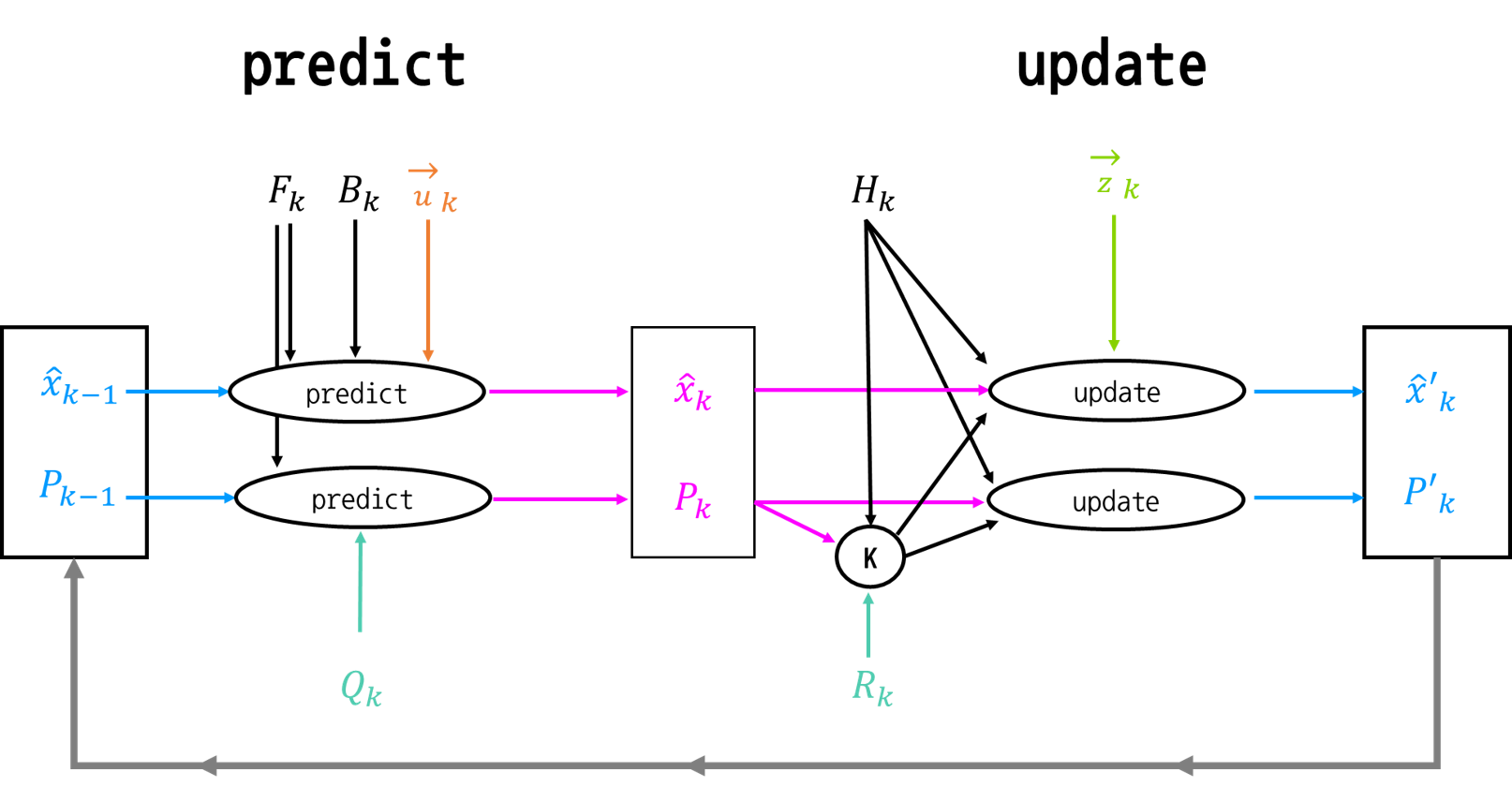
8. 칼만 필터 Flow

• 마지막으로 지금 까지 학습한 칼만 필터의 Flow를 보면서 글을 마무리 하겠습니다.
• 글을 읽어주셔서 감사합니다.