
자율주행을 위한 라이다(Lidar) 센서와 라이다 포인트 클라우드 처리 방법
2021, Jan 10
- 참조 : REC.ON : Autonomous Vehicle (FastCampus)
- 참조 : http://www.kibme.org/resources/journal/20210513134622527.pdf
- 이번 글에서는 라이다 관련된 내용을 종합적으로 정리하기 위한 글입니다. 다소 중복된 내용이 여러번 언급될 수 있으니 참조하여 글을 읽어주시면 됩니다.
목차
-
라이다 포인트 클라우드 처리 방법
-
자율주행에서의 라이다 동향
- 먼저 이번 글의 첫번째 목적은 아래와 같은 5가지의 프로세스를 하나씩 접근해 보는 것입니다.
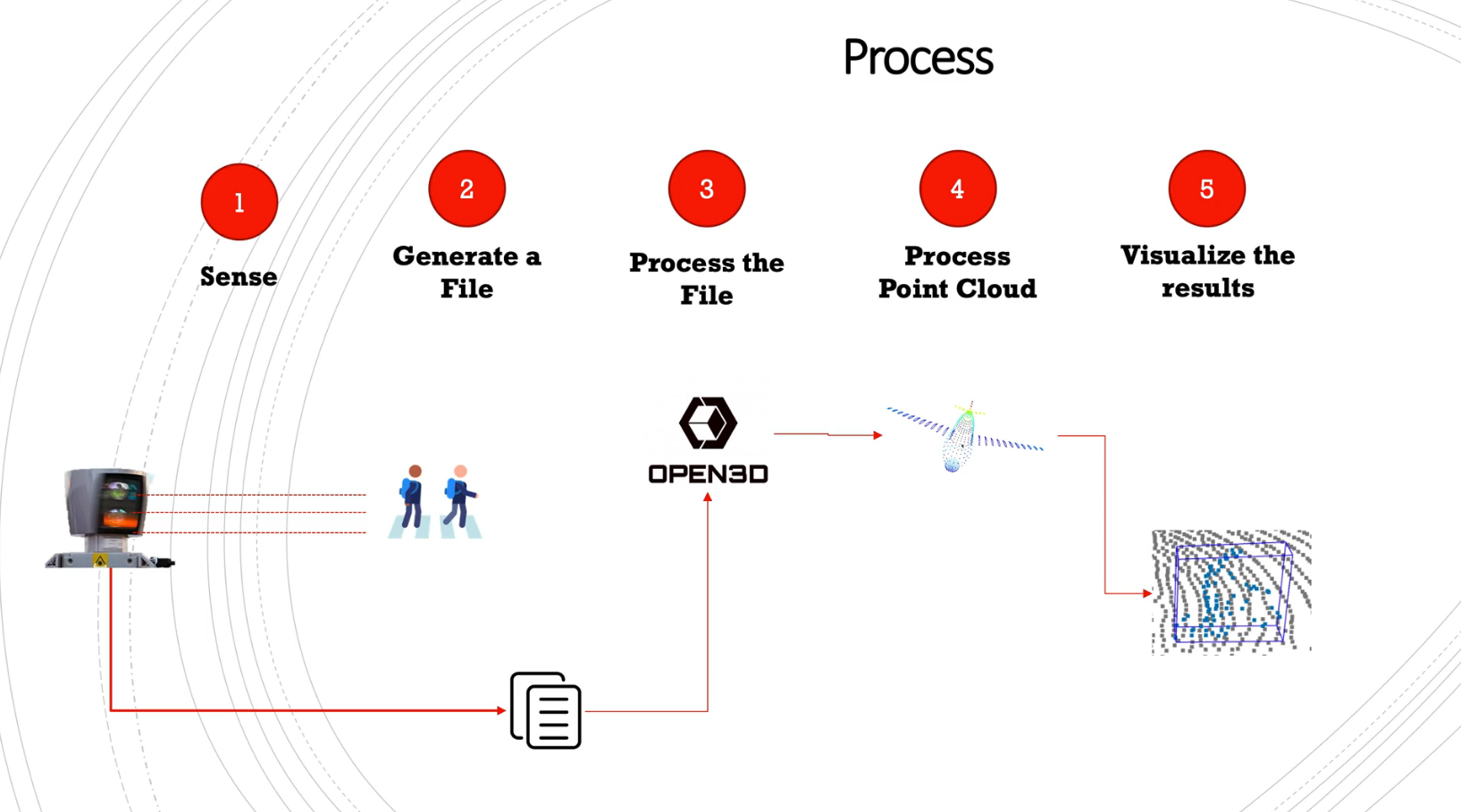
- ①
Sense: 라이다 센서는 빛 (레이저)를 송신하고 주변 물체로 부터 반사되어 다시 수신하여 물체의 위치를 확인합니다. 하드웨어적인 상세 내용은 글 후반부의자율주행에서의 라이다 동향에서 부터 살펴보시길 바랍니다. - ②
Generate a File: 라이다 센서를 통하여 인식한 결과를 통해 raw data를 생성합니다. 공개된 라이다 데이터셋은 보통 가공이 되어 있는 데이터인 반면에 직접 라이다를 통해 얻은 데이터는 노이즈도 섞여있고 포인트가 필요 이상으로 많이 있기도 합니다. - ③
Process the File: 라이다 데이터를 읽으면 포인트 클라우드 형태로 되어있습니다. 3D에서 포인트 클라우드 형태로 데이터를 읽기 위해서open3D라는 패키지를 사용할 예정입니다. - ④
Process Point Cloud: 라이다 데이터에서 의미 있는 정보를 찾기 위하여 포인트를 샘플링 하기도하고 추가적인 알고리즘을 이용하여 포인트들을 클러스터링을 하기도 합니다. 이번 글에서는 Unsupervised 방식으로bounding box를 적용하여 물체를 찾는 간단한 방법을 다루어 볼 예정입니다. - ⑤
Visualize the results: 포인트 클라우드 처리가 끝난 결과를 시각화해서 보는 단계를 의미합니다. 위 그림과 같이 포인트 클라우드 상에서bounding box가 잘 생성되었는 지 살펴보도록 하겠습니다.
라이다와 포인트 클라우드
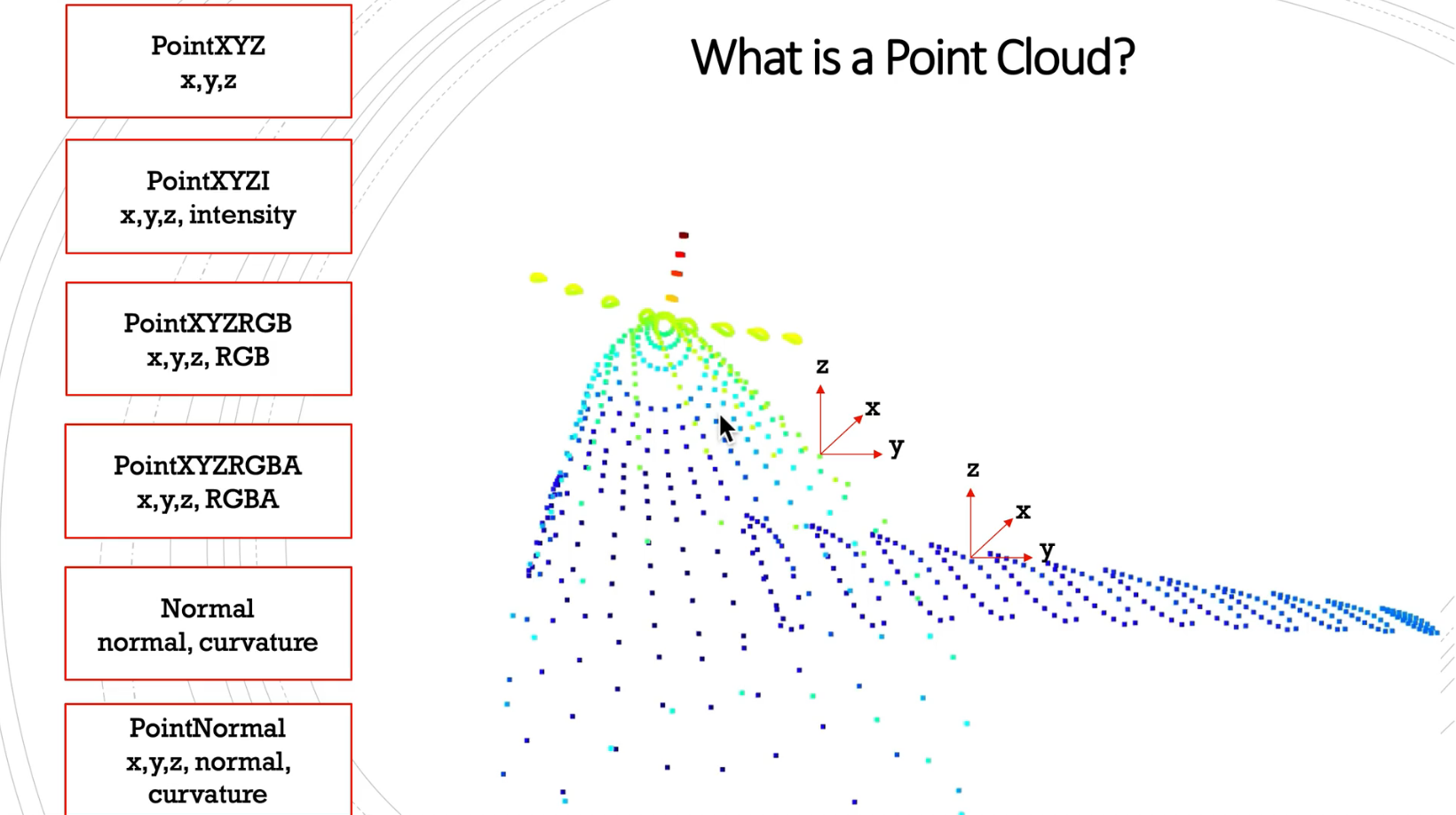
- 포인트 클라우드는 대표적으로 위 그림과 같이 6개의 포맷으로 저장될 수 있습니다.
- 공통적으로 가지고 있는 정보는 3차원 공간 상에서
XYZ 좌표정보이며 추가적으로intensity정보를 많이 사용합니다. - 라이다로 취득한 3차원 포인트 클라우드에서는 가까운 물체가 멀리 있는 물체에 비해 조밀하게 샘플링 되는 특징이 있습니다. 또한 멀리 있는 물체일수록 반사되어 돌아오는 신호의 강도가 약해지고 큰 노이즈를 포함하기 쉽습니다. 이러한 성질을 이용하여 라이다를 통해 얻은 포인트 클라우드에는 3차원 좌표와 함께 반사되어 돌아온 신호의 강도를 나타내는 반사도의 세기 정보가 포함되는데 이 정보를
intensity라고 합니다.
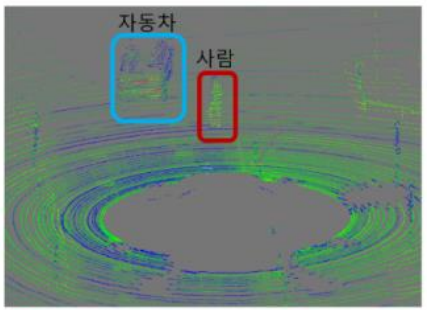
- 위 그림의 왼쪽에서는 포인트 클라우드의 색이 녹색과 파란색으로 비교적 반사도 세기가 낮고 자동차 번호판 부분은 붉은색으로 비교적 높은 세기를 가집니다. 반사도 세기에 영향을 미치는 요인들은 여러가지가 있는데 레이저 펄스가 통과하는 매질이나 물체의 표면과 펄스가 만나는 각도, 대상 물체 표면의 반사율에 따라서 돌아오는 신호의 세기가 결정됩니다. 같은 재질이더라도 물질의 색상에 따라서 반사도가 다를 수도 있습니다.
- 이와 같은 특성은 빛이 어떤 물질 특성에 잘 반사되는 지 또는 잘 흡수되는 지를 생각하면 쉽게 이해하실 수 있습니다.
- 앞의 비행기 포인트 클라우드에서도 이와 같은 intensity가 반영되어 색으로 표현되어 있음을 알 수 있습니다.
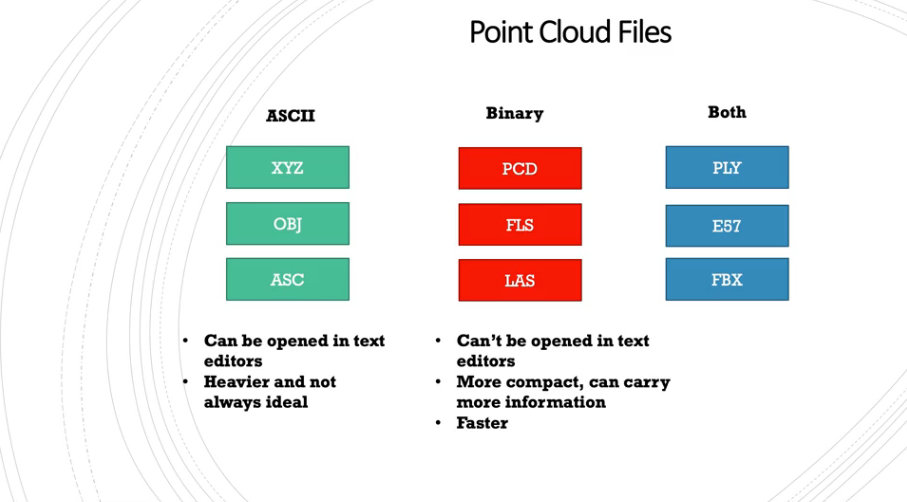
- 포인트 클라우드를 저장할 때, 대표적으로 ASCII 형식과 Binary 형식을 사용합니다. 잘 알려진 바와 같이 ASCII는 바로 텍스트에서 읽을 수 있지만 용량이 굉장히 커진다는 단점이 있습니다.
- 반면 Binary 파일은 텍스트 형태로 읽을 수 없지만 좀 더 compact 하여 용량이 작고 더 많은 정보를 가질 수 있고 읽을 때 더 빠르게 읽을 수 있습니다. 따라서 Binary 형태로 저장하고 읽어서 쓰는 것이 일반적입니다. 앞으로 Binary 파일은 bin 파일로 명칭하겠습니다.
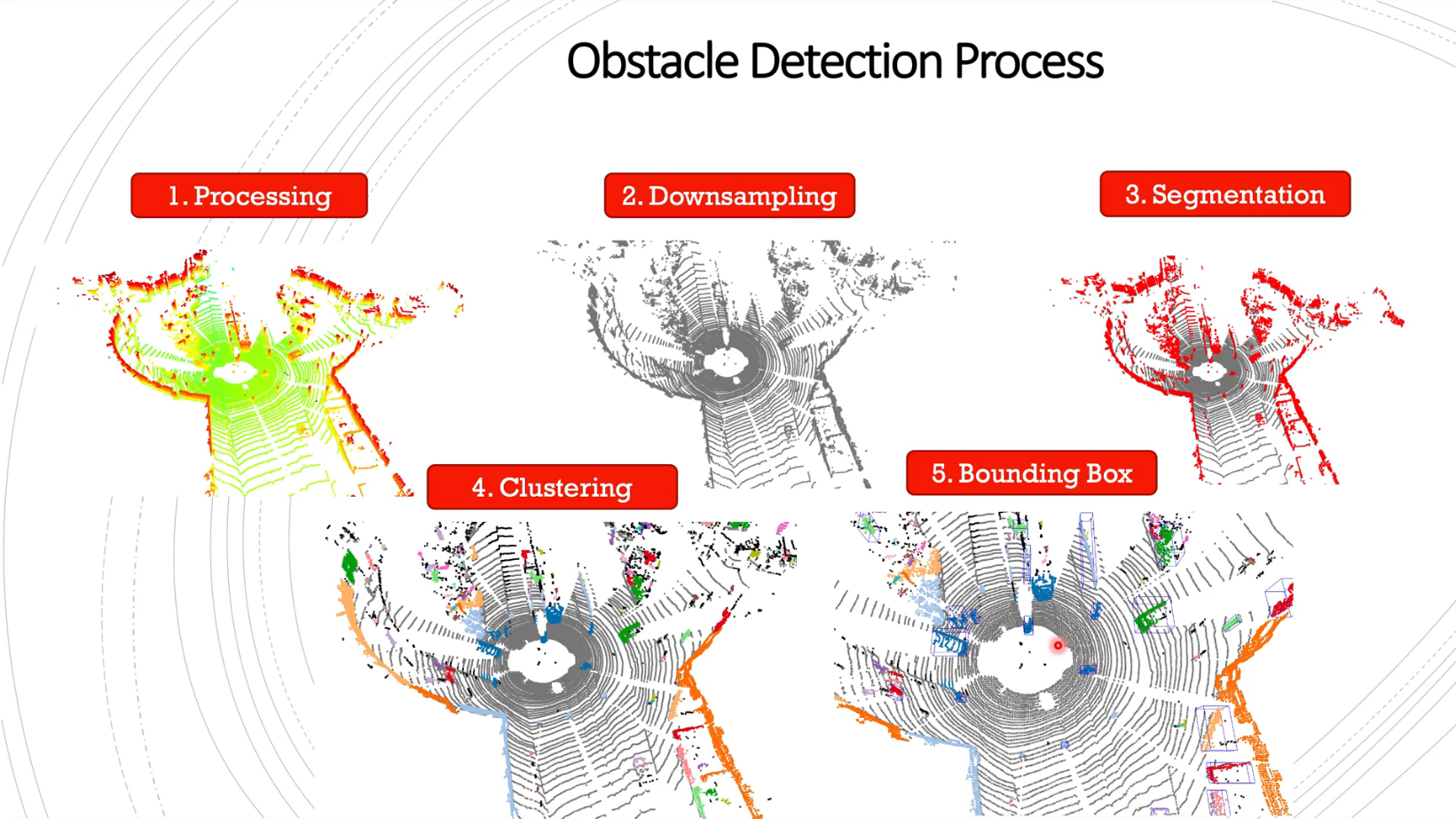
- ①
Processing: bin 파일을 읽으면 1번과 같은 형태의 많은 포인트 클라우드가 생성됩니다. - ②
Downsampling: 따라서 2번과 같이 Downsamping을 통하여 중복된 포인트 클라우드 수를 줄여줍니다. - ③
Segmentation: Downsampling된 포인트 들을 의미 단위로 나누는 작업을 합니다. 예를 들어 어떤 포인트는 바닥이고 어떤 포인트는 벽인지 등을 구분합니다. 본 글에서는 간단한 방식으로 Segmentation을 적용할 예정입니다. - ④
Clustering: Segmentation 작업을 통하여 클래스가 분류되면 거리를 기반으로 점들을 클러스터링 하여 필요한 객체 단위로 묶습니다. - ⑤
Bounding Box: Segmentation과 Clustering 과정을 통해 점들이 클래스와 거리 별로 구분이 되게 되면 Bounding Box를 사용하여 객체의 위치를 표시할 수 있습니다. - 이와 같은 ① ~ ⑤ 가 흔히 사용하는
Obstacle Detection Process방법입니다. 이번 글에서도 이와 같은 방식을 이용하여 어떻게 라이다 포인트 클라우드를 처리하는 지 살펴보도록 하겠습니다.
- 라이다 데이터를 다루기 위해서는 라이다를 다루기 위한 포인트 클라우드 라이브러리와 데이터셋이 필요합니다. 아래 링크를 통해 현재 많이 사용하는 라이다 포인트 클라우드 처리를 위한 라이브러리와 데이터셋을 확인할 수 있습니다.
Point Cloud Libraries: https://github.com/openMVG/awesome_3DReconstruction_list#mesh-storage-processingLiDAR Datasets: https://boschresearch.github.io/multimodalperception/dataset.html
Processing : open3d를 이용한 포인트 클라우드 처리
- 포인트 클라우드를 처리하기 위하여 3D 포인트 클라우드를 시각화해서 보기 위해
python에서open3d라이브러리를 사용해보도록 하겠습니다. 추가적으로 numpy, matplotlib, pandas 또한 설치하여 데이터를 다루는 데 활용하고PPTK패키지를 설치하여 더 개선된 시각화를 사용해 보도록 하겠습니다.
pip install open3dpip install numpypip install matplotlibpip install pandaspip install pptk
open3d의 documentation은 아래 링크에서 확인할 수 있습니다.- 링크 : http://www.open3d.org/docs/release/
- 기본적인
open3d사용법에 대한 튜토리얼은 다음 링크에서 확인할 수 있습니다.- 링크 : http://www.open3d.org/docs/release/tutorial/geometry/pointcloud.html
- 위 그림과 같이
open3d나pptk모두 라이다 포인트 클라우드를 읽는 데 문제는 없습니다.pptk의 장점은 라이다 포인트의 좌표를 직접 표시해준다는 장점이 있습니다.
- 이번 글에서 사용할 데이터는
KITTI에서 제공하는data_object_velodyne데이터로 약 29 GB 용량을 가지는 데이터 입니다. - KITTI 사이트에 접속하시고 Download Velodyne point clouds, if you want to use laser information (29 GB) 항목을 클릭하셔서 다운받으시면 됩니다.
- 위 데이터는
bin형식의 파일이고 아래에 설명할convert파일을 통하여bin → PCD로 포맷 변환이 가능합니다.bin은 효율적으로 데이터를 저장하고 읽기 위해 이와 같이 저장하고 실제 사용할 때에는PCD라는 확장자의 파일을 사용하는 것이 일반적입니다. - 본 글에서 주로 사용하는
pcd파일은KITTI의 샘플 데이터입니다. 아래 코드를 따라하려면 아래 링크를 통해 샘플 데이터를 다운받아서 사용하시면 됩니다.- 링크 : https://drive.google.com/file/d/1txU0Ou5VluSgqqBTJTC6G64s-pfDlccR/view?usp=sharing
- 아래 코드는
KITTI의bin데이터를pcd형태로 바꾸는 코드입니다.
import argparse
import open3d as o3d
import numpy as np
import struct
import os
def get_args():
parser = argparse.ArgumentParser()
parser.add_argument('--src_path', required = True)
parser.add_argument('--dest_path', required = True)
parser.add_argument('--size_float', default = 4, type=int)
args = parser.parse_args()
return args
if __name__ == "__main__":
args = get_args()
if os.path.exists(args.dest_path) == False:
os.makedirs(args.dest_path)
files_to_open = os.listdir(args.src_path)
for file_to_open in files_to_open:
print("write : ", file_to_open)
# list_pcd = []
# with open (args.src_path + os.sep + file_to_open, "rb") as f:
# byte = f.read(args.size_float * 4)
# while byte:
# x,y,z,intensity = struct.unpack("ffff", byte)
# list_pcd.append([x, y, z])
# byte = f.read(args.size_float*4)
# np_pcd = np.asarray(list_pcd)
np_pcd = np.fromfile(args.src_path + os.sep + file_to_open, dtype=np.float32).reshape((-1, 4))
np_pcd = np_pcd[:, :3]
pcd = o3d.geometry.PointCloud()
v3d = o3d.utility.Vector3dVector
pcd.points = v3d(np_pcd)
file_to_save = args.dest_path + os.sep + os.path.splitext(file_to_open)[0] + ".pcd"
o3d.io.write_point_cloud(file_to_save, pcd)
- 위 코드를
bin_to_pcd.py로 저장했다고 가정하였을 때, 파이썬 코드 사용은 다음과 같습니다.
python bin_to_pcd.py --src_path=/home/desktop/data_object_velodyne/training/velodyne --dest_path=/home/desktop/data_object_velodyne/training/velodyne_pcd
- 저장된
pcd파일은 다음 코드를 통해 읽은 후open3d나pptk로 시각화 할 수 있습니다.
import open3d as o3d
pcd = o3d.io.read_point_cloud("000000.pcd")
# visualization with open3d
open3d.visualization.draw_geometries([pcd])
# visualization with pptk
v = pptk.viewer(pcd.points)
- 파이썬에서
open3d의open3d.cpu.pybind.geometry.PointCloud객체 형태로 파일을 읽게 된다면 이 값은numpy로 변경할 수 있습니다. numpy로 변경하게 되면 파이썬에서 다양한 목적으로 쉽게 사용할 수 있습니다. - 다음 코드는 읽은
pcd파일을 numpy로 변경하거나 임의의 numpy 파일을 다시 point cloud 객체로 변환하는 방법입니다.
import open3d as o3d
# point cloud → numpy
pcd = o3d.io.read_point_cloud("000000.pcd")
pcd_np = np.asarray(pcd.points)
print(pcd_np)
# array([[896.994 , 48.7601 , 82.2656 ],
# [906.593 , 48.7601 , 80.7452 ],
# [907.539 , 55.4902 , 83.6581 ],
# ...,
# [806.665 , 627.363 , 5.11482],
# [806.665 , 654.432 , 7.51998],
# [806.665 , 681.537 , 9.48744]])
# numpy → point cloud
A = np.random.random((1000, 3)) * 1000
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(A)
# open3d.visualization.draw_geometries([pcd])
v = pptk.viewer(pcd.points)
# v = pptk.viewer(np.asarray(pcd.points))
- 위 코드와 같이 pcd → numpy 형태로 변형할 수 있고 반대로 임의의 numpy 값을 pcd로 변형하여 시각화 할 수 있습니다. 단, 이 때, pcd로 변형될 수 있도록 좌표값에 대한 정보를 3열을 이용하여 나타내어야 합니다.
pptk.viewer에 numpy 타입의 데이터를 직접 입력해 주는 방식도 사용 가능합니다.
Voxel Grid Downsampling
- 앞에서 살펴본 포인트 클라우드의 수가 중복된 위치에 필요 이상으로 촘촘히 있는 것을 확인할 수 있습니다.
- 흔히 센서를 통해 얻은 데이터는 원본 데이터를 사용하기보다 원본 데이터를 일정한 간격으로 줄이는
downsampling방법을 통해 처리를 해서 사용합니다. - 이와 같이 사용하는 이유는 실제 포인트 클라우드를 처리할 때, 효율적으로 처리하기 위함입니다. 원본 데이터를 그대로 사용할 경우 정보는 많으나 데이터를 처리하는 데 시간이 너무 많이 필요하기 때문입니다.
- 이미지에서도 이와 비슷하게 이미지를
downsampling하여 실제 알고리즘을 처리할 때 필요한 시간을 줄이기도 하는데, 이와 같은 목적입니다.
- 라이다 포인트 클라우드에서 downsampling 하는 흔한 방법은
Voxel Grid기반의 downsampling 입니다. Voxel Grid는 3D 상의 cube 이며Voxel Grid Downsampling은 이 Voxel Grid 내부에 점 1개만 유지하고 나머지는 필터해서 제거하는 방식입니다. 즉, Voxel Grid 내부에 점이 여러개 있다고 하더라도 1개만 남고 나머지는 없어지므로 유사한 위치에 과도하게 많은 정보를 제거한다는 뜻이 됩니다.
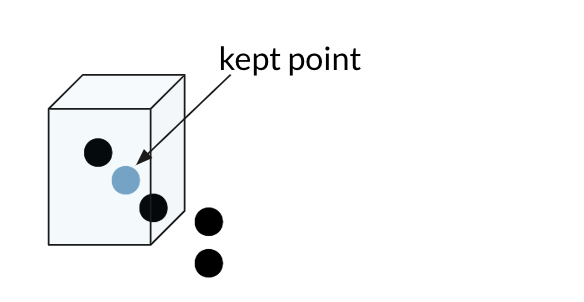
- 위 그림과 같이 1개의 Voxel Grid에서는 1개의 점만 남기고 나머지는 모두 지워버려 downsampling을 합니다. 이 경우 파라미터는
Voxel Grid의 크기가 됩니다. 앞으로 다룰voxel_size의 단위는meter입니다. 따라서 0.1m, 0.2m 등과 같은 길이가 많이 사용됩니다. open3d의 documentation에 따르면 한 개의Voxel Grid에 포함된 포인트 클라우드들을 대상으로 평균을 내어 평균 위치의 포인트를 한 개 생성하고 기존의 포인트 들은 제거하는 방식을 통하여 downsampling 하는 것으로 알려져 있습니다.
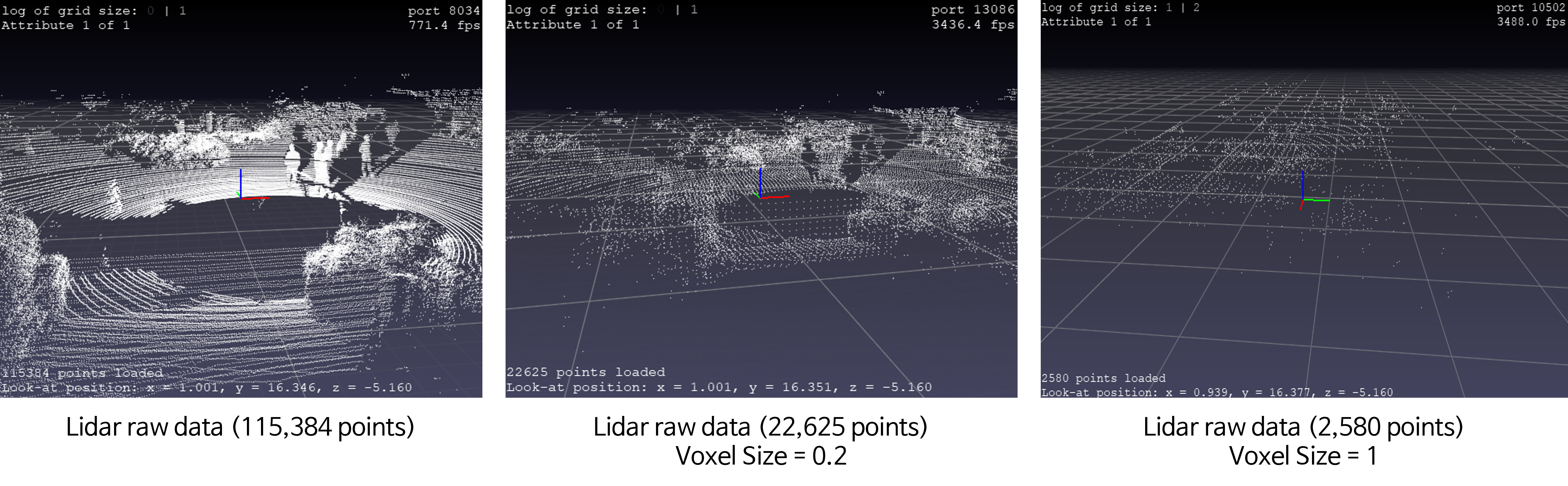
- 위 그림은 왼쪽부터 downsampling 하기 이전, 0.2의 voxel size로 downsampling을 한것 그리고 1의 voxel size로 downsampling을 한 것을 차례대로 시각화 한 것입니다.
- voxel size가 커질수록 3D 공간 상에서 필터링 되는 점이 많아지기 때문에 좀 더 sparse 해지게 됩니다.
- 아래 코드의
voxel_size값을 통해 크기를 조절할 수 있습니다.
print(f"Points before downsampling: {len(pcd.points)} ")
# Points before downsampling: 115384
pcd = pcd.voxel_down_sample(voxel_size=0.2)
print(f"Points after downsampling: {len(pcd.points)}")
# Points after downsampling: 22625
v = pptk.viewer(pcd.points)
- 추가적인 downsampling 방법으로는
ROI (Region Of Interest)영역을 기반으로 downsampling 하는 방법이 있습니다. 이 방법은 내가 관심있는 영역이 10m 라면 10m 이외의 모든 점은 제거하는 방법입니다. 간단하면서도 내가 필요로 하는 포인트만 사용한다는 점에서 굉장히 효율적인 방법입니다.
- 추가적으로
pcd = pcd.uniform_down_sample(every_k_points=5)와 같은 방법으로uniform_down_sample또한 적용할 수 있습니다.
Outlier 제거
open3d를 이용하여 outlier를 제거하는 대표적인 방법은statistical outlier removal방법과radius outlier removal방법이 있습니다.
statistical outlier removal
statistical outlier removal은 포인트 클라우드에서neighbor라는 단위로 그룹을 묶은 다음 포인트들 간의distance기준 평균과 표준 편차를 구하고std_ratio라는threshold값을 설정하여 거리의 편차가 큰 포인트를 outlier로 정의합니다.- 따라서 정해야 할 파라미터로
nb_neighbors즉, 그룹을 묶을 갯수와std_ratio라는 threshold 입니다. - 아래는
statistical outlier removal을 적용하는 코드이며 계산 효율을 위해down_sample이 필요할 수 있습니다.
# pcd = pcd.voxel_down_sample(voxel_size=0.5)
pcd, inliers = pcd.remove_statistical_outlier(nb_neighbors=20, std_ratio=2.0)
inlier_cloud = pcd.select_by_index(inliers)
outlier_cloud = pcd.select_by_index(inliers, invert=True)
inlier_cloud.paint_uniform_color([0.5, 0.5, 0.5])
outlier_cloud.paint_uniform_color([1, 0, 0])
o3d.visualization.draw_geometries([inlier_cloud, outlier_cloud])
nb_neighbors와std_ratio의 크기 변화에 따라 어떻게 outlier가 검출이 되는 지 원하는 방향에 맞게 사용하면 됩니다.
radius outlier removal
- 그 다음 방법으로
radius outlier removal방식을 설명하겠습니다. radius outlier removal은 구(sphere)를 그리고 구(sphere) 내부에 포인트의 갯수가 일정 갯수 이하만 있으면 outlier로 제거하는 방식입니다. 즉, 듬성 듬성 존재하는 점들을 제거하기 좋은 방법입니다.- 파라미터는 2개가 사용되며 첫번째로
nb_points는 구 안에nb_points이하의 포인트가 존재하면 outlier로 정할 수 있는 임계값이고radius는 구의 반지름에 해당합니다. 단위는 m 입니다.radius의 크기가 커지면 계산량이 많아져서 느려집니다.
# pcd = pcd.voxel_down_sample(voxel_size=0.5)
pcd, inliers = pcd.remove_radius_outlier(nb_points=20, radius=0.5)
inlier_cloud = pcd.select_by_index(inliers)
outlier_cloud = pcd.select_by_index(inliers, invert=True)
inlier_cloud.paint_uniform_color([0.5, 0.5, 0.5])
outlier_cloud.paint_uniform_color([1, 0, 0])
o3d.visualization.draw_geometries([inlier_cloud, outlier_cloud])
pcd = pcd.select_by_index(inliers)

- 위 예제는 0.5 m 구 를 그렸을 때, 점이 20개 이하인 점들을 대상으로 제거한 것입니다. 따라서 듬성 듬성 있는 점들에 대하여 빨간색 즉, outlier로 표시된 것을 확인할 수 있습니다.
RANSAC을 이용한 도로와 객체 구분
- 지금까지 포인트 클라우드를 읽은 다음 기본적인 downsamping 이외의 처리는 하지 않았습니다. 지금부터 살펴볼 내용은
RANSAC을 이용하여 도로와 객체를 분리하는 방법에 대하여 알아보도록 하겠습니다. 수많은 포인트 클라우드에서 도로와 객체를 분리만 해도 상당히 많은 수의 포인트가 필터링 됩니다.
RANSAC에 대한 상세한 내용은 아래 링크에서 참조할 수 있습니다.
RANSAC은inlier와outlier를 구분하는 간편하면서도 효과적인 알고리즘 입니다. 도로와 객체를 분리하기 위하여RANSAC을 사용하는 이유는 포인트 클라우드가 형성되는 패턴에 따라서 도로를inlier로 두고 객체를outlier로 두면 간단하면서 효율적으로 두 클래스를 분리할 수 있습니다.
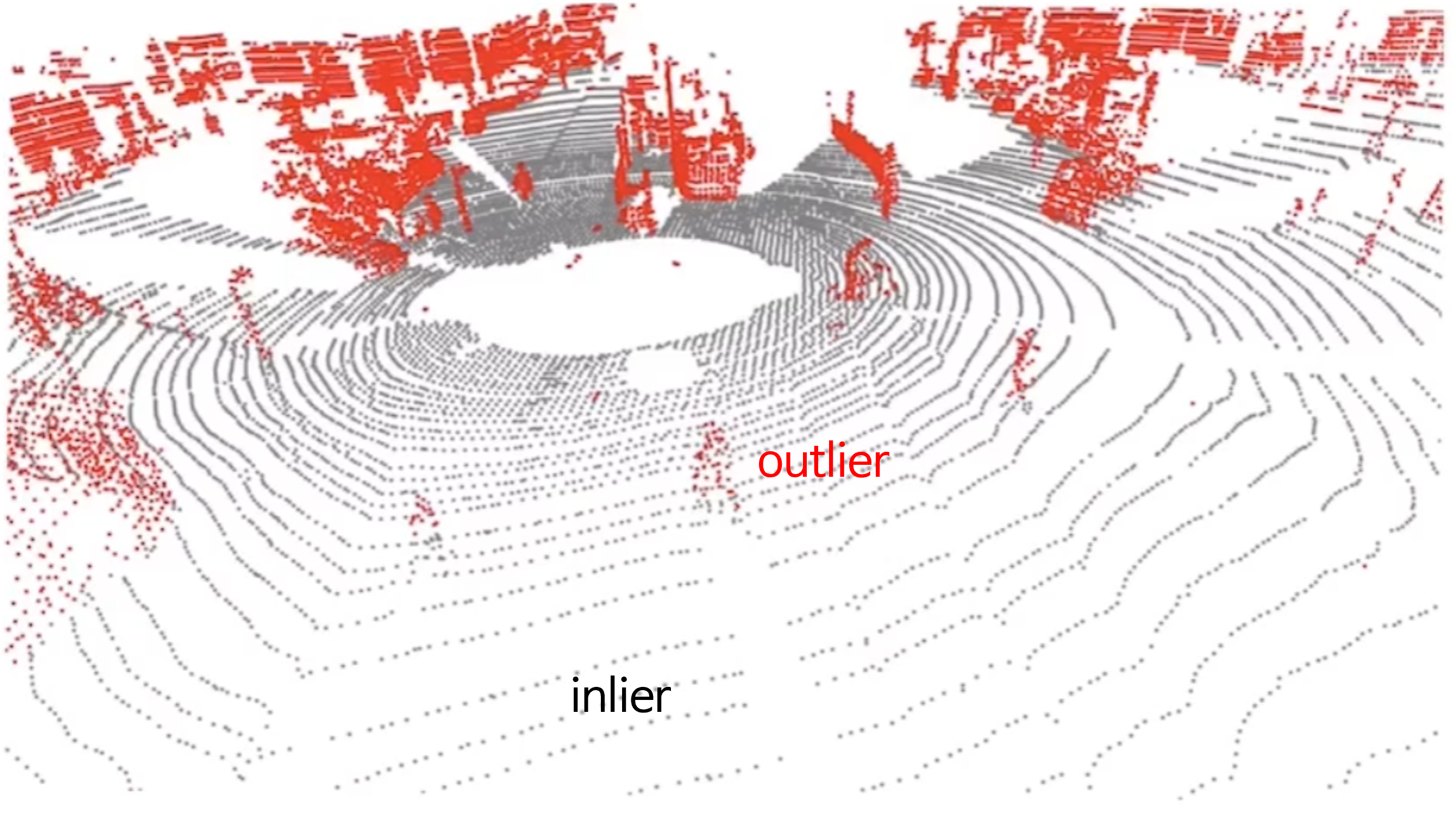
- 위 그림과 같이 도로는
inlier로 구분할 수 있고 객체는outlier형태로 구분할 수 있습니다. 도로와 같은 경우 객체와 다르게 등고선 형태로 쭉 펴져 있는 것을 볼 수 있는데 이러한 성질을 이용하는 것입니다.
- RANSAC의 자세한 내용은 앞에서 공유한 RANSAC (RANdom SAmple Consensus) 개념 및 실습 내용을 참조하시고 간단하게 컨셉만 공유해 보도록 하겠습니다.
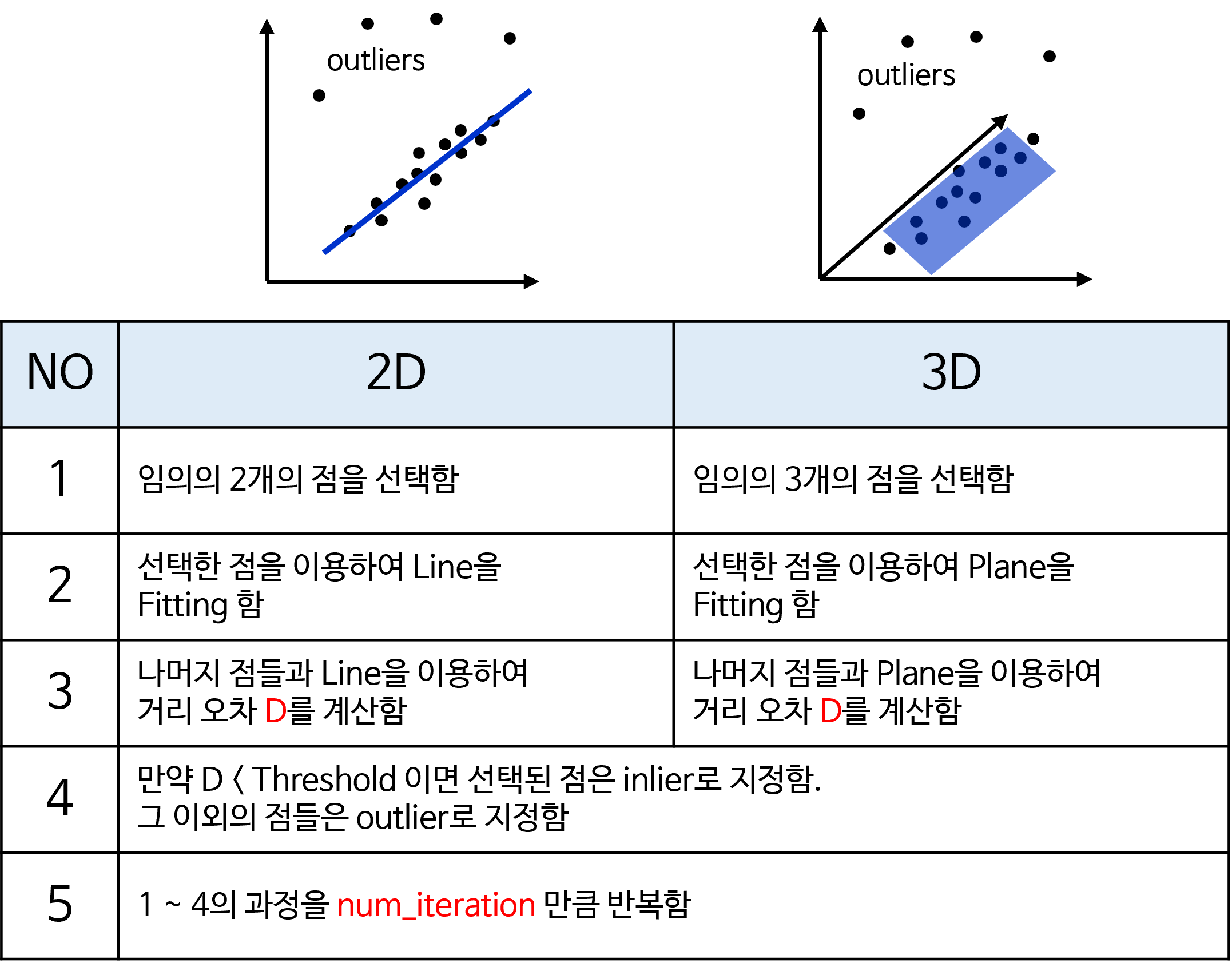
- RANSAC의 기본 원리에 따라 2차원에서는 2개의 점을 선택하고 선택된 점을 이용하여 Line을 Fitting 한 뒤 Line과 점들 간의 오차를 구하고 오차와 내가 선택한 Threshold 값의 차이가 얼만큼 차이가 나는 지 구합니다. 이 차이가 사전에 정한 Threshold 보다 작으면 inlier로 선택되는 구조입니다.
- 3차원에서는 추가적으로 3개의 점을 선택하고 3개의 점을 통해서 만들 수 있는 Plane을 이용하여 inlier와 outlier를 구하게 됩니다.
- 이 때,
inlier로 선택된 점들은 평평한 평면에 가까운 점들로 도로에 해당하고outlier로 선택된 점들은 평면과 거리가 먼 점들로 객체에 해당하게 됩니다.

- 위 그림을 보면 빨간색은
inlier로 구분된 점들이고 회색점은outlier로 구분된 점들입니다.

- 평면을 옆에서 살펴보면 평평한 평면에 fitting 될 수 있는 점들이
inlier로 선택된 것을 확인할 수 있습니다.
- 이와 같은 segmentation을 하기 위한 코드는 아래와 같습니다.
t1 = time.time()
plane_model, inliers = pcd.segment_plane(distance_threshold=0.3, ransac_n=3, num_iterations=100)
inlier_cloud = pcd.select_by_index(inliers)
outlier_cloud = pcd.select_by_index(inliers, invert=True)
inlier_cloud.paint_uniform_color([0.5, 0.5, 0.5])
outlier_cloud.paint_uniform_color([1, 0, 0])
t2 = time.time()
print(f"Time to segment points using RANSAC {t2 - t1}")
o3d.visualization.draw_geometries([inlier_cloud, outlier_cloud])
- 위 코드에서는
inlier를 도로로 구분하였고outlier를 도로이외의 포인트로 구분하였습니다. 본 글에서 다루는 방식은 객체를 찾아나아가는 과정이므로 도로는 제거해야 합니다 따라서 다음과 같이 포인트를 적용하면 도로를 제거할 수 있습니다.
plane_model, road_inliers = pcd.segment_plane(distance_threshold=0.3, ransac_n=3, num_iterations=100)
pcd = pcd.select_by_index(road_inliers, invert=True)
- 위 코드에서 구한
plane_model은 찾은 평면의 식을 나타냅니다. 평면이기 때문에 식은 다음과 같습니다.
- \[ax + by + cz + d = 0\]
- 위 식에서 \(a, b, c, d\) 계수가 차례대로
plane_model에 저장됩니다.
- 만약 도로가 평지가 아니라 약간의 오르막/내리막이 존재한다면 위 식과 같은 평면으로는 지면을 모델링 할 수 없습니다. 대신에 곡면을 이용해야 합니다.
- 다음 코드는 1차식 즉, 평면과 2차식 즉, 2차 곡면을 동일한
RANSAC방식으로 추정하는 코드입니다. 어떤 면을 선택해야 하는 지는 다양한 기준을 실험해 보면서 선택할 수 있습니다. 아래는 단순히inlier갯수를 이용하여 모델링한 것입니다. 함수의 출력은 앞의pcd.segment_plane과 호환이 되도록 구성하였습니다. min_samples의 갯수는 1차 평면의 경우 최소 점 3개를 선택해야 하므로 3개를 지정하였고 2차 곡면의 경우 6개의 점을 선택해야 하므로 6개를 지정하였습니다.
import numpy as np
from sklearn.linear_model import RANSACRegressor
from sklearn.preprocessing import PolynomialFeatures
def get_segment_plane(pcd, distance_threshold, num_iterations):
degress = [1, 2]
max_inliers = []
max_inliers_degree = None
for degree in degress:
pcd_points = np.array(pcd.points)
X = pcd_points[:, :2]
Z = pcd_points[:, 2]
# Polynomial features for quadratic model
poly_features = PolynomialFeatures(degree=degree, include_bias=True)
X_poly = poly_features.fit_transform(X)
# Apply RANSAC
ransac = RANSACRegressor(min_samples=3*degree, residual_threshold=0.3, max_trials=500)
ransac.fit(X_poly, Z)
# Retrieve the inlier mask, then find the indices of inliers
inlier_mask = ransac.inlier_mask_
inliers = np.nonzero(inlier_mask)[0]
if len(max_inliers) < len(inliers):
max_inliers = inliers
max_inliers_degree = degree
# Print the coefficients and intercept
plane_model = ransac.estimator_.coef_
# intercept = ransac.estimator_.intercept_
return coefficients, max_inliers
DBSCAN을 이용한 포인트 클라우드 클러스터링
- 지금까지
downsampling과outlier제거 그리고road제거 까지 적용하였습니다. 아직까지 생존한 포인트 클라우드들은 객체의 후보가 될 수 있는 포인트들입니다. - 객체의 후보가 될 수 있는 포인트들을 그룹화하여 묶은 다음에 마지막에는 bounding box화 하는 것이 목표입니다.
- 그러면 먼저 그룹화하여 묶을 수 있는 대표적인 알고리즘인
DBSCAN과HDBSCAN을 적용하는 방법을 살펴보도록 하겠습니다.
- 그룹화 방식은
Unsupervised Learning방식을 이용하여 클러스터링하는 방식을 사용할 것입니다. 이와 같은 클러스터링 방식 중 어느 정도 성능이 괜찮은 방식이DBSCAN (Density-Based Spatial Clustering of Applications with Noise)과HDBSCAN (Hierarchical Density-Based Spatial Clustering of Applications with Noise)으로 알려져 있습니다.
Clustering으로 유명한 알고리즘으로 K-means 알고리즘이 있습니다.K-means는 \(K\) 개의 센터점을 기준으로 distance가 가까운 점들을 그룹화하는 방법입니다. 조금만 더 자세하게 설명하면 다음과 같습니다.- ① \(K\) 개의 점을 랜덤으로 뽑습니다.
- ② 모든 점들에 대하여 랜덤으로 뽑은 \(K\) 개의 점과 군집화를 합니다. 이 때, 각각의 점들은 가장 가까운 \(K\) 개의 점의 클러스터에 할당됩니다.
- ③ 각 클러스터의 센터점은 각 클러스터의 중심점으로 변경됩니다.
- ④ 앞의 ②, ③ 과정을 특정 시점 또는 변경이 발생하지 않을 때 까지 반복하여 클러스터링을 완료합니다.
- 이러한
K-means클러스터링의 방식을Centroids기반 클러스터링 방식이라고도 합니다. - 작동 방식으로 판단할 때,
K-means의 경우 \(K\) 개의 클러스터할 그룹이 있다는 정보가 있을 때 유용하게 사용할 수 있습니다.
- 반면에 포인트 클라우드 속에서 클러스터링할 객체의 수는 알 수 없습니다. 따라서
K-means를 이용하여 클러스터링 하는 방식은 적합하지 않을 수 있습니다. 또한K-means는Centroid방식이기 때문에 클러스터가 구(sphere) 형태로 나타날 수 있습니다. 하지만 임의의 객체의 형상은 알 수 없습니다.
- 반면에 3D world 상에서 의미있는 객체가 되려면 어느 정도의 포인트가 밀집해 있는 지 정도는 가늠할 수 있습니다. 이러한 밀집 정도를
Density라고 하며Density는 객체의 형태와도 무관하게 동작할 수 있습니다. - 따라서 앞으로 사용해 볼
DBSCAN및HDBSCAN은Density기반 클러스터링 방식이라고 합니다. 동작 방식은 간단히 다음과 같습니다.- ① 임의의 한 점을 선택 합니다.
- ② 특정
distance인 \(\epsilon\) 이내에 속하는 점들을neighbor로 정의할 수 있습니다. 만약 선택한 점이 최소한의 이웃 \(n\) 개를 가진다면 선택한 한 점과neighbor를 그룹으로 묶습니다. (\(\epsilon\) : radius of the neighborhood, \(n\) : minimum number of points in the neighborhood to form a dense region) - ③ 앞의 ② 과정을 recursive하게 계속 반복하여
neighbor가 추가되지 않을 때 까지 반복합니다. - ④ 추가된
neighbor가 없으면 클러스터링을 끝내고 선택되지 않은 새로운 점에서 부터 ① ~ ③ 과정을 다시 시작합니다.
- 이 과정을
DBSCAN이라고 하며DBSCAN의 경우neighbor인 지 판단하기 위한distance인 \(\epsilon\) 와 최소한의 이웃 조건인 \(n\) 을 하이퍼파라미터로 가지게 됩니다.
open3d의 함수를 이용하여 아래와 같이 구현할 수 있으며cluster_dbscan의 파라미터인eps가 m 단위의 거리인 \(\epsilon\) 이 되고min_points가 최소한의 이웃 조건인 \(n\) 이 됩니다.
import matplotlib.pyplot as plt
# CLUSTERING WITH DBSCAN
t3 = time.time()
with o3d.utility.VerbosityContextManager(o3d.utility.VerbosityLevel.Debug) as cm:
labels = np.array(pcd.cluster_dbscan(eps=0.60, min_points=30, print_progress=False))
max_label = labels.max()
print(f'point cloud has {max_label + 1} clusters')
colors = plt.get_cmap("tab20")(labels / max_label if max_label > 0 else 1)
colors[labels < 0] = 0
pcd.colors = o3d.utility.Vector3dVector(colors[:, :3])
t4 = time.time()
print(f'Time to cluster outliers using DBSCAN {t4 - t3}')
o3d.visualization.draw_geometries([pcd])
HDBSCAN을 이용한 포인트 클라우드 클러스터링
DBSCAN알고리즘이 더 발전되어 \(\epsilon\) 을 고려하지 않고Density즉,min_cluster_size만 고려하는 방식을HDBSCAN이라고 합니다.min_cluster_size는 말 그대로 클러스터로 묶기 위한 최소한의 포인트 갯수를 의미하며 이 값만 지정하면 하이퍼파라미터는 필요로 하지 않습니다.
import hdbscan
import matplotlib.pyplot as plt
# CLUSTERING WITH HDBSCAN
t3 = time.time()
clusterer = hdbscan.HDBSCAN(min_cluster_size=30, gen_min_span_tree=True)
clusterer.fit(np.array(pcd.points))
labels = clusterer.labels_
max_label = labels.max()
print(f'point cloud has {max_label + 1} clusters')
colors = plt.get_cmap("tab20")(labels / max_label if max_label > 0 else 1)
colors[labels < 0] = 0
pcd.colors = o3d.utility.Vector3dVector(colors[:, :3])
t4 = time.time()
print(f'Time to cluster outliers using HDBSCAN {t4 - t3}')
o3d.visualization.draw_geometries([pcd])
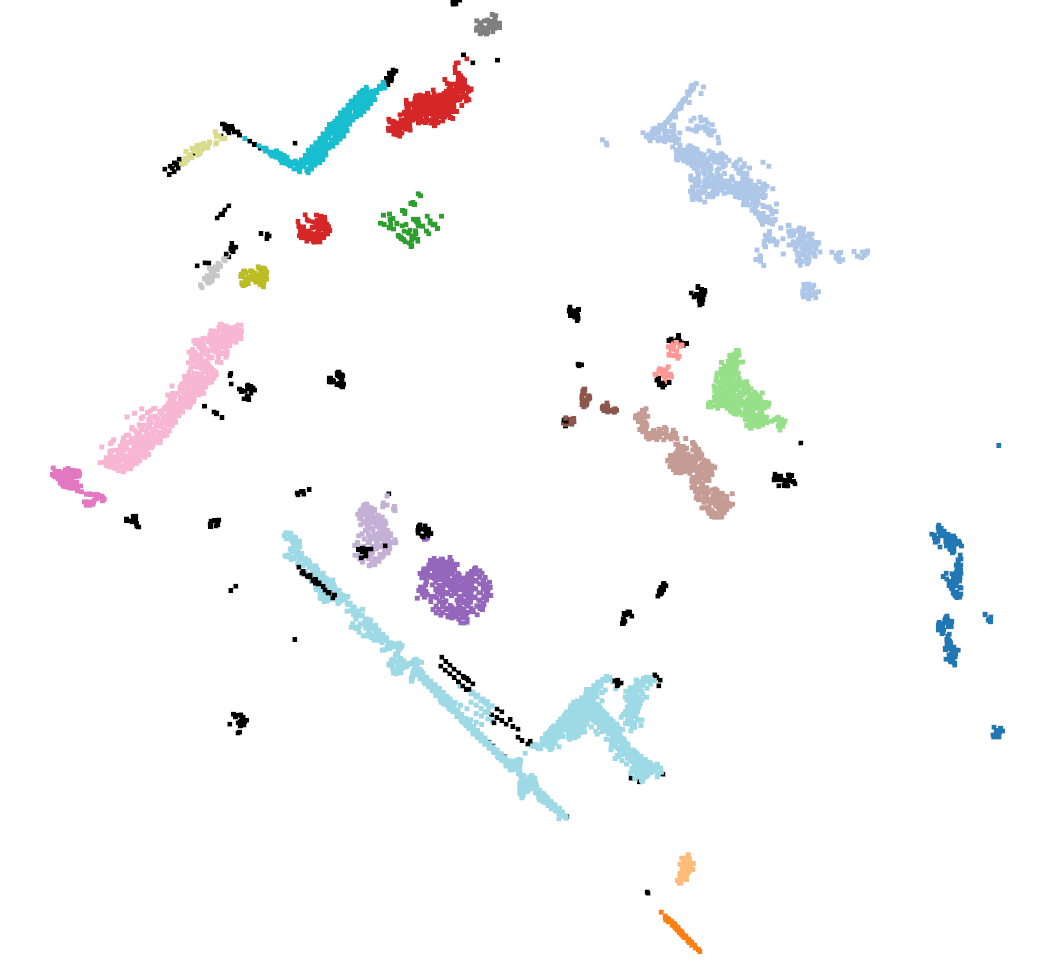
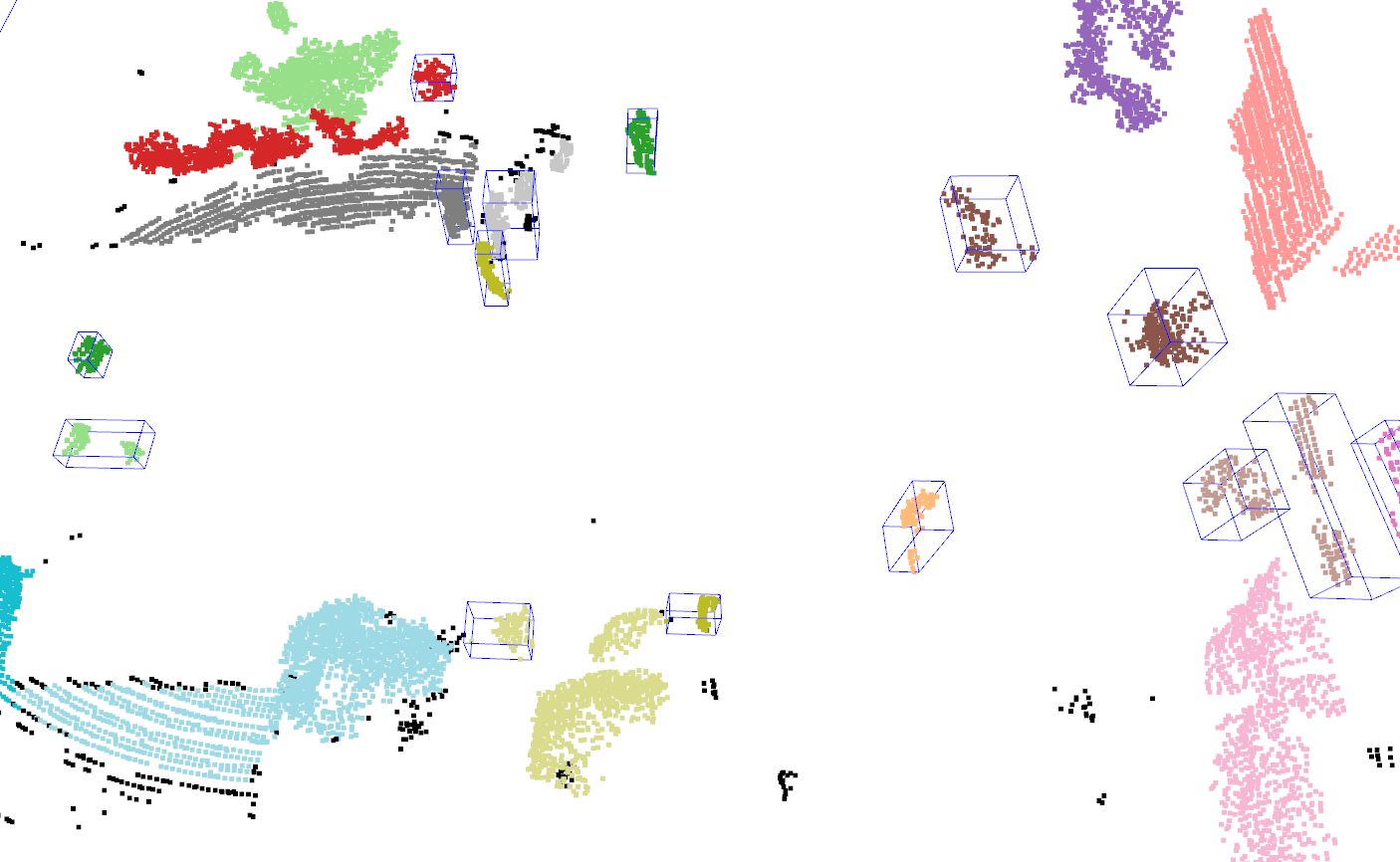
- 위 출력 결과는
HDBSCAN을 이용하여 클러스터링한 결과를 컬러값을 적용하여 시각화한 결과입니다. 검정색 포인트들은 클러스터링 되지 못한 포인트들입니다.
3D Bounding Box 생성
- 앞에서
HDBSCAN을 통하여 클러스터링 까지 완료하였습니다. 클러스터링된 포인트 정보를 이용하여open3d의get_axis_aligned_bounding_box()함수를 통해bounding box정보를 추출할 수 있습니다. 코드는 다음과 같습니다.
import pandas as pd
bbox_objects = []
indexes = pd.Series(range(len(labels))).groupby(labels, sort=False).apply(list).tolist()
MAX_POINTS = 300
MIN_POINTS = 50
for i in range(0, len(indexes)):
nb_points = len(pcd.select_by_index(indexes[i]).points)
if (nb_points > MIN_POINTS and nb_points < MAX_POINTS):
sub_cloud = pcd.select_by_index(indexes[i])
bbox_object = sub_cloud.get_axis_aligned_bounding_box()
bbox_object.color = (0, 0, 1)
bbox_objects.append(bbox_object)
print("Number of Boundinb Box : ", len(bbox_objects))
list_of_visuals = []
list_of_visuals.append(pcd)
list_of_visuals.extend(bbox_objects)
o3d.visualization.draw_geometries(list_of_visuals)
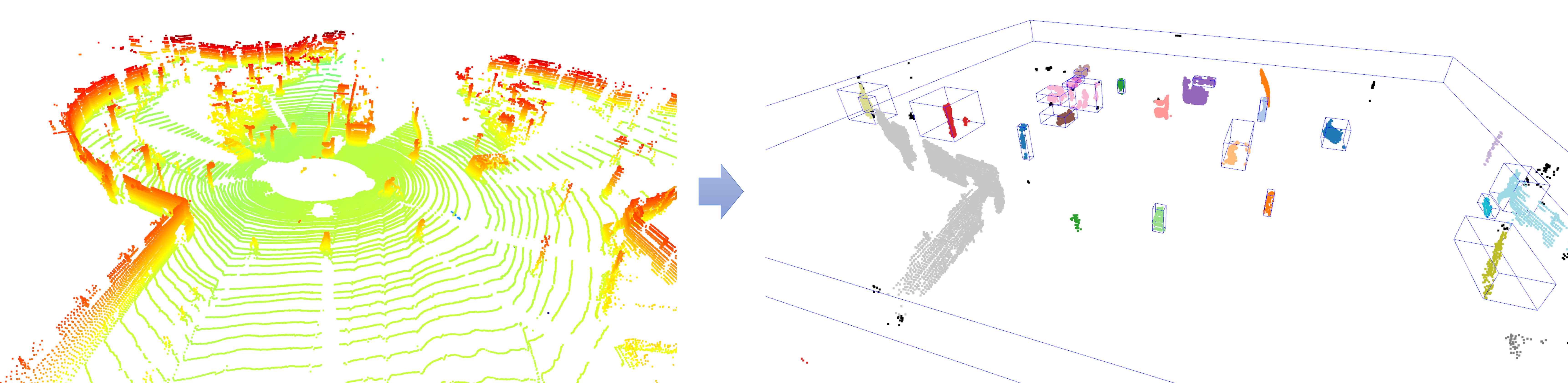
객체 인식을 위한 전체 코드
- 지금까지 살펴본 내용을 모두 정리하면 아래 코드에서 확인할 수 있습니다. 전체 순서는 다음과 같습니다.
- ①
downsampling - ②
remove outliers - ③
segment plane with RANSAC - ④
clustering with HDBSCAN - ⑤
generate 3D Bounding Box
import open3d as o3d
import numpy as np
import time
pcd_path = "./000000.pcd"
pcd = o3d.io.read_point_cloud(pcd_path)
# downsampling
pcd_1 = pcd.voxel_down_sample(voxel_size=0.1)
# remove outliers
pcd_2, inliers = pcd_1.remove_radius_outlier(nb_points=20, radius=0.3)
# segment plane with RANSAC
plane_model, road_inliers = pcd_2.segment_plane(distance_threshold=0.1, ransac_n=3, num_iterations=100)
pcd_3 = pcd_2.select_by_index(road_inliers, invert=True)
# CLUSTERING WITH HDBSCAN
import matplotlib.pyplot as plt
import hdbscan
clusterer = hdbscan.HDBSCAN(min_cluster_size=30, gen_min_span_tree=True)
clusterer.fit(np.array(pcd_3.points))
labels = clusterer.labels_
max_label = labels.max()
print(f'point cloud has {max_label + 1} clusters')
colors = plt.get_cmap("tab20")(labels / max_label if max_label > 0 else 1)
colors[labels < 0] = 0
pcd_3.colors = o3d.utility.Vector3dVector(colors[:, :3])
# generate 3D Bounding Box
import pandas as pd
bbox_objects = []
indexes = pd.Series(range(len(labels))).groupby(labels, sort=False).apply(list).tolist()
MAX_POINTS = 300
MIN_POINTS = 50
for i in range(0, len(indexes)):
nb_points = len(pcd_3.select_by_index(indexes[i]).points)
if (nb_points > MIN_POINTS and nb_points < MAX_POINTS):
sub_cloud = pcd_3.select_by_index(indexes[i])
bbox_object = sub_cloud.get_axis_aligned_bounding_box()
bbox_object.color = (0, 0, 1)
bbox_objects.append(bbox_object)
print("Number of Boundinb Box : ", len(bbox_objects))
list_of_visuals = []
list_of_visuals.append(pcd_3)
list_of_visuals.extend(bbox_objects)
# o3d.visualization.draw_geometries([pcd])
o3d.visualization.draw_geometries(list_of_visuals)

- 샘플 데이터를 한개 더 살펴보도록 하겠습니다. 코드는 동일하게 사용하였고 결과만 공유해보겠습니다.
- 샘플 데이터 : https://drive.google.com/file/d/18m5o8dwgCp-h75YW8Ej648bKBES-rb5v/view?usp=sharing
- 위 결과를 살펴보면 앞에서 사용한 알고리즘들의 파라미터 튜닝이 필요해 보이며 추가적인 보완 알고리즘 또한 필요할 수 있습니다.
- 지금까지 살펴본 내용은 일반적인 포인트 클라우드를 처리하는 방법 중 하나이며 이와 같은 방법을 통하여 전처리 및 Unsupervised 방식으로 클러스터링을 할 수 있음을 알 수 있었습니다.
Point Cloud Alignment via Iterative Closest Point 실습
ICP (Iterative Closest Point)는 2개의 포인트 클라우드 간의 차이를 최소화하는 알고리즘으로 3D 데이터를 다룰 때 많이 사용되는 알고리즘 입니다.ICP는 포인트 클라우드를 합칠 때 사용하는 방법이므로 기본적으로 필요한 전체 포인트 클라우드를 한번에 취득하지 못하는 한계 때문에 이와 같은 알고리즘을 필요로 합니다.- 예를 들어
3D Scanning을 한 이후Reconstruction을 할 때,ICP는 개체 또는 장면의 여러 스캔을 정렬하여 완전한 3D 모델을 생성하는 데 사용됩니다.ICP는 이 때, 서로 다른 포인트 클라우드를 합치고 스캔 간의 불일치를 해결하는 데 도움이 됩니다. 로보틱스분야에서는ICP를 이용하여 로봇의Localization을 할 때 사용할 수 있습니다. 현재 센서 판독값을 기존 map 또는 이전 판독값과 정렬하여 로봇의 현재 위치를 이해하는 데 사용할 수 있습니다.자율 주행 차량에서도ICP는 차량의 센서 데이터를 지도 또는 이전 판독값과 정렬하는 데 사용할 수 있습니다. 이와 같은 정렬은 Perception 및 Planning 등에 사용됩니다.
- 연속적인 포인트 클라우드가 형성될 때, 다른 센서값 또는 이전의 포인트 클라우드와 어떻게 잘 결합하여 사용할 지에 대한 알고리즘이
ICP가 됩니다. - 상세 내용은 다음 링크에서 확인 가능합니다.
- 링크 : https://gaussian37.github.io/autodrive-lidar-icp/
Point-to-Point Vs. Point-to-Plane
- 이번 글에서는
open3d의 API를 이용하여 2개의 포인트 클라우드를 어떻게ICP적용할 수 있는 지 방법을 살펴보도록 하겠습니다. - 대표적인
ICP방법으로Point-to-Point방식과Point-to-Plane방식을 각각 사용해볼 예정입니다. - 먼저
Point-to-Point ICP는 다음과 같은 절차를 가집니다.- ①
Correspondence Finding: For each point in the source point cloud, find the closest point in the target point cloud. - ②
Transformation Estimation: Compute the rigid transformation (rotation and translation) that minimizes the mean squared error between the corresponding points. - ③
Transformation Application: Apply the transformation to the source point cloud. - ④
Iteration: Repeat steps 1-3 until convergence, i.e., the change in error is below a certain threshold.
- ①
point-to-point ICP를 위한loss function은corresponding points간sum of squared Euclidean distances를 기본적으로 사용합니다.
- 다음으로
Point-to-Plane ICP에 대하여 살펴보겠습니다. point-to-plane ICP는surface normal을 이용하는ICP의 한 종류 입니다. 알고리즘의 절차는 다음과 같습니다.- ①
Correspondence Finding: For each point in the source point cloud, find the closest plane in the target point cloud. The plane is defined by a point in the target cloud and its normal vector. - ②
Transformation Estimation: Compute the rigid transformation that minimizes the sum of squared distances from each source point to its corresponding plane in the target cloud. - ③
Transformation Application: Apply the transformation to the source point cloud. - ④
Iteration: Repeat steps 1-3 until convergence.
- ①
point-to-plane ICP를 위한loss function은source points로 부터 대응되는target point cloud에서의 대응되는planes까지sum of squared distances를 기본적으로 사용합니다.
- 두 가지 대표적인
ICP알고리즘을 살펴보면point-to-plane ICP가geometric structure of the surface를 고려하므로 노이즈에 더 강건합니다. 하지만surface normal을 사전에 필요로 하고 계산 복잡도도 더 높다는 단점도 있습니다. 따라서point-to-plane ICP는 데이터에 노이즈가 많거나 point cloud에 대한 정보가 없을 경우에 사용하는 것이 좋습니다. - 반면에
point-to-point ICP는 단순히point간의euclidean distance만을 고려하기 때문에 과정이 단순한 반면 노이즈에 민감할 수 있습니다. 따라서point-to-point ICP는 노이즈가 덜하고 초깃값이 어느 정도 잘 정렬되어 있는 데이터에 사용하는 것이 좋습니다.
- 아래 코드의
source파일 : https://drive.google.com/file/d/1ra4MRmDh74QWwrWxqcoQ2qUUG_8YXm2z/view?usp=sharing - 아래 코드의
target파일 : https://drive.google.com/file/d/1J1FuTNPetYsftUOrckc3eNqxVwR74wOL/view?usp=sharing - 2개의 데이터는 노이즈가 덜하고 초깃값이 어느 정도 잘 정렬되어 있습니다. 따라서
point-to-point ICP만 사용하여도 충분한 것을 확인할 수 있습니다.
import numpy as np
import time
import open3d as o3d
import pandas as pd
import matplotlib.pyplot as plt
import copy
source = o3d.io.read_point_cloud("source.ply")
target = o3d.io.read_point_cloud("target.ply")
def draw_registration_result(source, target, transformation):
source_temp = copy.deepcopy(source)
target_temp = copy.deepcopy(target)
source_temp.paint_uniform_color([1, 0, 0])
target_temp.paint_uniform_color([0, 0, 1])
source_temp.transform(transformation)
o3d.visualization.draw_geometries([source_temp, target_temp])
threshold = 1.0
trans_init = np.identity(4)
draw_registration_result(source, target, trans_init)
print("Initial alignment")
evaluation = o3d.pipelines.registration.evaluate_registration(
source, target, threshold, trans_init)
print(evaluation)
# Initial alignment
# RegistrationResult with fitness=1.046892e-01, inlier_rmse=8.311949e-01, and correspondence_set size of 192
# Access transformation to get result.
########################## point-to-point ICP ##############################
print("\n\nApply point-to-point ICP")
reg_p2p = o3d.pipelines.registration.registration_icp(
source, target, threshold, trans_init,
o3d.pipelines.registration.TransformationEstimationPointToPoint())
print(reg_p2p)
print("Transformation is:")
print(reg_p2p.transformation)
draw_registration_result(source, target, reg_p2p.transformation)
# Apply point-to-point ICP
# RegistrationResult with fitness=9.411123e-01, inlier_rmse=2.790346e-01, and correspondence_set size of 1726
# Access transformation to get result.
# Transformation is:
# [[ 0.98046308 0.07335189 -0.18251481 1.32404862]
# [-0.07317525 0.99728929 0.00771128 -0.11099725]
# [ 0.1825857 0.00579494 0.98317286 -1.42716579]
# [ 0. 0. 0. 1. ]]
############################################################################
########################## point-to-plane ICP ##############################
print("\n\nApply point-to-plane ICP")
source.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
target.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
reg_p2l = o3d.pipelines.registration.registration_icp(
source, target, threshold, trans_init,
o3d.pipelines.registration.TransformationEstimationPointToPlane())
print(reg_p2l)
print("Transformation is:")
print(reg_p2l.transformation)
draw_registration_result(source, target, reg_p2l.transformation)
# Apply point-to-plane ICP
# RegistrationResult with fitness=9.323882e-01, inlier_rmse=2.793996e-01, and correspondence_set size of 1710
# Access transformation to get result.
# Transformation is:
# [[ 9.66789671e-01 1.58338593e-01 -2.00615607e-01 1.36196330e+00]
# [-1.54972254e-01 9.87384826e-01 3.24777823e-02 -2.02984836e-01]
# [ 2.03227292e-01 -3.09331810e-04 9.79131540e-01 -1.36642907e+00]
# [ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
############################################################################
- 위 코드를 수행한 결과 일치하지 않은 포인트 클라우드를
Point-to-Point방식과Point-to-Plane방식으로ICP를 적용하였고 유사한 수준에서inlier_rmse를 얻을 수 있었습니다. source→target으로 적용하기 위해 필요한transformation행렬 또한 유사한 수준에서 구할 수 있음도 확인할 수 있습니다.
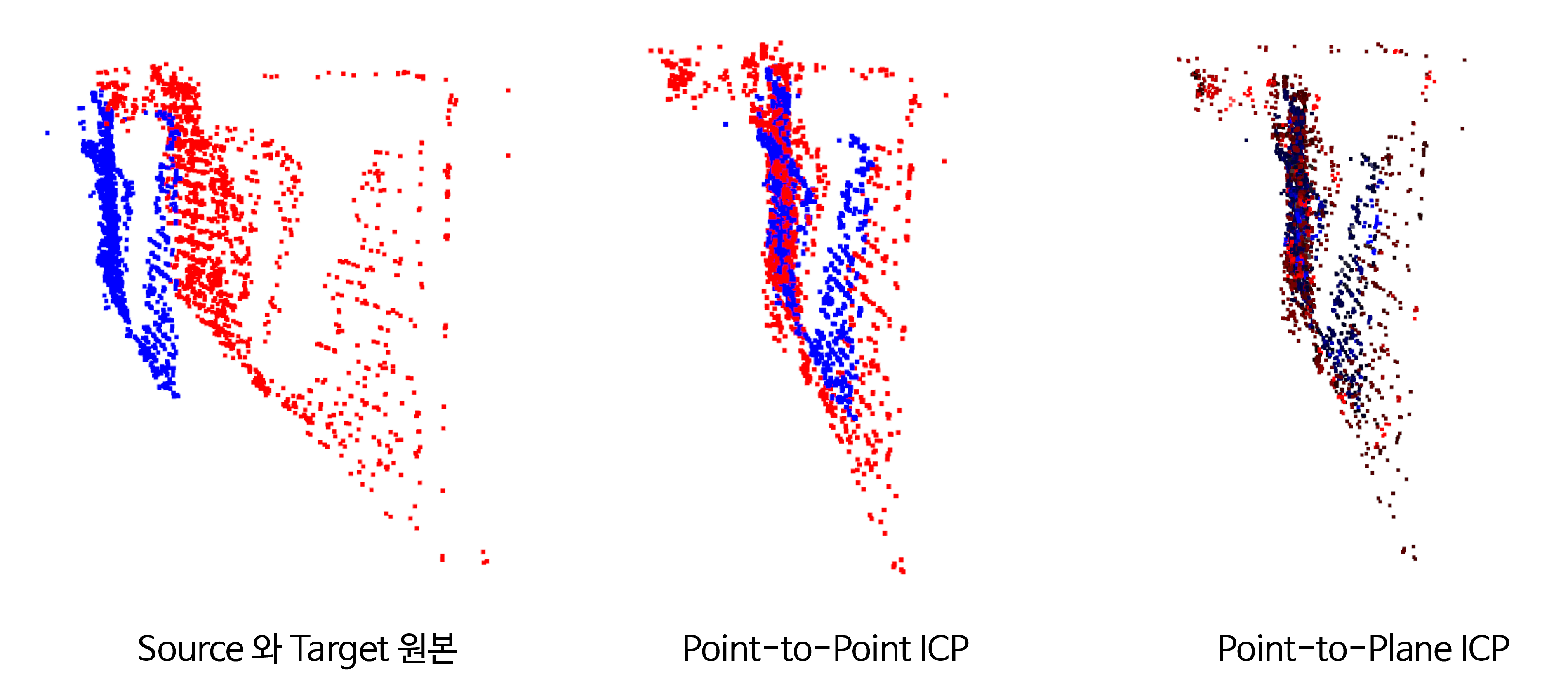
- 위 그림의 결과를 살펴보면
ICP를 적용하였을 때, 두 개의 포인트 클라우드가 겹치도록 위치 변환이 정상적으로 적용된 것을 확인할 수 있습니다.
Point-to-Plane Vs. Generalized ICP
- 논문 : https://www.roboticsproceedings.org/rss05/p21.pdf
- 참조 : https://gaussian37.github.io/autodrive-lidar-gicp/
Point-to-Plane ICP에 이어 많이 사용하는ICP방법론으로Generalized ICP가 있습니다.- 앞에서 설명한
Point-to-Point ICP또는Point-to-Plane ICP의 방법론은 두 포인트 클라우드 셋의best alignment를 찾아서 거리 차이값을 최소화 하는 방법을 사용하였습니다. 이 방법론은 데이터에 노이즈가 있거나 초깃값에 영향을 많이 받는다는 단점이 있습니다. - 반면
Generalized ICP는probabilistic framework개념을 도입하여 앞서 언급한 단점을 개선하고자 하였습니다. 이름 그대로 일반화하여 사용할 수 있는ICP방법론이며 다양한 환경에서의ICP를 진행할 때, 현재까지 베이스로 많이 사용하는 방법론 입니다.
- 이번에는
open3d에서 제공하는 샘플 데이터를 이용하여Point-to-Plane ICP대비Generalized ICP의 좋은 성능을 한번 확인해 보도록 하겠습니다. 물론 파라미터 튜닝에 따른 성능 차이는 발생할 수 있으니 참고만 해주시기 바랍니다.
import numpy as np
import time
import open3d as o3d
import pandas as pd
import matplotlib.pyplot as plt
import copy
demo_icp_pcds = o3d.data.DemoICPPointClouds()
source = o3d.io.read_point_cloud(demo_icp_pcds.paths[0])
target = o3d.io.read_point_cloud(demo_icp_pcds.paths[1])
def draw_registration_result(source, target, transformation):
source_temp = copy.deepcopy(source)
target_temp = copy.deepcopy(target)
source_temp.paint_uniform_color([1, 0, 0])
target_temp.paint_uniform_color([0, 0, 1])
source_temp.transform(transformation)
o3d.visualization.draw_geometries([source_temp, target_temp])
print("\n\nApply point-to-plane ICP")
demo_icp_pcds = o3d.data.DemoICPPointClouds()
source = o3d.io.read_point_cloud(demo_icp_pcds.paths[0])
target = o3d.io.read_point_cloud(demo_icp_pcds.paths[1])
source.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
target.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
reg_p2l = o3d.pipelines.registration.registration_icp(
source, target, threshold, trans_init,
o3d.pipelines.registration.TransformationEstimationPointToPlane())
print(reg_p2l)
print("Transformation is:")
print(reg_p2l.transformation)
draw_registration_result(source, target, reg_p2l.transformation)
# Apply point-to-plane ICP
# RegistrationResult with fitness=1.000000e+00, inlier_rmse=2.660825e-01, and correspondence_set size of 198835
# Access transformation to get result.
# Transformation is:
# [[ 0.80415634 0.0446264 -0.5927403 1.71318193]
# [-0.28280136 0.90581483 -0.31547248 1.26215451]
# [ 0.52283455 0.42131696 0.74103714 -1.38225719]
# [ 0. 0. 0. 1. ]]
print("\n\nApply Generalized ICP")
demo_icp_pcds = o3d.data.DemoICPPointClouds()
source = o3d.io.read_point_cloud(demo_icp_pcds.paths[0])
target = o3d.io.read_point_cloud(demo_icp_pcds.paths[1])
trans_init = np.identity(4)
source_down_sample = source.voxel_down_sample(0.1)
target_down_sample = target.voxel_down_sample(0.1)
max_correspondence_distances = 0.3
reg_gicp = o3d.pipelines.registration.registration_generalized_icp(
source, target, max_correspondence_distances, trans_init, o3d.pipelines.registration.TransformationEstimationForGeneralizedICP())
print(reg_gicp)
print("Transformation is:")
print(reg_gicp.transformation)
draw_registration_result(source, target, reg_gicp.transformation)
# Apply Generalized ICP
# RegistrationResult with fitness=7.213871e-01, inlier_rmse=5.392053e-02, and correspondence_set size of 143437
# Access transformation to get result.
# Transformation is:
# [[ 0.84047262 0.00661921 -0.54181359 0.64381443]
# [-0.14759452 0.96491234 -0.2171636 0.81044623]
# [ 0.52136516 0.26248878 0.81195936 -1.48451717]
# [ 0. 0. 0. 1. ]]
- 위 그림에서 파란색 포인트 클라우드를 빨간색 포인트 클라우드에 맞추는 것을 하는 것이
ICP의 목적입니다. Generalized ICP의 성능이 확실히 안정적임을 알 수 있습니다.ICP알고리즘에는 꽤 다양한 종류가 있습니다. 많은 파생된 방법을 알기 전에Generalized ICP방법론을 충분히 이해하는 것이 좋은 시작이 될 것입니다.
자율주행에서의 라이다 동향
자율주행 요소 기술
- 최근들어
라이다를 사용해야 하는 지에 대한 유무가 논쟁이 되고 있고 테슬라는 라이다는 물론 레이더도 사용하지 않으려고 하고 있습니다. 전 세계적으로 이런 논쟁이 있지만라이다센서 자체의 특성이 있기 때문에 이 글에서 한번 살펴보도록 하겠습니다.
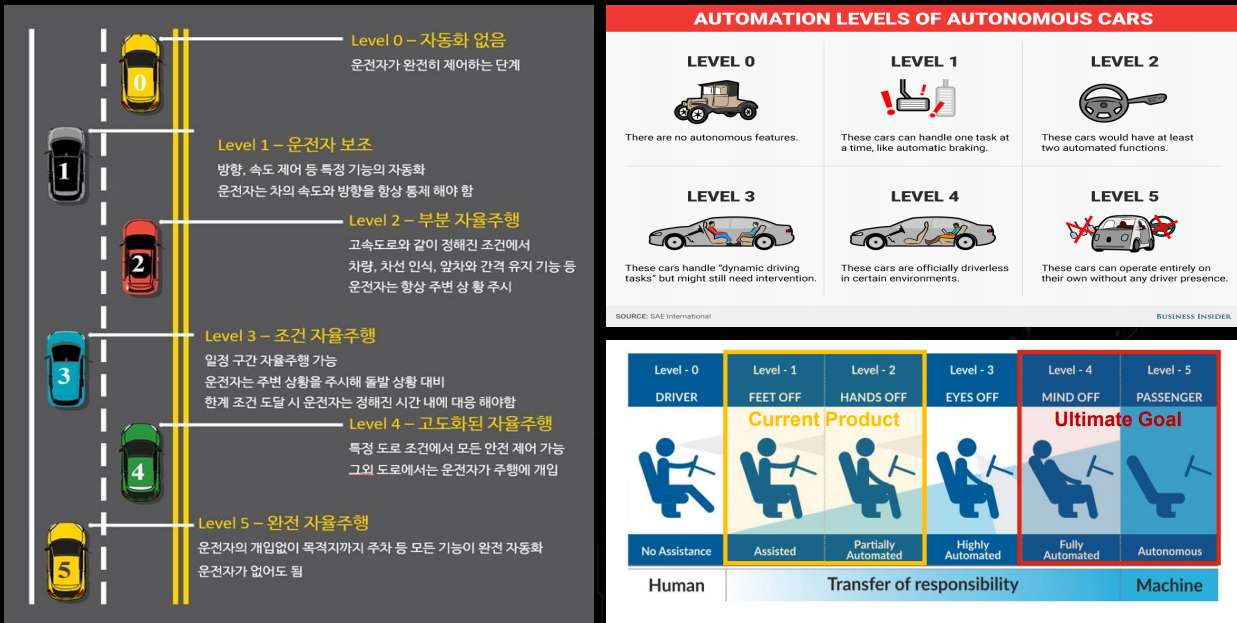
- 위 표는 이제 많은 사람들이 알고 계시는 자율주행의 6단계를 나타냅니다. 이번 글에서 다룰
라이다는 레벨 2단계 이상에서의 자율주행을 구현하기 위하여 사용되고 있습니다. 일반적으로 라이다를 사용하여 자율주행을 구현할 때, 현재 수준으로는 레벨 3의 양산차 판매 또는 레벨4의 로보택시 서비스를 판매하는 것을 목표로 하고 있습니다.
- 자율주행을 구현하기 위하여 센서를 통한
감지,주변 객체 인지,위치 추정,경로 계획 및 제어등이 필요합니다. - 이 기능들을 구현하기 위하여 가장 기본이 되는 센서를 통한
감지가 매우 중요하기 떄문에 다양한 센서들이 사용됩니다.
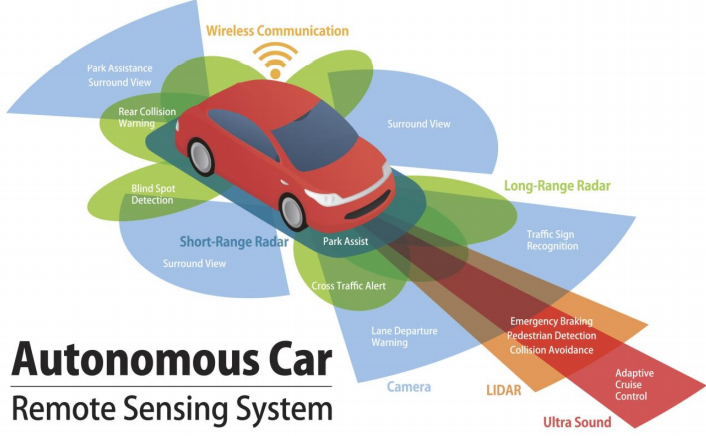
- 위 그림과 같이 자율주행을 구현하기 위하여 다양한 센서를 사용하고 있습니다. 센서들마다 특성이 있기 때문에 서로 다른 센서가 보완해 주고 있습니다. (현 시점으로 테슬라는 카메라, 초음파 센서만 사용하고 있긴 하지만…)
- 대표적으로
GPS,IMU,카메라,레이더등이 있고 자율주행에서 사용하는HD Map그리고 이 글에서 다룰라이다가 있습니다. 먼저라이다를 써야하는 이유를 살펴보기 전에 다른 센서의 특성을 간략하게 살펴보고라이다가 가지는 장점을 다루어 보겠습니다.
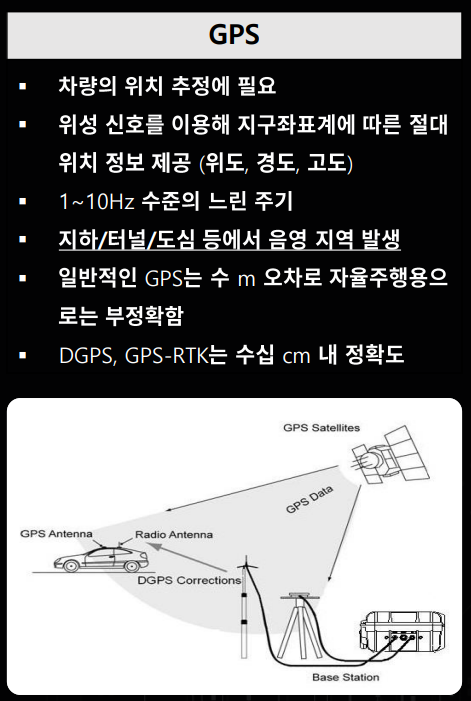
- 먼저
GPS (Global Positioning System)센서는 차량의 위치를 추정하는 데 사용되는 센서입니다. 위성으로 부터 신호를 받아서 차량의 절대적인 좌표를 얻게 되는데 문제는 현재 제공되는 GPS의 오차 수준이 미터 단위 정도의 정확도 밖에 제공하고 있지 못하기 때문에 자율 주행에 필요한 수십 cm 단위의 정확도를 달성하기 위해서는 주변에 있는 통신 인프라와 함께 통신하는 DGPS나 GPS-RTK와 같은 기술들이 필요합니다. - 또한
GPS는 고층 빌딩이 둘러 쌓여있거나 지하 터널에서는 순간적으로 신호를 받지 못하는 경우가 발생할 수 있습니다. 모든 판단을 센서를 통하여 하는 자율 주행 시스템의 경우 순간적인 신호 끊김도 위험하기 때문에 GPS 만으로는 위치 추정이 어렵습니다.
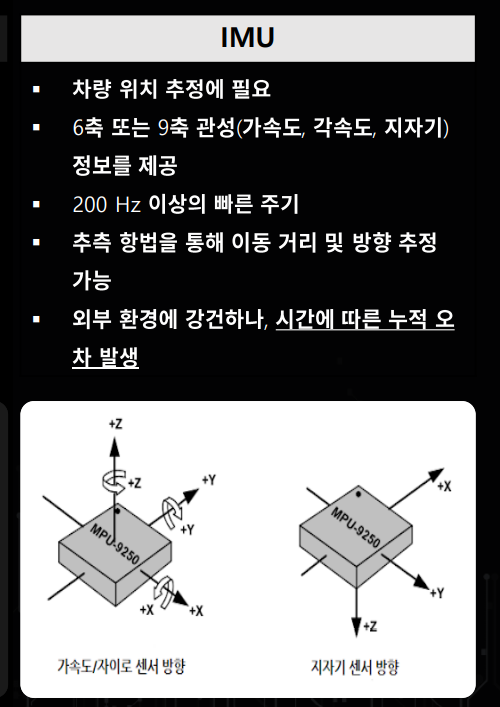
- 그래서 함꼐 사용되는 센서가
IMU (Inertial Measurement Unit)입니다.IMU는 순간순간 자동차의 속도, 가속도 및 이동 방향을 관성 정보를 이용하여 측정하는 센서입니다. 따라서 순간적인 차량의 이동 정보를GPS와 함께 이용하여 차량의 위치를 추적하는데 사용됩니다. IMU센서는 순간 순간 위치를 파악할 수 있으나 매 순간 위치에 센서의 오차가 있을 수 있고 이 오차가 계속 누적이 되면 차이가 발생할 수 있으므로 최근에는 카메라, 레이더, 라이다 등이 같이 사용되게 됩니다.
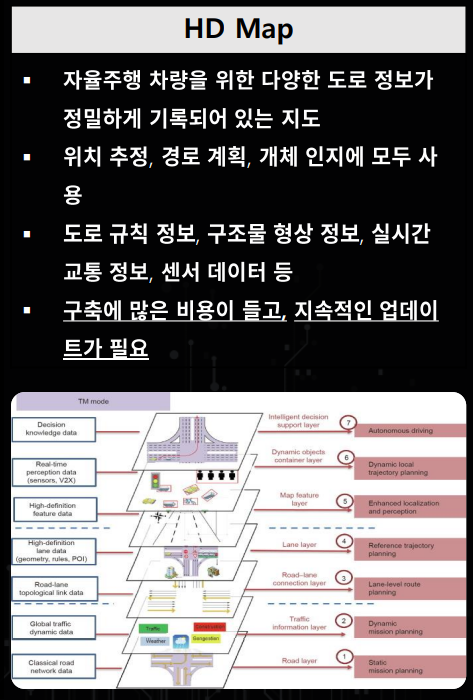
HD (High-definition) map이란 단순히 내비게이션에 사용되는 지도 정보 뿐 아니라 자율 주행 차량이 이동하는 도로 환경 정보 (차선, 가드레일 등)를 알수 있으므로 위치를 판단할 때 사용할 수 있습니다.- 하지만
HD map을 구축하는 데 굉장히 많은 비용이 들고 한번 구축했다고 하더라도 지속적인 업데이트가 필요하기 때문에 모든 지역의 HD map을 구축하는 데 한계가 있습니다.

- 자율 주행 자동차 및 ADAS에서 가장 많이 사용되는
카메라같은 경우 풍부한 텍스쳐 정보를 담고 있는 영상 정보를 얻을 수 있습니다. - 카메라 센서의 한계점으로 지적되는 주변 환경에 취약하다는 단점이 있어서 최근에는 레이더나 라이다와 함께 사용되고 있습니다.
- 최근에 딥러닝 기술의 발달로 더욱 높은 정확도로 자율 주행에 필요한 정보를 카메라를 통해 얻고 있는 추세입니다.
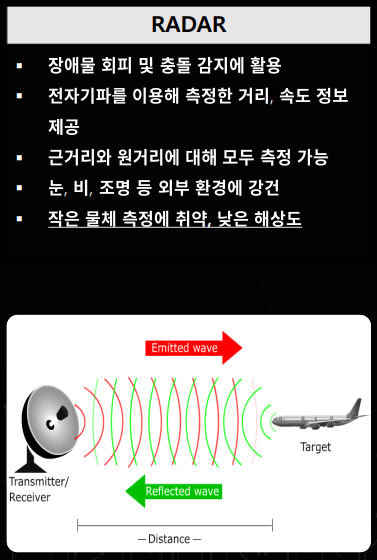
- 카메라와 달리
레이더, RADAR(Radio Detection and Ranging)는전자파를 이용하여 거리나 속도 정보를 자율 주행 자동차에 제공합니다. 레이더 같은 경우 원거리 물체를 측정하는 데 용이하고 특히 눈, 비, 조명과 같은 주변 환경에 굉장히 강건하여 악조건 환경에 자율 주행 시스템의 판단을 돕는데 사용되고 있습니다. - 하지만 레이더의 경우 아직 까지 해상도가 낮기 때문에 레이더 센서의 값만을 가지고 감지된 물체가 차량인지 사람인 지 판단하는 데에는 한계가 있습니다. 현재 수준으로는 물체의 구분보다는 물체의 유무 판단에 적합합니다.
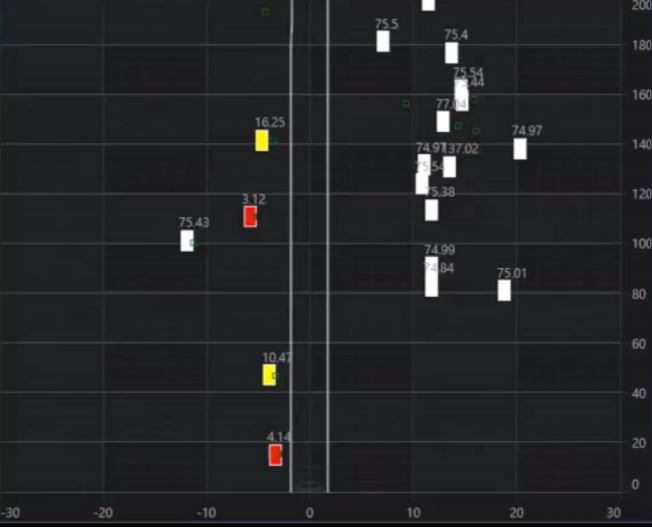
- 위 그림은 레이더를 통하여 도로 위의 물체를 파악하여 위치를 표시한 예시입니다.
- 지금 까지 라이다 센서를 제외한 자율 주행에 많이 사용되는 센서들의 특성에 대하여 간략하게 알아보았습니다.
라이다 센서
- 그러면 이 글의 주제인 라이다에 대하여 알아보도록 하겠습니다.

라이다, LIDAR(Light Detection and Rangin)는 빛 즉레이저를 이용하여 고해상도의 3차원 정보를 제공하는 센서입니다.
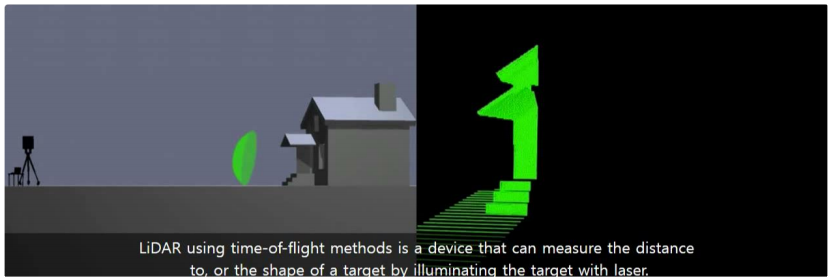
- 위 그림과 같이 라이다는 레이저를 송출하고 레이저가 물체에 맞고 반사되어 돌아오는 시간을 계산하여 빛의 이동 시간을 계산하고 이를 통해 주변 환경에 대한 3차원 형상을 측정합니다.
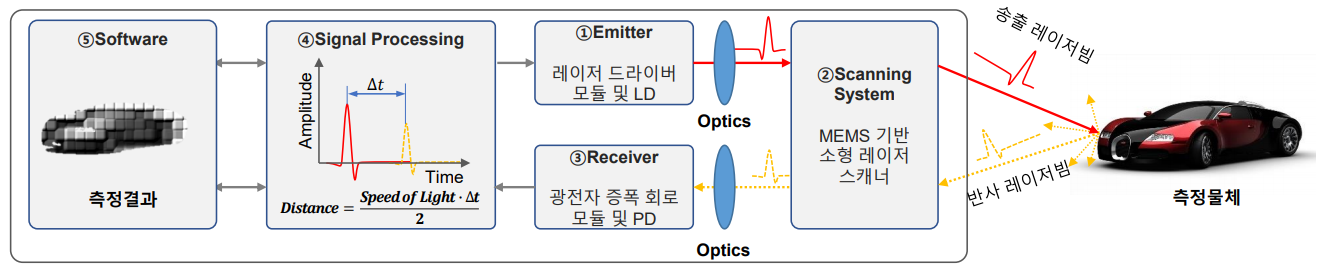
- 좀 더 상세하게 알아보면 라이다의 프로세는 위 그림과 같습니다.
- ①
Emitter: 레이저를 송출하는 역할을 합니다. - ②
Scanning System: 송출한 레이저를 주변 환경에 맞게 조사하는 역할을 합니다. - ③
Receiver: 반사되어 들어오는 빛을 다시 측정하는 역할을 합니다. - ④
Signal Processing:Emitter~Receiver까지 걸린 시간을 이용하여 각 포인트 마다의 거리를 계산하는 역할을 합니다. - ⑤
Software:Signal Processing을 통해 얻은 각 Point 정보를 이용하여 주변 물체에 대한 측정 결과를 제공합니다.
- 라이다의 특성 상 카메라에 비해서 눈, 비, 안개, 조명과 같은 주변 환경 등에 강건하기도 하고 레이더에 비해서 고해상도의 3차원 형상 정보를 제공하고 있어서 레이더, 카메라와 함꼐 주변 환경을 감지할 수 있습니다.

- 라이다를 이용하면 위 그림과 같이 주변 환경의 3D 정보를 수많은 점들의 뭉치인 point cloud 형태로 나타낼 수 있습니다.
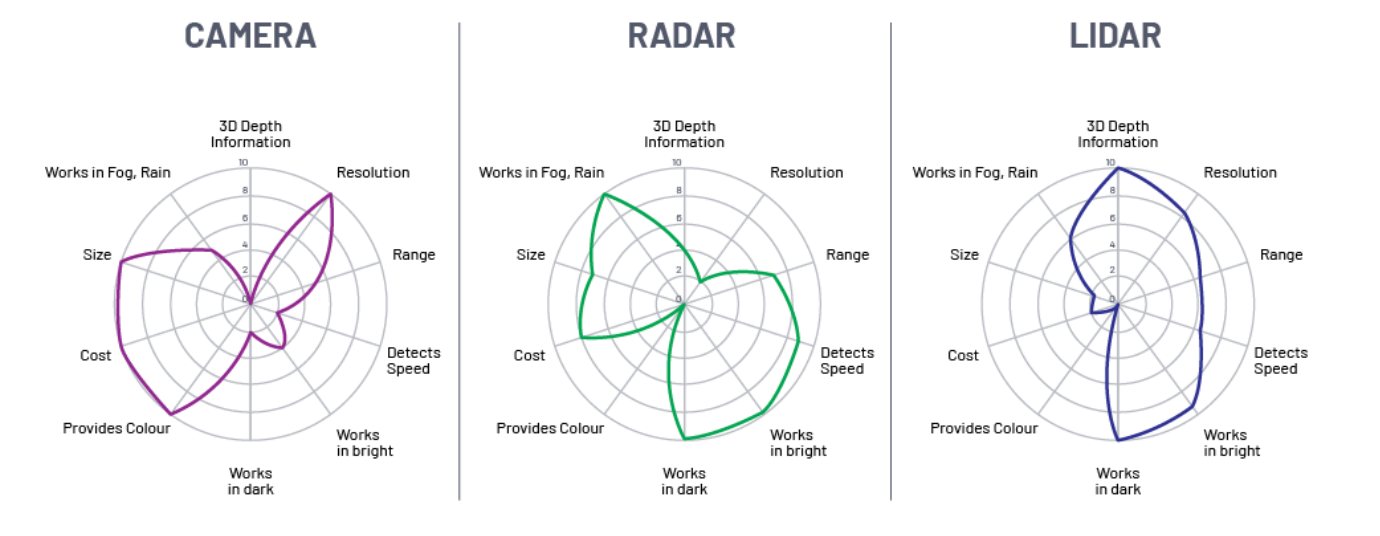
- 지금까지 알아본 센서 중에 흔히 가장 많이 사용되고 다루어지는 센서는 카메라, 레이더, 라이다 센서입니다.
- 위 표와 같이 각 센서는 장단점의 영역이 다르게 분포되어 있음을 알 수 있습니다. 즉, 단일 센서로는 모든 영역을 다 커버할 수 없습니다. 따라서 다양한 센서의 센서 퓨전을 통하여 서로의 장단점을 보완하는 것이 추세입니다.
- 특히 정교한 3D 데이터를 측정하기 위해서는 라이다가 독보적인 것을 알 수 있습니다.