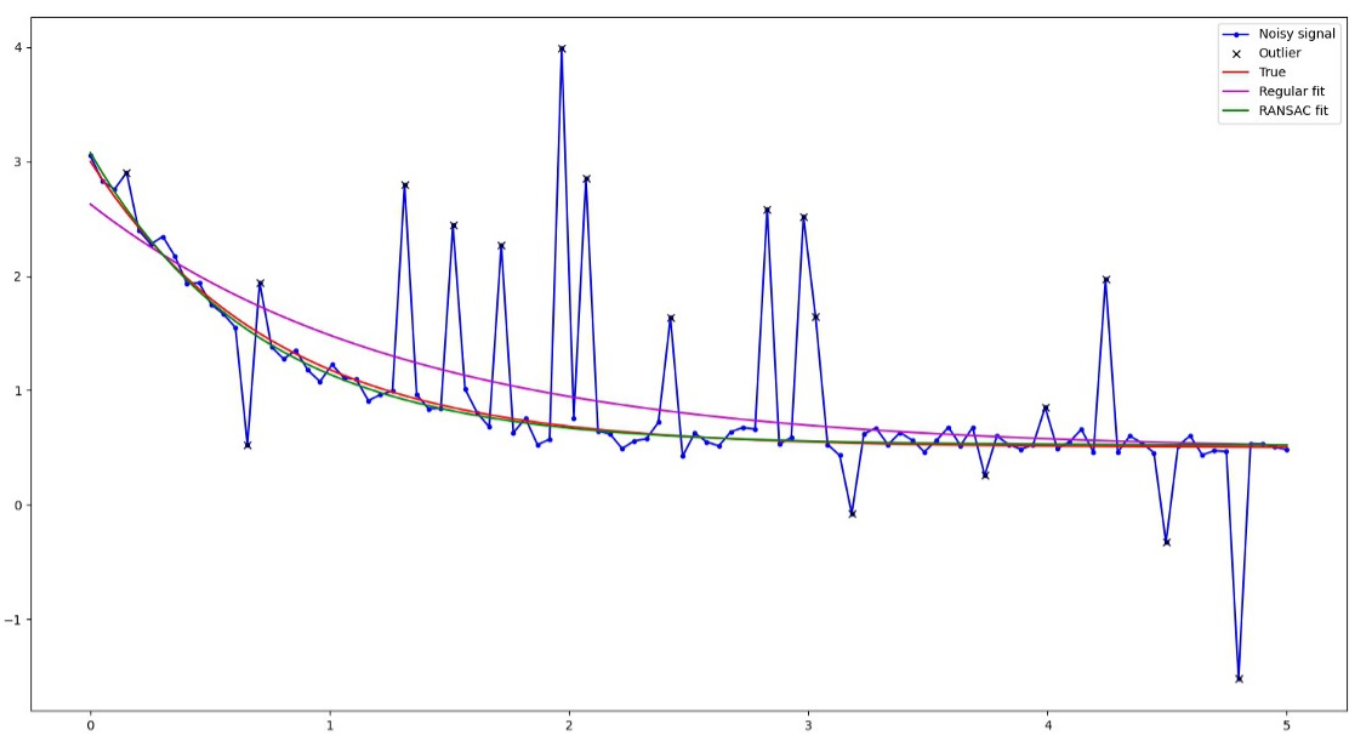
RANSAC (RANdom SAmple Consensus) 개념 및 실습
2022, Mar 20
- 참조 : https://gnaseel.tistory.com/33
- 참조 : https://scikit-learn.org/stable/auto_examples/linear_model/plot_ransac.html
- 참조 : https://www.youtube.com/watch?v=Q7FqV_bglHo
- 참조 : https://github.com/anubhavparas/ransac-implementation
목차
-
RANSAC 이란
-
RANSAC의 필요성
-
RANSAC 개념
-
RANSAC의 파라미터 셋팅법
-
Early Stop 사용법
-
RANSAC의 장단점
-
RANSAC Python Code
-
Lo-RANSAC 개념
-
Lo-RANSAC Python Code
-
Computer Vision에서의 RANSAC 활용
RANSAC 이란
RANSAC은Random Sample Consensus의 줄임말로 데이터를 랜덤하게 샘플링하여 사용하고자 하는 모델을 fitting한 다음 fitting 결과가 원하는 목표치 (합의점, Consensus)에 도달하였는 지 확인하는 과정을 통해 모델을 데이터에 맞게 최적화하는 과정을 의미합니다.- 따라서
RANSAC은 특정 모델식이나 알고리즘을 의미하는 것은 아니며① 데이터 샘플링,② 모델 fitting,③ 목표치 도달 확인이라는 3가지 과정을 반복적으로 수행하는 과정을 의미합니다. - 선형 함수 모델, 다항 함수 모델, 다양한 비선형 함수 모델 등 어떤 모델과 상관없이
모델 fitting과정을 적용하면 되므로RANSAC은 모델을 fitting 하는 일종의Framework라고 말하기도 합니다.
RANSAC의 필요성
- 앞의 설명을 참조하면
RANSAC이라는 방법론을 사용하지 않더라도 모델 fitting이라는 과정이 있기 때문에 굳이RANSAC절차를 거치지 않아도 됩니다. 그럼에도 불구하고RANSAC이 널리 사용되는 이유는 무엇일까요?
RANSAC이 널리 사용되는 이유는 다음 3가지를 동시에 만족하는 유연한 방법론이기 때문입니다.- ①
outliers에 강건한 모델을 만들 수 있습니다. - ②
outliers에 강건한 모델을 만드는 방법 중 매우 단순한 방법이므로 구현이 쉽고 응용하기도 쉽습니다. - ③ 어떤 모델을 사용하여도
RANSAC을 이용할 수 있으므로 임의의 모델을outliers에 강건하게 만들 수 있습니다.
RANSAC은 간단한 절차에도outliers에 강건한 모델 fitting을 할 수 있다는 이유로 널리 사용되고 있습니다.- 특히 컴퓨터 비전 관련 문제 해결 시, 다양한 이유로 노이즈나 오인식이 발생하게 되고 이러한 문제에 강건한 모델 설계를 위하여
RANSAC은 현재까지 많이 사용되고 있습니다.
RANSAC 개념
- 앞에서 언급한 바와 같이
RANSAC은① 데이터 샘플링,② 모델 fitting,③ 목표치 도달 확인과정을 거치며 최적의 모델 fitting을 하게 됩니다. - 가장 기본적인
RANSAC의 과정은 아래 flow-chart와 같습니다.
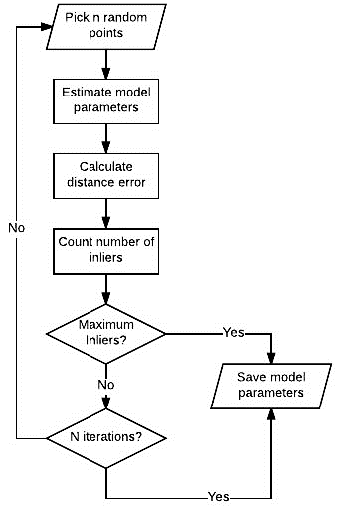
- ①
Pick n random points:inlier와outlier가 섞여 있는 전체 데이터셋에서 \(n\) 개의 데이터 (포인트)를 랜덤 샘플합니다. \(n\) 의 갯수를 정하는 내용은 본 글의 뒷부분에서 다룰 예정입니다. - ②
Estimate model parameters: 랜덤 샘플 데이터를 이용하여 사용하고자 하는 모델을 fitting 합니다. 본 글에서는 다항함수(polynomial function)를 사용하므로 다항 함수의 파라미터를 fitting 하는 방법을 사용하여 랜덤 샘플 데이터에 맞춰서 fitting 합니다. - ③
Calculate distance error: ② 과정을 통해 fitting한 모델과 전체 데이터에 대하여 error를 구합니다. - ④
Count number of inliers: ③ 과정에서 구한 error를 통해 각 데이터가inlier인 지outlier인 지 판단합니다. 이 때 판단하는 근거는threshold기준을 정하여 판단합니다.threshold가 크면 많은 실제outlier또한inlier가 될 수 있으므로 적당한 수준으로 정해야하며 본 글에서는 실험적으로threshold를 정하는 방법을 소개합니다. - ⑤
Maximum Inliers ?:inlier목표치 또는inlier데이터 비율의 목표치가 있고 현재 fitting한 모델이 이 목표치를 달성하였다면iteration을 끝낼 수 있습니다. 이와 같은 방법을early stop전략이라고 합니다. 만약 목표치를 달성하면 모델을 저장하고 전체 프로세스를 끝냅니다. 만약 목표치를 달성하지 못하였다면iteration을 반복합니다. - ⑥
N iterations ?: 위 flow-chart를 통해 최대 \(N\) 번의iteration을 반복하여RANSAC과정을 거치게 됩니다. \(N\) 이 커질수록 시도할 수 있는 횟수가 많아지기 때문에 좋은 모델을 선택할 수 있는 가능성이 커집니다. 하지만 그만큼 수행시간이 늘어나게 됩니다. 본 글의 뒷부분에서는 적당한 크기의 \(N\) 을 선택하는 방법을 소개하며 선택된 \(N\) 값을max iteration횟수로 지정하여 사용합니다.
- 이와 같은 전체 flow를 이용하여 기본적인
RANSAC이 동작하게 됩니다. 위 flow-chart를 구체적인 예시를 통해 한번 살펴보도록 하겠습니다.
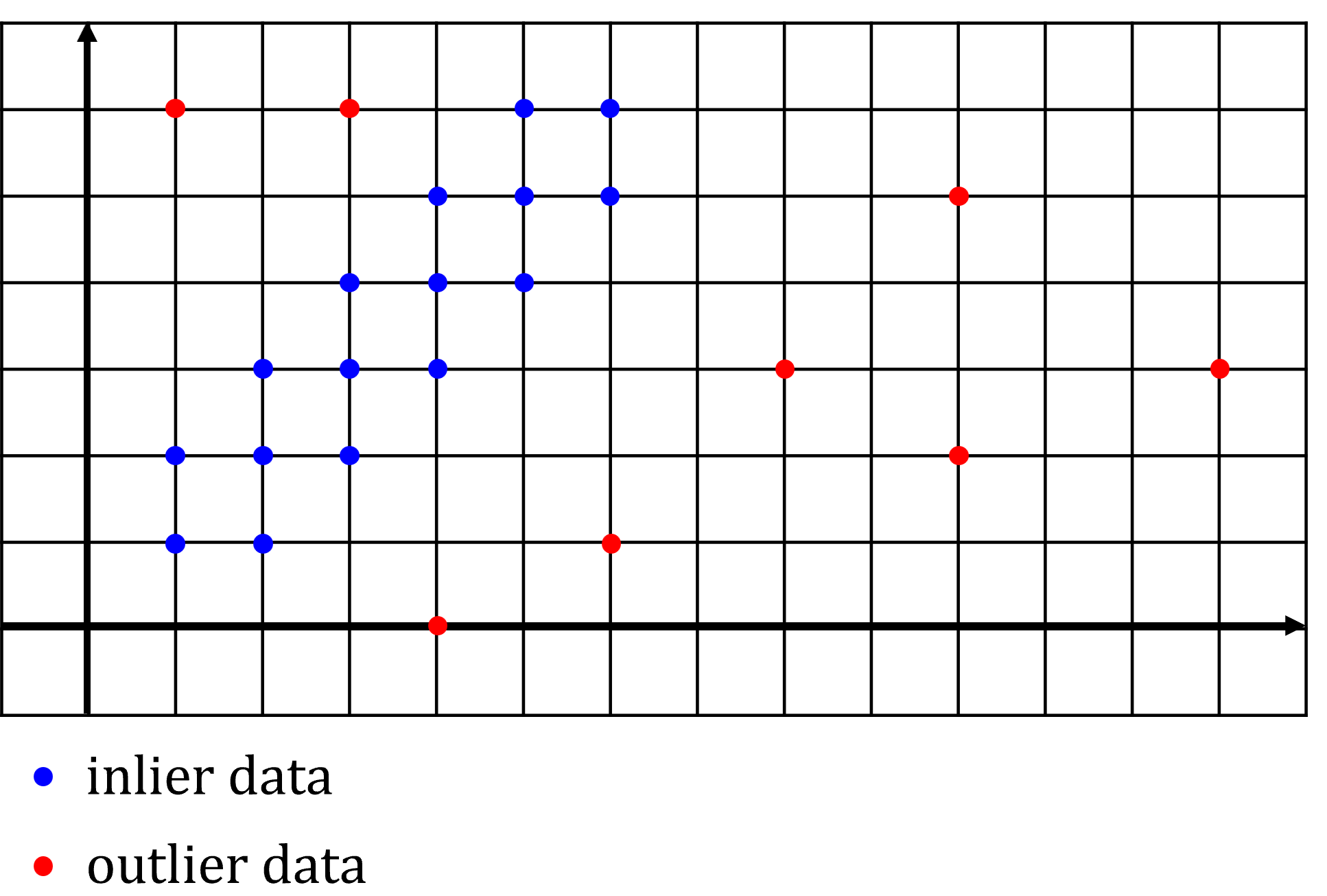
- 위 그림과 같은 데이터 셋이 있다고 가정하겠습니다. 가로축의 값 \(X\) 에 따른 \(y\) 값을 추정하는 모델링에 관한 데이터셋이며 파란색은
inlier데이터, 빨간색은outlier데이터입니다.
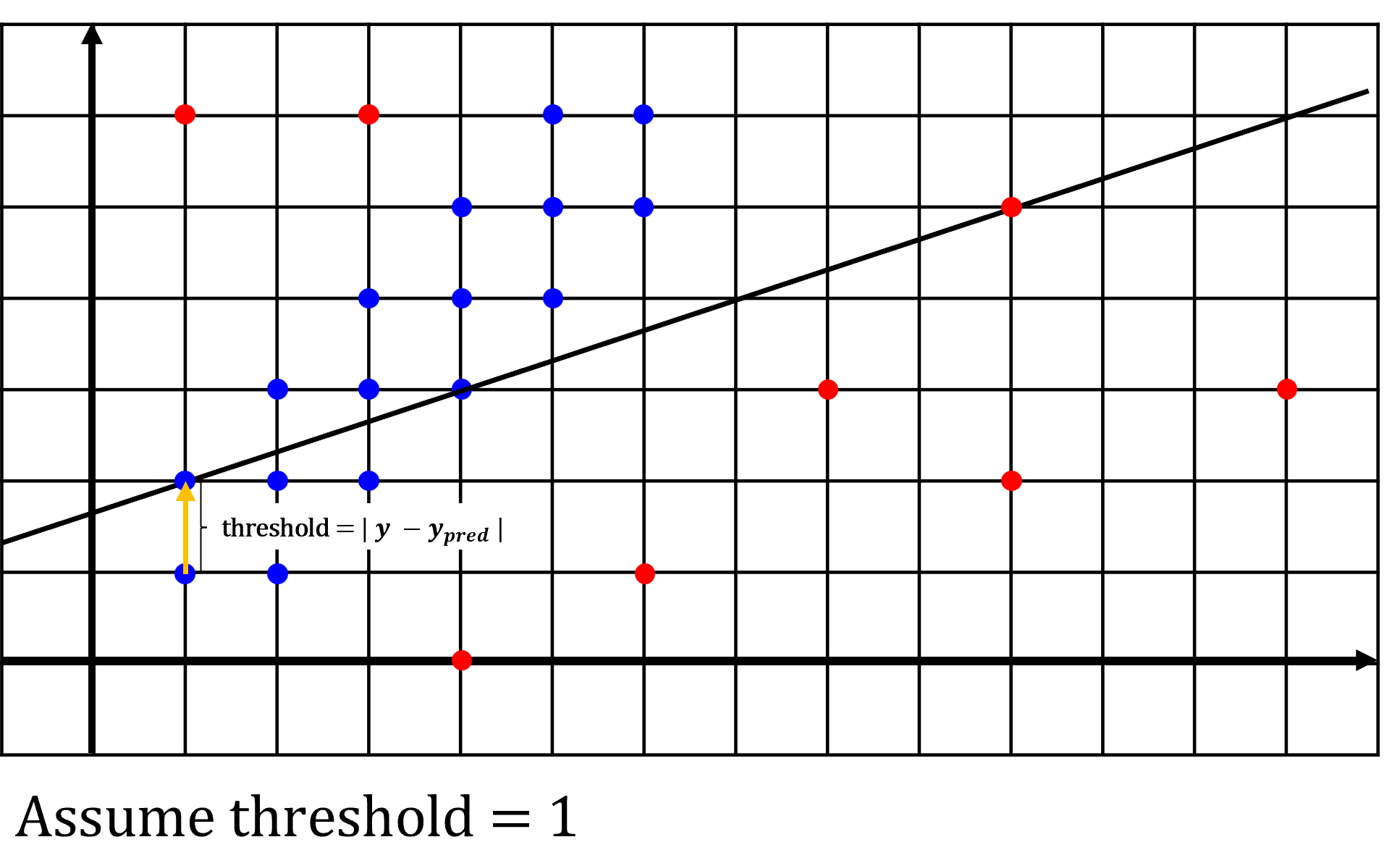
- 예제에서 ④
Count number of inliers과정을 위한threshold는 1로 가정하며 `threshold 계산은 \(\vert y - y_{\text{pred}} \vert\) 로 계산합니다. 그래프 상으로는 세로축 방향 포인트와 선의 길이로 생각하셔도 됩니다. - 본 예제에서는 선형 모델을 사용할 예정이므로 매 iteration마다 샘플링할 데이터의 수는 2개를 사용합니다. 직선을 긋기 위해서는 최소 2개의 데이터가 필요로 하기 때문에 2개의 데이터를 랜덤 샘플링하며
RANSAC에서는 모델링을 위한 최소 포인트를 샘플링 하는 것이 유리하기 때문에 단 2개의 데이터만 샘플링 합니다. 이와 관련된 내용은 본 글 뒷부분에 자세히 설명되어 있습니다.
- 예제에서는 ⑤
Maximum Inliers ?의 기준을inlier데이터의 비율이 50 % 이상인 경우로 가정하겠습니다. 즉, fitting된 모델을 이용하여threshold = 1을 기준으로inlier데이터의 비율을 계산하였을 때, 50 % 이상이면iteration을 종료하겠습니다.
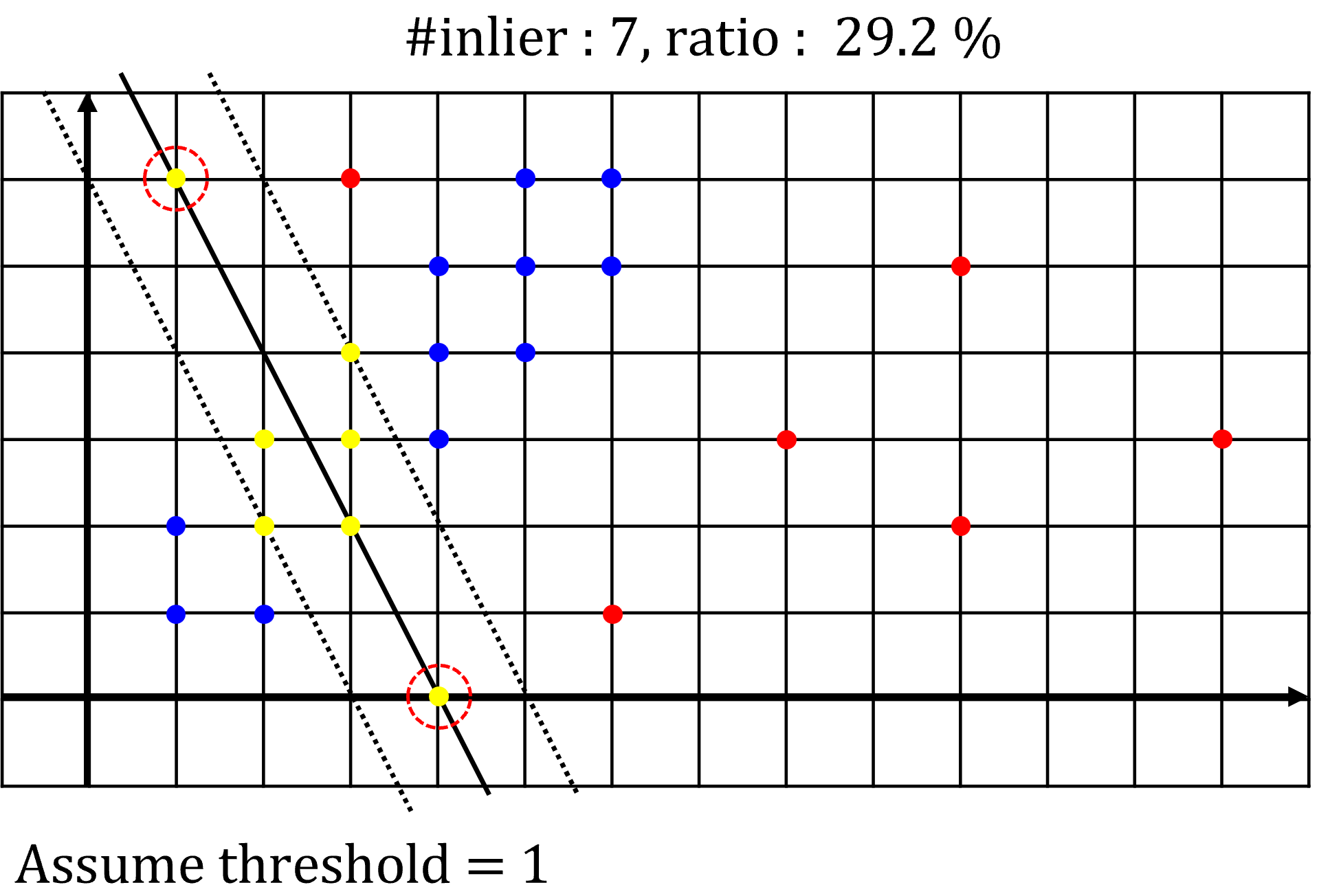
- 먼저 첫번째 예제입니다. 위 그림에서 빨간색 점선 원으로 선택된 2개의 포인트가 랜덤 샘플링된 포인트 입니다. 이 2개의 점을 잇는 선이 fitting한 선형 모델이 됩니다. 이 선을 기준으로
threshold가 1인 범위를 검은색 점선으로 그렸습니다. - 노란색 점들은 fitting한 모델을 기준으로
threshold이내에 존재하여inlier로 판단되는 점들입니다. 위 예제에서는 7개의 점이inlier로 판된되었으며 전체 데이터에서의 비율은 29.2 % 입니다. 따라서 flow-chart의 종료 조건인 50 % 를 초과하지 못하였으므로RANSAC을 종료하지 못하고 다시iteration을 반복하게 됩니다.
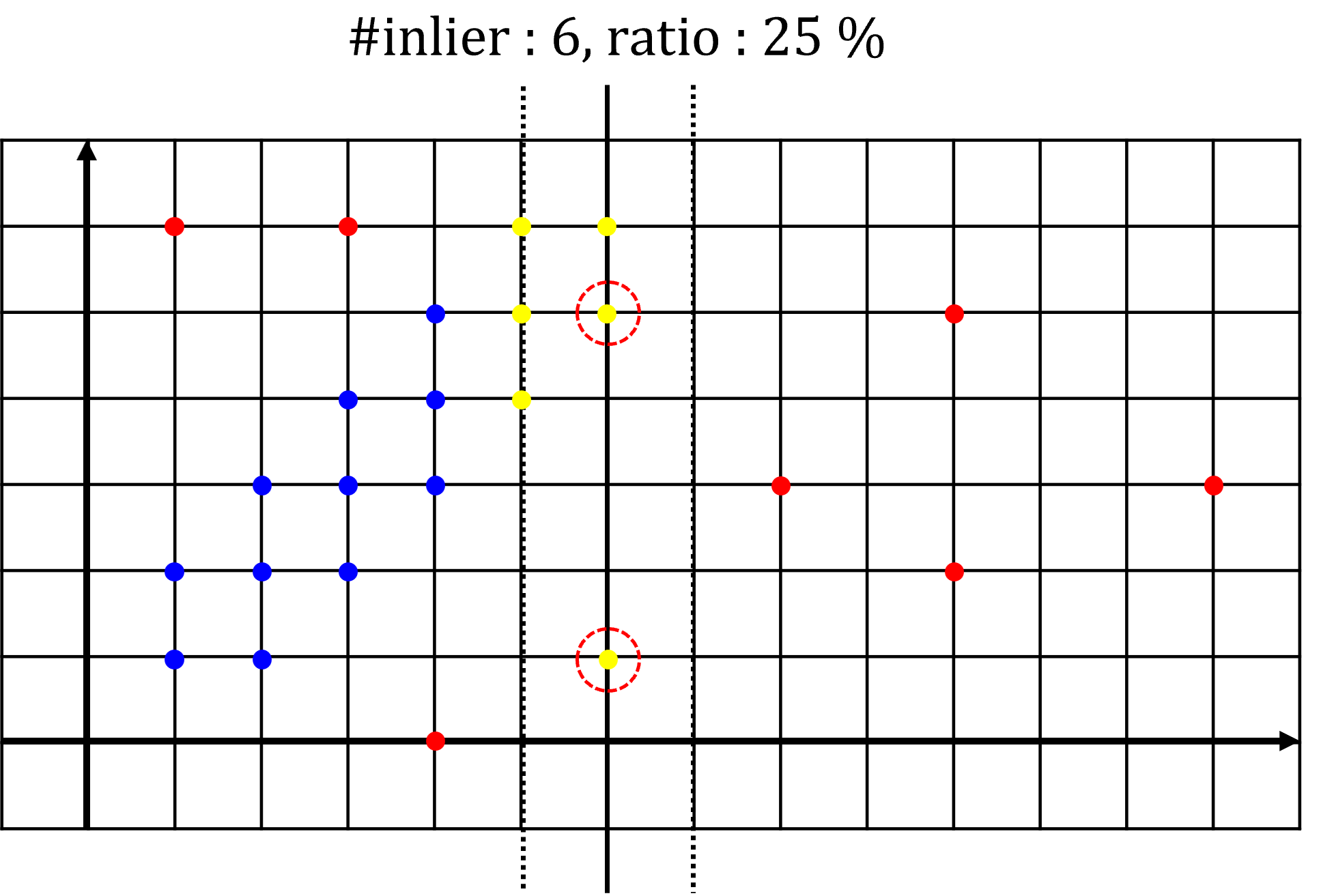
- 두번째 예제에서도 동작 방식 및 확인해야 할 점은 첫번째 예제와 동일합니다. 여기서 주의 깊게 볼 점은 새롭게 fitting한 모델의
inlier갯수가 첫번째 예제 경우보다 더 적다는 점입니다. 이와 같은 경우에는 fitting된 모델이 갱신되지 못합니다. 따라서 첫번째 예제의 fitting한 모델이 아직 까지는 최적의 모델이 됩니다.
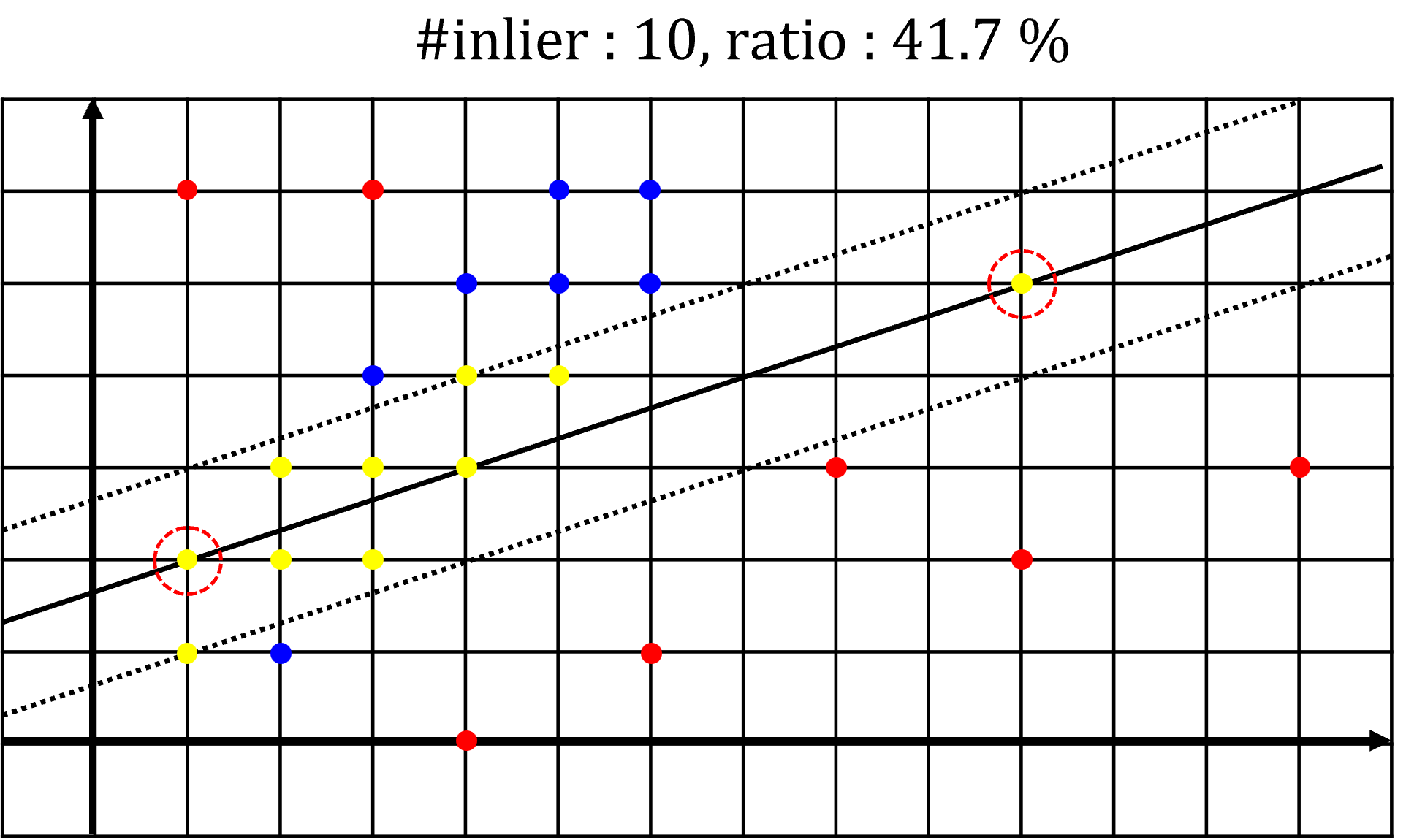
- 세번째 예제에서는 첫번째 예제보다
inlier갯수가 늘어났으므로 최적의 모델은 세번재 예제에서 구한 모델로 갱신이 됩니다. 하지만RANSAC종료 목표치인inlier데이터 비율 50 %를 만족하지 못하였으므로iteration은 계속 반복합니다.
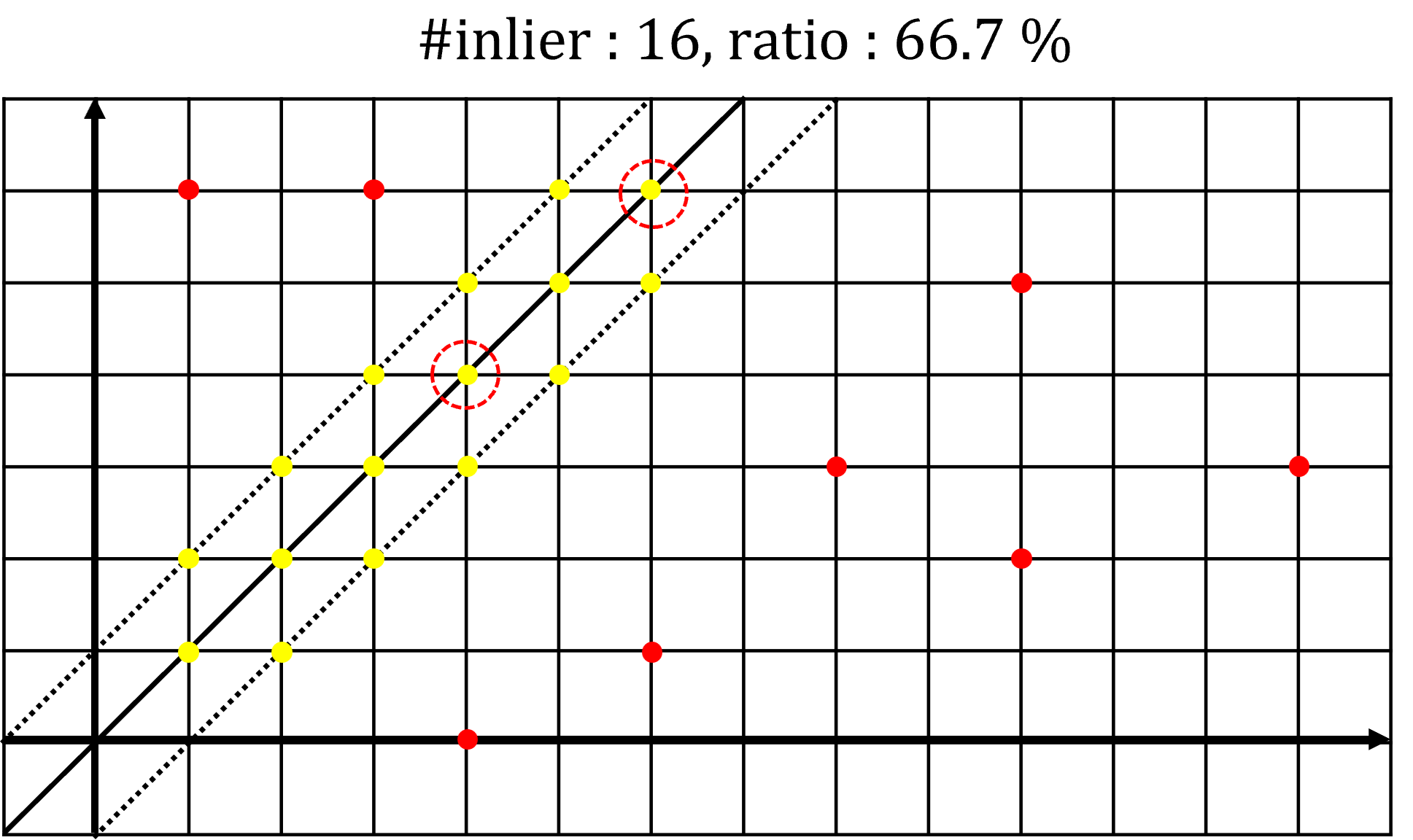
- 네번째 예제에서는 세번째 예제보다
inlier갯수가 늘어났고inlier데이터 비율도 66.7 %로 50%를 초과하였습니다. 따라서RANSAC종료조건을 만족하므로 전체 프로세스를 종료합니다. 네번째 예제에서 구한 모델이 최적의 모델이므로 이 모델의 결과가 최종 갱신됩니다.
- 이와 같은 과정을 거치는 방법이 기본적인
RANSAC방법입니다. 지금부터는 예제를 설명하면서 언급한 파라미터들을 어떻게 설정하는 지 그 방법에 대하여 살펴보도록 하겠습니다.
RANSAC의 파라미터 셋팅법
- 앞에서 살펴본
RANSAC의 개념 중 설정해 주어야 하는 파라미터가 3개 있습니다.threshold와sample size그리고sampling number입니다. threshold는 fitting한 모델을 이용하여 데이터 셋에서의inlier가 몇 개인지 파악하는 데 사용하는 기준값이었습니다. 이 값을 어떤 값으로 사용하는 지에 따라서 모델의 성능이 달라지게 됩니다. 매우 중요한 값이므로threshold를 정하는 다양한 접근 방법이 연구가 되었습니다. 사용중인 데이터셋의 통계적인 접근 방법이나 데이터셋에 대한 전문적인 지식으로 접근하는 방법등도 있지만 본 글에서는 가장 간단하고 확실한Grid Search와 같은 방법으로 여러개의threshold를 시도해보고 적합한threshold를 찾는 방법을 사용해 볼 예정입니다.- 여러
threshold에 따른 모델 fitting 양상을 보는 것이 좋은 모델을 선정하는 데 중요한 역할을 합니다.
- 단,
threshold에 따른 변화를 살펴보기 위해서는 다른 파라미터인sample size와sampling number는 가능한 고정한 후 실험을 하는 것이 편리합니다. 일반적으로sample size와sampling number를 설정하기 위해서 다음 식을 이용합니다.
- \[p = 1 - (1 - (1 - e)^m)^{N}\]
- \[p \text{ : Probability of obtaining a sample consisting only of inliers – sampling success}\]
- \[e \text{ : ratio of outliers in dataset}\]
- \[m \text{ : Number of data sampled per time}\]
- \[N \text{ : Number of algorithm iterations}\]
- 위 식이 정의된 배경은 다음과 같습니다.
- \[p(\text{fail once}) = \text{ do not select only inliers}\]
- \[1 - p \text{ : At least, one random sample set is free from outliers}\]
- \[1 - p = 1 - (1 - e)^{m}\]
- \[p(\text{fail N times}) = \text{ select at least one outlier in all N times}\]
- \[1 - p \text{ : At least, one random sample set is free from outliers}\]
- \[1 - p = (1 - (1 - e)^{m})^{N}\]
- \[\therefore \quad p = 1 - (1 - (1 - e)^m)^{N}\]
- 위 식에서 \(p\) 는
inlier로 이루어진 샘플을 얻을 확률이고 기대하는 값이기도 합니다. 따라서 \(p = 0.99\) 와 같이 매우 큰 값으로 설정합니다. 따라서 \(p\) 는 상수와 비슷하게 사용할 수 있습니다. - 그 다음 \(e\) 는 실제 데이터 확인을 통하여
outlier의 비율을 확인해서 정할 수 있습니다. 만약outlier의 비율을 알 수 없으면 보수적으로 0.5로 적용할 수도 있습니다. 실제로outlier의 비율이 0.5 정도가 된다면 노이즈가 굉장히 많은 데이터이기 때문입니다. 단, 식을 이용하여 전체 경향을 살펴보면outlier의 비율이 커질수록 시행 횟수가 늘어나게 됩니다. 아래 표의 각 셀은 확률 \(p\) 와 샘플링 횟수 \(m\) (도표에서는 \(s\) 로 표기함)에 따른 필요 시행횟수를 의미합니다. \(p\) 가 커질수록 \(m\) 이 커질수록 시행횟수가 늘어나야 하고outlier의 비율이 커질수록 시행횟수 또한 커져야 합니다.
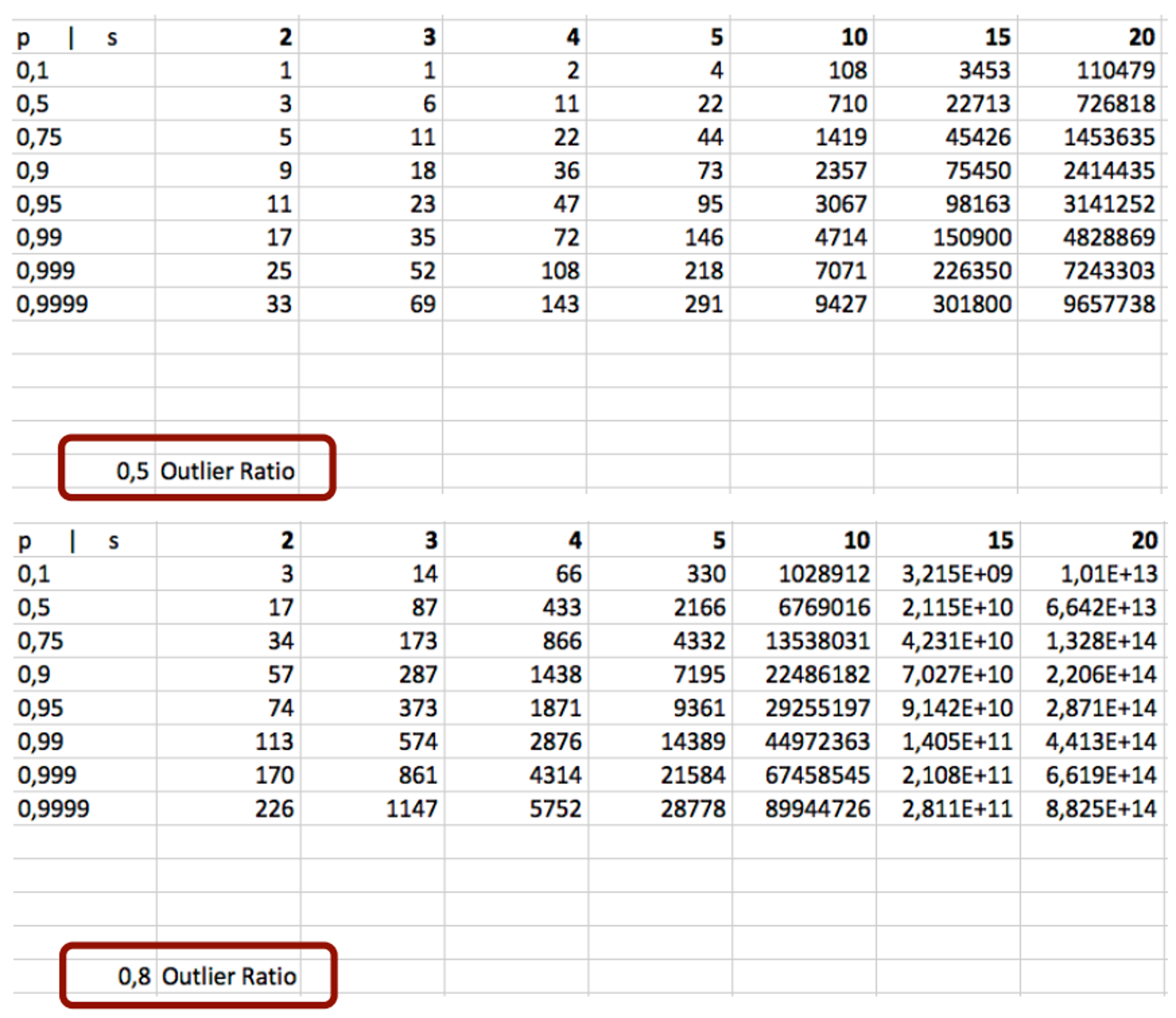
- 실제 정해주어야 하는 값은 \(m, N\) 입니다. \(m\) 은 크기가 작을수록 \(p\) 의 값이 1에 가까워지고 \(N\) 은 크기가 클수록 \(p\) 의 값이 1에 가까워 집니다.
- 예를 들어 \(m\) 이 클수록 샘플링 해야 하는 데이터의 수가 많아지기 때문에
outlier가 선택될 가능성이 더 커지게 됩니다. 즉inlier로만 이루어진 샘플을 얻을 확률이 낮아지므로 \(p\) 가 작아지게 됩니다. - 실제 값의 변화를 확인하여도 이유로 \(m\) 이 커질수록 \(p\) 가 작아지게 됩니다.\(e\) 가 비율이므로 \(1 - e\) 는 1보다 작은 값이고 \(m\) 만큼 거듭제곱이 되므로 \(m\) 이 커질수록 \((1 - e)^m\) 은 더욱 더 작아지게 됩니다. 따라서 \(p\) 또한 작아지도록 반영됩니다.
- 이러한 이유로 모델링에 필요한 최소 갯수를 샘플링 하는 방법을 많이 사용합니다. 예를 들면 선형 모델을 모델링할 때에는 2개의 샘플만 있으면 되기 때문에 \(m = 2\) 가 될 수 있습니다. 2차 모델의 경우 3개의 샘플이 필요하므로 \(m = 3\) 이 됩니다. 따라서
RANSAC에 사용되는 모델에 따라서 \(m\) 은 자동으로 결정될 수 있습니다.
- 따라서 \(p = 1 - (1 - (1-e)^{m})^{N}\) 에서 \(N\) 을 제외하고 모두 정할 수 있습니다. 직접적으로 \(N\) 을 구하기 위하여 다음과 같이 식을 정리할 수 있습니다.
- \[\begin{align} N &= \frac{\log{(1 - p)}}{\log{(1 - (1-e)^{m})}} \\ &= \frac{\log{(1 - 0.99)}}{\log{(1 - (1 - 0.5)^{m})}} \end{align}\]
- 위 식을 조건으로 살펴보았을 때, \(m = 1\) 일 때, \(N \approx 7\), \(m = 2\) 일 때, \(N \approx 16\) 등으로 \(m = 3\) 일 때, \(N \approx 34\), \(m = 4\) 일 때, \(N \approx 71\), … 과 같이 급격하게 증가하는 것을 볼 수 있습니다.
- 즉, 모델의 복잡도가 커질수록 모델 fitting을 하기 위한 최소 필요한 샘플링 수가 많아지고 그만큼 반복 수행을 많이 해야 원하는 \(p\) 의 확률로
inlier데이터를 뽑아낼 수 있습니다. 이러한 이유로 \(N\) 이 커지게 됩니다.
Early Stop 사용법
RANSAC을 통해 반복적으로 모델을 최적화 할 때, 적합한 모델을 찾았다면 더 이상 모델 fitting 작업을 할 필요가 없습니다. 따라서 다음과 같이 3가지 파라미터를 정하여RANSAC을 일찍 끝내는Early Stop을 사용하는 것이 좋습니다. 3가지 파라미터는 다음과 같습니다.
- ①
min iteration: 모델 fitting을 위한 최소 반복 횟수를 의미합니다. - ②
max iteration: 모델 fitting을 위한 최대 반복 횟수로 최대 반복 횟수 만큼 반복하면 모델 fitting이 실패하였음을 의미합니다. - ③
stop inlier ratio: 반복 작업을 끝내기 위한 최소inlier의 비율을 의미합니다. 따라서inlier의 비율이stop inlier ratio를 초과하면RANSAC작업을 끝냅니다.
- 앞에서 다룬 \(N\) 을 구하는 방법을 통하여 \(N\) 값을 얻은 뒤
max iteration으로 설정하고stop inlier ratio의 비율을 예상되는inlier의 비율을 통하여 정하거나, 실험적으로 의미있는 비율을 정하여 설정하면 효과적으로Early Stop을 적용할 수 있습니다.
RANSAC의 장단점
- 지금까지 살펴본 내용으로 설명을 하면 ①
RANSAC의 가장 큰 장점은outlier에 강건한 모델이라는 점입니다. 이 장점이RANSAC을 사용하는 가장 큰 이유이기도 합니다. 따라서outlier가 어느 정도 섞여있어도 그것들을 무시하고 모델링 할 수 있습니다. - 그리고 ②
RANSAC은outlier에 강건한 모델을 설계하는 방법 중 가장 쉬운 방법입니다.inlier의 갯수만 세면 되기 때문에 구현도 쉽고 어떠한 모델이라도 적용하기도 쉽습니다.
- 반면 ①
RANSAC은 랜덤 샘플이라는 방법을 이용하므로Non-deterministic하다는 단점이 있습니다. 즉, 같은 데이터 셋을 이용하여 모델링하더라도 매번 실행 결과가 다를 수 있다는 것입니다. 이 점은 관점에 따라서RANSAC의 장점이 될 수도 있고 단점이 될 수도 있다고 생각합니다. 하지만 모델의 재현성 관점에서는 단점이라고 볼 수 있습니다. - 두번째 단점은
RANSAC의 가장 치명적인 단점입니다. 만약outlier가 노이즈 처럼 생기지 않고 특정 분포를 가지게 되면 모델이outlier를 fitting 할 수 있습니다. 따라서 데이터 셋을 미리 확인하고outlier가 얼만큼 있는 지와outlier가 특정 패턴 및 분포를 가지는 지 사전에 확인하는 것은 매우 중요합니다. 만약 특정 분포를 가진다면 오히려 다른 방법으로outlier를 사전에 제거하는 것도 좋은 접근이 될 수 있기 때문입니다. - 또한
RANSAC은threshold파라미터에 큰 영향을 받는다는 단점이 있습니다.threshold를 너무 작게 설정하면 모델이 안정적으로 fitting이 되지 않을 수 있고 데이터의 변화에 민감하게 반응합니다. 반면threshold를 크게 잡으면outlier까지inlier로 판단할 수 있으므로 모델이 정상적으로 fitting할 수 없게됩니다. 뿐만 아니라inlier의 분포가 계속 변하게 된다면threshold기준 또한 adaptive하게 변해야 할 수 있습니다. 이러한 모든 것들을 반영하여threshold를 정하는 것이 어렵다는 것이RANSAC의 주요 단점 중의 하나입니다. - 마지막으로
RANSAC은Loss를 기반으로 동작하는 L1, L2 Loss와는 다르게Loss를 기반으로 모델 fitting을 하지 않습니다. 이러한 동작 방식이 다른 알고리즘과 연계되어 한번에Loss를 계산하는pipeline에 연결시킬 수 없다는 점이 단점이 될 수 있습니다. 왜냐하면 다양한 알고리즘이 머신러닝, 딥러닝 방식의 학습 방식으로 이루어지기 때문에 같은pipeline으로 연결할 수 있으면 한번에 전체pipeline을 학습할 수 있어서 효율적이기 때문입니다.
RANSAC Python Code
- 앞에서 다룬 내용을 파이썬 코드를 통하여 살펴보도록 하겠습니다. 살펴볼 내용은 다항함수를 이용하여 모델 fitting 하는 것이며 전체 데이터셋에서 80%는 약간의 노이즈만 추가하고 20%는 꽤 심한 변형을 주어
outlier가 되도록 하였습니다. 따라서early stop의stop inlier ratio는 0.8을 사용하고자 합니다. - 다항함수를 이용하는 것이므로 본 글에서는
np.polyfit또는scipy.optimize.curve_fit을 사용하여 모델 fitting 하는 방법을 사용하였습니다.
- 아래 코드의 전체적인 프로세스는 다음과 같습니다.
- ① 노이즈가 섞인 데이터를 생성합니다. 노이즈 또한 랜덤하게 생성합니다.
- ② \(p = 0.99, e = 0.5\) 인 조건에서
sampling number\(N\) 을 구하고 이 값을max iteration으로 사용합니다. 아래 코드의get_sampling_number함수가 이 내용에 해당합니다. - ③
threshold후보군을 작은 값부터 사용하여early stop을 만족하는 만족하는threshold를 찾습니다. 아래 코드의get_inlier_threshold함수가 이 내용에 해당합니다. - ④ 새로운 데이터를 생성한 다음에 앞에서 사용한
threshold와early stop을 이용하여RANSAC이 유효하게 동작하는 지 확인합니다. 아래 코드의get_model_with_ransac함수가 이 내용에 해당합니다.
import numpy as np
import math
import matplotlib.pyplot as plt
def get_sampling_number(sample_size, p=0.99, e=0.5):
'''
sample size : Number of sample size per every iterations
p : Desired probability of choosing at least one sample free of outliers
e : Estimated probability that a point is an outlier
'''
# Calculate the required number of iterations based on the formula
n_iterations_calculated = math.ceil(math.log(1 - p) / math.log(1 - (1 - e)**sample_size))
print(f"Calculated number of iterations: {n_iterations_calculated}")
return n_iterations_calculated
def get_inlier_threshold(thresholds, data, polynomial_degree, sample_size,
min_iteration, max_iteration, stop_inlier_ratio, verbose=False):
early_stop_flag = False
inlier_threshold = None
for threshold in thresholds:
best_fit = None
best_error = 0
for i in range(max_iteration):
# Randomly select sample points
subset = data[np.random.choice(len(data), sample_size, replace=False)]
x_sample, y_sample = subset[:, 0], subset[:, 1]
# Fit a line to the sample points
p = np.polyfit(x_sample, y_sample, polynomial_degree)
# Compute error
y_pred = np.polyval(p, X)
error = np.abs(y - y_pred)
# Count inliers
inliers = error < threshold
n_inliers = np.sum(inliers)
# Update best fit if the current model is better
if n_inliers > best_error:
print("threshold : {}, index : {}, n_inliers : {}".format(threshold, i, n_inliers))
best_fit = p
best_error = n_inliers
if (i > min_iteration) and (n_inliers/len(data)) >= stop_inlier_ratio:
early_stop_flag = True
inlier_threshold = threshold
if early_stop_flag:
break
if verbose:
# Best curve
y_best = np.polyval(best_fit, X)
# Plotting
plt.scatter(X, y, label='Data Points')
plt.plot(X, y_best, color='red', label='RANSAC Fit')
plt.legend()
plt.show()
if early_stop_flag:
break
return inlier_threshold
def get_model_with_ransac(data, polynomial_degree, threshold, sample_size,
min_iteration, max_iteration, stop_inlier_ratio, verbose=False):
early_stop_flag = False
inlier_threshold = None
best_fit = None
best_error = 0
for i in range(max_iteration):
# Randomly select sample points
subset = data[np.random.choice(len(data), sample_size, replace=False)]
x_sample, y_sample = subset[:, 0], subset[:, 1]
# Fit a line to the sample points
p = np.polyfit(x_sample, y_sample, polynomial_degree)
# Compute error
y_pred = np.polyval(p, X)
error = np.abs(y - y_pred)
# Count inliers
inliers = error < threshold
n_inliers = np.sum(inliers)
# Update best fit if the current model is better
if n_inliers > best_error:
best_fit = p
best_error = n_inliers
if (i > min_iteration) and (n_inliers/len(data)) >= stop_inlier_ratio:
early_stop_flag = True
inlier_threshold = threshold
print("index : {}, n_inliers : {}".format(i, n_inliers))
if early_stop_flag:
break
if verbose:
# Best curve
y_best = np.polyval(best_fit, X)
# Plotting
plt.scatter(X, y, label='Data Points')
plt.plot(X, y_best, color='red', label='RANSAC Fit')
plt.legend()
plt.show()
return early_stop_flag, best_fit
- 위에서 정의한 함수들을 이용하면 아래와 같이 실행할 수 있습니다.
# Generate synthetic data
np.random.seed(0)
n_points = 100
X = np.linspace(0, 10, n_points)
y = 3 * X + 10 + np.random.normal(0, 3, n_points)
# Add outliers
n_outliers = 20
X[-n_outliers:] += int(30 * np.random.rand())
y[-n_outliers:] -= int(50 * np.random.rand())
X = np.expand_dims(X, -1)
y = np.expand_dims(y, -1)
data = np.hstack([X, y])
threshold_cadidates = [1,2,4,8,16,32,64,128]
threshold_cadidates.sort()
sample_size = 2
max_iteration = get_sampling_number(sample_size)
threshold = get_inlier_threshold(
threshold_cadidates, data, polynomial_degree=1, sample_size=sample_size,
min_iteration=-1, max_iteration=max_iteration, stop_inlier_ratio=0.50, verbose=True)
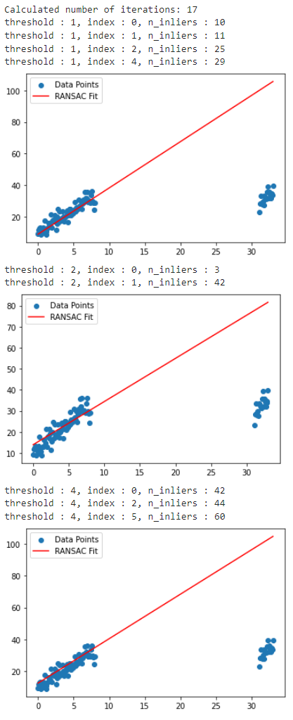
- 위 그림과 같이
threshold=4를 사용하는 것으로 구하였고 위 파라미터를 기준으로RANSAC을 수행하면 다음과 같습니다.
# Generate synthetic data
np.random.seed(np.random.seed())
n_points = 100
X = np.linspace(0, 10, n_points)
y = 3 * X + 10 + np.random.normal(0, 3, n_points)
# Add outliers
n_outliers = 20
X[-n_outliers:] += int(30 * np.random.rand())
y[-n_outliers:] -= int(50 * np.random.rand())
X = np.expand_dims(X, -1)
y = np.expand_dims(y, -1)
data = np.hstack([X, y])
success, param = get_model_with_ransac(data, polynomial_degree=1, threshold=threshold, sample_size=sample_size,
min_iteration=-1, max_iteration=max_iteration, stop_inlier_ratio=0.75, verbose=True)
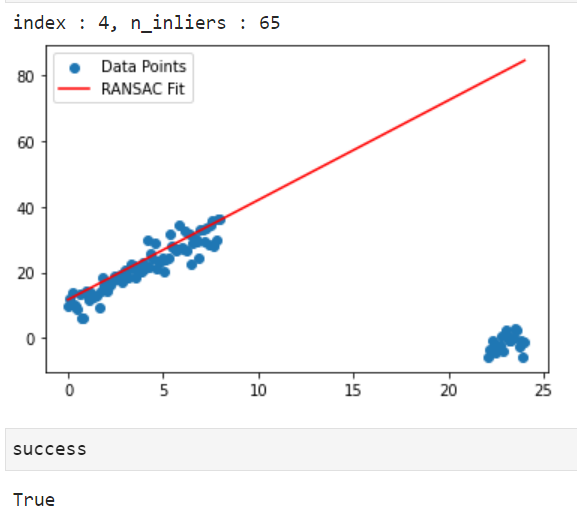
- 이번에는 동일한 함수를 이용하여 2차 함수를 모델링 해보겠습니다. 절차는 동일합니다.
import numpy as np
import math
import matplotlib.pyplot as plt
# Generate synthetic data
np.random.seed(0)
n_points = 100
X = np.linspace(-10, 10, n_points)
y = 2 * X**2 + 3 * X + 4 + np.random.normal(0, 10, n_points)
# Add outliers
n_outliers = 20
X[-n_outliers:] += int(30 * np.random.rand())
y[-n_outliers:] -= int(500 * np.random.rand())
X = np.expand_dims(X, -1)
y = np.expand_dims(y, -1)
data = np.hstack([X, y])
threshold_cadidates = [1,2,4,8,16,32,64,128]
threshold_cadidates.sort()
sample_size = 3
max_iteration = get_sampling_number(sample_size)
threshold = get_inlier_threshold(
threshold_cadidates, data, polynomial_degree=2, sample_size=sample_size,
min_iteration=-1, max_iteration=max_iteration, stop_inlier_ratio=0.50, verbose=True)
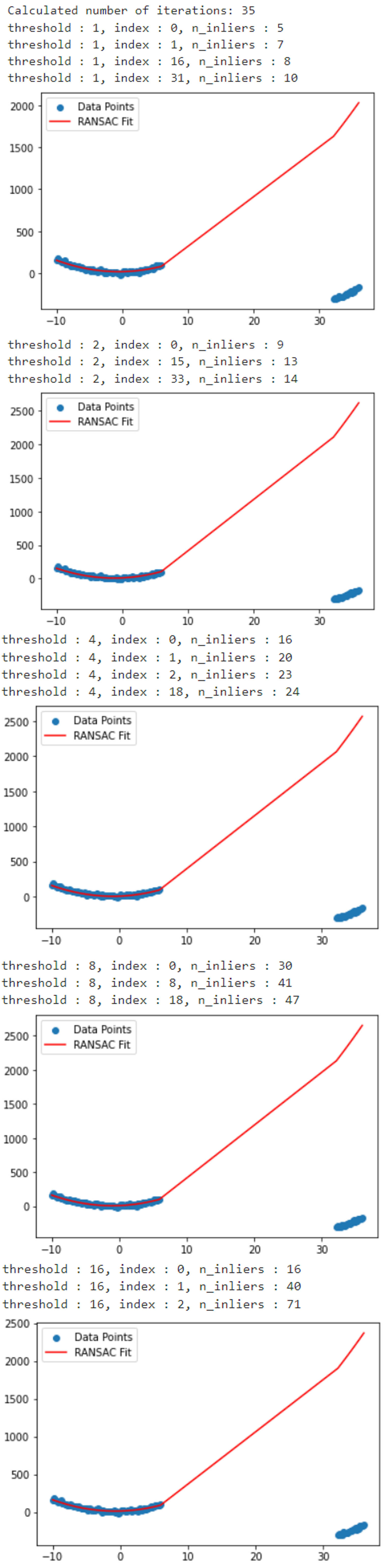
- 위 그림과 같이
threshold=16을 사용하는 것으로 구하였고 위 파라미터를 기준으로RANSAC을 수행하면 다음과 같습니다.
# Generate synthetic data
np.random.seed(np.random.seed())
n_points = 100
X = np.linspace(-10, 10, n_points)
y = 2 * X**2 + 3 * X + 4 + np.random.normal(0, 10, n_points)
# Add outliers
n_outliers = 20
X[-n_outliers:] += int(30 * np.random.rand())
y[-n_outliers:] -= int(500 * np.random.rand())
X = np.expand_dims(X, -1)
y = np.expand_dims(y, -1)
data = np.hstack([X, y])
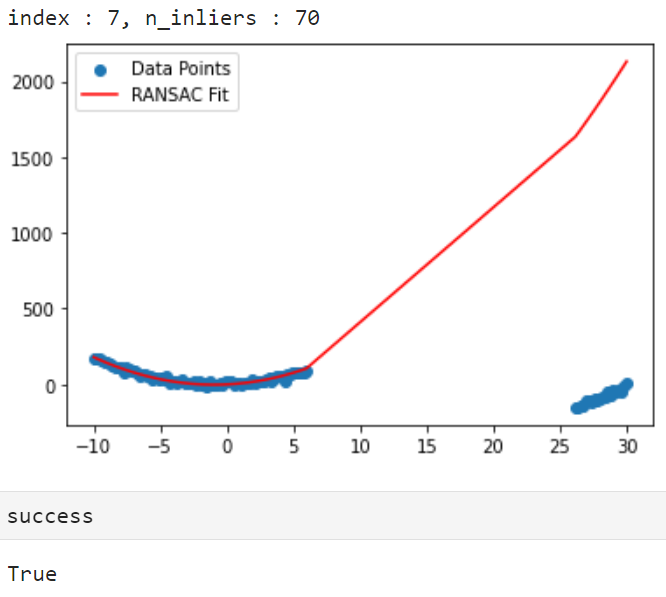
success, param = get_model_with_ransac(data, polynomial_degree=2, threshold=threshold, sample_size=sample_size,
min_iteration=-1, max_iteration=max_iteration, stop_inlier_ratio=0.50, verbose=True)
Lo-RANSAC 개념
- 지금까지 다룬
RANSAC의 아쉬운점은 좋은 모델을 찾았음에도 다음 iteration에서 완전히 다른 랜덤 샘플을 추출하기 때문에 이전 시도와 상관없이 새로운 샘플 데이터로RANSAC을 진행한다는 점입니다. Lo-RANSAC은Locally Optimized RANSAC의 줄임말로inlier데이터는inlier데이터 주변에 모인다는 특성을 이용하여RANSAC의 결과에서inlier들만을 이용하여local영역에서의 최적화를 더 진행하는 과정을 의미합니다.- 핵심 방법론은 ①
RANSAC을 수행한 후 ②inlier를 기준으로 한번 더RANSAC을 수행하고 ③inlier로 선별된 데이터를 이용하여local optimization을 한다는 것입니다. - 연산 과정이 추가되기 때문에 전체 연산이 더 늘어나는 것으로 보일 수 있으나
early stop전략과 잘 엮어서 쓰면 기본적인RANSAC에 비해 짧은iteration만으로도 높은 정확성을 가진 모델을 얻을 수 있습니다.
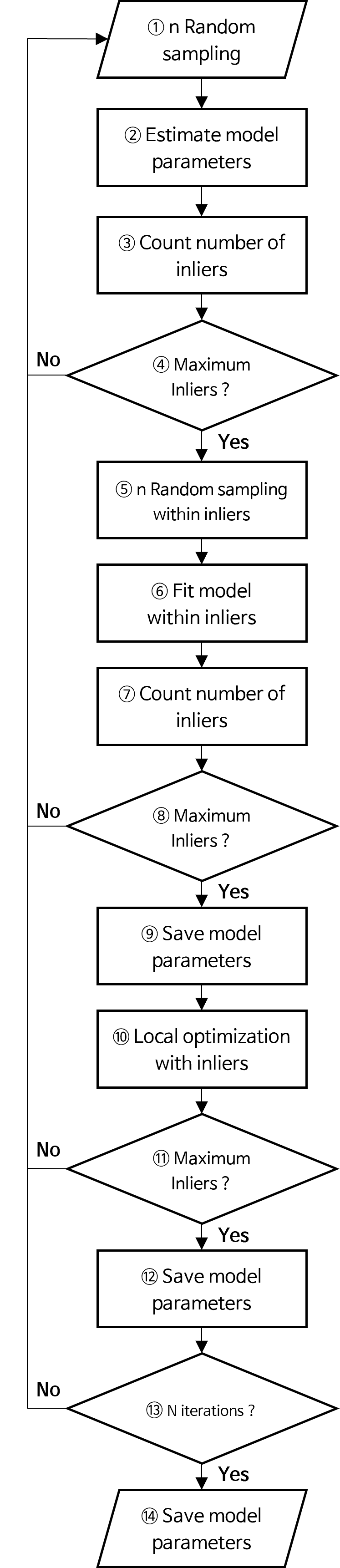
Lo-RANSAC의 전체 과정은 다음과 같습니다.- ① \(n\) 개의 데이터를 랜덤 샘플링 합니다.
- ② 랜덤 샘플한 데이터를 이용하여 모델 fitting을 합니다.
- ③ fitting된 모델을 이용하여 전체 데이터의
error를 계산하고 이 값과threshold를 이용하여inlier의 갯수를 카운트합니다. - ④ 기존에 기록된 최대
inlier갯수를 초과하면 다음 스텝으로 넘어가고 초과하지 못하면 ① 작업으로 돌아갑니다. 최대inlier갯수를 초과하였다는 뜻은local optimization을 할 만큼 가치있는 랜덤 샘플링이 되었다는 것을 의미합니다. - ⑤, ⑥, ⑦
inlier를 기준으로 앞에서 수행한 ①, ②, ③ 작업을 그대로 수행합니다. ①, ②, ③의 경우 전체 데이터에서 랜덤 샘플링한 후RANSAC작업을 한 것에 반해 ⑤, ⑥, ⑦ 은 한번 모델을 fitting한 결과를 기준으로inlier에서 랜덤 샘플링한 후RANSAC작업을 한 것에 차이가 있습니다. - ⑧
inlier기준으로RANSAC한 결과가 현재까지 기록된 최대inlier갯수를 초과하는 지 확인합니다. 초과한다면 다음 스텝으로 넘어가고 초과하지 못하면 ① 작업으로 돌아갑니다. - ⑨ 최대
inlier를 달성하였으므로 모델을 저장합니다. 이 지점에서 최대inlier를 달성한 것의 의미는inlier내에서 샘플링 하는 것이 의미가 있다는 뜻이며inlier가 유효하다는 것을 의미합니다. 따라서 다음 스텝에서inlier데이터 전체를 이용한local optimization을 시도해 볼 수 있는 상황이 됩니다. - ⑩
inlier데이터 전체를 이용하여local optimization을 합니다.polynomial함수의 경우inlier데이터 전체를 이용하여curve fitting을 해볼 수 있습니다. 또는Levenberg-Marquardt Optimization과 같은 최적화 방법론을 이용하여 모델을 최적화할 수 있습니다. - ⑪
local optimization의 결과가 최대inlier를 달성하였는 지 확인합니다. - ⑫ 최대
inlier를 달성하였으므로 모델을 저장합니다. - ⑬ 최대 N 번
iteration을 반복하였는 지 확인합니다.iteration을 더 반복해야 하면 ① 과정부터 다시 시작합니다. N번 모두iteration이 끝났다면Lo-RANSAC과정을 끝냅니다. - ⑭ 최종적으로 선택된 모델을 저장합니다.
- 위 flow-chart에서 ⑤ ~ ⑪ 과정이 기본적인
RANSAC과 대비하여 개선된 내용입니다. 다소 연산 과정이 늘어나 보일 수 있지만,early stop과 같이 쓸 경우iteration을 몇 번 반복하지 않고 끝낼 수 있으므로 효과가 좋을 수 있습니다.
Lo-RANSAC Python Code
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def get_sampling_number(sample_size, p=0.99, e=0.5):
'''
sample size : Number of sample size per every iterations
p : Desired probability of choosing at least one sample free of outliers
e : Estimated probability that a point is an outlier
'''
# Calculate the required number of iterations based on the formula
n_iterations_calculated = math.ceil(math.log(1 - p) / math.log(1 - (1 - e)**sample_size))
print(f"Calculated number of iterations: {n_iterations_calculated}")
return n_iterations_calculated
def polynomial(x, *coeffs):
return np.polyval(coeffs, x)
def fit_polynomial(subset, degree):
x, y = subset[:, 0], subset[:, 1]
params, _ = curve_fit(lambda x, *coeffs: polynomial(x, *coeffs), x, y, p0=[1]*(degree+1))
return params
def count_inliers(model, data, threshold):
x, y = data[:, 0], data[:, 1]
y_pred = np.polyval(model, x)
return np.where(np.abs(y - y_pred) < threshold)[0]
def local_optimization(model, inliers, degree):
return fit_polynomial(inliers, degree)
def lo_ransac_polynomial(data, degree=2, min_iterations=-1, max_iterations=100, threshold=1.0, stop_inlier_ratio=0.9):
best_model = None
max_inliers = 0
total_data = len(data)
for i in range(max_iterations):
# Step 1: Random Sampling
subset = data[np.random.choice(total_data, degree+1, replace=False)]
# Step 2: Fit Initial Model
model = fit_polynomial(subset, degree)
# Step 3: Count Inliers
inliers_idx = count_inliers(model, data, threshold)
inliers = data[inliers_idx]
# Step 4: Check Initial Model
if len(inliers) < max_inliers:
continue
# Step 5: Random Sampling within inliers
inner_subset = inliers[np.random.choice(len(inliers), degree+1, replace=False)]
# Step 6: Fit Model within inliers
inner_model = fit_polynomial(inner_subset, degree)
# Step 7: Count Inliers
inner_inliers_idx = count_inliers(inner_model, data, threshold)
inner_inliers = data[inner_inliers_idx]
# Step 8: Check Inner RANSAC Model and Save Best Model
if len(inner_inliers) > max_inliers:
best_model = inner_model
max_inliers = len(inner_inliers)
else:
continue
# Step 9: Local Optimization with inliers
refined_model = fit_polynomial(inner_inliers, degree)
refined_inliers = count_inliers(refined_model, data, threshold)
# Step 10: Check Local Optimization and Save Best Model
if len(refined_inliers) > max_inliers:
best_model = refined_model
max_inliers = len(refined_inliers)
# Step 11: Early stopping condition based on inlier ratio
inlier_ratio = max_inliers / total_data
if i >= min_iterations and inlier_ratio >= stop_inlier_ratio:
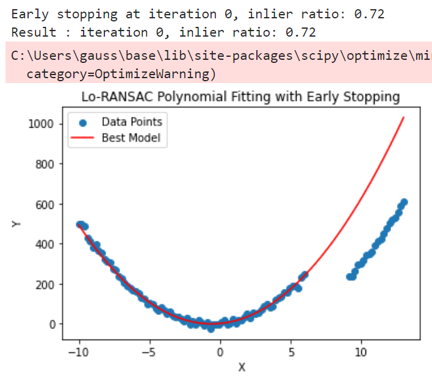
print(f"Early stopping at iteration {i}, inlier ratio: {inlier_ratio}")
break
print(f"Result : iteration {i}, inlier ratio: {inlier_ratio}")
return best_model
# Generate example data
np.random.seed(np.random.seed())
n_points = 100
X = np.linspace(-10, 10, n_points)
y = (np.random.random()*10)*X**2 + (np.random.random()*10)*X + np.random.normal(0, 10, n_points)
# Add outliers
n_outliers = 20
X[-n_outliers:] += int(10 * np.random.rand())
y[-n_outliers:] -= int(20 * np.random.rand())
X = np.expand_dims(X, -1)
y = np.expand_dims(y, -1)
data = np.hstack([X, y])
sample_size = 3
max_iteration = get_sampling_number(sample_size)
# Run Lo-RANSAC
best_model = lo_ransac_polynomial(data, degree=2, min_iterations=-1, max_iterations=max_iteration, threshold=16.0, stop_inlier_ratio=0.6)
# Plot the data and the best model
plt.scatter(data[:, 0], data[:, 1], label='Data Points')
x_values = np.linspace(min(data[:, 0]), max(data[:, 0]), 400)
y_values = np.polyval(best_model, x_values)
plt.plot(x_values, y_values, color='r', label=f'Best Model')
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Lo-RANSAC Polynomial Fitting with Early Stopping')
plt.show()
Computer Vision에서의 RANSAC 활용
- 참조 : https://www.ipb.uni-bonn.de/html/teaching/msr2-2020/sse2-11-ransac.pdf
- 컴퓨터 비전에서
RANSAC을 사용하는 대표적인 사례는 유사한 2개의 이미지에서 같은 위치를 나타내는 점들을 이용하여homography\(H\) 행렬을 구하거나fundamental matrix등을 구하는 것에 많이 사용됩니다. 왜냐하면 각각의 이미지에서 같은 위치의 점인Feature point를 찾고 어떤 점이 같은 점인 지 매칭을 해주는Feature matching단계까지outlier들이 많이 발생하기 때문입니다. - 따라서
outlier에 강건한RANSAC을 많이 사용합니다. 다음 2가지 예제를 살펴보도록 하겠습니다.
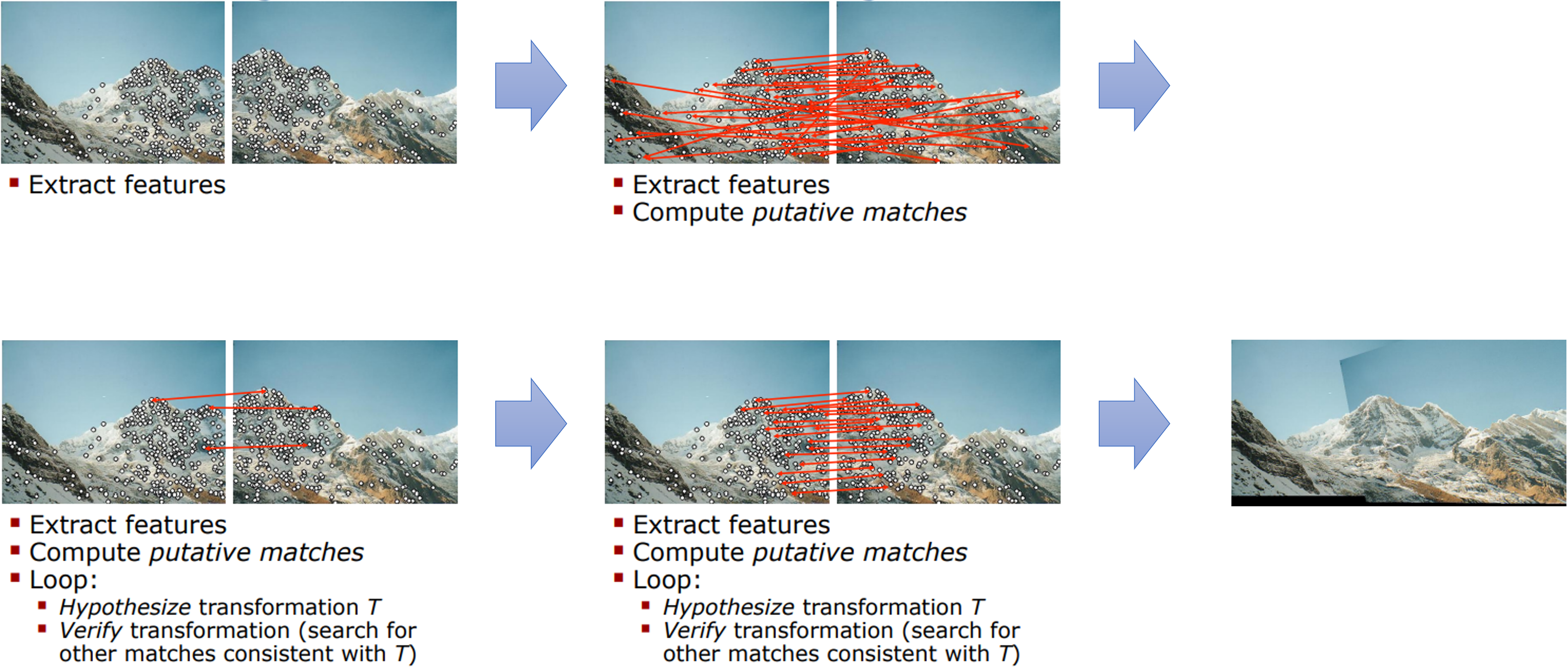
- 위 예제에서는 2개의 이미지를 이어붙이는 이미지 스티칭을 위하여 연결해야 하는 지점을 찾은 후 오른쪽 이미지를 왼쪽 이미지에 이어 붙일 수 있도록 변환하는
homography를 찾는 과정으로 볼 수 있습니다. - 2번째 과정에서의
feature matning결과를 보면 잘 연결이 된 점들도 있지만 연결이 잘못된outlier들도 생긴것을 볼 수 있습니다. 이러한 점들을 제거한 후homography를 구하고자RANSAC을 사용합니다.

- 이번 예제도 앞의 예시와 유사합니다. 촬영 위치가 다른 2개의 이미지에서 같은 이미지 지점을 찾는 것이 목적이 됩니다. 따라서
feature point를 추출하여 이미지 상의 어떤 지점을 기준으로 같은 이미지 지점을 비교할 지 정합니다. 그 다음feature matching을 이용하여feature들을 연결한 것이 두번째 그림입니다. 이번 예시에서도 잘 연결된 feature들이 있지만 잘못 연결된 점들도 보입니다. 이러한 점들을inlier,outlier로 구분하여 필요한inlier를 사용하는 것이RANSAC의 실제 사용 사례가 될 수 있습니다.