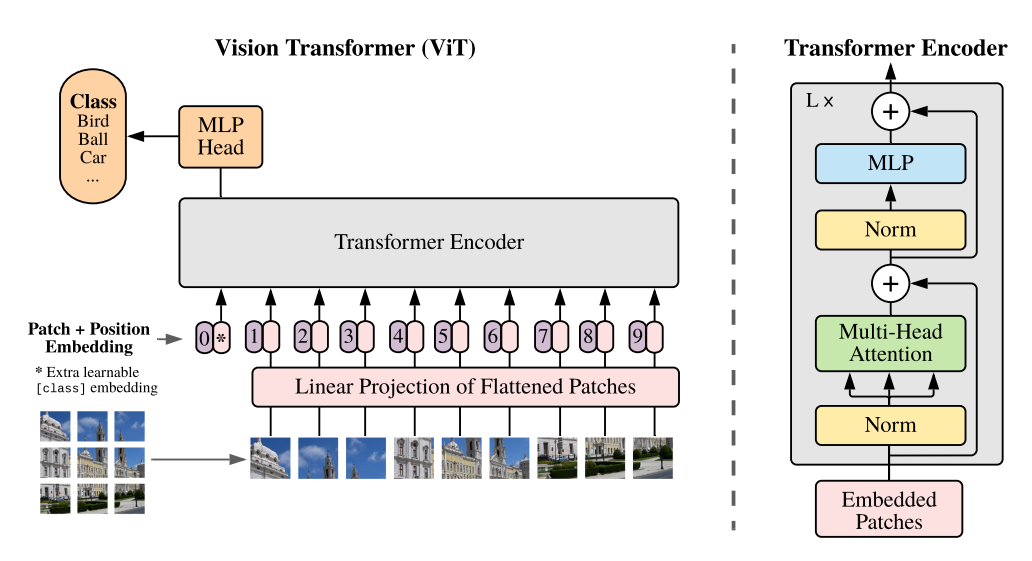
Vision Transformer (AN IMAGE IS WORTH 16X16 WORDS, TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE)

deep learning 관련 글 목차

• 이번 글에서는 Vision Transformer라는 이름으로 유명한 AN IMAGE IS WORTH 16X16 WORDS : TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE 논문 내용에 대하여 알아보도록 하겠습니다.
• 이 글을 명확하게 이해하기 위해서 아래 두 글을 먼저 읽기를 권장 드립니다.
  • ① Attention에 관하여
  • ② Transformer에 관하여

목차

• Vision Transformer

• Vision Transformer 학습

• Vision Transformer 결과 및 해석

• Pytorch를 이용한 Vision Transformer 구현

Vision Transformer

• Vision Transformer는 Transformer의 전체 아키텍쳐를 크게 변경하지 않은 상태에서 이미지 처리를 위한 용도로 사용되는데 의의가 있습니다.
• 기존의 이미지 분야에서 attention 기법을 사용할 경우 대부분 CNN과 함께 사용되거나 전체 CNN 구조를 유지하면서 CNN의 특정 구성 요소를 대체하는 데 사용되어 왔습니다.
• 또는 attention 만을 이용한 모델도 있었지만 기존의 CNN을 기반으로 하는 모델의 성능을 넘지는 못하였습니다.
• 하지만 Vision Transformer에서는 CNN에 의존하지 않고 이미지 패치의 시퀀스를 입력값으로 사용하는 transformer를 적용하여 CNN 기반의 모델의 성능을 넘는 성능을 보여주었습니다. 이미지를 이미지 패치의 시퀀스로 입력하는 방법은 뒤에서 다루겠습니다.

• 모델의 자세한 구조를 알아보기 전에 Vision Transformer의 장단점에 대하여 먼저 알아보도록 하겠습니다.
• Vision Transformer의 대표적인 장점은 다음과 같습니다.
  • ① transformer 구조를 거의 그대로 사용하기 때문에 확장성이 좋습니다. 기존의 attention 기반의 모델들은 이론적으로 좋음에도 불구하고 특성화된 attention 패턴 때문에 효과적으로 다른 네트워크에 확장하기가 어려웠습니다.
  • ② transformer가 large 스케일 학습에 우수한 성능이 있다는 것이 검증되었기 때문에 이와 같은 효과를 그대로 얻을 수 있습니다.
  • ③ transfer learning 시 CNN 보다 학습에 더 적은 계산 리소스를 활용할 수 있습니다.
• 반면 Vision Transformer의 단점은 다음과 같습니다.
  • ① inductive bias의 부족으로 인하여 CNN 보다 데이터가 많이 요구됩니다.
• inductive bias라는 것은 모델이 처음보는 입력에 대한 출력을 예측하기 위하여 사용하는 가정이라고 말할 수 있습니다. 예를 들어 CNN의 경우 translation equivariance, locality를 가정합니다.
• 먼저 translation equivariance는 입력 위치가 변하면 출력 또한 위치가 변한다는 것을 가정하는 것입니다.

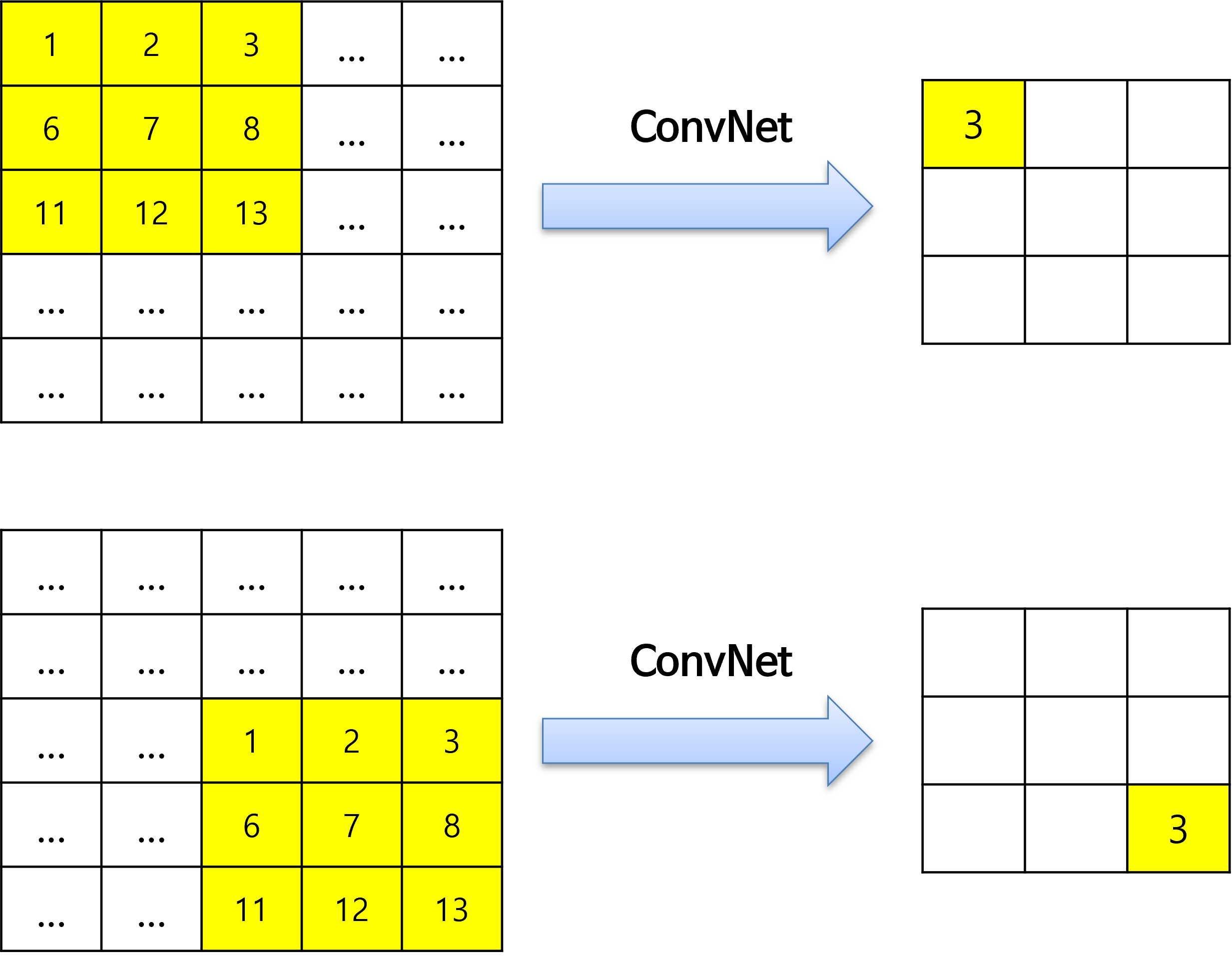
• 위 그림을 보면 입력의 위치 변화에 따라 출력의 위치 변화가 되는 것을 가정합니다. 즉, CNN에서는 입력값의 위치가 변하면 출력값의 위치도 같이 변하면서 값을 유지시킴으로써 추출되는 feature를 유지합니다.
• CNN에서는 inductive bias 가정을 두기 때문에 단순한 MLP 보다 좋은 성능을 가집니다. MLP에서는 완전히 같은 값을 가지는 패치의 위치가 조금 달라지더라도 flatten한 벡터값이 달라지고 그에 따라 fully connected 연산 시 weight가 모두 달라지기 때문에 결과값이 완전히 달라지게 됩니다.

• locality는 Convolution 연산을 할 때, 이미지 전체에서 Convolution 필터가 이미지의 일부분만 보게 되는데 이 특정 영역만을 보고 Convolution 필터가 특징을 추출할 수 있다는 것을 가정하는 것입니다.

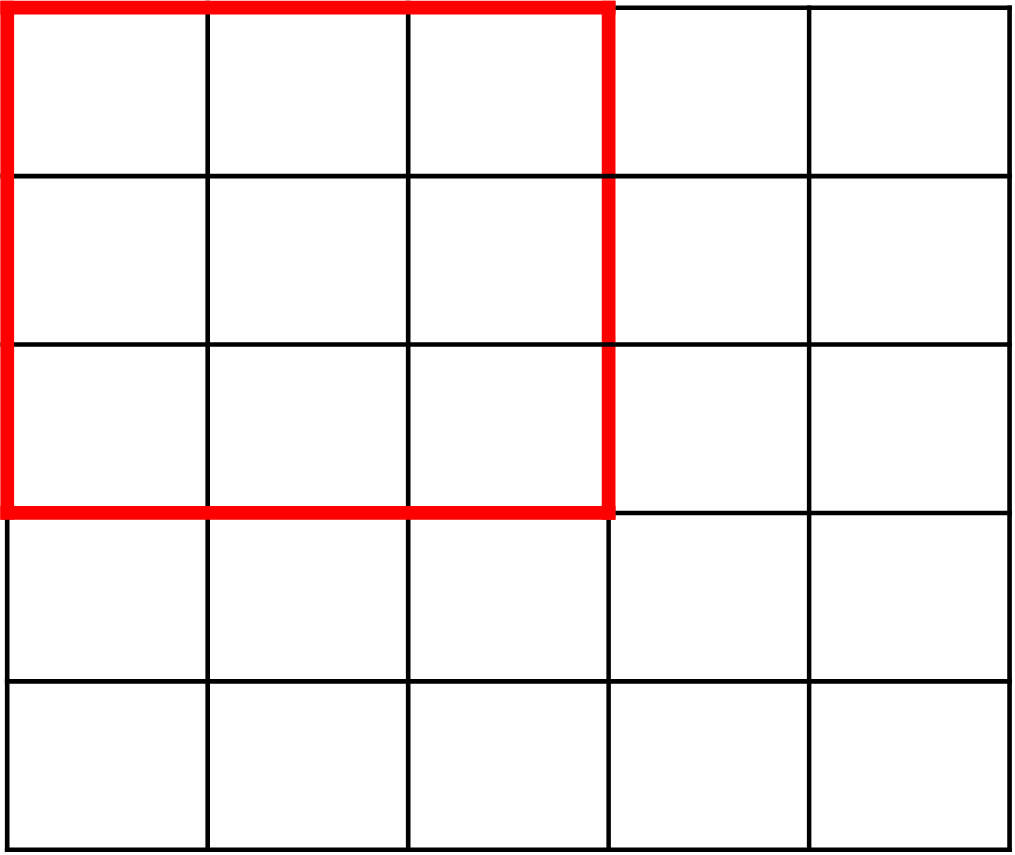
• 즉 위와 같은 이미지에서 빨간색의 3 x 3 영역만 보더라도 특징을 추출할 수 있다는 것을 의미합니다.
• 이러한 CNN의 2가지 가정을 통하여 CNN이 단순한 MLP 모델보다 더 좋은 성능을 낼 수 있다고 해석할 수 있습니다.

• 반면 transformer 모델은 attention 구조만을 사용하게 됩니다. attention은 CNN과 같이 local receptive field를 보는 것이 아니라 데이터 전체를 보고 attention할 위치를 정하는 메커니즘이기 때문에 이 패턴을 익히기 위해서 CNN 보다 더 많은 데이터를 필요로 하게 됩니다. 따라서 불충분한 데이터양으로 학습을 하게 되면 일반화 성능이 떨어지게 됩니다.
• 예를 들어 이미지넷 데이터 셋 정도 (중간 사이즈 정도의 데이터셋)를 학습에 사용할 경우 유사한 크기의 ResNet 보다 성능이 낮아지는 것을 확인하였습니다.
• 하지만 large scale 데이터셋을 이용하면 CNN 보다 높은 성능을 얻을 수 있음을 확인하였습니다. 따라서 large scale 데이터셋에서 학습을 하고 transfer learning을 이용하는 것이 효과적으로 transforemr를 사용하는 방법입니다.
• 논문에서는 large sclae 데이터셋인 ImageNet 21K나 JFT-300M으로 사전 학습을 하고 CIFAR-10으로 transfer learning을 하였을 때 높은 정확도를 가짐을 보여주었습니다.

• 그러면 Vision Transformer의 Architecture에 대하여 알아보도록 하겠습니다.

• Vision Transformer는 기본적인 Transformer의 Encoder를 그대로 가져와서 사용합니다. 따라서 Transformer에 맞는 입력값을 그대로 가져와서 사용해야 합니다.
• Transformer에서는 시퀀스 데이터를 ① Embedding을 하고 ② Positional Encoding 을 추가해 주었습니다. Vision Transformer에서도 동일한 방식을 거치게 됩니다. 순서는 다음과 같습니다.
• ① Transformer와 동일한 구조의 입력 데이터를 만들기 위해서 이미지를 패치 단위로 쪼개고 각 패치를 왼쪽 상단에서 오른쪽 하단의 순서로 나열하여 시퀀스 데이터 처럼 만듭니다.
• ② Transformer에서 Embedding된 데이터는 벡터값을 가지므로 각 패치는 flatten 하여 벡터로 변환해 줍니다.
• ③ 각 벡터에 Linear 연산을 거쳐서 Embedding 작업을 합니다.
• ④ Embedding 작업의 결과에 클래스를 예측하는 클래스 토큰을 하나 추가 합니다.
• ⑤ 클래스 토큰이 추가된 입력값에 Positional Embedding을 더해주면 Vision Transformer의 입력이 완성이 됩니다. 이미지에서도 각 패치의 위치가 중요하기 때문에 Positional Embedding을 적용해 주게 됩니다.

• ① ~ ⑤ 과정을 거쳐서 입력을 만들어 주게 되면 Transformer Encoder를 L번 반복을 하게 되고 입력값과 동일한 크기의 출력값을 마지막에 얻을 수 있습니다.
• Transformer Encoder의 출력 또한 클래스 토큰과 벡터로 이루어져 있습니다. 여기서 클래스 토큰만 사용하여 위 아키텍쳐의 MLP Head를 구성하고 이 MLP Head를 이용하여 MLP를 하면 최종적으로 클래스를 분류할 수 있습니다.

• 각 과정을 좀 더 자세하게 살펴보도록 하겠습니다.

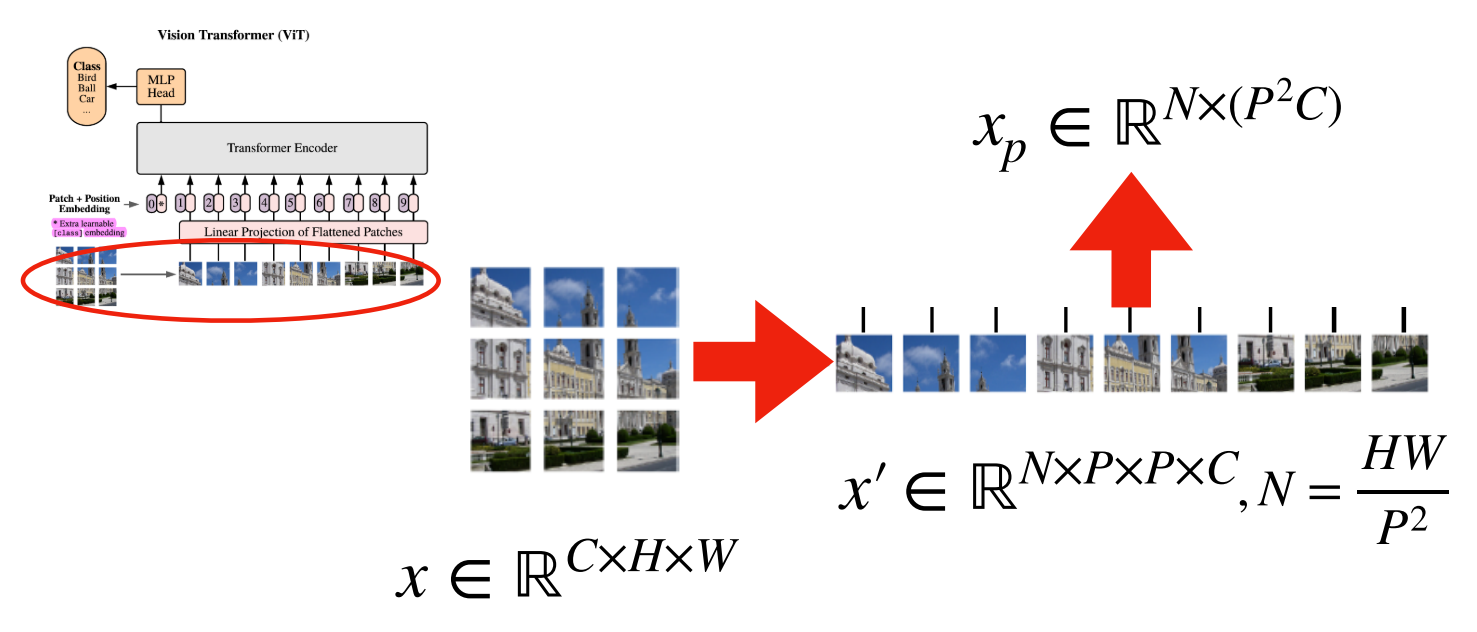
• 위 그림의 기호 중 (C, H, W)는 각각 Channel, Height, Width를 의미하며 P는 Patch의 크기를 나타냅니다. 각 패치는 (C, P, P)의 크기를 가지게 되며 이 때 N은 나뉘어진 패치의 갯수를 의미합니다.
• 각 패치를 위의 ② 과정 (flatten)을 거쳐 벡터로 만들면 각 벡터의 크기는 \(P^{2}C\) 가 되고 이 벡터가 N 개가 됩니다. 이 N개의 벡터를 합친 것을 \(x_{p}\) 라고 합니다.
• 예를 들어 (3, 256, 256) 크기의 이미지를 입력으로 받고 P=16을 사용한다면, 각 패치의 크기는 (3, 16, 16)이 되고 패치의 갯수는 16 X 16 개가 됩니다. 이 패치를 flatten 하게 되면 \(3 * 16 * 16 = 768\) 이므로 768 크기의 벡터를 16 X 16개 가지게 됩니다. 이 값을 시퀀스 데이터로 나타내면 (256, 768)의 형태로 표현할 수 있습니다.

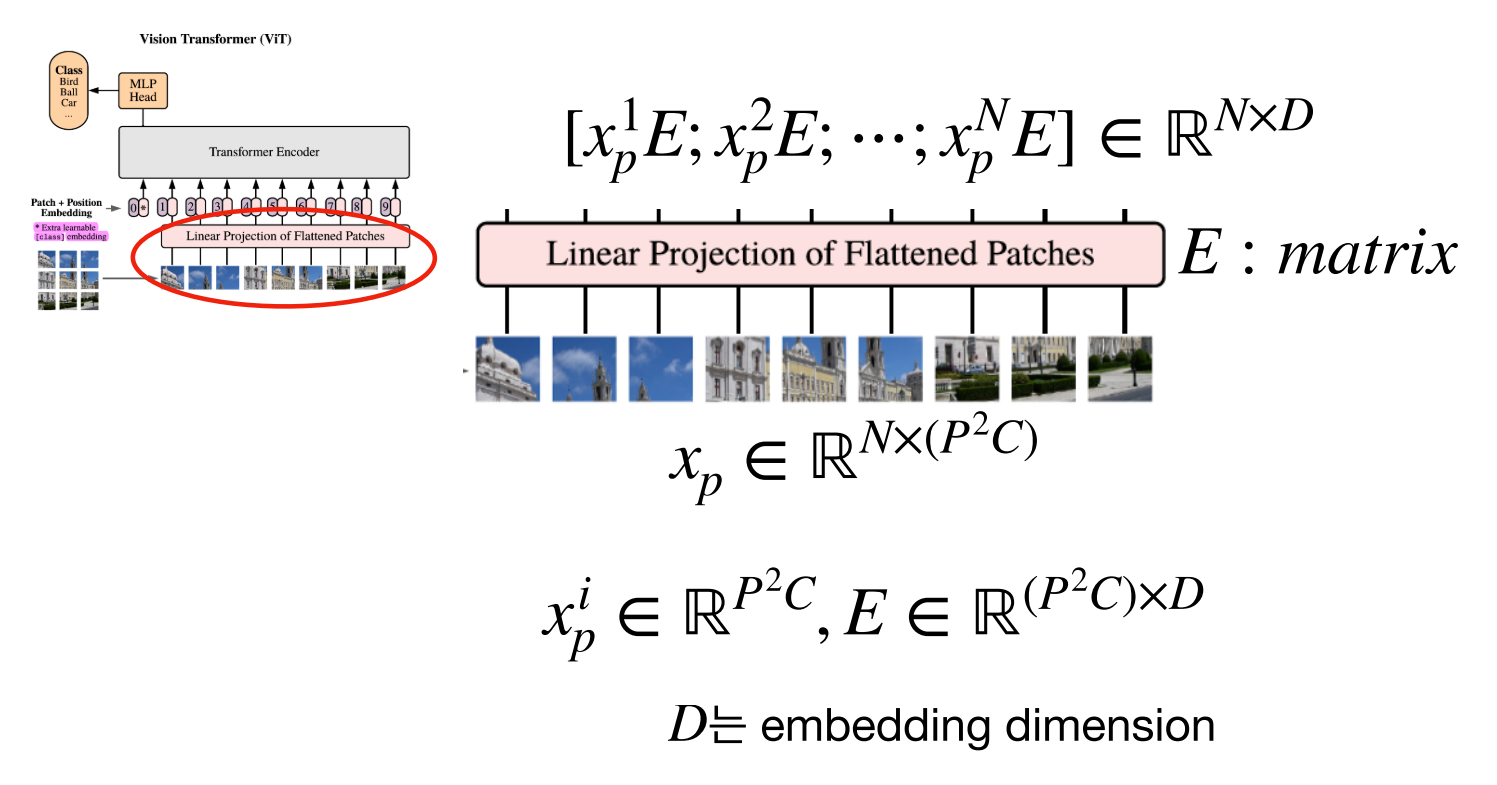
• 앞에서 생성한 \(x_{p}\) 를 Embedding 하기 위하여 행렬 \(E\) 와 연산을 해줍니다. \(E\) 의 shape은 ( \(P^{2}C, D\) ) 가 됩니다. \(D\) 는 Embedding dimension 로 \(P^{2}C\) 크기의 벡터를 \(D\) 로 변경하겠다는 의미입니다.
• 따라서 \(x_{p}\) 의 shape은 ( \(N, P^{2}C\) ), \(E\) 의 shape은 ( \(P^{2}C, D\) )으로 곱 연산을 하면 (N, D)의 크기를 가지게 됩니다.
• 배치 사이즈까지 고려하게 된다면 (B, N, D)의 크기를 가지는 텐서를 가지게 됩니다.

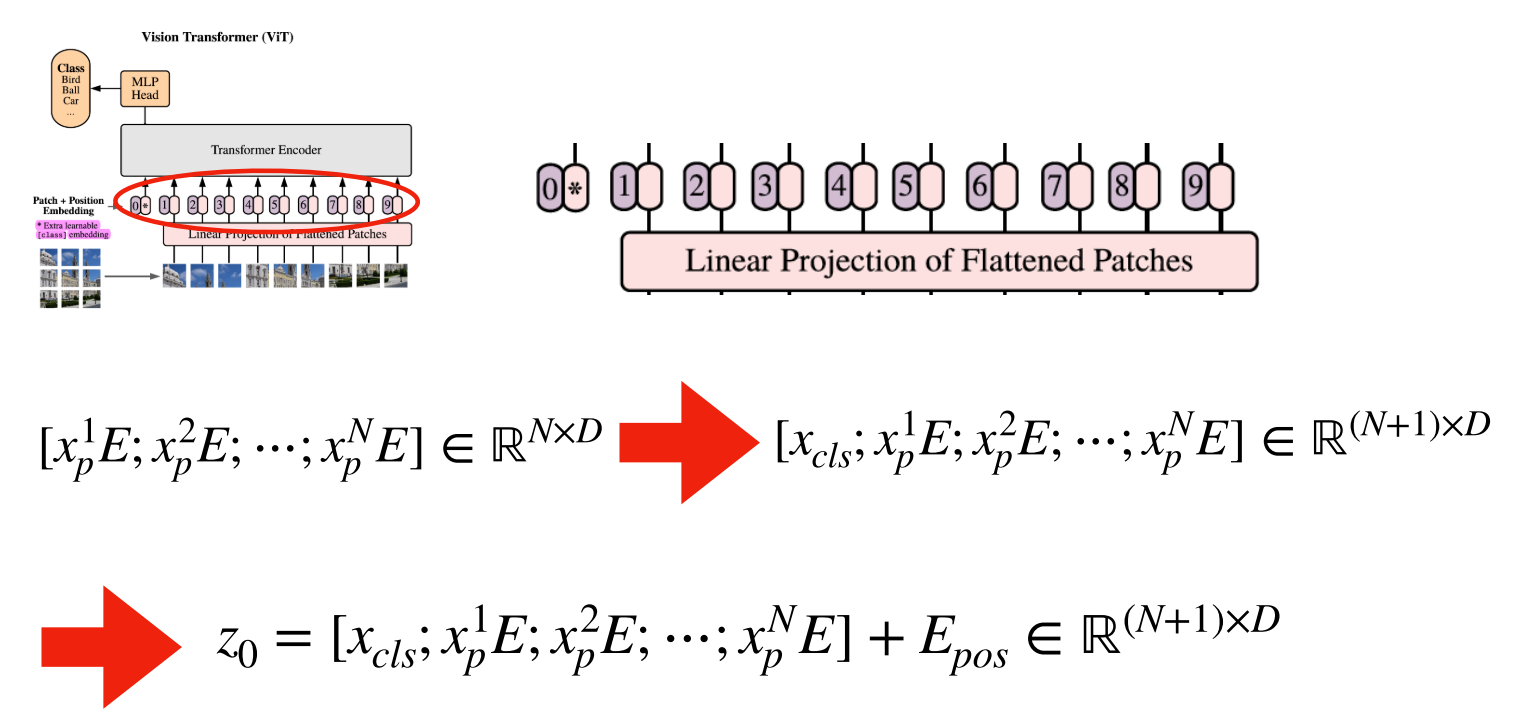
• Embedding한 결과에 클래스 토큰을 위 그림과 같이 추가합니다. 그러면 (N, D) 크게의 행렬이 (N+1, D)의 크기가 됩니다. 클래스 토큰은 학습 가능한 파라미터를 입력해 주어야 합니다.
• 마지막으로 Positional Encoding을 추가하기 위하여 (N+1, D) 크기의 행렬을 더해주면 입력값 \(z_{0}\) 준비가 마무리가 됩니다.

• 지금까지 과정을 CIFAR-10 데이터 예시로 다시 한번 살펴보면 다음과 같습니다.
• CIFAR-10 = (3, 32, 32)
• P = 4
• N = 32 * 32 / (4 * 4) = 64
• 이 때, \(x_{p} \in \mathbb{R}^{64 \times 48}\) 이 됩니다.
• D = 128 이면 Embedding 결과 \(\mathbb{R}^{64 \times 128}\) 이 됩니다.
• 클래스 토큰 추가 시 \(\mathbb{R}^{65 \times 128}\) 이 되고 이 값에 Positional Embedding \(\mathbb{R}^{65 \times 128}\) 을 더해줍니다. 따라서 \(z_{0} \in \mathbb{R}^{65 \times 128}\) 이 됩니다.

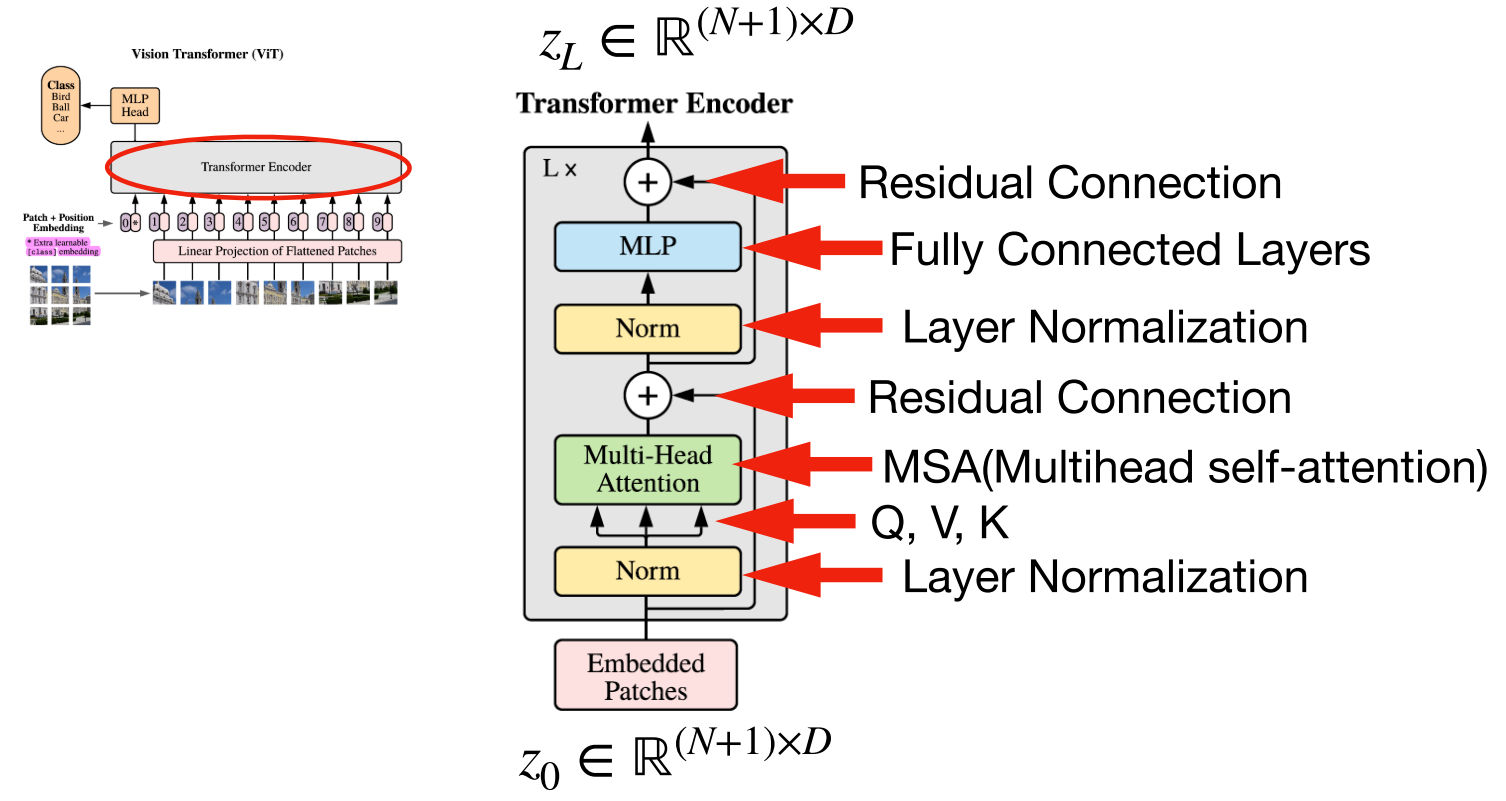
• Transformer의 Encoder는 \(L\) 번 반복하기 위해 입력과 출력의 크기가 같도록 유지합니다.
• Vision Transformer에서 사용된 아키텍쳐는 기존의 Transformer Encoder와 조금 다르지만 큰 맥락은 유지합니다. 기존의 Transformer Encoder에서는 Multi-Head Attention을 먼저 진행한 다음에 LayerNorm을 진행하지만 순서가 바뀌어 있는 것을 알 수 있습니다.
• 입력값 \(z_{0}\) 에서 시작하여 \(L\) 번 반복 시 \(z_{L}\) 이 최종 Encoder의 출력이 됩니다.
• 위 구조에서 사용된 Multihead Attention은 Self Attention 이므로 Multihead Self Attention 즉, MSA로 표현하겠습니다.

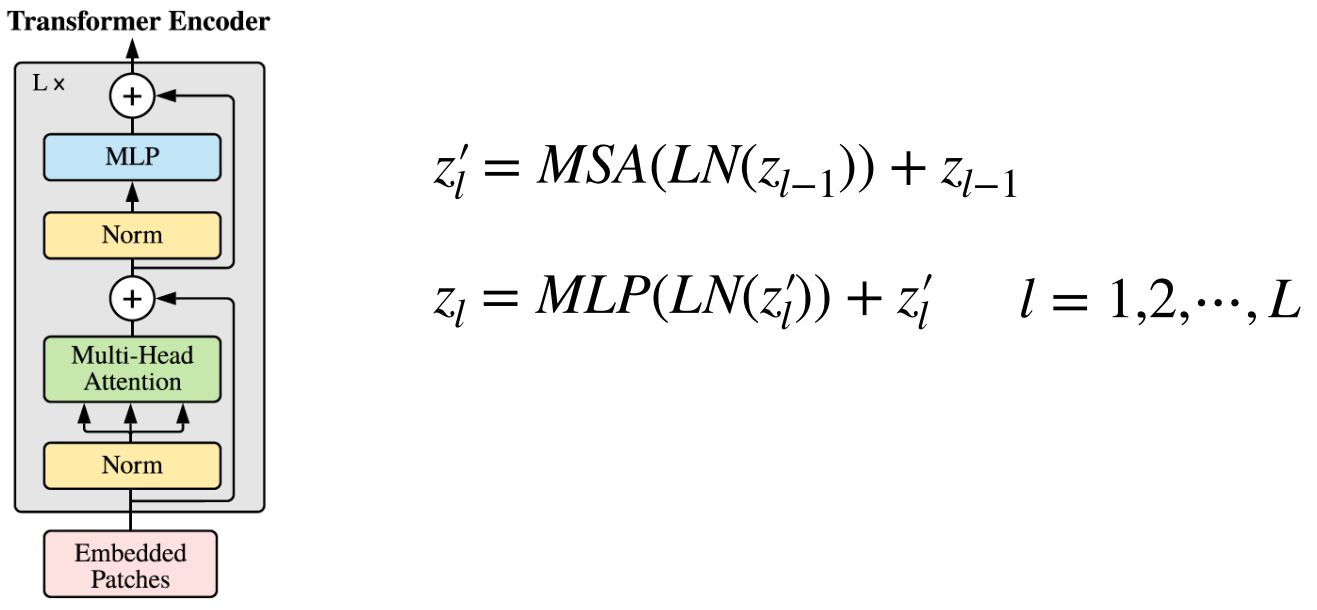
• 위 식과 같이 LM (LayerNorm), MSA, MLP 연산을 조합하면 Transformer Encoder를 구현할 수 있습니다.

• Layer Normalization은 D 차원에 대하여 각 feature에 대한 정규화를 진행합니다.
• Transformer Encoder가 L번 반복할 때, \(i\) 번째에서의 입력을 \(z_{i}\) 라고 하겠습니다.

• \[z_{i} = [ z_{i}^{1}, z_{i}^{2}, z_{i}^{3, }, \cdots , z_{i}^{N}, z_{i}^{N+1} ] \tag{1}\]

• Layer Normalization은 D 차원 방향으로 각 feature에 대하여 정규화를 진행하므로 다음 식을 따릅니다.

• \[\text{LN}(z_{i}^{j}) = \gamma \frac{z_{i}^{j} - \mu _{i}}{\sigma_{i}} + \beta \tag{2}\]
• \[= \gamma \frac{z_{i}^{j} - \mu _{i}}{\sqrt{\sigma_{i}^{2} + \epsilon}} + \beta \tag{3}\]

• 위 식에서 \(\gamma, \beta\) 는 학습 가능한 파라미터이며 식(3)의 분모 변경은 분산이 0에 가까워졌을 때, 처리하기 위한 트릭입니다.

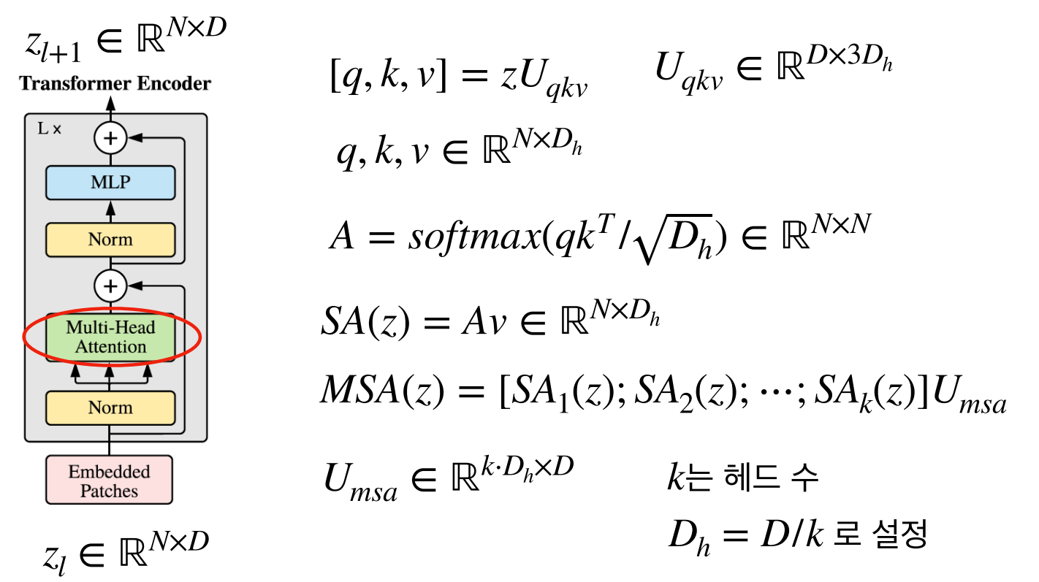
• Multi-Head Attention에 대하여 알아보도록 하겠습니다. Notation의 표기를 간단히 하기 위하여 입출력을 \(z_{l} \in \mathbb{R}^{N+1 \times D} \to z_{l} \in \mathbb{R}^{N \times D}\) 로 사용하였습니다.
• Attention 구조에 맞게 q(query), k(Key), v(value) 를 가지며 self attention 구조에 맞게 다음 식과 같이 q, k, v가 구성됩니다.

• \[q = z \cdot w_{q} \quad (w_{q} \in \mathbb{R}^{D \times D_{h}}) \tag{4}\]
• \[k = z \cdot w_{k} \quad (w_{k} \in \mathbb{R}^{D \times D_{h}}) \tag{5}\]
• \[v = z \cdot w_{v} \quad (w_{v} \in \mathbb{R}^{D \times D_{h}}) \tag{6}\]
• \[[q, k, v] = z \cdot U_{qkv} \quad (U_{qkv} \in \mathbb{R}^{D \times 3D_{h}}) \tag{7}\]

• q, k, v를 한번에 연산하기 위해서 식 (7)과 같이 사용하기도 합니다.

• \[A = \text{softmax}(\frac{q \cdot k^{T}}{\sqrt{D_{h}}}) \in R^{N \times N}\tag{8}\]
• \[\text{SA}(z) = A \cdot v \in R^{N \times D_{h}} \tag{9}\]
• \[\text{MSA}(z) = [\text{SA}_{1}(z); \text{SA}_{2}(z); \cdots ; \text{SA}_{k}(z)] U_{msa} \tag{10}\]

• 식 (8), 식(9)를 이용하여 각 head에서의 self attention 결과를 뽑고 식 (10)을 이용하여 각 head의 self attention 결과를 묶은 다음에 Linear 연산을 통해 최종적으로 Multi-head Attention의 결과를 얻을 수 있습니다.
• 식 (10) 에서 self attention의 결과를 묶은 것의 shape은 (N, \(D_{h}\) , k) 이고 \(U_{mha}\) 의 shape은 (k, \(D_{h}\) , D) 이므로 연산의 결과는 (N, D) 가 됩니다. 이 과정을 통해 Transformer Encoder의 입력과 같은 shape을 가지도록 조절할 수 있습니다.

• 실제 Multi-Head Attention을 구현할 때, 각 head의 \(q, k, v\) 에 대한 연산을 따로 하지 않고 한번에 처리할 수 있습니다.

• \[\text{head 1} : q_{1} = z \cdot w_{q}^{1}, k_{1} = z \cdot w_{k}^{1}, v_{1} = z \cdot w_{v}^{1} \tag{11}\]
• \[\text{head 2} : q_{2} = z \cdot w_{q}^{2}, k_{2} = z \cdot w_{k}^{2}, v_{2} = z \cdot w_{v}^{2} \tag{12}\]

• 위 식과 같이 같은 구조의 head 에서 weight만 달라지게 되므로 다음과 같이 한번에 묶어서 연산할 수 있습니다.

• \[\text{Single Head} : q, k, v \in \mathbb{R}^{N \times D_{h}} \to \text{Multi Head} : q, k, v \in \mathbb{R}^{N \times k \times D_{h}} \tag{13}\]

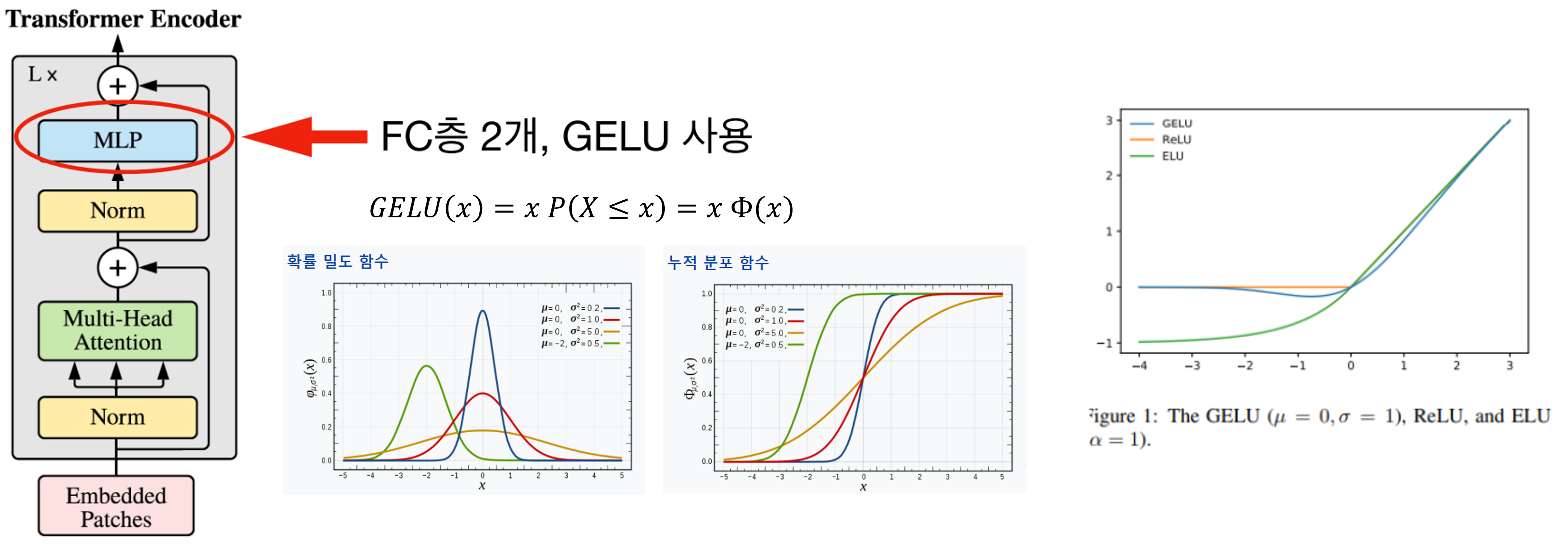
• 마지막으로 MLP 과정을 거치고 이 때, GELU Activation을 사용합니다.
• GELU는 입력값과 입력값의 누적 정규 분포의 곱을 사용한 형태입니다. 이 함수 또한 모든 점에서 미분 가능하고 단조 증가 함수가 아니므로 Activation 함수로 사용 가능하며 입력값 \(x\) 가 다른 입력에 비해 얼마나 큰 지에 대한 비율로 값이 조정되기 때문에 확률적인 해석이 가능해 지는 장점이 있습니다.

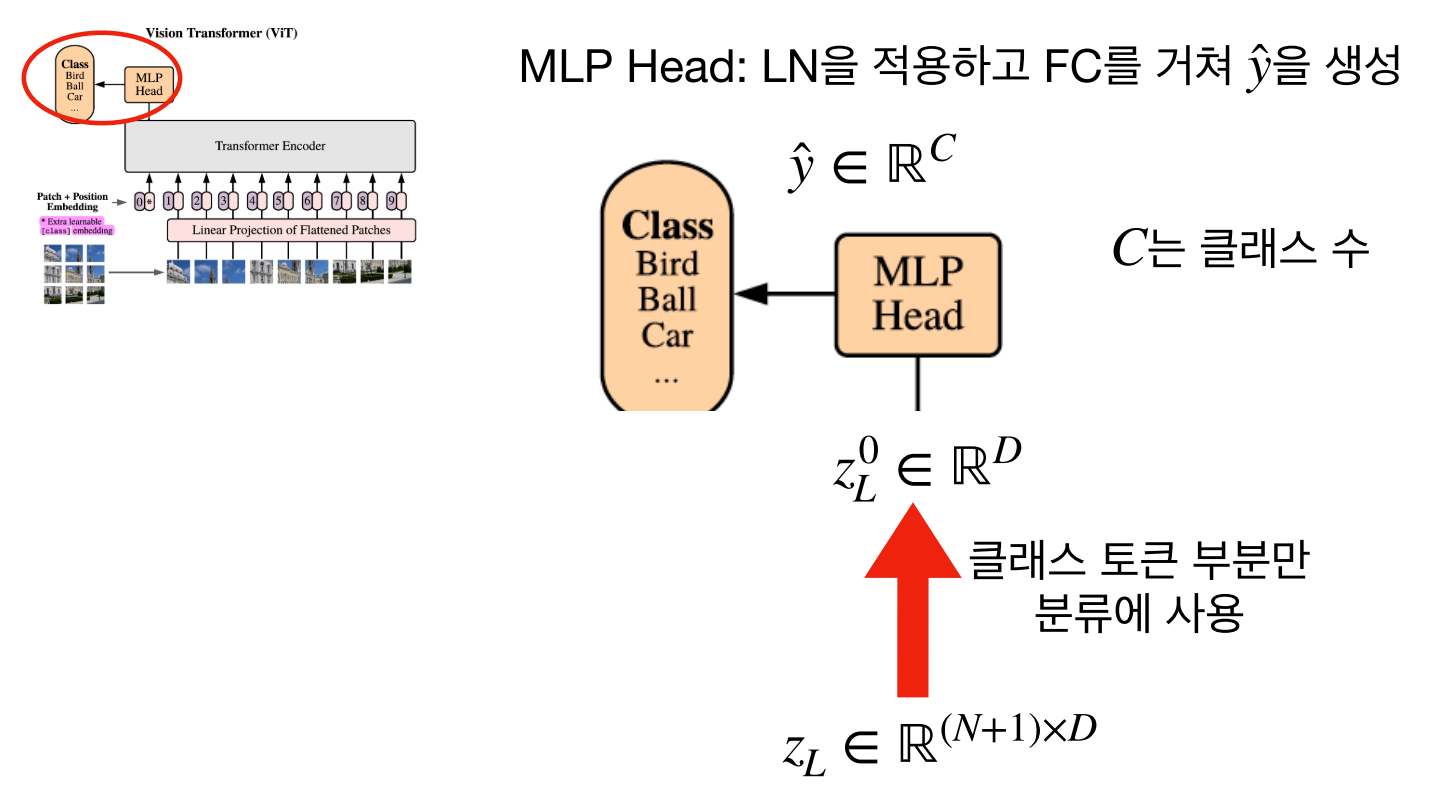
• L번 반복한 Transformer Encoder의 마지막 출력에서 클래스 토큰 부분만 분류 문제에 사용하게 되며 마지막에 추가적인 MLP를 이용하여 클래스를 분류하게 됩니다.

Vision Transformer 학습

• Vision Transformer를 학습할 때, 다음과 같은 방식을 사용하고 있습니다. 차례 차례 정리해 보면 아래와 같습니다.
• ① large 데이터셋으로 사전학습 후 더 작은 데이터셋에 대해 fine-tune하는 방식 (이미지 resize 및 MLP 헤드 부분을 클래스 수에 맞게 교체합니다.)
• ② 학습을 위해 large 데이터셋인 ImageNet, ImageNet-21k, JFT 사용
• ③ 전처리는 Resize, RandomCrop, RandomHorizontalFlip 사용
• ④ 광범위하게 Dropout 적용 (qkv-prediction 부분 제외)
• ⑤ ImageNet, CIFAR10/100, 9-task VTAB 등 데이터셋에 대해 transfer learning을 진행

• 사전 학습 조건은 다음과 같습니다.
• Optimizer : ADAM
• 스케줄링 : linear learning rate decay
• weight decay : 0.1 (강한 regularization 사용)
• 배치 사이즈 : 4,096
• Label smoothing 사용 (regularization 사용)
• validation accuracy 기준 early-stopping

• transfer learning 학습 조건은 다음과 같습니다.
• Optimizer : SGD 모멘텀
• 스케줄링 : cosine learning rate decay
• weight decay : 미적용
• grad clipping 적용
• 배치 사이즈 : 512

Vision Transformer 결과 및 해석

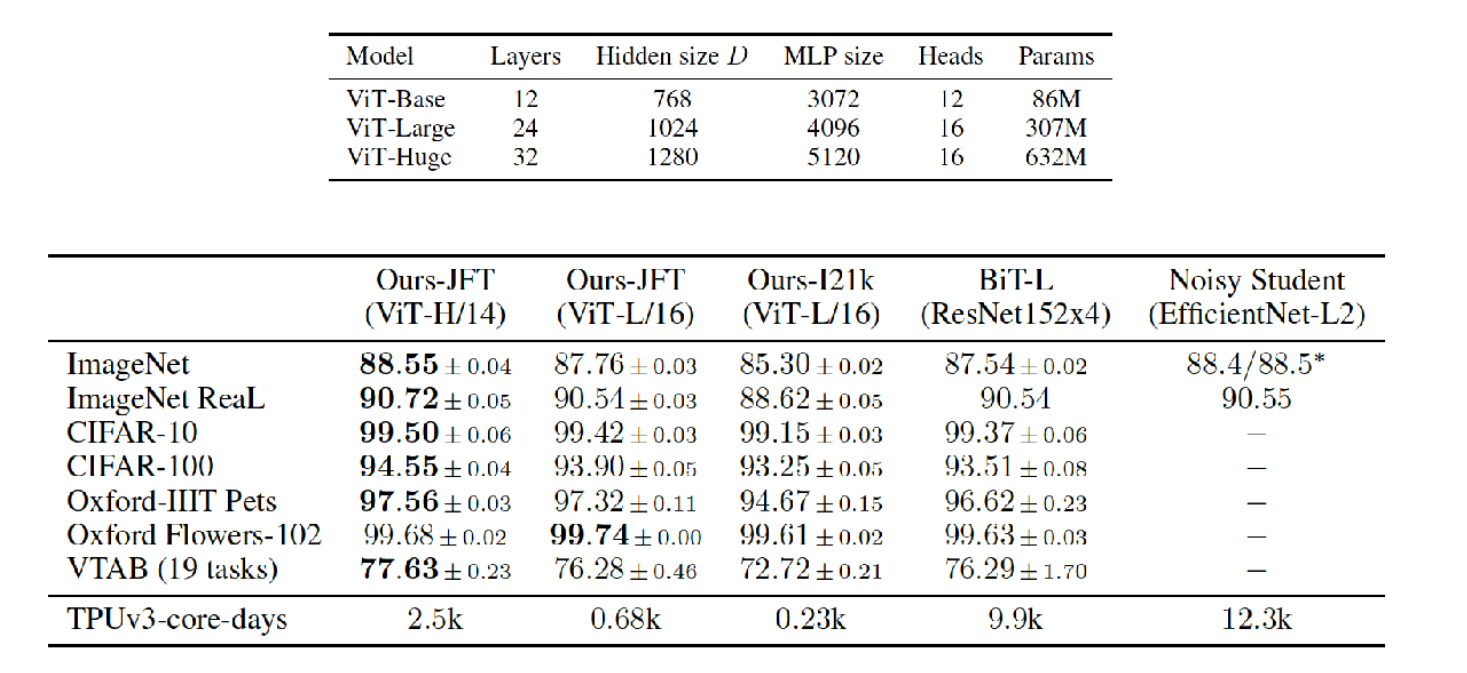
• 테스트는 ViT-Base, Vit-Large, Vit-Huge 3가지 모델에 대하여 진행하였습니다. 아래 표의 /14, /16은 패치 크기를 나타냅니다.
• 두번째 표에서 성능을 살펴보면 CNN 모델에 비해 성능이 좋다는 것을 보여주고자 합니다. 특히, 학습 시간도 절약한 것이 인상적입니다.

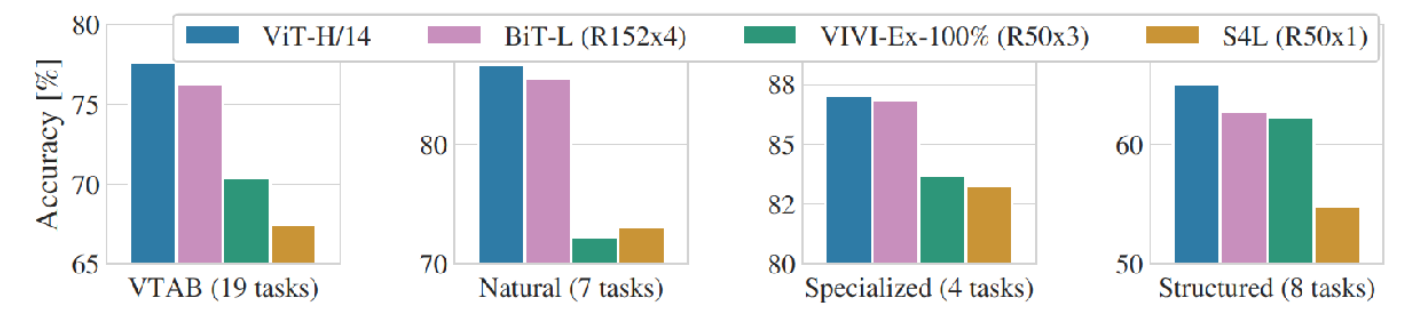
• 데이터의 특성에 따라 정확도가 달라질 수 있기 때문에, 여러 데이터의 유사한 종류의 데이터를 묶어서 성능을 비교하였습니다. 이 때에도 ViT의 성능이 좋은 점을 보여주고자 하였습니다.

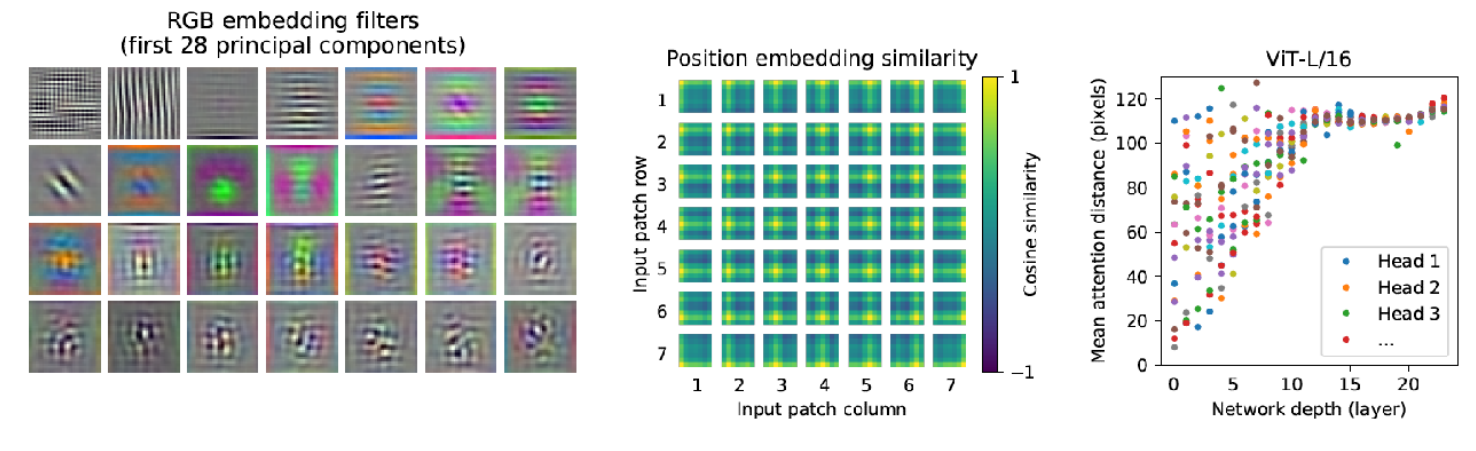
• 가장 왼쪽의 RGB embedding filter 그림의 시사점은 ViT 또한 CNN과 같은 형태로 학습이 되었다는 점입니다. RGB embedding filter는 Transformer Encoder에 입력되기 전 Embedding을 할 때 사용한 filter를 의미합니다. 이 filter의 일부분을 가져와서 시각화 하였을 때, 위 그림과 같은 형태가 나타납니다. 핵심은 CNN에서의 low level layer에서와 유사한 형태의 결과가 시각화로 나타난다는 점입니다. 즉, CNN 처럼 학습이 잘 되었다는 것을 의미합니다.
• 중간의 Positional Embedding Similarity 그림의 시사점은 Positional Embedding이 데이터의 위치를 잘 위미하도록 학습이 잘 되었다는 점입니다. Positional Embedding 에는 각 패치 마다 대응되는 Embedding 벡터가 존재합니다. 모든 패치 \(p(_{i}, p_{j} )\) 에 대하여 cosine similarity를 구하였을 때 각 row, col에 해당하는 부분의 패치가 similarity가 높은 것을 통해 Position이 의미가 있도록 학습이 잘 되었다는 것을 확인할 수 있습니다.
• 가장 오른쪽의 그래프는 attention이 관심을 두는 위치의 편차를 나타냅니다. low level layer에서는 가까운 곳에서부터 먼 곳까지 모두 살펴보는 반면 high level layer로 전체적으로 본다는 것을 의미합니다. y축의 distance의 의미는 어떤 query 위치를 기준으로 의미있는 영역까지의 평균 거리를 나타냅니다. 이 거리가 짧을수록 가까운 영역에 대하여 attention을 한다는 것이고 이 거리가 길수록 먼 영역에 대하여 attention을 한다는 것을 의미합니다.
• CNN 또한 convolution 연산의 특성상 layer가 깊어질수록 점점 더 큰 영역을 보게되는데 Vision Transformer 또한 그러한 성질을 가지는 것을 확인할 수 있었습니다.

Pytorch를 이용한 Vision Transformer 구현

import torch
import torch.nn as nn

class LinearProjection(nn.Module):

    def __init__(self, patch_vec_size, num_patches, latent_vec_dim, drop_rate):
        super().__init__()
        self.linear_proj = nn.Linear(patch_vec_size, latent_vec_dim)
        self.cls_token = nn.Parameter(torch.randn(1, latent_vec_dim))
        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, latent_vec_dim))
        self.dropout = nn.Dropout(drop_rate)

    def forward(self, x):
        batch_size = x.size(0)
        x = torch.cat([self.cls_token.repeat(batch_size, 1, 1), self.linear_proj(x)], dim=1)
        x += self.pos_embedding
        x = self.dropout(x)
        return x

class MultiheadedSelfAttention(nn.Module):
    def __init__(self, latent_vec_dim, num_heads, drop_rate):
        super().__init__()
        device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
        self.num_heads = num_heads
        self.latent_vec_dim = latent_vec_dim
        self.head_dim = int(latent_vec_dim / num_heads)
        self.query = nn.Linear(latent_vec_dim, latent_vec_dim)
        self.key = nn.Linear(latent_vec_dim, latent_vec_dim)
        self.value = nn.Linear(latent_vec_dim, latent_vec_dim)
        self.scale = torch.sqrt(latent_vec_dim*torch.ones(1)).to(device)
        self.dropout = nn.Dropout(drop_rate)

    def forward(self, x):
        batch_size = x.size(0)
        q = self.query(x)
        k = self.key(x)
        v = self.value(x)
        q = q.view(batch_size, -1, self.num_heads, self.head_dim).permute(0,2,1,3)
        k = k.view(batch_size, -1, self.num_heads, self.head_dim).permute(0,2,3,1) # k.t
        v = v.view(batch_size, -1, self.num_heads, self.head_dim).permute(0,2,1,3)
        attention = torch.softmax(q @ k / self.scale, dim=-1)
        x = self.dropout(attention) @ v
        x = x.permute(0,2,1,3).reshape(batch_size, -1, self.latent_vec_dim)

        return x, attention

class TFencoderLayer(nn.Module):
    def __init__(self, latent_vec_dim, num_heads, mlp_hidden_dim, drop_rate):
        super().__init__()
        self.ln1 = nn.LayerNorm(latent_vec_dim)
        self.ln2 = nn.LayerNorm(latent_vec_dim)
        self.msa = MultiheadedSelfAttention(latent_vec_dim=latent_vec_dim, num_heads=num_heads, drop_rate=drop_rate)
        self.dropout = nn.Dropout(drop_rate)
        self.mlp = nn.Sequential(nn.Linear(latent_vec_dim, mlp_hidden_dim),
                                 nn.GELU(), nn.Dropout(drop_rate),
                                 nn.Linear(mlp_hidden_dim, latent_vec_dim),
                                 nn.Dropout(drop_rate))

    def forward(self, x):
        z = self.ln1(x)
        z, att = self.msa(z)
        z = self.dropout(z)
        x = x + z
        z = self.ln2(x)
        z = self.mlp(z)
        x = x + z

        return x, att

class VisionTransformer(nn.Module):
    def __init__(self, patch_vec_size, num_patches, latent_vec_dim, num_heads, mlp_hidden_dim, drop_rate, num_layers, num_classes):
        super().__init__()
        self.patchembedding = LinearProjection(patch_vec_size=patch_vec_size, num_patches=num_patches,
                                               latent_vec_dim=latent_vec_dim, drop_rate=drop_rate)
        self.transformer = nn.ModuleList([TFencoderLayer(latent_vec_dim=latent_vec_dim, num_heads=num_heads,
                                                         mlp_hidden_dim=mlp_hidden_dim, drop_rate=drop_rate)
                                          for _ in range(num_layers)])

        self.mlp_head = nn.Sequential(nn.LayerNorm(latent_vec_dim), nn.Linear(latent_vec_dim, num_classes))

    def forward(self, x):
        att_list = []
        x = self.patchembedding(x)
        for layer in self.transformer:
            x, att = layer(x)
            att_list.append(att)
        x = self.mlp_head(x[:,0])

        return x, att_list

deep learning 관련 글 목차