
Pytorch Conv2d 함수 다루기
2019, Sep 27
- 참조 : https://gaussian37.github.io/dl-concept-covolution_operation/
- 참조 : https://pytorch.org/docs/stable/index.html
목차
Pytorch의 Conv2D 연산 정리
- Pytorch로 Computer vision을 한다면 반드시 사용하는
conv2d에 대하여 정리하겠습니다.
torch.nn.Conv2d(
in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
groups=1,
bias=True,
padding_mode='zeros'
)
conv2d에서 사용되는 파라미터는 위와 같습니다. 여기서 입력되어야 하는 파라미터는in_channels,out_channels,kernel_size입니다.- 나머지 파라미터는 기본값이 입력이 되어있고 기본값들이 일반적으로 많이 사용되는 값들입니다.
- 먼저 위 함수는 input 값에 2d convolution 연산을 적용하는 함수 입니다.
- input size는 \((N, C_{in}, H, W)\) 이고 output은 \((N, C_{out}, H_{out}, W_{out})\) 입니다.
- 여기서 \(N\)은 batch size이고 \(C\)는 채널의 수를 나타냅니다. \(H, W\)는 각각 height와 width를 나타냅니다.
- 이 기호들을 이용하여 식을 자세하게 나타내면 다음과 같습니다. 조금 어렵게 표현되어 있긴 하지만 자세히 살펴보면 어렵진 않습니다.
- \[\text{out}(N_{i}, C_{out}) = \text{bias}(C_{\text{out}_{j}}) + \sum_{k=0}^{C_{\text{in}}-1} \text{weight}(C_{\text{out}}, k) \otimes \text{input}(N_{i}, k)\]
- 여기서 \(\otimes\)는 2D convolution 연산을 뜻합니다.
stride를 설정하기 위해 숫자 또는 튜플을 받습니다.padding은 zero-padding할 사이즈를 입력 받습니다.dilation은 atrous 알고리즘으로도 불리고 필터(커널) 사이의 간격을 의미합니다.group은 입력 채널과 출력 채널 사이의 관계를 나타내고 옵션은 다음과 같습니다.group=1이면 모든 입력은 모든 출력과 convolution 연산이 됩니다. 일반적으로 알려진 convolution 연산과 같습니다.groups=2이면 입력을 2그룹으로 나누어서 각각 convolution 연산을 하고 그 결과를 concatenation을 합니다.groups=in_channels이면 각각의 인풋 채널이 각각의 아웃풋 채널에 대응되어 convolution 연산을 하게 됩니다. 그 사이즈는out_channels // in_channels가 됩니다.
kernel size, stride, padding, dilation은 int 나 tuple이 될 수 있고 int이면 width와 height에 동시에 같은 값이 적용됩니다.- 특히
group=in_channels이고out_channels == K * in_channels이면depthwise convolution이라고 합니다.- 이 개념은
Xeption이나mobilenet에서 대표적으로 사용되고 있습니다.
- 이 개념은
- 아래는 예제입니다.
>>> # With square kernels and equal stride
>>> m = nn.Conv2d(16, 33, 3, stride=2)
>>> # non-square kernels and unequal stride and with padding
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
>>> # non-square kernels and unequal stride and with padding and dilation
>>> m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2), dilation=(3, 1))
>>> input = torch.randn(20, 16, 50, 100)
>>> output = m(input)
- 위에 내용만 숙지하고 특히
dilation과group의 개념만 잘 이해하면 충분히 사용하는 데 문제는 없을 것입니다.
- 이번에는 MNIST 데이터 셋을 이용하여 Conv2d를 한번 다루어 보도록 하겠습니다.
- 먼저 아래 코드를 통해 간단하게 DataLoder를 하겠습니다.
import torch
from torchvision import datasets, transforms
batch_size = 1
train_loader = torch.utils.data.DataLoader(
datasets.MNIST(
root = "datasets/", # 현재 경로에 datasets/MNIST/ 를 생성 후 데이터를 저장한다.
train = True, # train 용도의 data 셋을 저장한다.
download = True,
transform = transforms.Compose([
transforms.ToTensor(), # tensor 타입으로 데이터 변경
transforms.Normalize(mean = (0.5,), std = (0.5,)) # data를 normalize 하기 위한 mean과 std 입력
])
),
batch_size=batch_size,
shuffle=True
)
- 위 MNIST 데이터 셋을 읽어 들여서 다음과 같이 실행하여 shape을 알아보겠습니다.
image, label = next(iter(train_loader))
print(image.shape, label.shape)
# torch.Size([1, 1, 28, 28]) torch.Size([1])
- 네트워크를 구성할 때 기본적으로 다음 패키지는 import를 해야 합니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
- 앞에서 설명한 것 처럼 다음 3가지 필수 속성에 유념해서
Conv2d를 사용해 보겠습니다.
nn.Conv2d(
in_channels = 1,
out_channels = 20,
kernel_size = 5,
stride = 1
)
# Conv2d(1, 20, kernel_size=(5, 5), stride=(1, 1))
- 그러면 위 Conv2d를 이용하여 layer를 만들어 보겠습니다. 이 때, device도 지정해 보겠습니다.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
layer = nn.Conv2d(in_channels = 1, out_channels = 3, kernel_size = 3, stride = 1).to(device)
print(layer)
# Conv2d(1, 3, kernel_size=(3, 3), stride=(1, 1))
- 위 layer가 현재 가지고 있는 weight를 보려면
.weight를 이용하여 살펴볼 수 있습니다.
print(layer.weight)
# Parameter containing:
# tensor([[[[ 0.1651, 0.2933, -0.1360],
# [-0.0189, 0.0794, 0.0879],
# [-0.1197, 0.2944, 0.2361]]],
# [[[-0.2551, -0.0717, 0.0259],
# [ 0.2137, 0.3300, -0.3100],
# [-0.1889, -0.3203, -0.1923]]],
# [[[-0.2630, 0.1230, -0.1499],
# [ 0.0073, 0.2863, 0.1842],
# [-0.0092, 0.1429, 0.1623]]]], requires_grad=True)
print(layer.weight.shape)
# torch.Size([3, 1, 3, 3])
- 위 layer의 weight가 가지는 shape을 살펴보면 (3, 1, 3, 3)임을 확인할 수 있습니다. 이것은 차례대로
(out_channels, in_channels, kernel_height, kernel_width)의 크기를 가집니다. - 한 가지 예를 더 들면 다음과 같습니다.
layer = nn.Conv2d(in_channels = 10, out_channels = 20, kernel_size =(3, 5), stride = 1).to(device)
print(layer.weight.shape)
# torch.Size([20, 10, 3, 5])
- 만약 위에서 다룬
layer.weight를 numpy로 변형하고 싶어서layer.weight.numpy()라고 호출을 하면 다음과 같은 에러가 발생합니다. Can't call numpy() on Variable that requires grad. Use var.detach().numpy() instead.- pytorch에서 weight는 학습 가능한 상태이기 때문에 바로 numpy()를 이용하여 뽑아낼 수 없도록 하였습니다.
- 이 때,
detach().numpy()를 통하여 그래프에서 빼서 gradient의 영향을 받지 않도록 할 수 있습니다. - 그러면 다음 코드를 통하여 weight의 크기를 컬러로 시각화 해보겠습니다. 논문에서 많이 사용하는 방법입니다.
weight = layer.weight.detach().numpy()
import matplotlib.pyplot as plt
plt.imshow(weight[0, 0, :, :], 'jet')
plt.colorbar()
plt.show()
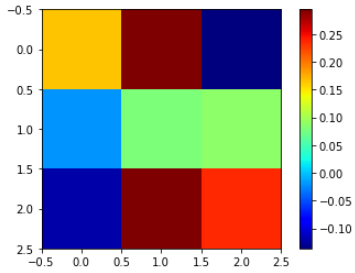
Conv2D를 이용한 산술 연산
- 앞에서 설명한
nn.Conv2d를 이용하면 기본적인 산술 연산 (+, -, *, /)을 할 수 있습니다. 편의상 산술 연산을 (+, *)로 정의하겠습니다. 설명드리는 내용은 convolution 연산 정리 를 바탕으로 진행해 보겠습니다. - 아래 내용은 입력 데이터
X에 대하여 채널 별로 특정값을 곱셈과 덧셈을 하는 연산입니다.convolution이 아닌 일반적인 산술 연산으로 표현하면 다음과 같습니다.
import torch
import torch.nn.functional as F
X = torch.rand(2, 5, 16, 16)
B, C, H, W = X.shape
mul_vals = [1.0, 2.0, 3.0, 4.0, 5.0]
add_vals = [5.0, 4.0, 3.0, 2.0, 1.0]
result1 = X * torch.Tensor(mul_vals).reshape(1, C, 1, 1) + torch.Tensor(add_vals).reshape(1, C, 1, 1)
- 위 코드에서는 첫번째 채널에는 1.0을 곱한 뒤 5.0을 더합니다. 두번째 채널은 2.0을 곱한 뒤 4.0을 더합니다.
- 위 연산을
convolution으로 적용하려면1x1 kernel을 이용한1x1 convolution을 적용하면 각 데이터 별 연산이 가능합니다. 1x1 convolution의weight값에 곱하고자 하는scalar값을 대입하고bias값에 더하고자 하는scalar값을 대입하면1x1 convolution연산 과정에서 곱셈과 덧셈을 적용할 수 있습니다.- 이 때, 채널 별 다른 값으로 연산하려면
convolution의group갯수를 입력 채널의 갯수와 동일하게 지정하면 채널의 갯수가 그룹의 갯수만큼 분할되어 채널 별로 곱셈과 덧셈을 적용할 수 있습니다. 해당 내용은 convolution 연산 정리의group에서 확인할 수 있습니다.
- 이 내용을 통하여
convolution연산을 구현하면 다음과 같습니다.
import torch
import torch.nn as nn
X = torch.rand(2, 5, 16, 16)
B, C, H, W = X.shape
mul_vals = [1.0, 2.0, 3.0, 4.0, 5.0]
add_vals = [5.0, 4.0, 3.0, 2.0, 1.0]
result1 = X * torch.Tensor(mul_vals).reshape(1, C, 1, 1) + torch.Tensor(add_vals).reshape(1, C, 1, 1)
conv_arithmetic = nn.Conv2d(in_channels=C, out_channels=C, kernel_size=1, stride=1, padding=0, groups=C, bias=True)
conv_arithmetic.weight.data[:] = torch.Tensor(mul_vals).reshape(conv_arithmetic.weight.data.shape)
conv_arithmetic.bias.data[:] = torch.Tensor(add_vals).reshape(conv_arithmetic.bias.data.shape)
result2 = conv_arithmetic(X)
torch.allclose(result1, result2)
- 두 결과 값이 같은 것을 확인할 수 있습니다.
- 위
convolution연산을 함수화 한다면F.conv2d를 이용할 수 있습니다. 다음과 같습니다.
import torch
import torch.nn as nn
X = torch.rand(2, 5, 16, 16)
B, C, H, W = X.shape
mul_vals = [1.0, 2.0, 3.0, 4.0, 5.0]
add_vals = [5.0, 4.0, 3.0, 2.0, 1.0]
result1 = X * torch.Tensor(mul_vals).reshape(1, C, 1, 1) + torch.Tensor(add_vals).reshape(1, C, 1, 1)
def conv_arithmetic_operation(X, mul_vals, add_vals):
B, C, H, W = X.shape
assert len(mul_vals) == C, "The number of multiplication values must be same with input channels"
assert len(add_vals) == C, "The number of add values must be same with input channels"
_weight = torch.zeros(C, 1, 1, 1)
_weight[:, 0, 0, 0] = torch.Tensor(mul_vals)
_bias = torch.zeros(C)
_bias[:] = torch.Tensor(add_vals)
return F.conv2d(X, weight=_weight, bias=_bias, groups=C)
result3 = conv_arithmetic_operation(X, mul_vals, add_vals)
torch.allclose(result1, result3)
- 만약 모든 채널에 2.0을 곱한 뒤 -1.0을 더하고 싶으면 다음과 같이 응용할 수 있습니다.
import torch
import torch.nn as nn
X = torch.rand(2, 5, 16, 16)
B, C, H, W = X.shape
mul_vals = [2.0] * C
add_vals = [-1.0] * C
result1 = X * 2.0 - 1.0
def conv_arithmetic_operation(X, mul_vals, add_vals):
B, C, H, W = X.shape
assert len(mul_vals) == C, "The number of multiplication values must be same with input channels"
assert len(add_vals) == C, "The number of add values must be same with input channels"
_weight = torch.zeros(C, 1, 1, 1)
_weight[:, 0, 0, 0] = torch.Tensor(mul_vals)
_bias = torch.zeros(C)
_bias[:] = torch.Tensor(add_vals)
return F.conv2d(X, weight=_weight, bias=_bias, groups=C)
result3 = conv_arithmetic_operation(X, mul_vals, add_vals)
torch.allclose(result1, result3)