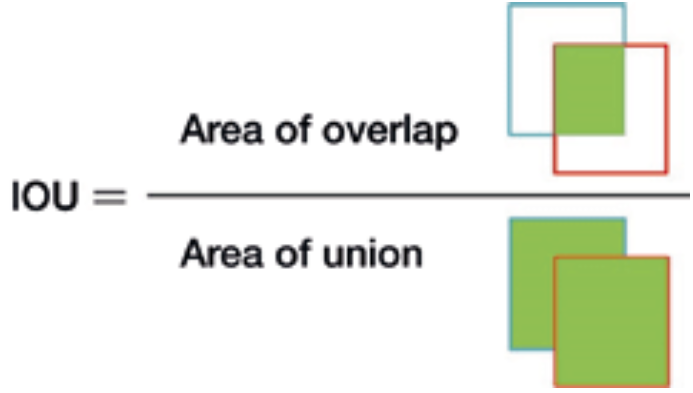
다양한 IOU(Intersection over Union) 구하는 법

알고리즘 관련 글 목차

목차

• IoU의 정의

• 두 영역이 직사각형이고 각 축과 수평할 때 IoU

• 두 영역이 임의의 (회전한) 볼록 다각형일 때 IoU

IoU의 정의

• 이번 글에서는 IoU(Intersection Over Union)을 구하는 방법에 대하여 알아보도록 하겠습니다.
• IoU의 개념에 대해서는 많은 영상 및 블로그에서 다루고 있으니 간단하게만 설명하도록 하겠습니다. 아래 참조글을 참조하셔도 됩니다.
  • 참조 : https://inspace4u.github.io/dllab/lecture/2017/09/28/IoU.html

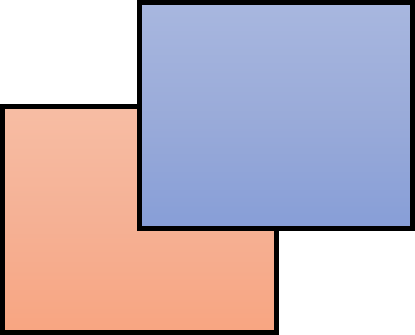
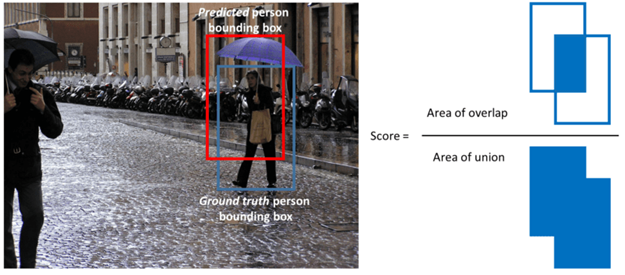
• 두 영역이 위 처럼 겹칠 때, 얼만큼 겹친다고 정량적으로 나타낼 수 있는 방법이 IoU가 됩니다.

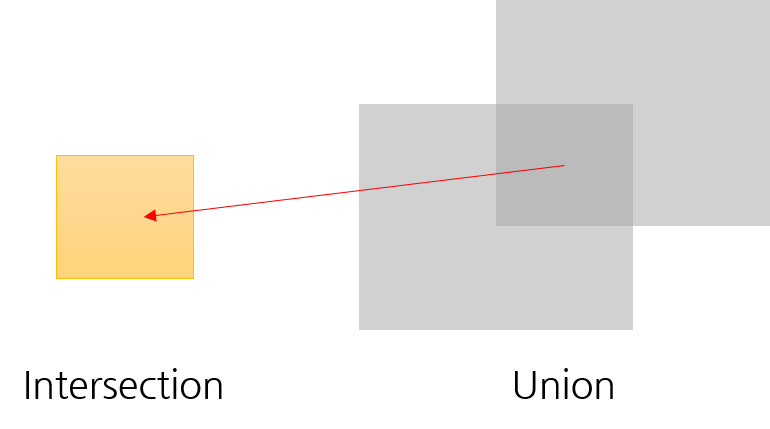
• 여기서 I에 해당하는 Intersection은 두 영역의 교집합이 되고 U에 해당하는 Union은 두 영역의 합집합이 됩니다.
• 이 값을 구하기 위해서는 두 영역에 대한 정보를 이용하여 Intersection을 먼저 구하고 \(A \cup B = A + B - A \cap B\)를 이용하여 Union의 값을 구하면 됩니다.

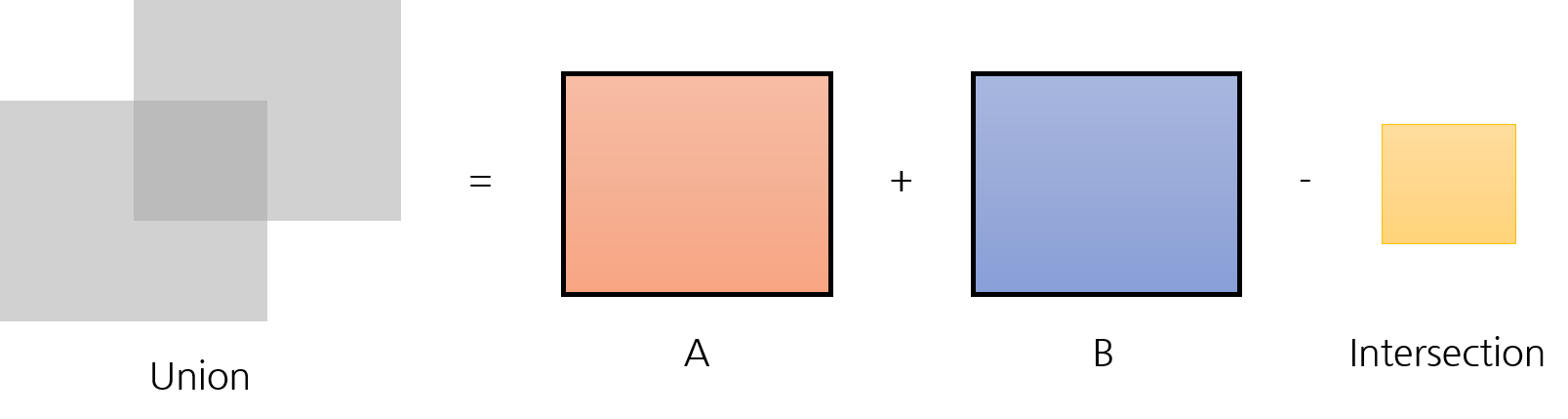
• 즉 위와 같이 구하면 됩니다. 그러면 어떻게 위의 그림과 같이 구할 수 있는지 2가지 경우로 나누어서 살펴보도록 하겠습니다.
• 첫번째로 살펴 볼 경우는 두 영역이 직사각형이고 각 축과 수평할 때 IoU 입니다. 일반적인 bounding box가 있을 때 사용하는 방법입니다.
• 두번째 방법은 두 영역이 임의의 볼록 다각형일 때 IoU 입니다. 좀 더 유연하게 적용할 수 있는 방법인 반면에 ccw, 두 선분의 교차의 개념이 필요합니다.

두 영역이 직사각형이고 각 축과 수평할 때 IoU

• 출처 : https://subscription.packtpub.com/book/big_data_and_business_intelligence/9781789346640/6/ch06lvl1sec51/calculating-an-intersection-over-a-union-between-two-images
• 먼저 설명의 편의를 위하여 스크린 좌표계가 아닌 직교 좌표계에서 설명하도록 하겠습니다.
  • 즉, (0, 0)을 기준으로 오른쪽이 x축의 양의 방향 위쪽이 y축의 양의 방향입니다.
• 위 그림처럼 구하려는 영역이 X축 Y축과 수평한 형태의 반듯한 직사각형인 형태가 있습니다.
• 이 때에 각 직사각형의 좌표 두개만 알면 IoU를 계산할 수 있습니다. 필요한 좌표 2개는 각각 바운딩 박스의 왼쪽 하단 좌표와 우측 상단 좌표입니다. 즉, (x축 최소, y축 최소), (x축 최대, y축 최대) 좌표가 필요합니다.
• 그러면 각각의 직사각형의 넓이는 쉽게 구할 수 있습니다.(x축 최대 값- x축 최소 값) * (y축 최대 값 - y축 최소 값)를 이용하여 단순히 직사각형의 넓이를 구하면 되기 때문입니다.
• 가장 핵심이 되는 것은 intersection 입니다.

intersection_x_length = min(max_x1, max_x2) - max(min_x1, min_x2);
intersection_y_length = min(max_y1, max_y2) - max(min_y1, min_y2);

• 기존의 영역 A, B가 모두 직사각형 형태이기 때문에 intersection 또한 직사각형 형태로 나타납니다.
• intersection의 x축에 평행한 변의 길이와 y축에 평행한 변의 길이는 위 코드와 같이 A와 B 직사각형에서 각 축 최대 값 중 작은것을 선택하고 각 축 최대 값 중 작은 것을 선택하면 변이 선택이 됩니다.

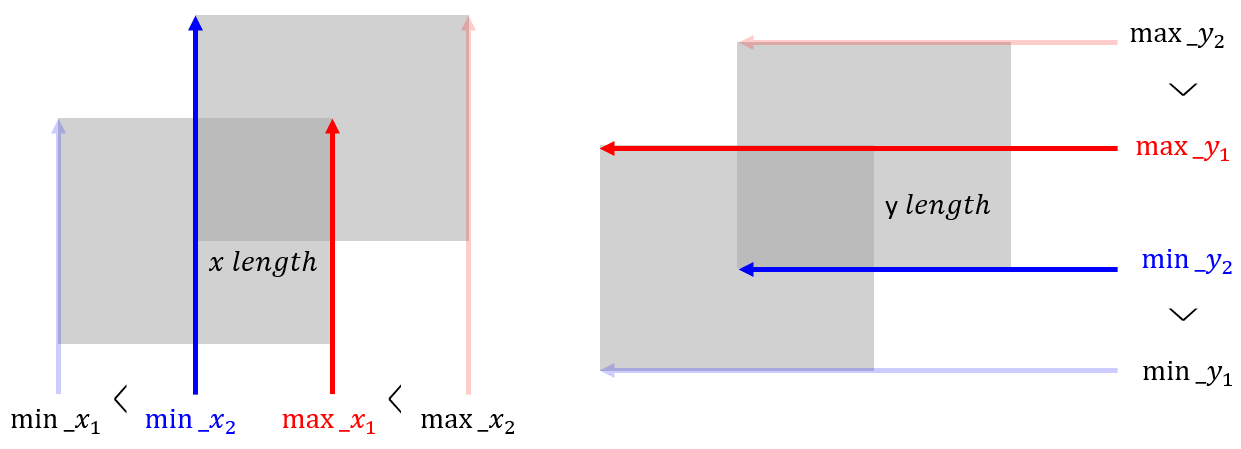
• 즉, 위 그림과 같이 만들 수 있습니다.
• 위 그림처럼 두 영역의 좌표값이 각각 2개씩 들어오게 되면 쉽게 IoU를 계산할 수 있게 됩니다.

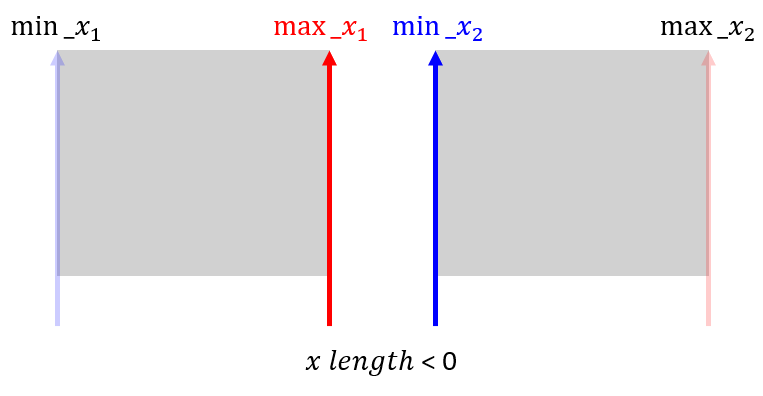
• 만약 두 영역이 겹치지 않으면 x축의 길이와 y축의 길이가 음수가 되게 됩니다.
• 따라서 길이가 양수인 경우에만 겹치는 것으로 간주하고 IoU를 구하면 됩니다.
• 다음 예를 한번 살펴보도록 하겠습니다.

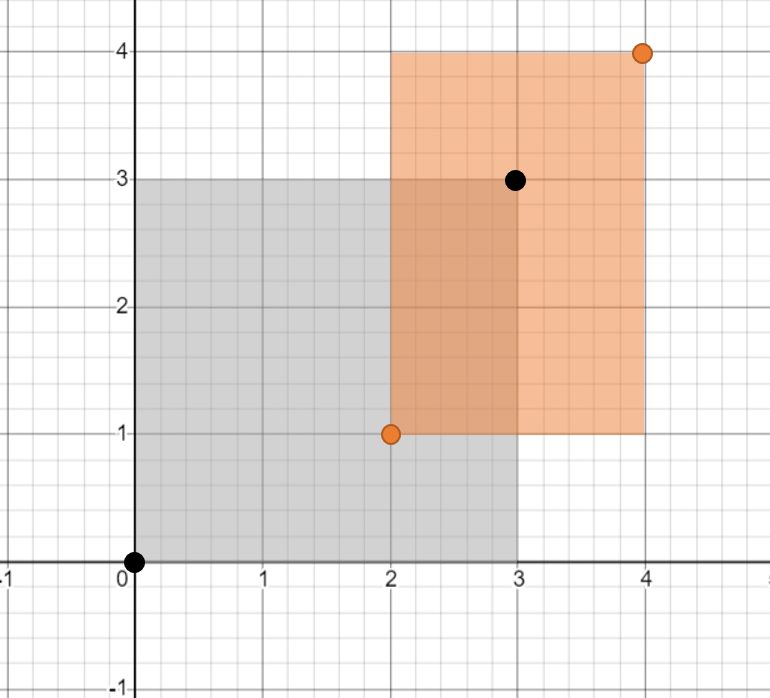
• 위 그림에서 IoU는 Intersection : 2, Union : 13 으로 2 / 13 = 0.1538.. 입니다.
• 코드를 통해 살펴보도록 하겠습니다.

• 위 예제에서 나온 결과 또한 0.1538..로 같은 결과가 나온 것을 확인할 수 있습니다.

두 영역이 임의의 (회전한) 볼록 다각형일 때 IoU

• 앞에서는 반듯한 직사각형 2개를 다루었기 때문에 문제가 상당히 간단하였습니다.
• 이번에는 임의의 볼록 다각형 2개의 IoU를 구하는 방법에 대하여 알아보도록 하겠습니다.
• 이 글을 이해하기 위해서는 ccw, 다각형의 넓이 계산, 선분의 교차 그리고 다각형 내부의 점을 사전에 이해하셔야 하며 더 간단한 방법이 있으면 공유 부탁드립니다.

• 먼저 방법은 다음과 같습니다.
  • ① 먼저 두 볼록 다각형 A, B의 교차 점을 구합니다.
  • ② A의 꼭지점 중에 B의 내부에 있는 점과 반대로 B의 꼭지점 중에 A에 있는 점을 구합니다.
  • ①과 ②에서 구한 꼭지점들을 반시계 방향으로 정렬합니다. (넓이를 구하기 위한 목적)
  • 정렬한 꼭지점들을 이용하여 Intersection을 구할 수 있습니다.

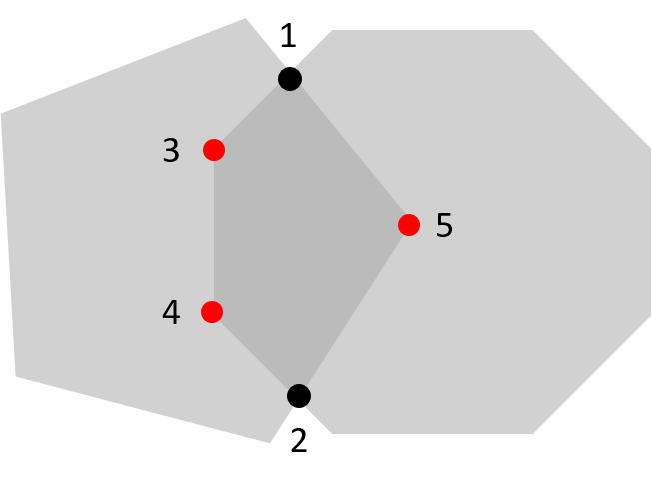
• 예를 들어 위 그림에서 5각형을 A, 8각형을 B라고 가정해 보겠습니다.
• 먼저 두 다각형의 교차점을 구하여 검은색 점으로 표현하였습니다.
• 그 다음 빨간색 점은 각 다각형의 꼭지점이 다른 다각형의 내부에 위치할 때입니다.
• 이 꼭점들을 반시계 방향으로 정렬합니다. 2-5-1-3-4
• 정렬한 꼭지점들을 이용하여 Intersection의 넓이를 구할 수 있습니다.

• 먼저 ① 과정인 두 볼록 다각형 A, B의 교차점을 구하는 방법은 A의 5개의 선분과 B의 8개의 선분 총 40쌍을 가지고 교차하는 지 살펴보면 됩니다. (선분의 교차)
• 그 다음 ② 과정은 A의 꼭지점이 5개가 B의 내부에 있는지 확인하고 반대로 B의 꼭지점 8개가 A의 내부에 있는 지 확인합니다.(다각형 내부의 점 확인)
• 마지막으로 점을 정렬할 때, 반시계 방향으로 점들을 정렬합니다. (좌표를 반시계 방향으로 정렬)
• 정렬한 좌표들을 이용하여 Intersection에 해당하는 넓이를 구합니다. (n각형의 넓이 계산)

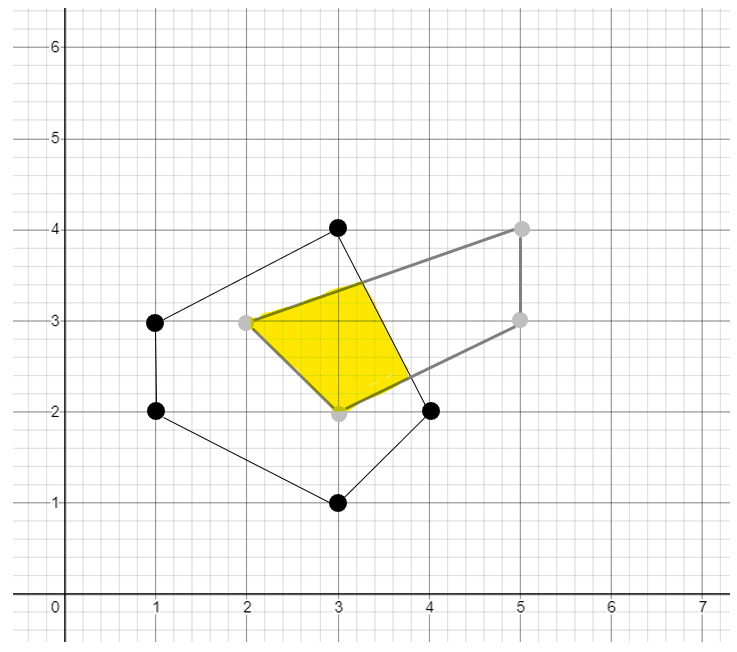
• 그러면 위 예제를 이용하여 intersection을 구해보도록 하겠습니다.
• 오각형의 좌표는 (1, 2), (3, 1), (4, 2), (3, 4), (1, 3) 이고 사각형의 좌표는 (2, 3), (3, 2), (5, 3), (5, 4) 입니다.

알고리즘 관련 글 목차