선분의 교차 여부 확인
2020, Jan 02
- 이번 글에서는 선분의 교차 여부를 확인하는 방법에 대하여 알아보도록 하겠습니다.
- 두 선분의 교차 여부를 확인할 때 사용하는 알고리즘은 CCW(Counter ClockWise)입니다. 이 알고리즘을 기반으로 설명해 보도록 하겠습니다.
- 먼저 한 선분을 나타낼 때 필요한 것은 두 점입니다. 따라서 두 선분의 교차 여부를 확인하기 위해서는 두 선분이 필요하고 각 선분당 두 점이 필요하므로 총 4개의 점이 필요 합니다.
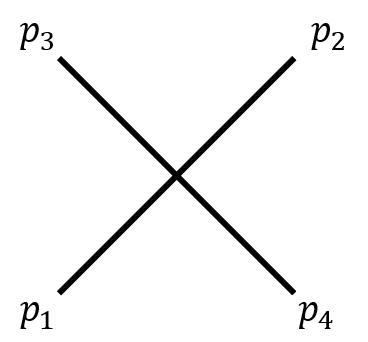
- 위와 같이 2개의 선분이 있고 선분이 교차할 때 위와 같은 방식으로 교차될 수 있습니다.
- 여기서 \(p_{1} , p_{2}\)를 이은 선분을 \(p_{1} \to p_{2}\) 방향으로의 벡터 \(v_{1}\) 이라고 하면 \(v_{1} = p_{2} - p_{1}\)이 됩니다.
- 같은 원리로 \(v_{2} = p_{3} - p_{1}\) 이라고 하고 \(v_{3} = p_{4} - p_{1}\) 이라고 하겠습니다. 이 두 벡터는 위 그림의 선분은 아니나 방향을 확인하기 위하여 도입하였습니다..
- 이 때, 확인해 볼 것은 \(v_{1}, v_{2}\)의 방향과 \(v_{1}, v_{3}\)의 방향 입니다.
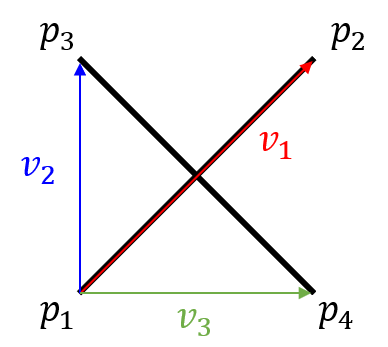
- 위 그림에서 \(v_{1} \to v_{2}\)로의 회전 방향은
반시계방향이므로 ccw의 결과는 양수가 나옵니다. - 반면 \(v_{1} \to v_{3}\)로의 회전 방향은
시계방향이므로 ccw의 결과는 음수가 나옵니다. - 위와 같은 케이스의 선분의 교차에서는 위 방법으로 벡터 쌍들의 ccw를 구하고 그 방향이 다르면 선분이 교차한다고 말할 수 있습니다.
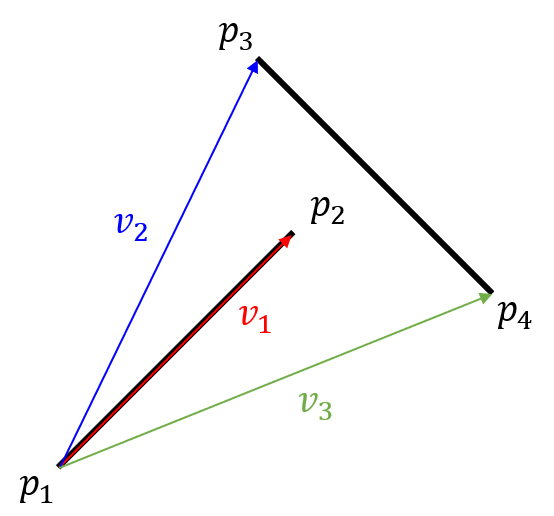
- 하지만 만약 위와 같은 경우에는 벡터의 회전 방향이 다르지만 선분이 교차하지 않습니다.
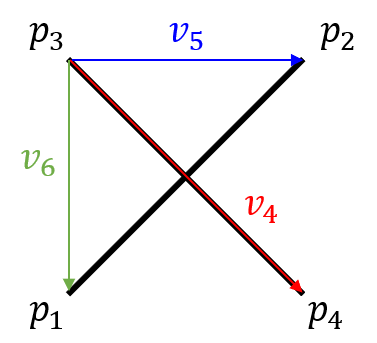
- 이 때에는 위와 같은 방향으로도 벡터들의 방향성을 확인하면 됩니다. 즉, \(v_{4} = p_{4} - p_{3}\), \(v_{5} = p_{2} - p_{3}\), \(v_{6} = p_{1} - p_{3}\) 일 때, \(v_{4} \to v_{5}\)로는 반시계 방향을 띄고 \(v_{4} \to v_{6}\)은 시계 방향을 띄므로 앞의 조건과 같이 벡터들의 방향성이 다름을 통하여 선분이 교차한다고 말할 수 있습니다.
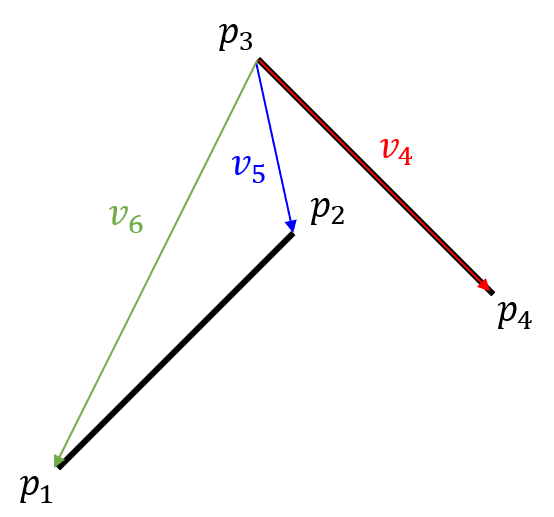
- 위 그림을 보면 앞의 조건인 \(v_{1}, v_{2}, v_{3}\)에서의 관계는 만족하였지만 방금 다룬 \(v_{4}, v_{5}, v_{6}\)의 관계에서는 같은 방향으로 회전하기 때문에 (\(v_{4} \to v_{5}\)와 \(v_{4} \to v_{6}\) 모두 시계 방향으로 회전) 교차하지 않음을 알 수 있습니다.

- 즉, 여기 까지 정리하면 p1 - p2 - p3 의 방향과 p1 - p2 - p4의 방향이 반대이고 p3 - p4 - p1의 방향과 p3 - p4 - p2의 방향도 반대이어야 합니다.
- 함수로 정리하면
ccw(p1, p2, p3) * ccw(p1, p2, p4) < 0&ccw(p3, p4, p1) * ccw(p3, p4, p2) < 0이 되어야 합니다.
- 위에서 다룬 케이스는 일반적인 선분의 교차이고 2가지 한계 상황에 대하여 더 다루어 보도록 하겠습니다.
- 첫번째는 4개의 점 중 3개의 점이 같은 직선상의 있는 경우이고 두번째는 4개의 점 모두 같은 직선 상에 있는 경우 입니다.
- 먼저 3개의 점이 같은 직선상에 있는 경우 부터 다루어 보도록 하겠습니다.
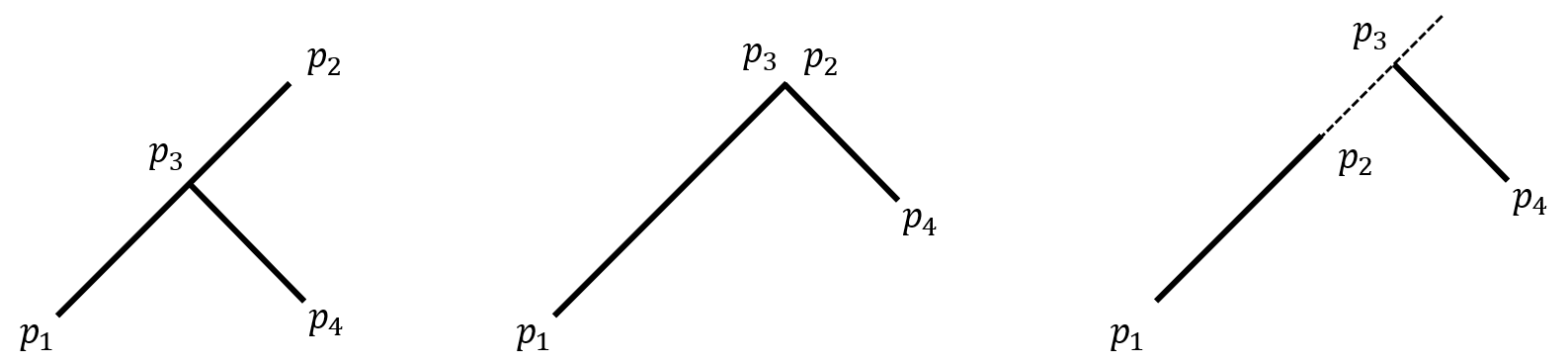
- 위 같은 경우는 p1, p2, p3가 모두 같은 직선상에 있는 케이스 입니다. 만약 위와 같은 경우도 선분이 교차 한다고 가정한다면 p1 - p2 - p3의 ccw는 동일선상에 있으므로 0이 나오게 됩니다.
- 즉,
ccw(p1, p2, p3) * ccw(p1, p2, p4) == 0만 만족하거나 또는ccw(p3, p4, p1) * ccw(p3, p4, p2) == 0만 만족하는 경우(둘 중에 하나만 0인 경우)에만 3점이 같은 직선에 속하게 되고 문제의 정의에 따라서 선분이 교차한다고 할 수 있습니다. - 그러면 위 두 식 모두 0을 만족하게 되는 경우를 다루어 보겠습니다. 그 케이스 바로 4개의 점들이 모두 같은 직선 상에 있는 경우입니다.

- 위 그림과 같이 4개의 점들이 같은 선상에 있는 경우에서 두 선이 겹치려면 위 그림의 아래 케이스 처럼 겹치는 방법이 있습니다.
- 겹치는 관계를 가지려면 좌표의 대소 관계를 비교하였을 때 p2가 p3보다 크고 p4가 p1 보다 커야합니다.
- 이 때 좌표의 대소 관계는 축의 순서를 정하고 그 축의 각 값의 대소 관계를 비교하는 것입니다.
- 예를 들어 x축 y축 순서를 가지고 p1의 x값이 p2의 x 값보다 크다면 p1 > p2이고 만약 x값이 같다면 p1의 y값이 p2의 y값보다 크다면 p1 > p2가 됩니다.
- 정리하면 p1, p2가 이루는 직선과 p3, p4가 이루는 직선이 있고 p1 < p2와 p3 < p4를 만족한다고 할 때,
p3 < p2 && p1 < p4를 만족하면 두 직선은 교차합니다.