Asymmetric Exponential

본 글에서 다루는 함수는 개인적으로 종종 사용하여 정리한 함수 입니다. 함수의 이름은 비대칭 지수 함수, Asymmetric Exponential로 정의 하였습니다.

이 함수는 다음 조건을 만족합니다.
① center 기준으로 지수적으로 증가하는 부분과 지수적으로 감소하는 부분이 존재합니다.
② low ~ center 범위는 지수적으로 감소하고 center ~ high 범위는 지수적으로 증가합니다. 따라서 low < center < high 크기 대소를 가집니다.
③ 생성되는 sample의 갯수는 지정할 수 있으며 low ~ center 범위와 center ~ high 범위의 범위 차이를 고려하여 sampling이 됩니다. 예를 들어 low ~ center 범위 대비 center ~ high 범위가 2배 크다면 2배 더 많이 sample을 뽑습니다.
④ rate 변수를 통하여 증가 폭을 증가시킵니다. rate 변수가 클수록 center 부근에서는 천천히 증감하고 low, high 근처에서는 많이 증감합니다.

이 함수는 center 부근에서는 작은 간격으로 구간을 나누고 center에서 멀어질수록 큰 간격으로 구간을 나누고자 할 때 사용할 수 있습니다. 단순히 등간격으로 low ~ high 까지의 범위를 나누는 것과 차이가 있습니다.

import numpy as np
import matplotlib.pyplot as plt

def exponential_formula(start, end, num_samples, rate):
    """
    Generates an exponential sequence between start and end.

    Parameters:
    - start (float): The starting value of the sequence.
    - end (float): The ending value of the sequence.
    - num_samples (int): Number of samples in the sequence.
    - rate (float): The rate of exponential growth.

    Returns:
    - numpy.ndarray: An array containing the exponential sequence.
    """
    t = np.linspace(0, 1, num_samples)
    scaled_values = start + (end - start) * (np.exp(rate * t) - 1) / (np.exp(rate) - 1)
    return scaled_values

def asymmetric_exponential_sampling(num_samples, center, low, high, rate=3):
    """
    Generates an asymmetric exponential sequence around a center value.

    Parameters:
    - num_samples (int): Total number of samples in the sequence.
    - center (float): The central value around which the sequence is generated.
    - low (float): The lower bound of the sequence.
    - high (float): The upper bound of the sequence.
    - rate (float): The rate of exponential growth.

    Returns:
    - numpy.ndarray: An array containing the asymmetric exponential sequence.
    """

    assert low < center and center < high, f"center:{center} is not on the range between low:{low} and high:{high}"
    # Calculate the number of samples from low to center and center to high
    num_low_to_center = int(num_samples * (center - low) / (high - low))
    num_center_to_high = num_samples - num_low_to_center

    # Generate sequence from low to center 
    low_sequence = exponential_formula(center, low, num_low_to_center, rate)[::-1]

    # Generate sequence from center to high (remove duplicated center value)
    high_sequence = exponential_formula(center, high, num_center_to_high, rate)[1:]

    # Combine sequences, excluding duplicate center value
    sequences = np.concatenate([low_sequence, high_sequence])
    return sequences

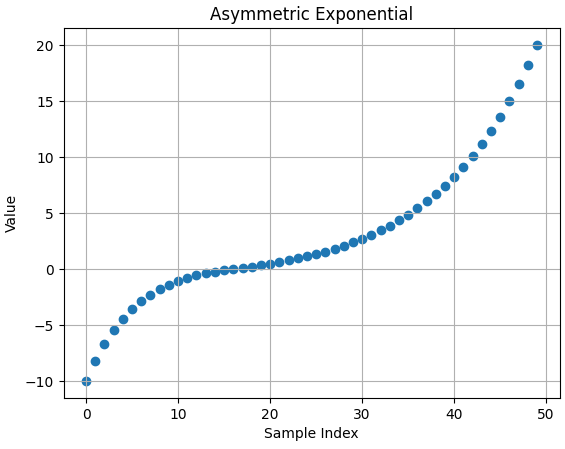
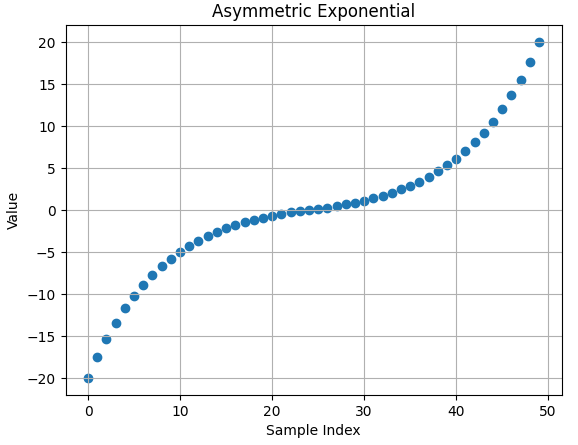
먼저 기본적인 샘플링 방식입니다. -20 ~ 0, 0 ~ 20 범위에서 50개의 샘플을 추출하는 예시입니다.

# Example usage
num_samples = 50
center = 0
low = -20
high = 20

sequences = asymmetric_exponential_sampling(num_samples + 1, center, low, high)

# Plotting the sequence
plt.scatter(np.arange(num_samples), sequences)
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Asymmetric Exponential')
plt.grid()
plt.show()

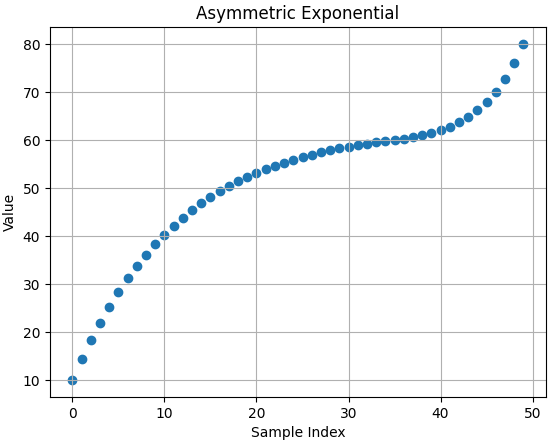
$Drawing$

아래는 10 ~ 60, 60 ~ 80 의 범위에서 샘플링하는 방식입니다. center 기준으로 구간의 범위가 비대칭적이므로 비대칭적 갯수로 샘플이 추출된 것을 볼 수 있습니다.

# Example usage
num_samples = 50
center = 60
low = 10
high = 80

sequences = asymmetric_exponential_sampling(num_samples + 1, center, low, high)

# Plotting the sequence
plt.scatter(np.arange(num_samples), sequences)
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Asymmetric Exponential')
plt.grid()
plt.show()

$Drawing$

Calculus 관련 글 목차