최적화 이론 기초 정리 (Gradient Descent, Newton Method, Gauss-Newton, Levenberg-Marquardt 등)

Calculus 관련 글 목차

사전 지식 필요 : 최소제곱법
사전 지식 필요 : Gradient, Jacobian, Hessian 개념
참조 : https://people.duke.edu/~hpgavin/ExperimentalSystems/lm.pdf
참조 : https://towardsdatascience.com/bfgs-in-a-nutshell-an-introduction-to-quasi-newton-methods-21b0e13ee504
참조 : https://youtu.be/C6DCtQjKkdY

이번 글에서는 최적화 기법을 이용할 때, 가장 기본적으로 사용되는 기법들에 대하여 다루어 보려고 합니다. 본 글에서 다룬 내용은 최적화 기법의 가장 기초적인 내용이며 풀고자 하는 문제에 맞게 각 기법들을 적용하여 사용하시면 됩니다.
다루는 알고리즘으로는 Gradient Descent(그래디언트 디센트), Newton Method(뉴턴 방법), Gauss-Newton Method(가우스 뉴턴 방법), Levenberg-Marquardt Method(르벤버그 마쿼트 방법), Quasi Newton Method(쿼시 뉴턴 방법), Lagrange Multiplier(라그랑주 승수법)이며 추가적으로 딥러닝에서 사용되는 Gradient Descent의 개선 알고리즘인 SGD, Mini-Batch Gradient Descent, Momentum, RMSProp, Adam을 다룹니다.
본 글을 읽기 전에 위에 명시되어 있는 최소제곱법과 Gradient, Jacobian, Hessian 개념 개념 숙지가 필요한 점 참조 부탁 드립니다.

Gradient Descent
Newton Method
Gradient Descent for Non-Linear Least Squares
Weighted Residuals
Newton Method for Non-Linear Least Squares
Gauss-Newton Method for Non-Linear Least Squares
Levenberg-Marquardt Method for Non-Linear Least Squares
Levenberg-Marquardt Method for Non-Linear Least Squares w/ Trial
Quasi Newton Method for Non-Linear Least Squares
Lagrange Multiplier
SGD
Mini-Batch Gradient Descent
Momentum
RMSProp
Adam

Gradient Descent

Newton Method

참조 : https://gaussian37.github.io/math-mfml-intro_to_optimisation/#newton-raphson-method-1

Gradient Descent for Non-Linear Least Squares

\[w_{\text{new}} = w_{\text{old}} - \lambda J_{r}^{T} r\]

Weighted Residuals

Gradient Descent에서 업데이트 해야 할 변화량 $\Delta$ 는 $J_{r}^{T} r$ 과 $\lambda$ 의 곱에 의하여 정의 되었습니다.
이 때, $\Delta$ 를 연산하기 위해 사용되는 Residual $r$ 을 단순히 $J_{r} r$ 로 연산하는 것이 아닌 업데이트 할 파라미터에 가중치를 부여하는 방법을 사용할 수 있습니다. 예를 들어 가중치를 부여하는 행렬을 $W$ 라고 명하였을 때, $J_{r} W r$ 과 같이 사용할 수 있습니다.
여기서 사용하는 가중치 행렬 $W$ 는 파라미터를 업데이트할 때, 어떤 파라미터에 좀 더 큰 업데이트를 적용할 지 업데이트 양을 조절하는 역할을 합니다. $W$ 행렬을 구성하는 별도의 방법이 있으면 사전 지식을 이용하여 활용해 볼 수 있지만 추가적인 정보가 없는 상태라면 Residual을 이용하여 $W$ 를 구성해 볼 수도 있습니다.

Residual은 에러값이므로 다음과 같이 표현할 수 있습니다.

\[y = f(\hat{x}) + \epsilon \quad (\epsilon \text{= Residual})\]
\[\epsilon = y - f(\hat{x})\]

통계 분석시에 Residual을 $\epsilon$ 으로 많이 표현하기 때문에 위 식과 같이 적어보았습니다. 중요한 것은 Residual은 정답값과 예측값의 차이인 에러를 나타내는 것이며 흔히 확률 분포를 생각 할 때, 노이즈로 간주되기도 합니다.
통계적 추정을 할 때, 자주 차용되는 가정 중 하나는 노이즈가 정규 분포를 따른 다는 것입니다. 이와 같은 가정을 이용하면 문제를 단순화 시킬 수 있습니다.
만약 에러값인 Residual이 정규분포를 따른다고 가정하면 에러값의 평균이 0이고 표준 편차는 $\sqrt{\text{Residual}^{2}}$ , 분산은 $\text{Residual}^{2}$이 됩니다.
이 때, $\text{Residual}^{2}$ 이 클수록 분산이 큰 것이고 노이즈가 크다는 것을 의미합니다. 분산이 크다는 의미는 데이터의 분포가 넓게 퍼져서 상대적으로 중요한 의미를 가지기 어렵다고 해석할 수도 있습니다. 따라서 $\text{Residual}^{2}$ 의 값이 큰 파라미터는 업데이트 시, 가중치를 낮추는 방향으로 업데이트를 유도할 수 있습니다.
이와 같은 방법을 이용하여 $W$ 행렬을 생성하려면 $1 / \text{Residual}^{2}$ 를 통해 구한 벡터를 $W$ 의 대각 성분으로 채우고 나머지 값은 0인 대각 행렬을 만들어서 $W$ 를 생성할 수 있습니다. 코드로 나타내면 다음과 같습니다.

# Estimate variances from residuals 
residuals = y - predict(x)
estimated_variances = residuals**2

weights = 1 / estimated_variances
W = np.diag(weights)

위 식을 통해 구한 $W$ 는 다음과 같이 파라미터 업데이트 시 사용될 수 있습니다.

\[w_{\text{new}} = w_{\text{old}} - \lambda J_{r}^{T} \color{red}{W} r\]

# python code style
J.T @ W @ r

가중치 행렬은 Least Squares에서도 사용됩니다. Least Squares의 기본적인 구조에서 앞에서 설명한 방식과 같은 방식으로 $W$ 를 만들어 Weighted Least Squares라는 방법론을 적용할 수 있습니다. 즉, 다음과 같이 기본적인 Least Squares식을 변경하여 Weighted Least Squares을 만들 수 있습니다.

\[(A^{T}A)^{-1}A^{T}b \quad \Rightarrow \quad (A^{T}WA)^{-1}A^{T}Wb\]

이번 글에서 다룰 Newton Method, Gauss-Newton Method, Levenberg-Marquardt Method들은 비선형 Least Squares 방법론이므로 동일한 방식으로 $W$ 를 적용할 수 있습니다.

가중치 행렬을 구성하는 방법은 모두 같으므로 앞으로 다룰 최적화 방법론에서 $W$ 는 생략한 상태로 식 및 코드를 진행하도록 하겠습니다. 실제 문제를 접근할 때에는 앞에서 소개한 바와 같이 Residual을 이용하여 $W$ 를 구한 다음 파라미터 업데이트 시 적용해 볼 수 있습니다.

Newton Method for Non-Linear Least Squares

앞에서 배운 newton method에서는 $f(x) = 0$ 의 해를 찾기 위하여 다음과 같이 식을 정의 후 iteration을 통하여 $f(x) = 0$ 를 만족하는 해를 점진적으로 찾아 갔습니다.

\[x_{i+1} = x_{i} - \frac{f(x_{i})}{f'(x_{i})}\]

문제의 관점을 조금 바꾸어서 단순히 $f(x) = 0$ 의 $f(x)$ 가 임의의 다항식이 아니라 Objective Function이라고 가정해 보겠습니다. 물론 Objective Function 또한 앞에서 정의한 다항식과 동일하게 표현될 수 있지만 의미상으로 정답 $y_{i}$ 와 예측값 $\hat{y}_{i}$ 간의 차이를 정의한 함수라고 생각해 보겠습니다.
이번에 다룰 예제 함수는 다음과 같은 함수입니다.

\[y = a \cdot e^{-wt}\]

위 식에서 $a$ 는 상수이고 구하고자 하는 파라미터는 $w$ 입니다. $t$ 가 입력값이고 $y$ 가 출력값입니다.
위 함수식을 이용하여 Objective Function을 SSE(Sum of Square Error) 형태로 아래와 같이 정의하겠습니다. 사용되는 데이터의 갯수는 $n$ 개로 이번 글에서는 8개의 데이터 샘플을 사용할 예정입니다.

\[\text{SSE} = \sum_{i=1}^{n}(y_{i} - \hat{y}_{i})^{2} = \sum_{i=1}^{n}(y_{i} - a e^{-wt_{i}})\]

SSE는 convex function으로 아래로 볼록한 형태를 가지게 됩니다. 따라서 critical point (임계점)을 찾기 위해 SSE의 1차 미분이 0이되는 지점을 찾는 문제로 변환하여 풀 수 있습니다.
newton metehod를 이용하여 이 문제를 접근한다면 다음과 같이 식을 정의할 수 있습니다.

\[w_{\text{new}} = w_{\text{old}} - \frac{f'(w_{\text{old}})}{f''(w_{\text{old}})}\]
\[\text{SSE} = \sum_{i} (y_{i} - a e^{-wt_{i}})\]
\[\frac{\partial \text{SSE}}{\partial w} = \sum_{i=1}^{n}2(y_{i} - ae^{-wt_{i}}) \cdot t_{i}ae^{-wt_{i}}\]
\[\frac{\partial^{2} \text{SSE}}{\partial w^{2}} = \sum_{i=1}^{n} -2y_{i}t_{i}t_{i}a e^{-wt_{i}} - ((2ae^{-wt_{i}})(-t_{i}t_{i}ae^{-wt_{i}}) + (-2t_{i}ae^{-wt_{i}})(t_{i}ae^{-wt_{i}}))\]

위 식들을 이용하여 newton method를 적용하면 다음과 같습니다.

\[w_{\text{new}} = w_{\text{old}} - \frac{\left(\frac{\partial \text{SSE}}{\partial w}\right)}{\left(\frac{\partial^{2}\text{SSE}}{\partial w^{2}}\right)}\]

단순히 1차 미분과 2차 미분을 이용하여 $w_{\text{old}} \to w_{\text{new}}$ 로 업데이트 한다는 것에서 앞에서 살펴본 다차 방정식의 해를 구하는 것과 큰 차이는 없습니다.

이번에는 위 함수에서 상수 $a$ 를 파라미터로 변경하여 다음과 같이 2개의 변수 $w = (w_{1}, w_{2})$ 를 가지는 multivariable function으로 변경해 보도록 하겠습니다.
최종적으로 구하고자 하는 형태가 vector-valued multivariable function에서의 최적화이기 때문입니다.

\[y = w_{1} \cdot e^{-w_{2}t}\]
\[w_{\text{new}} = w_{\text{old}} - \frac{f'(w_{\text{old}})}{f''(w_{\text{old}})}\]
\[\begin{bmatrix}w_{0(\text{new})} \\ w_{1(\text{new})} \end{bmatrix} = \begin{bmatrix} w_{0(\text{old})} \\ w_{1(\text{old})} \end{bmatrix} - H^{-1}G\]
\[G (\text{Gradient}) = \begin{bmatrix} \frac{\partial f}{\partial w_{1}} \\ \frac{\partial f}{\partial w_{2}} \end{bmatrix} = \begin{bmatrix} e^{-w_{2}t} \\ -w_{1}te^{-w_{2}t} \end{bmatrix}\]
\[H (\text{Hessian}) = \begin{bmatrix} \frac{\partial^{2}f}{\partial w_{1}^{2}} & \frac{\partial^{2}f}{\partial w_{1} \partial w_{2}} \\ \frac{\partial^{2}f}{\partial w_{2} \partial w_{1}} & \frac{\partial^{2}f}{\partial w_{2}^{2}} \end{bmatrix} = \begin{bmatrix} 0 & -t e^{-w_{2}t} \\ -t e^{-w_{2}t} & w_{1}t^{2}e^{-w_{2}t} \end{bmatrix}\]

위 식에서 $H^{-1}$ 과 $G$ 는 newton method에서 각각 아래 값과 대응됩니다.

\[f'(w) = G\]
\[\frac{1}{f''(w)} = H^{-1}\]

따라서 newton method를 이용하여 Objective Function을 최적화 할 때, 위 식을 통하여 점진적으로 해를 구할 수 있습니다.
위 식을 통하여 아래 데이터에 대하여 $w_{1}, w_{2}$ 을 최적화 해보려고 합니다.

t = [0, 20, 40, 60, 80, 100, 120, 140]
y = [147.8, 78.3, 44.7, 29.5, 15.2, 7.8, 3.2, 3.9]

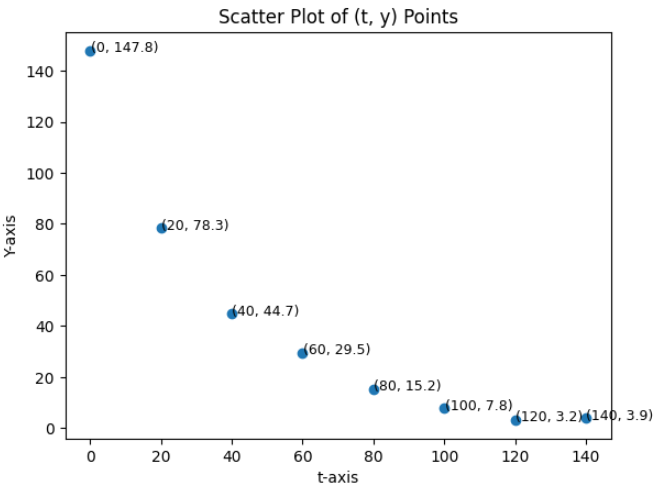
$Drawing$

위 데이터는 총 8개의 쌍으로 다음과 같이 기호로 적을 수 있습니다.

\[\begin{bmatrix} x_{0} & y_{0} \\ x_{1} & y_{1} \\ x_{2} & y_{2} \\ x_{3} & y_{3} \\ x_{4} & y_{4} \\ x_{5} & y_{5} \\ x_{6} & y_{6} \\ x_{7} & y_{7} \end{bmatrix} = \begin{bmatrix} 0 & 147.8 \\ 20 & 78.3 \\ 40 & 44.7 \\ 60 & 29.5 \\ 80 & 15.2 \\ 100 & 7.8 \\ 120 & 3.2 \\ 140 &3.9 \end{bmatrix}\]

그런데 newton method를 이용하여 최적화 하려고 하면 각 데이터에 대하여 Hessian을 구해야 하는 복잡함이 발생합니다. 따라서 각 행마다 다음과 같이 Hessian을 구하여 표현해 주어야 합니다.

\[H_{0} = \begin{bmatrix} 0 & -(0) e^{-w_{2}(0)} \\ -(0) e^{-w_{2}(0)} & w_{1}(0)^{2}e^{-w_{2}(0)} \end{bmatrix}\]
\[H_{1} = \begin{bmatrix} 0 & -(20) e^{-w_{2}(20)} \\ -(20) e^{-w_{2}(20)} & w_{1}(20)^{2}e^{-w_{2}(20)} \end{bmatrix}\]
\[\vdots\]
\[H_{7} = \begin{bmatrix} 0 & -(140) e^{-w_{2}(140)} \\ -(140) e^{-w_{2}(140)} & w_{1}(140)^{2}e^{-w_{2}(140)} \end{bmatrix}\]

예를 들어 least squares와 같은 경우에는 $Ax = b$ 에서 $x = (A^{T}A)^{-1}A^{T} b$ 와 같이 해를 구할 때, 모든 데이터 성분을 2차원 행렬 ( $(n, m)$ ) $A$ 와 벡터 $b$ 에 표현합니다.
하지만 newton method를 이용하여 최적해를 구할 때에는 Hessian으로 인하여 하나의 식으로 표현한다면 2차원 행렬인 Hessian을 행의 요소로 가지는 3차원 텐서로 표현해주어야 하는 복잡함이 발생합니다. (Hessian을 이용한 newton method의 출력은 matrix-valued multivariable function이 됩니다.) 그리고 2차 편미분에 대한 실제 계산도 복잡합니다.
따라서 newton method를 least squares와 같이 표현하여 계산 복잡도를 줄이는 방법이 필요합니다. 이러한 문제를 개선한 알고리즘이 Gauss-Newton Method입니다. (따라서 Newton Method를 non-linear least squares 문제를 풀기 위해 직접적으로 사용하는 경우는 다루지 않습니다.)

Gauss-Newton Method for Non-Linear Least Squares

Gauss-Newton Method는 optimization 문제를 풀 때, 2차 미분을 사용하는 Hessian 대신에 1차 미분을 사용하는 Gradient를 이용하여 근사해를 구하는 방식입니다. 이 때, Gradient를 $n$ 개의 function에 대하여 (vector-valued multivariable function) 적용하므로 Jacobian을 이용하게 됩니다.
Jacobian을 이용하여 Gauss-Newton Method에서 표현하고자 하는 것은 least squares(최소제곱법)를 반복적(iterative)으로 적용하는 것입니다.
이 방식을 통해 linear function의 해를 구하는 least squares를 non-linear function의 해를 구하는 non-linear least squares로 표현하는 것이 Gauss-Newton Method의 핵심이라고 말할 수 있습니다.
linear function의 해는 least squares를 한번 적용하여 해 또는 근사해를 구할 수 있습니다. 반면 non-linear function의 해는 linear function에 사용되는 least suqares를 단 한번 적용해서 근사해를 바로 구하기 어렵기 때문에 반복적으로 적용하며 점근적으로 근사해를 찾아갑니다.

이번에는 newton method for optimization 부분에서 다룬 내용을 이어서 어떻게 Gauss-Newton Method를 통해 non-linear least squares를 해결하는 지 살펴보도록 하겠습니다.

\[y = w_{1} \cdot e^{-w_{2}t}\]
\[\text{SSE} = \sum_{i}^{n} (y_{i} - w_{1} \cdot e^{-w_{2}t})^{2}\]
\[\text{Let } r_{i} = (y_{i} - w_{1} \cdot e^{-w_{2}t}). \ \ r \text{: residual}\]
\[\text{SSE} = \sum_{i=1}^{n} r_{i}^{2} = r^{t} r\]

chain rule을 이용하여 편미분을 적용해 보도록 하겠습니다.

\[\frac{\partial \text{SSE}}{\partial w_{j}} = 2 \sum_{i}^{n} r_{i} \cdot \frac{\partial r_{i}}{w_{j}} \to \sum_{i}^{n} r_{i} \cdot \frac{\partial r_{i}}{w_{j}}\]
\[\because \text{Constant(2) are deleted. It does not affect parameter estimation.}\]

아래와 같이 함수의 곱의 미분법에 따라 $\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}}$ 를 정의할 수 있습니다.
\[r(x) = f(x)g(x)\]
\[r'(x) = f'(x)g(x) + f(x)g'(x)\]

\[\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} = \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} + r_{i}\frac{\partial^{2} r_{i}}{\partial w_{j}\partial w_{k}} \right)\]

여기까지는 앞에서 다룬 newton method와 동일합니다. 앞에서 제기한 newton method의 문제점인 표현 및 계산의 복잡성을 단순화하고 least squares의 구조를 가질 수 있도록 식을 변경하기 위해서는 $\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}}$ 를 아래와 같이 단순화 해야 합니다.

\[\begin{align} \frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} &= \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} + \color{red}{r_{i}\frac{\partial^{2} r_{i}}{\partial w_{j}\partial w_{k}}} \right) \\ &\approx \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} \right) = J_{r}^{T}J_{r} \end{align}\]

위 식의 빨간색 부분은 2차 미분으로 값이 매우 작아지기 때문에 생략하여도 결과에 큰 영향이 없다는 점과 빨간색 부분을 생략함으로써 파라미터 업데이트 부분을 least squares 형태로 나타낼 수 있다는 특징이 있습니다. 이 부분은 바로 뒤에서 살펴보도록 하겠습니다.
이와 같이 식을 정리함으로써 SSE의 1차 미분과 2차 미분의 결과는 다음과 같이 Jacobian으로 표현할 수 있습니다.

\[\frac{\partial \text{SSE}}{\partial w_{j}} \approx \sum_{i}^{n} r_{i} \cdot \frac{\partial r_{i}}{w_{j}} = J_{r}^{T} r\]
\[\frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} \approx \sum_{i}^{n} \left( \frac{\partial r_{i}}{\partial w_{j}}\frac{\partial r_{i}}{\partial w_{k}} \right) = J_{r}^{T} J_{r}\]

위 결과값을 이용하면 newton method에서 사용하였던 $G$ 와 $H$ 는 다음과 같이 정의 됩니다.

\[G = \frac{\partial \text{SSE}}{\partial w_{j}} \approx J_{r}^{T} r\]
\[H = \frac{\partial^{2} \text{SSE}}{\partial w_{j} \partial w_{k}} \approx J_{r}^{T} J_{r}\]

따라서 newton method에서 사용하였던 파라미터 업데이트 수식을 다음과 같이 변경할 수 있습니다.

\[\begin{align} \begin{bmatrix}w_{0(\text{new})} \\ w_{1(\text{new})} \end{bmatrix} &= \begin{bmatrix} w_{0(\text{old})} \\ w_{1(\text{old})} \end{bmatrix} - H^{-1}G \\ &= \begin{bmatrix} w_{0(\text{old})} \\ w_{1(\text{old})} \end{bmatrix} - (J_{r}^{T} J_{r})^{-1}J_{r}^{T} r \end{align}\]

앞에서 빨간색 식 부분을 생략하는 방식을 통해 Hessian을 근사화하여 위 식과 같이 나타내는 이유는 파라미터 업데이트를 least squares(최소제곱법) 방식을 이용하여 업데이트하기 위함입니다.
먼저 파라미터를 업데이트하는 $(J_{r}^{T} J_{r})^{-1}J_{r}^{T} r$ 부분은 최소제곱법에서 사용한 수식과 같습니다. 최소제곱법에서는 $Ax = b$ 에서 $x$ 의 해를 구할 때, $x = (A^{T}A)^{-1}A^{T}b$ 와 같은 형식을 이용하여 해 또는 근사해를 구하였습니다.

\[(A^{T}A)^{-1}A^{T}b \quad \text{ Vs. } \quad (J_{r}^{T} J_{r})^{-1}J_{r}^{T} r\]

앞에서 residual은 정답값과 파라미터를 통해 추정한 값 간의 오차인데 이 오차는 파라미터가 아직 업데이트가 완전히 되지 않아서 생긴 오차입니다. 따라서 residual은 업데이트해야 할 $\Delta w$ 와 gradient의 곱으로 생긴 크기 만큼 발생합니다.

$Drawing$

위 그림은 Jacobian을 설명하기 위한 참조 그림입니다. $y_{2}$ 와 $y_{1}$ 의 차이는 $f'(x) \Delta x$ 만큼 차이가 나는 것으로 표현하였습니다.
이 때, $\Delta x$ 는 앞에서 표현한 $\Delta w$ 에 대응되고 $f'(x)$ 는 gradient에 대응됩니다.
즉, $y_{1}$ 을 추정값, $y_{2}$ 를 정답값이라고 가정한다면 $y_{1} \to y_{2}$ 로 근사화해 나아가는 것이 residual을 줄이는 것과 동일하게 생각할 수 있으므로 최적화 문제를 푸는 것이 됩니다.

이 때, 함수가 여러개이므로 residual의 gradient 대신에 Jacobian을 적용합니다. 따라서 $J_{r} \Delta w = r$ 로 residual을 표현할 수 있습니다.
실제 구하고자 하는 값은 residual을 최소화하는 $w$ 를 구하고 싶으므로 최적의 $w$ 를 구하기 위한 $w$ 의 변경량인 $\Delta w$ 를 구하기 위하여 다음과 같이 least squares를 적용할 수 있습니다.

\[J_{r} \Delta w = r\]
\[\Delta w = (J_{r}^{T} J_{r})^{-1}J^{T} r\]

따라서 업데이트해야 할 $\Delta w$ 를 구해서 $w$ 에 반영하여 다음과 같이 $w_{\text{old}} \to w_{\text{new}}$ 로 업데이트 하는 것이 문제를 해결하는 방법이 됩니다.
\[w_{\text{new}} = w_{\text{old}} - (J_{r}^{T} J_{r})^{-1}J_{r}^{T} r\]

업데이트 해야 할 $\Delta w$ 를 least squares를 이용하여 구한 후 $w$ 를 업데이트 하는데, 이 과정에서 한번의 least squares만을 이용하여 해를 구하지 않고 종료 조건이 만족될 때 까지 least squares를 반복하여 해 또는 근사해를 구하게 됩니다.
이와 같이 반복적인 근사화를 거치는 이유는 non-linear function에 least squares를 사용하기 때문입니다. 만약 linear function에서 least squares를 사용한다면 한번의 least squares를 적용하여 최적해를 찾을 수 있기 때문에 반복적인 근사화를 거치지 않습니다.
대표적으로 linear regression의 경우 residual의 기울기가 0이 되는 지점에서 유일한 최솟값을 가지기 때문에 한번의 least squares를 통하여 최솟값을 구할 수 있지만 지금까지 다룬 비선형 예제에서는 기울기가 0이되는 지점이 유일하지 않기 때문에 local minimum을 선형 함수로 근사화하여 해를 구한 것입니다. 따라서 Gauss-Newton method는 global minimum을 찾아가기 위하여 반복적으로 해를 찾아가는 과정을 거칩니다.

Gauss-Newton Method의 파라미터 업데이트 식을 살펴보면 $J_{r}^{T} r$ 에 $(J_{r}^{T}J_{r})^{-1}$ 가 곱해져서 파라미터를 업데이트 합니다. 이 값은 Hessian 근사값의 역행렬이므로 Gradient가 곡률(curvature)에 반비례한 만큼 업데이트 됩니다. Gradient의 변화가 크면 (즉, 곡률이 크면) 파라미터 업데이트 크기를 줄이고 Gradient의 변화가 작으면 (곡률이 작으면) 파라미터 업데이트 크기를 키워서 해를 찾아갑니다.
따라서 Gauss-Newton Method의 경우 주변 곡률 상황을 살펴보면서 Gradient의 크기를 조절하기 때문에 좀 더 빠르게 해를 찾을 수 있다는 장점이 있습니다.

지금까지 살펴본 예제는 파라미터가 $w_{1}, w_{2}$ 2개이므로 Jacobian이 다음과 같이 정의 됩니다.

\[\frac{\partial r_{i}}{\partial w_{1}} = -e^{-w_{2} t_{i}}\]
\[\frac{\partial r_{i}}{\partial w_{2}} = t_{i}w_{1}e^{-w_{2} t_{i}}\]
\[J_{r} = \begin{bmatrix} \frac{\partial r_{1}}{\partial w_{1}} & \frac{\partial r_{1}}{\partial w_{2}} \\ \frac{\partial r_{2}}{\partial w_{1}} & \frac{\partial r_{2}}{\partial w_{2}} \\ \vdots & \vdots \\ \frac{\partial r_{n}}{\partial w_{1}} & \frac{\partial r_{n}}{\partial w_{2}} \end{bmatrix} = \begin{bmatrix} -e^{-w_{2} t_{1}} & t_{1}w_{1}e^{-w_{2} t_{1}} \\ -e^{-w_{2} t_{2}} & t_{2}w_{1}e^{-w_{2} t_{2}} \\ \vdots & \vdots \\-e^{-w_{2} t_{3}} & t_{3}w_{1}e^{-w_{2} t_{3}} \end{bmatrix}\]

앞에서 이번 예제의 실제 데이터로 다음 데이터를 사용하기로 하였습니다. 따라서 아래 값을 대입해 줍니다.

t = [0, 20, 40, 60, 80, 100, 120, 140]
y = [147.8, 78.3, 44.7, 29.5, 15.2, 7.8, 3.2, 3.9]

\[J_{r} = \begin{bmatrix} -e^{-w_{2} t_{1}} & t_{1}w_{1}e^{-w_{2} t_{1}} \\ -e^{-w_{2} t_{2}} & t_{2}w_{1}e^{-w_{2} t_{2}} \\ \vdots & \vdots \\-e^{-w_{2} t_{3}} & t_{3}w_{1}e^{-w_{2} t_{3}} \end{bmatrix} = \begin{bmatrix} -e^{-w_{2}(0)}=-1 & (0)w_{1}e^{-w_{2}(0)}=0 \\ -e^{-20 w_{2}} & 20 w_{1}e^{-20 w_{2}} \\ \vdots & \vdots \\ -e^{-140 w_{2}} & 140 w_{1}e^{-140 w_{2}} \end{bmatrix}\]

파이썬 코드를 통하여 Jacobian을 구하면 다음과 같습니다.

from sympy import symbols, Matrix, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

# Initial values (0, 0)
params = np.array([0, 0]).reshape(2, 1)
# Define symbolic variables for the parameters and points
w1, w2 = symbols('w1 w2')

t = [0, 20, 40, 60, 80, 100, 120, 140]
y = [147.8, 78.3, 44.7, 29.5, 15.2, 7.8, 3.2, 3.9]

# Define the residual function for a single point
residuals = Matrix([])
for t_i, y_i in zip(t, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([y_i - w1 * sp.exp(-w2 * t_i)]))

residuals_func = lambdify([w1, w2], residuals, 'numpy')
r = residuals_func(params[0][0], params[1][0]) 

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w1, w2])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w1, w2], jacobian, 'numpy')

# Print the Jacobian matrix
Jr = jacobian_func(params[0][0], params[1][0])

위 코드에서 정의된 residuals의 결과는 다음과 같습니다.

$Drawing$

위 코드에서 정의된 jacobian의 결과는 다음과 같습니다.

$Drawing$

residual_func와 jacobian_func를 이용하여 Gauss-Newton Method를 다음과 같이 적용할 수 있습니다.
max_iteration최대 반복 횟수이고 threshold는 이전 파라미터와 현재 업데이트한 파라미터 간의 차이가 있는 지 확인하기 위한 값입니다. 따라서 max_iteration을 초과하거나 threshold 이하의 업데이트 양이 발생하면 Gauss-Newton Method를 종료합니다.

max_iteration = 30
threshold = 1e-7
prev_params = None
for i in range(max_iteration):
    # update parameters
    r = residuals_func(params[0][0], params[1][0])
    Jr = jacobian_func(params[0][0], params[1][0])
    update = np.linalg.pinv(Jr.T @ Jr) @ Jr.T @ r
    params -= update

    #### print out changes of parameters ###
    print("index:{}".format(i))
    if i > 0:
        print("prev_params: {}".format(prev_params.reshape(-1)))
    print("params:{}".format(params.reshape(-1)))
    print("update:{}\n".format(update.reshape(-1)))
    
    # check if updates are effective
    if i > 0:
        if np.sqrt(np.sum((prev_params - params)**2)) < threshold:
            break
            
    prev_params = params.copy()

# index:0
# params:[41.3  0. ]
# update:[-41.3   0. ]

# index:1
# prev_params: [41.3  0. ]
# params:[104.125        0.02173123]
# update:[-62.825       -0.02173123]

# index:2
# prev_params: [104.125        0.02173123]
# params:[145.08506266   0.02968753]
# update:[-40.96006266  -0.00795629]

# index:3
# prev_params: [145.08506266   0.02968753]
# params:[146.4444568    0.02918536]
# update:[-1.35939414  0.00050216]

# ...

# index:8
# prev_params: [146.42449511   0.02917939]
# params:[146.4244951    0.02917939]
# update:[0.00000001 0.        ]

파라미터 추정 결과 식은 다음과 같습니다.

\[146.4245 \cdot e^{-0.0292 t}\]

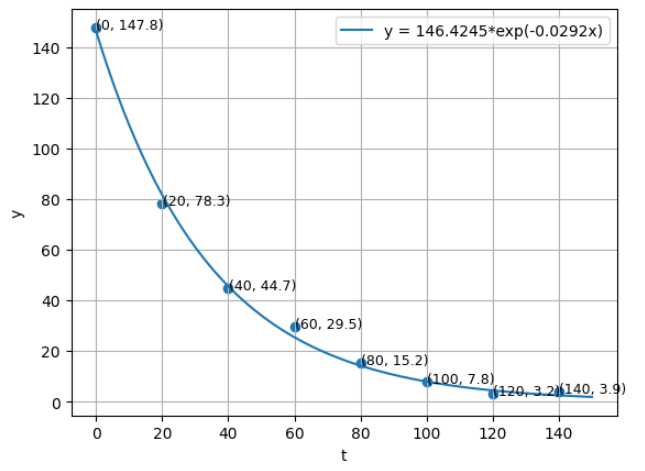
$Drawing$

따라서 위 그래프와 같이 샘플 데이터를 잘 표현하는 함수 파라미터를 구할 수 있음을 확인하였습니다.

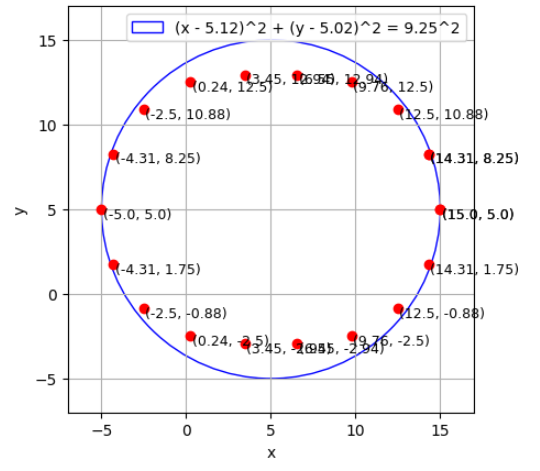
새로운 문제에 접근할 때에는 ① residual의 식 정의, ② 데이터 입력, ③ Gauss-Newton Method 부분 일부 수정을 통하여 새로운 문제를 해결할 수 있습니다.
그 다음으로 원의 방정식에서 필요한 파라미터를 찾는 예제를 살펴보도록 하겠습니다.

x = [15.0, 14.31, 12.5, 9.76, 6.55, 3.45, 0.24, -2.5, -4.31, -5.0, -4.31, -2.5, 0.24, 3.45, 6.55, 9.76, 12.5, 14.31, 15.0, 14.31]
y = [5.0, 8.25, 10.88, 12.5, 12.94, 12.94, 12.5, 10.88, 8.25, 5.0, 1.75, -0.88, -2.5, -2.94, -2.94, -2.5, -0.88, 1.75, 5.0, 8.25]

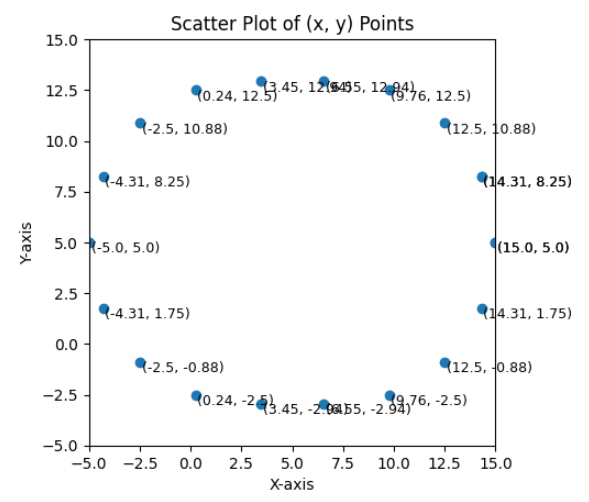
$Drawing$

원의 방정식은 다음과 같이 파라미터가 3개 입니다. 앞선 예제의 표현 방식과 동일하게 표현하기 위해 $w_{i}$ 로 표현하겠습니다.

\[(x - a)^{2} + (y - b)^{2} = r^{2}\]
\[\to (x - w_{1})^{2} + (y - w_{2})^{2} = w_{3}^{2}\]

원의 방정식에 맞게 파라미터 추정을 할 수 있도록 일부 코드를 수정하였습니다. 다음과 같습니다.

from sympy import symbols, Matrix, sqrt, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

params = np.array([0.0, 0.0, 0.0]).reshape(3, 1)

# Define symbolic variables for the circle parameters and points
w1, w2, w3 = symbols('w1 w2 w3') 

# Define the residual function for a single point
residuals = Matrix([])
for x_i, y_i in zip(x, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([sqrt((x_i - w1)**2 + (y_i - w2)**2) - w3]))

residuals_func = lambdify([w1, w2, w3], residuals, 'numpy')
r = residuals_func(params[0][0], params[1][0], params[2][0]) 
# print(r)

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w1, w2, w3])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w1, w2, w3], jacobian, 'numpy')

jacobian_result = jacobian_func(params[0][0], params[1][0], params[2][0])
# print(jacobian_result)

max_iteration = 30
threshold = 1e-7
prev_params = None
for i in range(100):
    r = residuals_func(params[0][0], params[1][0], params[2][0])
    Jr = jacobian_func(params[0][0], params[1][0], params[2][0])
    update = np.linalg.pinv(Jr.T @ Jr) @ Jr.T @ r
    params -= update

    print("index:{}".format(i))
    if i > 0:
        print("prev_params: {}".format(prev_params.reshape(-1)))
    print("params:{}".format(params.reshape(-1)))
    print("update:{}\n".format(update.reshape(-1)))
    
    if i > 0:
        if np.sqrt(np.sum((prev_params - params)**2)) < threshold:
            break
            
    prev_params = params.copy()

# index:0
# params:[5.45288523 6.14610515 7.28317812]
# update:[-5.45288523 -6.14610515 -7.28317812]

# index:1
# prev_params: [5.45288523 6.14610515 7.28317812]
# params:[5.13924744 4.95227765 9.20964762]
# update:[ 0.31363778  1.19382749 -1.9264695 ]

# index:2
# prev_params: [5.13924744 4.95227765 9.20964762]
# params:[5.12422646 5.02125385 9.25367991]
# update:[ 0.01502098 -0.0689762  -0.0440323 ]

# index:3
# prev_params: [5.12422646 5.02125385 9.25367991]
# params:[5.1236288  5.01748587 9.25393801]
# update:[ 0.00059767  0.00376798 -0.0002581 ]

# ...

# index:7
# prev_params: [5.12358414 5.01768123 9.25393944]
# params:[5.12358414 5.0176812  9.25393944]
# update:[ 0.00000001  0.00000003 -0.        ]

파라미터 추정 결과는 다음과 같습니다. (파라미터 값은 반올림 하였습니다.)

\[(x - 5.12)^{2} + (y - 5.02)^{2} = 9.25^{2}\]

$Drawing$

Levenberg-Marquardt Method for Non-Linear Least Squares

앞에서 Gauss-Newton Method를 이용하여 non-linear least squares 문제를 해결하는 방법을 다루었습니다.
Gauss-Newton Method의 단점 중 하나는 계산 과정 중 $(J_{r}^{T} J_{r})^{-1}$ 이라는 역행렬이 있어 역행렬이 없을 경우 수치적으로 불안정해질 수 있다라는 점입니다. 따라서 이 문제를 개선한 방법 중 유명한 방법인 Levenberg-Marquardt Method에 대하여 살펴보도록 하겠습니다.
먼저 앞에서 다룬 Gradient Descent와 Gauss-Newton Method의 차이점에 대하여 다시 확인해 보도록 하겠습니다. 왜냐하면 non-linear least squares 문제를 푸는 Levenberg-Marquardt Method는 Gradient Descent와 Gauss-Newton Method의 조합으로 이루어졌기 때문입니다.

Gradient Descent for Non-Linear Least Squares : $w_{\text{new}} = w_{\text{old}} - \lambda J_{r}^{T} r$

Gauss-Newton Method for Non-Linear Least Squares : $w_{\text{new}} = w_{\text{old}} - (J_{r}^{T}J_{r})^{-1}J_{r}^{T} r$

두 방법론의 공통점은 업데이트 크기를 결정하는 부분이 $J_{r}^{T} r$ 로 residual과 residual의 변화량(미분)인 Jacobian을 이용하여 파라미터를 업데이트 한다는 점입니다.

반면 차이점은 Gradient Descent의 경우 $J_{r}^{T} r$ 에 $\lambda$ 라는 learning rate가 곱해져서 파라미터 업데이트가 되기 때문에 Gradient의 크기에 비례한 만큼 파라미터를 업데이트하게 됩니다.
하지만 Gauss-Newton Method의 경우 $J_{r}^{T} r$ 에 $(J_{r}^{T}J_{r})^{-1}$ 가 곱해져서 파라미터를 업데이트 합니다. 이 값은 Hessian 근사값의 역행렬이므로 Gradient가 곡률(curvature)에 반비례한 만큼 업데이트 됩니다. 따라서 Gradient의 변화가 크면 (즉, 곡률이 크면) 파라미터 업데이트 크기를 줄이고 Gradient의 변화가 작으면 (곡률이 작으면) 파라미터 업데이트 크기를 키워서 해를 찾아갑니다.
Gauss-Newton Method의 경우 주변 곡률 상황을 살펴보면서 Gradient의 크기를 조절하기 때문에 좀 더 빠르게 해를 찾을 수 있다는 장점이 있습니다. 하지만 $(J_{r}^{T}J_{r})^{-1}$ 에 대한 수치 불안정성이 있어 발산의 위험성이 있습니다.

일반적으로 Gauss-Newton Method의 수렴 속도가 Gradient Descent보다 빠릅니다. 앞에서 설명한 곡률에 따른 비율 조정으로 좀 더 빠르게 해를 찾아갈 수 있다는 점이 Gauss-Newton Method의 장점이 됩니다.
일반적으로 Gradient Descnet의 Learning Rate인 $\lambda$ 를 $0.001$ 과 같이 정한다는 가정이라면 Gauss-Newton Method 에서 사용하는 $(J_{r}^{T}J_{r})^{-1}$ 의 값이 곡률이 작은 경우에는 $\lambda$ 보다 커지고 곡률이 큰 경우에는 $\lambda$ 보다 작아집니다. 즉, 동적으로 Learning Rate를 조절할 수 있어 수렴 속도가 빠른 것입니다.

따라서 일반적으로는 Gauss-Newton Method를 사용하여 빠르게 수렴하는 방법을 취하는 대신에 수렴이 정상적으로 되지 않는 상황에서는 Gradient Descent를 이용하여 안정적으로 수렴시키는 방식을 취하는 것이 대안이 될 수 있습니다. 이 컨셉이 Levenberg-Marquardt Method의 핵심입니다.

수렴이 정상적으로 되지 않는 상황은 residual의 변화를 통해 확인할 수 있습니다. 일반적으로 Gauss-Newton Method를 이용하여 정상적으로 수렴해 나아간다면 residual의 크기가 점점 줄어들어야 합니다. 반면 residual의 크기가 줄어들지 않는 상황은 수렴하지 않는 상황이라고 생각할 수 있습니다. 이와 같은 경우에 Gradient Descent 방법의 비중을 높여 안정적으로 수렴하도록 유도합니다.

\[w_{\text{new}} = w_{\text{old}} - (J_{r}^{T}J_{r} + \mu \cdot \text{diag}(J_{r}^{T}J_{r}))^{-1}J_{r}^{T} r\]
\[\mu \text{: damping factor}\]
\[\text{As the damping factor gets larger, it gets closer to Gradient Descent.}\]
\[\text{As the damping factor gets smaller, it gets closer to Gauss Newton Method.}\]

위 수식에서 $\mu > 0$ 는 damping factor라고 부르며 이 값에 따라서 파라미터 업데이트 방식이 Gradient Descent에 가까워질 지 또는 Gauss-Newton Method에 가까워질 지 결정됩니다.

만약 극단적으로 $\mu$ 가 0이 된다면 식은 다음과 같이 변경되어 Gauss-Newton Method와 동일해 집니다.

\[w_{\text{new}} = w_{\text{old}} - (J_{r}^{T}J_{r} + 0 \cdot \text{diag}(J_{r}^{T}J_{r}))^{-1}J_{r}^{T} r = w_{\text{old}} - (J_{r}^{T}J_{r})^{-1}J_{r}^{T} r\]

반면 $\mu$ 가 극단적으로 커지면 식은 다음과 같이 변경될 수 있습니다. 즉, Gradient Descent 방식과 유사해 집니다.

\[w_{\text{new}} = w_{\text{old}} - (J_{r}^{T}J_{r} + \alpha \cdot \text{diag}(J_{r}^{T}J_{r}))^{-1}J_{r}^{T} r \approx w_{\text{old}} - \mu J_{r}^{T} r \quad (\alpha \text{ : large number})\]

이와 같이 damping factor $\mu$ 에 따라서 알고리즘의 성격이 바뀌기 때문에 상황에 따라서 damping factor를 조절할 수 있어야 합니다. damping factor를 조절하는 방식 중 Residual의 크기가 점점 작아지면 정상 수렴이라 가정하고 $\mu$ 값을 줄여서 Gauss-Newton Method에 가깝도록 반영하는 방법이 사용 됩니다.
반면 Residual의 크기가 작아지지 않으면 발산할 가능성이 있다라고 가정합니다. (이와 같은 경우 선택적으로 파라미터 업데이트를 보류하고 $\mu$ 값을 증가시켜 안정적인 Gradient Descent에 가깝도록 반영할 수 있습니다. 아래 flow-chart에는 이 부분이 반영되어 있습니다.)
기본적으로 $\mu$ 값을 증감 시키는 factor를 $\nu = 10 > 0$ 을 많이 사용합니다. $\mu$ 감소 시 $\mu = \mu / \nu$ 로 적용하고 $\mu$ 증가 시 $\mu = \mu \cdot \nu$ 로 적용합니다.

추가적으로 damping factor가 커지면 수치적으로 안정적인 이유에 대하여 설명하면 다음과 같습니다.
- ① 행렬의 대각 성분의 크기가 커지면 invertible 해지는 경향이 있습니다. 예를 들어 대각 행렬은 항상 invertible 합니다.
- ② 추가적으로 Hessian의 Determinant로 Global Optimization의 여부를 알 수 있는데, Hessian의 Determinant가 양수이면 Global Optimization이 가능한 형태가 됩니다. damping factor가 속한 행렬 전체는 Hessian을 근사한 행렬입니다. 행렬의 대각 성분이 큰 양수가 될수록 Positive Definite Matrix가 될 가능성이 높아지는데 Positive Definite Matrix는 양의 고유값들만 가지게 됩니다. 이 때, 고유값의 곱이 Determinant가 되므로 행렬의 대각 성분이 큰 양수가 될수록 Determinant가 양수가 될 가능성이 커집니다. 뿐만 아니라 Determinant가 양수가 될 가능성이 커지고 대각 성분 또한 실제 양수가 될 가능성이 커지므로 Global Optimization이 될 가능성 또한 커집니다.
이와 같은 이유로 $\mu$ 값이 커지면 ① 역행렬을 가지는 경향이 커진다는 것과 ② Global Optimization을 만족하는 경향이 커진다는 이유로 수치적으로 안정화 됩니다.

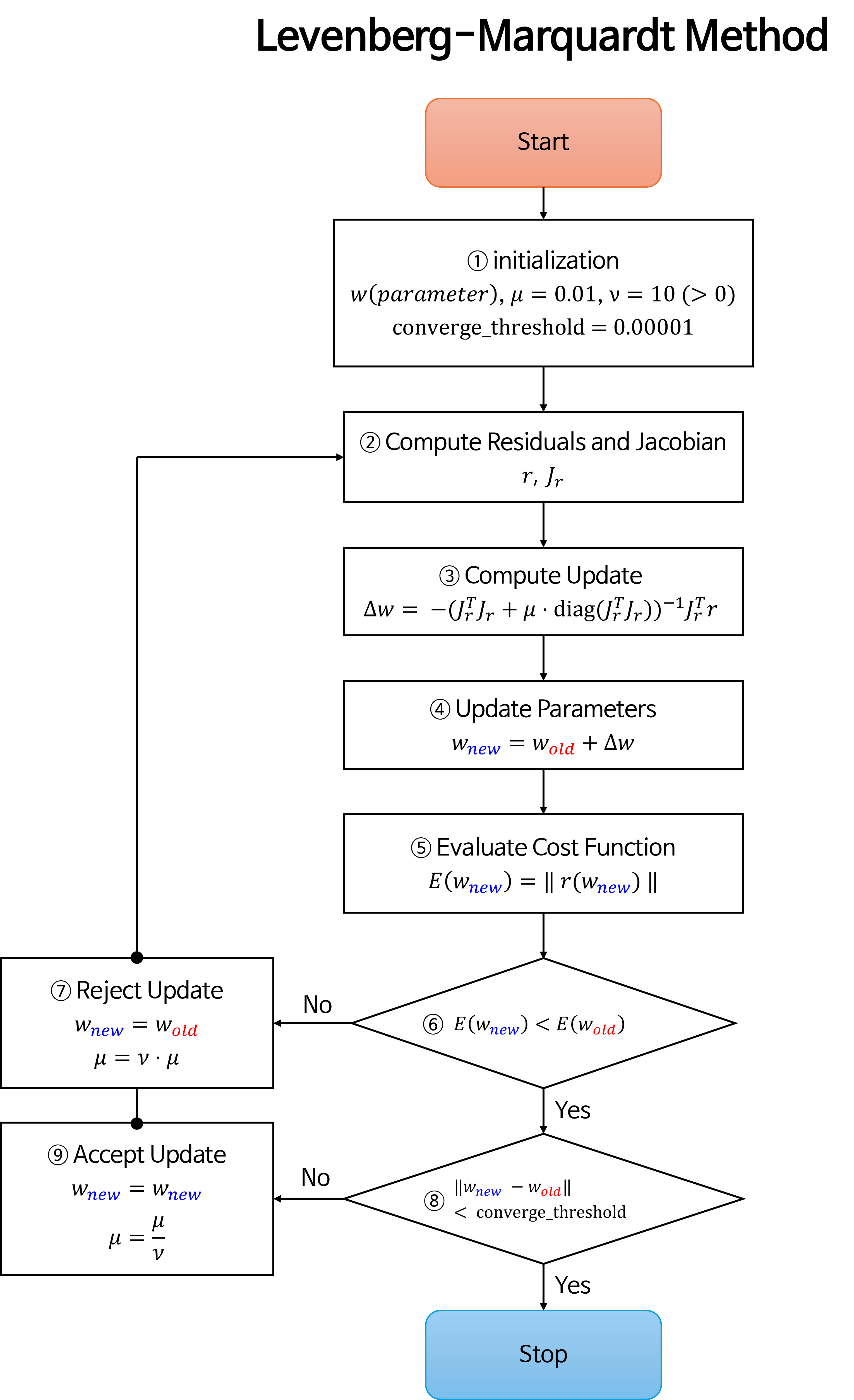
Levenberg-Marquardt Method의 전체적인 알고리즘을 flow-chart로 나타내면 다음과 같습니다.

$Drawing$

지금까지는 Levenberg-Marquardt Method의 이론적 배경에 대하여 살펴보았습니다.
이번에는 앞에서 살펴본 예제보다 약간 복잡도가 있는 Damped Oscillation Formula예제를 이용하여 Levenberg Marquardt Method를 사용하였을 때, Gauss-Newton Method를 사용하였을 때보다 안정적으로 수렴하는 것을 살펴보도록 하겠습니다.

아래 예제에서는 Damped Oscillation Formula에 따라 다음과 같이 식을 정의 하였습니다.

\[y = A \cdot e^{-\lambda \cdot x} \cos{(\omega \cdot x + \phi)} + C\]
\[A \text{ : amplitude}\]
\[\lambda \text{ : damping coefficient}\]
\[\omega \text{ : angular frequency}\]
\[\phi \text{ : phase shift}\]
\[C \text{ : vertical shift}\]

위 식을 앞에서 다룬 예제들과 같이 파라미터를 다음과 같이 $w_{i}$ 로 간소화하여 사용하겠습니다.

\[\to y = w_{0} \cdot e^{-w_{1} \cdot x} \cos{(w_{2} \cdot x + w_{3})} + w_{4}\]

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, Matrix, sqrt, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

# True parameters
A_true = 2
lambda_true = 0.1
omega_true = 2 * np.pi / 5
phi_true = 0.5
C_true = 1

# Generate data points
x = np.linspace(0, 20, 30)
y = A_true * np.exp(-lambda_true * x) * np.cos(omega_true * x + phi_true) + C_true

# Round the points to 2 decimal places
x = np.round(x, 2).tolist()
y = np.round(y, 2).tolist()

# Print the points
print("x =", x)
# x = [0.0, 0.69, 1.38, 2.07, 2.76, 3.45, 4.14, 4.83, 5.52, 6.21, 6.9, 7.59, 8.28, 8.97, 9.66, 10.34, 11.03, 11.72, 12.41, 13.1, 13.79, 14.48, 15.17, 15.86, 16.55, 17.24, 17.93, 18.62, 19.31, 20.0]
print("y =", y)
# y = [2.76, 1.38, -0.07, -0.62, -0.03, 1.17, 2.1, 2.18, 1.47, 0.54, 0.03, 0.23, 0.92, 1.57, 1.76, 1.42, 0.85, 0.45, 0.47, 0.83, 1.26, 1.46, 1.33, 0.99, 0.71, 0.65, 0.83, 1.1, 1.27, 1.24]

위 코드를 통하여 $(x, y)$ 데이터를 $A = 2, \lambda = 0.1, \omega= \frac{2\pi}{5}, \phi = 0.5, C = 1$ 파라미터를 이용하여 생성하였습니다.

$Drawing$

위 그림이 Damped Oscillation Formula 에서 참조한 Damped Oscillation Formula의 예시입니다.

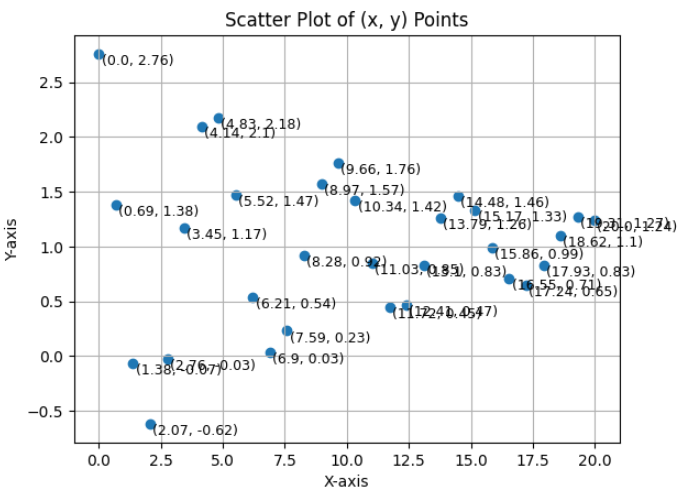
$Drawing$

위 그림이 코드를 통해 생성한 예제입니다. 좌상단부터 점들을 이어서 그리면 Oscillation을 관측할 수 있습니다.

Gauss-Newton Method

먼저 Gauss-Newton Method를 이용하여 파라미터 추정을 하면 다음과 같습니다.

num_params = 5
params = np.random.rand(num_params).reshape(num_params, 1)

# Define symbolic variables for the circle parameters and points
w0, w1, w2, w3, w4 = symbols('w0 w1 w2 w3, w4') 

# Define the residual function for a single point
residuals = Matrix([])
for x_i, y_i in zip(x, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([w0 * sp.exp(-w1 * x_i) * sp.cos(w2 * x_i + w3) + w4 - y_i]))

residuals_func = lambdify([w0, w1, w2, w3, w4], residuals, 'numpy')
r = residuals_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
# print(r)

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w0, w1, w2, w3, w4])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w0, w1, w2, w3, w4], jacobian, 'numpy')

jacobian_result = jacobian_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
# print(jacobian_result)

max_iteration = 50
threshold = 1e-5
prev_params = None
for i in range(max_iteration):
    r = residuals_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
    Jr = jacobian_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
    update = np.linalg.pinv(Jr.T @ Jr) @ Jr.T @ r
    params -= update

    print("index:{}".format(i))
    if i > 0:
        print("prev_params: {}".format(prev_params.reshape(-1)))
    print("params:{}".format(params.reshape(-1)))
    print("update:{}\n".format(update.reshape(-1)))
    
    if i > 0:
        if np.sqrt(np.sum((prev_params - params)**2)) < threshold:
            break
            
    prev_params = params.copy()

# index:0
# params:[-0.624676    2.30179744 -2.30671177 37.76048577  5.24782737]
# update:[  0.39962068  -2.26936801   2.12682433 -38.11397284  -6.63437497]

# index:1
# prev_params: [-0.624676    2.30179744 -2.30671177 37.76048577  5.24782737]
# params:[  -3.9341092    36.43396877 -219.96593882  185.79090885    1.01711128]
# update:[   3.3094332   -34.13217134  217.65922705 -148.03042308    4.23071609]

# index:2
# prev_params: [  -3.9341092    36.43396877 -219.96593882  185.79090885    1.01711128]
# params:[  -3.49213454   36.43396877 -219.96593882  186.60300529    0.94793103]
# update:[-0.44197466  0.         -0.         -0.81209644  0.06918025]

# index:3
# prev_params: [  -3.49213454   36.43396877 -219.96593882  186.60300529    0.94793103]
# params:[  -3.51234232   36.43396877 -219.96593882  186.39130536    0.94793103]
# update:[ 0.02020778 -0.         -0.          0.21169993 -0.        ]

# ...

# index:6
# prev_params: [  -3.51375076   36.43396877 -219.96593882  186.38292922    0.94793103]
# params:[  -3.51375076   36.43396877 -219.96593882  186.38292922    0.94793103]
# update:[ 0. -0. -0.  0.  0.]    

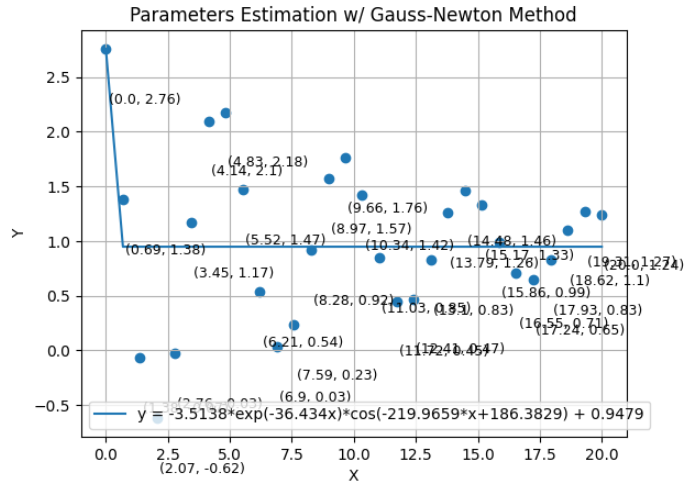
$Drawing$

앞선 쉬운 예제와는 다르게 Gauss-Newton Method는 수렴에 실패한 것을 확인할 수 있습니다. 다양하게 실험을 해 보아도 수렴이 잘 되지 않았습니다.

Levenberg-Marquardt Method

num_params = 5
params = np.random.rand(num_params).reshape(num_params, 1)

# Define symbolic variables for the circle parameters and points
w0, w1, w2, w3, w4 = symbols('w0 w1 w2 w3, w4') 

# Define the residual function for a single point
residuals = Matrix([])
for x_i, y_i in zip(x, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([w0 * sp.exp(-w1 * x_i) * sp.cos(w2 * x_i + w3) + w4 - y_i]))

residuals_func = lambdify([w0, w1, w2, w3, w4], residuals, 'numpy')
r = residuals_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
# print(r)

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w0, w1, w2, w3, w4])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w0, w1, w2, w3, w4], jacobian, 'numpy')

jacobian_result = jacobian_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
# print(jacobian_result)

max_iteration = 50
converge_threshold = 1e-5
mu = 0.01
nu = 10
prev_params = None
for i in range(max_iteration):
    r = residuals_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
    Jr = jacobian_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0]) 
    update = np.linalg.pinv(Jr.T @ Jr + mu * np.diag(np.diag(Jr.T @ Jr))) @ Jr.T @ r
    params -= update

    print("index:{}".format(i))
    if i > 0:
        print("prev_params: {}".format(prev_params.reshape(-1)))
    print("params:{}".format(params.reshape(-1)))
    print("update:{}\n".format(update.reshape(-1)))
    
    if i > 0:
        E_old = np.sum(residuals_func(prev_params[0][0], prev_params[1][0], prev_params[2][0], prev_params[3][0], prev_params[4][0])**2)
        E_new = np.sum(residuals_func(params[0][0], params[1][0], params[2][0], params[3][0], params[4][0])**2)
        if E_new < E_old:                   
            if np.sqrt(np.sum((prev_params - params)**2)) < converge_threshold:
                break
            else:
                # params = params.copy() 
                mu = mu / nu
        else:
            params = prev_params.copy()
            mu = mu * nu
                
    prev_params = params.copy()

# index:0
# params:[0.21561101 0.03815262 0.52028444 0.75913489 1.0330242 ]
# update:[ 0.53048438 -0.0217913   0.0354741  -0.50188437 -0.97090691]

# index:1
# prev_params: [0.21561101 0.03815262 0.52028444 0.75913489 1.0330242 ]
# params:[0.48145848 0.23137313 0.44070408 1.92344109 1.03481424]
# update:[-0.26584746 -0.1932205   0.07958036 -1.1643062  -0.00179004]

# index:2
# prev_params: [0.48145848 0.23137313 0.44070408 1.92344109 1.03481424]
# params:[ 3.34563941  1.67963651  1.51289747 -3.40649195  1.10638248]
# update:[-2.86418093 -1.44826339 -1.07219339  5.32993304 -0.07156824]

# ...

# index:24
# prev_params: [1.99920146 0.10026304 1.25684614 0.49679209 0.99929372]
# params:[1.99920345 0.1002633  1.25684608 0.49679235 0.99929372]
# update:[-0.00000199 -0.00000026  0.00000006 -0.00000026 -0.        ]

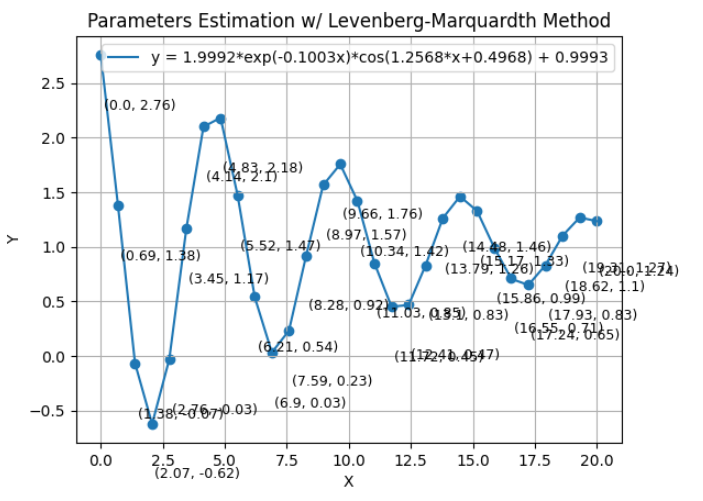
$Drawing$

반면 Levenberg-Marquardt Method를 이용하였을 때에는 위 결과와 같이 수렴이 되었습니다. 하지만 Newton Method계열의 알고리즘이 초깃값을 잘못 설정하면 수렴이 잘 되지 않는다는 점은 Levenberg-Marquardt Method에서도 나타남을 확인하였습니다. (초깃값에 따라 가끔씩 수렴을 하지 않습니다.)
따라서 Levenberg-Marquardt Method를 사용할 때에도 각 문제에 맞는 적절한 초깃값 설정은 매우 중요합니다.
글 뒷 부분에서 몇가지 실험들을 더 다루겠지만 알고리즘을 강건하게 설계하는 것도 중요하지만 Newton Method 계열의 최적화에서는 초깃값을 잘 잡는 것이 무엇보다 중요합니다.
컴퓨터 비전에서 사용하는 대표적인 Levenberg-Marquardt Method의 사용처인 Camera Calibration 또는 Bundle Adjustment에서도 사전에 알고리즘을 통하여 적절한 초깃값을 구한 다음에 최적화를 시작합니다. 이 부분에서 Levenberg-Marquardt Method 의 방법론을 개선하기 보다 초깃값을 개선하는 것이 최종 성능 개선에 효과적일 수 있습니다.

Levenberg-Marquardt Method for Non-Linear Least Squares w/ Trial

이번에는 몇가지 최적화 예제를 통하여 Levenberg-Marquardt Method를 이용한 방법을 다루어 보도록 하겠습니다. 이번 챕터에서 제안한 내용은 개인적인 경험으로 작성해 본 것이며 풀고자 하는 문제에 따라 아래 방법이 비효율적일 수도 있음을 감안하고 읽으시면 좋겠습니다.
앞에서 설명한 순서도에서 알고리즘의 강건성 향상 및 해를 구하기 쉽게 몇가지 셋팅을 변경하였습니다.
특히, 초깃값 설정이 잘못되었을 때, 초깃값을 다시 구하는 과정을 추가하여 수렴 가능성을 높였습니다. 초깃값을 실제 구할 수 있는 환경에서는 다시 예측을 하여 초깃값을 구할 수 있으며 그렇지 않은 경우에는 다시 랜덤값으로 초깃값을 셋팅합니다. 이와 같이 여러 번의 초깃값 셋팅을 시도한다는 점에서 Trial이라고 붙였습니다.

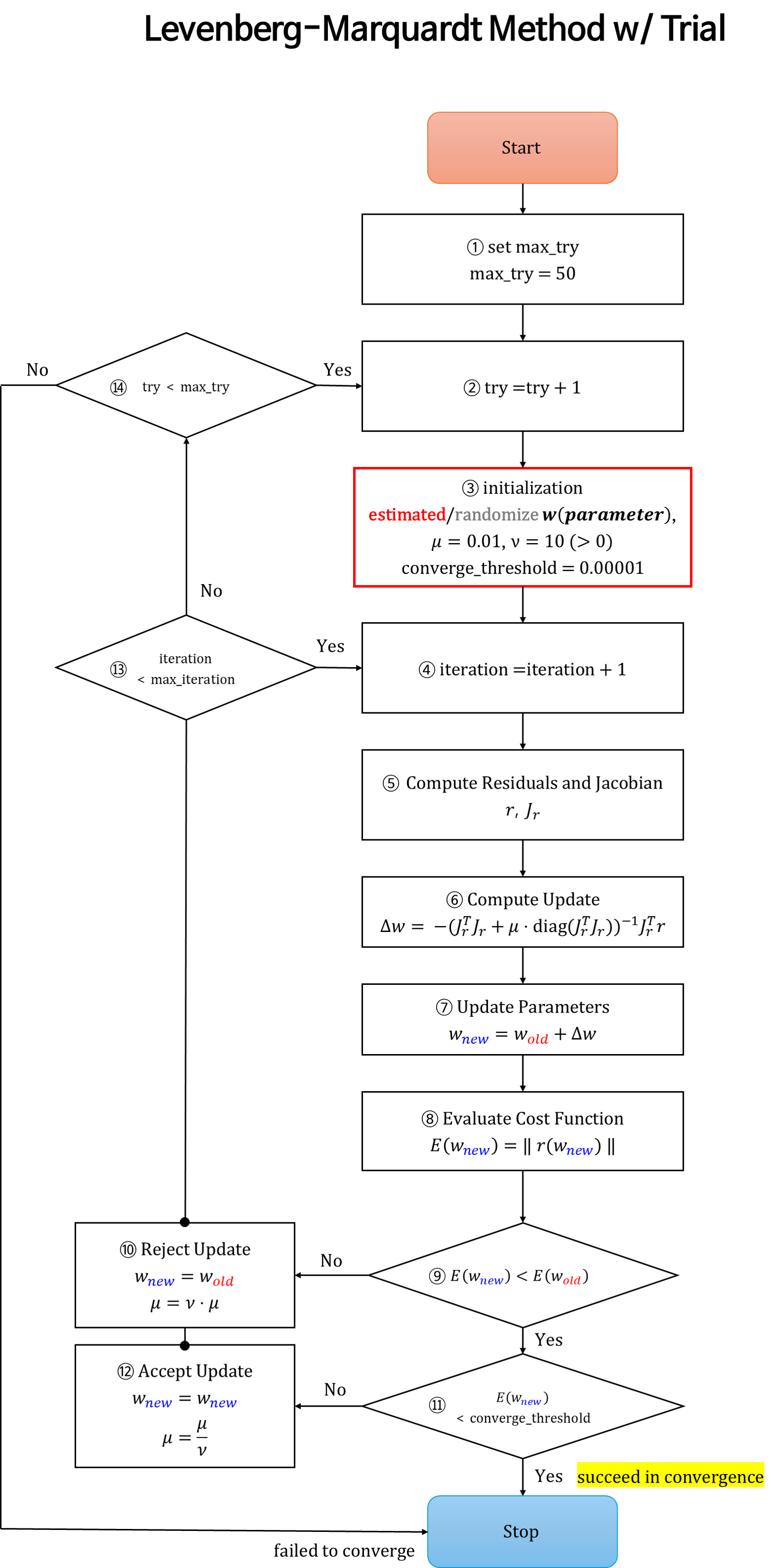
$Drawing$

① set max try : 앞에서 다룬 Levenberg-Marquardt Method와 가장 큰 차이 입니다. 이 부분은 ③의 파라미터 값을 다시 초기화 하기 위한 최대 try 횟수를 지정하는 부분입니다.
② try + 1 : 각 try 별 최대 시도 가능한 횟수를 카운트 하는 부분입니다. 이 부분은 ③ 과정과 연관되어 있으며 최대 try 횟수만큼 initialization을 할 수 있는 기회가 주어집니다.
③ initialization : 추정해야 할 파라미터와 그 이외의 하이퍼 파라미터를 셋팅하는 과정입니다. 하이퍼 파라미터 셋팅은 실험적으로 정할 수 있습니다. 추정해야 할 파라미터에 대한 정보가 없다면 예상되는 범위에서 임의의 초깃값을 줄 수 있습니다. 만약 추정해야 할 파라미터를 다른 알고리즘을 이용하여 근사값으로 추정할 수 있다면 가능한 정답과 유사하게 초깃값을 셋팅하는 것이 좋습니다. (초깃값을 잘 설정하는 것이 최적화의 성능을 높이는 데 매우 중요합니다.). 하이퍼 파라미터 또한 각 문제에 맞게 적합하게 설정해야 합니다.
④ iteration + 1 : 각 iteration 별 최대 최적화 횟수를 카운트하는 부분입니다. 이 부분은 ⑬과 연결되며 ⑬에서 최대 최적화 횟수를 초과하면 새로운 try를 시작합니다.
⑤, ⑥, ⑦ Compute Residuals and Jacobian : 앞에서 다룬 Levenberg-Marquardt Method 내용과 동일합니다.
⑧ Evaluate Cost Function : 최적화 진행 상태를 확인하기 위하여 Error 값의 크기를 계산합니다.
⑨ $\text{E}(w_{\text{new}}) \lt \text{E}(w_{\text{old}})$ : Error 값의 크기가 작아지는 지 확인합니다. 만약 Error 값이 작아진다면 정상 수렴이라고 가정합니다. 반대로 Error 값이 커진다면 정상 수렴 상태가 아니라고 판단하고 ⑩ 과정으로 진행됩니다.
⑩ Reject Update : 정상 수렴이 아니라고 가정하고 파라미터 업데이트를 하지 않습니다. 수렴이 안정적이지 않으므로 Levenberg-Marquardt Method에서 제안한 damping factor의 크기를 증가시켜 Gradient Descent에 가깝도록 알고리즘에 반영하여 좀 더 안정적인 최적화 방법을 수행합니다.
⑪ $\text{E}(w_{\text{new}}) \lt \text{converge_threshold}$ : Error 값의 크기가 ③에서 정한 converge_threshold 값보다 작아졌다면 수렴했다고 판단하고 알고리즘을 종료합니다.
⑫ Accept Update : ⑤, ⑥, ⑦ 과정을 통해 정상 수렴은 하였지만 아직 목표(converge_threshold) 지점까지 최적화가 진행되지 않은 상태입니다. 따라서 현재까지 최적화한 파라미터 결과를 채택하고 damping factor를 줄여 Gauss-Newton Method에 가깝도록 알고리즘에 반영합니다. damping factor가 줄어들어 최적화 수렴 속도가 증가할 것을 기대합니다.
⑬ iteration < max_iteration : 현재 초깃값 기준의 최적화 반복(iteration)이 최대 가능한 반복 횟수에 도달한 지 확인합니다. 아직 반복 횟수가 남았다면 현재 상태에서 계속 최적화 반복을 하게 되고 반복 횟수를 모두 다 채웠는데 목표 지점에 도달하지 못하였다면 새로운 try로 넘어가게 됩니다.
⑭ try < max_try : 새로운 초깃값 환경에서 최적화를 시도할 수 있는 지 최대 시도 횟수를 확인합니다. 아직 시도 횟수가 남았다면 새로운 초깃값을 통하여 최적화를 시도해 봅니다. 만약 최대 시도 횟수를 도달하였다면 수렴을 실패한 것으로 결론을 내립니다.

⑭에서 수렴 실패에 도달하지 않도록 잘 구성하는 방법은 빨간색 상자인 ③에서의 파라미터 초깃값 셋팅과 하이퍼파라미터 셋팅에 달려 있습니다. 따라서 각 문제 별 해당 값들을 잘 설정하는 것이 매우 중요합니다.

example 1. double gaussian

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, Matrix, sqrt, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

# True parameters
A1_true = 3
mu11_true = 2
mu12_true = 3
sigma1_true = 8.0

A2_true = 2
mu21_true = -10
mu22_true = -20
sigma2_true = 10

C_true = 0.5

# Generate data points
np.random.seed(0)  # For reproducibility
x1 = np.linspace(-30, 30, 20)
x2 = np.linspace(-30, 30, 20)
x1, x2 = np.meshgrid(x1, x2)
x1 = x1.flatten()
x2 = x2.flatten()
y = (A1_true * np.exp(-((x1 - mu11_true)**2 + (x2 - mu12_true)**2) / (2 * sigma1_true**2)) +
     A2_true * np.exp(-((x1 - mu21_true)**2 + (x2 - mu22_true)**2) / (2 * sigma2_true**2)) +
     C_true)

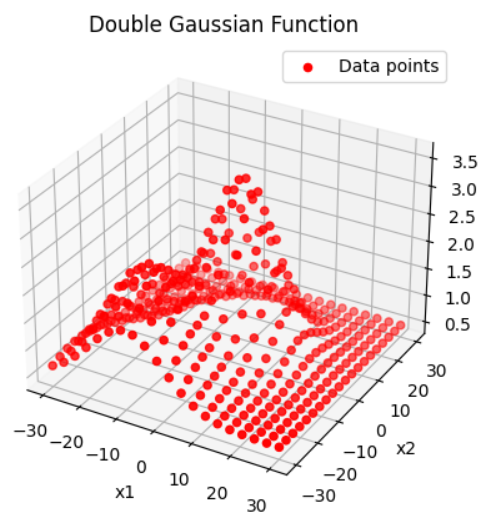
위 코드를 통해 생성된 데이터의 분포는 다음과 같습니다. 2개의 가우시안 분포를 사용하여 peak 점이 2개인 것을 확인할 수 있습니다.

$Drawing$

num_params = 9

# Define symbolic variables for the circle parameters and points
A1, mu11, mu12, sigma1, A2, mu21, mu22, sigma2, C = symbols('A1 mu11 mu12 sigma1 A2 mu21 mu22 sigma2 C') 

# Define the residual function for a single point
residuals = Matrix([])
for x1_i, x2_i, y_i in zip(x1, x2, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([
        A1 * sp.exp(-((x1_i - mu11)**2 + (x2_i - mu12)**2) / (2 * sigma1**2)) +
        A2 * sp.exp(-((x1_i - mu21)**2 + (x2_i - mu22)**2) / (2 * sigma2**2)) +
        C - y_i
    ]))

residuals_func = lambdify([A1, mu11, mu12, sigma1, A2, mu21, mu22, sigma2, C], residuals, 'numpy')
r = residuals_func(
    params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], params[5][0], params[6][0], params[7][0], params[8][0]
) 

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([A1, mu11, mu12, sigma1, A2, mu21, mu22, sigma2, C])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([A1, mu11, mu12, sigma1, A2, mu21, mu22, sigma2, C], jacobian, 'numpy')

jacobian_result = jacobian_func(
    params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], params[5][0], params[6][0], params[7][0], params[8][0]
) 


max_try = 100
max_iterations = 50
converge_threshold = 1e-5

nu = 10
max_mu = 1000

is_converged = False

min_error = 1e10
best_params = None

for try_index in range(max_try):    
    sample_range = np.random.randint(0, 50) * 1.0
    params = np.random.normal(0.0, 1.0, num_params).reshape(num_params, 1) * sample_range - (sample_range//2)
                       
    mu = 0.01
    prev_params = None    
    
    for i in range(max_iterations):
        r = residuals_func(
            params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
            params[5][0], params[6][0], params[7][0], params[8][0]
        )
        Jr = jacobian_func(
            params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
            params[5][0], params[6][0], params[7][0], params[8][0]
        ) 

        try:
            update = np.linalg.pinv(Jr.T @ Jr + mu * np.diag(np.diag(Jr.T @ Jr))) @ Jr.T @ r
        except:
            continue
            
        params -= update
        
        if i > 0:
            E_old = np.sum(residuals_func(
                prev_params[0][0], prev_params[1][0], prev_params[2][0], prev_params[3][0], prev_params[4][0], 
                prev_params[5][0], prev_params[6][0], prev_params[7][0], prev_params[8][0]
            )**2)
            
            E_new = np.sum(residuals_func(
                params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
                params[5][0], params[6][0], params[7][0], params[8][0]
            )**2)

            if E_new < E_old:
                # params = params.copy() 
                mu = mu / nu

                if E_new < error_minimized_threshold:
                    is_converged = True
                    print("try_index: {}, iter:{}, mu: {}, E: {}, Delta E Ratio: {}, best:{}".format(try_index, i, mu, E_new,(abs(E_new - E_old) / E_new), E_new < min_error))
                    break
            else:
                params = prev_params.copy()
                mu = mu * nu

        prev_params = params.copy()
        
        # initial parameters are not good.
        if mu > max_mu:            
            break

    if E_new < min_error:
        min_error = E_new
        best_params = params.copy()       
    
    if is_converged:
        break
    print("try_index: {}, iter:{}, mu: {}, E: {}, Delta E Ratio: {}, best:{}".format(try_index, i, mu, E_new,(abs(E_new - E_old) / E_new), E_new < min_error))

print("----------------------------------------------------")
print("is_converged:{}".format(is_converged))
print("min_error:{}".format(min_error))
print("best_params:{}".format(best_params))

# try_index: 0, iter:49, mu: 0.001, E: 37.59036006390082, Delta E Ratio: 0.0009055930280118061, best:False
# try_index: 1, iter:17, mu: 1000.0000000000001, E: 206.97039034172724, Delta E Ratio: 0.0, best:False
# try_index: 2, iter:16, mu: 10000.0, E: 206.97039034172724, Delta E Ratio: 0.0, best:False
# try_index: 3, iter:49, mu: 0.001, E: 253.55132760813837, Delta E Ratio: 0.20343546505090918, best:False
# try_index: 4, iter:49, mu: 0.001, E: 123.05221503956174, Delta E Ratio: 0.001298832607611588, best:False
# try_index: 5, iter:49, mu: 1.0000000000000004e-29, E: 69.68654315711306, Delta E Ratio: 0.0, best:False
# try_index: 6, iter:22, mu: 10000.0, E: 206.97039034172425, Delta E Ratio: 0.0, best:False
# try_index: 7, iter:49, mu: 1.0000000000000003e-05, E: 188.08049497093316, Delta E Ratio: 1.8382487061751123e-11, best:False
# try_index: 8, iter:26, mu: 10000.0, E: 206.9703903417273, Delta E Ratio: 2.7464517396403543e-16, best:False
# try_index: 9, iter:49, mu: 1e-05, E: 66.5634463887767, Delta E Ratio: 0.020826578787656726, best:False
# try_index: 10, iter:9, mu: 1.0000000000000002e-07, E: 6.692776332216131e-06, Delta E Ratio: 7494.505843092161, best:True
# ----------------------------------------------------
# is_converged:True
# min_error:6.692776332216131e-06
# best_params:[[  2.99990612]
#  [  2.0002813 ]
#  [  3.00050697]
#  [ -7.9997588 ]
#  [  1.99953022]
#  [ -9.99761198]
#  [-20.00092243]
#  [ 10.00184881]
#  [  0.50001135]]

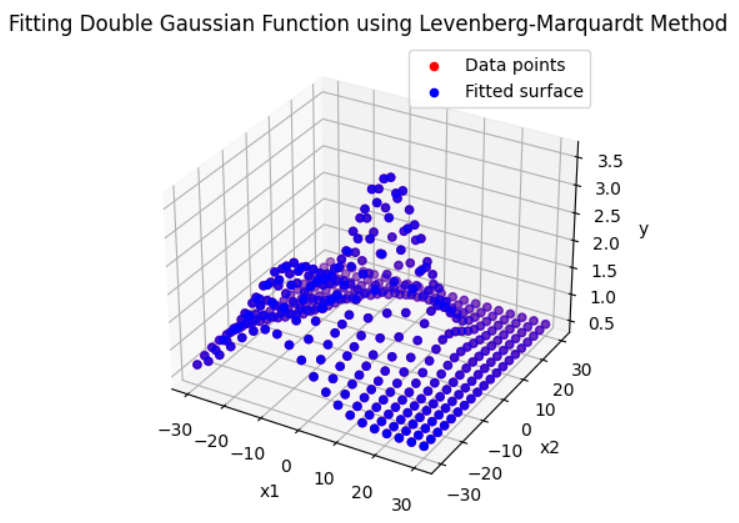
$Drawing$

위 그래프를 보면 생성된 데이터와 fitting된 결과가 유사한 것을 확인할 수 있습니다. 전체 에러는 6.692776332216131e-06로 수렴하였습니다.

앞으로 살펴볼 2개의 예제는 Test functions for optimization에서 선정하였습니다.

example 2. Beale function

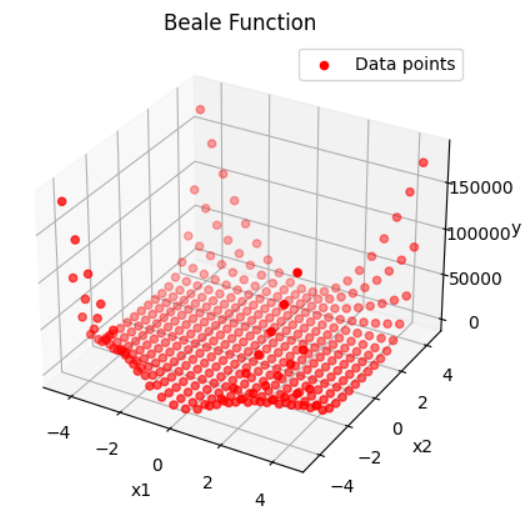
\[f(x_{1}, x_{2}) = (1.5 - x_{1} + x_{1}x_{2})^{2} + (2.25 - x_{1} + x_{1}x_{2}^{2})^{2} + (2.625 - x_{1} + x_{1}x_{2}^{3})^{2}\]
\[-4.5 \le x_{1}, x_{2} \le 4.5\]
\[\to f(x_{1}, x_{2}) = (w_{0} + w_{1}x_{1} + w_{2}x_{1}x_{2})^{2} + (w_{3} + w_{4}x_{1} + w_{5}x_{1}x_{2}^{2})^{2} + (w_{6} + w_{7}x_{1} + w_{8}x_{1}x_{2}^{3})^{2}\]

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, Matrix, sqrt, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

# Generate data points
x1 = np.linspace(-4.5, 4.5, 20)
x2 = np.linspace(-4.5, 4.5, 20)
x1, x2 = np.meshgrid(x1, x2)
x1 = x1.flatten()
x2 = x2.flatten()

w0_true = 1.5
w1_true = -1
w2_true = 1
w3_true = 2.25
w4_true = -1
w5_true = 1
w6_true = 2.625
w7_true = -1
w8_true = 1

y = (w0_true + w1_true*x1 + w2_true*x1*x2)**2 + (w3_true + w4_true*x1 + w5_true*x1*(x2**2))**2 + (w6_true + w7_true*x1 + w8_true*x1*(x2**3))**2

위 코드를 통해 생성된 데이터의 분포는 다음과 같습니다.

$Drawing$

num_params = 9

# Define symbolic variables for the circle parameters and points
w0, w1, w2, w3, w4, w5, w6, w7, w8= symbols('w0, w1, w2, w3, w4, w5, w6, w7, w8') 

# Define the residual function for a single point
residuals = Matrix([])
for x1_i, x2_i, y_i in zip(x1, x2, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([
        (w0 + w1*x1_i + w2*x1_i*x2_i)**2 + (w3 + w4*x1_i + w5*x1_i*(x2_i**2))**2 + (w6 + w7*x1_i + w8*x1_i*(x2_i**3))**2 - y_i
    ]))

residuals_func = lambdify([w0, w1, w2, w3, w4, w5, w6, w7, w8], residuals, 'numpy')

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w0, w1, w2, w3, w4, w5, w6, w7, w8])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w0, w1, w2, w3, w4, w5, w6, w7, w8], jacobian, 'numpy')

max_try = 100
max_iterations = 50
converge_threshold = 1e-5

nu = 10
max_mu = 1000

is_converged = False

min_error = 1e10
best_params = None

for try_index in range(max_try):    
    sample_range = np.random.randint(0, 10) * 1.0
    params = np.random.normal(0.0, 1.0, num_params).reshape(num_params, 1) * sample_range - (sample_range//2)
                       
    mu = 0.01
    prev_params = None    
    
    for i in range(max_iterations):
        r = residuals_func(
            params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
            params[5][0], params[6][0], params[7][0], params[8][0]
        )
        Jr = jacobian_func(
            params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
            params[5][0], params[6][0], params[7][0], params[8][0]
        ) 

        try:
            update = np.linalg.pinv(Jr.T @ Jr + mu * np.diag(np.diag(Jr.T @ Jr))) @ Jr.T @ r
        except:
            continue
            
        params -= update
        
        if i > 0:
            E_old = np.sum(residuals_func(
                prev_params[0][0], prev_params[1][0], prev_params[2][0], prev_params[3][0], prev_params[4][0], 
                prev_params[5][0], prev_params[6][0], prev_params[7][0], prev_params[8][0]
            )**2)
            
            E_new = np.sum(residuals_func(
                params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
                params[5][0], params[6][0], params[7][0], params[8][0]
            )**2)

            if E_new < E_old:
                # params = params.copy() 
                mu = mu / nu

                if E_new < error_minimized_threshold:
                    is_converged = True
                    print("try_index: {}, iter:{}, mu: {}, E: {}, Delta E Ratio: {}, best:{}".format(try_index, i, mu, E_new,(abs(E_new - E_old) / E_new), E_new < min_error))
                    break
            else:
                params = prev_params.copy()
                mu = mu * nu

        prev_params = params.copy()
        
        # initial parameters are not good.
        if mu > max_mu:            
            break

    if E_new < min_error:
        min_error = E_new
        best_params = params.copy()       
    
    if is_converged:
        break
    print("try_index: {}, iter:{}, mu: {}, E: {}, Delta E Ratio: {}, best:{}".format(try_index, i, mu, E_new,(abs(E_new - E_old) / E_new), E_new < min_error))

print("----------------------------------------------------")
print("is_converged:{}".format(is_converged))
print("min_error:{}".format(min_error))
print("best_params:{}".format(best_params))

# try_index: 0, iter:20, mu: 1.0000000000000002e-14, E: 2.0731271064710485e-06, Delta E Ratio: 42580.35465329452, best:True
# ----------------------------------------------------
# is_converged:True
# min_error:2.0731271064710485e-06
# best_params:[[ 1.50000433]
#  [-1.00000307]
#  [ 0.99999666]
#  [-2.25      ]
#  [ 0.99999621]
#  [-0.99999999]
#  [ 2.625     ]
#  [-0.99999998]
#  [ 1.        ]]

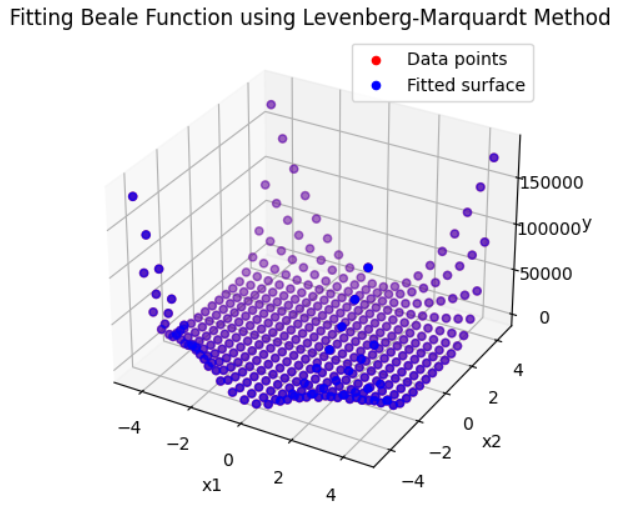
$Drawing$

위 그래프를 보면 생성된 데이터와 fitting된 결과가 유사한 것을 확인할 수 있습니다. 전체 에러는 2.0731271064710485e-06로 수렴하였습니다.

example 3. Goldstein-Price function

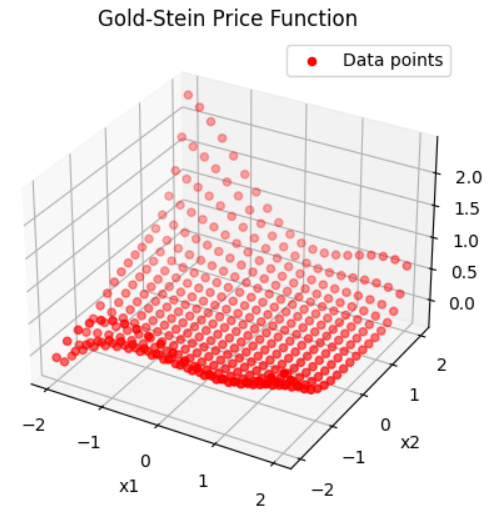
\[\begin{align} f(x_1, x_2) &= \left[1 + (x_1 + x_2 + 1)^2 \left(19 - 14x_1 + 3x_1^2 - 14x_2 + 6x_1 x_2 + 3x_2^2\right) \right] \\ &\cdot \left[30 + (2x_1 - 3x_2)^2 \left(18 - 32x_1 + 12x_1^2 + 48x_2 - 36x_1 x_2 + 27x_2^2 \right) \right] \end{align}\]
\[-2 \le x_{1}, x_{2} \le 2\]
\[\begin{align} \to f(x_1, x_2) &= \left[1 + (x_1 + x_2 + 1)^2 \left(w_{0} + w_{1}x_1 + w_{2}x_1^2 + w_{3}x_2 + w_{4}x_1 x_2 + w_{5}x_2^2\right) \right] \\ &\cdot\left[w_{6} + (w_{7}x_1 + w_{8}x_2)^2 \left(w_{9} + w_{10}x_1 + w_{11}x_1^2 + w_{12}x_2 + w_{13}x_1 x_2 + w_{14}x_2^2 \right) \right] \end{align}\]

import numpy as np
import matplotlib.pyplot as plt
from sympy import symbols, Matrix, sqrt, lambdify
import sympy as sp
import numpy as np
np.set_printoptions(suppress=True)

# Generate data points
x1 = np.linspace(-2, 2, 20)
x2 = np.linspace(-2, 2, 20)
x1, x2 = np.meshgrid(x1, x2)
x1 = x1.flatten()
x2 = x2.flatten()

w0_true = 19
w1_true = -14
w2_true = 3
w3_true = -14
w4_true = 6
w5_true = 3
w6_true = 30
w7_true = 2
w8_true = -3
w9_true = 18
w10_true = -32
w11_true = 12
w12_true = 48
w13_true = -36
w14_true = 27

y = ( (1 + (x1 + x2 + 1)**2) * \
       (w0_true + w1_true*x1 + w2_true*x1**2 + w3_true*x2 + w4_true*x1*x2 + w5_true*x2**2) ) * \
    ( (w6_true + (w7_true*x1 + w8_true*x2)**2) * \
       (w9_true + w10_true*x1 + w11_true*x2**2 + w12_true*x2 + w13_true*x1*x2 + w14_true*x2**2) )

위 코드를 통해 생성된 데이터의 분포는 다음과 같습니다.

$Drawing$

num_params = 15

# Define symbolic variables for the circle parameters and points
w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14 = symbols('w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14') 

# Define the residual function for a single point
residuals = Matrix([])
for x1_i, x2_i, y_i in zip(x1, x2, y):
    residuals = residuals.row_insert(residuals.shape[0], Matrix([
        ((1 + (x1_i + x2_i + 1)**2)*(w0 + w1*x1_i + w2*x1_i**2 + w3*x2_i + w4*x1_i*x2_i + w5*x2_i**2))*
        ((w6 + (w7*x1_i + w8*x2_i)**2)*(w9 + w10*x1_i + w11*x2_i**2 + w12*x2_i + w13*x1_i*x2_i + w14*x2_i**2)) - y_i
    ]))

residuals_func = lambdify([w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14], residuals, 'numpy')

# Compute the Jacobian matrix of the residual function
jacobian = residuals.jacobian([w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14])

# Convert the Jacobian to a numerical function using lambdify
jacobian_func = lambdify([w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14], jacobian, 'numpy')

max_try = 100
max_iterations = 50
converge_threshold = 1e-5

nu = 10
max_mu = 1000

is_converged = False

min_error = 1e10
best_params = None

for try_index in range(max_try):    
    sample_range = np.random.randint(0, 100) * 1.0
    params = np.random.normal(0.0, 1.0, num_params).reshape(num_params, 1) * sample_range - (sample_range//2)
                       
    mu = 0.01
    prev_params = None    
    
    for i in range(max_iterations):
        r = residuals_func(
            params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
            params[5][0], params[6][0], params[7][0], params[8][0], params[9][0], 
            params[10][0], params[11][0], params[12][0], params[13][0], params[14][0]          
        )
        Jr = jacobian_func(
            params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
            params[5][0], params[6][0], params[7][0], params[8][0], params[9][0], 
            params[10][0], params[11][0], params[12][0], params[13][0], params[14][0]             
        ) 

        try:
            # print("gradient_clipping : ", max_gradient_norm, gradient_norm)
            update = np.linalg.pinv(Jr.T @ Jr + mu * np.diag(np.diag(Jr.T @ Jr))) @ Jr.T @ r
        except:
            print("?????")
            continue
            
        params -= update
        
        if i > 0:
            E_old = np.sum(residuals_func(
                prev_params[0][0], prev_params[1][0], prev_params[2][0], prev_params[3][0], prev_params[4][0], 
                prev_params[5][0], prev_params[6][0], prev_params[7][0], prev_params[8][0], prev_params[9][0], 
                prev_params[10][0], prev_params[11][0], prev_params[12][0], prev_params[13][0], prev_params[14][0]
            )**2)
            
            E_new = np.sum(residuals_func(
                params[0][0], params[1][0], params[2][0], params[3][0], params[4][0], 
                params[5][0], params[6][0], params[7][0], params[8][0], params[9][0], 
                params[10][0], params[11][0], params[12][0], params[13][0], params[14][0]                
            )**2)

            if E_new < E_old:
                # params = params.copy() 
                mu = mu / nu

                if E_new < error_minimized_threshold:
                    is_converged = True
                    print("try_index: {}, iter:{}, mu: {}, E: {}, Delta E Ratio: {}, best:{}".format(try_index, i, mu, E_new,(abs(E_new - E_old) / E_new), E_new < min_error))
                    break
            else:
                params = prev_params.copy()
                mu = mu * nu

        prev_params = params.copy()
        
        # initial parameters are not good.
        if mu > max_mu:            
            break

    if E_new < min_error:
        min_error = E_new
        best_params = params.copy()       
    
    if is_converged:
        break
    print("try_index: {}, iter:{}, mu: {}, E: {}, Delta E Ratio: {}, best:{}".format(try_index, i, mu, E_new,(abs(E_new - E_old) / E_new), E_new < min_error))

print("----------------------------------------------------")
print("is_converged:{}".format(is_converged))
print("min_error:{}".format(min_error))
print("best_params:{}".format(best_params))

# try_index: 0, iter:6, mu: 10000.0, E: 75523658650766.72, Delta E Ratio: 0.0, best:False
# try_index: 1, iter:49, mu: 1e-15, E: 2130294165632.0605, Delta E Ratio: 6.405066488527749e-06, best:False
# try_index: 2, iter:42, mu: 1.0000000000000004e-08, E: 7.61306899046107e-12, Delta E Ratio: 348427159246.9762, best:True
# ----------------------------------------------------
# is_converged:True
# min_error:7.61306899046107e-12
# best_params:[[-10.81778709]
#  [  7.97100101]
#  [ -1.70807165]
#  [  7.97100101]
#  [ -3.41614329]
#  [ -1.70807165]
#  [210.7857465 ]
#  [  5.30139285]
#  [ -7.95208928]
#  [ -4.49953559]
#  [  7.99917438]
#  [-81.82790802]
#  [-11.99876156]
#  [  8.99907117]
#  [ 72.07891425]]

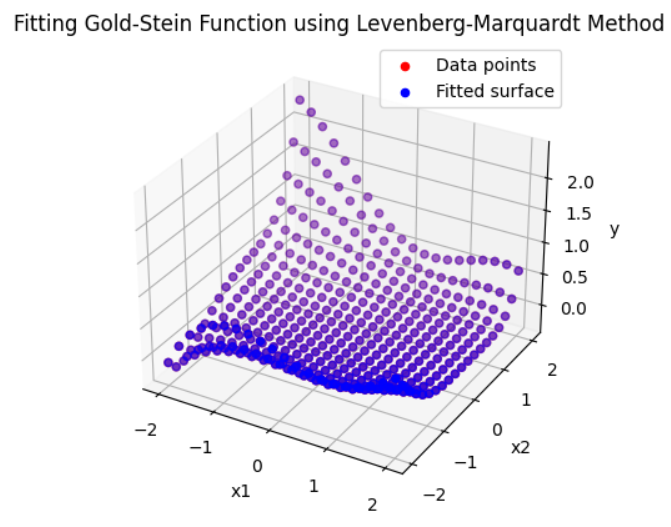
$Drawing$

위 그래프를 보면 생성된 데이터와 fitting된 결과가 유사한 것을 확인할 수 있습니다. 전체 에러는 7.61306899046107e-12로 수렴하였습니다.
하지만 파라미터의 값이 실제 파라미터 값과는 다른 것을 볼 수 있습니다. 파라미터가 많아져서 모델의 자유도가 높아진 만큼 위 데이터 분포를 표현할 수 있는 방법이 많아진 것으로 이해할 수 있습니다. 따라서 생성된 데이터 영역인 $-2 \le x_{1}, x_{2} \le 2$ 이외의 영역에서는 기존 모델과 다른 값을 추정할 가능성이 큽니다. 이와 같은 이유로 파라미터 추정이 필요한 전 데이터 영역에 골고루 데이터를 생성하여 파라미터를 추정 하는 것이 중요함을 알 수 있습니다.

Test functions for optimization에서 다른 예제 또한 테스트 해볼 수 있습니다. 이 때, 적절한 초깃값 범위를 잘 선정하는 것에 유의하시면 됩니다.

Quasi Newton Method for Non-Linear Least Squares

Lagrange Multiplier

지금부터는 Deep Learning에서 많이 사용하는 Gradient Descent를 응용한 최적화 방법등을 다루어 보도록 하겠습니다.
앞에서 다룬 Newton Method 기반의 최적화 방법은 최적화에 강건하고 수렴 속도가 빠르다는 장점이 있지만 $(J_{r}^{T} J_{r})^{-1}$ 와 같은 역행렬 연산이 필요하고 대량의 데이터를 모두 이용하여 최적화 할 때 메모리에 비효율적인 측면이 있어 파라미터 최적화에 어려움이 있습니다. (GPU 메모리 초과 및 학습 시간 증가 문제)
따라서 Deep Learning 이외의 small dataset을 이용한 최적화 알고리즘을 사용할 때에는 Newton Method 기반의 최적화 알고리즘이 주요한 방법으로 사용되는 반면에 Deep Learning과 같이 large dataset을 이용한 최적화 알고리즘은 주로 Gradient Descent 기반의 최적화 알고리즘을 사용합니다.

목차

Gradient Descent

Newton Method

Gradient Descent for Non-Linear Least Squares

Weighted Residuals

Newton Method for Non-Linear Least Squares

Gauss-Newton Method for Non-Linear Least Squares

Levenberg-Marquardt Method for Non-Linear Least Squares

Gauss-Newton Method

Levenberg-Marquardt Method

Levenberg-Marquardt Method for Non-Linear Least Squares w/ Trial

example 1. double gaussian

example 2. Beale function

example 3. Goldstein-Price function

Quasi Newton Method for Non-Linear Least Squares

Lagrange Multiplier

SGD

Mini-Batch Gradient Descent

Momentum

RMSProp

Adam