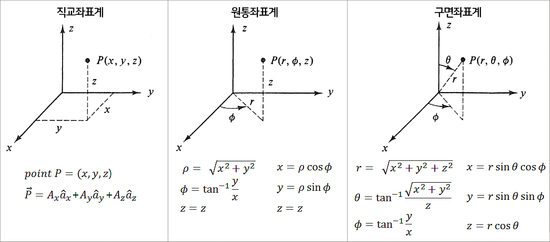
직교 좌표계, 원통 좌표계 및 구면 좌표계

Calculus 관련 글 목차

• 이번 글에서는 원통 좌표계와 구면 좌표계에 대하여 알아보도록 하겠습니다.

목차

• 직교 좌표계, 원통 좌표계, 구면 좌표계

• Forward-Left-Up 좌표계에서의 좌표계 변환

• Right-Down-Forward 좌표계에서의 좌표계 변환

직교 좌표계, 원통 좌표계, 구면 좌표계

• 3차원 좌표계에서 일반적으로 많이 사용하는 직교 좌표계는 임의의 점 $P = (x, y, z)$ 로 나타냅니다.
• 반면 이 글에서 다룰 원통 좌표계(Cylindrical Coordinate) 또는 구면 좌표계(Spherical Coordinate)는 직교좌표계의 $x, y, z$ 좌표를 다른 방식으로 표현합니다.
• 원통 좌표계나 구면 좌표계를 사용하는 이유는 다양한 상황에서 이와 같은 좌표계를 사용하였을 때, 미적분 계산이 편리해지는 상황이 발생하기 때문입니다. 원통 좌표계의 경우 원통형으로 생긴 물체나 원형 케이블에서의 연산이 필요할 때 직교 좌표계를 사용할 때보다 계산이 편리해 집니다. 케이블에서의 전자기학 등을 생각해 보시면 이해가 되실 것입니다. 이와 같은 이유로 구면 좌표계의 경우에는 구형 물체나 3차원 상에서의 물체의 운동을 표현할 때, 계산의 편리함을 얻을 수 있습니다.
• 이번 글에서는 간단히 직교 좌표계, 원통 좌표계, 구면 좌표계 간의 어떤 관계가 있는 지 살펴보고자 합니다. 추가적으로 3차원 상에서 많이 사용하는 오른손 좌표계에서의 좌표 변환 뿐 아니라 카메라 좌표계에서의 좌표 변환도 다루어 보도록 하겠습니다.

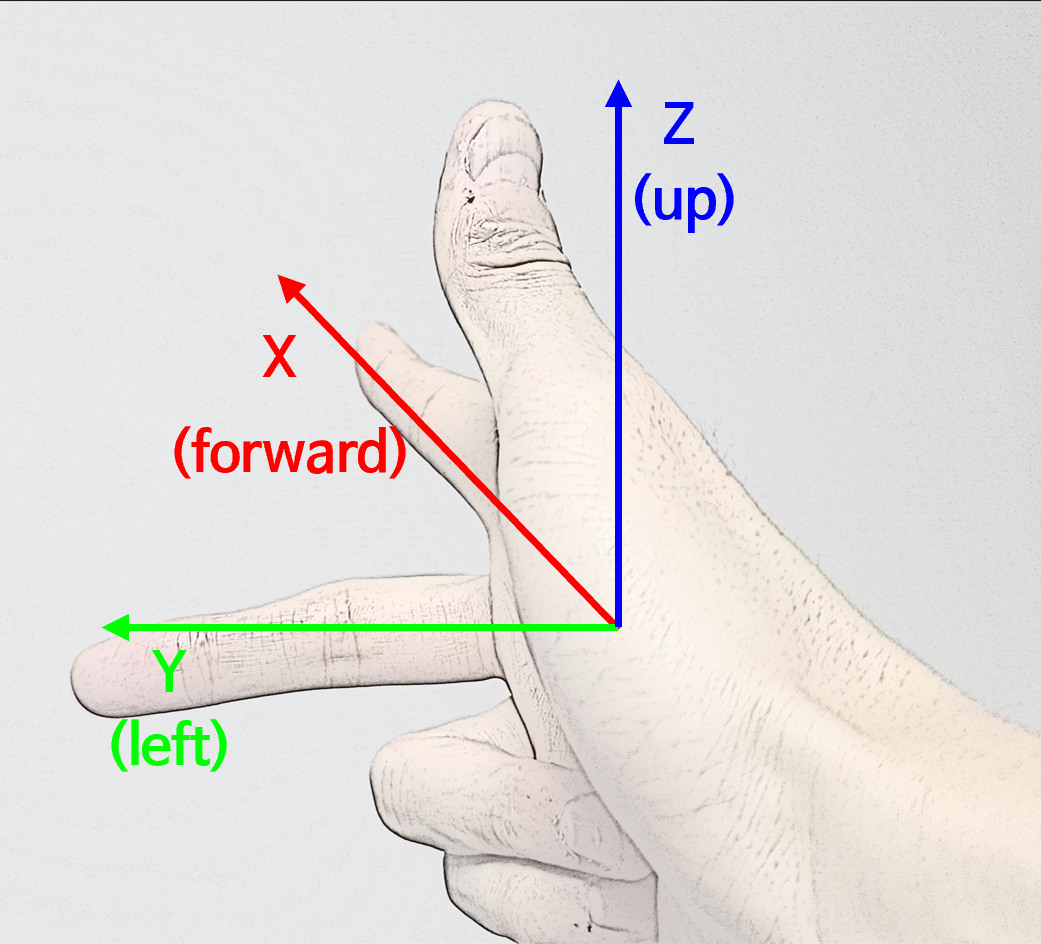
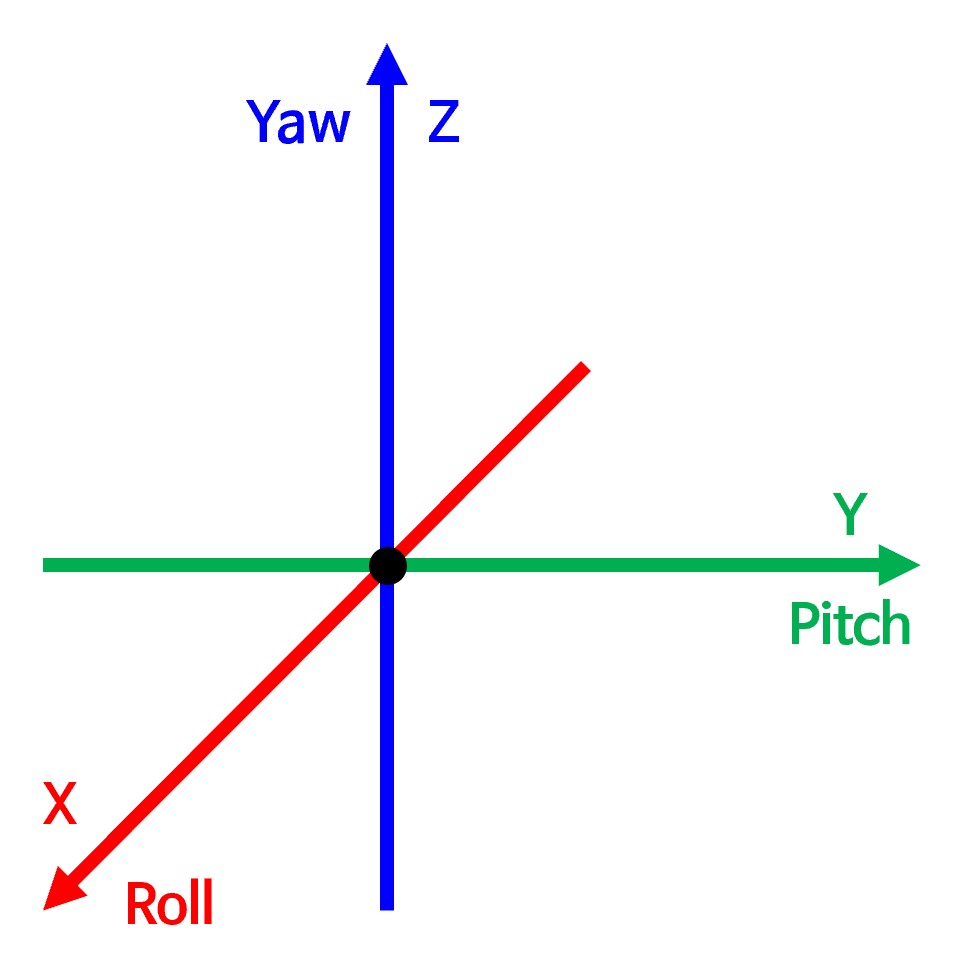
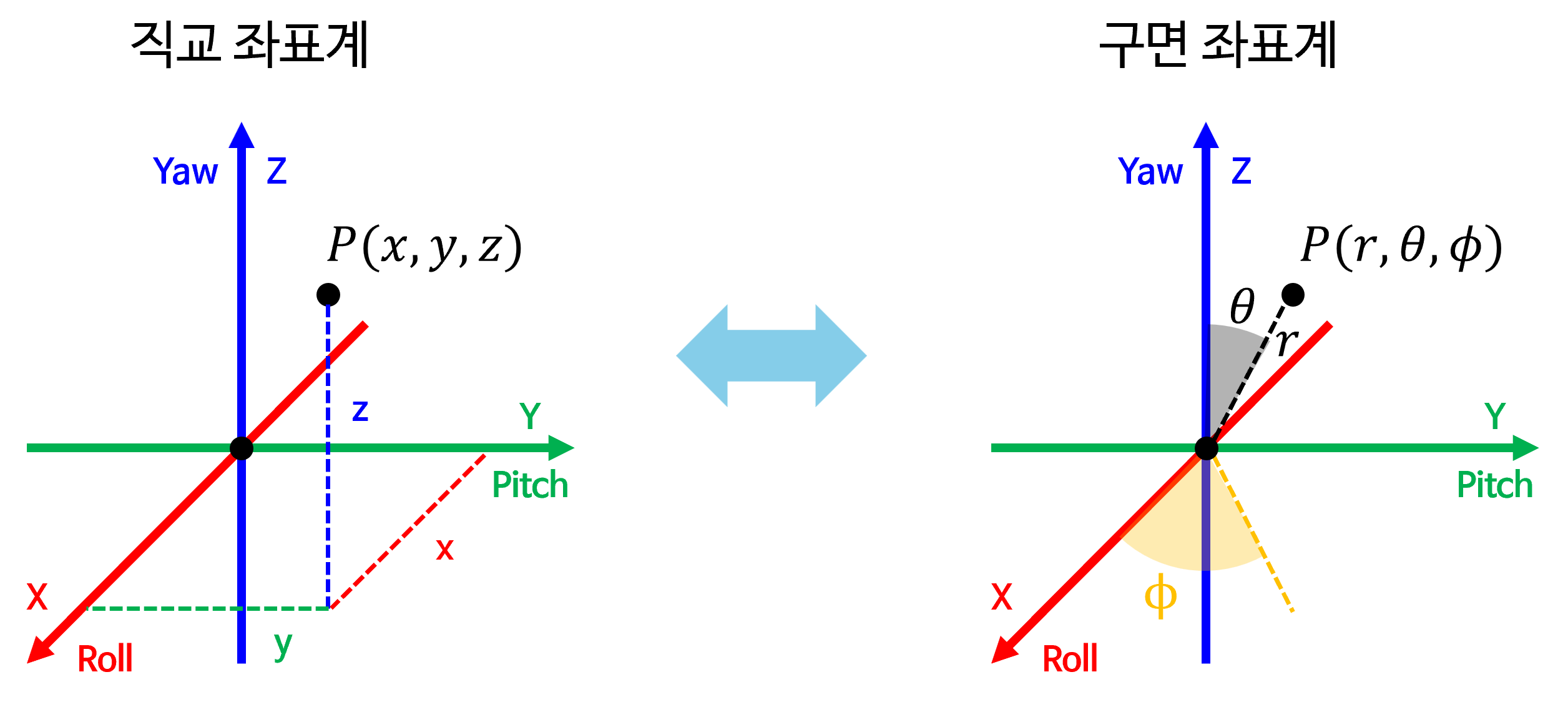
• 이 글에서 다루는 오른손 좌표계는 위 그림과 같이 검지가 $X$ 축, 중지가 $Y$ 축, 엄지가 $Z$ 축으로 표현되는 좌표계를 의미합니다. $X, Y, Z$ 축 순서로 Forward, Left, Up 이므로 이 글에서는 줄여서 FLU(Forward-Left-Up) 좌표계 라고 표현하겠습니다.

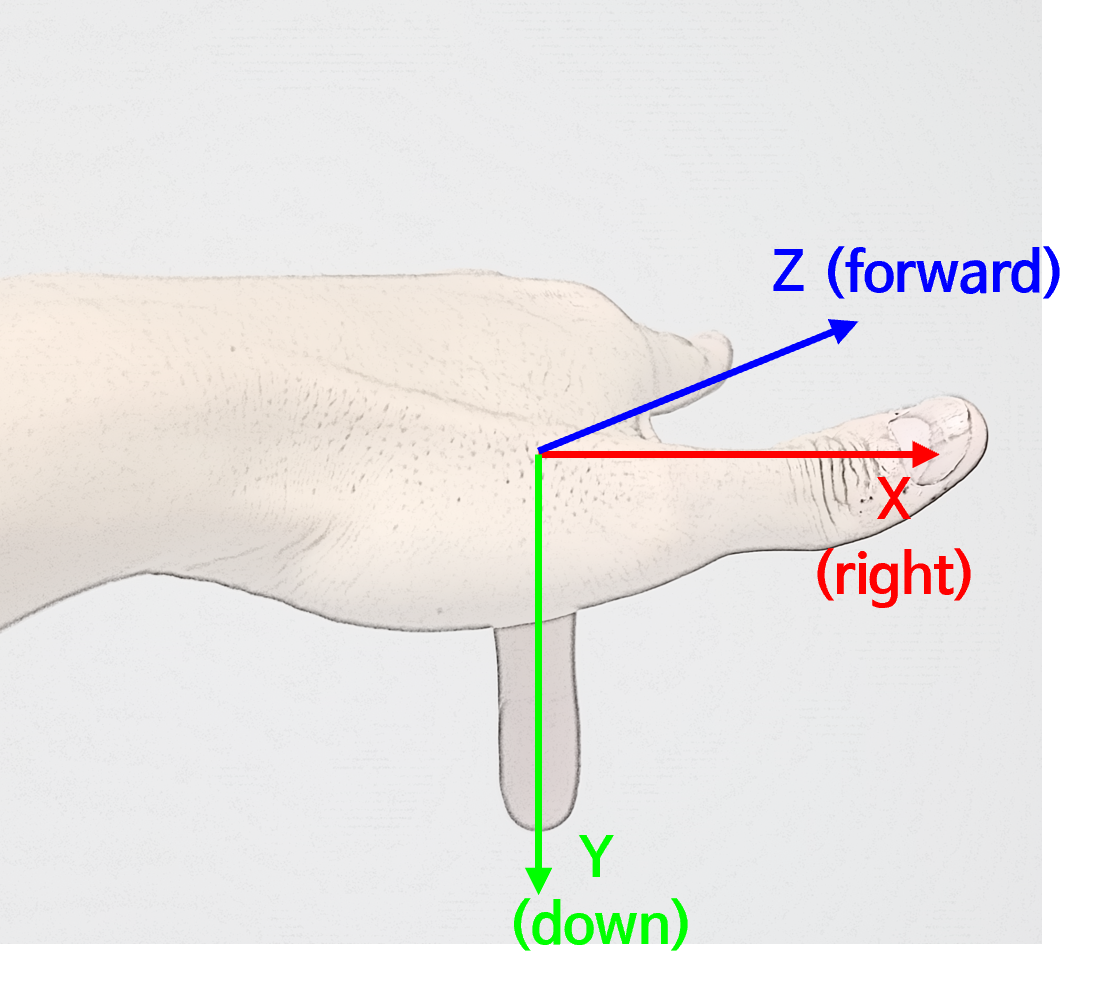
• 반면 카메라 좌표계 (또는 왼손 좌표계)는 다음과 같이 엄지가 $X$ 축, 중지가 $Y$ 축, 검지가 $Z$ 축으로 표현되는 좌표계를 의미합니다. $X, Y, Z$ 축 순서로 Right, Down, Forward 이므로 이 글에서는 줄여서 RDF(Right-Down-Forward) 좌표계 라고 표현하겠습니다.

• 먼저 개념을 이해하기 위해 원통 좌표계와 구면 좌표계의 표현 방식에 대하여 살펴보도록 하겠습니다.

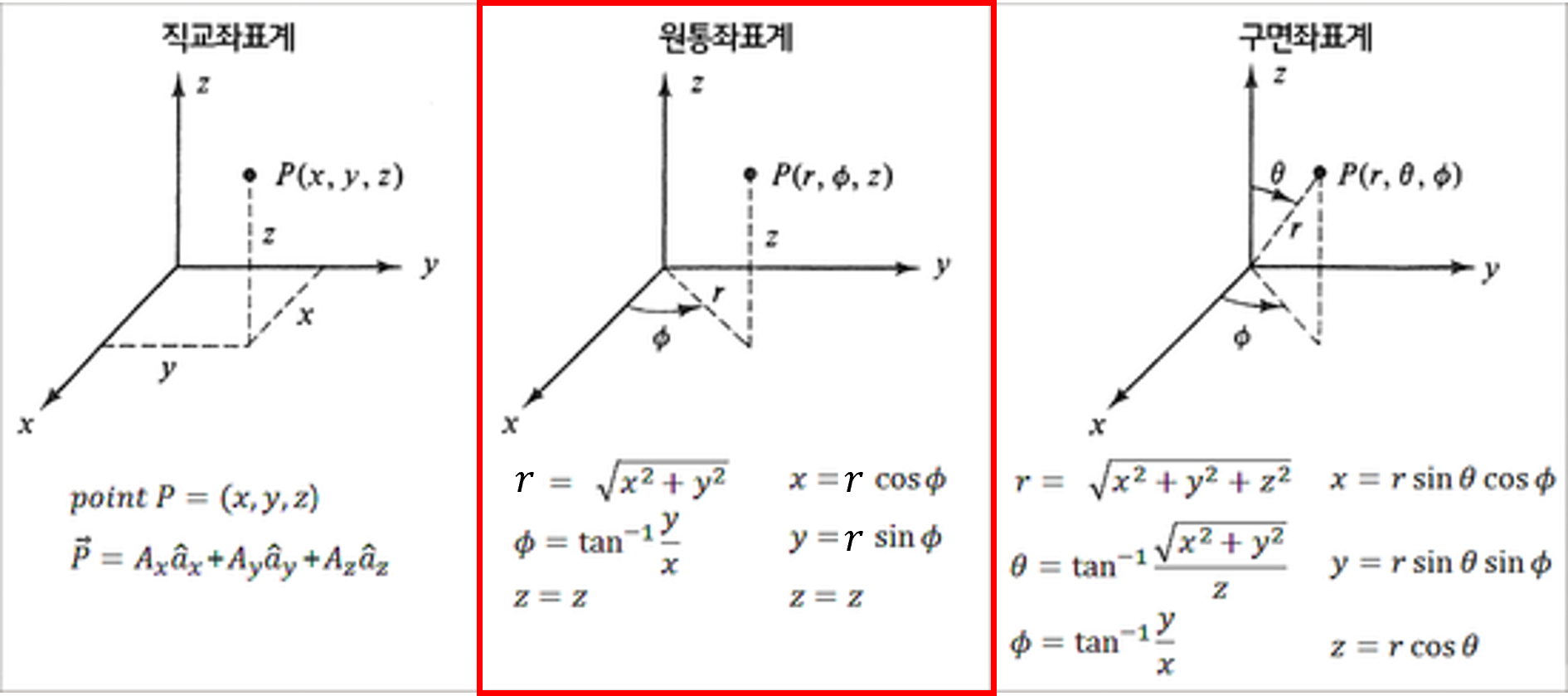
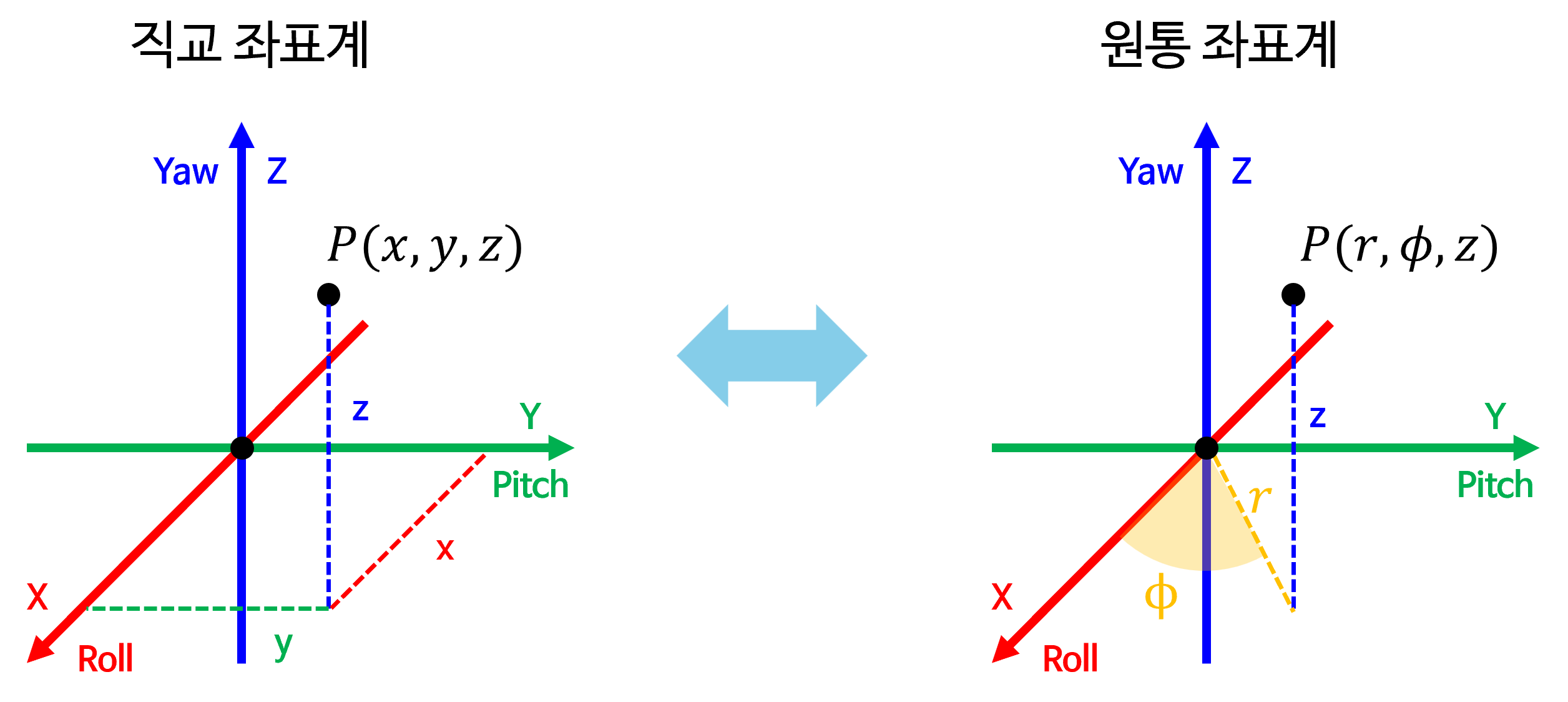
• 위 그림의 가운데 좌표계가 원통 좌표계입니다. FLU 좌표계에서 $X$ 축에서 $Y$ 축 방향으로의 회전 각도를 $\phi$ 로 나타내며 이 각도를 azimuth angle이라고 부릅니다. 점 $P$ 를 $XY$ 평면에 투영하였을 때, 원점과 점 $P$ 의 거리(distance)를 $r$ 로 나타냅니다. $z$ 는 직교 좌표계와 동일하게 사용됩니다.
• 원통 좌표계는 기존에 사용하는 직교 좌표계의 $x, y$ 좌표 표현을 사용하는 대신에 $\phi, r$ 을 이용하여 좌표위 위치를 나타냅니다. 회전 각도와 원점으로 부터의 거리인 $\phi, r$ 을 이용하여 점의 위치를 나타내기 때문에 원과 같은 곡면을 표현하기 유리해지며 높이는 그대로 $z$ 를 사용하기 때문에 원기둥의 표면을 좌표로 나타내기 쉬운 장점이 있습니다.

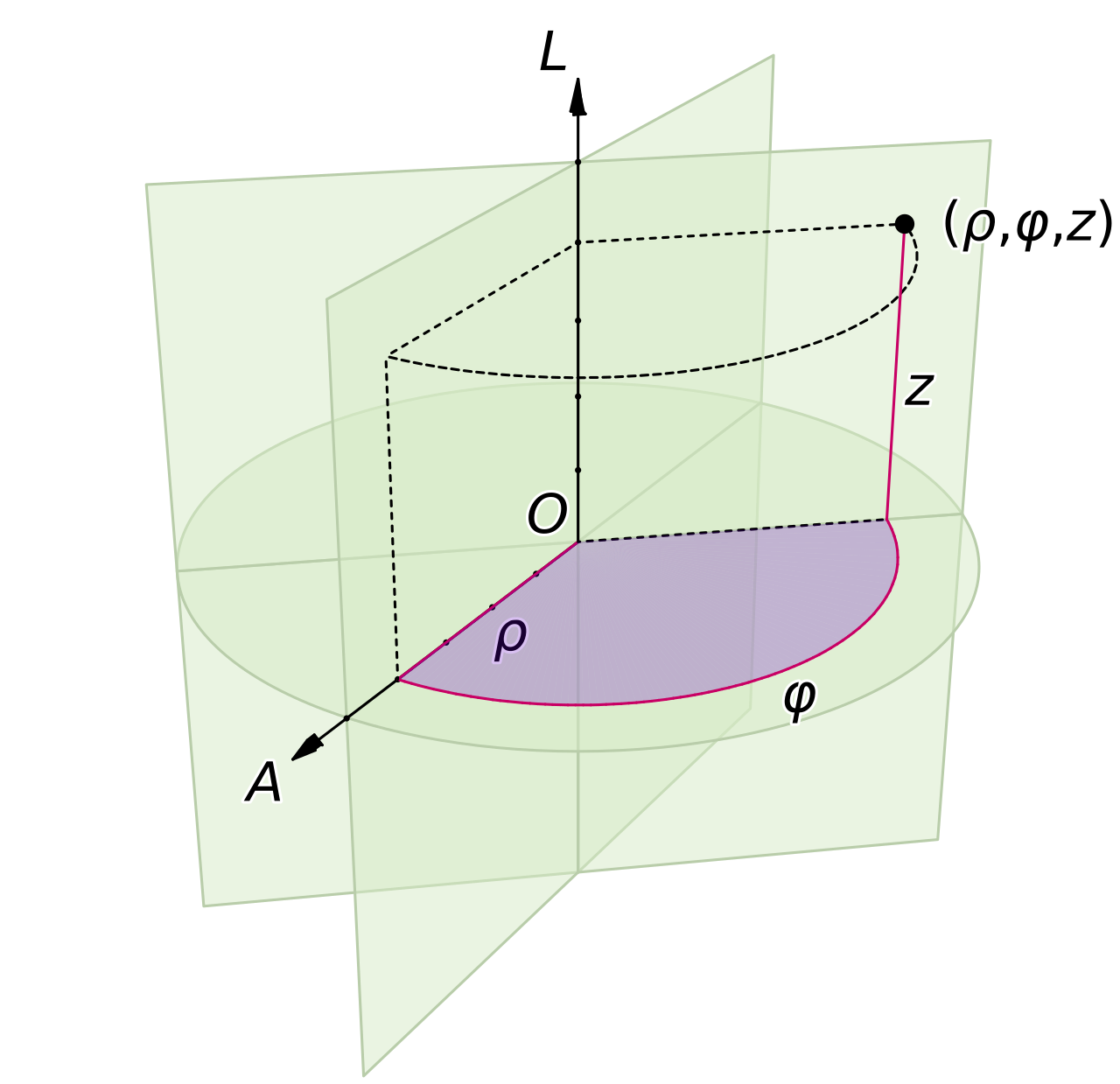
• 위 그림을 참조하면 원통 좌표계의 의미를 이해하시는 데 도움이 되실 것입니다.
• 앞에서 직교 좌표계와 비교하기 위하여 $X, Y, Z$ 축을 그대로 사용하였지만 위 그림의 $A$ 에 해당하는 $\phi$ 의 시작점을 나타내는 축은 Polar Axis라 하고 높이를 나타내는 $L$ 은 Longitudinal Axis라고 합니다.

• 위 그림의 가장 오른쪽 좌표계는 구면 좌표계를 나타냅니다. 원통 좌표계와 비교하면 $r$ 의 의미가 달라진 점과 $z$ 대신에 $\theta$ 를 사용하여 점 $P$ 를 표현하였다는 점입니다. 원통 좌표계에서는 $r = \sqrt{x^{2} + y^{2}}$ 인 반면 구면 좌표계에서는 $r = \sqrt{x^{2} + y^{2} + z^{2} }$ 으로 정의됩니다. 구면 좌표계에서의 $\theta$ 는 elevation 또는 inclination 이라고 하며 높이 축으로 부터 아래로 내려오는 각도를 의미합니다.
• 이와 같이 $\phi, \theta, r$ 을 이용하여 점 $P$ 를 나타내면 $x, y, z$ 를 사용하지 않고도 점의 위치를 표현할 수 있으며 구 형태 표면에서의 좌표를 나타낼 때 용이합니다.

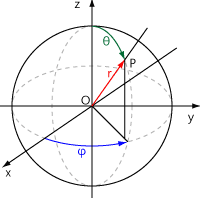
• 추가적으로 참고 자료에 따라 표기 방법이 다른 경우가 발생하여 그 부분을 정하고 넘어가고자 합니다.

• 위 내용은 위키피디아에서 발췌한 내용입니다. 왼쪽의 경우가 물리학이나 공학에서 많이 사용하는 표기법입니다. 즉, azimuth angle에 $\phi$ 를 사용하고 elevation angle에 $\theta$ 를 사용합니다. 본 글에서도 이 표기법을 따를 예정입니다.
• 반면에 오른쪽 표기 방법은 수학에서 많이 사용하는 방법이라고 합니다. 참조하시면 되겠습니다.

Forward-Left-Up 좌표계에서의 좌표계 변환

• 지금 부터는 FLU 좌표계에서 직교 좌표계, 원통 좌표계, 구면 좌표계의 변환 방법과 코드를 살펴보도록 하겠습니다.

• FLU 좌표계는 위 축의 방향과 같이 $X, Y, Z$ 축이 정의된 형태를 의미합니다. 앞에서 계속 살펴본 것과 동일한 축 방향입니다. 글 아랫 부분에서는 RDF 좌표계에서의 변환 방법을 다루어 볼 예정이므로 FLU 좌표계와 비교해서 살펴보면 도움이 될 것 같습니다.

직교 좌표계와 원통 좌표계 간의 좌표 변환

• 먼저 위 그림과 같이 FLU 좌표계에서의 직교 좌표계와 원통 좌표계 간의 변환에 대하여 살펴보도록 하겠습니다.

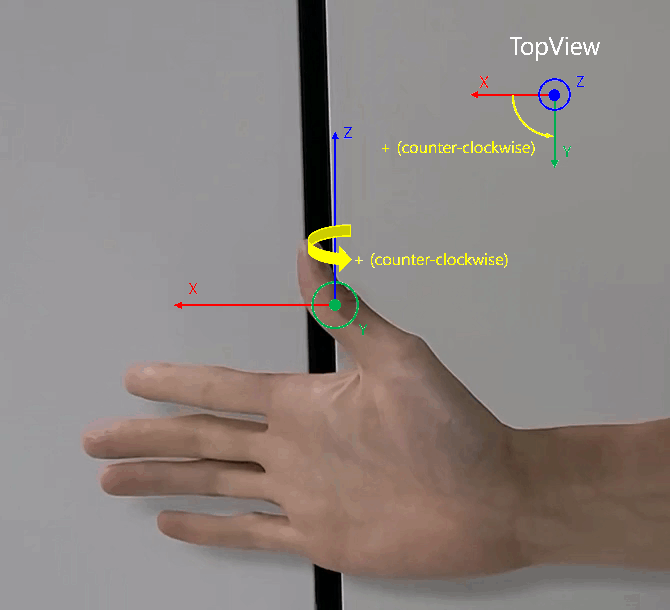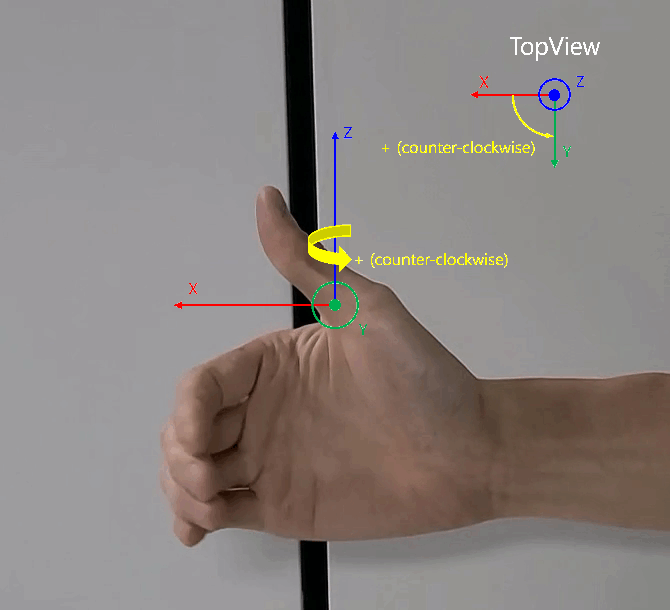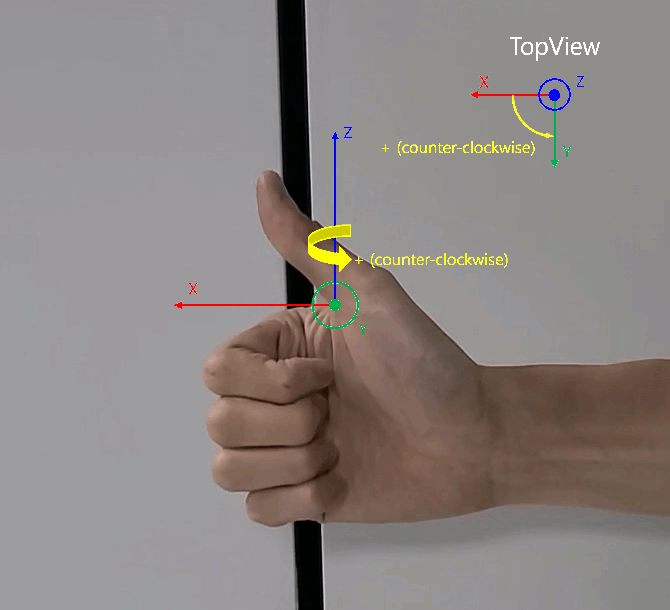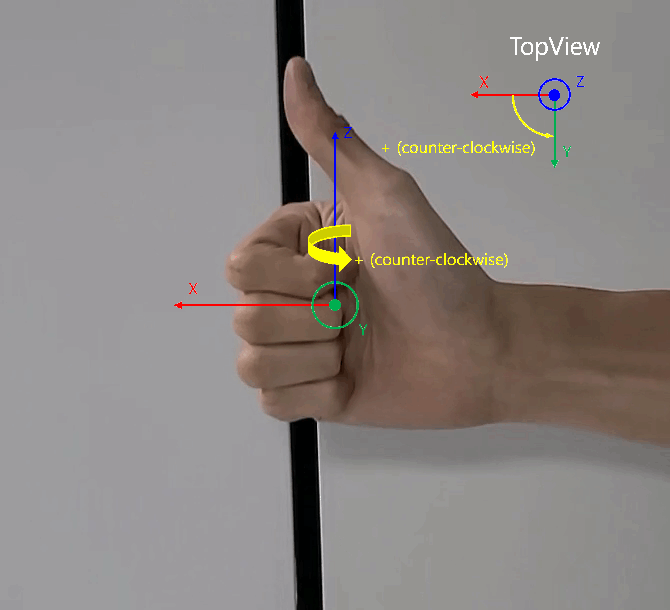
• 원통 좌표계에서 $X, Y$ 평면 상에 회전 각도인 $\phi$ 는 위 영상과 같이 오른손을 전/후 방향의 축 ($X$ 축) 에서 좌/우 방향의 축 ($Y$ 축)을 손으로 감쌋을 때, 감싸는 회전 방향인 반시계 방향과 같습니다. 이 내용을 바탕으로 아래 글을 읽으시면 됩니다.

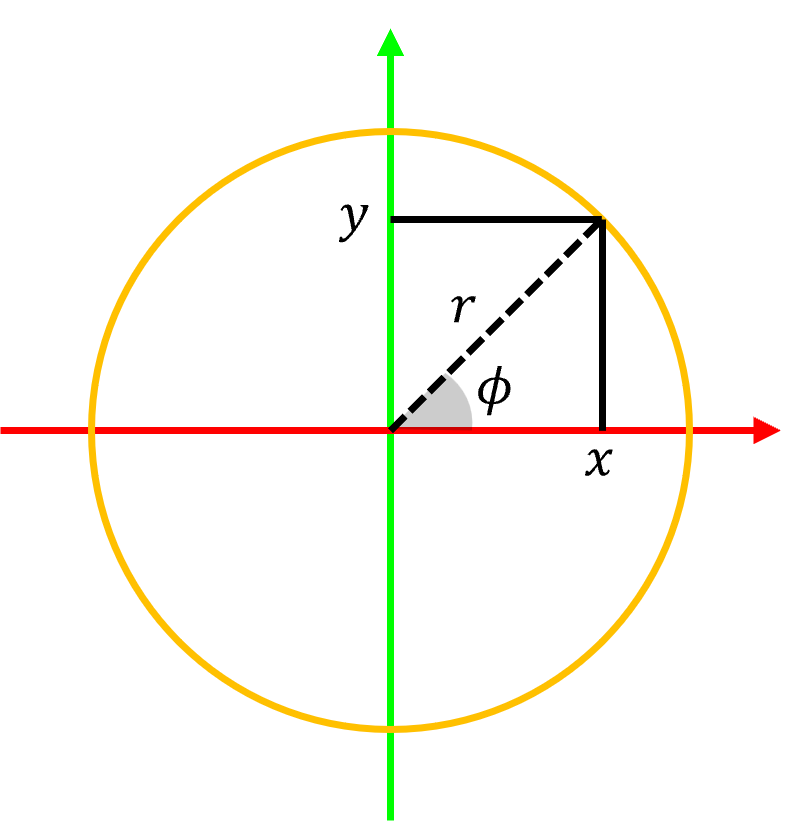
• 원통의 반지름인 $r$ 은 위 그림에서 다음과 같이 쉽게 얻을 수 있습니다.

• $$r = \sqrt{x^{2} + y^{2}}$$

• 그리고 $\phi$ 는 직교 좌표계의 $x, y$ 를 이용하여 다음과 같이 구할 수 있습니다.

• $$\phi = \tan^{-1}(\frac{y}{x})$$

• 위 내용과 같이 $x, y, z$ 를 이용하여 $r, \phi, z$ 를 쉽게 구할 수 있습니다.

• 반대로 $r, \phi$ 를 알고있을 때, 삼각함수를 이용하면 직교 좌표계 $x, y$ 로 변환할 수 있습니다.

• $$x = r \cos{(\phi)}$$
• $$y = r \sin{(\phi)}$$

• 따라서 다음과 같이 직교 좌표계와 원통 좌표계 간의 변환 관계를 정의할 수 있습니다.

직교 좌표계와 구면 좌표계 간의 좌표 변환

• 이번에는 직교 좌표계와 구면 좌표계 간의 변환 관계를 정의해 보도록 하겠습니다.

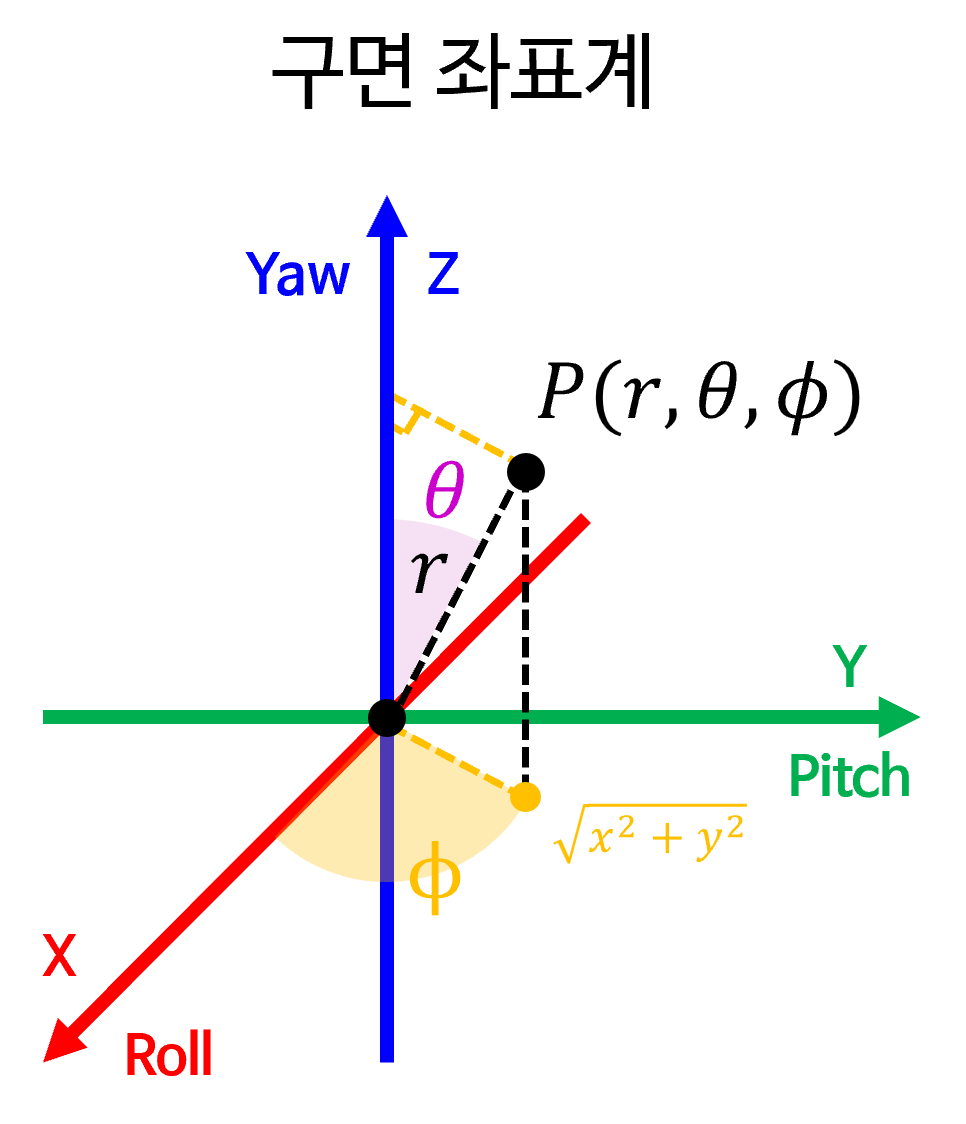
• 위 그림과 같이 3차원 상의 점 $P$ 를 구하기 위해 필요한 값을 하나씩 구해보면 다음과 같습니다.

• $$r = \sqrt{x^{2} + y^{2} + z^{2}}$$
• $$\phi = \tan^{-1} \frac{y}{x}$$

• 위 그림에서 $r$ 은 원점과 $x, y, z$ 의 직선 거리이므로 $\sqrt{x^{2} + y^{2} + z^{2}}$ 로 구할 수 있으며 $\phi$ 는 원통 좌표계와 동일한 방법으로 구할 수 있습니다.
• 다음으로 $\theta$ 를 구하기 위해서는 $\theta$ 를 사이각으로 하고 빗변이 $r$, 밑변이 $z$ 인 삼각형을 이용하면 다음과 같이 구할 수 있습니다.

• $$\theta = \cos^{-1} \left(\frac{z}{r} \right)$$

• 반대로 구면 좌표계 값인 $r, \theta, \phi$ 를 알고 있을 때, 직교 좌표계 값인 $x, y, z$ 는 삼각함수를 이용하여 쉽게 구할 수 있습니다.

• $$z = r \cos{(\theta)}$$

• 사잇각을 $\theta$ 로 하는 삼각형에서 삼각비를 이용하면 $z$ 를 쉽게 구할 수 있습니다.
• 그 다음으로 원점과 주황색 점 사이의 거리는 방금 사용한 삼각형에서의 삼각비를 이용하여 $r \sin{(\theta)}$ 로 구할 수 있으므로 (평행한 2개의 주황 점선을 참조하면 됩니다.) 다음과 같이 $x, y$ 에 접근할 수 있습니다.

• $$x = r \sin{(\theta)} \cos{(\phi)}$$
• $$y = r \sin{(\theta)} \sin{(\phi)}$$

• 따라서 다음과 같이 직교 좌표계와 구면 좌표계 간의 변환 관계를 정의할 수 있습니다.

원통 좌표계와 구면 좌표계 간의 좌표 변환

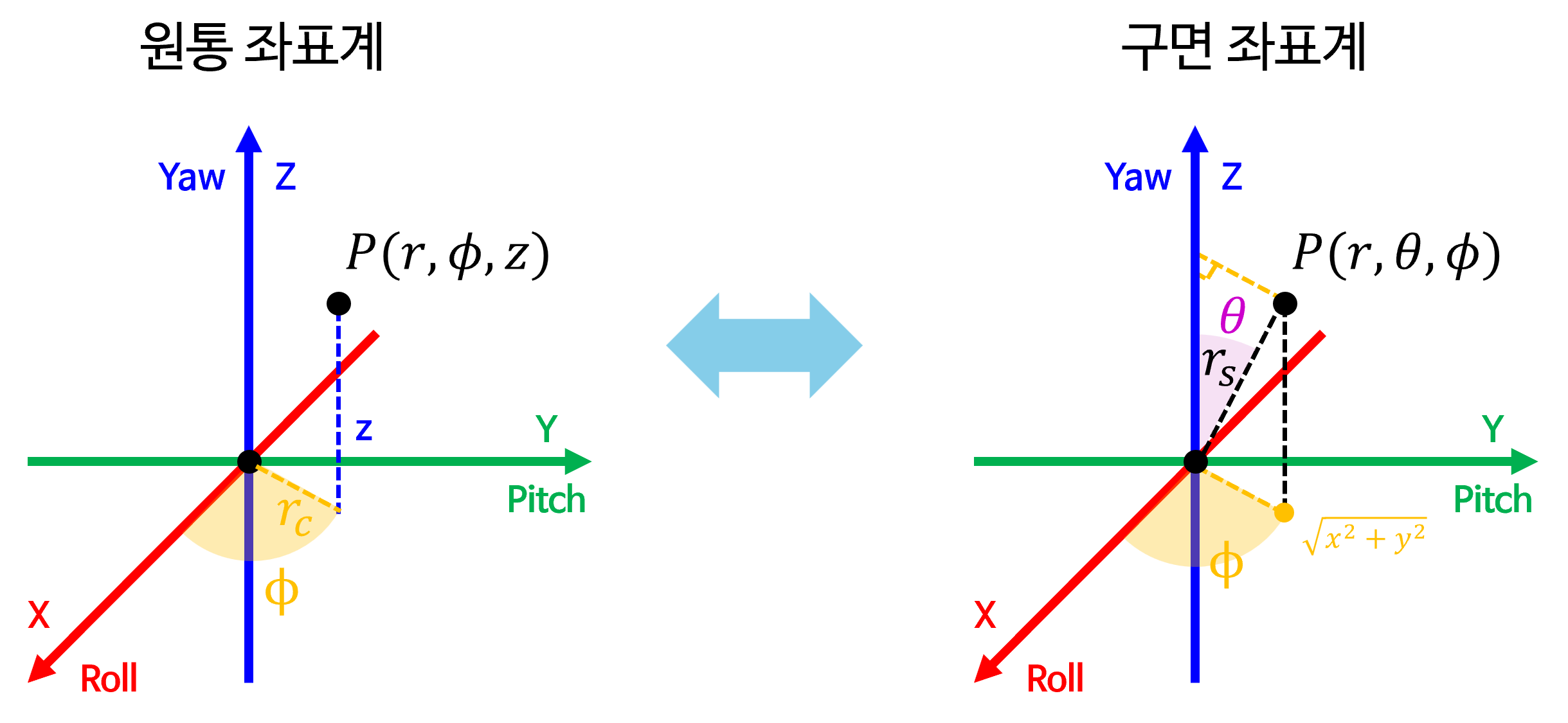
• 마지막으로 원통 좌표계와 구면 좌표계간의 좌표 변환에 대하여 살펴보도록 하겠습니다. 두 좌표계 모두 $r$ 이 사용되므로 원통 좌표계에서는 $r_{c}$ 로 사용하고 구면 좌표계에서는 $r_{s}$ 로 사용하도록 하겠습니다.
• 먼저 두 좌표계 모두 azimuth 각도로 $\phi$ 를 사용합니다. 원통 좌표계에서 구면 좌표계의 $r_{s}, \theta$ 를 구하기 위해서는 $r_{c}, z$ 와 삼각비를 활용하면 쉽게 구할 수 있습니다.

• $$r_{s} = \sqrt{r_{c}^{2} + z^{2}}$$
• $$\theta = \tan^{-1}{(\frac{r_{c}}{z})}$$

• 반면 구면 좌표계에서 $r_{s}, \theta$ 를 이용하여 $r_{c}, z$ 를 구하는 방법 또한 삼각비를 활용하면 쉽게 구할 수 있습니다.

• $$r_{c} = r_{s} \sin{(\theta)}$$
• $$z = r_{s} \cos{(\theta)}$$

• 정리하면 다음과 같이 원통 좌표계와 구면 좌표계를 변환할 수 있습니다.

Python Code

• 지금까지 살펴본 내용을 파이썬 코드를 이용하여 정리하면 다음과 같습니다.

import numpy as np

def cartesian_to_cylindrical(x, y, z):
    r = np.sqrt(x**2 + y**2)
    phi = np.arctan2(y, x)
    return r, phi, z

def cartesian_to_spherical(x, y, z):
    r = np.sqrt(x**2 + y**2 + z**2)
    phi = np.arccos(z / r)
    theta = np.arctan2(y, x)
    return r, theta, phi

def cylindrical_to_cartesian(r, phi, z):
    x = r * np.cos(phi)
    y = r * np.sin(phi)
    return x, y, z

def cylindrical_to_spherical(r_c, phi, z):
    r_s = np.sqrt(r_c**2 + z**2)
    theta = np.arctan2(r_c, z)
    return r_s, theta, phi

def spherical_to_cartesian(r, theta, phi):
    x = r * np.sin(phi) * np.cos(theta)
    y = r * np.sin(phi) * np.sin(theta)
    z = r * np.cos(phi)
    return x, y, z

def spherical_to_cylindrical(r_s, theta, phi):
    r_c = r_s * np.sin(theta)
    z = r_s * np.cos(theta)
    return r_c, phi, z

# Main Conversion Dispatcher Function

def convert_coordinates(src_system, dst_system, coordinates):
    if src_system == "cartesian" and dst_system == "cylindrical":
        return cartesian_to_cylindrical(*coordinates)
    elif src_system == "cartesian" and dst_system == "spherical":
        return cartesian_to_spherical(*coordinates)
    elif src_system == "cylindrical" and dst_system == "cartesian":
        return cylindrical_to_cartesian(*coordinates)
    elif src_system == "cylindrical" and dst_system == "spherical":
        return cylindrical_to_spherical(*coordinates)
    elif src_system == "spherical" and dst_system == "cartesian":
        return spherical_to_cartesian(*coordinates)
    elif src_system == "spherical" and dst_system == "cylindrical":
        return spherical_to_cylindrical(*coordinates)
    else:
        raise ValueError("Invalid source or destination coordinate system.")

# Example usage
point = (1, 1, 1)  # Cartesian coordinates
src_system = "cartesian"
dst_system = "cylindrical"
converted_point = convert_coordinates(src_system, dst_system, point)
print(f"Converted from {src_system} to {dst_system}:", converted_point)

Right-Down-Forward 좌표계에서의 좌표계 변환

• 카메라 데이터를 사용하지 않거나 카메라에서의 좌표축을 고려하지 않는다면 아래 글은 생략하여도 무관합니다.

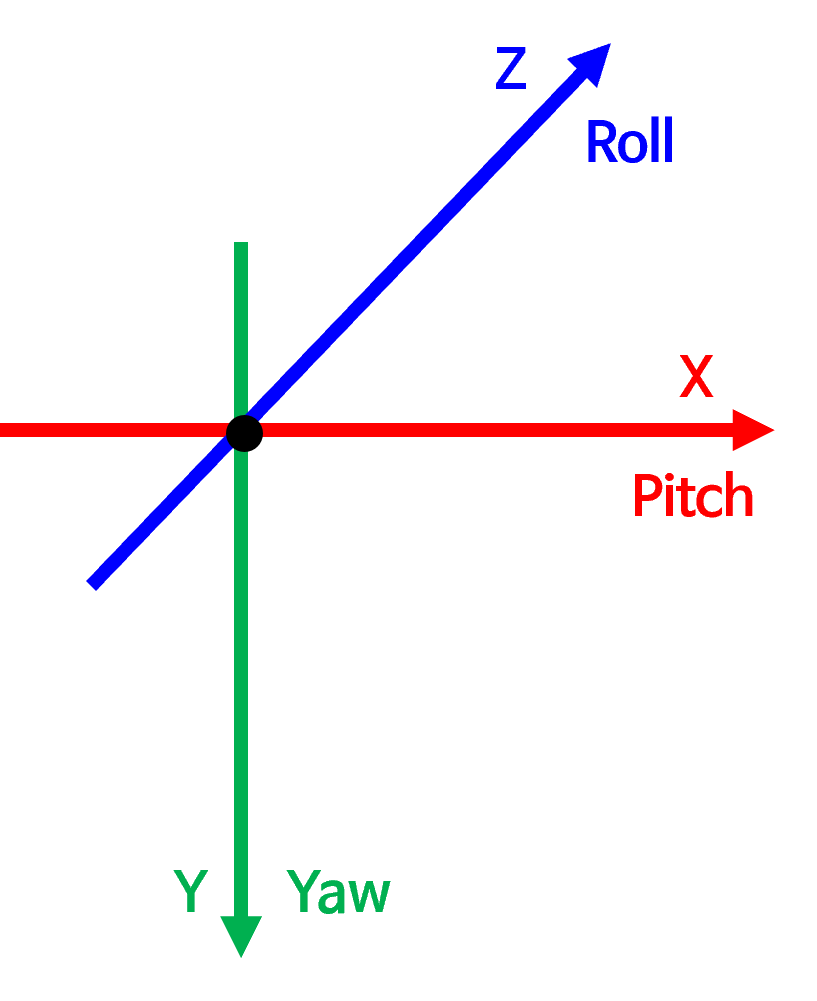
• 위 그림과 같이 RDF 좌표계는 카메라를 이용할 때 주로 사용되는 좌표 축입니다. 가로축이 $X$, 세로축이 $Y$ 이고 앞으로 향하는 방향이 $Z$ 가 되며 이 방향의 값을 Depth 라고 부릅니다.
• 본 글을 통하여 직교 좌표계를 사용하는 카메라 영상의 값을 앞에서 다룬 원통 좌표계와 구면 좌표계를 이용하여 어떻게 다루는 지 살펴보도록 하겠습니다.

직교 좌표계와 원통 좌표계 간의 좌표 변환

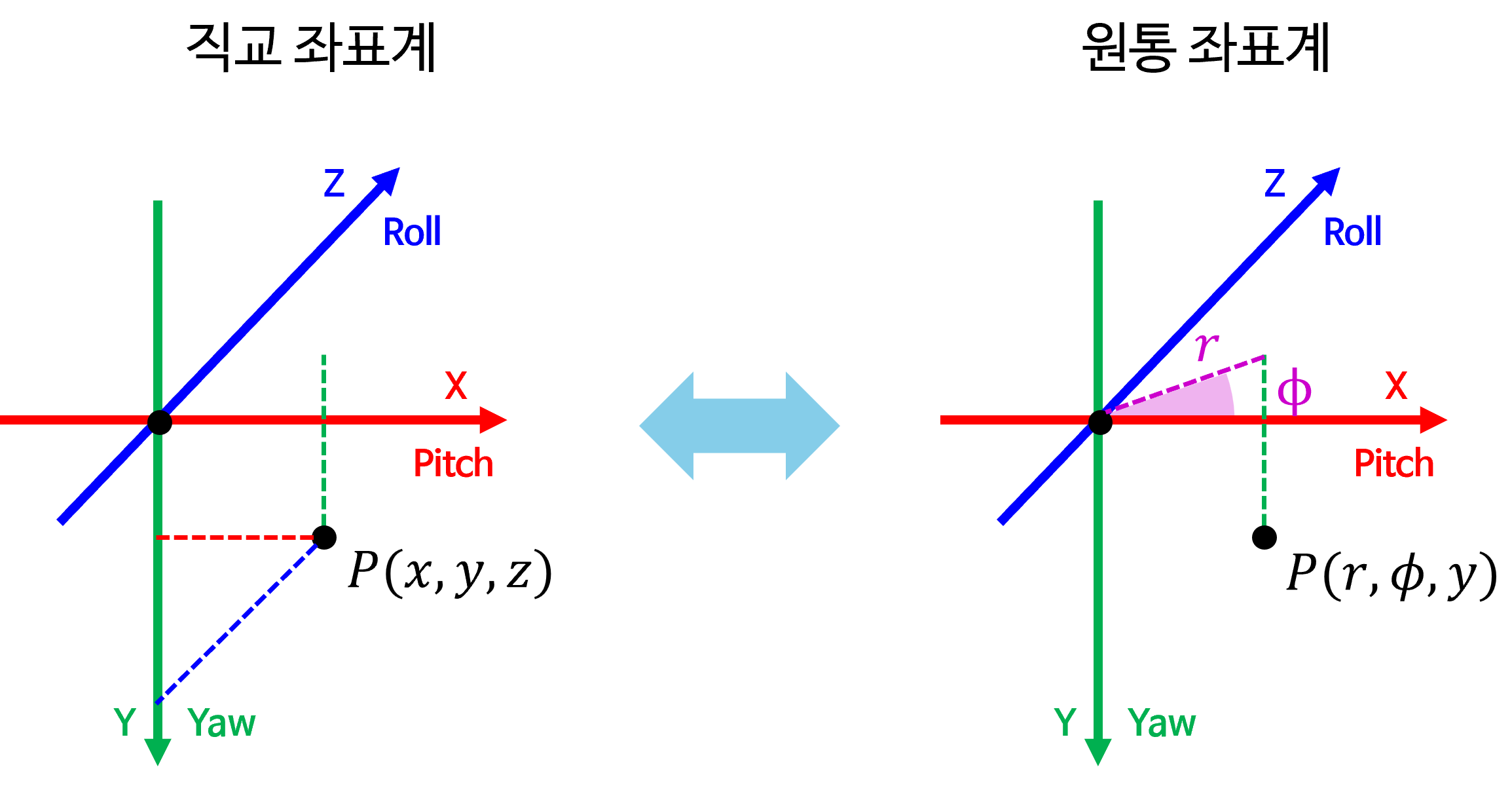
• 위 그림은 RDF 좌표계 기준으로 직교 좌표계와 원통 좌표계 간의 변환 관계를 보여줍니다.

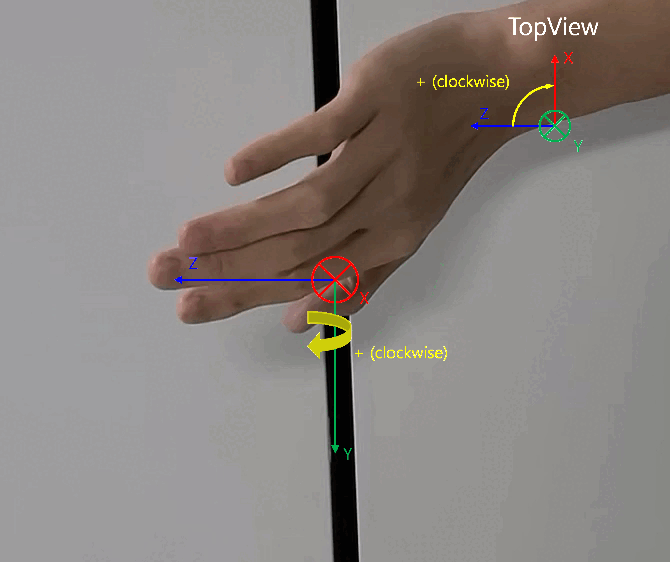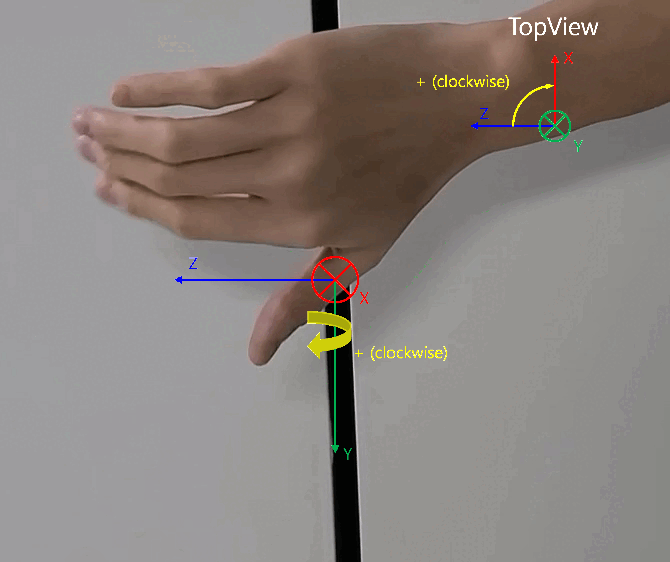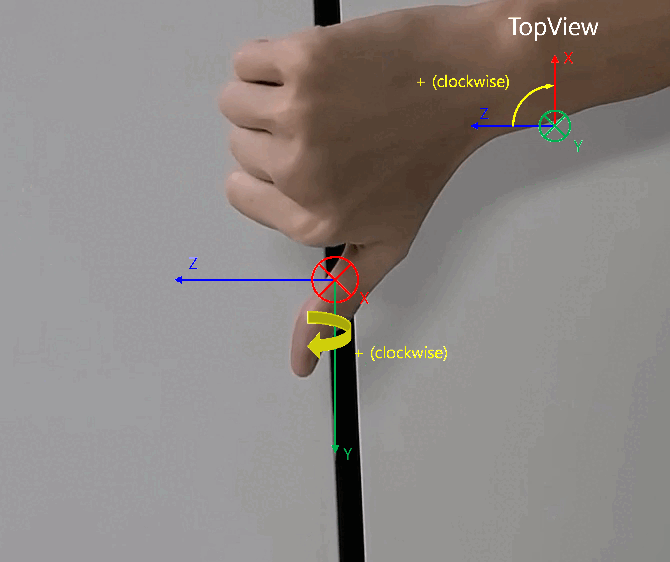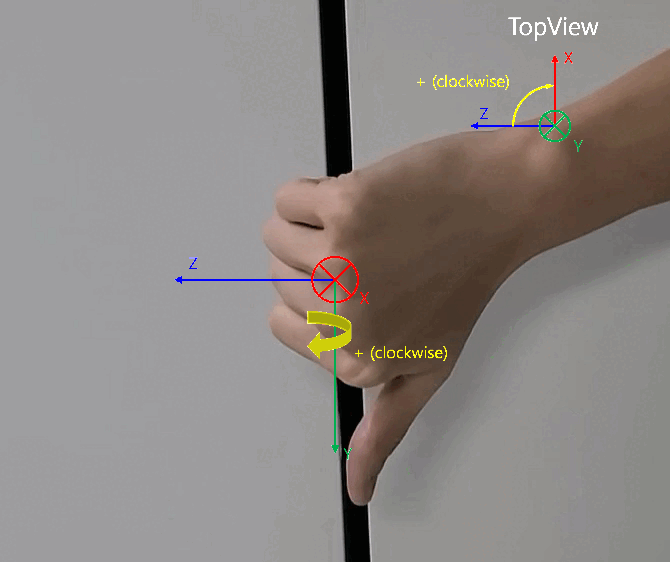
• 원통 좌표계에서 $X, Z$ 평면 상에 회전 각도인 $\phi$ 는 위 영상과 같이 오른손을 전/후 방향의 축 ($Z$ 축) 에서 좌/우 방향의 축 ($X$ 축)을 손으로 감쌋을 때, 감싸는 회전 방향인 시계 방향과 같습니다. 이 내용을 바탕으로 아래 글을 읽으시면 됩니다.

• 위 설명과 같은 이유로 FLU 좌표계에서 $\phi$ 는 전후방 축인 Forward 양의 방향축에서 좌우 수평축인 Left 양의 방향축으로의 회전 각도를 나타낸 것과 같이 RDF 좌표계에서도 $\phi$ 는 전후방 축인 Forward 양의 방향축에서 좌우 수평축인 Right 양의 방향축으로의 회전 각도를 나타냅니다.

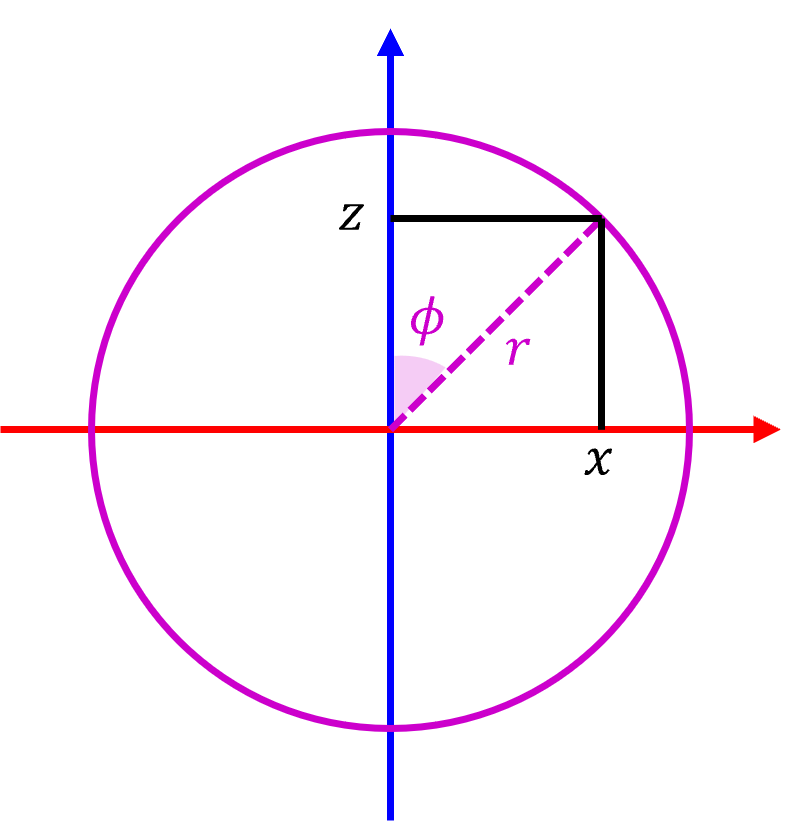
• 앞에서 다룬 내용과 유사하게 $X$ 축과 $Z$ 축이 이루는 평면에서 $x, z$ 좌표를 이용하면 위 그림과 같이 쉽게 $r, \phi$ 를 구할 수 있습니다. $y$ 값은 직교 좌표계와 원통 좌표계 같은 값을 사용합니다. 따라서 직교 좌표계의 $x, y, z$ 값을 이용하면 원통 좌표계의 $r, \phi, y$ 를 다음과 같이 구할 수 있습니다.

• $$r = \sqrt{x^{2} + z^{2}}$$
• $$\phi = \tan^{-1}(\frac{x}{z})$$
• $$y = y$$

• 반대로 원통 좌표계의 $r, \phi, y$ 를 이용하여 직교 좌표계의 $x, y, z$ 를 구하려면 삼각함수를 이용하여 변환할 수 있습니다.

• $$x = r \sin{(\phi)}$$
• $$y = y$$
• $$z = r \cos{(\phi)}$$

• 따라서 다음과 같이 직교 좌표계와 원통 좌표계 간의 변환 관계를 정의할 수 있습니다.

직교 좌표계와 구면 좌표계 간의 좌표 변환

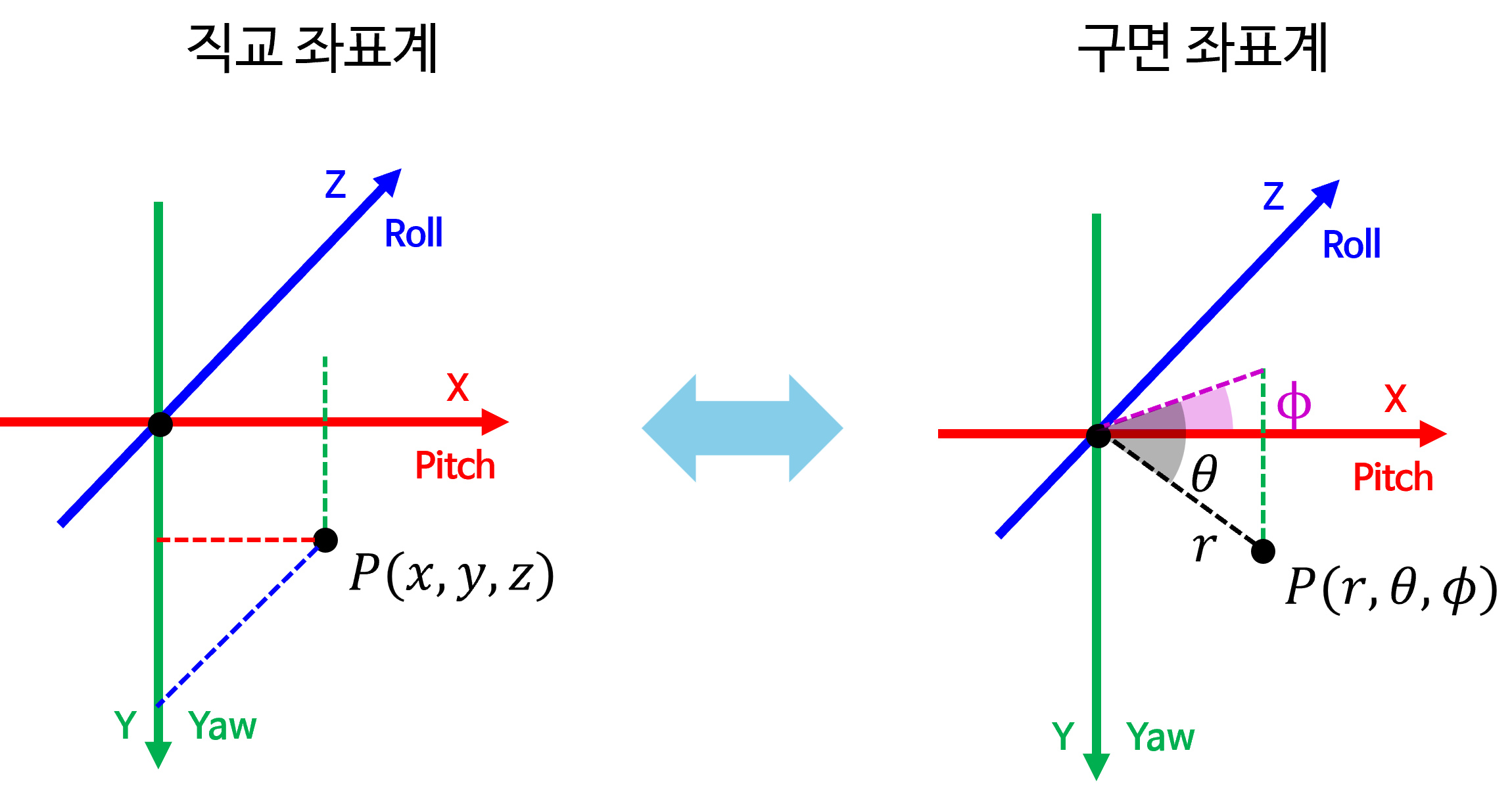
• 이번에는 직교 좌표계와 구면 좌표계 간의 변환 관계를 정의해 보도록 하겠습니다.

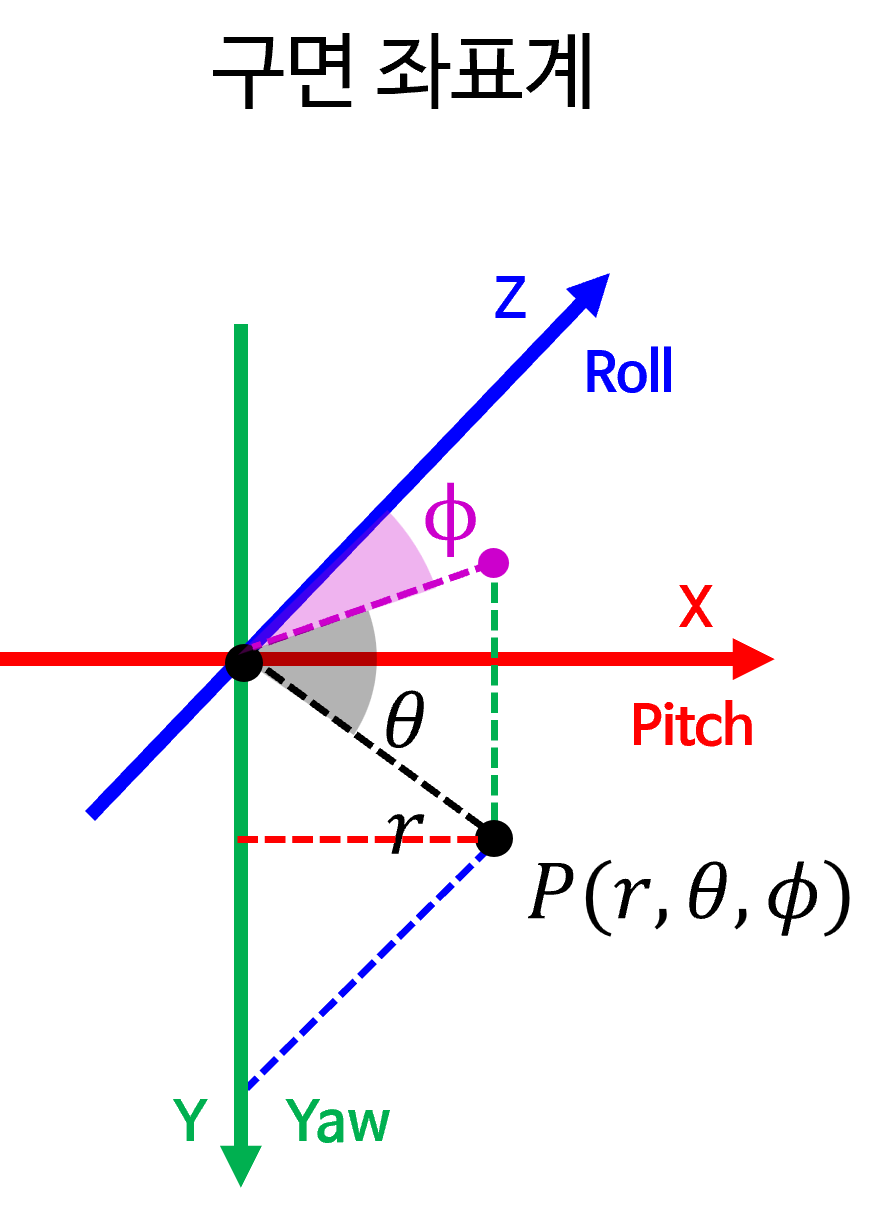
• 위 그림과 같이 3차원 상의 점 $P$ 를 구하기 위해 필요한 값을 하나씩 구해보면 다음과 같습니다.

• $$r = \sqrt{x^{2} + y^{2} + z^{2}}$$
• $$\phi = \tan^{-1}(\frac{x}{z})$$

• 구면 좌표계에서도 $r, \phi$ 는 원통 좌표계와 동일한 방식으로 구할 수 있습니다.
• 반면 $\theta$ 의 정의는 $X, Z$ 축이 생성하는 평면을 시작으로 생성되는 각도가 됩니다. 이와 같이 정의 하는 이유는 카메라 좌표계에서 $Z$ 축이 Forward로 향하는 원점을 Principal Point로 삼기 때문에 이 부분을 기준으로 $\theta$ 의 회전각을 구하기 위함입니다.
• 즉, $Z$ 축을 기준으로 수평 방향으로의 회전 각도를 $\phi$, 수직 방향으로의 회전 각도를 $\theta$ 로 정의하는 것이 RDF 좌표계에서 $\phi, \theta$ 를 정의하는 방법입니다. FLU 좌표계와 다른 이유는 RDF 좌표계를 전통적으로 사용하는 카메라 좌표계와 대응하여 사용하기 위함입니다.

• 따라서 $\theta$ 를 구하기 위해서는 $\theta$ 를 사이각으로 하고 빗변이 $r$, 높이가 $y$ 인 삼각형을 이용하면 다음과 같이 구할 수 있습니다.

• $$\theta = \sin^{-1}{\left(\frac{y}{r} \right)}$$

• 반대로 구면 좌표계 값인 $r, \theta, \phi$ 를 알고 있으면, 직교 좌표계 값인 $x, y, z$ 는 삼각 함수를 이용하여 쉽게 구할 수 있습니다.
• 먼저 사잇각을 $\theta$ 로 하는 삼각형에서 삼각비를 이용하면 $y$ 를 쉽게 구할 수 있습니다.

• $$y = r \cdot \sin{(\theta)}$$

• 그 다음 위 그림에서 원점과 보라색 점 사이의 거리는 방금 사용한 삼각형에서의 삼각비를 이용하면 $r \cos{(\theta)}$ 로 구할 수 있으므로 다음과 같이 $x, z$ 에 접근할 수 있습니다.

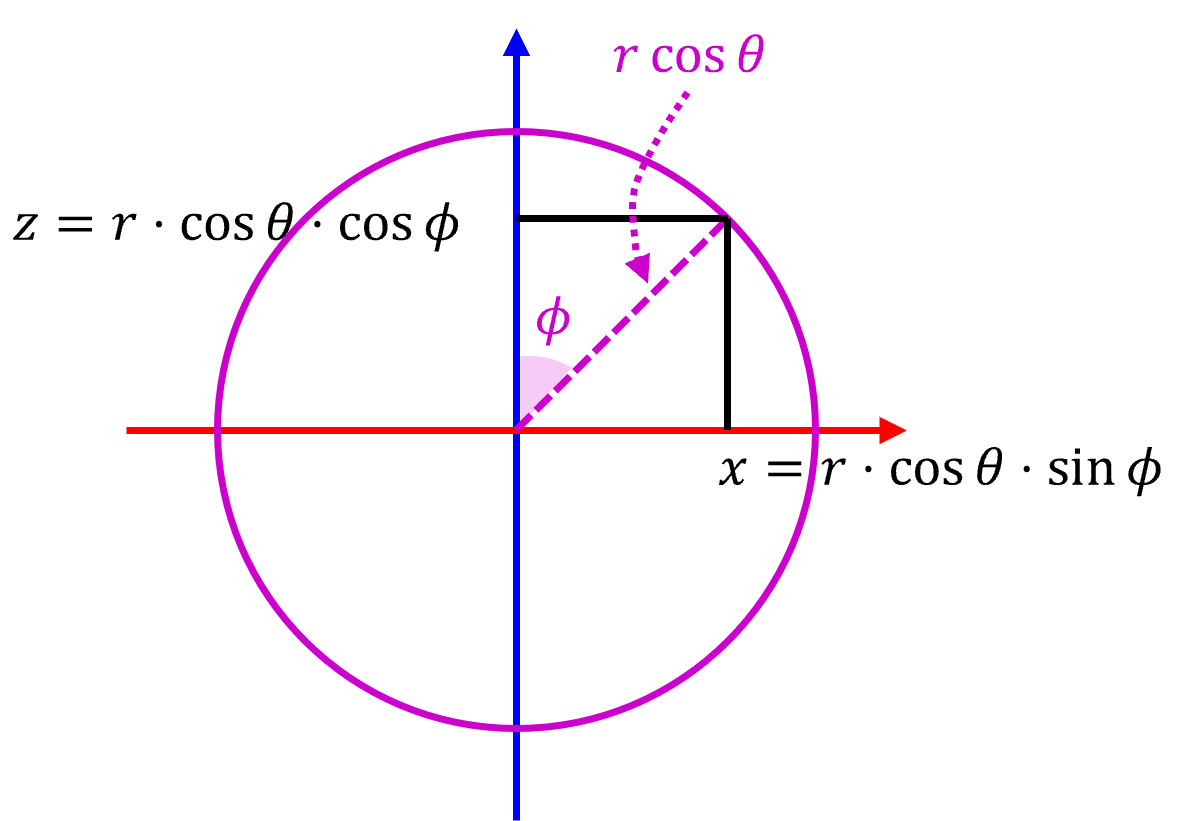
• $$x = r \cdot \cos{(\theta)} \cdot \sin{(\phi)}$$
• $$z = r \cdot \cos{(\theta)} \cdot \cos{(\phi)}$$

• 따라서 다음과 같이 직교 좌표계와 구면 좌표계간의 변환 관계를 정의할 수 있습니다.

원통 좌표계와 구면 좌표계 간의 좌표 변환

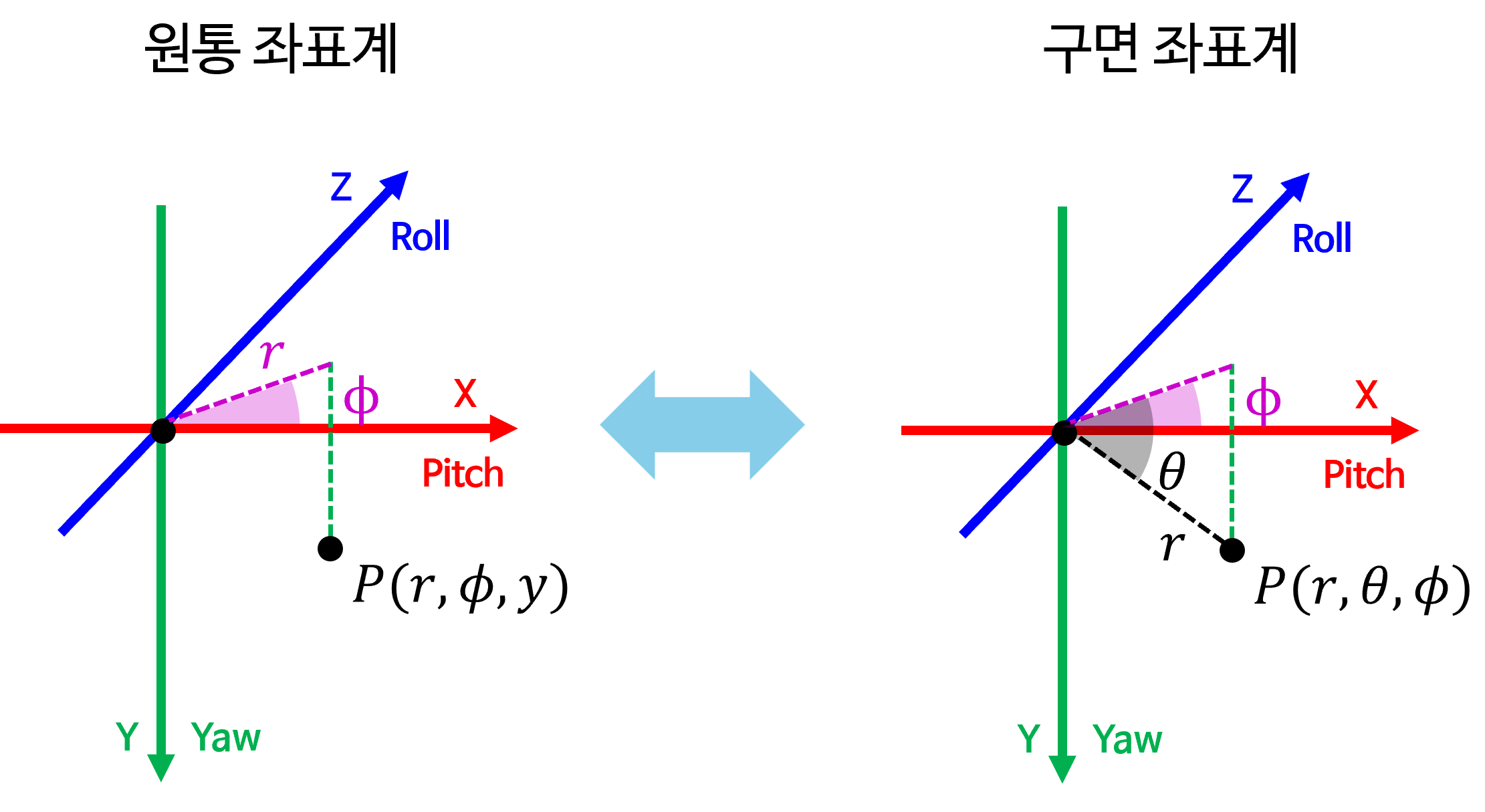
• 마지막으로 원통 좌표계와 구면 좌표계간의 좌표 변환에 대하여 살펴보도록 하겠습니다. FLU 좌표계 예제와 마찬가지로 두 좌표계 모두 $r$ 이 사용되므로 원통 좌표계에서는 $r_{c}$ 로 사용하고 구면 좌표계에서는 $r_{s}$ 로 사용하도록 하겠습니다.
• 먼저 두 좌표계 모두 azimuth 각도로 $\phi$ 를 사용합니다. 원통 좌표계에서 구면 좌표계의 $r_{s}, \theta$ 를 구하기 위해서는 $r_{c}, y$ 와 삼각비를 활용하면 쉽게 구할 수 있습니다.

• $$r_{s} = \sqrt{r_{c}^{2} + y^{2}}$$
• $$\theta = \tan^{-1}{(\frac{y}{r_{c}})}$$

• 반면 구면 좌표계에서 $r_{s}, \theta$ 를 이용하여 $r_{c}, y$ 를 구하는 방법 또한 삼각비를 활용하면 쉽게 구할 수 있습니다.

• $$r_{c} = r_{s} \cos{(\theta)}$$
• $$y = r_{s} \sin{(\theta)}$$

• 정리하면 다음과 같이 원통 좌표계와 구면 좌표계를 변환할 수 있습니다.

Python Code

• 지금까지 살펴본 내용을 파이썬 코드를 이용하여 정리하면 다음과 같습니다.

import numpy as np

def cartesian_to_cylindrical_RDF(x, y, z):
    r = np.sqrt(x**2 + z**2)
    phi = np.arctan2(x, z)
    return r, phi, y

def cylindrical_to_cartesian_RDF(r, phi, y):
    x = r * np.sin(phi)
    z = r * np.cos(phi)
    return x, y, z

def cartesian_to_spherical_RDF(x, y, z):
    r = np.sqrt(x**2 + y**2 + z**2)
    theta = np.arcsin(y / r)
    phi = np.arctan2(x, z)
    return r, theta, phi

def spherical_to_cartesian_RDF(r, theta, phi):
    x = r * np.cos(theta) * np.sin(phi)
    y = r * np.sin(theta)
    z = r * np.cos(theta) * np.cos(phi)
    return x, y, z

def spherical_to_cylindrical_RDF(r_s, theta, phi):
    r_c = r_s * np.cos(theta)
    y = r_s * np.sin(theta)
    return r_c, phi, z

def cylindrical_to_spherical_RDF(r_c, phi, z):
    r_s = np.sqrt(r_c**2 + y**2)
    theta = np.arctan2(y, r_c)
    return r_s, theta, phi


def convert_coordinates_RDF(src_system, dst_system, coordinates):
    if src_system == "cartesian" and dst_system == "cylindrical":
        return cartesian_to_cylindrical_RDF(*coordinates)
    elif src_system == "cartesian" and dst_system == "spherical":
        return cartesian_to_spherical_RDF(*coordinates)
    elif src_system == "cylindrical" and dst_system == "cartesian":
        return cylindrical_to_cartesian_RDF(*coordinates)
    elif src_system == "cylindrical" and dst_system == "spherical":
        return cylindrical_to_spherical_RDF(*coordinates)
    elif src_system == "spherical" and dst_system == "cartesian":
        return spherical_to_cartesian_RDF(*coordinates)
    elif src_system == "spherical" and dst_system == "cylindrical":
        return spherical_to_cylindrical_RDF(*coordinates)
    else:
        raise ValueError("Invalid source or destination coordinate system.")

# Example usage
point = (1, 1, 1)  # Cartesian coordinates
src_system = "cartesian"
dst_system = "cylindrical"
converted_point = convert_coordinates_RDF(src_system, dst_system, point)
print(f"Converted from {src_system} to {dst_system}:", converted_point)

Calculus 관련 글 목차