
페이저 (Phasor)
2021, Mar 01
- 참조 : https://angeloyeo.github.io/2019/06/18/phasor.html
- 이번 글에서는 물리학 또는 신호 처리에서 사용되는
Phasor의 정의에 대하여 간략하게 알아보도록 하겠습니다. - 먼저
정현파(sinusoidal wave)의 의미에 대하여 알아보겠습니다. 정현파는 막대기의 회전 운동을 통하여 유도할 수 있습니다. 다음 그림을 참조하면 쉽게 이해할 수 있습니다.
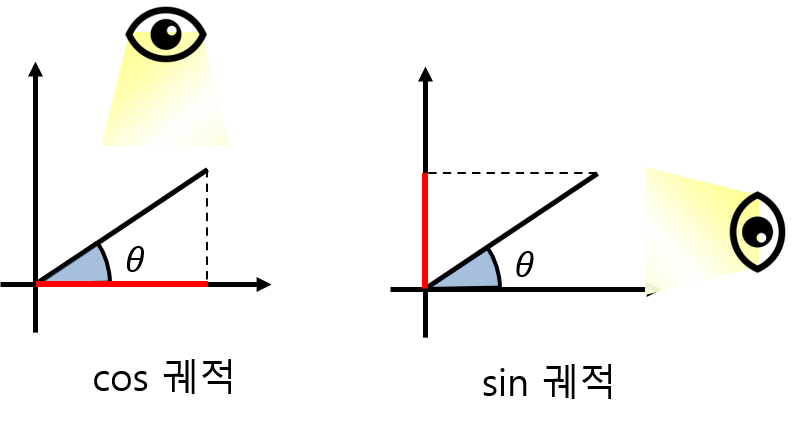
- cos 함수의 궤적은 위 그림과 같이 어떤 선을 반시계 방향으로 각도 \(\theta\) 만큼 회전할 때, 위에서 바라본 그림자(빨간색 선) 길이의 자취로 생각할 수 있습니다.
- 반면 sin 함수의 궤적은 오른쪽에서 바라본 그림자 길이의 자취로 생각할 수 있습니다.
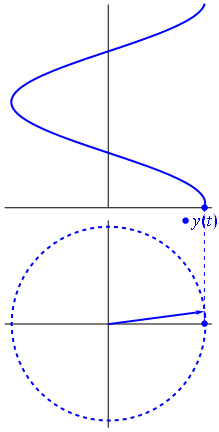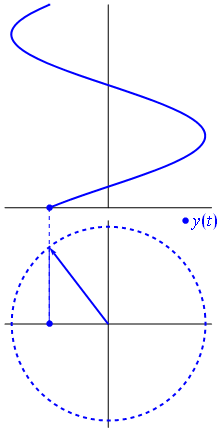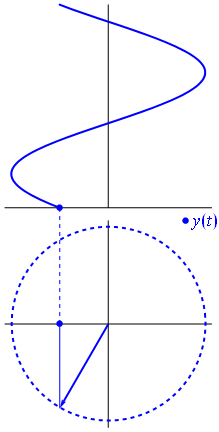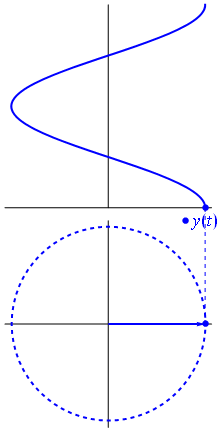
- 위 그림은 cos 함수를 나타낸 것입니다. 막대의 움직임이 반시계 방향으로 점점 증가함에 따라서 위에서 바라본 그림자의 길이를 자취로 나타낸 형태입니다.
- 중요한 점은 sin, cos 모두 같은 형태 및 방향으로 움직이는 막대를 보는 방향에 따라서 다르게 값을 나타낸다는 점입니다. 즉, 보는 방향만 90도 만큼 이동하면 같은 관점에서 바라보므로 같은 값을 가지게 됩니다. 이 점이 cos, sin 함수의 관계라고 말할 수 있습니다.
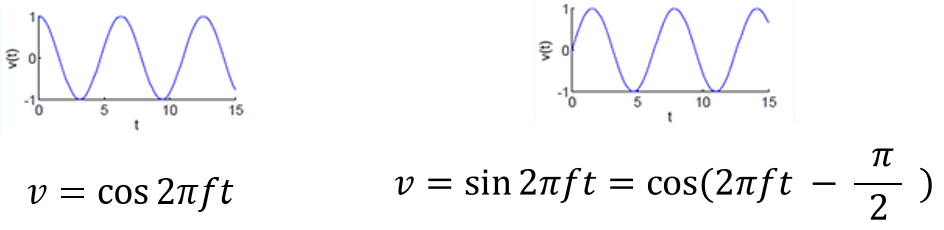
- 즉, 위 식과 같이 sin이나 cos 모두 cos 함수로 환원해서 생각할 수 있다는 점입니다.
phasor의 중요한 전제는 모든 정현파를 cos으로 환원해서 생각하는 것입니다. 따라서 sin은 cos이 \(\pi / 2\) 만큼 이동한 것으로 생각하면 됩니다.
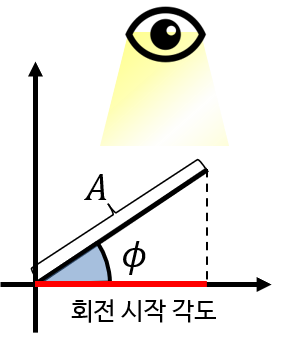
- 그러면, 좀 더 개념을 확장해 보도록 하겠습니다. 사용할 변수는 \(A, \phi, f, t\) 입니다.
- ① \(A\) : 위 그림에서는 막대의 길이에 해당하며 진폭과 관련 있습니다.
- ② \(\phi\) : 위 그림에서 회전을 시작하는 처음 각도에 해당합니다. 따라서 cos 함수의 시작점을 뜻합니다.
- ③ \(f\) : 주파수를 뜻하며 위 그림에서는 막대가 반시계방향으로 회전하는 주기와 관련 있습니다.
- ④ \(t\) : cos 함수에서의 \(x\)축에 해당하는 값입니다.
- 위 그림과 같이 막대의 길이가 \(A\), 회전을 시작하는 처음 각도가 \(\phi\), 주파수가 \(f\) 일 때, 막대 그림자의 궤적은 다음과 같이 표현할 수 있습니다.
- \[\begin{align} A\cos{(2\pi f t + \phi)} &= A\cos{(\phi)}\cos{(2\pi ft)} - A\sin{(\phi)}\sin{(2\pi f t)} \\ &= X \cos{(2\pi f t)} - Y \sin{(2\pi f t)} \end{align}\]
- 위 식과 같이 sin, cos 함수를 이용하여 식을 분해하면 \((X, Y) = (A\cos{\phi}, A\sin{phi})\)를 얻어낼 수 있습니다. 이 관점이
phasor분석의 핵심 아이디어 입니다. 주파수 성분이 고정되어 있다면 \(X, Y\)의 값을 이용하여 막대의 길이 \(A\)와 시작 각도 \(\phi\)인 막대의 회전 운동을 간단하게 나타낼 수 있습니다. - 따라서 \((X, Y) = (A\cos{\phi}, A\sin{phi})\)를 이용하여
벡터의 회전 운동을 표현할 수 있습니다.
phasor에서는 2차원 벡터를 표현해주는 좌표계로 복소 평면을 사용합니다. 왜냐하면 허수는 회전을 의미하기 때문입니다.- 따라서 벡터는 다음과 같은 형태로 사용할 수 있습니다.
- \[(X,Y) = (A\cos(\phi), A\sin(\phi)) = X + jY = A\cos{(\phi)} + j A \sin{(\phi)}\]
- 위 식을 오일러 공식을 이용하면 다음과 같이 나타낼 수 있습니다.
- \[A \times exp(j\phi)\]
- 간단하게 막대기의 길이 \(A\)와 각도 \(\phi\)만을 이용하여 나타낼 수 있습니다. 이 경우 앞에서도 가정한 바와 같이 주파수가 고정되어 있는 경우입니다.
- \[A \angle \phi \ \ \ \ \text{(polar coordinate representation)}\]
- 이와 같이 위에서 정의한 식 모두 하나의 회전 운동하는 막대기를 표현할 수 있게 되며, 주파수가 고정되어 있다고 가정한다면 네 개의 표현 방법은 모두 같은 현상을 표현한 것입니다.