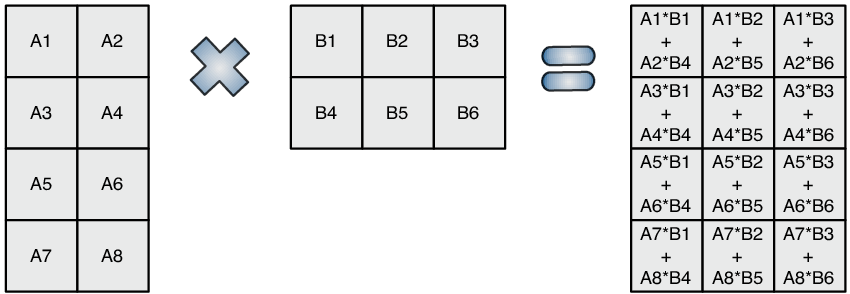
블록 행렬 곱 (block matrix multiplication)
2020, Aug 26
- 참조 : https://ximera.osu.edu/la/LinearAlgebra/MAT-M-0023/main
- 참조 : https://math.stackexchange.com/questions/787909/block-matrix-multiplication
- 이번 글에서는 행렬 곱을 효율적으로 하기 위한
블록 행렬 곱 연산 (block matrix multiplication)에 대하여 간략하게 알아보도록 하겠습니다. 블록 행렬 곱 연산은 간단하게 말하여 행렬의 모든 원소 값들을 한번에 연산하는 것이 아니라 영역 별로 따로 연산하는 것을 뜻합니다. 이와 같이 문제의 범위를 여러 단위로 분할하고 최종적으로 합치는 방법을 통해 연산량을 줄일 수 있어서 많이 사용됩니다.
- 예를 들어 다음과 같이 2 x 2 크기의 \(A, B\) 행렬이 있다고 가정해 보겠습니다. 이 때, 행렬의 곱은 다음과 같이 나타낼 수 있습니다.
- \[AB = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]\cdot \left[ \begin{array}{cc} b_{11} & b_{12} \\ b_{21} & b_{22} \end{array} \right] = \left[ \begin{array}{cc} a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\ a_{21}b_{11}+a_{22}b_{21} & a_{22}b_{12}+a_ {22}b_{22} \end{array} \right]\]
- 만약 위 행렬의 각 원소인 \(a_{ij}, b_{ij}\)가 스칼라 값이 아니라 행렬이라면 어떻게 될까요?
- \[AB = \left[ \begin{array}{c|c} A_{11} & A_{12} \\\hline A_{21} & A_{22} \end{array} \right]\cdot \left[ \begin{array}{c|c} B_{11} & B_{12} \\\hline B_{21} & B_{22} \end{array} \right] = \left[ \begin{array}{c|c} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22} \\\hline A_{21}B_{11}+A_{22}B_{21} & A_{22}B_{12}+A_{22}B_{22} \end{array} \right]\]
- 이 경우, 표기만 조금 바꾸어서 위 식과 같이 쓸 수 있습니다. 다만 이 값은 스칼라 값이 아니기 때문에 영역을 표시하는 선을 그어서 나타내었습니다.
- 이와 같이 행렬 곱 연산을 하다 보면 전혀 영향을 끼치지 않는 원소들 끼리의 연산도 고려해야 하기 때문에 계산 비효율성이 발생할 수 있는데, 위 연산과 같이 모든 영역을 한번에 계산하지 않는 방식을 통하여 계산 효율성을 증가할 수 있습니다.
- 그러면 조금 더 구체적인 예시를 통하여 이 연산의 방식을 살펴보도록 하겠습니다.
- \[\begin{equation*} A = \left[ \begin{array}{rr|rrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ \hline 2 & -1 & 4 & 2 & 1 \\ 3 & 1 & -1 & 7 & 5 \end{array} \right] = \left[ \begin{array}{cc} I_{2} & O_{23} \\ P & Q \end{array} \right] \end{equation*}\]
- \[\begin{equation*} B = \left[ \begin{array}{rr} 4 & -2 \\ 5 & 6 \\ \hline 7 & 3 \\ -1 & 0 \\ 1 & 6 \end{array} \right] = \left[ \begin{array}{c} X \\ Y \end{array} \right] \end{equation*}\]
- 위 식에서 행렬 \(A\)를 살펴보면 \(I_{2}\) 부분은 단위 행렬이고 \(O_{23}\)은 영행렬 그리고 나머지 \(P, Q\)는 특정 값을 가지는 행렬에 해당합니다. 반면 행렬 \(B\)에서는 \(X, Y\)로 블록을 나누었는데 그 이유는 행렬 \(A\)의 \(P, Q\)와 연산을 하기 위하여 사이즈를 나눈 것입니다.
- 이 의미 단위로 연산을 하면 단위 행렬과 영행렬 덕분에 계산 과정이 많이 생략이 되게 됩니다. 아래 식을 살펴보겠습니다.
- \[\begin{equation*} AB = \left[ \begin{array}{cc} I & O \\ P & Q \end{array} \right] \left[ \begin{array}{c} X \\ Y \end{array} \right] = \left[ \begin{array}{c} IX + OY \\ PX + QY \end{array} \right] = \left[ \begin{array}{c} X \\ PX + QY \end{array} \right] = \left[ \begin{array}{rr} 4 & -2 \\ 5 & 6 \\ \hline 30 & 8 \\ 8 & 27 \end{array} \right] \end{equation*}\]
- 위 식과 같이 의미있는 연산은 \(PX + QY\)로 문제가 단순화 됩니다.
- 예제 하나를 더 보면서 이 글을 마무리 하겠습니다.
- \[\begin{equation*} A = \left[ \begin{array}{rr|rr} 2 & -1 & 3 & 1 \\ 1 & 0 & 1 & 2 \\ \hline 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \quad B = \left[ \begin{array}{rr|r} 1 & 2 & 0 \\ -1 & 0 & 0 \\ \hline 0 & 5 & 1 \\ 1 & -1 & 0 \end{array} \right] \end{equation*}\]
- \[AB = \left[ \begin{array}{cc} P & Q \\ O_{22} & I_{2} \end{array} \right] \cdot \left[ \begin{array}{cc} X & O_{21} \\ Y & Z \end{array} \right] = \left[ \begin{array}{cc} PX + QY & QZ \\ Y & Z \end{array} \right]\]
- \[\begin{equation*} AB = \left[ \begin{array}{rr|r} 4 & 18 & 3 \\ 3 & 5 & 1 \\ \hline 0 & 5 & 1 \\ 1 & -1 & 0 \end{array} \right] \end{equation*}\]