
Companion Matrix
2020, Aug 26
- 이번 글에서는
companion matrix에 대하여 간단하게 살펴보도록 하겠습니다.
companion matrix는일계수 다항식 (Monic Polynomial)을 행렬 형태로 나타내는 방법으로 볼 수 있습니다.일계수 다항식이란 다음과 같은 형태의 다항식을 의미합니다.
- \[x^{n} + c_{n-1}x^{n-1} + \cdots + c_{2}x^{2} + c_{1}x + c_{0}\]
- 일계수 다항식의 형태가 다음과 같다고 가정해 보겠습니다.
- \[p(x) = c_{0} + c_{1}x + \cdots + c_{n-1}x^{n-1} + x^{n}\]
- 이 때
Companion Matrix\(C(p)\) 는 다음과 같습니다.
- \[C(p) = \begin{bmatrix} 0 & 0 & \cdots & 0 & -c_{0} \\ 1 & 0 & \cdots & 0 & -c_{1} \\ 0 & 1 & \cdots & 0 & -c_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & -c_{n-1} \end{bmatrix}\]
- 만약 \(C(p)\) 행렬을 \(p(x)\) 다항식으로 표현하고 싶다면 \(C(p)\) 을
특성 방정식 (Characteristic Equation)으로 표현하면 됩니다.
- \[\text{det}(C(p) - \lambda I) = 0\]
- 예시를 통해 특성 방정식이 \(p(x)\) 가 됨을 살펴보도록 하겠습니다.
- \[p(x) = x^{3} + x^{2} + x + 1\]
- \[C(p) = \begin{bmatrix} 0 & 0 & -1 \\ 1 & 0 & -1 \\ 0 & 1 & -1 \end{bmatrix}\]
- \[\text{det}(C(p) - \lambda I) = 0\]
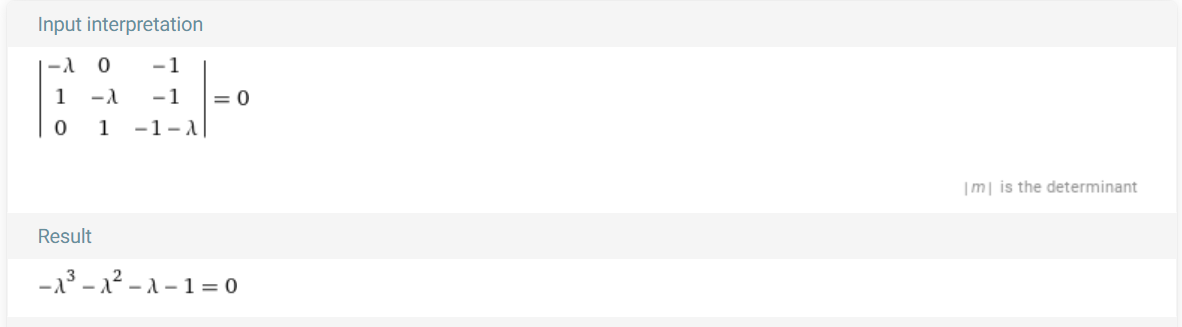
- 위 예시와 같이 \(C(p)\) 의 특성 방정식이 \(p(x)\) 가 됨을 예시를 통하여 확인하였습니다.
- 기본적으로 특성 방정식은 행렬의 고유값을 구하기 위한 방정식입니다. \(C(p)\) 의 특성 방정식이 \(p(x)\) 와 같으므로 \(C(p)\) 의 특성 방정식을 통해 고유값을 구한다는 것은 \(p(x)\) 의 해를 구하는 것과 동일하다는 것을 뜻합니다.
- 따라서 \(C(p)\) 의 고유값을 구하는 방법을 통하여 \(p(x)\) 의 해를 구할 수 있습니다.