LU 분해와 Cholesky (촐레스키) 분해

선형대수학 관련 글 목차

이번 글에서는 선형대수학에서 많이 사용되는 LU 분해와 LU 분해의 특수 형태인 Cholesky 분해에 대하여 다루어 보도록 하겠습니다.

LU 분해

어떤 행렬 $A$ 가 주어졌을 때, $A$ 를 2개 이상의 행렬의 곱으로 나타내는 것을 행렬의 분해라고 합니다. 많이 쓰는 용어로는 factorization 또는 decomposition 이라고 합니다.
만약 어떤 행렬 $A$ 를 다음과 같이 분해하였을 때, 이를 LU 분해라고 합니다.

\[A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ j & 1 & 0 \\ k & l & 1 \end{bmatrix} \begin{bmatrix} m & n & o \\ 0 & p & q \\ 0 & 0 & r \end{bmatrix} = LU\]

\[L = \begin{bmatrix} 1 & 0 & 0 \\ j & 1 & 0 \\ k & l & 1 \end{bmatrix}\]
\[U = \begin{bmatrix} m & n & o \\ 0 & p & q \\ 0 & 0 & r \end{bmatrix}\]

위 식에서 $L$ 은 하삼각 행렬 (lower triangle matrix)를 의미하며 대각선 원소는 모두 1이 됩니다. $U$ 는 상삼각 행렬 (upper triangle matrix)라고 합니다.

LU 분해는 가우스 소거법을 통해 도출할 수 있습니다. $3 \times 3$ 행렬의 예시를 통해 가우스 소거법을 통한 LU 분해를 진행해 보도록 하겠습니다.

\[\begin{bmatrix} 1 & 2 & 4 \\ 3 & 8 & 14 \\ 2 & 6 & 13 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 13 \\ 4 \end{bmatrix}\]

가우스 소거법을 적용해 보도록 하겠습니다. 위 행렬에서 ① 1 행을 3배를 한 뒤 2행에서 빼고 (2행 = 2행 - 3 x 1행) ② 1행의 2배를 해서 3행에서 빼주면 (3행 = 3행 - 2 x 1행) 다음과 같습니다.

\[\begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 2 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \\ -2 \end{bmatrix}\]

이 때, ① 1 행을 3배를 한 뒤 2행에서 빼는 것과 ② 1행의 2배를 해서 3행에서 빼는 것을 행렬식으로 표현하면 다음과 같습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix}\]

따라서 앞에서 가우스 소거법을 적용한 것은 위 행렬식을 좌/우변에 곱하는 것과 같은 작업입니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 4 \\ 3 & 8 & 14 \\ 2 & 6 & 13 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ 13 \\ 4 \end{bmatrix}\]

\[\Rightarrow \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 2 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \\ -2 \end{bmatrix}\]

이 때, 여기서 사용된 행렬은 이후에 LU 분해 시 사용됩니다.

\[\color{red}{\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix}}\]

가우스 소거법을 계속 진행해 보도록 하겠습니다.

\[\begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 2 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \\ -2 \end{bmatrix}\]

이번에는 3행에서 2행을 빼면 (3행 = 3행 - 2행) 다음과 같습니다.

\[\begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \\ -6 \end{bmatrix}\]

이 결과는 다음 행렬을 곱한 것과 같습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}\]

따라서 다음과 같이 해석할 수 있습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 2 & 5 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} 3 \\ 4 \\ -2 \end{bmatrix}\]

\[\Rightarrow \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \\ -6 \end{bmatrix}\]

이 때, 가우스 소거법을 정의하는 행렬을 표시하면 다음과 같습니다.

\[\color{blue}{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}}\]

가우스 소거법을 통해 정의된 빨간색과 파란색 행렬을 순서대로 곱하면 다음과 같습니다.

\[\color{blue}{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}} \color{red}{\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix}} = \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 1 & -1 & 1 \end{bmatrix}\]

따라서 다음과 같이 위 행렬을 이용하면 다음과 같이 상삼각행렬을 구할 수 있습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 1 & -1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 4 \\ 3 & 8 & 14 \\ 2 & 6 & 13 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix}\]

\[\Rightarrow \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 1 & -1 & 1 \end{bmatrix} A = \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix}\]

위 식에서 좌변의 행렬에 역행렬을 곱하여 우변으로 넘기면 다음과 같습니다.

\[A = \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 1 & -1 & 1 \end{bmatrix}^{-1} \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix}\]

이 때, 하삼각 행렬의 역행렬은 다음과 같이 정형화 할 수 있습니다.

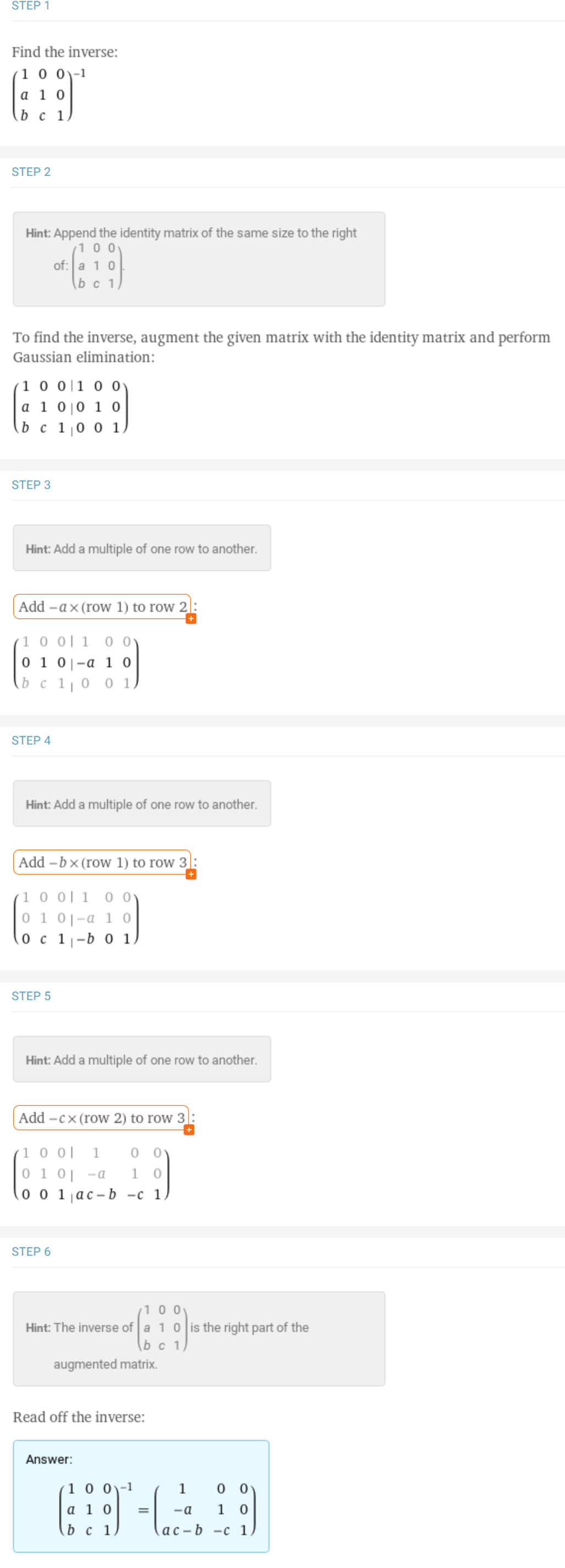
$Drawing$

\[\begin{bmatrix} 1 & 0 & 0 \\ a & 1 & 0 \\ b & c & 1 \end{bmatrix}^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ -a & 1 & 0 \\ ac-b & -c & 1 \end{bmatrix}\]

따라서 다음과 같이 정리할 수 있습니다.

\[\begin{align} A &= \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 1 & -1 & 1 \end{bmatrix}^{-1} \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix} \\ = \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix} \end{align}\]

분해된 행렬의 왼쪽은 하삼각행렬로 분해되고 오른쪽은 상삼각행렬로 분해됩니다. 그리고 하삼각행렬의 대각성분은 모두 1로 표현할 수 있습니다.

\[A = LU = \begin{bmatrix} 1 & 0 & 0 \\ j & 1 & 0 \\ k & l & 1 \end{bmatrix} \begin{bmatrix} m & n & o \\ 0 & p & q \\ 0 & 0 & r \end{bmatrix}\]

LU 분해는 지금까지 살펴본 바와 같이 가우스 소거법을 행렬로 표현한 것입니다. 따라서 다음과 같이 2 x 2 행렬과 3 x 3 행렬에 대하여 정형화 할 수 있습니다. 아래 내용은 가우스 소거법을 통하여 구한 것입니다.

\[A = LU\]
\[\text{ where } A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \quad L = \begin{bmatrix} 1 & 0 \\ \frac{c}{a} & 1 \end{bmatrix}, \quad U = \begin{bmatrix} a & b \\ 0 & d - \frac{bc}{a} \end{bmatrix}\]

\[A = LU\]
\[\text{ where } \\ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{bmatrix},\]
\[L = \begin{bmatrix} 1 & 0 & 0 \\ \frac{d}{a} & 1 & 0 \\ \frac{g}{a} & \frac{h - \frac{bg} {a}}{e - \frac{bd}{a}} & 1 \\ \end{bmatrix}, \quad U = \begin{bmatrix} a & b & c \\ 0 & e - \frac{bd}{a} & f - \frac{cd}{a} \\ 0 & 0 & i - \frac{cg}{a} - \frac{(h - \frac{bg}{a})(f - \frac{cd}{a})}{e - \frac{bd}{a}} \\ \end{bmatrix}\]

LDU 분해

LDU 분해는 LU 분해의 확장판이며 D는 Diagonal Matrix를 뜻하며 LU 분해의 U에 해당하는 Upper Triangular Matrix를 다음과 같이 분해하는 것입니다.

\[U = \begin{bmatrix} m & n & o \\ 0 & p & q \\ 0 & 0 & r \end{bmatrix} =\begin{bmatrix} m & 0 & 0 \\ 0 & p & 0 \\ 0 & 0 & r \end{bmatrix} \begin{bmatrix} 1 & n/m & o/m \\ 0 & 1 & q/p \\ 0 & 0 & 1 \end{bmatrix}\]

위 식을 보면 $U$ 를 $DU'$ 로 분해한 형태이고 $D$ 의 대각 성분과 $U$ 의 대각 성분이 같습니다. 분해된 식을 살펴보면 $U'$ 와 같이 분해되는 것은 자명합니다.
따라서 LDU 분해를 적용하면 다음과 같습니다.

\[\begin{align} A &= \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ j & 1 & 0 \\ k & l & 1 \end{bmatrix} \begin{bmatrix} m & n & o \\ 0 & p & q \\ 0 & 0 & r \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ j & 1 & 0 \\ k & l & 1 \end{bmatrix} \begin{bmatrix} m & 0 & 0 \\ 0 & p & 0 \\ 0 & 0 & r \end{bmatrix} \begin{bmatrix} 1 & n/m & o/m \\ 0 & 1 & q/p \\ 0 & 0 & 1 \end{bmatrix} \\ &= LDU \end{align}\]

따라서 앞에서 구한 예제를 LDU 분해해 보도록 하겠습니다.

\[\begin{align} A = LU &= \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 4 \\ 0 & 2 & 2 \\ 0 & 0 & 3 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix}1 & 2 & 4 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} \end{align}\]

대칭행렬의 LDU 분해

대칭행렬을 LDU 분해 하였을 때, $A = LDU = LDL^{T}$ 로 분해되는 것을 확인해 보도록 하겠습니다.
이 성질이 많이 사용되는 이유는 임의의 행렬 $B$ 를 $BB^{T}$ 로 곱하면 항상 대칭행렬이 되기 때문입니다. 즉, 다음과 같은 형태로 식 전개 시 많이 사용됩니다.

\[BB^{T} = A = LDL^{T}\]

먼저 기본적인 내용을 예제를 통하여 좀 더 자세하게 살펴보도록 하겠습니다. 먼저 다음 행렬 $A$ 를 분해해 보도록 하겠습니다.

\[\begin{align} A &= \begin{bmatrix} 2 & 2 & -4 \\ 2 & 1 & -2 \\ -4 & -2 & 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ -2 & -2 & 1 \end{bmatrix} \begin{bmatrix} 2 & 2 & -4 \\ 0 & -1 & 2 \\ 0 & 0 & -3 \end{bmatrix} = LU_{1} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ -2 & -2 & 1 \end{bmatrix} \begin{bmatrix} 2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -3 \end{bmatrix} \begin{bmatrix} 1 & 1 & -2 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{bmatrix} = LDL^{T} \end{align}\]

위 형태의 일반화를 위하여 $3 \times 3$ 크기의 행렬을 대수적으로 표현해 보도록 하겠습니다.

\[A = \begin{bmatrix} a & x & y \\ x & b & z \\ y & z & c \end{bmatrix}\]

먼저 1열에 대하여 가우스 소거법을 통하여 LU 분해를 진행해 보도록 하겠습니다.

\[\begin{align} \begin{bmatrix} 1 & 0 & 0 \\ -\frac{x}{a} & 1 & 0 \\ -\frac{y}{a} & 0 & 1 \end{bmatrix} A &= \begin{bmatrix} 1 & 0 & 0 \\ -\frac{x}{a} & 1 & 0 \\ -\frac{y}{a} & 0 & 1 \end{bmatrix} \begin{bmatrix} a & x & y \\ x & b & z \\ y & z & c \end{bmatrix} \\ &= \begin{bmatrix} a & x & y \\ 0 & -\frac{x^{2}}{a} + b & -\frac{xy}{a} + z \\ 0 & -\frac{xy}{a} + z & -\frac{y^{2}}{a} + c \end{bmatrix} \end{align}\]

\[\alpha = -\frac{x^{2}}{a} + b\]
\[\beta = -\frac{xy}{a} + z\]
\[\gamma = -\frac{y^{2}}{a} + c\]

\[\Rightarrow \begin{bmatrix} a & x & y \\ 0 & -\frac{x^{2}}{a} + b & -\frac{xy}{a} + z \\ 0 & -\frac{xy}{a} + z & -\frac{y^{2}}{a} + c \end{bmatrix} = \begin{bmatrix} a & x & y \\ 0 & \alpha & \beta \\ 0 & \beta & \gamma \end{bmatrix}\]

이번에는 2열에 대하여 가우스 소거법을 진행해 보도록 하겠습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{\beta}{\alpha} & 1 \end{bmatrix} \begin{bmatrix} a & x & y \\ 0 & \alpha & \beta \\ 0 & \beta & \gamma \end{bmatrix} = \begin{bmatrix} a & x & y \\ 0 & \alpha & \beta \\ 0 & 0 & -\frac{\beta^{2}}{\alpha} + \gamma \end{bmatrix}\]

지금까지 적용한 가우스 소거법을 행렬로 표현하면 다음과 같습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{\beta}{\alpha} & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ -\frac{x}{a} & 1 & 0 \\ -\frac{y}{a} & 0 & 1 \end{bmatrix} A = \begin{bmatrix} a & x & y \\ 0 & \alpha & \beta \\ 0 & 0 & -\frac{\beta^{2}}{\alpha} + \gamma \end{bmatrix}\]
\[L^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{\beta}{\alpha} & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ -\frac{x}{a} & 1 & 0 \\ -\frac{y}{a} & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ -\frac{x}{a} & 1 & 0 \\ \frac{x}{a}\frac{\beta}{\alpha}-\frac{y}{a} & -\frac{\beta}{\alpha} & 1 \end{bmatrix}\]
\[L^{-1}A = \begin{bmatrix} a & x & y \\ 0 & \alpha & \beta \\ 0 & 0 & -\frac{\beta^{2}}{\alpha} + \gamma \end{bmatrix} = U_{1}\]
\[U_{1} = \begin{bmatrix} a & x & y \\ 0 & \alpha & \beta \\ 0 & 0 & -\frac{\beta^{2}}{\alpha} + \gamma \end{bmatrix} = \begin{bmatrix} a & 0 & 0 \\ 0 & \alpha & 0 \\ 0 & 0 & -\frac{\beta^{2}}{\alpha} + \gamma \end{bmatrix} \begin{bmatrix} 1 & \frac{x}{a} & \frac{y}{a} \\ 0 & 1 & \frac{\beta}{\alpha} \\ 0 & 0 & 1 \end{bmatrix} = DU_{2}\]

앞에서 다음 관계를 보였었습니다.

\[\begin{bmatrix} 1 & 0 & 0 \\ a & 1 & 0 \\ b & c & 1 \end{bmatrix}^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ -a & 1 & 0 \\ ab-b & -c & 1 \end{bmatrix}\]

따라서 $L$ 은 다음을 만족하며 $L^{T}, D$ 는 다음과 같이 정의 됩니다.

\[L = \begin{bmatrix} 1 & 0 & 0 \\ \frac{x}{a} & 1 & 0 \\ \frac{y}{a} & \frac{\beta}{\alpha} & 1 \end{bmatrix}\]
\[L^{T} = \begin{bmatrix} 1 & \frac{x}{a} & \frac{y}{a} \\ 0 & 1 & \frac{\beta}{\alpha} \\ 0 & 0 & 1 \end{bmatrix}\]
\[D = \begin{bmatrix} a & 0 & 0 \\ 0 & \alpha & 0 \\ 0 & 0 & -\frac{\beta^{2}}{\alpha} + \gamma \end{bmatrix}\]

위 값들을 이용하여 $A = LDL^{T}$ 를 만족합니다.

Cholesky 분해

참조 : 양의 정부호 행렬 (Positive Definite Matrix)

Cholesky 분해는 행렬 $A$ 가 양의 정부호 행렬 (Positive Difinite Matrix) 임을 가정한 상태에서 LU 분해를 하는 방법입니다. $A$ 가 양의 정부호 행렬 (Positive Difinite Matrix)이면 대칭 행렬임을 만족합니다. (역은 성립하지 않음)
즉 양의 정부호 행렬 $A$ 는 대칭 행렬이므로 $A = LDL^{T}$ 로 분해 가능한데, 양의 정부호 행렬이라는 특성으로 인하여 유일하게 $A = LL^{T}$ 로 분해된다는 특성을 가집니다.
유일하게 분해된다는 성질을 이용하여 Cholesky 분해는 식의 전개나 해를 구할 때, 자주 사용됩니다. 그러면 Cholesky 분해에 대하여 알아보도록 하겠습니다.

행렬 $A$ 가 양의 정부호 행렬이면 대칭행렬이므로 $A = LDL^{T}$ 로 분해가 가능함은 앞에서 다루었습니다. 이 때, $D = L^{T}AL$ 또한 양의 정부호 행렬임을 만족합니다. 따라서 $D$ 의 모든 대각원소는 양수입니다. 따라서 $D$ 는 제곱근으로 분해될 수 있습니다. 이 성질을 이용하면 $A = LL^{T}$ 로 분해 가능합니다.

\[D = \begin{bmatrix} d_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & d_{n} \end{bmatrix}\]
\[\sqrt{D} = \begin{bmatrix} \sqrt{d_{1}} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \sqrt{d_{n}} \end{bmatrix}\]
\[(\sqrt{D})^{2} = D\]

\[L_{1} = L\sqrt{D}\]
\[L_{1}L_{1}^{T} = L\sqrt{D}\sqrt{D}^{T}L^{T} = LDL^{T} = A\]

따라서 $A$ 가 양의 정부호 행렬이면 $L$ 이 존재하여 $A = LL^{T}$ 로 분해됩니다.
아래는 예제를 통하여 $A = LL^{T}$ 로 분해되는 과정을 살펴본 결과입니다.

\[\begin{align} A &= \begin{bmatrix} 2 & 4 & 4 \\ 4 & 14 & 8 \\ 4 & 8 & 14 \\ \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 2 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 4 & 4 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 2 & 0 & 1 \end{bmatrix} \begin{bmatrix} 2 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{bmatrix} \begin{bmatrix} 1 & 2 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ &=\begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 2 & 0 & 1 \end{bmatrix} \begin{bmatrix} \sqrt{2}^{2} & 0 & 0 \\ 0 & \sqrt{6}^{2} & 0 \\ 0 & 0 & \sqrt{6}^{2} \end{bmatrix} \begin{bmatrix} 1 & 2 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 2 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \sqrt{2} & 0 & 0 \\ 0 & \sqrt{6} & 0 \\ 0 & 0 & \sqrt{6} \\ \end{bmatrix} \begin{bmatrix} \sqrt{2} & 0 & 0 \\ 0 & \sqrt{6} & 0 \\ 0 & 0 & \sqrt{6} \\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \\ &= \begin{bmatrix} \sqrt{2} & 0 & 0 \\ 2\sqrt{2} & \sqrt{6} & 0 \\ 2\sqrt{2} & 0 & \sqrt{6} \\ \end{bmatrix} \begin{bmatrix} \sqrt{2} & 2\sqrt{2} & 2\sqrt{2} \\ 0 & \sqrt{6} & 0 \\ 0 & 0 & \sqrt{6} \\ \end{bmatrix} \\ &= LL^T \end{align}\]

앞에서 언급한 바와 같이 양의 정부호 행렬 $A$ 는 Cholesky 분해가 유일한 값으로 분해된다는 점을 이용하여 사용된다고 하였습니다. 이 내용을 살펴보면 다음과 같습니다.

\[A = LDL^{T}\]
\[A = L_{1}L_{1}^{T} \quad (L_{1} = L\sqrt{D})\]
\[L \text{ : Lower triangular matrix with all diagonal elements being 1}\]
\[D \text{ : Diagonal matrix. All diagonal matrix elements are positive numbers}\]
\[L \text{ : Lower triangular matrix with all diagonal elements being positive numbers}\]
\[L_{1}L_{1}^{T} = L(\sqrt{D})(\sqrt{D})^{T}L_{T} = LDL^{T} = A\]

마지막으로 $3 \times 3$ 행렬과 같이 Cholesky 분해가 많이 사용되는 행렬의 형태에서는 아래와 같이 정형화 하여 사용할 수도 있습니다.

\[A = LL^{T}\]
\[\begin{align} \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} &= \begin{bmatrix} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \end{bmatrix} \begin{bmatrix} l_{11} & l_{21} & l_{31} \\ 0 & l_{22} & l_{32} \\ 0 & 0 & l_{33} \end{bmatrix} \\ &= \begin{bmatrix} l_{11}^{2} & l_{11}l_{21} & l_{11}l_{31} \\ l_{11}l_{21} & l_{21}^{2} + l_{22}^{2} & l_{21}l_{31} + l_{22}l_{32} \\ l_{11}l_{31} & l_{21}l_{31} + l_{22}l_{32} & l_{31}^{2} + l_{32}^{2} + l_{33}^{2} \end{bmatrix} \end{align}\]

위 식을 정리하면 다음 값들을 순차적으로 구할 수 있습니다.

\[l_{11} = \sqrt{a_{11}}\]
\[l_{21} = a_{21} / l_{11}\]
\[l_{22} = \sqrt{a_{22} - l_{21}^{2}}\]
\[l_{31} = a_{31} / l_{11}\]
\[l_{32} = (a_{32} - l_{31}l_{21}) / l_{22}\]
\[l_{33} = \sqrt{a_{33} - l_{31}^{2} - l{32}^{2}}\]

앞에서 다룬 예제를 다시 위 식을 통해 구하면 다음과 같습니다.

\[A = \begin{bmatrix} 2 & 4 & 4 \\ 4 & 14 & 8 \\ 4 & 8 & 14 \\ \end{bmatrix}\]
\[l_{11} = \sqrt{a_{11}} = \sqrt{2}\]
\[l_{21} = a_{21} / l_{11} = 4 / \sqrt{2} = 2\sqrt{2}\]
\[l_{22} = \sqrt{a_{22} - l_{21}^{2}} = \sqrt{14 - 8} = \sqrt{6}\]
\[l_{31} = a_{31} / l_{11} = 4 / \sqrt{2} = 2\sqrt{2}\]
\[l_{32} = (a_{32} - l_{31}l_{21}) / l_{22} = (8 - 2\sqrt{2}2\sqrt{2}) / \sqrt{6} = 0\]
\[l_{33} = \sqrt{a_{33} - l_{31}^{2} - l{32}^{2}} = \sqrt{14 - 8 - 0} = \sqrt{6}\]
\[\therefore \quad L = \begin{bmatrix} \sqrt{2} & 0 & 0 \\ 2\sqrt{2} & \sqrt{6} & 0 \\ 2\sqrt{2} & 0 & \sqrt{6} \\ \end{bmatrix}\]

이와 같이 앞에서 다룬 결과와 동일한 값을 얻을 수 있습니다.

선형대수학 관련 글 목차