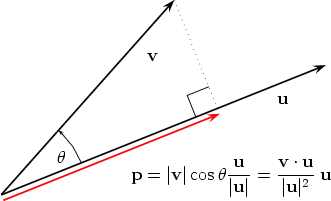
벡터의 내적 (inner product)와 벡터의 정사영 (projection)

2020, Aug 26    

선형대수학 글 목차

• 참조 : 이득우의 게임 수학

• 본 글에서는 벡터의 내적의 내용과 대표적인 벡터의 내적의 사용처인 정사영 (projection)에 대하여 간략히 다루어 보도록 하겠습니다. 추가적으로 벡터의 내적을 활용하는 몇가지 예시를 더 살펴보겠습니다.
• 벡터의 정사영 부분이 필요하시면 아래 scalar projection → vector projection 부분부터 읽어보시면 됩니다.

목차

• 벡터의 내적 정의 및 성질

• scalar projection → vector projection

• vector projection 바로 구하기

• 두 벡터의 방향 확인과 시야 판별

• 조명 효과 표현

벡터의 내적 정의 및 성질

• 벡터의 내적은 같은 차원의 두 벡터가 주어졌을 때, 벡터를 구성하는 각 성분을 곱한 후 이들을 더해 스칼라 값을 만들어내는 연산을 의미합니다.

• \[\vec{u} = (a, b)\]
• \[\vec{v} = (c, d)\]
• \[\vec{u} \cdot \vec{v} = a \cdot c + b \cdot d\]

• 벡터의 내적은 곱셈과 덧셈으로 구성되어 있으므로 교환 법칙은 성립합니다.
• 벡터의 결과가 스칼라이므로 결합 법칙은 성립하지 않습니다.
• 벡터의 덧셈에 대한 분배법칙은 성립합니다.

• 같은 벡터를 내적하면 벡터의 크기를 제곱한 결과가 나옵니다.

• \[(x, y) \cdot (x, y) = x^{2} + y^{2}\]
• \[\therefore \vec{v} \cdot \vec{v} = \vert \vec{v} \vert^{2}\]

• 내적은 교환법칙과 분배법칙이 성립하기 때문에 아래와 같이 두 벡터 합의 내적은 두 벡터의 크기로 표현할 수 있습니다.

• \[(\vec{u} + \vec{v}) \cdot (\vec{u} + \vec{v}) = \vec{u} \cdot \vec{u} + \vec{v} \cdot \vec{v} + 2(\vec{u} \cdot \vec{v}) = \vert \vec{u} \vert^{2} + \vert \vec{v} \vert^{2} + 2(\vec{u} \cdot \vec{v})\]

내적과 삼각함수와의 관계

• 벡터의 내적은 아래 그림과 같이 두 벡터의 사이각에 대한 cos 함수와 비례하는 특징을 가집니다.

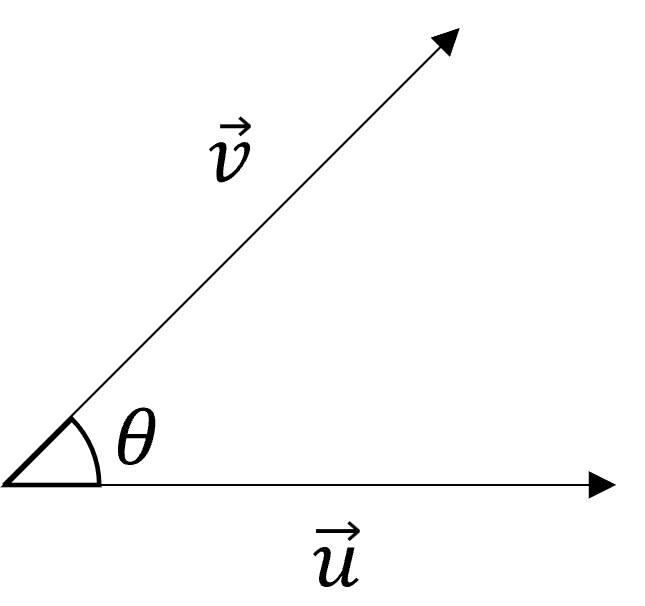
• \[\vec{u} \cdot \vec{v} = \vert \vec{u} \vert \vert \vec{v} \vert \cos{(\theta)}\]

• 위 식이 유도된 방법을 살펴보면 다음과 같습니다.

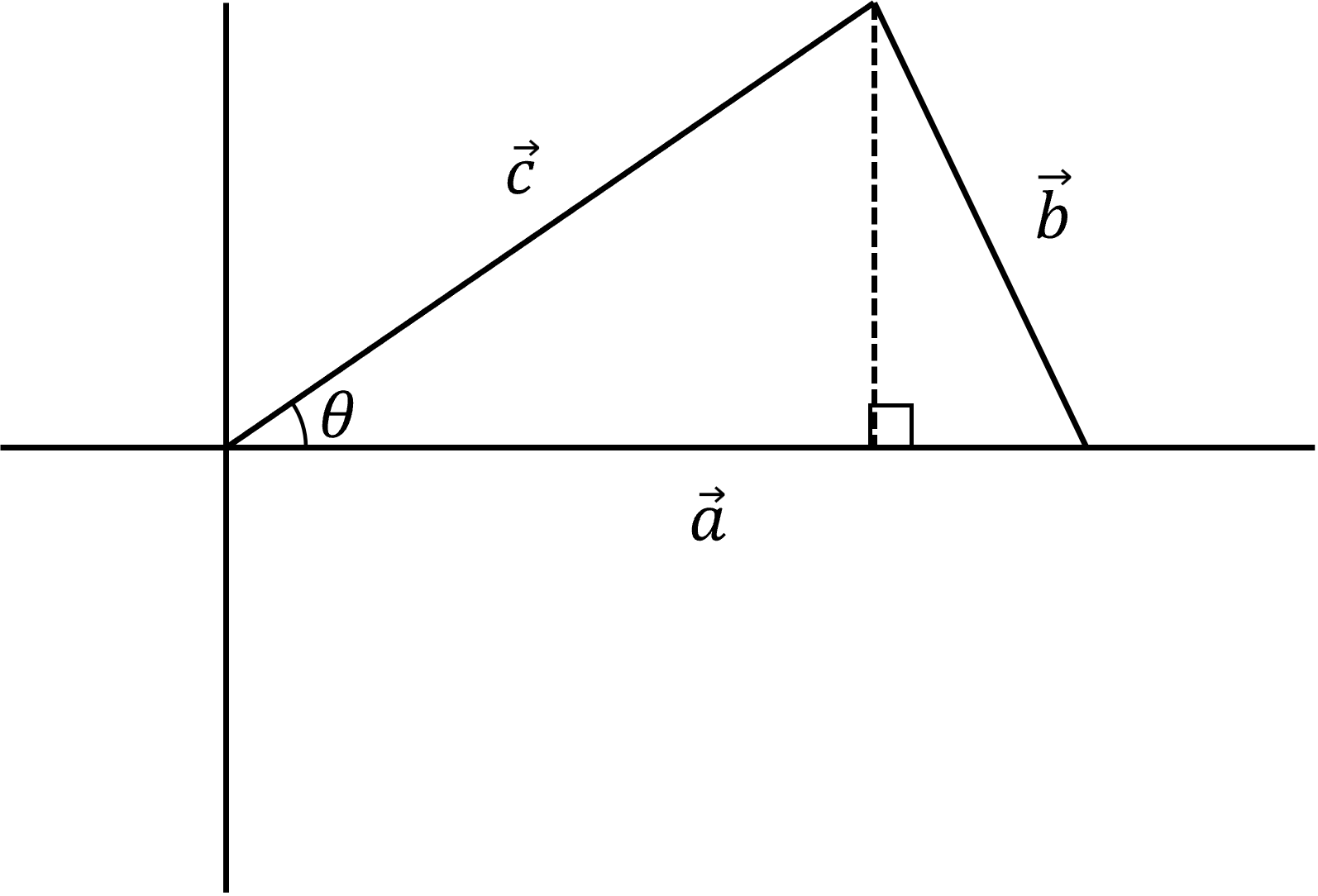
• \[\vec{b} = \vec{a} - \vec{c}\]

• 위 식을 이용하여 식을 전개해 보도록 하겠습니다.

• \[\begin{align} \vert \vec{b} \vert^{2} &= \vec{b} \cdot \vec{b} \\ &= (\vec{a} - \vec{c}) \cdot (\vec{a} - \vec{c}) \\ &= \vert \vec{a} \vert^{2} + \vert \vec{c} \vert^{2} -2\vec{a}\vec{c} \tag{1} \end{align}\]

• 다음으로 다음과 같이 식을 전개해 보도록 하겠습니다.

• \[\begin{align} \vert \vec{b} \vert^{2} &= \vert \vec{c} \vert^{2}\sin^{2}{(\theta)} \\ &= (\vert \vec{a} \vert - \vert \vec{c} \vert \cos{(\theta)})^{2} + \vert \vec{c} \vert^{2}\sin^{2}{(\theta)} \quad (\because (\vert \vec{a} \vert - \vert \vec{c} \vert \cos{(\theta)}) = 0) \\ &= \vert \vec{a} \vert^{2} - 2 \vert \vec{a} \vert \vert \vec{c} \vert \cos{(\theta)} + \vert \vec{c} \vert^{2} \cos^{2}{(\theta)} + \vert \vec{c} \vert^{2}\sin^{2}{(\theta)} \\ &= \vert \vec{a} \vert^{2} + \vert \vec{c} \vert^{2} - 2 \vert \vec{a} \vert \vert \vec{c} \vert \cos{(\theta)} \tag{2} \end{align}\]

• 식 (1) 과 식 (2)을 이용하여 정리하면 벡터의 내적 식을 구할 수 있습니다.

• \[\vert \vec{a} \vert^{2} + \vert \vec{c} \vert^{2} -2\vec{a}\vec{c} = \vert \vec{a} \vert^{2} + \vert \vec{c} \vert^{2} - 2 \vert \vec{a} \vert \vert \vec{c} \vert \cos{(\theta)}\]
• \[\vec{a} \cdot \vec{c} = \vert \vec{a} \vert \vert \vec{c} \vert \cos{(\theta)} \tag{3}\]

• 식 (3)에서 두 벡터 \(\vec{a}, \vec{c}\) 의 크기가 1이면 두 벡터의 내적은 \(cos{(\theta)}\) 가 됩니다.

• \[\vec{u} \cdot \vec{v} = \cos{(\theta)} \quad (\text{where, } \vert \vec{u} \vert = 1, \vert \vec{v} \vert = 1)\]

• 이와 같은 원리를 이용하면 두 벡터의 내적이 0인 경우에 대한 조건이 \(\cos{(\theta)} = 0\) 이 되는 것을 알 수 있으며 이 때 사이각은 90도 또는 270도인 경우 임을 알 수 있습니다.
• 대표적인 직교하는 벡터는 표준 기저 벡터가 있습니다. (1, 0) 과 (0, 1) 은 가장 기본적인 표준 기저 벡터이며 두 벡터의 내적은 0이되고 좌표계 상에서도 직교함을 알 수 있습니다.

• scalar projection → vector projection

• 먼저 scalar projection에서 vector projection으로 확장하는 관점에서 vector projection에 대하여 알아보겠습니다.
• scalar projection은 한 벡터에서 다른 벡터로 projection을 하였을 때 projection된 벡터의 시작점에서 projection된 지점까지의 거리(크기)를 나타냅니다.
• 반면 vector projection은 projection된 벡터의 시작점에서 projection된 지점까지의 거리만큼의 크기를 가지는 벡터를 나타냅니다.
• 그러면 두 벡터 \(r, s\) 가 있고 벡터 \(s\) 를 벡터 \(r\) 에 projection 시킨다는 가정하에 scalar projection과 vector projection을 구하는 방법에 대하여 알아보겠습니다.

• 먼저 scalar projection 방법에 대하여 알아보도록 하겠습니다.

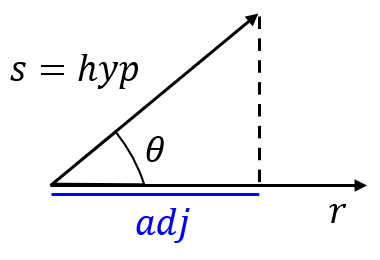
• \[\cos{\theta} = \frac{\text{adj}}{\color{blue}{\text{hyp}}} = \frac{\text{adj}}{\color{blue}{\vert s \vert}}\]
• \[\text{adj} = \vert s \vert \cos{\theta}\]

• 위 식을 두 벡터의 내적의 성질에 접목시켜 보겠습니다. 두 벡터의 내적은 다음을 따릅니다.

• \[r \cdot s = \vert r \vert \vert s \vert \cos{\theta}\]

• 따라서 앞의 식을 접목시키면 다음과 같습니다.

• \[\text{adj} = \vert s \vert \cos{\theta} = \frac{r \cdot s}{\vert r \vert} = \hat{r} \cdot s\]

• 지금 까지가 scalar projection에 관한 내용이었습니다. 즉, 위 그림과 같이 두 벡터 \(r, s\)를 이용하여 파란색의 길이를 알 수 있습니다.
• 그럼 여기서 vector projection으로 개념을 확장시켜 보겠습니다. 아시다시피 벡터는 크기와 방향을 가집니다. 따라서 scalar projection에 방향을 추가하면 됩니다.

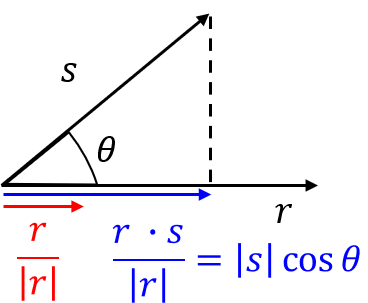
• \[\text{vector projection} = \text{scalar projection} \times \text{unit vector} = \frac{r \cdot s}{\vert r \vert} \cdot \frac{r}{\vert r \vert} = \frac{r \cdot s}{\vert r \vert \cdot \vert r \vert} \cdot r= \frac{r \cdot s}{r \cdot r} \cdot r\]

• unit vector를 포함한 형태로 나타내면 다음과 같습니다.

• \[\text{vector projection} = \text{scalar projection} \times \text{unit vector} = \frac{r \cdot s}{\vert r \vert} \cdot \frac{r}{\vert r \vert} = (\hat{r} \cdot s) \cdot \hat{r}\]

• 위 식은 scalar projection에서 구한 길이값에 방향인 유닛 벡터를 곱하여 vector projection을 하는 식입니다.
• 위 계산 과정을 보면 scalar projection은 projection 된 벡터의 유닛 벡터(\(\hat{r}\) )와 projection한 벡터(\(s\))의 내적이 됨을 알 수 있습니다.
• vector projection은 벡터이기 때문에 개념적으로 스칼라 값에 유닛 벡터를 곱하면 됩니다. 따라서 위 식과 같이 유도될 수 있습니다.

• vector projection 바로 구하기

• 이번에는 vector projection을 바로 구해보도록 하겠습니다.

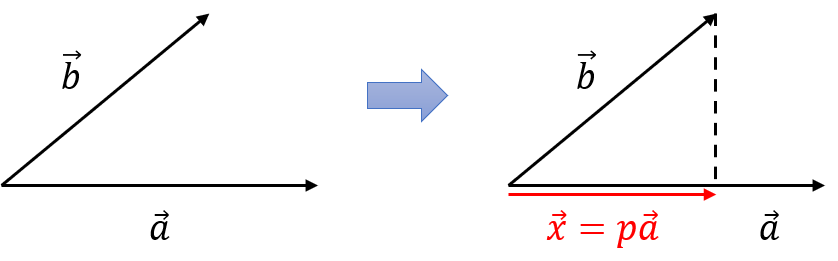
• 위 그림에서는 \(\vec{b}\)를 \(\vec{a}\)에 projection 시킵니다. 이것은 \(\vec{b}\)로부터 \(\vec{a}\)에 수직인점 까지의 길이를 가지며 \(\vec{a}\)와 같은 방향을 갖는 벡터를 찾는것을 의미합니다.
• 그리고 \(\vec{a}\)에서 projection 한 점 까지의 벡터를 \(\vec{x}\)로 나타내고 변수 \(p\)를 도입하여 \(\vec{x} = p \vec{a}\)로 정의하겠습니다.
• 먼저 projection한 벡터와 \(\vec{a}\)의 내적은 0입니다. 왜냐하면 사이각이 직각이기 때문에 앞에서 다룬 내적의 성질에 의해 0이 되게 됩니다.

• \[(\vec{b} - p\vec{a})^{T} \vec{a} = 0\]

• 위 관계식을 이용하여 \(p\)를 정의해 보겠습니다.

• \[\vec{b}^{T} \vec{a} - p\vec{a}^{T}\vec{a} = 0\]
• \[p = \frac{\vec{b}^{T}\vec{a}}{\vec{a}^{T}\vec{a}}\]
• \[\vec{x} = p \vec{a} = \frac{\vec{b}^{T}\vec{a}}{\vec{a}^{T}\vec{a}} \vec{a}\]

• 이번 방법에서도 앞에서 정리한 방법과 동일한 결과의 vector projection을 구할 수 있었습니다.
• 특히 두 unit vector의 내적은 1이기 때문에 \(\vec{a}\)가 unit vector라면 다음과 같습니다.

• \[\vec{x} = p\vec{a} = (\vec{b}^{T}\vec{a})\vec{a}\]

• 이와 같은 방법으로 벡터를 projection 하면 다양하게 사용될 수 있습니다. 가장 간단한 예시로 카메라 공간을 분석할 때에도 활용 할 수 있습니다.

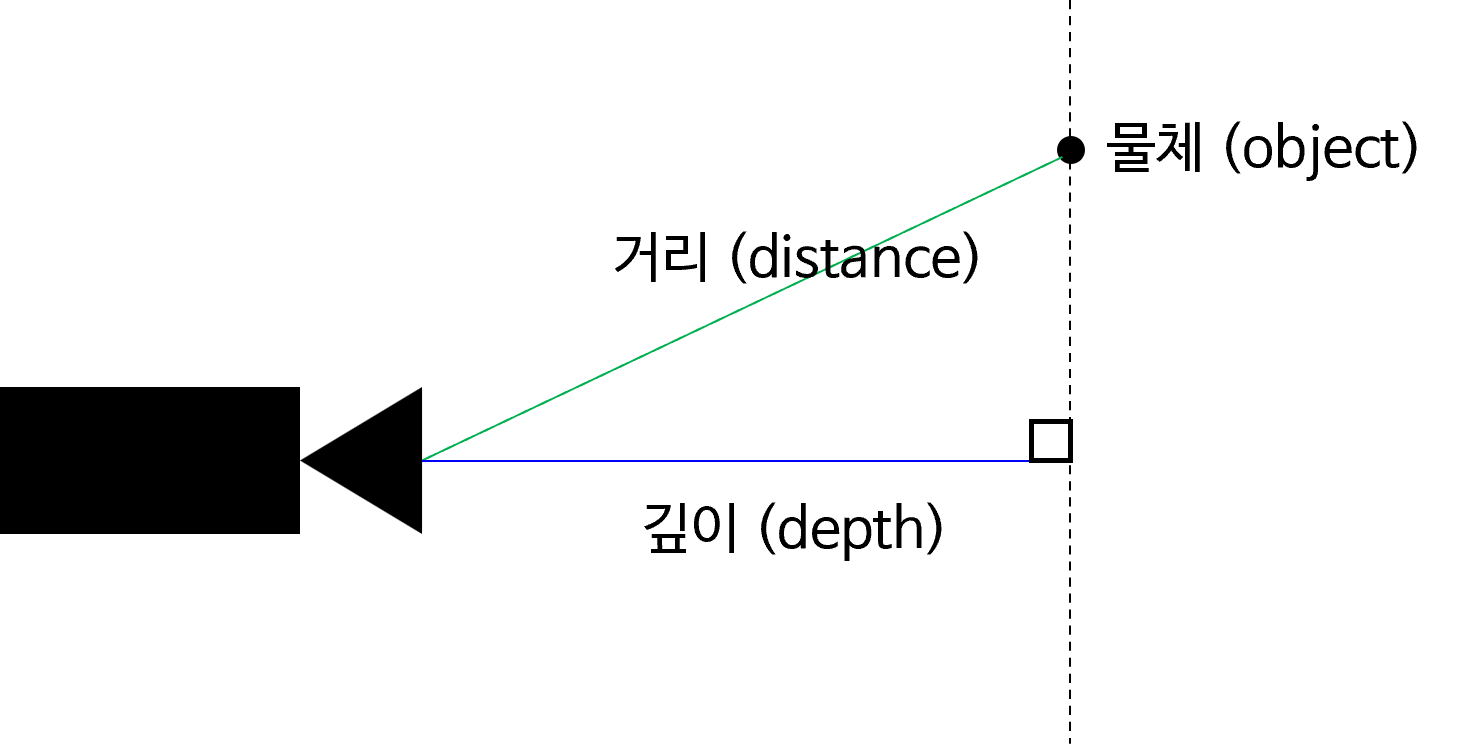
• 위 그림에서는 어떤 물체의 거리를 알 때, 카메라가 촬영하는 방향으로의 깊이 정보를 알고 싶을 때, projection을 통하여 구할 수 있음을 나타냅니다.

두 벡터의 방향 확인과 시야 판별

• 벡터의 내적 성질은 유용하게 사용 가능하며 projection을 구하는 것 이외에도 다양한 응용으로 사용할 수 있습니다.
• 대표적인 사용 방법으로 두 벡터의 방향 확인이 있습니다.
• 벡터의 내적으로 구할 때 벡터의 크기 값은 언제나 양수이므로 벡터 내적의 부호는 \(\cos{(\theta)}\) 가 결정하며 이 값은 다음과 같습니다.

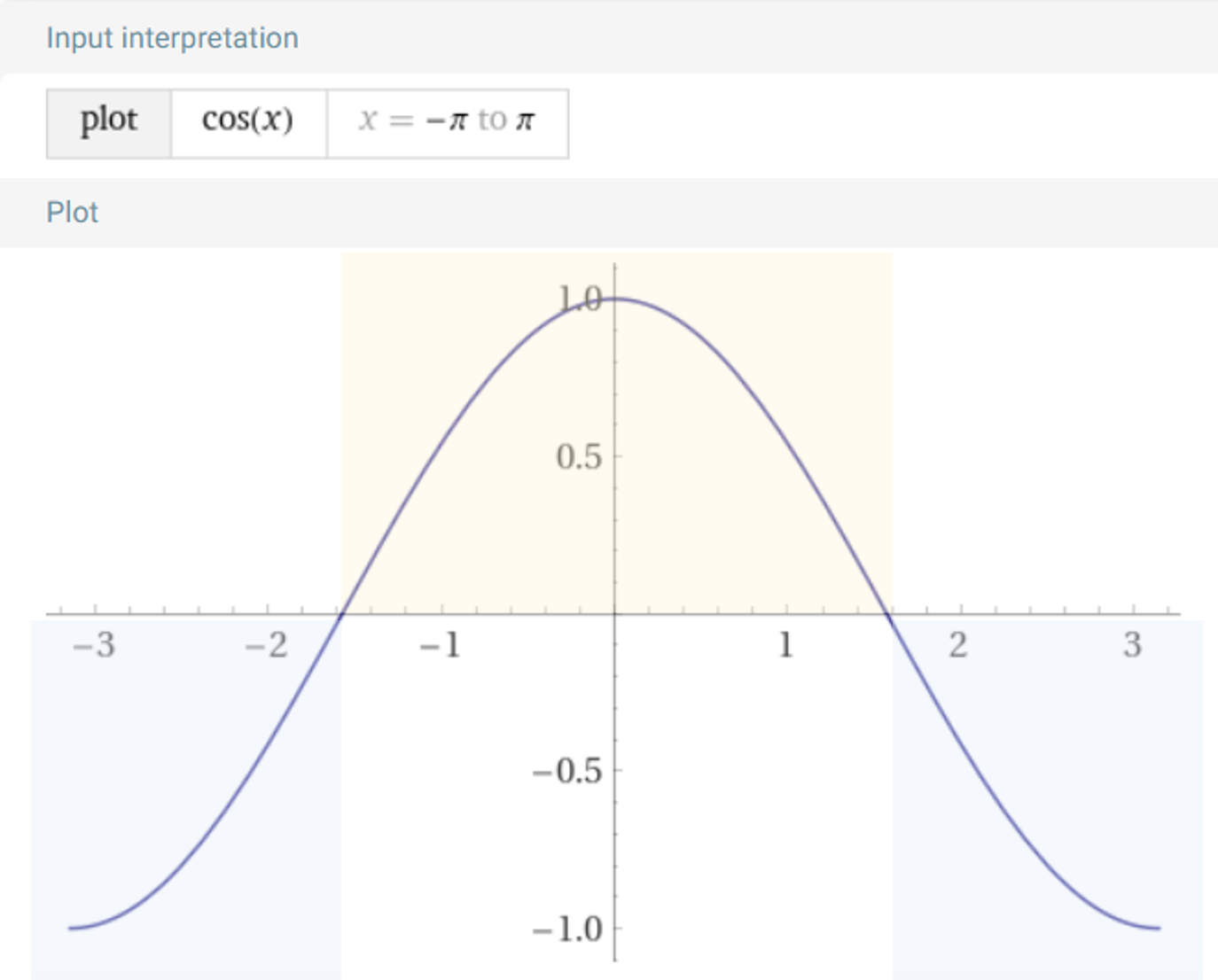
• 위 그래프와 같이 \(\cos{(\theta)}\) 는 주황색 영역에서 양수의 값을 가지고 파란색 영역에서 음수의 값을 가집니다. 즉, \(\theta = (-\pi/2, \pi/2)\) 까지는 양의 부호를 가지므로 벡터 내적의 부호를 이용하면 두 벡터의 방향을 알 수 있습니다.

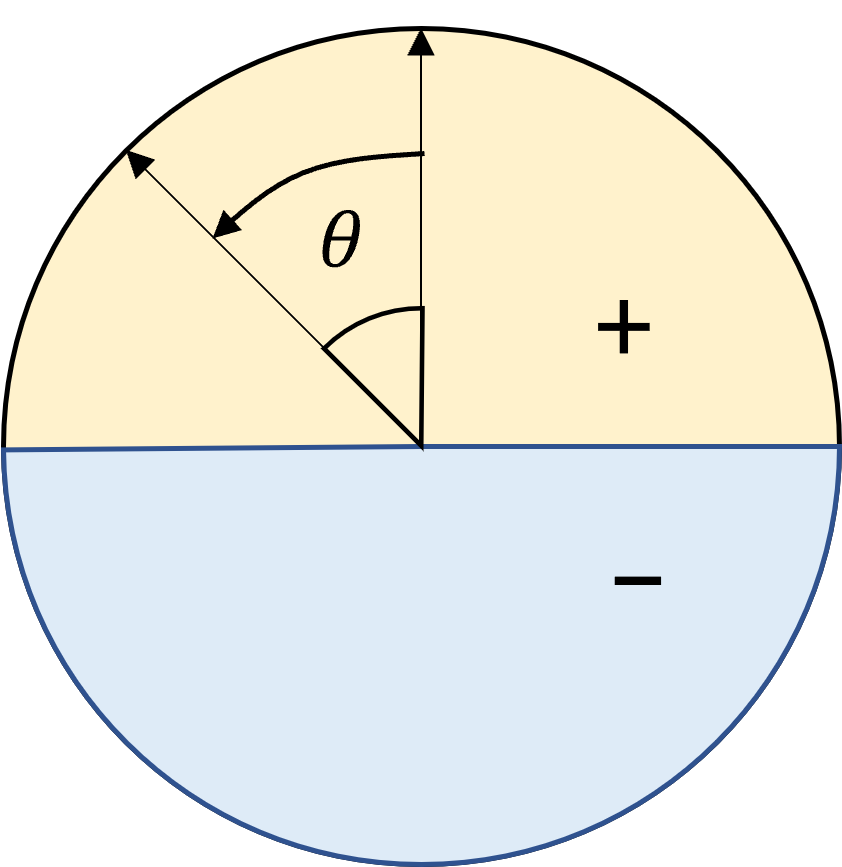
• 위 그림과 같이 벡터 내적의 결과가 양수이면 두 벡터는 같은 방향을 향하고 있습니다. 반면 벡터 내적의 결과가 음수이면 두 벡터는 다른 방향을 향하고 있다고 말할 수 있습니다.
• 이 방향을 카메라의 촬영 방향이라고 하면 벡터의 내적이 양수이면 같은 방향으로 바라보고 있다고 볼 수 있고 벡터의 내적이 음수이면 서로 반대 방향을 본다고 말할 수 있습니다.
• 마지막으로 벡터 내적의 결과가 0이면 두 벡터는 서로 직교합니다.

조명 효과 표현

• 조명 효과를 주기 위하여 빛의 반사를 표현할 때, Lambertian reflection 모델을 사용합니다. 내용은 굉장히 간단합니다.
• 어떤 광원이 물체를 향헤 직사광선을 발사할 때, 빛을 받아 표면에 반사되는 빛의 세기는 두 벡터가 만드는 사잇각의 \(\cos{(\theta)}\) 함수에 비례한다는 것이 Lambertian reflection 모델의 주요 내용입니다.

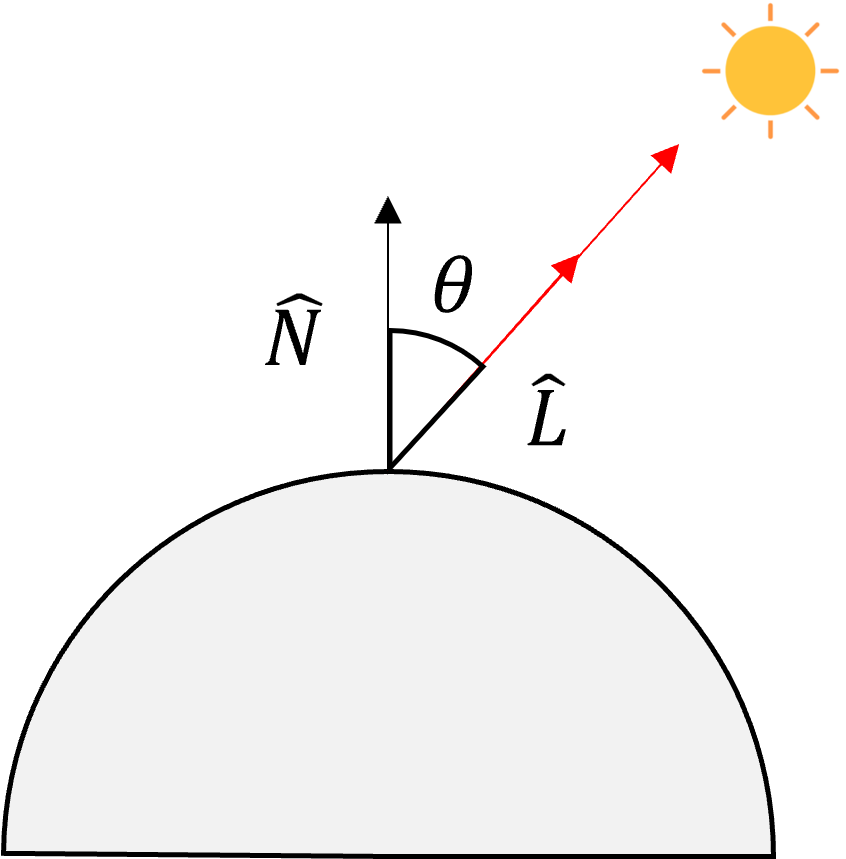
• 위 그림에서 \(\hat{N}\) 은 표면의 법선 벡터의 단위 벡터입니다. 즉, 표면이 향하는 방향의 벡터입니다. \(\hat{L}\) 은 표면에서 광원으로 향하는 벡터의 단위 벡터 입니다.
• 두 벡터가 모두 단위 벡터로 설정되었으므로 두 벡터의 내적으로 사용하면 Lambertian reflection 모델에 필요한 사잇각을 구할 수 있습니다.

• \[\hat{N} \cdot \hat{L} = \cos{(\theta)}\]

선형대수학 글 목차