sparse matrix (희소 행렬)와 CSR(Compressed Sparse Row)

참조 : https://en.wikipedia.org/wiki/Sparse_matrix#:~:text=The%20compressed%20sparse%20row%20(CSR,row%20indices%2C%20hence%20the%20name.
이번 글에서는 sparse matrix의 개념에 대하여 알아보도록 하겠습니다.

sparse matrix 또는 sparse array는 행렬의 대부분의 요소가 0인 행렬입니다. 반대로 대부분의 요소가 0이 아니면 행렬은 dense하다고 표현합니다. 값이 0 인 갯수를 전체 값의 총 수로 나눈 값 (예 : m × n 행렬의 경우 m × n)을 행렬의 희소성 또는 sparsity 라고합니다.

\[\begin{pmatrix} 11 & 22 & 0 & 0 & 0 & 0 & 0 \\ 0 & 33 & 44 & 0 & 0 & 0 & 0 \\ 0 & 0 & 55 & 66 & 77 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 88 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 99 \end{pmatrix}\]

예를 들어 위 sparse matrix의 경우 오직 9개의 값만 0이 아니고 26개는 모두 0입니다. 따라서 sparsity = 76 % 가 되고 density = 24 %가 됩니다.

sparse matrix는 대부분의 행렬의 값이 0이기 때문에 연산 시 필요없는 부분이 상당히 많아집니다. 따라서 행렬 연산에 수많은 0을 연산하는 것은 비효율적인 뿐 아니라 계산에서도 비효율적입니다.
따라서 sparse matrix를 좀 더 효율적으로 관리하기 위한 방법이 필요합니다. sparse matrix를 저장하기 위한 다양한 방법이 존재하는데 그 중 CSR(Compressed Sparse Row) 또는 CRS(Compressed Row Storage) 또는 Yale format으로 불리는 저장 방법에 대하여 다루어 보겠습니다.
이 방법은 3개의 벡터를 이용하여 행렬을 표현합니다. 각 벡터를 Data, Row, Col 이라고 부르겠습니다.

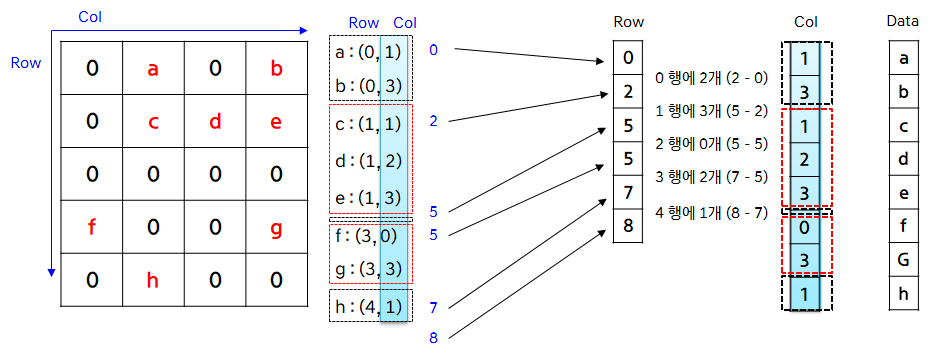
$Drawing$

가장 왼쪽의 행렬인 Sparse matrix를 이용하여 CSR을 만들어 보도록 하겠습니다.
Sparse matrix 에서 0이 아닌 a ~ h의 행과 열의 위치를 먼저 확인한 다음 행이 증가하고 그 다음 열이 증가하는 순서대로 임시 벡터를 만들어 보겠습니다.
먼저 Row를 만들기 위해 바로 전에 Non-zero값의 위치를 차례 대로 저장한 벡터에서 새로운 행이 시작하는 위치의 인덱스를 Row에 저장합니다. 예를 들어 첫번째 행의 시작 인덱스는 0입니다. 그 다음 새로운 행의 시작 위치는 2입니다. 그 다음 새로운 행의 시작 위치는 5입니다. 세번째 행은 모두 0이므로 다시 네번째 행의 시작점이 되고 시작 위치는 다시 5가 됩니다. 마지막 행의 시작 위치는 7이 됩니다. 그리고 마지막에는 벡터의 길이인 8만큼 추가로 입력해 줍니다.
Row를 이용하여 인접한 원소들 끼리 빼면 각 행에 Non-zero 값이 몇 개 인지 알 수 있습니다. 위 그림을 참조하시기 바랍니다.
Col은 앞의 임시 벡터의 열 값을 그대로 사용합니다.
Data 또한 임시 벡터가 작성된 순서대로 Non-zero 값을 그대로 사용합니다.

이와 같은 방법으로 Non-zero 값의 위치를 효율적으로 확인할 수 있습니다. (물론 이 예제에서는 행렬의 크기가 작아서 효과를 볼 순 없었지만…)
CSR 방법을 이용하면 0인 값의 위치는 접근하지 않고 필요한 요소만 연산하는 데 사용할 수 있습니다. CSR을 이용한 희소 행렬의 효율적인 행렬곱 연산 방법등은 현재 많이 연구되고 있고 GPU에 적용되기 위해 특히 많이 연구되고 있습니다.