특이값 분해(SVD)

선형대수학 관련 글 목차

• 참조 : https://darkpgmr.tistory.com/106
• 참조 : https://angeloyeo.github.io/2019/08/01/SVD.html
• 참조 : https://dowhati1.tistory.com/7
• 참조 : https://bskyvision.com/

• 아래 내용은 사전 지식 이므로 가능한 먼저 읽으시길 추천 드립니다.
• 고유값 분해 (EVD, Eigen Value Decomposition) : https://gaussian37.github.io/math-la-evd/

목차

• SVD 간단 정의

• SVD 계산 방법

• SVD 간단 예제

• SVD 의미 해석

• 고유값과 특이값

• SVD 관련 성질

• SVD with Python

• SVD의 활용

• SVD 연산 가속화

SVD 간단 정의

• SVD (Singular Value Decomposition), 특이값 분해는 고유값 분해와 같이 행렬을 대각화하는 방법 중 하나입니다. 고유값 분해는 정방 행렬에만 사용가능하고 정방 행렬 중 일부 행렬에 대해서만 적용 가능한 반면, 특이값 분해는 직사각형 행렬일 때에도 사용 가능하므로 활용도가 높습니다.
• 즉, 고유값 분해에서는 행렬 \(A\) 가 대칭 행렬 & 정사각행렬이면 \(A = PDP^{T} ( P : \text{orthogonal matrix}, D : \text{diagonal matrix} )\) 로 분해할 수 있으나 \(A\) 가 이 조건을 만족하지 못하는 경우에도 \((\text{orthogonal matrix}) \cdot (\text{diagonal matrix}) \cdot (\text{orthogonal matrix})\) 형태로 분해하고자 하는 것이 SVD의 목적입니다.

• m x n 크기의 행렬 \(A\) 를 특이값 분해하면 다음과 같이 분해됩니다.

• \[A = U \Sigma V^{t}\]
• \[A : m \times n \text{ (rectangular matrix)}\]
• \[U : m \times m \text{ (orthogonal matrix)}\]
• \[\Sigma : m \times n \text{ (diagonal matrix)}\]
• \[V : n \times n \text{ (orthogonal matrix)}\]

• 여기서 \(U, V\) 는 각각 서로 다른 직교 행렬이며 특이 벡터로 구성된 행렬입니다. \(\Sigma\) 는 특이값 \(\sigma_{1}, \sigma_{1}, \cdots \sigma_{r}\) 들을 대각요소로 갖고 있는 대각 행렬로서 특이값 행렬이라고 불립니다. \(\sigma_{r}\) 의 \(r\) 은 대각행렬의 rank를 의미합니다.
• 행렬 \(A\) 의 크기가 \(m \times n\) 이고 \(m \ge n\) 이라면 \(r\) 과의 관계는 다음과 같습니다.

• \[m \ge n \ge r\]

• 따라서 \(\Sigma\) 는 \(\text{rank}(A) = r\) 만큼의 대각 성분을 가지고 나머지 대각 성분은 0을 가지는 대각 행렬이 됩니다.

• \[\Sigma = \begin{bmatrix} \sigma_{1} & & & \\ & \sigma_{2} & & \\ & & \ddots & \\ & & & \sigma_{r} \\ & & & & \sigma_{r+1} \\ & & & & &\ddots \\ & & & & && \sigma_{n} \end{bmatrix}\]
• \[\sigma_{r+1}, \cdots \sigma_{n} = 0\]
• 특이값 행렬은 (m x n) 크기의 직사각행렬이므로 m과 n의 크기에 따라 다음과 같은 형태를 가질 수 있습니다.

• 직교 행렬(orthogonal matrix)와 대각 행렬(diagonal matrix)에 대한 성질을 살펴보면 다음과 같습니다. \(U\) 를 직교 행렬이라고 하겠습니다.

• \[UU^{T} = U^{T}U = I\]
• \[U^{-1} = U^{T}\]

• 벡터가 서로 직교한다고 하면 내적이 0이 됩니다. \(u\) 와 \(v\) 벡터가 직교한다면 다음 수식을 만족합니다.

• \[u^{T}v = 0\]

• 만약 \(n\) 차원 공간에서 행 방향과 열 방향에 대하여 서로 직교하는 \(n\) 개의 단위 벡터 (unit vector)를 이용하여 \(n\) 차원의 벡터를 만들면 직교 행렬이 됩니다.

• \[U = (u_{1}, u_{2}, ... , u_{n})\]

• 각 벡터가 단위 벡터이기 때문에 서로 다른 행 또는 열 끼리의 벡터의 내적 연산은 0이고 같은 행 또는 열 끼리의 벡터의 내적 연산은 1이므로 앞에서 언급한 조건이 만족합니다.

• \[UU^{T} = U^{T}U = I\]
• \[U^{-1} = U^{T}\]

• 이와 같이 \(A = U \Sigma V^{t}\) 는 분해되며 직교 행렬이 되는 \(U, V\) 의 성질 또한 살펴보았습니다.
• SVD를 구하는 근본적인 목적은 선형 연립방정식의 해를 찾거나 근사화 해를 찾기 위함입니다.
• 일반적으로 \(Ax = b\) 의 식에서 \(A\) 는 m x n 크기의 행렬이고 \(x, b\) 는 열벡터일 때, 이 식을 만족하는 열벡터 \(x\) 를 찾는 것이 선형 대수학의 근본적인 질문입니다.
• 이와 같은 문제를 풀 때, 크게 3가지 경우의 수가 발생합니다. ① 해가 1개 존재하는 경우, ② 해가 여러개 존재하는 경우, ③ 해가 존재하지 않아 근사화 하는 경우 ( \(\text{min} \Vert Ax - b \Vert\) ) 입니다.
• SVD를 이용하면 3가지 경우의 수에 대하여 모두 동일한 방법으로 접근할 수 있습니다. 따라서 SVD를 통하여 선형 연립방정식의 해를 찾거나 근사화 해를 찾기 위한 일반화 방법을 얻을 수 있습니다.

SVD 계산 방법

• 어떤 행렬 \(A\) 를 특이값 분해를 하면 \(U, \Sigma, V\) 로 분해가 됩니다. 그러면 어떤 방법으로 분해할 수 있을까요? 먼저 간단하게 분해 방법에 대하여 서술해보겠습니다.
• 행렬 \(A\) 의 특이값 (Singular Value)들은 \(AA^{T}\) 또는 \(A^{T}A\) 의 0이 아닌 고유값들에 루트를 적용한 것입니다. 이 때, \(AA^{T}\) 와 \(A^{T}A\) 는 동일한 고유값들을 가집니다. (이러한 이유는 글 아래에 설명을 참조하시면 됩니다.)
• 여기서 \(U\) 는 \(AA^{T}\) 의 고유벡터 행렬이고 \(V\) 는 \(A^{T}A\) 의 고유벡터 행렬입니다. 앞으로는 이 벡터들을 특이 벡터 (Singular vector)라고 하며 \(U\) 의 열벡터를 left singular vectors, \(V\) 의 열벡터를 right singular vectors라고 부르겠습니다. 정리하면 다음과 같습니다.

• \[\text{singular value} = \sqrt{\text{eigen value}}\]
• \[\text{left singular vector} = \text{eigen vector of } AA^{T}\]
• \[\text{right singular vector} = \text{eigen vector of } A^{T}A\]

• 고유값 분해에서 다룬 바와 같이 대칭 행렬 (symmetric matrix)은 항상 고유값 분해가 가능하며 직교 행렬 (orthogonal matrix)로 대각화 할 수 있습니다. \(AA^{T}\) 와 \(A^{T}A\) 는 모두 대칭 행렬이므로 고유값 분해가 가능하여 항상 \(U\) , \(V\) 를 구할 수 있습니다.
• 그리고 \(U\) 와 \(V\) 는 정규 직교 벡터들을 열벡터로 갖는 직교 행렬인데 처음 \(r\) 개의 열벡터는 0이 아닌 고유값들에 해당하는 고유벡터들로 채우면 되고 (고유값과 고유벡터의 짝이 맞아야 합니다.) 나머지는 그것들에 직교인 정규 직교 벡터를 자유롭게 찾아서 채워넣으면 됩니다. (이 부분은 아래 예제를 참조하시면 됩니다.)

• 이와 같은 방법을 사용하면 SVD를 할 수 있습니다. 여기서 \(A^{T}A\) 를 사용하는 이유는 \(A^{T}A\) 가 대칭 행렬이 되기 때문입니다.

• \[(AA^{T})^{T} = (A^{T})^{T}A^{T} = AA^{T}\]

• 대칭 행렬은 고유값 분해가 가능함을 이용하는 것이 SVD의 조건이고 따라서 \(AA^{T}\) 와 \(A^{T}A\) 를 모두 이용합니다.

• 따라서 두개의 정방 행렬 & 대칭 행렬인 \(AA^{T}\) 와 \(A^{T}A\) 를 이용하여 각각 고유값 분해를 하면 다음과 같이 분해할 수 있습니다.

• \[AA^{T} = UDU^{T}\]
• \[A^{T}A = VD'V^{T}\]

• 위 식에서 \(U, V\) 는 고유값 분해로 인하여 각각 직교 행렬이 됩니다. 직교 행렬의 역행렬은 대칭 행렬이 되므로 다음과 같이 식을 전개할 수 있습니다.

• \[AA^{T} = (U \Sigma V^{T}) \times (V \Sigma^{T} U^{T}) = U \Sigma^{2} U^{T} = U D U^{T}\]
• \[A^{T}A = (V \Sigma T^{T}) \times (T \Sigma^{T} B^{T}) = V \Sigma^{2} V^{T} = V D' V^{T}\]
• \[D = D' = \Sigma^{2}\]

• 따라서 \(AA^{T}\) 와 \(A^{T}A\) 의 고유값 분해 결과 대각 행렬 \(\Sigma\) 는 동일한 것을 확인할 수 있습니다.

• 이와 같은 성질을 이용하면 행렬 \(V\) 와 \(\Sigma\) 를 구하면 \(U\) 는 별도 계산하지 않고 구할 수 있습니다. 다음과 같습니다.

• ① \((A^{T}A)\) 의 고유값 \(\lambda_{i}\) 와 \(v_{i}\) 를 구합니다.
• ② 대각 행렬 \(\Sigma\) 를 구성합니다. 대각 행렬의 원소는 \(\sigma_{i} = \sqrt{\lambda_{i}}\) 이고 내림차순 순서로 정렬하여 구성합니다.
• ③ \(u_{i}\) 는 다음 수식을 이용하여 구합니다. 차례대로 전개해 보면 다음과 같습니다. (\(AA^{T}\) 의 고유값 고유벡터를 구하지 않아도 됩니다.)

• \[A = \sigma_{1}u_{1}v_{1}^{T} + \sigma_{2}u_{2}v_{2}^{T} + \cdots + \sigma_{r}u_{r}v_{r}^{T}\]

• 여기서 \(i\) 번째 벡터 하나만 다루어 보겠습니다.

• \[A = \sigma_{i} u_{i} v_{i}^{T}\]
• \[Av_{i} = \sigma_{i} u_{i} v_{i}^{T} v_{i}\]
• \[Av_{i} = \sigma_{i} u_{i}\]
• \[u_{i} = \frac{Av_{i}}{\sigma_{i}}\]

• 위 식의 \(u_{i}\) 를 구하는 방법을 통하여 행렬 \(U\) 를 한번에 구할 수 있습니다. 이 부분도 예제를 살펴보도록 하겠습니다.

• ④ 대각 원소의 순서에 맞게 직교 행렬 \(U, V\) 를 구성합니다.

• 그러면 실제 SVD를 계산하는 예제를 살펴보도록 하겠습니다.

SVD 간단 예제

• 아래 행렬 \(A\)를 특이값 분해 해보도록 하겠습니다. ① 먼저 \(AA^{T}\) 와 \(A^{T}A\) 를 각각 분해하여 \(U, \Sigma, V\) 를 모두 찾아보고 ② 두번째로는 \(A^{T}A\) 를 통하여 \(V\) 를 찾고 그 값을 이용하여 \(U\) 를 찾는 방법을 살펴보겠습니다.

• \[A = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}\]

• 먼저 행렬 \(A\)의 특이값들을 찾기 위해 \(AA^{T}\)와 \(A^{T}A\)의 고유값을 구합니다. 먼저 \(AA^{T}\)의 고유값부터 구해보도록 하겠습니다.

• \[AA^{T} = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix}\]

• 행렬 \(AA^{T}\)의 고유값이 \(\lambda_{1}, \lambda_{2}\)라고 하면 \(AA^{T}\)의 고유값들의 합 \(\lambda_{1} + \lambda_{2}\)은 \(AA^{T}\)의 대각요소들의 합과 같고, 고유값들의 곱 \(\lambda_{1}\lambda_{2}\)은 행렬식의 값과 같으므로 아래와 같습니다.

• \[\lambda_{1} + \lambda_{2} = 4, \lambda_{1}\lambda_{2} = 3\]

• 따라서 \(AA^{T}\) 의 고유값들은 3, 1이 됩니다. 이것들에 루트를 씌운 것이 행렬 \(A\) 의 특이값 (Singular Value)이 됩니다. 따라서 \(\sqrt{3}, 1\)이 특이값이 됩니다. 특이값 행렬 \(\Sigma\)는 특이값들을 대각요소로 갖고 있는 (m x n) 크기의 행렬로 이 문제에서는 (2 x 3) 행렬이 됩니다.

• \[\Sigma = \begin{bmatrix} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}\]

• 특이값 행렬의 고유값의 작성 순서는 큰 값을 기준으로 내림차순 순서로 작성하겠습니다. 이렇게 작성해야 하는 것은 아니나 고유값이 큰 값 순서대로 활용성이 커지기 때문에 이와 같은 방법을 흔히 사용합니다.
• 이번에는 \(A^{T}A\)의 고유값을 구해보도록 하겠습니다. 앞에서 설명한 바와 같이 동일하게 3, 1이 나올 것입니다.

• \[A^{T}A = \begin{bmatrix} 1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 1 \end{bmatrix}\]
• \[\vert A^{T}A - \lambda I \vert = \begin{vmatrix} 1-\lambda & -1 & 0 \\ -1 & 2-\lambda & -1 \\ 0 & -1 & 1-\lambda \end{vmatrix}\]
• \[(1-\lambda)^{2}(2-\lambda)-2(1-\lambda) = 0\]
• \[(1-\lambda)( (1-\lambda)(2-\lambda)-2 ) = 0\]
• \[(1-\lambda)(\lambda^{2} - 3\lambda) = 0\]
• \[\lambda(\lambda-1)(\lambda-3) = 0\]

• 3, 1, 0이 \(A^{T}A\)의 고유값으로 계산됩니다. 이 중에서 0이 아닌 고유값들은 3과 1이므로 \(AA^{T}\)의 고유값들과 동일함을 확인할 수 있습니다. 특이값행렬을 구했으므로 이번에는 특이벡터행렬인 \(U\)와 \(V\)를 구해보도록 하곘습니다.
• 먼저 \(U\)는 \(AA^{T}\)의 고유벡터들을 열로 가진 행렬이므로 \(AA^{T}\)의 고유벡터를 구해야 합니다.

• \[AA^{T}x = \lambda x\]
• \[(AA^{T} - \lambda I)x = 0\]

• 위 식에서 \(\lambda_{1} = 3, \lambda_{2} = 1\) 을 각각 대입하여 고유벡터 \(x_{1}, x_{2}\) 를 구해보도록 하겠습니다. 먼저 \(\lambda_{1} = 3\) 을 대입하여 구하면 다음과 같습니다.

• \[(AA^{T} - \lambda_{1}I)x_{1} = \begin{bmatrix} 2 - 3 & -1 \\ -1 & 2 - 3 \end{bmatrix} x_{1} = \begin{bmatrix} -1 & -1 \\ -1 & -1 \end{bmatrix} x_{1} = 0\]

• 위 조건을 만족시키는 정규직교인 고유벡터를 구하면 다음과 같습니다.

• \[x_{1} = \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 1 \end{bmatrix}\]

• 그리고 앞의 방식과 동일하게 \(AA^{T}\) 의 고유값 \(\lambda_{2} = 1\) 일 때의 고유벡터 \(x_{2}\) 를 찾으면 다음과 같습니다.

• \[(AA^{T} - \lambda_{1}I)x_{2} = \begin{bmatrix} 2 - 1 & -1 \\ -1 & 2 - 1 \end{bmatrix} x_{2} = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} x_{2} = 0\]

• 위 식을 만족시키는 정규직교인 고유벡터를 구하면 다음과 같습니다.

• \[x_{2} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix}\]

• 따라서 왼쪽 특이행렬 \(U\) 는 다음과 같습니다. \(x_{1}, x_{2}\) 의 순서는 고유값에 대응되며 앞에서 고유값이 큰 값을 기준으로 내림차순으로 사용하기로 하였습니다.

• \[U = \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix}\]

• 이와 동일한 방법으로 \(A^{T}A\)의 고유벡터들로 이루어진 오른쪽 특이벡터행렬 \(V\)를 구할 수 있습니다.

• \[x_{1} = \frac{1}{\sqrt{6}} \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}\]
• \[x_{2} = \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix}\]

• 고유값이 0에 해당하는 고유벡터는 다른 고유벡터와 직교인 임의의 정규직교벡터를 사용하면 됩니다. 일반적으로 다음과 같은 정규직교벡터를 사용하면 됩니다.

• \[x_{3} = \frac{1}{\sqrt{3}} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]

• 따라서 오른쪽 특이벡터행렬 \(V\) 는 다음과 같습니다.

• \[V = \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{-1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{-2}{\sqrt{6}} & 0 & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix}\]

• 이와 같이 \(\Sigma, U, V\)를 모두 구했으므로 \(A\)는 아래와 같이 특이값 분해가 됩니다.

• \[\begin{align} A &= \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} = U \Sigma V^{T} \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\ \frac{-1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{bmatrix} \end{align}\]

• 지금까지 \(AA^{T}\) 와 \(A^{T}A\) 를 각각 분해하여 \(U, \Sigma, V\) 를 구해보았습니다.
• 앞에서 아래 식을 통하여 \(A^{T}A\) 의 분해만으로도 \(U\) 를 구할 수 있음을 확인하였습니다.

• \[u_{i} = \frac{Av_{i}}{\sigma_{i}}\]

• 이번에는 위 식을 통하여 \(U\) 를 구할 수 있는 지 확인해 보도록 하겠습니다. \(V\) 와 \(\Sigma\) 는 앞에서 계산한 값을 사용하겠습니다.

• \[A = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}\]
• \[\sigma_{1} = \sqrt{3}\]
• \[v_{1} = \frac{1}{\sqrt{6}} \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}\]
• \[\begin{align} u_{1} &= \frac{Av_{1}}{\sigma_{1}} = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \frac{1}{\sqrt{6}} \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix} \frac{1}{\sqrt{3}} \\ &= \frac{1}{\sqrt{6}}\begin{bmatrix} -3 \\ 3 \end{bmatrix} \frac{1}{\sqrt{3}} \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 1 \end{bmatrix} \end{align}\]

• \[A = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}\]
• \[\sigma_{2} = 1\]
• \[v_{2} = \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix}\]

• \[\begin{align}u_{2} &= \frac{Av_{2}}{\sigma_{2}} = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} 1 \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} \end{align}\]

• 따라서 \(U\) 는 다음과 같이 정리할 수 있습니다.

• \[U = \begin{bmatrix} u_{1} & u_{2} \end{bmatrix} = \begin{bmatrix} -1/\sqrt{2} & 1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{bmatrix}= \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix}\]

• 따라서 \(AA^{T}\) 를 직접 분해하여 \(U\) 를 구한 결과와 동일한 것을 확인할 수 있습니다.

• 앞으로 실제 연산을 할 때에는 \(u_{i} = \frac{Av_{i}}{\sigma_{i}}\) 을 이용한 방식을 사용하겠습니다. 이 방법을 사용하면 연산량을 줄일 수 있고 일관된 방향의 고유 벡터를 구할 수 있기 때문입니다.
• 이 글의 뒷부분의 코드 연산도 이 방법을 사용할 예정입니다.

SVD 의미 해석

• SVD는 임의의 행렬 \(A\) 를 \(A = U \Sigma V^{T}\) 로 분해하는 것을 확인하였습니다. 즉, 분해된 각 성분은 역할이 있는데 그 역할에 대하여 간략하게 살펴보겠습니다.
• 임의의 행렬 \(A\) 는 어떤 벡터 \(x\) 를 \(x'\) 로 변환할 때 사용됩니다. 즉, \(x' = Ax\) 가 되므로 \(A\) 는 선형 변환의 역할로 사용됩니다.
• 행렬 \(A = U \Sigma V^{T}\) 에서 \(U, V\) 는 직교 행렬이고 \(\Sigma\) 는 대각 행렬 입니다. 직교 행렬은 회전 변환의 역할을 하고 대각 행렬은 스케일 변환을 하게 됩니다.
• 따라서 \(x' = Ax = U \Sigma V^{T} x\) 는 벡터 \(x\) 를 \(V^{T}\) 만큼 회전 변환을 한 후 \(\Sigma\) 만큼 스케일 변환을 한 다음에 다시 \(U\) 만큼 회전 변환을 적용하여 \(x \to x'\) 로 변환합니다. 그림으로 나타내면 다음과 같습니다.

• 따라서 SVD를 통해 얻은 특이값은 행렬의 스케일 변환에 사용됨을 알 수 있습니다.
• EVD (고유값 분해)에서는 고유값을 얻을 수 있고 이 고유값은 선형 변환에 의해 변환되지 않는 고유 벡터에 대한 스케일 값인 반면에 SVD에서 얻은 특이값은 선형 변환 자체의 스케일 값인 것을 알 수 있습니다. 즉, 선형 변환 \(A\) 에 의한 기하학적 변환은 특이값들에 의해서만 결정되는 것을 확인할 수 있습니다.

• determinant 관점에서 살펴보아도 의미는 동일하게 해석할 수 있습니다.

• \[A\mathbf{x} = U\Sigma V^{T}\mathbf{x}\]

• 위 식의 행렬 \(U, V\) 는 직교 행렬이고 직교 행렬의 det는 다음과 같습니다.

• \[\text{det}(UU^{T}) = 1\]
• \[\text{det}(VV^{T}) = 1\]

• 위 식을 전개하면 다음과 같습니다. 아래는 \(U\) 에 대해서만 전개하고 \(V\) 도 동일합니다.

• \[\text{det}(UU^{T}) = \text{det}(U)\text{det}(U^{T}) = \text{det}(U)\text{det}(U) = (\text{det}(U))^{2} = 1\]
• \[\therefore \quad \text{det}(U) = \pm 1\]

• 즉, determinant가 1 또는 -1이기 때문에 행렬 \(U, V\) 는 스케일의 변화를 주지 못함을 알 수 있습니다. (unimodular matrix)

• 따라서 스케일 변화는 \(\Sigma\)에 영향을 받습니다.

• SVD를 선형 변환 개념으로 다시 정리해 보면 다음과 같습니다.

• \[A_{mn}x_{n} = b_{m}\]

• 위 수식은 \(n\) 차원의 데이터 \(x\) 를 \(A\) 를 이용하여 선형 변환을 하면 \(m\) 차원의 데이터 \(b\) 가 된다는 것이며 변환 방법은 3가지의 순차적인 방법을 거칩니다.

• ① \(V^{T}_{nn}\) : \(n\) 차원 내에서의 직교 변환 (길이를 바꾸지 않고 방향만 변환함)
• ② \(\Sigma_{mn}\) : \(n \to m\) 차원으로의 변환 (각 차원에서의 길이(스케일) 변환을하며 \(\text{rank}(A) = r\) 차원만큼 실제 의미를 가집니다.)
• ③ \(U_{mm}\) : \(m\) 차원 내에서의 직교 변환

• \[U_{mm} \cdot (\Sigma_{mn} \cdot (V^{T}_{nn} \cdot x_{n})) = b_{m}\]

• SVD의 개념은 2D 이미지 변환의 Affine Transformation에서도 동일하게 사용됩니다.

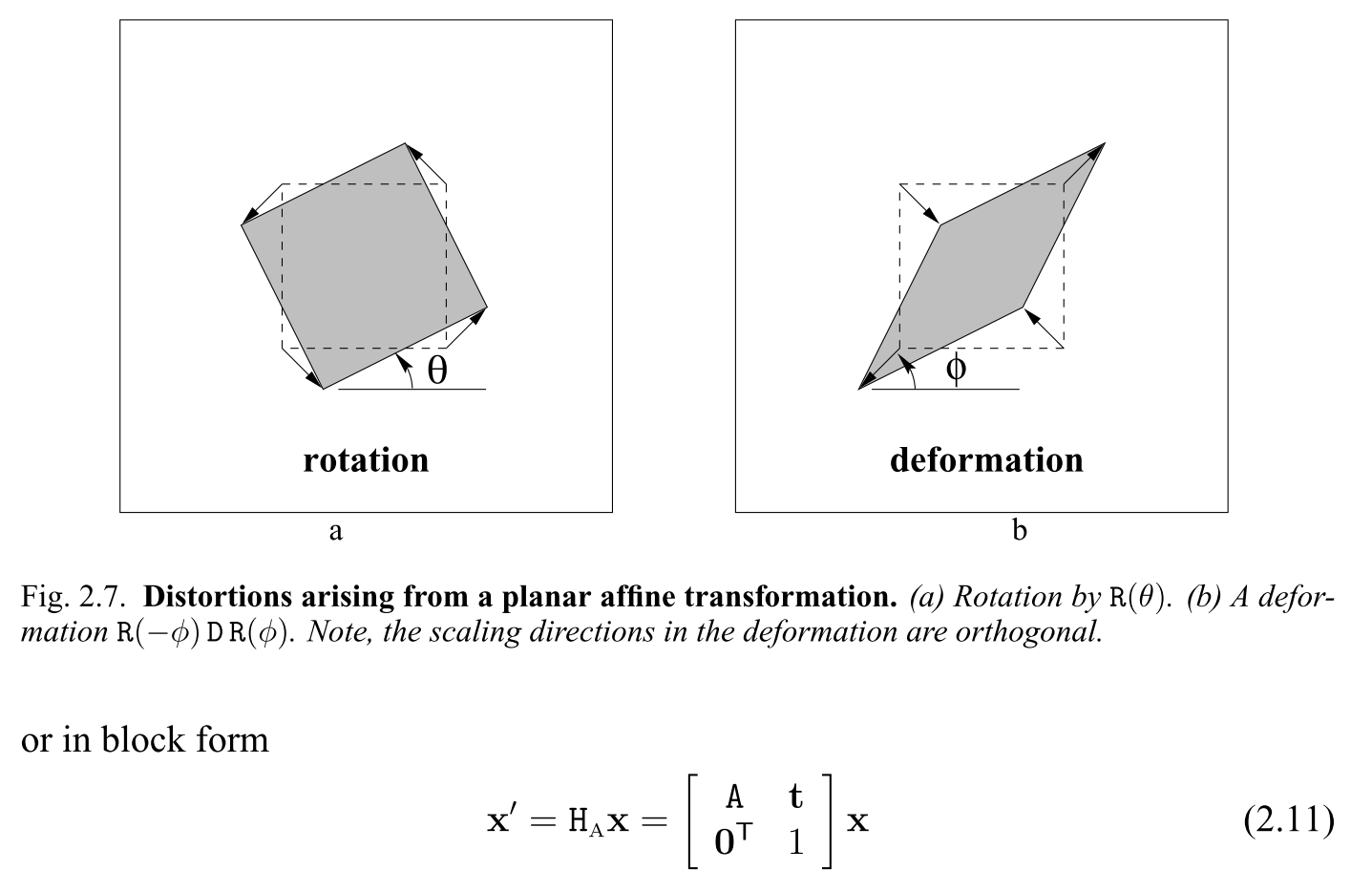
• Affine Transformation은 평행 성분과 면적 및 길이의 비율은 유지한 상태로 선형 변환을 하는 방법 입니다. Affine Transformation에서의 비율을 변환하는 인자가 Singular Value가 됩니다. 즉, \(U\), \(V\) 행렬만으로는 비율이 전혀 변하지 않지만 \(\Sigma\) 로 인하여 비율이 변하는 선형 변환이 발생한다는 것을 알 수 있습니다.

• SVD는 정방 행렬 뿐 아니라 직사각형 행렬에서도 사용할 수 있음을 확인하였습니다. 선형 변환의 관점을 \(m \times n\) 크기의 직사각형 행렬에서도 살펴보겠습니다.
• 만약 \(m \times n\) 크기의 행렬에서 \(m \gt n\) 이라면 \(\Sigma\) 에서 0을 덧붙여서 차원을 확장한 후 \(U\) 로 회전 변환을 하는 것입니다. ( \(Ax = U (\Sigma V^{T} x)\) ) 반면 \(m \lt n\) 이라면 투영을 통해 차원을 없애고 회전 변환을 하는 것입니다.
• 형태적인 변환은 \(\Sigma\) 의 값에 따라 달라지게 되고 차원의 변화는 \(U, V\) 를 따르게 됩니다.

고유값과 특이값

• 지금까지 살펴본 내용을 통해 다시 한번 고유값(eigen value)과 특이값(singular value)를 비교해 보도록 하겠습니다. 두 값 모두 매우 중요한 의미를 가지기 때문에 다시 한번 정리하고자 합니다.

eigen value

• 행렬 \(A \in \mathbb{M}^{n \times n}\) 가 \(n \times n\) 크기의 정사각행렬이고 벡터 \(v \in \mathbb{R}^{n}\) 가 \(n\) 개의 원소를 가진 열벡터라고 가정하겠습니다. 이 때, 고유값, 고유벡터의 정의에 따라 다음과 같이 식을 정의할 수 있습니다.

• \[Av = \lambda v\]

• 위 식에서 고유벡터 \(v\) 에 대응되는 고유값은 \(\lambda\) 가 되어 하나의 쌍을 이루게 됩니다.
• 고유값과 고유벡터는 행렬 \(A\) 가 정사각행렬일 때에만 존재합니다. 만약 행렬 \(A \in \mathbb{M}^{m \times n}\) 가 정사각행렬이 아니라고 가정해 보도록 하겠습니다. 행렬 연산에 따라서 \(v\) 는 \(n\) 개의 원소를 가지는 벡터이어야 합니다. 따라서 \(Av\) 는 \(m \times 1\) 의 크기를 가지는 열벡터의 결과를 얻습니다. 하지만 열벡터 \(v\) 의 크기가 \(n\) 임을 가정하였기 때문에 \(\lambda v\) 는 \(m \times 1\) 의 크기는 반드시 \(m = n\) 인 경우만 만족합니다. 따라서 행렬 \(A\) 가 정사각행렬인 경우에만 고유값, 고유벡터가 존재합니다.

singular value

• singular value는 앞에서 다룬 바와 같이 행렬 \(A^{T}A\) 의 eigen value를 찾는 것에서 시작합니다. \(A^{T}A\) 에서 행렬 \(A \in \mathbb{M}^{m \times n}\) 인 경우에 \(A^{T}A\) 는 항상 \(n \times n\) 크기의 정사각행렬이되며 \(A^{T}A\) 는 항상 symmetric 행렬을 만족합니다.
• 또한 \(A^{T}A\) 는 정사각행렬이기 때문에 항상 eigen value를 가지며 \(A^{T}A\) 는 Positive Semi-Definite Matrix이기 때문에 음수가 아닌 (0 또는 양수) eigen value를 가집니다. 따라서 singular value의 값은 다음과 같습니다.

• \[\sigma_{1} = \sqrt{\lambda_{1}}, \sigma_{2} = \sqrt{\lambda_{2}}, \cdots \sigma_{n} = \sqrt{\lambda_{n}}\]

• 간단히 정리하면 eigen value는 정사각행렬 \(A\) 의 고유값이고 singular value는 \(A^{T}A\) 의 고유값과 연관되어 있습니다. 행렬 \(A^{T}A\) 는 행렬 \(A\) 의 제곱 형태이기 때문에 square root를 적용하면 singular value를 구할 수 있습니다.

condition of eigen value = singular value

• eigen value와 singular value가 연관되어 있기 때문에 특정 조건에서는 두 값이 같아질 수 있습니다. 그 조건은 행렬 \(A\) 가 symmetric matrix ( \(A = A^{T}\) ) 인 경우입니다.

• \[Av = \lambda v\]
• \[A^{T}Av = A^{T}\lambda v = \lambda A^{T} v = \lambda (Av) (\because A=A^{T}) = \lambda^{2} v\]

• 즉, \(A^{T}A\) 의 고유값은 \(\lambda^{2}\) 임을 알 수 있습니다. 따라서 singular value는 \(\sqrt{\lambda^{2}} = \lambda\) 가 됩니다. (Positive Semi-Definite Matrix 조건 이용)

usage of eigen value = singular value

• symmetric matrix에서 eigen value와 singular value가 같아짐을 확인할 수 있었습니다. 대표적인 symmetric matrix는 covariance matrix입니다. 즉, covariance matrix의 eigen value/vector를 이용할 때, singular value를 구하는 방법을 이용할 수 있습니다.
• covariance matrix의 eigen vector는 데이터의 principal direction을 의미하고 대응되는 eigen valuee는 데이터가 얼만큼 퍼져있는 지 (spread) 정도를 나타냅니다. 따라서 eigen value를 통하여 각 eigen vector 방향으로의 variance를 구할 수 있습니다. 따라서 eigen value가 가장 큰 eigen vector가 principal axis(direction)의 의미를 가지게 됩니다. 이와 같은 접근 방식이 PCA (Principal Component Analysis)의 개념입니다.
• 정리하면 symmetric matrix일 때, eigen value와 singular value가 같은 값을 가지고 대표적인 경우가 covariance matrix입니다. 이 때, eigen value/vector가 의미 있게 사용되므로 SVD를 이용하여 이 값들을 구할 수도 있습니다.

SVD 관련 성질

• SVD를 다양한 관점에서 보면 SVD에 관련된 다양한 성질이 있음을 확인할 수 있습니다. SVD에 관한 다양한 성질을 나열해 보도록 하겠습니다. 아래 나열된 순서의 기준은 우선순위와는 무관합니다.

특이값 (고유값)이 모두 0 이상임을 확인

• SVD를 전개할 때 사용하는 \(AA^{T}\) 와 \(A^{T}A\) 의 고유값은 ① 모두 0 이상이며 ② 0이 아닌 고유값들은 서로 동일하다는 것입니다. 특이값이 고유값에 루트를 적용한 것이므로 고유값이 0보다 커야 하고 \(A = U \Sigma V^{T}\) 에서 하나의 행렬 \(\Sigma\) 를 사용하려면\(AA^{T}\) 와 \(A^{T}A\) 의 고유값은 같아야 합니다.
• 먼저 첫번째 조건인 \(AA^{T}\) 와 \(A^{T}A\) 의 고유값은 모두 0 이상임을 확인해 보도록 하겠습니다. 아래와 같이 고유값과 고유벡터의 정의를 이용하여 전개해 보겠습니다.

• \[A^{T}Av = \lambda v ( v \ne 0)\]
• \[v^{T}A^{T}Av = \lambda v^{T}v\]
• \[(Av)^{T}Av = \lambda v^{T}v\]
• \[\Vert Av \Vert^{2} = \lambda \Vert v \Vert^{2}\]

• 위 식에서 좌변과 우변이 제곱으로 모두 양수이어야 하기 때문에 \(\lambda \ge 0\) 이 되어야 합니다.

\(AA^{T}\) 와 \(A^{T}A\) 의 특이값 (고유값이) 동일함 확인

• 두번째 조건인 \(AA^{T}\) 와 \(A^{T}A\) 의 고유값이 서로 동일하다는 것을 확인해 보도록 하겠습니다.

• \[(A^{T}A)v = \lambda v\]
• \[A(A^{T}A)v = \lambda Av\]
• \[AA^{T}(Av) = \lambda (Av)\]

• 위 식에서 \(Av \ne 0\) 을 만족해야 한다면 마지막 식에서 \(AA^{T}\) 의 고유값이 \(\lambda\) 가 되며 첫번째 식에서 \(A^{T}A\) 의 고유값이 \(\lambda\) 임을 전제로 시작하였기 때문에 \(AA^{T}\) 와 \(A^{T}A\) 의 고유값은 \(\lambda\) 로 동일해 집니다.

• 정리하면 \(AA^{T}\) 와 \(A^{T}A\) 의 공통의 고유값은 \(\lambda_{1} \ge \lambda_{2} \ge \cdots \lambda_{r} \ge 0\) (\(\text{rank}(A) = \text{rank}(AA^{T}) = \text{rank}(A^{T}A) = r\)) 이 되고 루트를 적용한 값 \(\sqrt{\lambda_{1}} \ge \sqrt{\lambda_{2}} \ge \cdots \sqrt{\lambda_{r}} \ge 0\) (기호를 바꿔 쓰면) \(\sigma_{1} \ge \sigma_{2} \ge \cdots \sigma_{r} \ge 0\) 이 공통의 특이값이 됩니다.

고유(특이) 벡터 간의 관계

• \[A = U \Sigma V^{T}\]
• \[AV = U\Sigma\]

• 위 식의 \(U, V\) 를 벡터 단위로 나누어서 살펴보겠습니다.

• \[A \begin{bmatrix} v_{1} & v_{2} & \cdots \end{bmatrix} = \begin{bmatrix} u_{1} & u_{2} & \cdots \end{bmatrix} \begin{bmatrix} \sigma_{1} & & & \\ & \sigma_{2} & & \\ & & \ddots & \\ \end{bmatrix} = \begin{bmatrix} \sigma_{1}u_{1} & \sigma_{2}u_{2} & \cdots \end{bmatrix}\]

• 위 식의 각 성분을 일반화하여 표현하면 다음과 같이 적을 수 있습니다.

• \[Av_{i} = \sigma_{i}u_{i}\]

• 이 식에서 \(U, V\) 는 각각 직교행렬이므로 다음과 같은 성질을 얻을 수 있습니다.

• \[Av_{i} = \sigma_{i}u_{i}\]
• \[Av_{j} = \sigma_{j}u_{j}\]
• \[v_{i} \perp v_{j}\]
• \[u_{i} \perp u_{j}\]

• 위 식의 의미를 살펴보면 \(v_{i}, v_{j}\) 는 서로 직교이며 행렬 \(A\) 에 의하여 선형 변환이 되더라도 여전히 서로 직교함을 의미합니다. 선형 변환을 통하여 직교성질은 그대로 유지되며 크기만 \(\sigma_{i}, \sigma_{j}\) 에 의해 조절되었습니다.

Singular Value와 Singular Matrix의 차이점

• 참고로 SVD에서 언급하는 Singular와 특이 행렬 (Singular Matrix)에서의 Singular는 의미가 다릅니다.
• 일반적으로 Singular Matrix는 det(A) = 0 즉, 역행렬이 없는 행렬을 의미합니다.
• SVD에서의 Singular는 앞에서 설명한 Singular Value와 Singular Vector의 의미로 사용된다는 측면에서 차이가 있습니다. Singular Matrix의 의미 즉 역행렬이 없는 행렬과 같이 해석하려면 어떤 경우에 해당할까요?
• Singluar Value 중 0이 포함되면 역행렬이 없는 행렬에 해당합니다. 앞에서 살펴보았듯이 Singular Value가 스케일 변환에 해당하기 때문에 0배 만큼 스케일 변환이 되었다면 행렬 \(A\) 의 det(A) = 0을 만족합니다. 반면 Singular Value 가 모두 0보다 크면 역행렬이 존재하는 Non-Singular Matrix가 됩니다.
• 따라서 0보다 큰 Singular Value의 수는 \(r \le \text{min}(m, n)\) 이 되어야 Non-Singular Matrix가 됩니다.

SVD에서의 rank의 활용

• SVD에서 0이 아닌 고유값의 갯수가 \(\text{rank}(A) = r\) 이면 수식을 다음과 같이 줄여서 사용할 수 있습니다.

• \[A_{mn} = U_{mm} \Sigma_{mn} V^{T}_{nn} = u_{mr} \Sigma_{rr} V^{T}_{rn}\]

• 즉, Null Space 만큼의 값은 필요 없음을 의미하며 완전히 동일한 값을 얻을 수 있습니다.
• 따라서 \(A_{mn}\) 즉, \(m \times n\) 갯수의 모든 값을 \(m \times r + r + r \times n\) 의 갯수만으로 표현할 수 있음을 나타냅니다. 만약 \(r\) 의 크기가 작다면 필요한 값의 갯수가 작아지기 때문에 효율적으로 데이터를 저장할 수 있습니다. 이러한 성질은 데이터 압축 방법으로도 사용됩니다.

• 앞에서 다룬 간단한 예제를 통하여 확인해 보겠습니다. 앞의 2 X 3 크기의 행렬 \(A\) 의 \(\text{rank}(A) = 2\) 이기 때문에 Null Space인 1개의 차원을 제외해도 무관합니다.

• \[\begin{align} A &= \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} = U \Sigma V^{T} \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\ \frac{-1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{bmatrix} \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} \sqrt{3} & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\ \frac{-1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{bmatrix} \\ &= \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \end{align}\]

• 위 예제에서는 기존에 \(m \times n = 2 \times 3 = 6\) 개의 값을 저장해야 했고 특이값 분해와 rank 갯수 만큼 사용하여 값을 저장할 때, \(m \times r + r + r \times n = 2 \times 2 + 2 + 2 \times 3 = 12\) 개의 값을 저장해야 합니다. 이 예제에서는 기존 행렬의 크기가 매우 작기 때문에 효과가 없으나 \(r\) 의 크기가 작아질수록 효과그 크게 나타납니다.

• 이와 같은 접근 방법에서 추가적으로 사용하는 방식이 손실 압축 방식이 있습니다.
• 특이값 행렬을 구성할 때, 특이값을 큰 순서로 내림차순 하였습니다. 특이값이 작다면 그 만큼 스케일 변환에 영향을 주는 정도도 작기 때문에 영향도가 작은 성분끼리 모으기 위함입니다.
• 만약 특이값이 0이 아닌 양의 값이지만 작다고 판단되면 제외할 수 있습니다. 하지만 이 특이값과 이에 대응되는 특이 벡터를 제외하면 실제 정보가 손실되기 때문에 원본 데이터의 손실이 발생합니다. 이와 같은 방식을 손실 압축이라고 하며 뒤의 SVD의 활용에서 자세하게 다루어 보도록 하겠습니다.

SVD의 선형 연립 방정식 적용

• 특이값 분해의 가장 큰 목적 중의 하나는 선형 연립 방정식을 풀기 위함입니다. 즉, \(Ax = b\) 와 같은 식에서 \(x\) 를 찾기 위함입니다.

• 행렬 \(A\) 가 \(U \Sigma V^{T}\) 로 분해된다고 하였을 때, 벡터 \(x\) 를 \(V\) 행렬의 고유벡터 \(v_{i}\) 들을 이용하여 구성해 보도록 하겠습니다.

• \[\mathbf{x} = x_{1}v_{1} + x_{2}v_{2} + \cdots + x_{n}v_{n}\]

• 위 식과 같이 \(x\) 를 두고 \(Ax = b\) 를 전개해보도록 하겠습니다.

• \[Ax = b\]
• \[\begin{align} A\mathbf{x} &= (U \Sigma V^{T})\mathbf{x} = (U \Sigma)(V^{T}\mathbf{x}) \\ &= (U \Sigma)([v_{1}, v_{2}, \cdots , v_{n}]^{T}(x_{1}v_{1} + x_{2}v_{2} + \cdots + x_{n}v_{n})) \\ &= (U \Sigma)([x_{1}, x_{2}, \cdots, x_{n}]^{T}) \quad (\because v_{i}\cdot v_{j} = 0 \ (i \ne j ), v_{i}\cdot v_{j} = 1 \ (i = j )) \\ &= [\sigma_{1}u_{1}, \sigma_{2}u_{2}, \cdots, \sigma_{n}u_{n}] \cdot [x_{1}, x_{2}, \cdots, x_{n}]^{T} \\ &= \sigma_{1}x_{1}u_{1} + \sigma_{2}x_{2}u_{2} + \cdots + \sigma_{n}x_{n}u_{n} \\ &= \sigma_{1}x_{1}u_{1} + \sigma_{2}x_{2}u_{2} + \cdots + \sigma_{r}x_{r}u_{r} \quad (\because \text{rank(A) = r})\\ &= b \end{align}\]

• \[b = \sigma_{1}x_{1}u_{1} + \sigma_{2}x_{2}u_{2} + \cdots + \sigma_{r}x_{r}u_{r}\]

• 만약 \(b\) 를 \(U\) 의 고유벡터 \(u_{i}\) 들로 이루어진 값이라고 가정하면 다음과 같이 쓸 수 있습니다.

• \[b = b_{1}u_{1} + b_{2}u_{2} + \cdots + b_{m}u_{m}\]

• 따라서 관계를 다음과 같이 정의할 수 있습니다.

• \[\begin{align} b = (\sigma_{1}x_{1})u_{1} + (\sigma_{2}x_{2})u_{2} + \cdots + (\sigma_{r}x_{r})u_{r} \\ &= b_{1}u_{1} + b_{2}u_{2} + \cdots + b_{m}u_{m} \end{align}\]
• \[x_{i} = \frac{b_{i}}{\sigma_{i}}, \quad (1 \le i \le r)\]

• 위 식과 같이 SVD를 이용하여 구한 \(b\) 값을 보면 \(r\) 의 크기가 중요한 것을 알 수 있습니다. 또한 위 식의 전개 과정은 \(b\) 가 \(r\) 개의 고유 벡터 조합으로 나타낼 수 있다는 전제하에 전개된 것입니다. 따라서 다음과 같이 3가지 경우의 수를 따릅니다.

• ① \(r = n = m\) 일 때, 1개의 해가 존재합니다.

• ② \(r \lt \text{min}(m, n)\) 이고 \(b\) 가 \(r\) 개의 고유 벡터의 조합으로 나타낼 수 있으면 다양한 해가 존재합니다. ( \(r + 1\) ~ \(n\) 차원 까지의 값은 임의로 대입해서 \(n\) 차원의 해를 만들 수 있기 때문입니다.)

• ③ \(r \lt \text{min}(m, n)\) 이고 \(b\) 가 \(r\) 개의 고유 벡터의 조합으로 나타낼 수 없으면 해를 구할 수 없습니다. 이 경우 Least Squares를 이용하여 \(n\) 차원을 \(r\) 차원에 정사영 (projection)한 근사해를 구할 수 있습니다.

• 위 3가지 방법에 대해서는 아래 SVD의 활용에서 살펴보도로 하겠습니다.

SVD를 이용한 역행렬 구하기

• SVD를 이용하여 \(A = U \Sigma V^{T}\) 로 행렬을 분해할 수 있었습니다. 여기서 \(U, V\) 는 직교 행렬이고 \(\Sigma\) 는 대각 행렬입니다. 이 성질을 이용하면 쉽게 역행렬을 구할 수 있습니다.
• 직교 행렬의 역행렬은 전치 행렬입니다. 그리고 대각 행렬의 역행렬은 대각 성분 역수 적용 & 전치 행렬입니다. 즉 대각 행렬의 크기가 \((m \times n) \to (n \times m)\) 이 됩니다. 따라서 다음과 같이 식을 전개할 수 있습니다.

• \[A^{-1} = (U \Sigma V^{T})^{-1} = (V \Sigma^{-1} U^{T})\]

• 만약 \(A\) 가 \(m \times n\) 크기의 행렬 이었다면 \(A^{-1}\) 은 \(n \times m\) 크기의 행렬이 됩니다.
• 이와 같이 역행렬을 구하면 다른 방식으로 역행렬을 구한 경우와 동일한 값을 얻을 수 있으며 det(A) = 0과 같이 역행렬이 없거나 직사각행렬인 경우에도 역행렬을 구할 수 있는데 이와 같은 역행렬을 pseudo-inverse 라고 합니다. 이와 관련 활용도 SVD의 활용에서 다루어 보도록 하겠습니다.

• 앞에서 사용한 간단 예제를 통하여 pseudo-inverse를 구해보면 다음과 같습니다.

• \[\begin{align} A &= \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} = U \Sigma V^{T} \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\ \frac{-1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{bmatrix} \end{align}\]

• \[\begin{align} A^{-1} &= (U \Sigma V^{T})^{-1} = V \Sigma^{-1}U^{T} \\ &= \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{-1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{-2}{\sqrt{6}} & 0 & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{3}} & 0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} -1 & 1 \\ 1 & 1 \end{bmatrix} \\ &\approx \begin{bmatrix} -0.66666667 & -0.33333333 \\ 0.33333333 & -0.33333333 \\ 0.33333333 & 0.66666667 \end{bmatrix} \end{align}\]

• 위 식과 같이 역행렬 \(A^{-1}\) 을 구할 수 있습니다.

• \[AA^{-1} = \begin{bmatrix} -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} -0.66666667 & -0.33333333 \\ 0.33333333 & -0.33333333 \\ 0.33333333 & 0.66666667 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I\]

• 역행렬이 올바르게 구해졌는 지 확인 하면 위 식과 같이 \(AA^{-1} = I\) 가 나오는 것을 확인할 수 있습니다.

SVD with Python

• 이번 글에서는 \(u_{i} = \frac{Av_{i}}{\sigma_{i}}\) 를 이용 방식으로 코드를 구현하였습니다. 앞에서 설명한 내용과 같이 이 방식을 사용하면 고유값, 고유벡터를 한번만 구해도 되기 때문입니다.

def get_svd(A, num_dims=0, round_digit=0):
    # 고유값, 고유벡터를 구합니다. 
    eigenvalues, eigenvectors = np.linalg.eig(np.dot(A.T, A))
    
    # 특이값을 내림차순으로 정렬합니다.
    idx = eigenvalues.argsort()[::-1]
    singular_values = np.sqrt(eigenvalues)
    singular_values = singular_values[idx]

    # V의 고유벡터를 이용하여 U의 고유 벡터를 구합니다.
    U = np.zeros((A.shape[0], A.shape[0]))
    for i in range(A.shape[0]):
        U[:,i] = np.dot(A, eigenvectors[:,idx[i]]) / singular_values[i]

    V = eigenvectors[:,idx]

    Sigma = np.zeros((U.shape[0], V.shape[0]))
    np.fill_diagonal(Sigma, singular_values)
    
    # 표기의 간략화를 위하여 반올림 합니다.
    if round_digit > 0:
        U = np.round(U, round_digit)
        Sigma = np.round(Sigma, round_digit)
        V = np.round(V, round_digit)
    
    # 차원 축소를 하기 위하여 영향도가 큰 num_dims 만큼의 차원만 유지하고
    # 나머지 차원은 제거합니다.
    if num_dims > 0:
        U = U[:, :num_dims]
        Sigma = Sigma[:num_dims, :num_dims]
        V = V[:, :num_dims]

    return U, Sigma, V

def get_svd_composition(U, Sigma, V):
    return np.matmul(U, np.matmul(Sigma, V.T))

• 위 코드에서 get_svd(A) 함수를 통하여 A를 U, Sigma, V로 분해합니다. num_dims를 0보다 큰 값을 입력하면 특이값이 큰 순서대로 num_dims의 차원 만큼만 남기고 나머지는 제거하여 차원을 축소합니다.
• 위 코드에서 get_svd_composition(U, Sigma, V) 함수를 통하여 행렬 A를 복원할 수 있습니다.

import numpy as np

A = np.array([
    [-1, 1, 0],
    [0, -1, 1]
])

U, Sigma, V = get_svd(A)

print("Sigma:\n", Sigma, "\n")
# Sigma:
#  [[1.73205081 0.         0.        ]
#  [0.         1.         0.        ]]

print("Left Singular Vectors:\n", U, "\n")
# U : Left Singular Vectors:
#  [[ 0.70710678  0.70710678]
#  [-0.70710678  0.70710678]] 

print("Right Singular Vectors:\n", V, "\n")
# V : Right Singular Vectors:
#  [[-0.40824829 -0.70710678  0.57735027]
#  [ 0.81649658  0.          0.57735027]
#  [-0.40824829  0.70710678  0.57735027]] 

print("Composition:\n", get_svd_composition(U, Sigma, V), "\n")
# Composition:
#  [[-1.  1. -0.]
#  [-0. -1.  1.]] 

• 앞에서 수식으로 전개한 내용과 일부 다른 점이 있을 수 있습니다. 고유 벡터의 부호가 다를 수 있는데 이 점은 고유 벡터의 방향이 다르게 표현한 것일 뿐 무시하셔도 됩니다. (절대값이 다르지 않습니다.)

• 한가지 예시를 더 살펴보겠습니다.

import numpy as np

A = np.array([
    [1, 2, 3], 
    [4, 5, 6], 
    [7, 8, 9]
])

U, Sigma, V = get_svd(A)

print("Sigma:\n", Sigma, "\n")
# Sigma:
#  [[16.84810335  0.          0.        ]
#  [ 0.          1.06836951  0.        ]
#  [ 0.          0.          0.00000009]]

print("U : Left Singular Vectors:\n", U, "\n")
# U : Left Singular Vectors:
#  [[-0.21483724  0.88723069  0.00000015]
#  [-0.52058739  0.24964395  0.00000005]
#  [-0.82633754 -0.38794278 -0.00000007]] 

print("V : Right Singular Vectors:\n", V, "\n")
# V : Right Singular Vectors:
#  [[-0.47967118 -0.77669099  0.40824829]
#  [-0.57236779 -0.07568647 -0.81649658]
#  [-0.66506441  0.62531805  0.40824829]] 

print("Composition:\n", get_svd_composition(U, Sigma, V), "\n")
# Composition:
#  [[1. 2. 3.]
#  [4. 5. 6.]
#  [7. 8. 9.]] 

• Python의 Numpy에서 제공하는 np.linalg.svd를 이용하면 SVD를 쉽게 구할 수 있습니다. 앞에서 구현한 내용과 비교하여 살펴보겠습니다.

A = np.array([
    [-1, 1, 0],
    [0, -1, 1]
])

# U, Sigma, V
get_svd(A)
# (array([[ 0.70710678,  0.70710678],
#         [-0.70710678,  0.70710678]]),
#  array([[1.73205081, 0.        , 0.        ],
#         [0.        , 1.        , 0.        ]]),
#  array([[-0.40824829, -0.70710678,  0.57735027],
#         [ 0.81649658,  0.        ,  0.57735027],
#         [-0.40824829,  0.70710678,  0.57735027]]))

# U, Sigma, V_T
np.linalg.svd(A)
# (array([[-0.70710678,  0.70710678],
#         [ 0.70710678,  0.70710678]]),
#  array([1.73205081, 1.        ]),
#  array([[ 0.40824829, -0.81649658,  0.40824829],
#         [-0.70710678, -0.        ,  0.70710678],
#         [ 0.57735027,  0.57735027,  0.57735027]]))

• np.linalg.svd()의 Sigma는 대각 성분의 벡터값을 의미하고 V는 Transposed가 적용된 V.T가 반환됩니다.

SVD의 활용

• ① SVD를 이용하면 손실 압축을 할 수 있습니다. SVD를 이용하여 어떻게 이미지 압축을 하는 지 살펴보도록 하겠습니다.
• ② SVD를 이용하면 의사역행렬(Pseudo-Inverse)을 구할 수 있습니다. 역행렬이 없는 경우나 직사각 행렬과 같이 역행렬이 존재하지 않는 경우에도 역행렬을 만들 수 있도록 고안된 방법이므로 이 방법에 대하여 살펴보도록 하겠습니다.
• ③ SVD를 이용하여 선형 연립 방정식을 풀어보도록 하겠습니다. 의사역행렬을 이용하여 선형 연립 방정식을 풀거나 해가 없을 경우 근사해를 구할 수 있습니다.

• ① SVD를 이용하면 손실 압축을 할 수 있습니다.

• 아래 샘플 이미지를 살펴 보겠습니다. 아래 링크에서 샘플 이미지를 다운 받을 수 이씃ㅂ니다.
  • 링크 : https://drive.google.com/file/d/1scpXrkqZhUhmul7VTzZ43_rdFRxjFqar/view?usp=share_link

• 편의상 위 영상을 grayscale로 읽어서 채널 1의 이미지로 만든 다음 손실 압축을 해보도록 하겠습니다.
• 위 이미지의 해상도는 (768, 1024) 입니다.

import cv2
image = cv2.imread("image.jpg", cv2.IMREAD_GRAYSCALE)
print(image.shape)
# (768, 1024)

fig = plt.figure(figsize=(10, 13))
plt.imshow(image, cmap='gray')

• 아래 그림이 원본이며 저장하는 데 \(768 \times 1024 = 0.78\text{MB}\) 가 필요합니다.

image_float = image.astype(np.float32)
U, Sigma, V = get_svd(image_float, num_dims=0)
image_composition = get_svd_composition(U, Sigma, V)

fig = plt.figure(figsize=(10, 13))
plt.imshow(image_composition, cmap='gray')

• 위 코드와 같이 특이값 분해한 결과를 다시 합성하여 이미지로 나타낼 수 있습니다.

• 위 특이값 분해에서 실제 필요한 값은 \(768 \times 768 + 768 + 1024 \times 1024 = 1.6\text{MB}\) 입니다. 원본을 그대로 복원하며 이 경우에는 오히려 저장해야 할 값이 더 늘어났습니다.
• 이제 차원 축소를 통한 손실 압축을 해보도록 하겠습니다.

U, Sigma, V = get_svd(image_float, num_dims=100)
image_composition_100 = get_svd_composition(U, Sigma, V)

fig = plt.figure(figsize=(10, 13))
plt.imshow(image_composition_100, cmap='gray')

• 위 코드에서는 특이값을 100개만 사용하여 표현하였습니다. 이미지의 나뭇가지와 같은 디테일한 부분이 흐릿해진 것을 확인할 수 있습니다.
• 위 특이값 분해에서 실제 필요한 값은 \(768 \times 100 + 100 + 100 \times 1024 = 0.17\text{MB}\) 입니다. 원본에 비하여 1/4 이상으로 압축되었습니다.

U, Sigma, V = get_svd(image_float, num_dims=50)
image_composition_50 = get_svd_composition(U, Sigma, V)

fig = plt.figure(figsize=(10, 13))
plt.imshow(image_composition_50, cmap='gray')

• 위 코드에서는 특이값을 50개만 사용하여 표현하였습니다. 정보가 더 많이 손실 되었습니다.
• 위 특이값 분해에서 실제 필요한 값은 \(768 \times 50 + 50 + 50 \times 1024 = 0.08\text{MB}\) 입니다. 원본에 비하여 1/10 이상으로 압축되었습니다.

U, Sigma, V = get_svd(image_float, num_dims=10)
image_composition_10 = get_svd_composition(U, Sigma, V)

fig = plt.figure(figsize=(10, 13))
plt.imshow(image_composition_10, cmap='gray')

• 위 코드에서는 특이값을 10개만 사용하여 표현하였습니다. 이제 많이 흐려졌습니다.
• 위 특이값 분해에서 실제 필요한 값은 \(768 \times 10 + 10 + 10 \times 1024 = 0.017\text{MB}\) 입니다. 원본에 비하여 1/40 이상으로 압축되었습니다.

• 이와 같은 방식으로 정보의 손실 압축을 할 수 있습니다. 실제로 SVD 성질과 Discrete Cosine Transform을 이용하여 이미지를 압축하는 방식이 JPEG에 사용되는 방식입니다.

• 만약 RGB 이미지 전체에 대하여 SVD를 적용하고 싶으면 채널 방향으로 SVD를 적용하면 됩니다. 아래 코드를 참조하시면 됩니다.

def svd_compressor(image, order):
    """Returns the compressed image channel at the specified order"""
    
    # Create an array filled with zeros having the shape of the image
    compressed = np.zeros(image.shape)
    
    # Get the U, S and V terms (S = SIGMA)
    U, S, V = np.linalg.svd(image)
    
    # Loop over U columns (Ui), S diagonal terms (Si) and V rows (Vi) until the chosen order
    for i in range(order):
        Ui = U[:, i].reshape(-1, 1)
        Vi = V[i, :].reshape(1, -1)
        Si = S[i]
        compressed += (Ui * Si * Vi)
    
    return compressed

• 위 코드를 사용하며 RGB 이미지에 대하여 order를 변경하며 손실 압축의 정도를 살펴보도록 하겠습니다.

image = cv2.cvtColor(cv2.imread("image.jpg"), cv2.COLOR_BGR2RGB)
plt.figure(figsize=(20, 4))
orders = [1, 5, 10, 20, 50, 100, 200, 400, 600]
for i in range(len(orders)):
    
    # Use the compressor function
    order = orders[i]
    red_comp = svd_compressor(red_image, order)
    green_comp = svd_compressor(green_image, order)
    blue_comp = svd_compressor(blue_image, order)
    
    # Combine images
    color_comp = np.zeros((np.array(image).shape[0], np.array(image).shape[1], 3))
    color_comp[:, :, 0] = red_comp
    color_comp[:, :, 1] = green_comp
    color_comp[:, :, 2] = blue_comp
    color_comp = np.around(color_comp).astype(int)
    
    # Display the compressed colored image in the subplot
    plt.subplot(2, 5, i + 1)
    plt.title("Order = {}".format(order))
    plt.axis('off')
    plt.imshow(color_comp)

plt.suptitle('Compression at different orders')
plt.show()

② SVD를 이용하면 의사역행렬(Pseudo-Inverse)을 구할 수 있습니다.

• 앞에서 SVD를 이용하여 의사역행렬을 다음 식과 같이 구할 수 있음을 확인하였습니다.

• \[A^{-1} = (U \Sigma V^{T})^{-1} = (V \Sigma^{-1} U^{T})\]

• 이번에는 파이썬 코드를 이용하여 의사역행렬을 구해보도록 하겠습니다.

def get_inv(A):
    U, Sigma, V = get_svd(A)
    for idx, singular_value in enumerate(np.diag(Sigma)):
        Sigma[idx, idx] = 1/singular_value if singular_value > 1e-6 else 0        
    return np.matmul(V, np.matmul(Sigma.T, U.T))    

• 위 코드에서는 너무 작은 특이값에 의해 전에 값에 왜곡이 생기지 않도록 하기 위한 예외 처리가 추가되었습니다.

• 먼저 앞에서 살펴본 예제에 대한 의사역행렬을 구해보도록 하겠습니다.

A = np.array([
    [-1, 1, 0],
    [0, -1, 1]
])

print(get_inv(A))
# [[-0.66666667, -0.33333333],
# [ 0.33333333, -0.33333333],
# [ 0.33333333,  0.66666667]]

print(np.matmul(A, get_inv(A)))
# [[ 1., -0.],
#  [-0.,  1.]]

• numpy의 라이브러리에도 의사역행렬 함수가 있습니다. 이 값을 이용해 보면 값이 같은 것을 확인할 수 있습니다.

B = np.array([
    [1, 3, 5],
    [2, 4, 6], 
    [3, 7, 3]
])

print(get_inv(B))
# [[-1.875  1.625 -0.125]
#  [ 0.75  -0.75   0.25 ]
#  [ 0.125  0.125 -0.125]]

print(np.linalg.pinv(B))
# [[-1.875  1.625 -0.125]
#  [ 0.75  -0.75   0.25 ]
#  [ 0.125  0.125 -0.125]]

print(np.matmul(B, get_inv(B)))
# [[ 1. -0.  0.]
#  [-0.  1. -0.]
#  [ 0. -0.  1.]]

③ SVD를 이용하여 선형 연립 방정식을 풀어보도록 하겠습니다.

• 선형대수학에서 가장 중요한 문제 중 하나는 \(Ax = b\) 라는 선형 연립 방정식을 풀어내는 것입니다. 선형 연립 방정식을 풀 때 아래와 같은 4가지 경우가 발생합니다.

• 1 : \(Ax = b (b \ne 0)\)
  • 1.a : \(Ax = b (b \ne 0), \text{A is invertible}\)
  • 1.b : \(Ax = b (b \ne 0), \text{A is not invertible}\)

• 2 : \(Ax = 0\)
  • 2.a : \(Ax = 0 (\text{A is invertible})\)
  • 2.b : \(Ax = 0 (\text{A is not invertible}, x \ne 0 )\)

• 먼저 문제가 생기지 않는 부분은 역행렬이 존재하는 케이스 입니다. 즉, 1.a와 2.a 모두 역행렬이 존재하므로 모두 \(A\) 의 역행렬을 곱해주면 1.a의 경우 \(x = A^{-1}b\) 가 되고 2.a의 경우 \(x = 0\) 이 됩니다. 역행렬이 존재하려면 정사각행렬이기 때문에 이번 글에서 다룬 SVD가 꼭 필요하진 않습니다.
• 반면에 1.b와 2.b의 경우에는 역행렬이 없기 때문에 본 글에서 설명하는 SVD를 이용하여 풀 수 있습니다.

\(Ax = b (b \ne 0), \text{A is invertible}\)

• 앞에서 배운 pseudo-inverse를 이용하면 \(x = A^{-1}b\) 로 변환할 수 있습니다.
• 컴퓨터 비전에서 다루는 많은 문제들은 \(A\) 행렬의 크기가 \((m, n)\) 일 때, \(m\) 의 크기가 큰 경우가 많습니다. 왜냐하면 행 ( \(m\) ) 방향으로 식을 늘려서 쌓고 열 ( \(n\) ) 방향으로는 변수를 쌓기 때문입니다. 추정하고자 하는 변수보다 추정하는데 사용되는 식들이 많은 것이 일반적입니다.
• 따라서 행렬 \(A\) 는 보통 정사각행렬이 아닌 행의 크기가 더 큰 직사각행렬이므로 pseudo-inverse를 통해서 \(Ax = b\) 의 해를 구할 수 있습니다. 과정은 다음과 같습니다.

• \[A^{-1} = (U \Sigma V^{T})^{-1} = (V \Sigma^{-1} U^{T})\]
• \[x = A^{-1}b = (V \Sigma^{-1} U^{T}) b\]

\(Ax = 0 (\text{A is not invertible}, x \ne 0 )\)

• 이와 같은 형태에서는 \(A\) 를 pseudo-inverse를 적용하면 \(x = 0\) 이 되기 때문에 원하는 해를 구할 수 없습니다.
• 따라서 새로운 방법을 사용하여 \(Ax = 0\) 을 만족하는 \(x\) 를 구하거나 만족하는 해가 없다면 우변이 0이 아니지만 0에 가까운 \(Ax = \delta\) 가 될 수 있도록 만든 다음에 만족하는 \(x\) 를 구하도록 해야 합니다. 이 경우에도 svd를 사용할 수 있습니다.

• 방법은 \(A = U \Sigma V^{T}\) 에서 가장 작은 Singular Value에 대응되는 Right Singular Vector를 선택하는 것입니다. 예를 들어 가장 작은 Singular Value가 \(n\) 번째 값인 \(\sigma_{n}\) 이라면 행렬 \(V\) 의 \(n\) 번째 열벡터인 \(v_{n}\) 가 선택되고 문제는 다음과 같이 변형 됩니다.
• 아래 \(v_{n}\) 과 \(u_{m}\) 은 가장 작은 Singular Value와 대응되는 열벡터입니다.

• \[Ax = 0 \to Av_{n} = \sigma_{n}u_{m}\]

• 만약 Singular Value 중 가장 작은 값이 0이 된다면 \(Ax = \sigma_{n}u_{m} = 0 \cdot u_{m} = 0\) 이 유지가 되며 이 식을 만족시키는 \(x = v_{n}\) 또한 Right Singular Vector에서 찾을 수 있습니다.
• Singular Value 중 가장 작은 값이 0인데 0인 값이 여러개가 있다면 그 중 하나를 사용하여도 모두 \(Ax = 0\) 을 만족하므로 상관없습니다.
• 이와 같이 Right Singular Vector에서 해를 찾는 이유는 다음과 같습니다.

• \[Ax = 0\]
• \[Av_{n} = U \Sigma V^{T} v_{n} = U \Sigma (V^{T} v_{n})\]

• 위 식에서 \(A\) 는 (m, n) 의 크기를 가지는 행렬입니다. \((V^{T} v_{n})\) 는 \(n\) 번째 값만 1이고 나머지는 모두 0인 열벡터가 됩니다. 왜냐하면 \(V\) 는 정규 직교 행렬이기 때문에 \(v_{n}\) 와 \(v_{i} (n \ne i )\) 와의 inner product 연산은 0이고 \(v_{n}\) 와 \(v_{n}\) 의 연산은 1이 됩니다.
• 아래 식의 \(0_{(1)}\) 이나 \(1_{(n)}\) 의 아래첨자는 이해를 돕기 위해 행의 순서를 나타내었습니다.

• \[\begin{align} Av_{n} &= U \Sigma \begin{bmatrix} 0_{(1)} \\ 0_{(2)} \\ \vdots \\ 0_{(n-1)} \\ 1_{(n)} \end{bmatrix} \\ &= U \begin{bmatrix} \sigma_{1} & & & \\ & \sigma_{2} & & \\ & & \ddots & \\ & & & \sigma_{r} \\ & & & & \sigma_{r+1} \\ & & & & &\ddots \\ & & & & && \sigma_{n} \end{bmatrix} \begin{bmatrix} 0_{(1)} \\ 0_{(2)} \\ \vdots \\ 0_{(n-1)} \\ 1_{(n)} \end{bmatrix} \\ &= U \begin{bmatrix} 0_{(1)} \\ 0_{(2)} \\ \vdots \\ 0_{(m-1)} \\ \sigma_{n} \end{bmatrix} \\ &= \begin{bmatrix} u_{1} & u_{2} & \cdots & u_{m-1} & u_{m} \end{bmatrix} \begin{bmatrix} 0_{(1)} \\ 0_{(2)} \\ \vdots \\ 0_{(m-1)} \\ \sigma_{n} \end{bmatrix} = \sigma_{n}u_{m} \end{align}\]

• \[\therefore Av_{n} = \sigma_{n}u_{m}\]

• 앞에서 언급한 바와 같이 \(\sigma_{n}\) 즉, 가장 작은 Singular Value가 0이라면 다음과 같이 식이 정리됩니다.

• \[Av_{n} = \sigma_{n}u_{m} = 0 \cdot u_{m} = 0\]

• 따라서 \(Av_{n} = 0\) 이 되어 \(v_{n}\) 이 해가 됩니다.
• 위의 식과 같이 \(\sigma_{n} \ne 0\) 이면 문제는 다음과 같이 바뀌게 되며 만족하는 해는 \(v_{n}\) 이 됩니다.

• \[Ax = 0 \to Av_{n} = \sigma_{n}u_{m}\]

• 추가적으로 위 식에서 양변에 norm을 적용하면 \(u_{m}\) 의 경우 정규 직교 행렬의 열벡터이므로 norm은 1이 되고 다음과 같이 정리 됩니다.

• \[\Vert Av_{n} \Vert = \Vert \sigma_{n}u_{m} \Vert = \sigma_{n}\]

• 위 내용을 간략하게 파이썬으로 실습해보면 다음과 같습니다.

A = np.array([[1, 2, 4], [2, 6, 1], [3, 2, 4]])
# [[1 2 4]
#  [2 6 1]
#  [3 2 4]]

U, Sigma, V_T = np.linalg.svd(A)

print(U)
# [[ 0.48070787  0.44038034  0.75827772]
#  [ 0.66025596 -0.75083694  0.01749173]
#  [ 0.57704594  0.49224897 -0.65169697]]

print(Sigma)
# [8.56344207 4.00242988 1.28375037]

print(V_T)
# [[ 0.41249273  0.70964962  0.57118051]
#  [ 0.10380029 -0.6595401   0.74446783]
#  [-0.90502776  0.24779887  0.34571733]]

x = V_T.T[:, -1]
# [-0.90502776  0.24779887  0.34571733]


###### A@x와 Sigma[-1] * U[:, -1] 가 같으므로 위 수식 설명과 같이 전개되었습니다.#####
print(A@x)
# [ 0.9734393   0.02245501 -0.83661622]

print(Sigma[-1] * U[:, -1])
# [ 0.9734393   0.02245501 -0.83661622]



##### norm(A@x) 과 Sigma[-1] 가 같은 것을 확인할 수 있습니다. #####
print(np.linalg.norm(A @ x))
# 1.2837503655387381
print(Sigma[-1])
# 1.2837503655387383

SVD 연산 가속화

• 큰 크기의 행렬을 여러개 처리한다면 SVD 연산도 꽤 큰 연산 시간을 필요로 합니다.
• 행렬 연산과 같은 경우 cupy를 이용하여 cuda 연산을 사용하면 연산 시간을 줄일 수 있습니다. cupy 관련 내용은 아래 글을 참조해 주시기 바랍니다.
  • cupy 설치 및 사용 방법

• numpy와 cupy의 문법은 완전 동일하므로 아래 예제 코드를 통하여 실행 결과를 살펴보도록 하겠습니다.

import numpy as np
import cupy as cp
import time

start_time = time.time()
for _ in range(20):    
    A = np.random.randint(0, 255, (300, 500, 3)).astype(np.float32)
    U, Sigma, V = np.linalg.svd(A)
print(time.time() - start_time)
# 13.495264768600464

start_time = time.time()
A = np.random.randint(0, 255, (300, 500, 3*20)).astype(np.float32)
U, Sigma, V = np.linalg.svd(A)
print(time.time() - start_time)
# 10.183464288711548

start_time = time.time()
for _ in range(20):    
    A = cp.random.randint(0, 255, (300, 500, 3)).astype(cp.float32)
    U, Sigma, V = cp.linalg.svd(A)
print(time.time() - start_time)
# 4.324589967727661

start_time = time.time()
A = cp.random.randint(0, 255, (300, 500, 3*20)).astype(cp.float32)
U, Sigma, V = cp.linalg.svd(A)
print(time.time() - start_time)
# 3.8288321495056152

• 같은 행렬 연산을 cuda를 이용하면 시간을 절약할 수 있으므로 cupy 사용을 권장합니다.

선형대수학 관련 글 목차