Intro to Optimisation (newton-raphson method, gradient descent, lagrange multipliers)

mathematics for machine learning 글 목록

이번 글에서는 최적화(Optimisation) 하는 방법에 대하여 다루어 보려고 합니다. 이 글에서 다루는 최적화 방법은 최적화의 기본이 되는 간단한 방법들입니다.

newton-raphson method

지금 부터 살펴볼 newton-raphson method는 derivative를 이용하여 방정식을 풀어 보는 방법입니다.

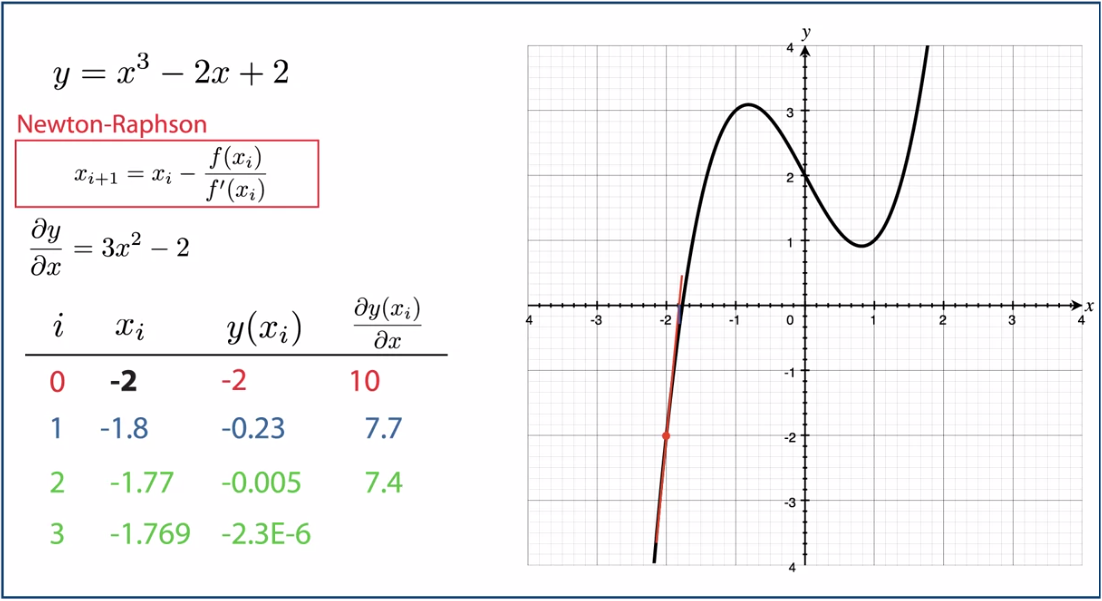
$Drawing$

newton-raphson method는 위 그림과 같이 반복적인 탐색을 통하여 방정식의 해를 찾는 방법입니다. 이 때 사용하는 점화식은 다음과 같습니다.

\[x_{i+1} = x_{i} - \frac{f(x_{i})}{f'(x_{i})}\]

위 식에 대한 유도는 newton-raphson method의 마지막 부분에서 테일러 급수를 이용하여 유도해 보도록 하겠습니다.
임의의 $x_{0}$에서 시작하여 위 점화식을 풀어갈 때, $x_{i}$가 수렴하게 되면 그 해는 $f(x_{i}) = 0$ 을 만족하게됩니다.
위 식에서 업데이트 되는 $- f(x_{i}) / f'(x_{i})$ 를 살펴보면 분자의 $f(x_{i})$는 함수 값으로 $x_{i}$가 실제 해에 가까워질 수록 $f(x_{i})$는 0에 수렴하게 됩니다. 따라서 분모인 $f'(x_{i})$ 값 크기를 조정해줍니다.
또한 $f'(x_{i})$도 업데이트 할 크기와 방향에 영향을 줍니다. $x_{i}$ 지점에서 함수값이 증가하면 기울기가 양수이고 감소하면 기울기가 음수이기 때문에 업데이트 할 방향에 영향을 주고 기울기 값에 따라서 업데이트 할 크기에도 영향을 줍니다.
위 예제에서는 -2를 $x$의 초깃값으로 시작해서 -1.769 근처에서 수렴시킵니다.
위 과정을 볼 때 newton-raphson method의 핵심은 초깃값을 어디서 부터 시작하는 지에 따라서 수렴 성능에 영향을 미칩니다.

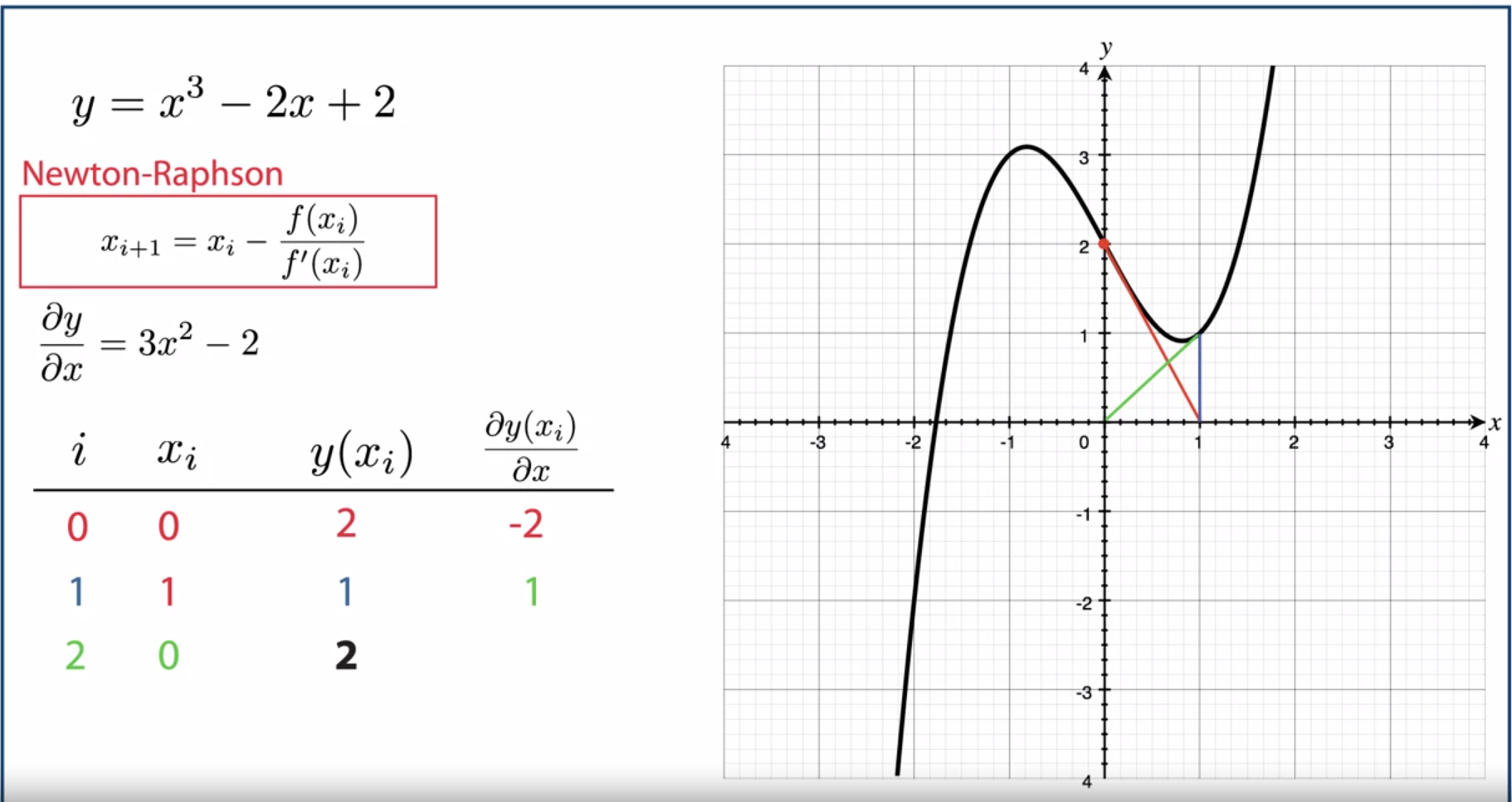
$Drawing$

위 예제에서는 $x_{0} = 0$으로 설정하였습니다. 이 경우에는 newton-raphson method가 수렴하지 않고 진동하게 됩니다. 업데이트 되는 부분이 해를 찾아갈 정도로 $x_{i}$의 값을 업데이트 해주지 못하기 때문입니다.

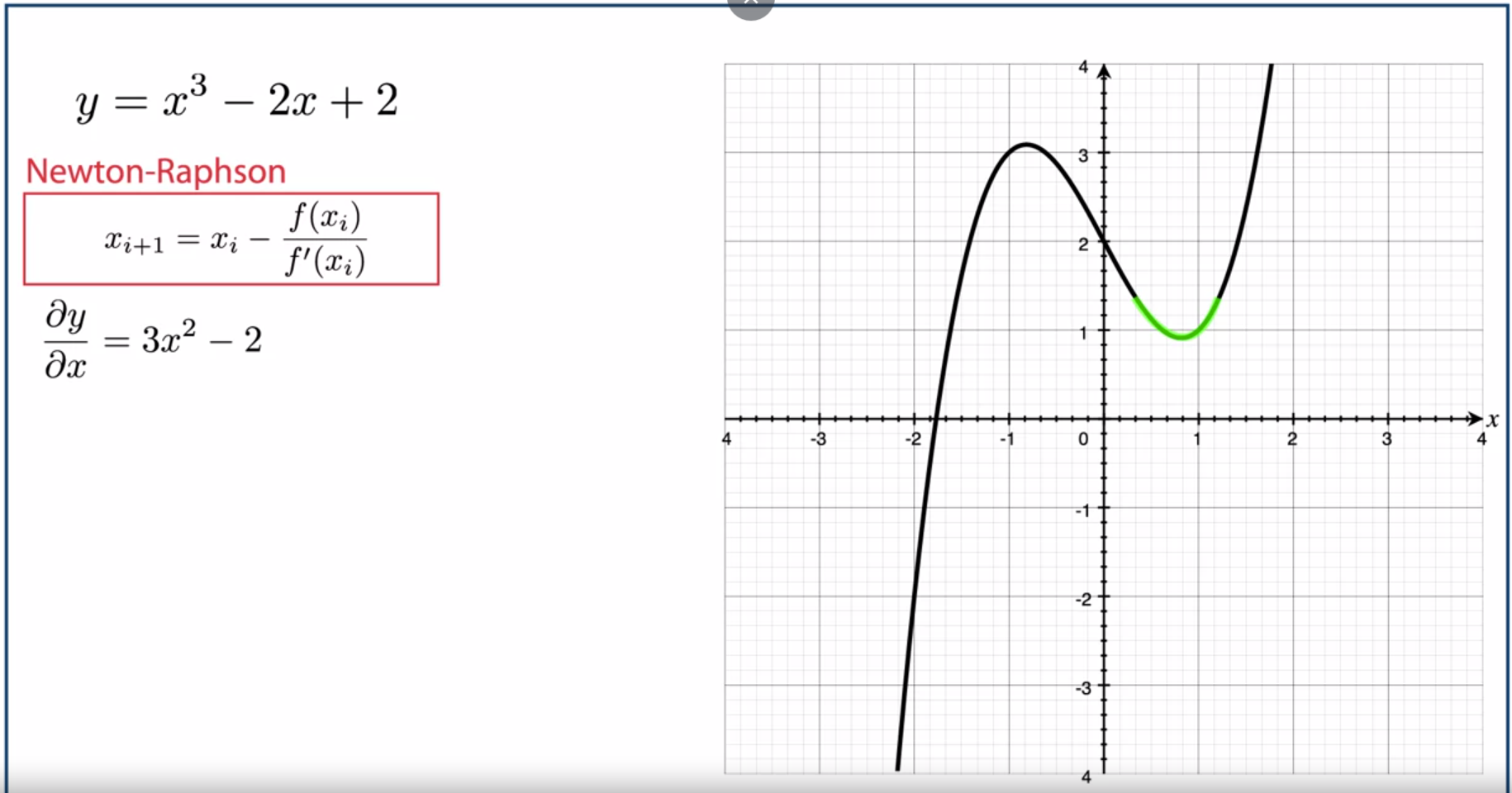
$Drawing$

위 문제와 유사하게 다른 곳에서 수렴하는 문제가 발생하는 경우가 생깁니다. 이 또한 업데이트가 되는 $- f(x_{i}) / f'(x_{i})$ 이 부분에서 해에 해당하는 $x$ 값으로 적당한 크기와 방향만큼 업데이트 되지 못하기 때문입니다.
특히 변곡점에서는 $f'(x_{i})$ 가 0에 가까워 져서 $- f(x_{i}) / f'(x_{i})$가 아주 큰 값을 가지기 때문에 변곡점에서의 newton-raphson method는 매우 취약합니다.

newton-raphson method는 위 경우와 같이 정확하게 방정식의 해를 못찾는 경우가 발생하긴 합니다. 그럼에도 초깃값 설정이 잘 되면 정확한 해를 근사할 수 있기 때문에 많이 사용되곤 합니다.

그러면 newton-raphson method가 어떤 방식으로 유도되었는 지 아래 예제를 통해 살펴보도록 하겠습니다.

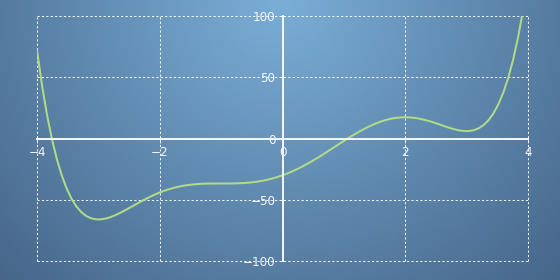
$Drawing$

\[f(x) = \frac{x^{6}}{6} - 3x^{4} + \frac{2x^{3}}{3} + \frac{27x^{2}}{2} + 18x -30\]

위 식과 그래프를 통해 확인할 수 있는 것은 $x = -4$와 $x = 1$ 부근에서 해를 찾을 수 있다는 것입니다. 이 정보와 newton-raphson method를 이용하여 해를 구해보도록 하겠습니다.
먼저 앞에서 다룬 newton-raphson method의 식을 유도하기 전에 테일러 급수에서 $f(x + \Delta x)$ 형태로 식 변형한 것에서 부터 시작해보도록 하겠습니다.
만약 $x_{0}$라는 임의의 값에서 선형화를 한다면 $f(x + \Delta x)$ 값을 다음과 같이 근사화 할 수 있습니다.

\[f(x_{0} + \Delta x) = f(x_{0}) + f'(x_{0}) \Delta x\]

만약 어떤 점에서 $f(x_{0} + \Delta x)$가 0으로 수렴한다고 가정하겠습니다. 그러면 $\Delta x$가 $x_{0}$에서 얼만큼 떨어져 있는 값인지 알 수 있습니다.

\[f(x_{0} + \Delta x) = 0 = f(x_{0}) + f'(x_{0}) \Delta x\]
\[\Delta x = -\frac{f(x_{0})}{f'(x_{0})}\]

위에서 $f(x_{0} + \Delta x) = 0$ 이라는 가정을 통해 이 함수의 해는 $x_{0} + \Delta x$가 됩니다. 따라서 $x_{0} + \Delta x = x_{1}$ 이라고 새로운 $x_{1}$를 도입하여 정의할 수 있습니다.
여기서 $x$의 인덱스를 일반화 하여 $i$로 나타내면 다음과 같습니다.

\[x_{i+1} = x_{i} + \Delta x\]

테일러 급수를 통하여 근사화 하는 대부분의 함수는 비선형 함수 입니다. 그래서 선형화로 한번에 정확한 값을 근사화 하는것은 어렵습니다. 따라서 임의의 점 $x_{0}$에서 함수의 해가 되는 $x_{0} + \Delta x$ 를 한번에 구하는 것은 어렵습니다. 하지만 임의의 점 $x_{0}$ 보다는 $x_{0} + \Delta x$가 좀 더 해에 가까운 값이 되는 것을 이용할 수 있습니다. 즉, 계속 반복하여 점점 실제 해에 가까워지도록 하는 것입니다.

위 예제를 이용하여 해를 구해보도록 하겠습니다.

\[f(x) = \frac{x^{6}}{6} - 3x^{4} + \frac{2x^{3}}{3} + \frac{27x^{2}}{2} + 18x -30\]
\[f'(x) = x^{5} - 12x^{3} -2x^{2} + 27x + 18\]

실제 해가 -4 근처이기 때문에 초기값을 -4로 정하고 $x_{i+1} = x_{i} - \frac{f(x_{i})}{f'(x_{i})}$ 을 이용하여 근사해를 구해보겠습니다.

def f (x) :
  return x**6/6 - 3*x**4 - 2*x**3/3 + 27*x**2/2 + 18*x - 30

def d_f (x) :
  return x**5 -12*x**3-2*x**2+27*x + 18

x = -4

d = {"x" : [x], "f(x)": [f(x)]}
for i in range(0, 20):
  x = x - f(x) / d_f(x)
  d["x"].append(x)
  d["f(x)"].append(f(x))

pd.DataFrame(d, columns=['x', 'f(x)'])

#            x          f(x)
# 0  -4.000000  7.133333e+01
# 1  -3.811287  1.223161e+01
# 2  -3.763093  6.515564e-01
# 3  -3.760224  2.198858e-03
# 4  -3.760214  2.531156e-08
# 5  -3.760214  1.421085e-13
# 6  -3.760214  4.263256e-14
# 7  -3.760214  4.263256e-14
# 8  -3.760214  4.263256e-14
# 9  -3.760214  4.263256e-14
# 10 -3.760214  4.263256e-14
# 11 -3.760214  4.263256e-14
# 12 -3.760214  4.263256e-14
# 13 -3.760214  4.263256e-14
# 14 -3.760214  4.263256e-14
# 15 -3.760214  4.263256e-14
# 16 -3.760214  4.263256e-14
# 17 -3.760214  4.263256e-14
# 18 -3.760214  4.263256e-14
# 19 -3.760214  4.263256e-14
# 20 -3.760214  4.263256e-14

결과를 보면 -3.760에서 수렴한 것을 볼 수 있습니다.
같은 방법으로 초깃값을 1.5 정도에서 시작해 보면 1.05에서 수렴하는 또다른 해를 근사화 할 수 있습니다.
위 코드를 이용할 때, 주의해야 할 점은 앞에서 설명한 바와 같이 변곡점에서는 기울기가 0에 가까워지므로 divided by zero 오류가 발생할 수 있다는 것입니다. 예를 들어 초깃값을 2로 설정하면 그 문제가 나타납니다.

newton-raphson method는 상당히 간단하며 유명한 방법으로 파이썬은 scipy에 구현이 이미 되어 있습니다. 다음 코드를 참조하시기 바랍니다.

from scipy import optimize

def f (x) :
  return x**6/6 - 3*x**4 - 2*x**3/3 + 27*x**2/2 + 18*x - 30
  
x0 = 3.1
optimize.newton(f, x0)
# 1.063070629709697

지금 까지 newton-raphson method에 대하여 살펴보았습니다. 이 방법을 이용하여 방정식의 해를 찾을 떄 가장 중요한 것은 초깃값을 어디서 설정하는 지 입니다. 아래 방법은 초깃값 설정에 대한 팁입니다.
① 변곡점 주변과 같이 graident가 너무 작은 곳 근처에서는 설정하지 않는 것이 좋습니다. 변곡점 주변에서 진동하거나 원하는 방향과 다른 방향으로 떨어질 수 있습니다.
② $- \frac{f(x_{i})}{f'(x_{i})}$ 에 따라 -, 함수 값, 기울기의 연산 결과가 양수인지 음수 인지 판단하여 가까운 해의 방향으로 근접하는 지 확인할 수 있습니다.

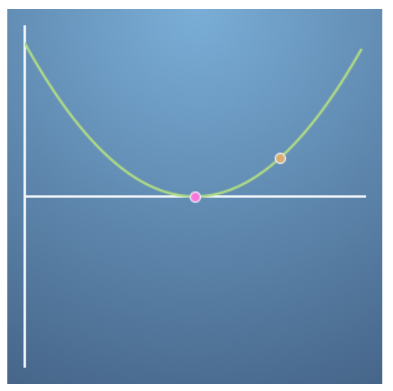
$Drawing$

위와 같은 경우 주황색 점이 초깃값이고 분홍색 점이 최적화 할 점일 때, ① 변곡점 근처에 있지 않고 ② 업데이트 항의 연산 결과 부호는 -이므로(-, +(함수값), +(기울기)) 주황색 → 분홍색점으로 이동할 수 있습니다.

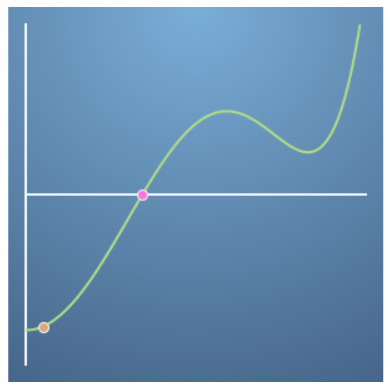
$Drawing$

위 그래프의 경우 주황색 점이 변곡점 근처에 있으므로 확실하게 최적화 될 지 잘 모릅니다.

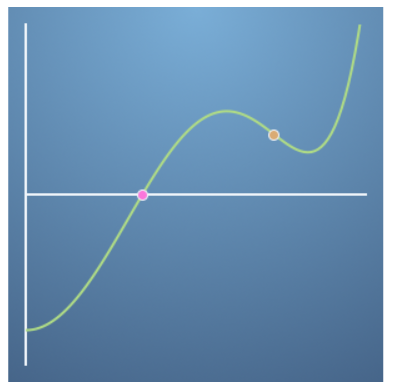
$Drawing$

위와 같은 경우 ① 변곡점 근처에 있지 않지만 ② 업데이트 항의 연산 결과는 부호는 +이므로(-, +(함수값), -(기울기)) 주황색 점은 오른쪽으로 이동하게 되어 최적화 할 수 없습니다.

gradient descent

앞에서 다룬 newton-raphson method는 gradient를 반복적으로 사용하여 $x$에 관한 단일 변수 함수의 해를 구하였습니다.
이 개념을 이용하여 다변수 함수에 적용해 보고 다변수 함수의 maxima 또는 minima를 찾는 데 응용해 보도록 하겠습니다.

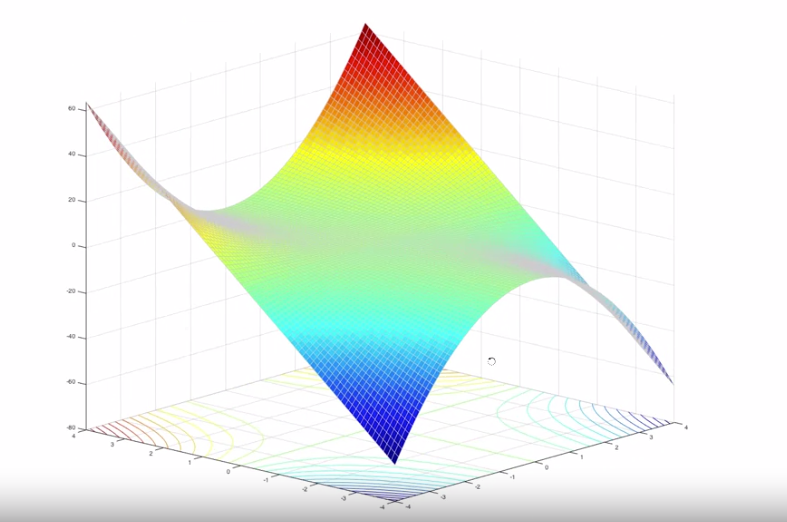
$Drawing$

위 그래프의 함수는 $f(x, y) = x^{2}y$를 따릅니다. 즉, 단일 변수의 함수가 아닙니다.
앞에서 newton-raphson method에서는 $f(x) = 0$을 만족하는 $x$를 찾는 것이 목적이었습니다.
여기서 풀 문제는 임의의 점 $(x, y)$에서 시작하여 그래프의 가장 낮은 지점으로 빠르게 가는 방법을 찾는 것입니다. 위 그래프를 보면 $(x, y)$값에 대응하는 값이 있고 이 값들이 등고선 형태로 그려집니다. 이를 언덕 형태로 보았을 때, 가장 아랫쪽인 지면에 가능 방법을 구하는 문제라고 생각하면 됩니다.

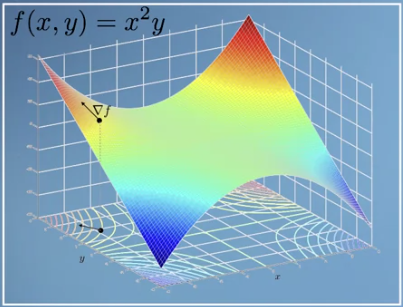
$Drawing$

newton-raphson method에서도 gradient를 구하여 $x_{i}$를 업데이틑 하는 방법을 사용하였습니다.
이번에도 같습니다. 좀더 직관적으로 받아들일 수 있는 것은 최적화 할 목적이 그래프의 가장 아래로 빠르게 내려가는 것이고 이는 가장 경사가 깊은 방향으로 내려가면 된다는 것입니다.
따라서 각 지점에서의 경사가 얼만큼인 지 확인하기 위해 $x, y$ 각각에 대하여 편미분을 해야 합니다.

\[f(x, y) = x^{2}y\]
\[\frac{df}{dx} = 2xy\]
\[\frac{df}{dy} = x^{2}\]
\[\nabla f = \begin{bmatrix} \frac{df}{dx} \\ \frac{df}{dy} \end{bmatrix}\]

위 식의 $\nabla f$를 gradient라 하고 줄여서 grad 라고 합니다.
grad는 어떤 지점 $(x, y)$에서 빠르게 내려가기 위한 경사입니다. grad 벡터의 경사를 키우려면 다른 벡터를 곱해서 내적을 해야 합니다. 이 때, 최대한 경사를 키우는 방법은 grad와 곱할 벡터가 grad와 평행한 벡터가 되도록 하는 것입니다. 왜냐하면 코사인 법칙에 따라 두 벡터의 곱이 최대가 되는 점은 사잇각이 0도가 되는 지점이기 때문입니다.

gradient를 데이터 사이언스에서 주로 다루는 문제와 접목시켜 보도록 하겠습니다. 위 그래프 $f(x, y) = x^{2}y$ 에서 높이는 모델이 추론한 값과 실제 정답 값과의 차이에 해당하는 error 라고 하겠습니다. 즉, $f(x, y)$는 얼만큼 에러가 있는 지 나타내는 에러 함수 입니다.
그러면 에러를 최소화 하는 것이 이 문제의 최적화 입니다. 비유하면 높은 에러에서 낮은 에러로 최적화 하는 것은 경사를 타고 아래로 내려오는 것과 같습니다.
이는 앞에서 gradient 경사를 키워서 빠르게 내려가는 것과 같은 목적입니다. 이 방법을 gradient descent 라고 합니다. 말 그대로 gradient를 하강시킨다는 뜻입니다. 이를 식으로 나타내면 다음과 같습니다.

\[S_{n+1} = S_{n} - \gamma \nabla f(S_{n})\]

위 식에서 $S_{n}$은 $n$ 번째 스텝의 위치 상태 즉, 에러를 나타냅니다. $\gamma$는 gradient에 대한 가중치 입니다. 중요한 것은 $\nabla f(S_{n})$ 입니다. 즉, $n$ 번째의 gradient에 해당합니다.
보통 위 식을 계속 반복할수록 에러 값은 줄어들게 됩니다.
하지만 위와 같은 에러 함수에는 전 영역에서 가장 작은 에러를 가지는 지점도 있는 반면 국소적으로 작은 에러를 가지는 지점도 있습니다. 이 때, 전 영역에서 가장 작은 에러를 가지는 쪽으로 최적화 되었으면 잘 된 것이지만 국소적으로 작은 에러를 가지는 지점으로 이동하게되면 이것은 최적화가 잘 안된 것입니다.
이 문제를 local minimum 이라고 합니다. 즉, 그 지점에 갇히게 되어 최적화가 덜 되게 됩니다.
그럼에도 불구하고 gradient descent 방법으로 에러를 최소화 하는 최적화 방법은 널리 사용되고 이 방법을 개선한 많은 방법이 딥러닝에서 활용되고 있습니다.

constrained optimisation method of lagrange multipliers

지금까지 grad를 이용하여 단일 변수, 다 변수 함수의 minima, maxima를 찾는 gradient descent에 대하여 다루어 보았습니다.
이번에는 constrained optimisaion method of Lagrange Multiplier에 대하여 알아보도록 하겠습니다.
이 내용은 앞에서 다룬 minima, maxmima를 찾을 때, 제약 조건을 적용하여 원하는 방향으로 최적화 하는 데 도움을 줍니다. 이 방법을 간단하게 lagrange multiplier 라고 하겠습니다.
먼저 앞에서 다룬 다 변수 함수의 gradient를 다시 한번 살펴보겠습니다.

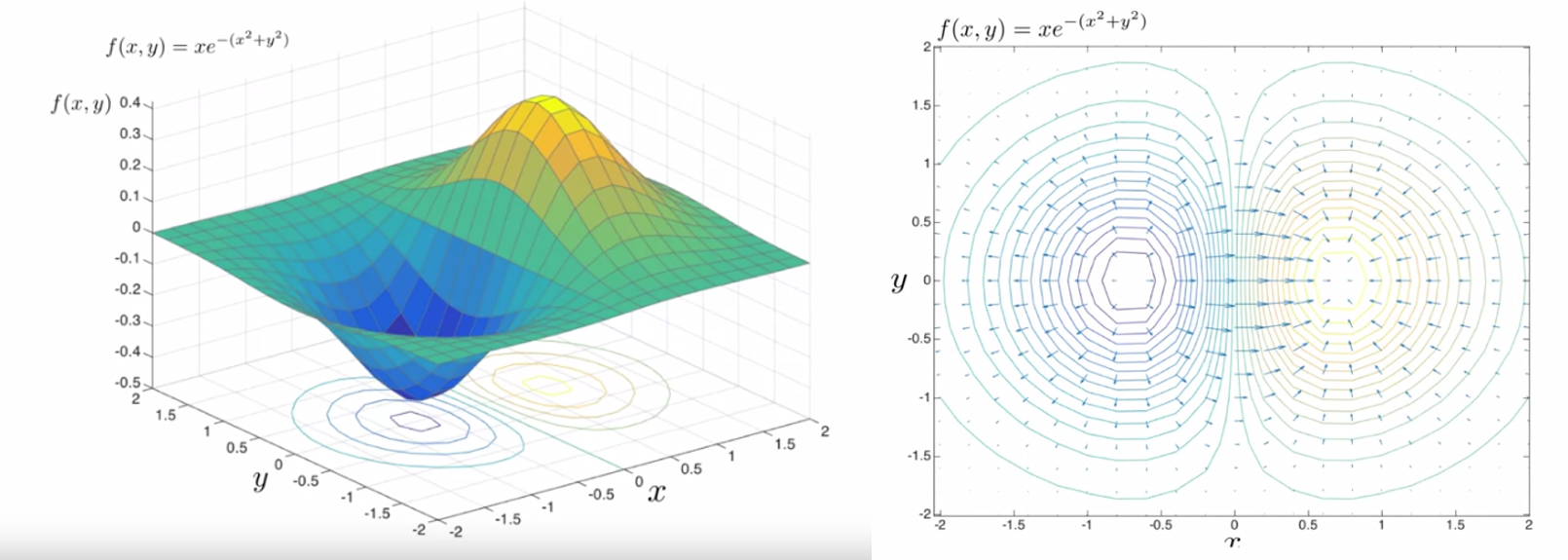
$Drawing$

위 그림의 오른쪽 등고선을 보면 gradient 벡터가 화살표 형태로 나와있는 것을 볼 수 있습니다. 화살표의 방향은 낮은값 → 높은값입니다.
그리고 각 gradient 벡터는 등고선과 수직 방향을 가집니다. 왜냐하면 gradient는 경사를 나타내고 등고선은 같은 값들을 선으로 이은 것이기 때문입니다. 따라서 gradient는 등고선과 수직형태를 이룹니다.
또한 그 지점의 변화량이 클수록 화살표의 길이는 길어집니다.

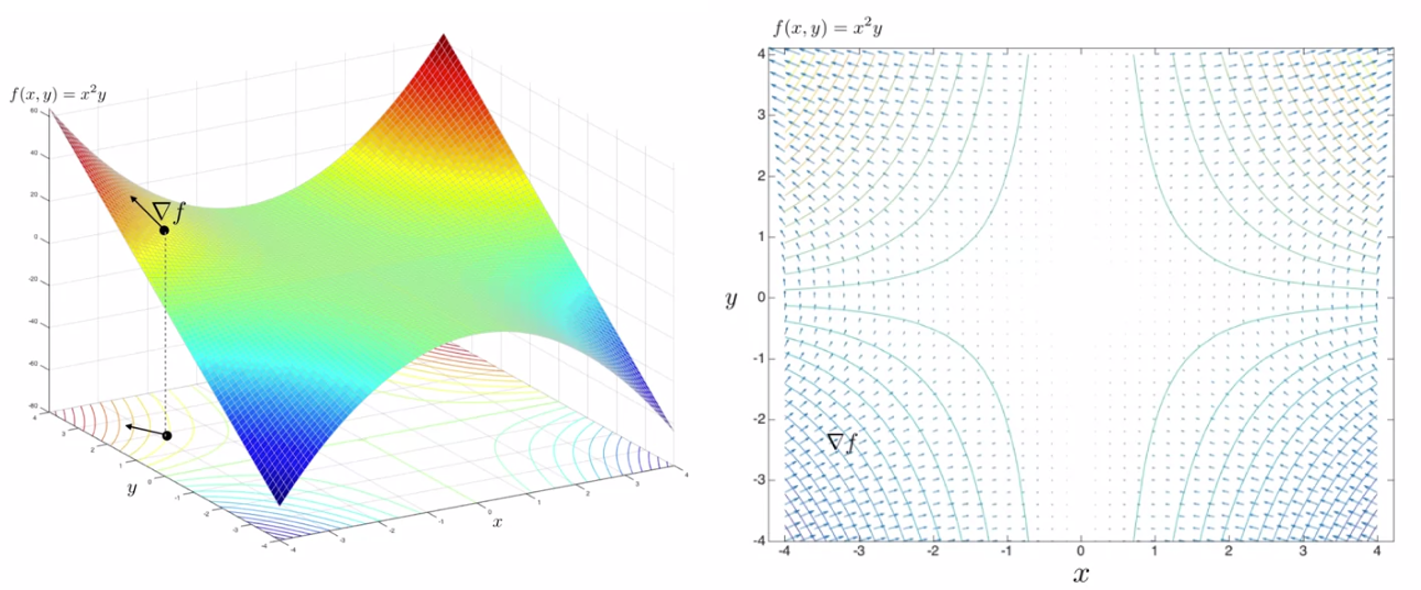
$Drawing$

위 예제도 동일합니다. 앞의 예제와 동일한 규칙으로 등고선과 gradient 벡터가 그려져 있습니다.
위 그림에서는 등고선 또는 3D 그래프를 보면 maxima, minima를 구할 수 있습니다.

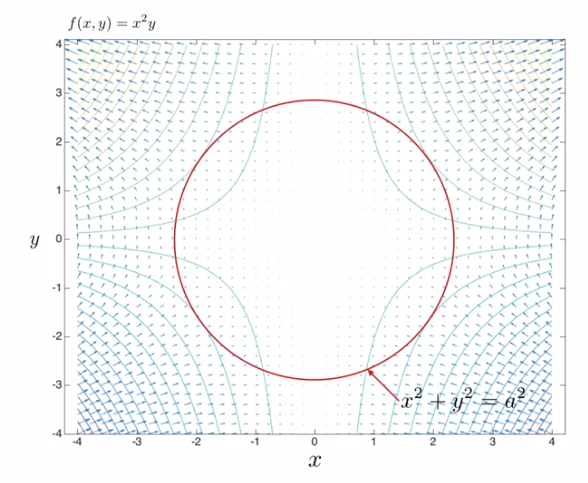
$Drawing$

하지만 만약 위 그림처럼 빨간색 원의 지점에서 minima, maxima로 최적화 하려고 한다면 어떻게 해야 할까요? 이 문제가 지금 다룰 constrained optimisation 입니다.

optimize : $f(x, y) = x^{2}y$
constrain : $g(x, y) = x^{2} + y^{2} = a^{2}$

위 그래프의 등고선은 optimize에 해당하는 식이고 원은 constrain에 해당하는 식입니다.

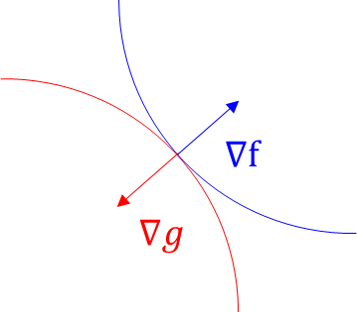
$Drawing$

이 때, 위 그림과 같이 $f(x, y)$의 gradient와 $g(x, y)$의 gradient가 같은 지점의 최댓값과 최솟값을 찾으면 그 점이 바로 constrained optimisation 입니다.
즉, $f(x, y)$의 gradient를 $\nabla f$라 하고 $g(x, y)$의 gradient를 $\nabla g$ 라고 한다면 $\nabla f = \lambda \nabla g$를 만족하는 지점에서 최적화가 됩니다.
이 때 $\lambda$를 Lagrange Multiplier 라고 합니다. 그러면 $x, y$ 각각에 대하여 편미분을 한 후 식을 전개해 보도록 하겠습니다.

\[\nabla f = \nabla(x^{2}y) = \begin{bmatrix} 2xy \\ x^{2} \end{bmatrix} = \lambda \nabla g = \lambda \begin{bmatrix} 2x \\ 2y \end{bmatrix}\]

\[\text{about dx : } \quad 2xy = \lambda 2x \quad \to \quad y = \lambda\]
\[\text{about dy : } \quad x^{2} = \lambda 2y = 2y^{2} \quad \to \quad x = \pm \sqrt{2}y\]
\[x^{2} + y^{2} = a^{2} = 3y^{2} \quad \to \quad y = \pm a / sqrt{3}\]

따라서 $x, y$ 조합에 따라서 4가지 경우가 발생합니다.

\[\frac{a}{\sqrt{3}} \begin{bmatrix} \sqrt{2} \\ 1 \end{bmatrix}, \quad \frac{a}{\sqrt{3}} \begin{bmatrix} \sqrt{2} \\ -1 \end{bmatrix}, \quad \frac{a}{\sqrt{3}} \begin{bmatrix} -\sqrt{2} \\ 1 \end{bmatrix}, \quad \frac{a}{\sqrt{3}} \begin{bmatrix} -\sqrt{2} \\ -1 \end{bmatrix}\]

위 값을 $f(x, y)$에 대입하면 다음과 같이 값을 얻을 수 있습니다.

\[\frac{2a^{3}}{3\sqrt{3}} , \quad -\frac{2a^{3}}{3\sqrt{3}}, \quad \frac{2a^{3}}{3\sqrt{3}}, \quad -\frac{2a^{3}}{3\sqrt{3}}\]

따라서 maxima는 $\frac{2a^{3}}{3\sqrt{3}}$ 이고 minima는 $-\frac{2a^{3}}{3\sqrt{3}}$로 구할 수 있습니다. 또한 lagrange multiplier는 $\lambda = \pm a/\sqrt{3}$ 으로 $\nabla f$와 $\nabla g$의 관계 또한 구할 수 있습니다.

이번에는 다른 예제와 코드를 이용하여 lagrange multiplier를 구해보도록 하겠습니다.
최솟값을 찾아야 할 함수 $f(X)$ 와 제약 함수 $g(X)$는 다음과 같습니다.

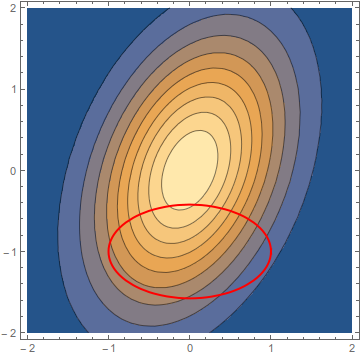
$Drawing$

\[f(X) = exp(-\frac{2x^{2} + y^{2} - xy}{2})\]
\[g(X) = x^{2} + 3(y + 1)^{2} -1 = 0\]

만약 제약 조건에 부합하는 최적점을 바로 찾으려면 상당히 복잡합니다.

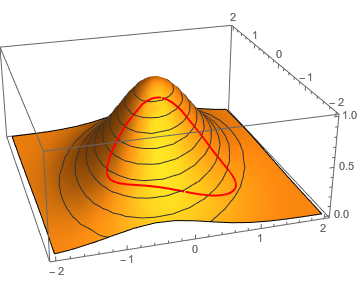
$Drawing$

위 그림과 같은 곡면에서 제약 조건을 적용한 최적 점을 바로 찾기는 상당히 어렵습니다.
여기서 lagrange multiplier를 도입해 보겠습니다.
함수의 gradient와 제약 조건의 gradient 모두 등고선에 수직이므로 아래와 같이 식을 사용할 수 있습니다.

\[\nabla f(X) = \lambda \nabla g(X)\]
\[\begin{bmatrix} \partial f / \partial x \\ \partial f / \partial y \end{bmatrix} = \lambda \begin{bmatrix} \partial g / \partial x \\ \partial g / \partial y \end{bmatrix}\]

또한 $g(X) = x^{2} + 3(y + 1)^{2} -1 = 0$ 식에 따라 하나의 벡터로 다음과 같이 정리해 보겠습니다.

\[\nabla \mathcal L (x, y, \lambda) = \begin{bmatrix} \frac{\partial f}{\partial x} - \lambda \frac{\partial g}{\partial x} \\ \frac{\partial f}{\partial y} - \lambda \frac{\partial g}{\partial y} \\ -g(X) \end{bmatrix} = 0\]

mathematics for machine learning 글 목록

목차

newton-raphson method

gradient descent

constrained optimisation method of lagrange multipliers

newton-raphson method

gradient descent

constrained optimisation method of lagrange multipliers