Taylor series 와 linearisation - gaussian37

Taylor series 와 linearisation

mathematics for machine learning 글 목록

이번 글에서 다룰 테일러 급수는 임의의 함수를 다항식 급수로 재 표현하는 방법입니다.
테일러 급수는 간단한 선형 근사법을 복잡한 함수에 사용합니다. 이 글에서는 먼저 단일변수를 이용한 테일러 급수의 공식을 유도하고 기계 학습과 관련된 이 결과의 몇 가지 중요한 결과에 대해 논의해 보겠습니다. 더 나아가 다변수 사례로 확장한 후 Jacobian과 Hessian이 어떻게 적용되는 지 살펴보겠습니다. 마지막에 다루는 다변수 테일러 급수에서는 앞에서 다룬 모든 내용을 총 집합 해서 설명해 보도록 하겠습니다.

목차

Taylor series for approximations
- Building approximate functions
- Power series
- Power series derivation : Maclaurin series
- Power series derivation : Taylor series
- Example of Taylor series
- Linearisation
Multivariable Taylor Series
테일러 급수의 사용 이유와 활용

Taylor series for approximations

이번 글에서는 복잡한 함수를 좀 더 간단한 함수를 이용하여 어떻게 근사화 할 수 있는 지 배워보려고 합니다.
근사화 하는 방법으로는 테일러 급수(taylor series)를 사용하려고 합니다.

Building approximate functions

테일러 급수는 어떤 함수를 근사화 하기 위해 사용하는 방법 중 하나입니다.
테일러 급수에 대하여 구체적으로 알아보기 이전에 그래프 상에서 근사화 하는 것이 어떤 의미를 가지는 지 한번 살펴보도록 하겠습니다.
예를 들어 닭을 오븐에 구울 때, 얼마나 오래 구울 지 시간을 구하는 함수가 있다고 가정해 보겠습니다.
이런 함수는 단순히 선형적이지 않을 뿐 아니라 많은 요소가 함수에 추가됭야 정확하게 추정할 수 있습니다.
예를 들어 다음과 같이 함수를 만들어 보겠습니다.

\[\text{t(m, OvenFactor, ChickenShapeFactor)} = 7.33m^{5} - 72.3m^{4} + 253m^{3} - 368m^{2} + 250m + 0.02 + \text{OvenFactor} + \text{ChickenShapeFactor}\]

위 식은 닭의 질량 \(m\)과 Oven과 Chicken의 특성에 따른 OvenFactor와 ChickenShapeFactor를 입력으로 받습니다.
만약 위 식이 닭을 얼만큼 구워야 할 지 잘 추정할 수 있는 식이라도 이 식은 사람들이 사용하기에 너무 복잡합니다.
따라서 추정 성능이 조금 떨어지더라도 식을 단순화 해서 사람들이 사용하기 쉽게 만들어 보려고 합니다.
먼저 사람들이 Oven과 Chicken은 비슷한 것을 사용한다고 가정하고 OvenFactor와 ChickenShapeFactor는 소거하겠습니다. 실제로 식을 단순화 시킬 때 큰 차이가 없을 것으로 생각하는 변수들은 동일하다고 가정하고 소거하는 방법을 사용하기도 합니다.
따라서 다음 식과 같이 두 Factor를 소거합니다.

\[\text{t(m)} = 7.33m^{5} - 72.3m^{4} + 253m^{3} - 368m^{2} + 250m + 0.02\]

위 식은 닭의 질량이 입력되었을 때, 오븐에 구울 최적의 시간을 산출하는 함수입니다.

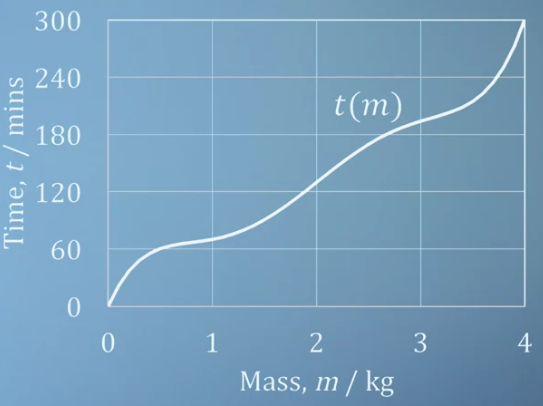
$Drawing$

앞의 식을 좌표 평면에 그리와 위 그래프와 같이 그릴 수 있습니다.
만약 슈퍼마켓에 파는 일반적인 닭의 무게가 1.5kg이라고 가정해 보겠습니다.

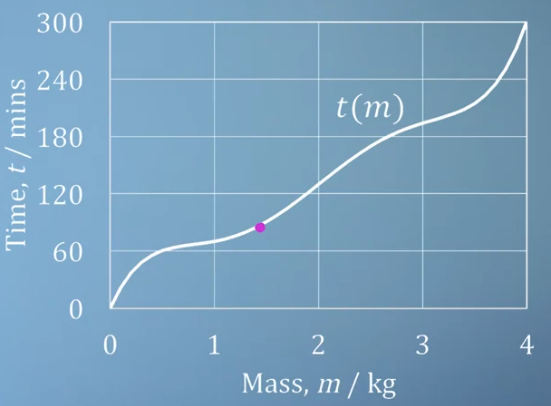
$Drawing$

1.5kg의 무게에 해당하는 시간은 그래프에 표시된 점의 y값에 해당합니다.

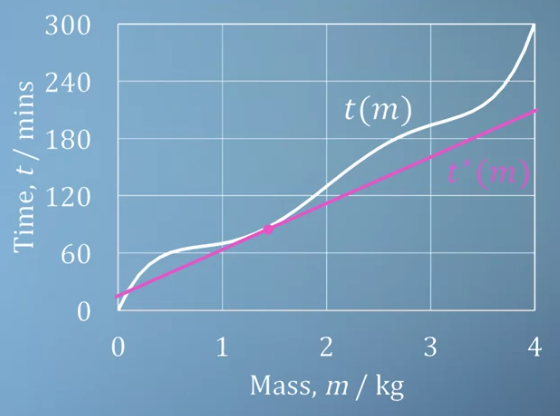
$Drawing$

위 그래프에서는 원래 그래프 \(t(m)\)을 1.5kg 지점에서 1차 미분하여 접선 \(t'(m)\)을 구하였습니다.
이 접선은 미분을 한 1.5kg 근방에서는 꽤나 근사가 잘 되었지만 1.5kg에서 멀어질수록 그 오차가 커지는 것을 알 수 있습니다.
하지만 예제에서 다루는 입력은 닭의 질량이므로 1.5kg에서 크게 벗어나지 않기 때문에 의미가 있습니다.

Power series

테일러 급수에 대하여 본격적으로 알아보기 이전에 간단한 컨셉에 대하여 먼저 다루어 보겠습니다.
먼저 테일러 급수는 멱급수(Power series)의 형태입니다. 테일러 급수의 형태를 보면 \(x^{n}\) 이고 \(n\)은 점점 증가합니다. 그리고 \(x^{n}\) 앞의 계수가 붙어있습니다. 예를 들어 다음과 같습니다.

\[g(x) = a + bx + cx^{2} + dx^{3} + \cdots\]

앞으로 살펴 볼 테일러 급수는 위 식과 같은 멱급수의 형태를 가지며 복잡한 식을 근사화 하는 목적으로 사용됩니다.
급수에 사용되는 \(n\)이 단순히 1차식을 사용할 수도 있는 반면 큰 차수도 사용할 수 있습니다. 큰 차수를 사용할수록 더 정교하게 근사화 가능합니다.
물론 많은 application 들은 매우 큰 차수 보다는 앞의 몇 차수 (1차, 2차, 3차 … 등)만을 사용하는 데, 낮은 차수 들의 합을 이용해서도 꽤나 근사화가 잘되기 때문입니다.
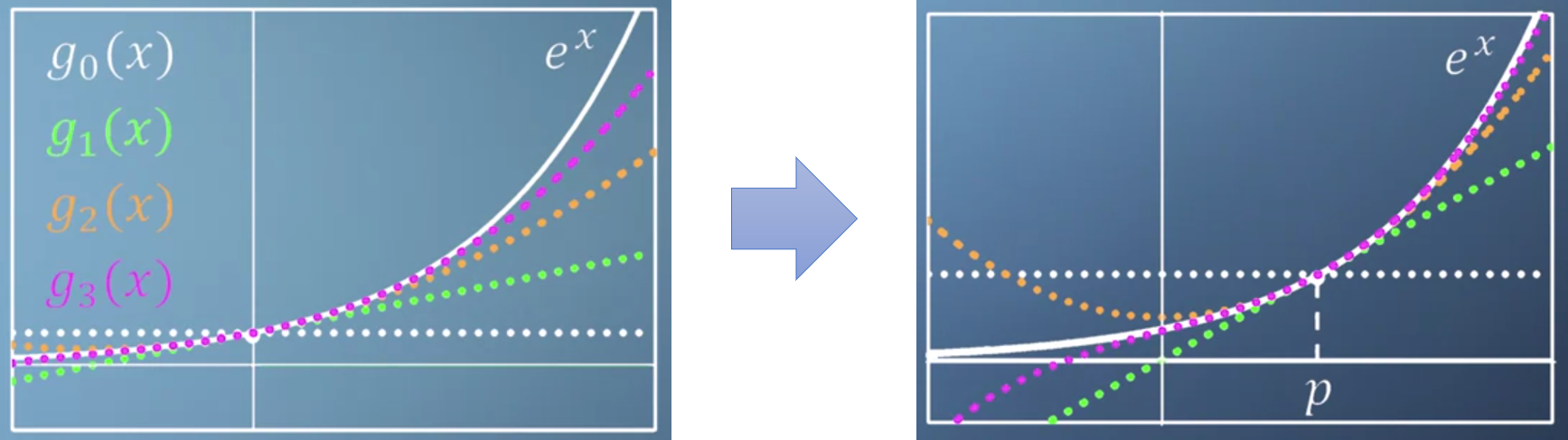
아래 예제에서는 ① 지수함수와 ② 6차 다항 함수에 대하여 0, 1, 2, 3 차로 각각 근사화 하는 예제를 보여줍니다.

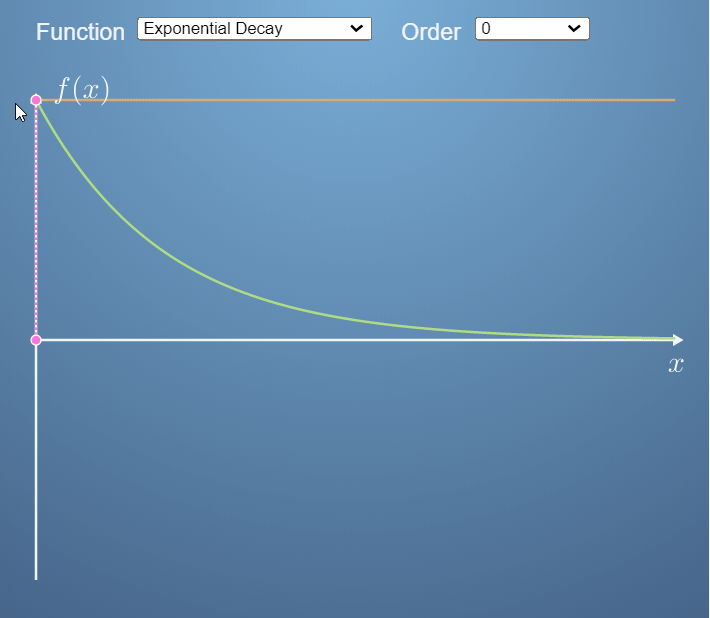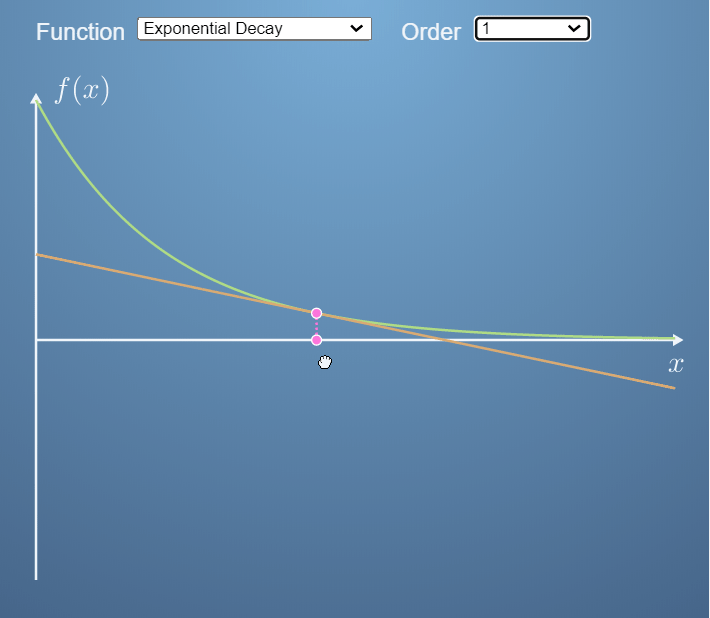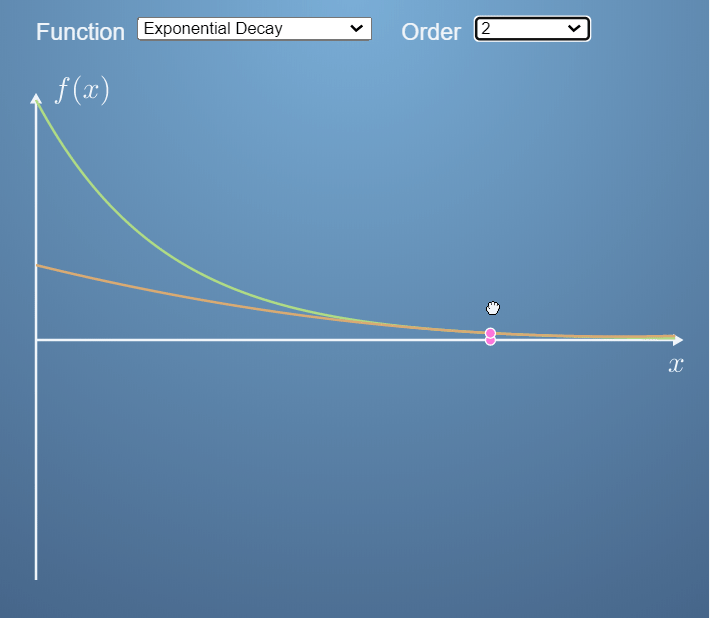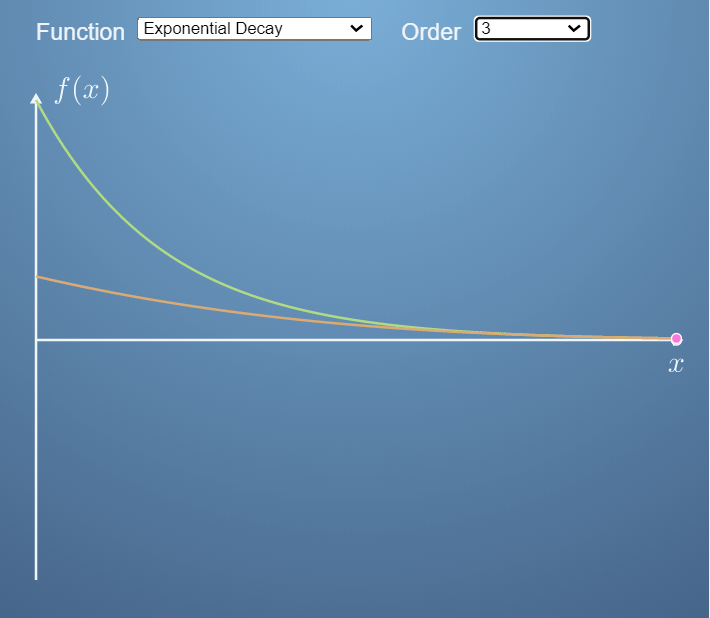
$Drawing$

$Drawing$

위 두 그림을 보면 0차 즉, x축에 평행한 직선 부터 3차 곡선 까지 지수함수와 다항함수의 각 x점에 접하는 곡선으로 근사화 하였습니다.
근사화 하는 함수의 차수가 증가할수록 더 정교하게 근사화 할 수 있음을 확인할 수 있습니다. 물론 차수가 늘어날수록 계산량도 늘어납니다.

정리해 보겠습니다. 앞에서 다룬 바와 같이 Taylor 계열 근사법은 power series로 볼 수도 있습니다. 이 근사법은 특히 수치적 방법을 사용할 때 종종 더 간단하고 평가하기 쉬운 함수를 만드는 데 사용됩니다. 다음 예제들을 보면 점점 증가하는 power serires를 통해 함수에 대한 추가 정보를 어떻게 얻어 나아갈 수 있는 지 이해할 수 있습니다.
아래 그림에서 0차, 2차, 4차 3개의 근사식은 \(x = 0\) 일 때 어떤 함수를 근사한 식이라고 하겠습니다. 이 경우 원래 함수는 \(\cos{(x)}\) 일 수 있습니다. (물론 가능한 다른 함수도 많습니다.)

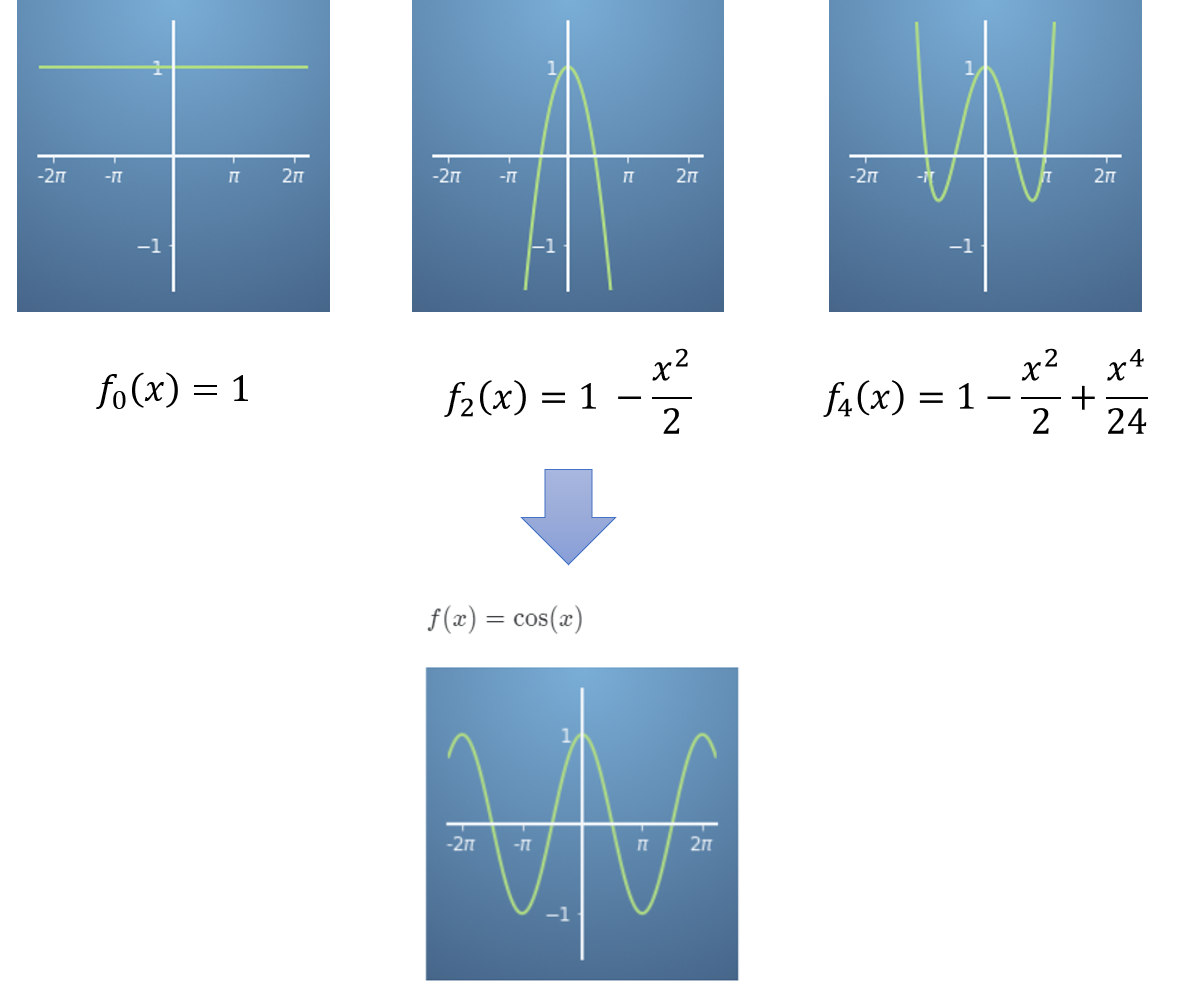
$Drawing$

위 그림을 보면 \(f(x) = \cos{(x)}\)는 근사식의 일부를 모두 포함합니다. 즉 접하는 것을 알 수 있습니다.

$Drawing$

반면 위 그림에서 1차 함수가 지수 함수를 근사한 것이라고 하였을 때, 이 근사는 잘못되었다고 판단할 수 있습니다. 왜냐하면 지수 함수와 접하지 않기 때문입니다.

Power series derivation : Maclaurin series

지금부터 멱급수(Power series)의 미분 형태에 대하여 알아보도록 하겠습니다. 앞에서 다루었듯이, 이 형태는 어떤 함수를 멱급수 형태로 근사화 시키기 위함입니다.
특히, 미분이 항상 가능한 연속 함수에서는 어떤 점에 대한 근사화를 할 수 있으면 모든 점에 대해서 근사화를 할 수 있어 식 전체를 멱급수 형태로 나타낼 수 있습니다. 다음과 같은 예시가 있습니다.

\[e^{x} = 1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \cdots\]

그러면 어떤 함수 \(f(x)\)가 있을 때, 그 함수를 \(x = 0\) 인 지점에서 근사화 시키는 방법을 살펴보도록 하겠습니다.

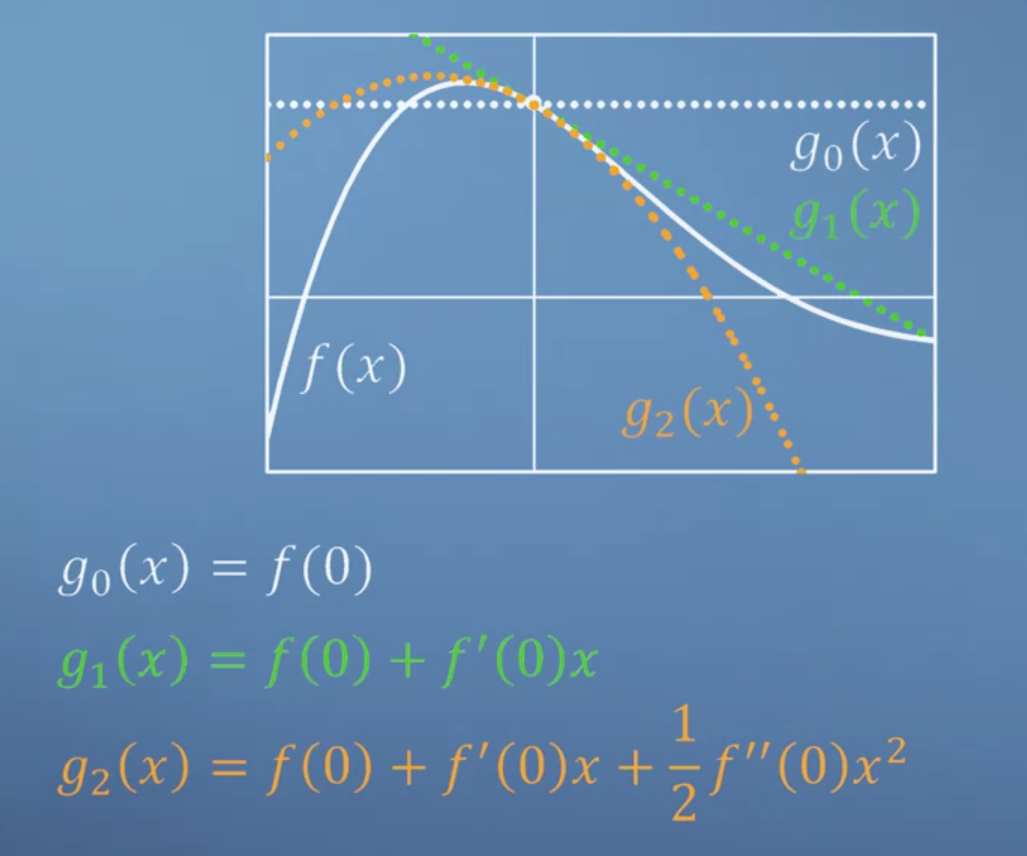
$Drawing$

위 그림에서 하얀색 곡선의 함수가 근사화 할 함수인 \(f(x)\)입니다.
이 함수를 \(x = 0\) 지점에서 0차 식으로 근사화한 식을 \(g_{0}(x)\) 라고 할 수 있습니다. 물론 근사화는 안되었습니다. 다만 \(f(0)\)인 지점과 \(g_{0}(0)\)의 지점은 교차하는 것을 확인할 수 있습니다.
그 다음으로 \(x = 0\) 지점에서 1차식으로 근사화 한 식 \(g_{1}(x)\)에 대하여 알아보겠습니다.
위 그래프의 식을 살펴보면 \(g_{1}(x)\)는 \(f(0)\) 인 지점을 접하는 1차 함수식입니다. 곡선에 접하는 1차식이므로 1차식의 기울기는 \(x = 0\) 지점의 미분값입니다. 따라서 \(f'(0)\)이 됩니다.
또한 위 그래프를 참고하면 1차식의 절편(bias)값은 \(f(0)\)의 값을 가지게 됩니다. 따라서 \(g_{1}(x) = f(0) + f'(0)x\)가 됩니다.

앞에서 유도한 \(g_{1}(x)\)를 \(g_{2}(x)\)를 구하는 과정 속에서 일반화 시켜서 유도해 보겠습니다. 근사화할 식이 2차식이므로 \(f(x)\)를 2차식의 일반식으로 두고 미분해 보겠습니다.

\[f(x) = ax^{2} + bx + c\]
\[f'(x) = 2ax + b\]
\[f''(x) = 2a\]

앞의 예제와 같이 \(x = 0\)에서의 값을 살펴보겠습니다.

\[f(0) = c\]
\[f'(0) = b\]
\[f''(0) = 2a\]

따라서 \(a = f''(0) / 2\), \(b = f'(0)\), \(c = f(0)\)이 됩니다. 따라서 이 값을 일반항에 대입하면 다음과 같습니다.

\[g_{2}(x) = c + bx + ax^{2} = f(0) + f'(0)x + \frac{f''(0)}{2}x^{2}\]

같은 논리를 이용하여 근사식이 3차식이라고 가정하여 \(g_{3}(x)\)에 대하여 풀어보도록 하겠습니다.

\[f(x) = ax^{3} + bx^{2} + cx + d\]
\[f^{(1)}(x) = 3ax^{2} + 2bx + c\]
\[f^{(2)}(x) = 6ax + 2b\]
\[f^{(3)}(x) = 6a\]
\[f^{(3)}(0) = 6a, \quad a = f^{(3)}(0) / 6\]

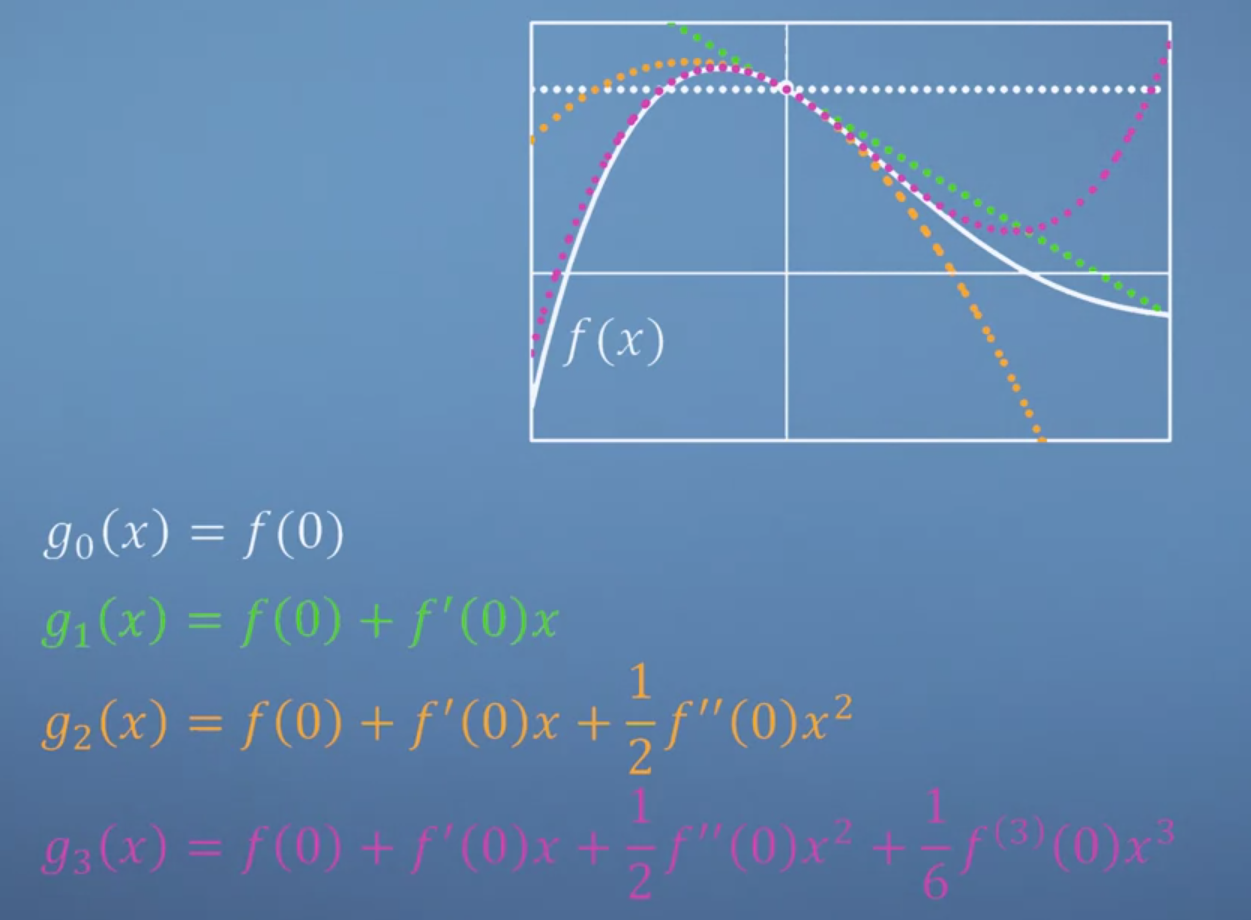
$Drawing$

위 그래프를 보면 조금 더 근사화가 잘 된 것을 알 수 있습니다. \(n\)차 다항식으로 근사학 식들을 살펴보면 공통점들이 있습니다. 이것들을 이용해 일반화 시키면 다음과 같습니다.

\[g_{0}(x) = f(0)\]
\[g_{1}(x) = f(0) + f^{(1)}(0)x\]
\[g_{2}(x) = f(0) + f^{(1)}(0)x + \frac{1}{2!}f^{(2)}(0)x^{2}\]
\[g_{3}(x) = f(0) + f^{(1)}(0)x + \frac{1}{2!}f^{(2)}(0)x^{2} + \frac{1}{3!}f^{(3)}(0)x^{3}\]
\[g_{4}(x) = f(0) + f^{(1)}(0)x + \frac{1}{2!}f^{(2)}(0)x^{2} + \frac{1}{3!}f^{(3)}(0)x^{3} + \frac{1}{4!}f^{(4)}(0)x^{4}\]

즉, \(n\) 차로 근사화 할 때에는 \(\frac{1}{n!} f^{(n)}(0) x^{n}\) 까지 점점 항을 추가하여 식을 만들어 나아갈 수 있습니다. 따라서 \(g_{n}(x)\)를 일반화 하면 다음과 같습니다.

\[g_{n}(x) = \sum_{n=0}^{\infty} \frac{1}{n!}f^{(n)}(0)x^{n}\]

위 내용을 한장으로 요약하면 다음과 같습니다.

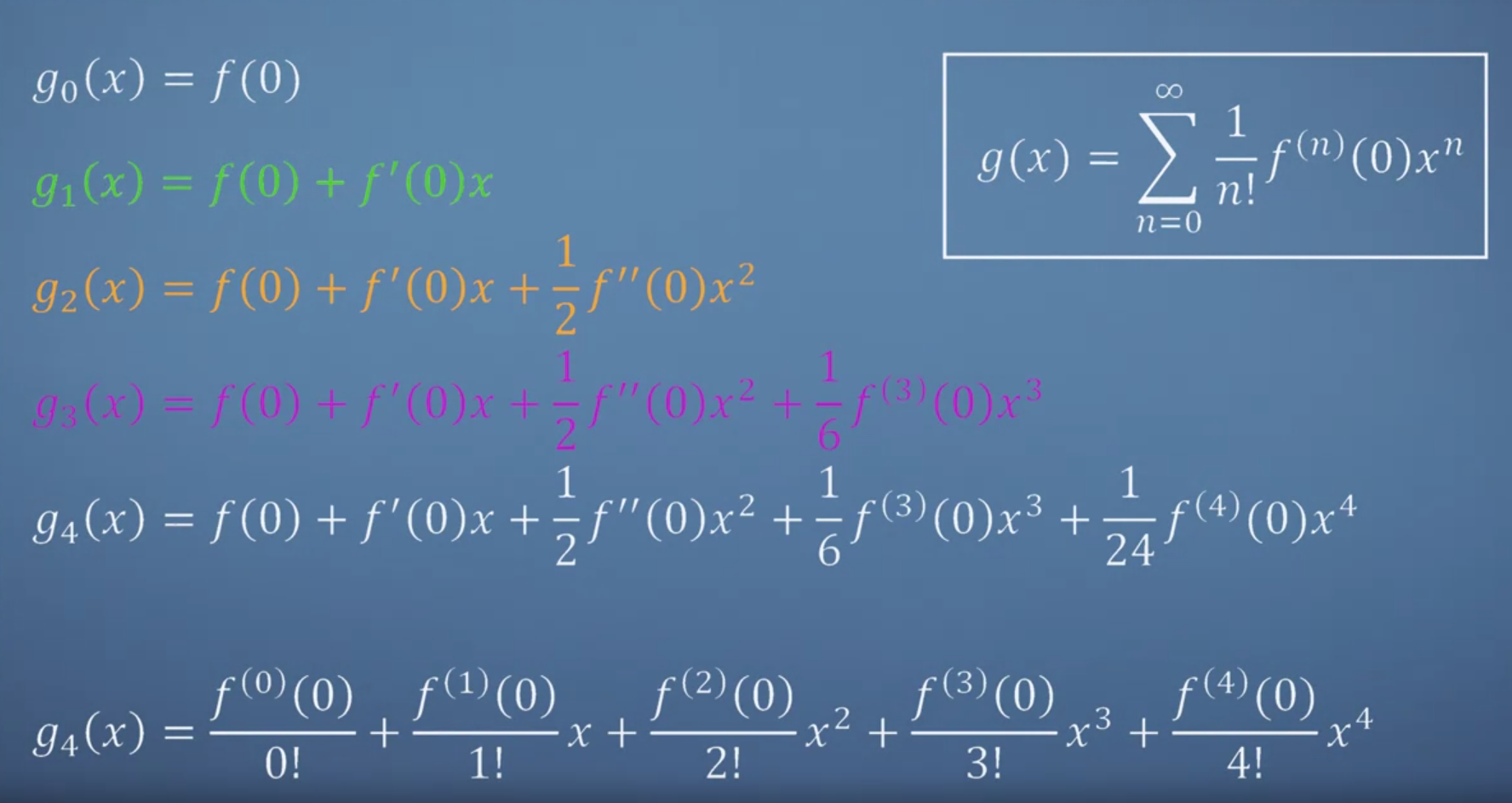
$Drawing$

위 식과 같이 \(x = 0\) 일 때 기준으로 식을 근사화 한 것을 Maclaurin Series (맥클로린 급수) 라고 합니다.
맥클로린 급수는 테일러 급수에서 \(x = 0\) 일 때에 한하여 적용한 특별한 경우입니다. 정확히는 맥클로린 급수를 모든 \(x\)에 대하여 확장한 것이 테일러 급수입니다. 그러면 테일러 급수에 대하여 본격적으로 알아보겠습니다.

Power series derivation : Taylor series

지금부터 앞에서 배운 맥클로린 급수를 이용하여 테일러 급수로 확장해 보도록 하겠습니다.

$Drawing$

맥클로린 급수는 미분 가능한 연속 함수 \(f(x)\)를 \(x = 0\) 위치에서 \(n\) 차 다항식으로 근사화 하면 모든 점에서 근사화 할 수 있다는 방법을 보여주었습니다.
테일러 급수는 맥클로린 급수의 조건인 \(x = 0\)을 \(x = p\)로 일반화 합니다. 즉, 어떤 점에서 \(n\) 차 다항식으로 근사화 할 수 있으면 모든 점에서 근사화 할 수 있는 것으로 범위를 확장합니다.

지금 부터는 임의의 점 \(p\)에서 근사화한 1차식을 통해 \(x =0\)이 아닌 임의의 점 \(x = p\)에서 근사화 하는 지 다루어 보도록 하겠습니다. \(n\)차의 원리는 동일하므로 1차식만 유도해도 전체를 이해하실 수 있습니다.

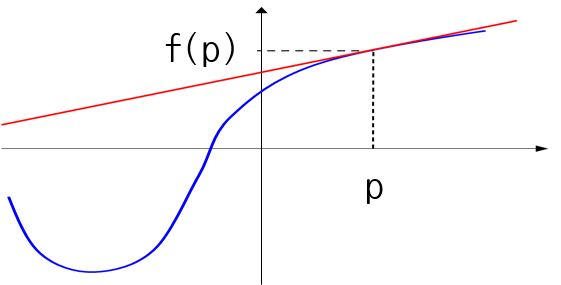
$Drawing$

\[y = mx + c\]
\[y = f'(p)x + c\]
\[f(p) = f'(p)p + c, \quad c = f(p) - f'(p)p\]
\[\therefore y = mx + c = f'(x)x + f(p) - f'(p)p\]
\[y = f'(p)(x - p) + f(p)\]

위 식을 차례 차례 살펴보면 어떻게 전개되는 지 알 수 있습니다. 맥클로린 급수와의 차이점은 \(x\) 대신 \((x - p )\)를 이용한다는 것이고 이것은 \(p\) 방향으로 평행이동 한 것과 같습니다.
따라서 아래와 같이 정리할 수 있습니다.

\[g_{0}(x) = f(p)\]
\[g_{1}(x) = f(p) + f'(p)(x-p)\]
\[g_{2}(x) = f(p) + f'(p)(x-p) + \frac{1}{2}f''(p)(x - p)^{2}\]
\[g(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(p)}{n!}(x - p)^{n}\]

$Drawing$

테일러 급수에 대하여 다시 정리해 보겠습니다. 테일러 급수는 미분 가능한 임의의 연속함수를 다항식을 이용하여 근사화 시킵니다. 테일러 급수는 임의의 점 \(x = p\)에서 멱급수 형태로 함수를 근사화 시키며 근사화된 식은 \(x = p\) 뿐 아니라 다른 \(x\) 값에서도 사용 가능합니다.
특히, \(x = 0\)에서 어떤 함수를 다항식으로 근사한 경우에 한하여 맥클로린 급수라고 합니다.
일반적으로 \(x = 0\) 일 때, 연산이 간단해 지기 때문에 맥클로린 급수를 많이 사용합니다. 경우에 따라서 \(x = 0\) 인 경우에 근사화 하지 못하는 경우가 있는데, 이 때 테일러 급수를 사용하면 됩니다.

Example of Taylor series

그러면 테일러 급수에 대한 2가지 예제를 살펴보도록 하겠습니다. 각 예제의 식은 \(\cos{(x)}\)와 \(1/x\) 입니다. 앞에서 설명한 바와 같이 특이한 경우가 아니면 맥클로린 급수를 사용하도록 하겠습니다.
그러면 먼저 \(f(x) = \cos{(x)}\)애 대하여 알아보도록 하겠습니다.

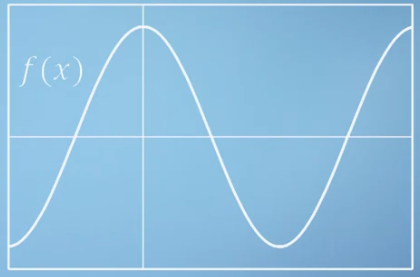
$Drawing$

위 그래프는 \(f(x) = \cos{(x)}\)의 그래프 입니다. 맥클로린 급수 식에 필요한 각 성분에 대하여 먼저 구해보면 다음과 같습니다.

\[f(x) = \cos{(x)}, \quad \therefore f(0) = \cos{(0)} = 1\]
\[f'(x) = -\sin{(x)}, \quad \therefore f'(0) = -\sin{(0)} = 0\]
\[f''(x) = -\cos{(x)}, \quad \therefore f''(0) = -\cos{(0)} = -1\]
\[f^{(3)}(x) = \sin{(x)}, \quad \therefore f^{(3)}(0) = \sin{(0)} = 0\]
\[f^{(4)}(x) = \cos{(x)}, \quad \therefore f^{(4)}(0) = \cos{(0)} = 1\]

그리고 맥클로린 함수인 \(g(x) = \sum_{n=0}^{\infty} \frac{f^{(n)(0)}}{n!}x^{n}\)에 대응하면 다음과 같습니다.

\[cos(x) = 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} - \frac{x^{6}}{720} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n)!}x^{2n}\]

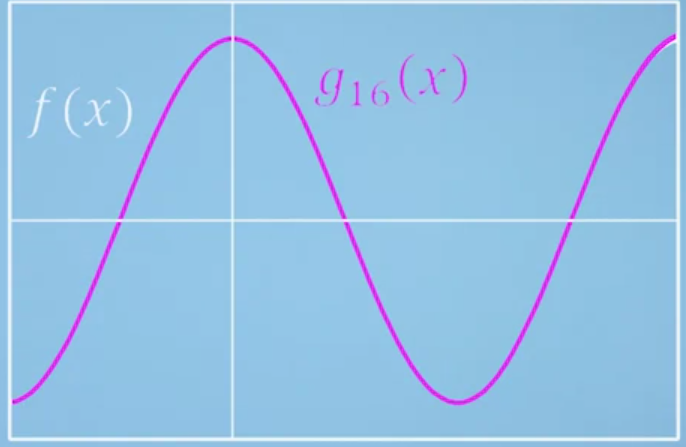
$Drawing$

참고로 16차 함수 정도로 근사하면 코사인 함수와 꽤나 유사하게 근사화 되는 것을 확인하실 수 있습니다.

그 다음으로 다루어 볼 함수는 \(f(x) = 1/x\) 함수입니다. 함수 형태는 아래와 같습니다.

$Drawing$

이 함수의 경우 맥클로린 급수를 사용하여 근사화 할 수 없습니다. 왜냐하면 \(x = 0\) 지점에서 연속적이지 않기 때문입니다. 따라서 테일러 급수를 사용하며 근사화 할 점은 계산량을 줄일 수 있는 \(x = 1\)로 잡겠습니다. 테일러 급수 전개에 필요한 각 성분을 구하면 다음과 같습니다.

\[f(x) = 1/x, \quad \therefore f(1) = 1/1 = 1\]
\[f'(x) = -1/x^{2}, \quad \therefore f'(1) = -1/1^{2} = -1\]
\[f''(x) = 2/x^{3}, \quad \therefore f''(1) = 2/1^{3} = 2\]
\[f^{(3)}(x) = -6/x^{4}, \quad \therefore f^{(3)}(1) = -6/1^{4} = -6\]
\[f^{(4)}(x) = 24/x^{5}, \quad \therefore f^{(4)}(1) = 24/1^{5} = 24\]

이 값들을 테일러 급수 인 \(g(x) = \sum_{n=0}^{\infty}\frac{f^{(n)}(p)}{n!}(x - p)^{n}\)에 대응하면

\[1/x = 1 - (x-1) + (x-1)^{2} - (x-1)^{3} + \cdots\]
\[1/x = \sum_{n=0}^{\infty}(-1)^{n}(x-1)^{n}\]

위 식과 같은 불연속 함수를 근사화 하면 다음과 같은 문제가 발생하게 됩니다.
① 테일러 급수를 통해 도출한 근사식을 실제 그려보면 \(x \gt 0\) 영역에서만 \(y\) 값을 가지게 됩니다. 이는 불연속 함수 \(f(x)\)를 근사화 했기 때문이고 그 중 \(x = 1\)을 포함하는 연속 구간의 식만 근사화 된것입니다.
② 연속 함수 근사화와 달리 상당히 불안정하게 근사화 하게 됩니다. 앞에서 살펴보았던 \(\cos{(x)}\)는 꽤나 근사화가 잘된 반면 \(1/x\)는 원래 함수 모양에 수렴하지 않습니다. 특히 점근선을 무시하는 근사화가 되곤합니다.

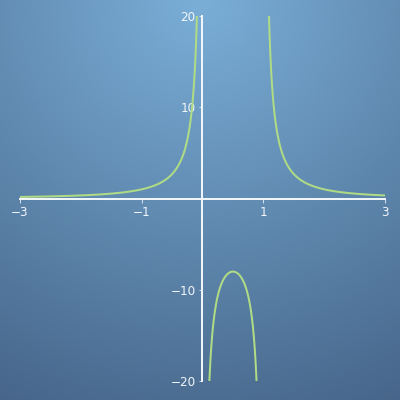
$Drawing$

예제를 한개 더 살펴보겠습니다. 위 그래프의 식은 \(f(x) = 2 / (x^{2} - x)\) 입니다. 이 식 또한 불연속적이기 때문에 테일러 급수로 근사화 하였을 때, 모든 영역을 근사화 할 수 없습니다.
예를 들어 \(x = 0.5\)에서 근사하면 \(0 \lt x \lt 1\) 영역에서의 함수값만 근사하게 됩니다. 반면 \(x = -3\) 에서 근사하면 \(x \lt 0\) 영역의 함수값만 근사하게 됩니다. 같은 이유로 \(x = 2\) 에서 근사하면 \(x \gt 1\) 영역의 함수값만 근사하게 됩니다.

Linearisation

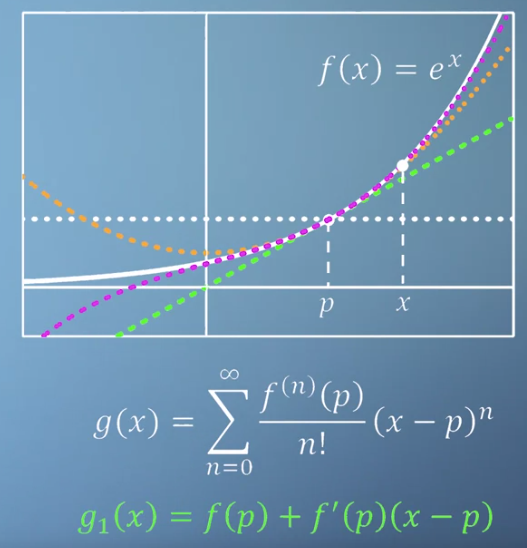
$Drawing$

앞에서 배운 바와 같이 어떤 함수 \(f(x)\)가 있을 때, 테일러 급수를 통하여 \(x = p\)에서 다항식의 멱급수로 근사화 할 수 있었습니다.
이 때, 근사한 일반식을 \(g(x)\)라 하면 1차식으로 근사한 식을 \(g_{1}(x)\) 형태로 사용하였습니다.
위 그림에서는 \(f(x)\)를 0, 1, 2, 3차 형태로 근사한 것을 점선으로 나타내었으며 그 중 초록색 선이 1차식으로 근사한 것입니다.
앞의 글 Basic Calculus에서 배운 바와 같이 변화량은 Rise Over Run 형태로 나타낼 수 있었습니다.

\[\text{Gradient} = \text{Rise} / \text{Run}\]
\[f'(p) = \text{Rise} / (x - p)\]

위 값의 분모를 각각 이항해 보면 다음과 같이 변형할 수 있습니다.

\[\text{Run} \times \text{Gradient} = \text{Rise}\]
\[(x - p) \times f'(p) = \text{Rise}\]

위 식에서 Run에 해당하는 것은 \(x\) 축에서의 증가량이고 ** p ** 만큼 증가하였으므로 \(\Delta p\)로 나타낼 수 있습니다.
즉, \(x - p = \Delta p\)가 되고 \(x = p + \Delta p\) 로 표현할 수 있습니다.

$Drawing$

따라서 위 그래프와 \(g_{1}(p + \Delta p)\) 처럼 정리 가능합니다.
그러면 앞에서 사용한 \(p\)를 \(x\)로 바꿔서 좀더 일반화 시켜보도록 하겠습니다. 식 자체의 변화는 전혀 없습니다.

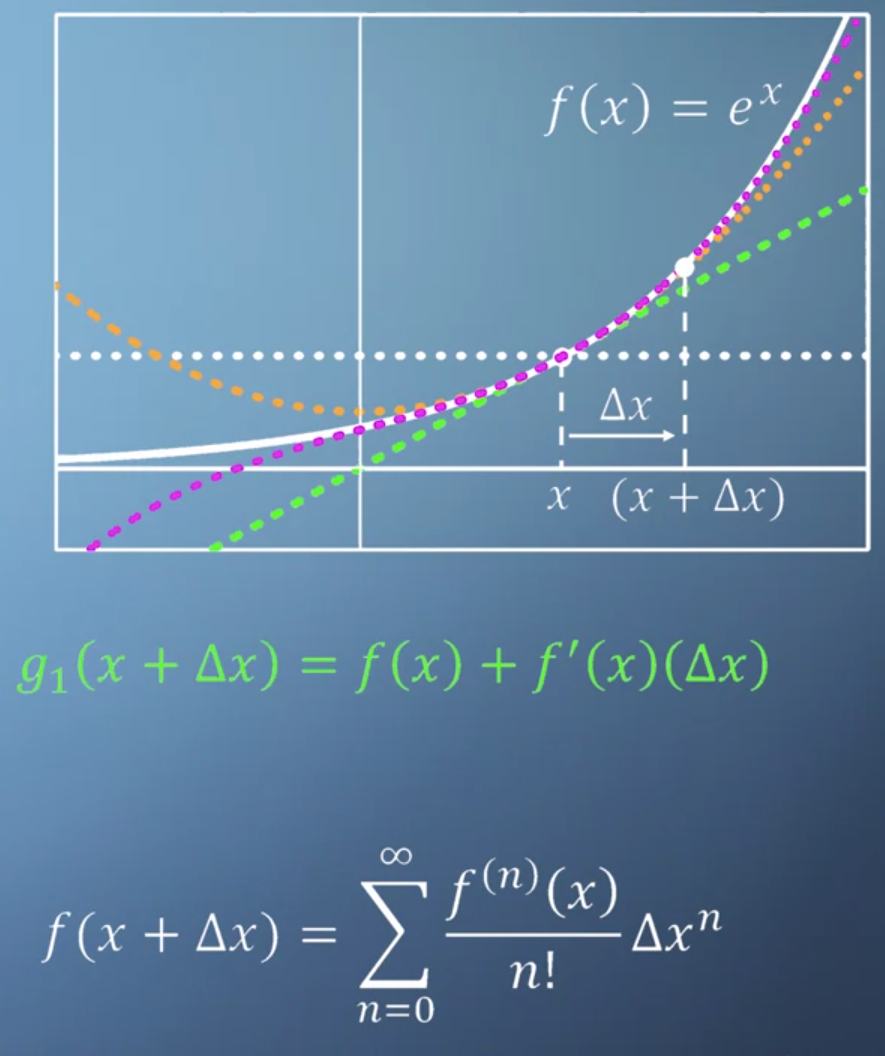
$Drawing$

위 그래프와 식처럼 테일러 급수를 새로운 형태로 나타낼 수 있습니다.

\[f(x + \Delta x) = \sum_{n = 0}^{\infty} \frac{f^{(n)(x)}}{n!} \Delta x^{n} = f(x) + f^{(1)}(x) \Delta x + \frac{f^{(2)}(x)}{2} \Delta x^{2} + \frac{f^{(3)}(x)}{6} \Delta x^{3} + \cdots\]

테일러 급수를 위 식과 같이 나타내었을 때, 주목할 점은 \(\Delta x\)입니다. 만약 \(\Delta x\) 값이 1보다 작은 값이라면 이 값의 제곱, 세제곱, n 제곱값은 계속 작아지므로 0에 수렴하게 됩니다.
위 식을 단순화 시켜 영향이 작은 \(\Delta x^{2}\) 부터 0에 수렴한다고 가정하면 아래와 같이 식을 단순화 시킬 수 있습니다.

\[f(x + \Delta x) = f(x) + f'(x)(\Delta x) + (0 + 0 + \cdots) = f(x) + f'(x)(\Delta x)\]

위 식과 같이 어떤 함수 \(f(x)\)를 0에 가까운 작은 값 \(\Delta x\)를 이용하여 근사화 할 때, 더해지는 값이 0에 가깝다고 판단되는 제곱, 세제곱, … , n제곱 항을 무시하여 간단하게 표시한 위 식을 선형화(linearisation) 라고 합니다.
이 컨셉으로 복잡한 함수를 단순한 선형 함수로 근사화 하여 값을 예측할 수 있습니다.

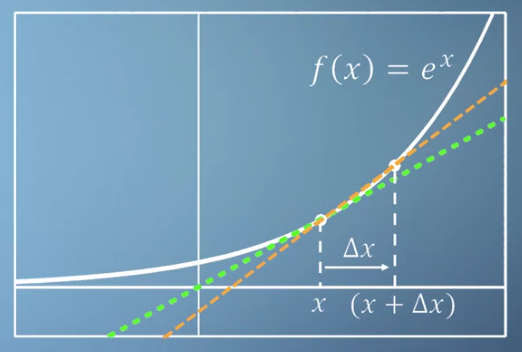
$Drawing$

linearisation을 앞에서 배운 rise over run과 비교하여 살펴보도록 하겠습니다.
위 그래프에서 지수 함수 \(f(x)\)를 \(\Delta x\)를 이용하여 1차식으로 근사화 한 것이 초록색 선입니다. 반면 주황색 선은 rise over run에 따라 \((x, f(x)), ((x + \Delta x), f(x + \Delta x))\) 를 연결한 직선입니다.
주황색 선은 실제 함수 \(f(x)\)를 이용하여 \(\Delta x\) 증가에 따른 변화율은 구한 것이므로 근사화 한 것이 아닌 정확한 값입니다.
반면 초록색 선은 테일러 급수의 원리에 따라서 근사화 한 값이기 때문에 같은 \(\Delta x\)를 이용하였다고 하더라도 주황색 선과 차이를 보입니다. 이 차이를 error 라고 하겠습니다.
그러면 error가 얼만큼인지 확인하기 위해 식을 변형해 보겠습니다.

\[f(x + \Delta x) = f(x) + f'(x)\Delta x + \frac{f''(x)}{2} \Delta x^{2} + \frac{f^{(3)}(x)}{6} \Delta x^{3} + \cdots\]
\[f'(x) = \frac{f(x + \Delta x) - f(x)}{\Delta x} - \frac{f''(x)}{2} \Delta x - \frac{f^{(3)}(x)}{6} \Delta x^{2} - \cdots\]

위의 첫번째 식을 \(f'(x)\)에 대하여 정리하면 두번째 식과 같이 정리할 수 있습니다.
두번째 식에서 우번의 첫번째 항이 바로 rise over run 입니다.
앞에서 linearisation을 위하여 두번째 식의 2번째 항 부터는 0에 수렴한다고 가정하여 아래 식과 같이 사용하였습니다.

\[f'(x) = \frac{f(x + \Delta x) - f(x)}{\Delta x} + 0\]

그러면 linearisation을 하였을 때의 error는 0에 수렴한다고 가정한 부분임을 알 수 있습니다. 즉 다음 식 부분이 실제 error에 해당합니다.

\[- \frac{f''(x)}{2} \Delta x - \frac{f^{(3)}(x)}{6} \Delta x^{2} - \cdots\]

여기서 다룬 기법은 컴퓨터가 문제를 해결할 때, 사람처럼 분석적인 방법으로 문제를 해결하는 것이 아닌 수치적으로 해결할 때 유용하게 사용됩니다. 그 내용은 다음 글에서 다루어 볼 예정입니다.

Multivariable Taylor Series

지금까지 배운 내용은 단일 변수일 때 적용한 테일러 급수이었습니다. 이번에는 차원을 늘려서 다변수에서 테일러 급수를 사용해 보도록 하겠습니다. 먼저 바로 앞에서 배운 내용을 다시 정리하면 다음과 같습니다.

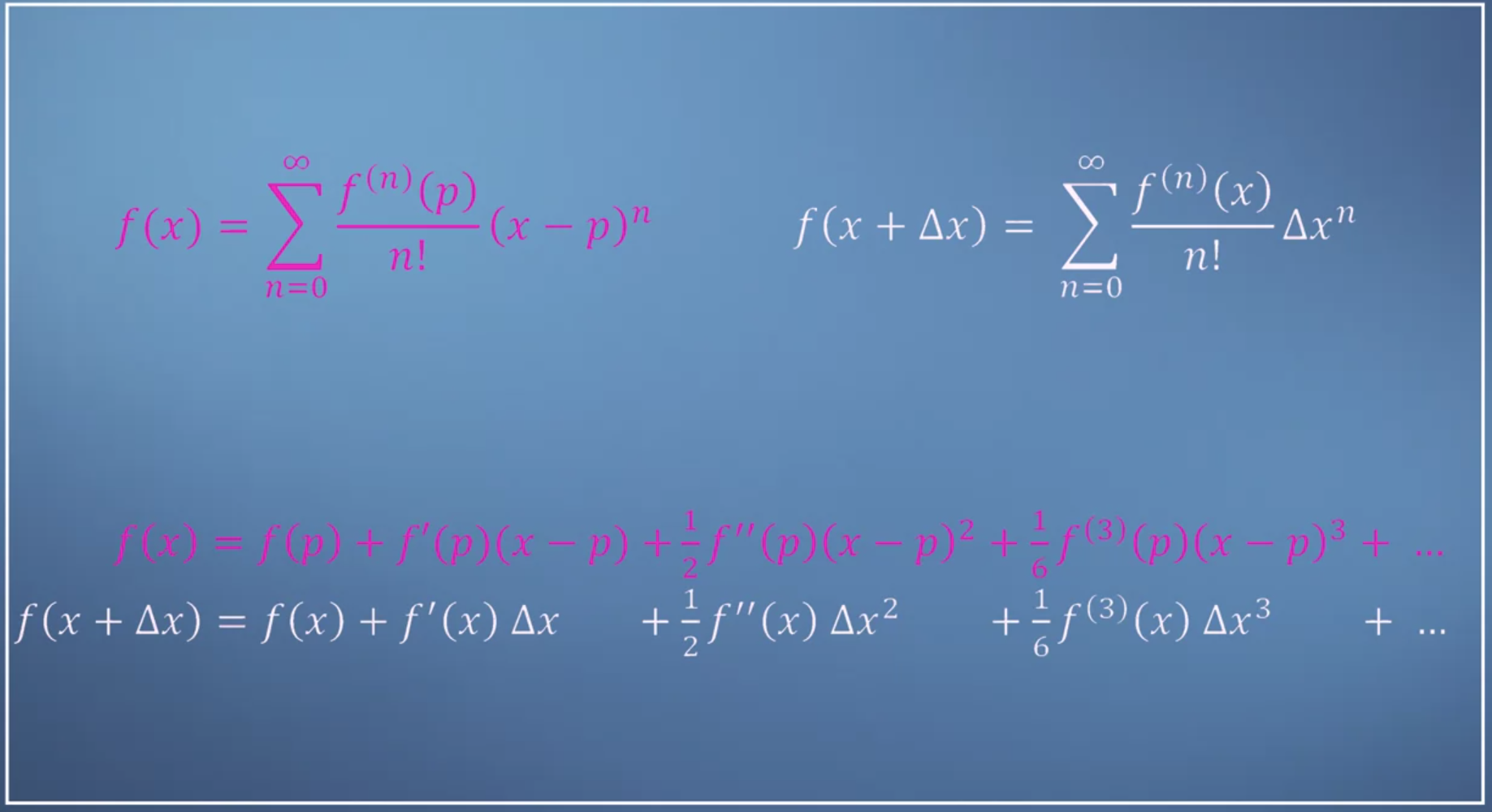
$Drawing$

\[f(x + \Delta x) = \sum_{n=0}^{\infty} \frac{f^{(n)(x)}}{n!} \Delta x^{n}\]
위 식의 변수는 \(x\) 입니다.
만약 변수를 늘려 \(f(x + \Delta x, y + \Delta y)\) 로 확장하면 어떻게 될까요?

$Drawing$

위 그림과 같이 가우시안 분포 형태의 그래프를 대상으로 이변량 테일러 급수에 대하여 알아보도록 하겠습니다.
앞에서 살펴 보았듯이 단일 변수에서는 0차로 근사화 하면 변수 축에 평행한 형태로 근사화 되었고 근사화 한 점의 함수값과 교차하는 형태를 가졌습니다.

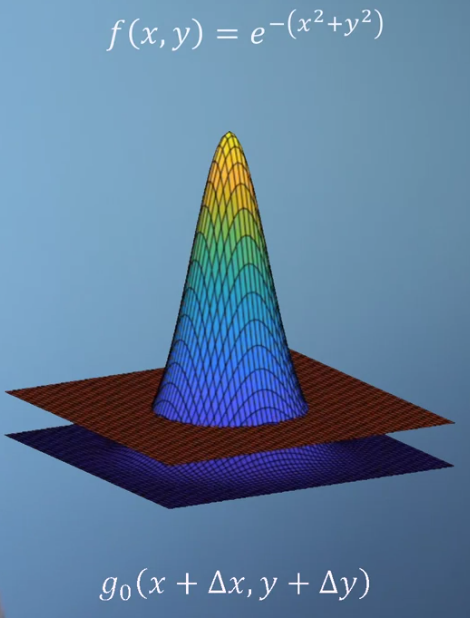
$Drawing$

이변량의 경우에도 0차로 근사화 한 경우 단일변량의 경우와 유사한 형태로 나타납니다. 위 그림을 참조하시기 바랍니다. 단순히 직선이 면으로 확장되었다고 보면 됩니다.
단인변량 함수에서 0차로 근사한 선과와 1차로 근사한 선의 차이점은 무엇일까요? 바로 기울기 입니다. 그러면 이변량의 경우에는 면에 기울기가 발생한다고 생각할 수 있습니다.

$Drawing$

위 그림을 보면 1차로 근사한 경우 기울기가 있는 면의 형태가 되는 것을 알 수 있습니다.

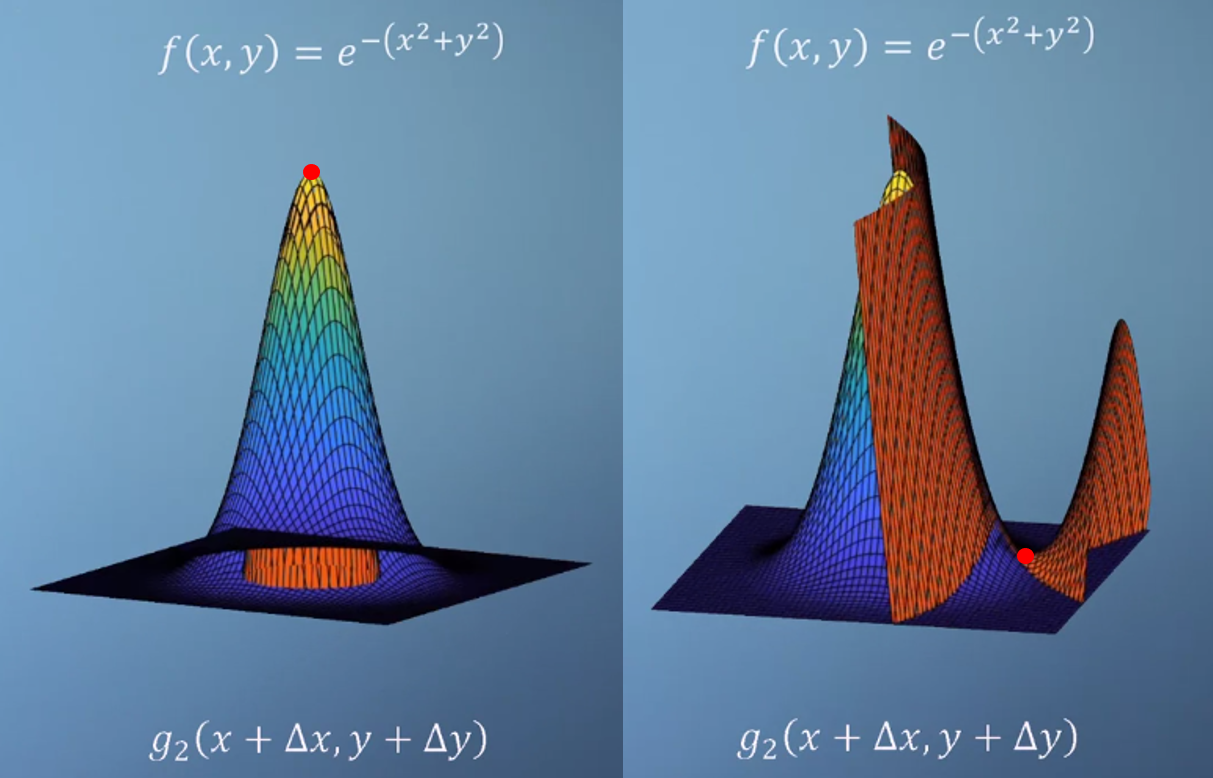
$Drawing$

위 그림은 2차식으로 근사한 경우입니다. 왼쪽 그림은 테일러 급수에서 근사하기 위해 사용한 지점이 꼭대기 점인 반면에 오른쪽 그림에서 근사하기 위해 사용한 지점은 지면에 있는 값에 해당합니다.
즉, 위 그림을 통해 어느 지점을 기준으로 근사화를 하느냐에 따라서 근사화 성능이 달라질 수 있음을 알 수 있습니다.

이번에는 이변량 테일러 급수의 식을 어떻게 전개하는 지 알아보도록 하겠습니다.
단일 변량의 경우 \(f(x + \Delta x)\) 형태로 나타낸 반면 이변량의 경우 \(f(x + \Delta x, y + \Delta y)\)로 나타낼 수 있습니다.
각 변수에 대하여 변화량을 계산하여 근사화 해야하므로 편미분을 사용합니다. 따라서 아래 식과 같이 0차, 1차, 2차에 대하여 편미분을 통해 테일러 급수를 전개할 수 있습니다.

\[f(x, y) \quad \text{ : 0th derivative}\]
\[(\partial_{x}f(x, y) \Delta x + \partial_{y}f(x, y) \Delta y) \quad \text{ : 1st derivative}\]
\[\frac{1}{2}(\partial_{xx}f(x, y) \Delta x^{2} + 2\partial_{xy}f(x, y)\Delta x \Delta y + \partial_{yy}f(x, y) \Delta y^{2}) \quad \text{ : 2nd derivative}\]

위 식에서 1차 미분을 한 항은 자코비안 행렬로 좀 더 간단하게 표현할 수 있습니다. 다음과 같습니다.

\[(\partial_{x}f(x, y) \Delta x + \partial_{y}f(x, y) \Delta y) \color{purple}{\to} \color{purple}{\begin{bmatrix} \partial_{x}f(x, y) & \partial_{y}f(x, y) \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}} \color{orange}{\to J_{f} \Delta x}\]

반면 2차 미분을 한 항은 헤시안 행렬로 좀 더 간단하게 표현할 수 있습니다. 다음과 같습니다.

\[\frac{1}{2}(\partial_{xx}f(x, y) \Delta x^{2} + 2\partial_{xy}f(x, y)\Delta x \Delta y + \partial_{yy}f(x, y) \Delta y^{2}) \color{purple}{\to \frac{1}{2} \begin{bmatrix} \Delta x, & \Delta y \end{bmatrix} \begin{bmatrix} \partial_{xx}f(x, y) & \partial_{xy}f(x, y) \\ \partial_{yx}f(x, y) & \partial_{yy}f(x, y) \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}} \color{orange}{\to \frac{1}{2} \Delta x^{t} H_{f} \Delta x}\]

참고로 자코비안과 헤시안 행렬의 개념은 다음 링크에서 확인하실 수 있습니다.
위 성분들을 합하여 표현하면 다음과 같습니다.

\[f(x + \Delta x, y + \Delta y) = f(x,y) + (\partial_{x}f(x, y) \Delta x + \partial_{y}f(x, y) \Delta y) + \frac{1}{2}(\partial_{xx}f(x, y) \Delta x^{2} + 2\partial_{xy}f(x, y)\Delta x \Delta y + \partial_{yy}f(x, y) \Delta y^{2})\]

\[f(x + \Delta x, y + \Delta y) = f(x,y) + \color{purple}{\begin{bmatrix} \partial_{x}f(x, y), & \partial_{y}f(x, y) \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix} + \frac{1}{2} \begin{bmatrix} \Delta x, & \Delta y \end{bmatrix} \begin{bmatrix} \partial_{xx}f(x, y) & \partial_{xy}f(x, y) \\ \partial_{yx}f(x, y) & \partial_{yy}f(x, y) \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix} + \cdots}\]

\[f(x + \Delta x, y + \Delta y) = f(x,y) + \color{orange}{J_{f} \Delta x + \frac{1}{2} \Delta x^{t} H_{f} \Delta x + \cdots}\]

예를 들어 다음 2가지 예제를 한번 풀어보겠습니다.
① \(f(x, y) = xy^{2}e^{-x^{4}-y^{2}/2}\) 식을 \((x, y) = (-1, 2)\)에서 1차 테일러 급수로 근사화 해보겠습니다. \(f(x, y)\)를 먼저 편미분 합니다.

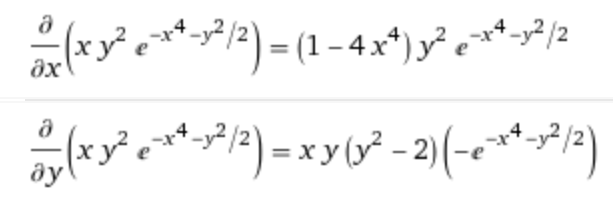
$Drawing$

그러면 \(f_{1}(-1 + \Delta x, 2 + \Delta y) = f(-1, 2) + \begin{bmatrix} \partial_{x}f(-1, 2) & \partial_{y}f(-1, 2) \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix}\)와 편미분한 결과를 이용하여 식을 풀면 아래와 같습니다.

\[f_{1}(-1 + \Delta x, 2 + \Delta y) = -4e^{-3} -12e^{-3}\Delta x + 4e^{-3}\Delta y\]

② \(f(x, y) = \sin{(\pi x - x^{2}y)}\) 식을 \((x, y) = (1, \pi)\)에서 2차 테일러 급수로 근사화 하려고 할 때, 헤시안 행렬을 구해보도록 하겠습니다.

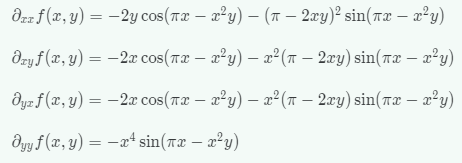
$Drawing$

위에서 구한 헤시안 행렬의 각 성분을 이용하고 \((x, y) = (1, \pi)\)를 직접 대입하여 \(\begin{bmatrix} \partial_{xx}f(x, y) & \partial_{xy}f(x, y) \\ \partial_{yx}f(x,y) & \partial_{yy}f(x, y) \end{bmatrix}\)를 구하면 아래와 같습니다.

\[H_{f} = \begin{bmatrix} -2\pi & -2 \\ -2 & 0 \end{bmatrix}\]

지금까지 테일러 급수와 매클로린 급수 그리고 선형화와 2D 테일러 급수 까지 모두 알아보았습니다. 이제 테일러 급수가 무엇인지는 정확히 알았으니 왜 사용하는 지 알아보도록 하겠습니다.

테일러 급수의 사용 이유와 활용

mathematics for machine learning 글 목록