가우시안 (Gaussian) 관련 내용 정리
2021, Dec 20
- 공학에서
가우시안과 관련된 내용은 너무나 중요한 개념입니다. 공부하면서 종종 쓰였단 가우시안과 관련된 개념들을 이 글에 정리하고자 하며 학습 범위가 깊어지는 글은 별도 링크를 달아두도록 하겠습니다.
목차
-
가우스 함수
-
가우스 적분 증명
-
가우시안 분포 공식 유도
-
1D, 2D, 3D 가우시안 분포
-
가우시안 PDF의 곱과 Convoltuion 연산
-
covariance와 zero-mean gaussian의 covariance
-
가우시안 혼합 모델(Gaussian Mixture Model)과 EM 알고리즘
-
가우시안 프로세스
-
가우시안 분포를 이용한 Anomaly Detection 응용
가우스 함수
- 가우스 함수 식은 다음과 같습니다.
- \[f(x) = a \cdot exp(-\frac{(x - b)^{2}}{c^{2}})\]
- 여기서 \(a (> 0), b, c\)는 실수입니다.
- 이 함수는 좌우 대칭의 종(bell) 모양의 곡선을 가지고 +/- 극한값을 입력으로 받으면 급격히 함수 값이 감소하게 됩니다.
- 매개변수 \(a\)의 역할은 종 모양 곡선의 꼭대기 높이가 되고 \(b\)는 꼭대기 중심의 위치가 됩니다. \(c\)는 종 모양의 너비를 결정합니다.
- 가우스 함수의 의미는 가우스 오차 함수의 미분값(도함수)이고 가우시안 분포의 밀도 함수가 됩니다.
가우스 적분 증명
- 위키피디아에 따른
가우스 적분(Gaussian integral)의 정의는 가우스 함수에 대한 실수 전체 범위의 적분으로 식은 다음과 같습니다.
- \[\int_{-\infty}^{\infty} e^{-x^{2}} dx = \sqrt{\pi}\]
- 가우스 적분의 증명을 이용하면 가우시안 분포 공식의 유도에도 사용할 수 있기 때문에, 가우스 적분의 증명을 어떻게 하는 지 알아보도록 하겠습니다.
- \[I = \int_{-\infty}^{\infty} e^{-x^{2}} dx\]
- \[I^{2} = \Biggl( \int_{-\infty}^{\infty} e^{-x^{2}} dx \Biggr)^{2} = \int_{-\infty}^{\infty} e^{-x^{2}} dx \int_{-\infty}^{\infty} e^{-y^{2}} dy\]
- 위 식에서 \(x\) 변수는 소위 말하는 더미 변수이므로 한 개의 \(x\)를 \(y\) 로 변경하였습니다.
- \[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^{2} + y^{2})} dx dy\]
- 식을 정리하면 위와 같이 두 변수 \(x, y\)에 대하여 정리할 수 있습니다.
- 이 식을 풀기 위해
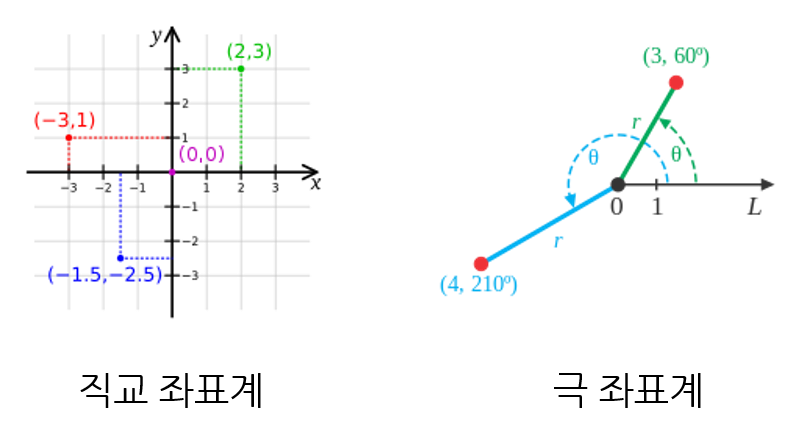
극 좌표계개념을 가져오도록 하겠습니다. 극 좌표계는 \((r, \theta)\)로 좌표 평면의 좌표를 표현하는 방법입니다. 여기서 \(\theta\)의 단위는radian입니다. 아래 그림을 참조하시기 바랍니다.
- 그러면 \(x, y\) 축을 이용하여 \((x, y)\)로 나타내는 직교 좌표계와 \((r, \theta)\)로 나타내는 극 좌표계의 관계를 살펴보면 다음과 같습니다.
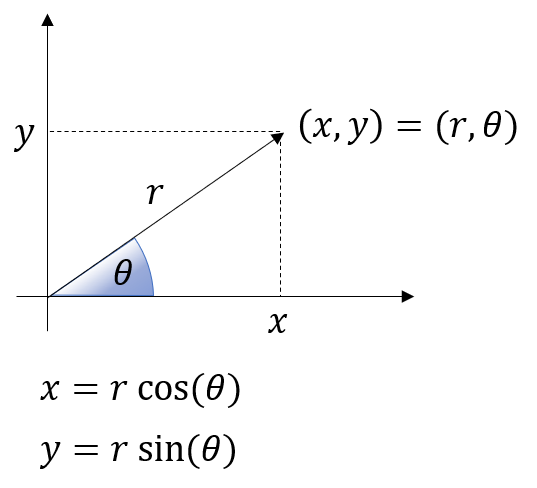
- 위 식에 따라서 \(x^{2} + y^{2} = r^{2}\)이 성립합니다. 물론 원의 방정식에 의한 관계라고 이해하셔도 무방합니다.
- \[x^{2} + y^{2} = (r \cos{(\theta)})^{2} + (r \sin{(\theta)})^{2} = r^{2}(\cos^{2}{(\theta)} + \sin^{2}{(\theta)}) = r^{2}\]
- 이렇게 직교 좌표계를 극 좌표계로 바꾸는 이유는 적분을 하기 위함입니다. 즉, 적분할 때, \(dx, dy\)를 \(dr, d\theta\)로 바꾸려고 합니다.
- 그러면 적분의 구간은 \(x : (-\infty, \infty), \ y : (-\infty, \infty) \to r : (0, \infty), \ \theta : (0, 2\pi)\)로 변경됩니다.
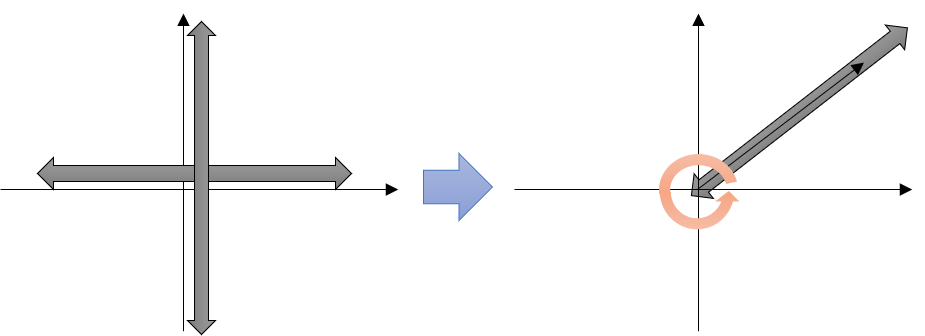
- 즉, 위 그림과 같이 기존의 직교 좌표계에서는 \(x, y\)의 값이 음의 무한대에서 양의 무한대의 영역의 범위를 가지게 되므로 좌표계 전체 영역을 적분 할 수 있는 반면 극 좌표계에서는 원점에서 시작하는 선 \(r\)의 길이가 0에서 양의 무한대의 영역의 범위를 가지고 그 선의 이동 영역이 0에서 \(2\pi\) 만큼의 범위를 가지게 되므로 똑같이 좌표계 전체 영역을 적분할 수 있게 됩니다.
- 따라서 적분하는 영역은 같으나 접근 방식이 다르다고 이해하시면 됩니다.
- 그러면 \(dx \cdot dy\)를 \(dr \cdot d\theta\)로 변환하면 그 변환 term은 얼만큼 곱해주어야 할까요? 아래 그림을 통하여 직교 좌표계에서의 미소 면적과 극 좌표계에서의
미소 면적의 차이를 알아보겠습니다.

- 먼저 직교 좌표계에서는 \(x, y\)의 변화량 \(dx, dy\)에 의해 증가한 미소 면적은 직사각형으로 \(dx \cdot dy\) 입니다.
- 반면 극 좌표계에서 \(r, \theta\)의 변화량 \(dr, d\theta\)에 의해 증가한 영역은 \(r \cdot dr \cdot d\theta\) 입니다.
- (먼저 추상적으로 설명해 보면) 다음과 같은 적분의 성질을 보면 적분 구간을 근사(approximation)하여 면적을 구하는 것을 볼 수 있습니다.

- 위 그림의 왼쪽 그림을 보면 곡선은 함수 \(r(\theta)\)를 따르고 \(\theta\)의 범위는 \([a, b]\)입니다. 이 때, 면적 \(R\)을 한번에 구하기 어렵기 때문에 다음 식을 통해서 근사화 하여 구할 수 있습니다.
- \[\frac{1}{2} \int_{a}^{b} r(\theta)^{2} d\theta\]
- 위 식을 유도해 보겠습니다. 오른쪽 그림과 같이 구간을 \(n\)개로 나누고 각 구간을 \(i = 1, 2, \cdots, n\)에서 \(\theta_{i}\)이 각 구간의 중점이라고 하고 극에 중심을 두는 부채꼴을 만듭니다.
- 이 때, 각 호의 반지름은 \(r(\theta_{i})\), 중심각은 \(\Delta \theta_{i}\)이면 호의 길이는 \(r(\theta_{i})\Delta \theta\)가 되고 넓이는 \(\frac{1}{2}r(\theta_{i})^{2} \Delta \theta\)가 됩니다. 따라서 총 넓이는 리만 합에 따라서 다음과 같이 정리됩니다.
- \[\sum_{i=1}^{n} \frac{1}{2} r(\theta_{i})^{2} \Delta \theta\]
- 리만 합의 정의에 따라 구간의 갯수 \(n\)이 증가할수록 그 극한값은 넓이 \(R\)에 가까워집니다.
- 이 성질을 이용하면 앞선 그림의 넓이 증가량을 \(\color{blue}{r \cdot d\theta} \cdot \color{red}{dr}\)의 사각형 넓이로 근사하여 생각할 수 있습니다. 리만 합에 의해 \(r, \theta\)의 값이 작은 단위로 나누어져서 합쳐진다면 실제 넓이에 가까워질 것이기 때문입니다.
- 즉, discrete 한 케이스의 \(\sum\)을 이용한 식의 구간을 무수히 많이 쪼개어서 합하게 되면 \(\int\) 형태의 합이 됩니다.
- 여기까지가 추상적이고 직관적인 설명이긴 합니다. 좀 더 구체적으로 알고 싶으면 아래 내용을 읽어보시면 도움이 됩니다. (넘어가셔도 됩니다.)
- 직교 좌표계에서는 미소 면적의 넓이를 \(dA = dx \cdot dy\)로 표시하였습니다.
- 그리고 \(x, y\)는 다음과 같이 \(r, \theta\)로 나타내어 졌습니다.
- \[x = r \cos{(\theta)}\]
- \[y = r \sin{(\theta)}\]
- 여기서 \(x, y\) 에 대하여 각각 \(r, \theta\)에의 변화량을 확인하기 위해
자코비안을 구해보면 다음과 같습니다. - 아래 자코비안의 1행, 2행은 각각 \(x, y,\)가 \(r, \theta\) 각각의 변화에 따라 얼만큼 변화를 가지는 지 나타냅니다.
- \[\frac{\partial(x, y)}{\partial(r, \theta)} = \begin{bmatrix} \partial x / \partial r & \partial x / \partial \theta \\ \partial y / \partial r & \partial y / \partial \theta \end{bmatrix} = \begin{bmatrix} \cos{(\theta)} & -r\sin{(\theta)} \\ \sin{(\theta)} & r\cos{(\theta)} \end{bmatrix}\]
- 변화의 scale을 구할 때,
determinant를 사용할 수 있습니다. 지금과 같은 2차원에서 변화의 총량은 변화하였을 때의넓이의 scale이 됩니다. 그러면 위에서 구한 자코비안의 determinant를 \(J\)라고 나타내면 다음과 같습니다.
- \[J = \begin{vmatrix} \cos{(\theta)} & -r\sin{(\theta)} \\ \sin{(\theta)} & r\cos{(\theta)} \end{vmatrix} = r \cos^{2}{(\theta)} + r \sin^{2}{(\theta)} = r\]
- 즉, \(r, \theta\)가 \(dr, d\theta\) 만큼 변할 때, 변화하는 양 scale은 \(J = r\) 이 됩니다.
- 따라서 직교 좌표계의 변화량과 극 좌표계의 변화량은 다음 관계를 가집니다.
- \[dA = dx \cdot dy = J \cdot dr \cdot d\theta = r \cdot dr \cdot d\theta\]

- 다시 확인해 보면 극 좌표계에서 \(r, \theta\)의 변화에 따른 변화량은 직관적인 설명과 자코비안을 통한 설명 모두 \(r \cdot dr \cdot d\theta\) 임을 확인할 수 있습니다.

- 변화량의 scale은 \(r\) 입니다. 따라서 호의 반지름의 길이인 \(r\)이 커질수록 미소 면적의 크기가 커짐을 확인할 수 있습니다.
- 지금 까지 확인한 내용인 직교 좌표계에서 극 좌표계로 변환을 통해 적분을 마무리 해보겠습니다.
- \[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-(x^{2} + y^{2})} \cdot dx \cdot dy = \int_{0}^{2\pi}\int_{0}^{\infty} e^{-r^{2}} \cdot r \cdot dr \cdot d\theta\]
- 이제 식이 깔끔하게 정리되었으니 단순 치환 적분을 통하여 문제를 풀어보겠습니다.
- \[-r^{2} = u\]
- \[-2r dr = du\]
- \[r dr = -\frac{1}{2} du\]
- \[\begin{split} \int_{0}^{2\pi}\int_{0}^{\infty} e^{-r^{2}} \cdot r \cdot dr \cdot d\theta &= \int_{0}^{2\pi}\int_{0}^{-\infty} e^{u} (-\frac{1}{2})du \cdot d\theta &= -\frac{1}{2} \int_{0}^{2\pi} [e^{u}]_{0}^{-\infty} d\theta &= \frac{1}{2} \int_{0}^{2\pi} d\theta = \pi \end{split}\]
- \[I^{2} = \pi = \Biggl( \int_{-\infty}^{\infty} e^{-x^{2}} dx \Biggr)^{2}\]
- \[\therefore \quad \int_{-\infty}^{\infty} e^{-x^{2}} dx = \sqrt{\pi}\]
가우시안 분포 공식 유도
- 참조 : https://www.alternatievewiskunde.nl/QED/normal.pdf
- 자료 : https://drive.google.com/file/d/1n_PeSlIzJRsbHmfUlGHSBuNh1AdDWx6e/view?usp=sharing
- 참조 : https://angeloyeo.github.io/2020/09/14/normal_distribution_derivation.html
가우시안 분포는정규 분포라는 이름으로 중고등학교 때 부터 이미 많이 사용되어 왔지만 그 공식의 유도는 많은 분들이 다루어 보지 못하였을 것으로 생각됩니다.- 이번 글에서는 가우시안 분포 공식을 유도해보도록 하겠습니다. 이 식의 유도는 위 2개의 글을 참조하여 작성하였습니다.
- 먼저 바로 앞에서 다룬 가우스 적분 증명 내용은 먼저 확인해 주시기 바랍니다.
- 먼저 가우시안 분포의 형태를 살펴보면 다음과 같습니다.
- \[f(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp{\biggl( -\frac{(x - \mu)^{2}}{2\sigma^{2}} \biggr) }\]
- 가우시안 분포를 유도하기 위하여 3가지 부분으로 나누어서 차례대로 유도해보겠습니다.
- \[f(x) = \color{blue}{\frac{1}{\sigma \sqrt{2\pi}}} \color{red}{\exp{\biggl(-\color{green}{\frac{(x - \mu)^{2}}{2\sigma^{2}}} \biggr) }}\]
- ① \(\color{red}{e^{-x^{2}}}\) 의 꼴을 유도해 보겠습니다.
- ② \(\color{blue}{\frac{1}{\sigma \sqrt{2\pi}}}\) 의 꼴을 유도해 보겠습니다.
- ③ \(\color{green}{\frac{(x-\mu)^{2}}{2\sigma^{2}}}\) 의 꼴을 유도해 보겠습니다.
Determining the Shape of the Distribution
- 그러면 먼저 가우시안 분포 \(f(x)\) 가 \(e^{-x^{2}}\) 형태의 꼴을 따르는 ① 식을 살펴보겠습니다.
- 이 식의 전개를 살펴보기 위하여
직교좌표계와극좌표계의 관계를 이용해야하기 때문에 다음과 같은 가정을 사용합니다.

- ⓐ 원점으로 같은 거리에 있는 점은 확률 값은 모두 같으므로 확률 밀도 함수는 회전 각도에 독립적입니다.
- ⓑ 사각형의 크기가 같을 때, 원점으로부터 사각형까지의 거리가 가까울수록 그 사각형의 확률밀도는 높습니다.
- ⓒ 사각형까지의 거리가 같을 떄에는 사각형의 넓이가 넓을 수록 확률밀도가 높습니다.
- 위 그림을 살펴보면 사각형 A, B, C는 크기는 같지만 원점을 중심으로 거리가 다르기 때문에 \(A \gt B \gt C\) 크기 순으로 확률 값을 가집니다.
- 반면 D, E, F는 원점으로 부터 사각형의 거리는 같지만 사각형의 크기가 차이가 나므로 \(F \gt E \gt D\) 크기 순으로 확률 값을 가집니다.
- 위 조건을 유심히 살펴보면 원점이 가장 나타날 확률이 높고 원점에서 멀어질수록 확률이 낮아지는 정규 분포 형태를 가짐을 알 수 있습니다. 즉, 정규 분포와 유사한 조건을 전제 조건으로 둔 것을 알 수 있습니다.

- 앞의 조건들을 전제 조건으로 위 그림의 Figure 2의 음영 처리된 면적이 선택될 확률을 살펴보겠습니다.
- 먼저 연속 확률 밀도 함수에서의 기댓값의 정의 \(\int x f(x) dx\) 에 따라 다음과 같이 음영 부분의 확률 밀도 함수를 표현하도록 하겠습니다.
- \[p(x) \Delta x = \int_{x}^{x + \Delta x} x f_x(x) dx\]
- \[p(y) \Delta y = \int_{y}^{y + \Delta y} y f_y(x) dy\]
- 또한 앞서 언급한 전제 조건 ⓐ, ⓑ, ⓒ에 따라서 원점을 기준으로
normal probability density function의 성질을 가짐을 알 수 있습니다. - 따라서 음영 지역을 선택할 확률은 \(p(x) \Delta x \cdot p(y) \Delta y\) 가 됩니다.
- 또한 ⓐ 조건에 따라 어떤 영역이라도 회전 각도에 독립적이므로 \(r, \theta\) 를 이용하여
극 좌표계로 확률값을 나타내면 직교좌표계 결과를 참조하여 \(g(r) \Delta x \Delta y\) 로 나타낼 수 있습니다. - 같은 음영 면적이 선택될 확률에 대하여
직교 좌표계상에서의 확률과극 좌표계상에서의 확률은 같아야 하므로 다음과 같이 식을 적을 수 있습니다.
- \[p(x) \Delta x \cdot p(y) \Delta y = g(r) \Delta x \Delta y\]
- \[g(r) = p(x) p(y)\]
-
여기서 \(g(r)\) 은 각의 변화에 대하여 독립적이므로 각 \(\theta\) 에 대하여 미분을 하면 변화량이 없으므로 0이 되어야 합니다. 따라서 위 식을 \(\theta\) 에 미분하면 다음과 같습니다.
- \[\frac{d p(x)}{d\theta}p(y) + \frac{d p(y)}{d\theta}p(x) = \frac{g(r)}{d\theta} = 0\]
- \[\Rightarrow \frac{d p(x)}{dx}\frac{dx}{d\theta}p(y) + \frac{d p(y)}{dy}\frac{dy}{d\theta}p(x) = 0\]
- \[\Rightarrow p(x)\frac{d p(y)}{dy}\frac{dy}{d\theta} + p(y)\frac{d p(x)}{dx}\frac{dx}{d\theta} = 0\]
- \[\Rightarrow p(x)p'(y)\frac{dy}{d\theta} + p(y)p'(x)\frac{dx}{d\theta} = 0\]
- 극 좌표계에서 \(x = r \cos{(\theta)}, y = r\sin{(\theta)}\) 이므로 \(x, y\) 를 \(\theta\) 에 미분하면 다음과 같습니다.
- \[\frac{dx}{d\theta} = -r\sin(\theta)\]
- \[\frac{dy}{d\theta} = r\cos(\theta)\]
- 이 값을 이용하여 식을 다시 전개하면 다음과 같습니다.
- \[p(x)p'(y)\frac{dy}{d\theta} + p(y)p'(x)\frac{dx}{d\theta} = 0\]
- \[\Rightarrow p(x)p'(y)(r\cos(\theta)) + p(y)p'(x)(-r\sin(\theta)) = 0\]
- 여기서 \(r\sin(\theta)=y\) 과 \(r\cos(\theta)=x\) 을 이용하면 다음과 같이 식을 정리할 수 있습니다.
- \[p(x)p'(y)x - p(y)p'(x)y = 0\]
- \[p(x)p'(y)x = p(y)p'(x)y\]
- \[\frac{p'(x)}{x p(x)} = \frac{p'(y)}{yp(y)} \ \ \ \ \ \cdots \text{(solved by separating variables)}\]
- 위 미분 방정식은 어떤 \(x, y\) 에 대하여 만족해야 하며 \(x, y\) 각각은 독립적이어야 합니다. 이 조건을 만족하려면 위 식이 항상 어떤 상수 값이 되어야 합니다.
- \[\frac{p'(x)}{x p(x)} = \frac{p'(y)}{yp(y)} = C\]
- 위 식의 좌변과 우변의 형태가 같기 때문에 좌변인 \(\frac{p'(x)}{x p(x)}\) 에 대하여 식을 풀어주면 같은 결과를 얻을 수 있으므로 다음 미분 방정식을 풀어줍니다.
- \[\frac{p'(x)}{x p(x)} = C\]
- \[\frac{x p(x)}{p'(x)} = C \ \ \ \ \text{C is constant.}\]
- \[x = C\frac{p'(x)}{p(x)}\]
- \[\text{applying integral } \Rightarrow \frac{1}{2}x^{2} = C \ln{(p(x))} + C'\]
- 위 식에서 \(C'\) 은 적분에 의해 생긴 또 다른 상수입니다. 따라서 합쳐서 적을 수 있습니다.
- \[\frac{1}{2}x^{2} - C' = C \ln{(p(x))}\]
- \[\frac{1}{2C}x^{2} - \frac{C'}{C} = \ln{(p(x))}\]
- \[p(x) = \exp{(\frac{1}{2C}x^{2} - \frac{C'}{C})} = \exp{\frac{1}{2C}x^{2}} \cdot \exp{-\frac{C'}{C}} = \exp{\frac{1}{2}c x^{2}} A\]
- 마지막 식에서 상수 \(1/C\) 는 \(c\) 로 다시 표현하였고 \(\exp{-\frac{C'}{C}} = A\) 로 표현하였습니다. 따라서 식을 정리하면 다음과 같습니다.
- \[p(x) = A e^{\frac{c}{2}x^{2}}\]
- 이 때, 앞에서 정의한 가정인 ⓑ 사각형의 크기가 같을 때, 원점으로부터 사각형까지의 거리가 가까울수록 그 사각형의 확률밀도는 높습니다. 조건으로 인하여 원점으로부터 거리가 가까울수록 확률이 높도록 식을 만들어야 하기 때문에 \(\exp{()}\) 내부의 값은 음수가 되도록 하여 지수승의 값이 0에 가까울수록 큰 값을 가지도록 하고 무한대에 가까워질수록 0에 가까운 값을 가지도록 만듭니다. 따라서 \(k > 0\) 인 양의 값을 도입하여 다음과 같이 식을 적을 수 있습니다.
- \[p(x) = A e^{-\frac{k}{2}x^{2}}\]
- 지금까지 살펴본 바로 가우시안 분포에서 첫번째 부분인 ① \(\color{red}{e^{-x^{2}}}\) 의 꼴을 유도하였습니다.
- \[f(x) = \color{blue}{\frac{1}{\sigma \sqrt{2\pi}}} \color{red}{\exp{\biggl(-\color{green}{\frac{(x - \mu)^{2}}{2\sigma^{2}}} \biggr) }}\]
- 그 다음으로 앞에서 유도한 식의
A의 값이 어떻게 \(\color{blue}{\frac{1}{\sigma \sqrt{2\pi}}}\) 을 만족하는 지 살펴보도록 하겠습니다.
Determining the Coefficient A
- 앞에서 정의한 \(p(x) = A e^{-\frac{k}{2}x^{2}}\) 확률 분포 또한 확률이기 때문에 곡선 아래의 전체 면적은 전체 확률값인 1이 되어야 합니다.
- 따라서 \(A\) 값을 적당하게 조정하여 면적의 값이 1이 되도록 만들어 \(A\) 의 값을 정해보도록 하겠습니다.
- \[\int_{-\infty}^{\infty} A e^{-\frac{k}{2}x^{2}} dx = 1\]
- \[\int_{-\infty}^{\infty} e^{-\frac{k}{2}x^{2}} dx = \frac{1}{A}\]
- \[\Rightarrow \biggl( \int_{-\infty}^{\infty} e^{-\frac{k}{2}x^{2}} dx \biggr)\biggl( \int_{-\infty}^{\infty} e^{-\frac{k}{2}y^{2}} dy \biggr) = \frac{1}{A^{2}}\]
- 위 식에서 \(x, y\) 각각은 독립적인 dummy 변수이므로 다음과 같이 적을 수 있습니다.
- \[\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-\frac{k}{2}(x^{2} + y^{2})} dy dx = \frac{1}{A^{2}}\]
- 위 식을 직교좌표계에서 극좌표계로 바꾸어서 쓰면 다음과 같이 바꿔 적을 수 있습니다.
- \[\int_{0}^{\infty} \int_{0}^{\infty} e^{-\frac{k}{2}(x^{2} + y^{2})} dy dx = \frac{1}{A^{2}}\]
- \[\Rightarrow \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-\frac{k}{2}r^{2}} r dr d\theta = \frac{1}{A^{2}}\]
- 적분을 풀기 위하여 다음과 같이 치환 적분을 해주려고 합니다. 다만, 계산 과정을 스킵하시고 싶으면 아래 울프람 알파의 결과만 확인하시기 바랍니다.
- 계산 과정은 다음과 같습니다. 먼저 위 적분을 풀기 위하여 다음과 같이 치환을 해줍니다.
- \[-\frac{1}{2}kr^{2} = u\]
- \[-krdr = du\]
- \[rdr = -\frac{1}{k} du\]
- 위 식을 이용하여 \(-\frac{1}{2}kr^{2} \to u\) , \(rdr \to -\frac{1}{k} du\) 형태로 모두 바꾸어 치환 적분하면 다음과 같습니다.
- \[\int_{\theta=0}^{\theta=2\pi} \int_{u=0}^{u=-\infty} e^{-\frac{k}{2}r^{2}} r dr d\theta = \frac{1}{4A^{2}}\]
- \[= \int_{\theta=0}^{\theta=2\pi} \int_{u=0}^{u=-\infty} e^{u} -\frac{1}{k} du d\theta\]
- \[= -\frac{1}{k} \int_{\theta=0}^{\theta=2\pi} \int_{u=0}^{u=-\infty} e^{u} du d\theta\]
- \[= -\frac{1}{k} \int_{\theta=0}^{\theta=2\pi} [e^{u}]_{0}^{-\infty} d\theta\]
- \[= -\frac{1}{k} \int_{\theta=0}^{\theta=2\pi} (-1) d\theta\]
- \[= \frac{2\pi}{k} = \frac{1}{A^{2}}\]
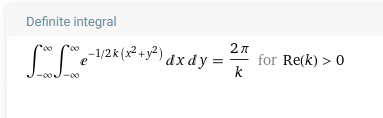
- 적분의 결과와 울프람 알파의 결과가 같은 것을 확인할 수 있습니다.
- 마지막 식을 \(A\) 에 대하여 정리해 보겠습니다. 앞에서 다룬 값은 확률밀도함수의 넓이와 관련된 것이므로 항상 양수이기 때문에 양의 값을 가지게 됨을 유의해야 합니다.
- \[A^{2} = \frac{k}{2\pi}\]
- \[A = \sqrt{\frac{k}{2\pi}}\]
- 따라서 \(A\) 는 위 식과 같이 구할 수 있고 지금 까지 구한 확률 분포를 살펴보면 다음과 같습니다.
- \[p(x) = \sqrt{\frac{k}{2\pi}} e^{-\frac{k}{2}x^{2}}\]
- 처음에 살펴본 가우시안 분포에서 ② \(\color{blue}{\frac{1}{\sigma \sqrt{2\pi}}}\) 과 \(\sqrt{\frac{k}{2\pi}}\) 를 비교하면 \(k = 1 / \sigma^{2}\) 에 대한 값을 확인하는 과정이 더 필요합니다. 마지막으로 \(k\) 에 대하여 알아보도록 하겠습니다.
Determining the Value of k
- 앞에서 구한 식의 미지수 \(k\) 를 구하기 위하여
평균과분산의 개념을 도입하여 식을 전개해 보도록 하겠습니다. 왜냐하면 \(k\) 값이 확률 분포에 사용되는 값이기 때문에평균,분산과 연관이 되어 있고 이 추가적인 식을 이용하여 미지수 \(k\) 를 풀 수 있기 때문입니다. - 먼저, 평균 \(\mu\) 와 분산 \(\sigma^{2}\) 은 다음과 같은 식으로 적을 수 있습니다.
- \[\mu = \int_{-\infty}^{\infty} x p(x) dx\]
- \[\sigma^{2} = \int_{-\infty}^{\infty} (x - \mu)^{2} p(x) dx\]
- 이 때, \(x\) 자체는 기함수 (odd function)이고 \(p(x) = \sqrt{\frac{k}{2\pi}} e^{-\frac{k}{2}x^{2}}\) 는 우함수 (even function)입니다. \(x p(x)\) 는 기함수와 우함수의 곱이므로
기함수입니다. - 음의 무한대와 양의 무한대 전체 범위에서 기함수의 평균은 0 입니다. 따라서 평균 식은 다음과 같이 정리됩니다.
- \[\mu = \int_{-\infty}^{\infty} x p(x) dx = 0\]
- 분산의 정의에 따라 아래 식은 다음과 같이 변경 가능합니다. (편차의 평균 → (제곱의 평균 - 평균의 제곱)), 링크를 참조해 주시기 바랍니다.
- \[\sigma^{2} = \int_{-\infty}^{\infty} (x - \mu)^{2} p(x) dx = \int_{-\infty}^{\infty} x^{2} p(x) dx - \mu^{2}\]
- \[\Rightarrow \sigma^{2} = \int_{-\infty}^{\infty} x^{2} p(x) dx - 0 = \int_{-\infty}^{\infty} x^{2} p(x) dx\]
- \[\Rightarrow \sigma^2 = \int_{-\infty}^{\infty}x^2\sqrt{\frac{k}{2\pi}}\exp\left(-\frac{1}{2}kx^2\right)dx =\sqrt{\frac{k}{2\pi}}\int_{-\infty}^{\infty}x^2\exp\left(-\frac{1}{2}kx^2\right)dx = \sqrt{\frac{k}{2\pi}}\int_{-\infty}^{\infty}x\cdot x\exp\left(-\frac{1}{2}kx^2\right)dx\]
- 위 적분식을 구하기 위하여 부분 적분법을 사용하겠습니다. (단순 계산 방법이므로 스킵하시고 아래 울프람 알파 결과만 확인하셔도 됩니다.)
- \[\begin{cases}u = x \\ du = 1\end{cases}\]
- \[\begin{cases} dv = x\exp\left(-\frac{1}{2}kx^2\right) \\ v = -\frac{1}{k}\exp\left(-\frac{1}{2}kx^2\right) \end{cases}\]
- \[\sqrt{\frac{k}{2\pi}}\left\lbrace\left[x\cdot\left(-\frac{1}{k}\right)\exp\left(-\frac{1}{2}kx^2\right)\right]_{-\infty}^{\infty}+\frac{1}{k}\int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}kx^2\right)dx\right\rbrace\]
- 식 중간의 대괄호 부분을 계산하면 0이 되므로 다음과 같이 정리할 수 있습니다.
- \[\sqrt{\frac{k}{2\pi}}\left\lbrace\frac{1}{k}\int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}kx^2\right)dx\right\rbrace = \sqrt{\frac{k}{2\pi}}\left(\frac{1}{k}\right)\sqrt{\frac{2\pi}{k}} = \frac{1}{k}\]
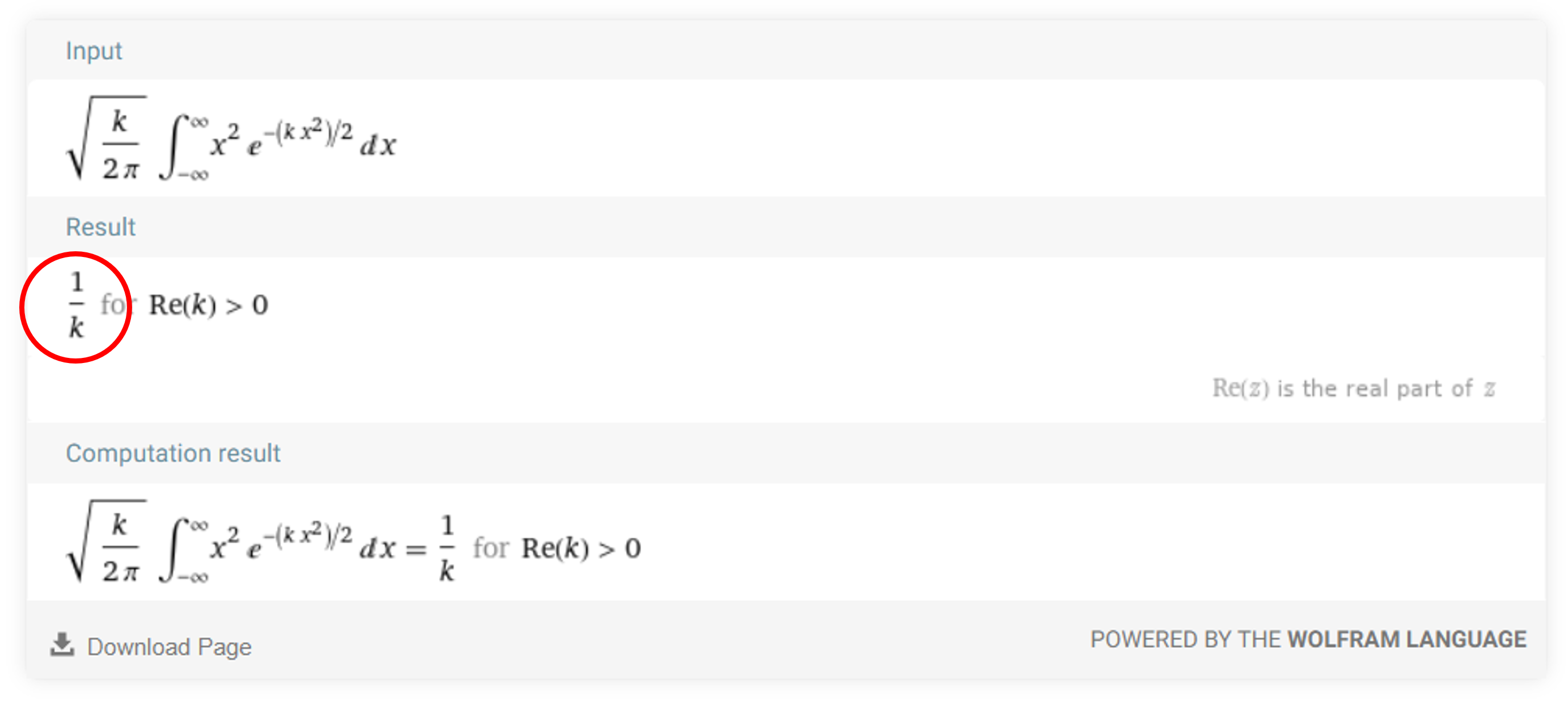
- 적분의 결과와 울프람 알파의 결과가 같은 것을 확인할 수 있습니다.
- \[\therefore k = \frac{1}{\sigma^{2}}\]
- 따라서 앞에서 구한 식에 \(k\) 를 대입하면 다음과 같이 정리할 수 있습니다.
- \[p(x) = \sqrt{\frac{k}{2\pi}} e^{-\frac{k}{2}x^{2}} = \sqrt{\frac{1}{\sigma^{2}2\pi}} e^{-\frac{1}{2}\sigma^{2}x^{2}}\]
- 위 식은 가우시안 분포의 수식에서 평균값이 0인 경우를 의미하며 평균값이 \(\mu\) 인 경우에는 \(x\) 를 \(x - \mu\) 로 평행이동 시켜주면 되므로 최종적인 가우시안 분포 공식은 다음과 같이 유도할 수 있습니다.
- \[p(x) = \frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]
1D, 2D, 3D 가우시안 분포
- 앞에서 유도한
가우시안 분포 공식의PDF (Probability Density Function)를 일반화 하면 다음과 같습니다.
- \[(2\pi)^{-\text{d}/2} \text{det}(\Sigma)^{-1/2}\exp{\left(-\frac{1}{2}(x - \mu)^{T}\Sigma^{-1}(x - \mu) \right)}\]
- \[\text{d: dimension}\]
- \[\text{Exists only when } \Sigma \text{ is Positive-Definite.}\]
- 앞에서 다룬 내용은 1차원 가우시안 분포의 식을 유도한 것이며 2, 3차원 가우시안 분포도 같은 형태로 나타낼 수 있습니다. 위 함수를 코드로 나타내면 다음과 같습니다.
def generalized_gaussian_pdf(X, mu, Sigma):
"""
Compute the probability density of a multivariate Gaussian for one or more points X.
Parameters
----------
X : ndarray of shape (n, d) or (d,)
Points at which to evaluate the pdf. Each row is a point in d dimensions.
mu : ndarray of shape (d,)
Mean vector of the Gaussian.
Sigma : ndarray of shape (d, d)
Covariance matrix (must be positive-definite).
Returns
-------
pdf_vals : ndarray of shape (n,)
The pdf value for each input point.
"""
X = np.atleast_2d(X) # Ensure X is (n, d)
d = mu.shape[0]
mu = mu.reshape(1, d) # Make mu broadcastable
Sigma_inv = np.linalg.inv(Sigma)
det_Sigma = np.linalg.det(Sigma)
# Normalization constant
denom = np.sqrt((2 * np.pi)**d * det_Sigma)
# Compute exponent for each row of X
diff = X - mu # shape (n, d)
exponent = -0.5 * np.sum(diff @ Sigma_inv * diff, axis=1)
pdf_vals = np.exp(exponent) / denom
return pdf_vals
- 위 함수를 이용하여 1D, 2D, 3D 가우시안 분포를 그려보도록 하겠습니다.
mu_1d = np.array([0.0])
Sigma_1d = np.array([[1.0]])
x_range=(-5,5)
num_points=200
x = np.linspace(*x_range, num_points)
pdf_vals = generalized_gaussian_pdf(x.reshape(-1,1), np.array(mu_1d), np.array(Sigma_1d))
plt.figure()
plt.plot(x, pdf_vals, 'b-', label='1D Gaussian')
plt.title(f'1D Gaussian (μ={mu_1d}, σ²={Sigma_1d})')
plt.xlabel('x')
plt.ylabel('pdf')
plt.grid(True)
plt.legend()
plt.show()
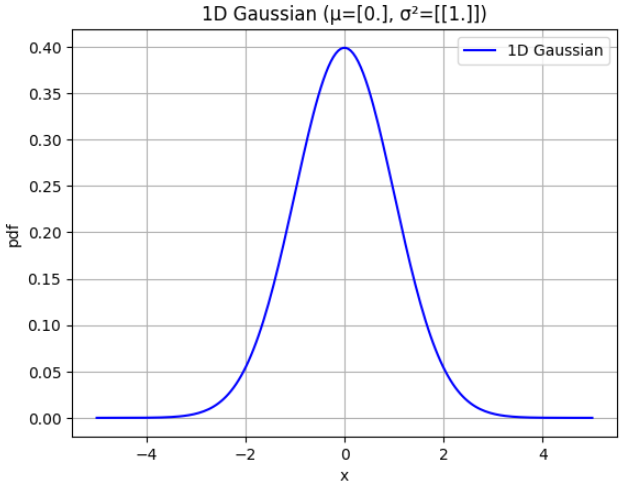
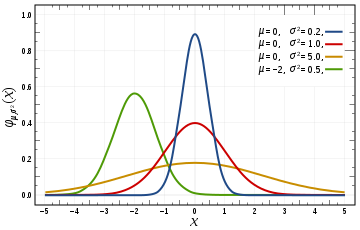
- 위 그래프는 \(\mu = 0, \sigma^{2} = 1.0\) 인 표준 정규 분포 그래프입니다.
- 다음으로 2D 가우시안 분포 그래프를 그려보도록 하겠습니다.
mu_2d = np.array([0.0, 0.0])
Sigma_2d = np.array([[1.0, 0.6],
[0.6, 2.0]])
xy_range=(-3,3)
num_points=100
x = np.linspace(*xy_range, num_points)
y = np.linspace(*xy_range, num_points)
X, Y = np.meshgrid(x, y)
# Flatten grid and evaluate pdf
XY = np.column_stack([X.ravel(), Y.ravel()])
pdf_vals = generalized_gaussian_pdf(XY, mu_2d, Sigma_2d)
pdf_vals = pdf_vals.reshape(X.shape)
plt.figure()
contour = plt.contourf(X, Y, pdf_vals, cmap='viridis')
plt.title(f'2D Gaussian (μ={mu_2d})')
plt.xlabel('x')
plt.ylabel('y')
plt.colorbar(contour, label='pdf')
plt.show()
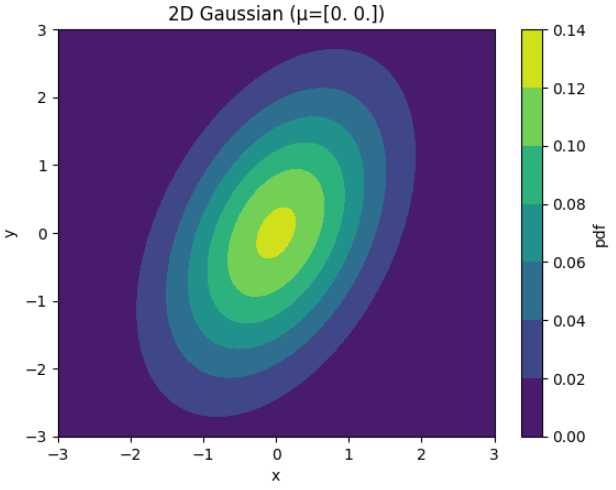
- 위 그래프는 2D 가우시안이므로 \(\mu, \Sigma\) 는 다음과 같이 2차원 값을 가집니다.
- \[\mu = \begin{bmatrix} 0.0 \\ 0.0 \end{bmatrix}\]
- \[\Sigma = \begin{bmatrix} 1.0 & 0.6 \\ 0.6 & 2.0 \end{bmatrix}\]
- 위 예제는 아래 링크의 위키피디아 예제를 이용하였습니다. 다음 그림을 보면 더 쉽게 이해할 수 있습니다.
- 링크: https://en.wikipedia.org/wiki/Multivariate_normal_distribution
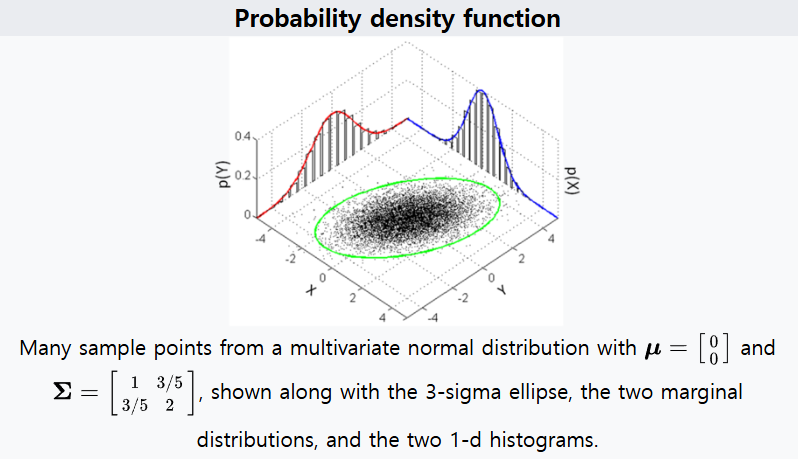
- 앞에서 시각화한 내용과 \(X, Y\) 축을 매칭해서 보면 기울어진 타원형이 어떤 방식으로 생성되었는 지 이해할 수 있을 것입니다.
- 마지막으로 3D 가우시안 분포를 그려보도록 하겠습니다. 시인성을 위하여
Probability Density가 낮은 값은 필터를 적용하였습니다.
mu_3d = np.array([0.0, 0.0, 0.0])
Sigma_3d = np.array([[1.0, 0.0, 0.0],
[0.0, 1.0, 0.0],
[0.0, 0.0, 1.0]]) # Standard isotropic Gaussian
# -----------------------------
# Create a regular grid in 3D space
# -----------------------------
n_points = 20 # Grid resolution per axis
grid_range = np.linspace(-3, 3, n_points)
X_grid, Y_grid, Z_grid = np.meshgrid(grid_range, grid_range, grid_range)
# Flatten grid to list of 3D points (n_points^3, 3)
points_3d = np.column_stack([X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel()])
# Compute the pdf for each point using the generalized function
pdf_values = generalized_gaussian_pdf(points_3d, mu_3d, Sigma_3d)
# -----------------------------
# Filter out low-density points
# -----------------------------
# Set a threshold: e.g., only keep points with density >= 5% of the maximum value.
threshold = 0.05 * pdf_values.max()
high_density_idx = pdf_values >= threshold
points_filtered = points_3d[high_density_idx]
pdf_filtered = pdf_values[high_density_idx]
# -----------------------------
# 3D Scatter Plot: visualize high density region
# -----------------------------
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
sc = ax.scatter(points_filtered[:, 0],
points_filtered[:, 1],
points_filtered[:, 2],
c=pdf_filtered, cmap='viridis', marker='o', s=30)
ax.set_title('3D Gaussian Density (High-Density Points Only)')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.colorbar(sc, label='pdf value')
plt.show()
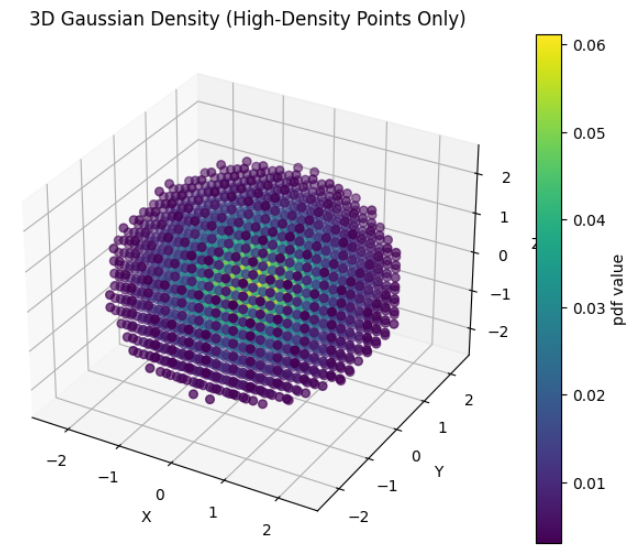
- 위 예제의 \(\mu, \Sigma\) 는 다음과 같습니다.
- \[\mu = \begin{bmatrix} 0.0 \\ 0.0 \\ 0.0 \end{bmatrix}\]
- \[\Sigma = \begin{bmatrix} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 1.0 \end{bmatrix}\]
- 위 예제는 간단한
Standard isotropic Gaussian형태입니다. \(\mu, \Sigma\) 를 변경하여 달라지는 형상을 관찰해 보면 3D 가우시안을 이해하는 데 도움이 될 것입니다.
가우시안 PDF의 곱과 Convoltuion 연산
- 아래 글은 가우시안 PDF의 곱과 Convolution 연산에 관한 내용을 다룹니다. 이 내용은 다소 긴 내용으로 별도 페이지를 작성하였으며 링크는 아래와 같습니다. 글을 읽기 전에 기억할 핵심 내용은 두 가우시안 분포의 곱은 가우시안 분포로 나타내어 진다라는 것입니다.
- 링크 : https://gaussian37.github.io/math-pb-product_convolution_gaussian_pdf/
covariance와 zero-mean gaussian의 covariance
- 가우시안 분포에서 공분산에 대하여 한번 알아보겠습니다.
- 다음과 같이 n 차원의 벡터 \(x\)와 평균 벡터 \(\mu\)가 있다고 가정해 보겠습니다.
- \[\boldsymbol x= \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\]
- 벡터를 자세히 살펴보면 다음과 같습니다.
- \[\boldsymbol x= \begin{bmatrix} \color{blue}{x_1} \\ \color{red}{x_2} \end{bmatrix}=\begin{bmatrix}\color{blue}{x_{11} \\ x_{12}\\\vdots\\ x_{1h}}\\\color{red}{x_{21}\\x_{22}\\\vdots\\ x_{2k}}\end{bmatrix}\tag{$n \times 1$}\]
- \[\boldsymbol\mu= \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}\]
- 이 때, covariance matrix는 다음과 같이 정의됩니다.
- \[\begin{bmatrix} \Sigma_{\color{blue}{11}} & \Sigma_{\color{blue}{1}\color{red}{2}} \\ \Sigma_{\color{red}{2}\color{blue}{1}} & \Sigma_{\color{red}{22}} \end{bmatrix} \tag {$n \times n$}\]
- 이 때, 공분산도 자세히 살펴보면 다음과 같습니다.
- \[\Sigma_{\color{blue}{11}}=\begin{bmatrix} \sigma^2({\color{blue}{x_{11}}}) & \text{cov}(\color{blue}{x_{11},x_{12}}) & \dots & \text{cov}(\color{blue}{x_{11},x_{1h}}) \\ \text{cov}(\color{blue}{x_{12},x_{11}}) & \sigma^2({\color{blue}{x_{12}}}) & \dots & \text{cov}(\color{blue}{x_{12},x_{1h}}) \\ \vdots & \vdots & & \vdots \\ \text{cov}(\color{blue}{x_{1h},x_{11}}) & \text{cov}(\color{blue}{x_{1h},x_{12}}) &\dots& \sigma^2({\color{blue}{x_{1h}}}) \end{bmatrix} \tag{$h \times h$}\]
- \[\Sigma_{\color{blue}{1}\color{red}{2}}= \begin{bmatrix} \text{cov}({\color{blue}{x_{11}}},\color{red}{x_{21}}) & \text{cov}(\color{blue}{x_{11}},\color{red}{x_{22}}) & \dots & \text{cov}(\color{blue}{x_{11}},\color{red}{x_{2k}}) \\ \text{cov}({\color{blue}{x_{12}}},\color{red}{x_{21}}) & \text{cov}(\color{blue}{x_{12}},\color{red}{x_{22}}) & \dots & \text{cov} \color{blue}{x_{12}},\color{red}{x_{2k}}) \\ \vdots & \vdots & & \vdots \\ \text{cov}({\color{blue}{x_{1h}}},\color{red}{x_{21}}) & \text{cov}(\color{blue}{x_{1h}},\color{red}{x_{22}}) & \dots & \text{cov}(\color{blue}{x_{1h}},\color{red}{x_{2k}}) \end{bmatrix}\tag{$h \times k$}\]
- \[\Sigma_{\color{red}{2}\color{blue}{1}} = \begin{bmatrix} \text{cov}({\color{red}{x_{21}}},\color{blue}{x_{11}}) & \text{cov}(\color{red}{x_{21}},\color{blue}{x_{12}}) & \dots & \text{cov}(\color{red}{x_{21}},\color{blue}{x_{1h}}) \\\text{cov}({\color{red}{x_{22}}},\color{blue}{x_{11}}) & \text{cov}(\color{red}{x_{22}},\color{blue}{x_{12}}) & \dots & \text{cov} \color{red}{x_{22}},\color{blue}{x_{1h}}) \\ \vdots & \vdots & & \vdots \\ \text{cov}({\color{red}{x_{2k}}},\color{blue}{x_{11}}) & \text{cov}(\color{red}{x_{2k}},\color{blue}{x_{12}}) & \dots & \text{cov}(\color{red}{x_{2k}},\color{blue}{x_{1h}}) \end{bmatrix}\tag{$k \times h$}\]
- \[\Sigma_{\color{red}{22}}=\begin{bmatrix} \sigma^2({\color{red}{x_{21}}}) & \text{cov}(\color{red}{x_{21},x_{22}}) & \dots & \text{cov}(\color{red}{x_{21},x_{2k}}) \\ \text{cov}(\color{red}{x_{22},x_{21}}) & \sigma^2({\color{red}{x_{22}}}) & \dots & \text{cov}(\color{red}{x_{22},x_{2k}}) \\ \vdots & \vdots & & \vdots \\ \text{cov}(\color{red}{x_{2k},x_{21}}) & \text{cov}(\color{red}{x_{2k},x_{22}}) &\dots& \sigma^2({\color{red}{x_{2k}}}) \end{bmatrix} \tag{$k \times k$}\]
- 일단 covariance에 대하여 알아보았는데, 먼저 확인해야 하는 것은 행과 열의 인덱스가 같은 부분은 \(\text{cov}\)가 아닌 분산의 형태인 \(\sigma^{2}\)으로 나타나 있는가 입니다.
- 만약 \(\text{cov}\)로 나타낸다면 예를 들면 \(\text{cov}{x_{11}, x_{11}}\)이 됩니다.
- 여기서 \(x_{i}, x_{j}\)가 벡터일 때, \(\text{cov}{x_{i}, x_{j}}\)를 풀어보면 다음과 같습니다.
- \[\text{cov}({x_{i}, x_{j}}) = E[ (x_{i} - \mu_{i})(x_{j} - \mu_{j})]\]
- 따라서 \(\text{cov}(x_{11}, x_{11}) = E[(x_{11} - \mu_{11})^{2}] = \sigma^{2}(x_{11})\)이 됩니다.
- 그러면 본론으로 들어가서
zero-mean gaussian distribution에 대하여 알아보겠습니다. - 대각 성분은 앞에서 다룬 것 처럼 \(\sigma^{2}(x_{ii})\) 형태가 됩니다.
- zero-mean gaussian에서는 대각 성분이 아닌 경우에는 모두 0이 됩니다.
- 대각 성분이 아닌 경우를 한번 살펴보면 다음과 같습니다.
- \[\text{cov}({x_{i}, x_{j}}) = E[ (x_{i} - \mu_{i})(x_{j} - \mu_{j}) ] = E[ (x_{i})(x_{j}) ] = E[x_{i}]E[x_{j}] = \mu_{i}\mu_{j} = 0\]
- zero-mean gaussian 이기 때문에 \(\mu\)는 모두 0이 되고 \(E(XY) = E(X)E(Y)\)이기 때문에 분리가 됩니다. 분리한 각각의 값이 또 평균이기 때문에 각 평균은 0이되어 최종적으로 \(\text{cov}{x_{i}, x_{j}}\)은 0이 됩니다.
- 따라서
zero-mean gaussian distribution에서 대각 성분은 분산이 되고 그 이외 성분은 모두 0이 됩니다.
- \[\Sigma_{}=\begin{bmatrix} \sigma^2({\color{blue}{x_{1}}}) & 0 & \dots & 0 \\ 0 & \sigma^2({\color{blue}{x_{2}}}) & \dots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0&\dots& \sigma^2({\color{blue}{x_{m}}}) \end{bmatrix} \tag{$h \times h$}\]