Pearson Correlation Coefficient와 Spearman Correlation Coefficient

통계학 관련 글 목록

• 참조 : 분산과 공분산 (variance and covariance)
• 참조 : 피어슨 상관 계수, 위키피디아
• 참조 : 스피어먼 상관 계수, 위키피디아

• 이번 글에서는 두 변수의 상관관계를 측정하는 대표적인 방식인 Pearson Correlation Coefficient와 Spearman Correlation Coefficient에 대하여 살펴보도록 하겠습니다.

목차

• Pearson Correlation과 Spearman Correlation의 비교

• Pearson Correlation의 정의와 예제

• Spearman Correlation의 정의와 예제

Pearson Correlation과 Spearman Correlation의 비교

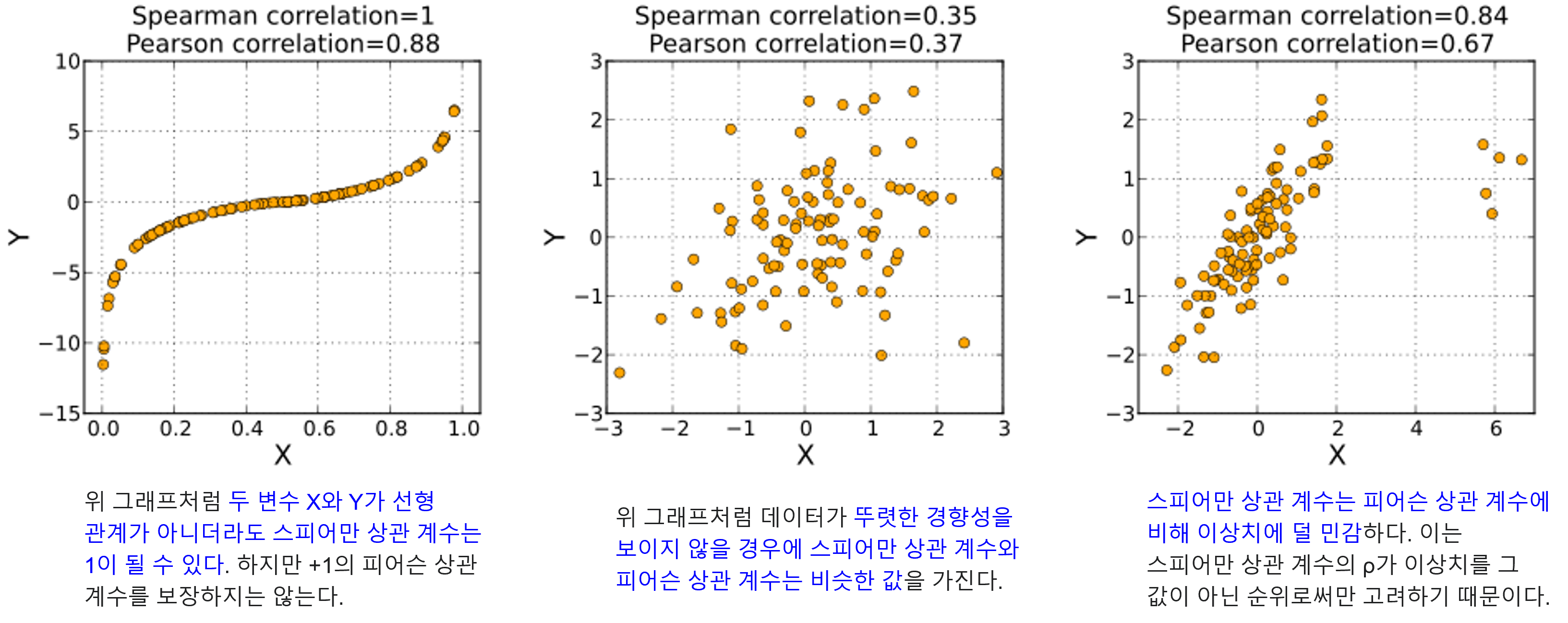
• 먼저 본 글에서 살펴 볼 Pearson Correlation과 Spearman Correlation의 특성에 대하여 먼저 살펴보도록 하겠습니다.

• 위 도표와 같이 Spearman Correlation이 아웃라이어에 좀 더 강건할 뿐 아니라 단조 증가 관계만 가지면 사용할 수 있기 때문에 처음 시도하기에 좀 더 용이합니다.
• 반면 두 변량이 선형 관계를 가지는 지 여부에 좀 더 초점을 두고자 한다면 Pearson Correlation을 사용할 수 있습니다.
• 따라서 본 글의 내용을 살펴 보기 전에 어떤 상관 관계를 사용해야 하는 지 위 도표를 보고 먼저 접근하는 과정이 필요합니다.

Pearson Correlation의 정의와 예제

• 먼저 Pearson Correlation에 대하여 살펴보도록 하겠습니다. 살펴볼 순서는 Pearson Correlation의 정의와 식의 의미이며 간단한 예시도 살펴보도록 하겠습니다.

Pearson Correlation의 정의

• 먼저 Pearson Correlation의 정의는 다음과 같습니다.

• $$\rho_{(X, Y)} = \frac{\text{COV}(X, Y)}{\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}} = \frac{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}} = \frac{\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\sqrt{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}}$$

• 위 식에서 분자는 변수 $X, Y$ 의 표본의 공분산을 의미하고 분모는 $X, Y$ 각각의 표본 표준 편차를 의미합니다. 이와 같이 Pearson Correlation의 정의에는 정규 분포를 가정하는 요소인 표본의 공분산과 표준편차가 존재하기 때문에 도표와 같이 정규 분포를 가정하는 데이터 셋에서 잘 동작합니다.
• 위 식에서 $\text{COV}(X, Y) = \frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})$ 는 두 변수의 공분산을 나타내며 공분산이 양수이면 두 확률변수는 서로 양의 관계가 있음을 의미하고 공분산이 음수이면 두 확률변수는 서로 음의 관계가 있음을 의미합니다.
• 하지만 공분산의 크기값이 상관관계의 강한 정도를 나타내는 것은 아닙니다. 왜냐하면 $X, Y$ 값 각각의 스케일이 있기 때문에 이 스케일을 통일시켜 주지 않으면 상관관계의 강한 정도를 비교할 수 없기 때문입니다.
• 따라서 공분산이 가장 크게 나타날 수 있는 경우를 분모로 나누어 주는 Normalization 과정을 통해 값의 스케일을 1 이하로 조정할 수 있습니다. 이 때, 공분산이 가장 크게 나타날 수 있는 경우가 $\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}$ 입니다. 즉, 다음 조건을 만족합니다.

• $$\vert \text{COV}(X, Y) \vert \le \sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}$$

• 이 식이 성립하는 조건은 Cauchy-Schwarz Inequality를 통해 증명이 가능합니다. 바로 아래 내용에서 왜 $\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}$ 가 공분산의 최댓값인 지와 Pearson Correlation의 범위가 왜 -1과 1 사이인 지 살펴보도록 하겠습니다.

Pearson Correlation의 범위가 -1과 1사이인 이유

• Pearson Correlation에서 값의 범위와 Normalization은 다음과 같은 Cauchy-Schwarz Inequality에 의하여 결정됩니다. Cauchy-Schwarz Inequality의 정의는 다음과 같습니다.

• $$\vert \langle a, b \rangle \vert \le \Vert a \Vert \cdot \Vert b \Vert$$
• $$\langle a, b \rangle \quad \text{ : inner product of vectors a and b.}$$
• $$\Vert a \Vert \quad \text{ : norm of vector a.}$$

• 위 식이 Cauchy-Schwarz Inequality의 정의이며 좌변의 값은 두 벡터 내적의 절대값을 의미하고 우변의 각 값은 벡터의 norm을 의미합니다.
• Pearson Correlation을 구할 때, 분자에 해당하는 Covariance의 정의는 다음과 같습니다.

• $$\vert \text{COV}(X, Y) \vert = \vert E[(X - \overline{X})(Y - \overline{Y})] \vert = \vert E[(X - \overline{X})]E[(Y - \overline{Y})] \vert$$

• 위 식에서 $(X - \overline{X})$ 와 $(Y - \overline{Y})$ 각각은 벡터를 의미하고 $(X - \overline{X})(Y - \overline{Y})$ 는 내적을 의미합니다.
• 따라서 위 내적과 관련된 식은 Pearson Correlation에서의 분자 요소에 해당하고 Cauchy-Schwarz Inequality에서는 좌변의 요소에 해당합니다.

• Pearson Correlation을 구할 때, 분모에 해당하는 식은 다음과 같습니다.

• $$\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)} = \sqrt{E[(X - \overline{X})^{2}]}\sqrt{E[(Y - \overline{Y})^{2}]}$$

• 어떤 벡터 $a$ 의 norm의 정의는 다음과 같습니다.

• $$\sqrt{a \cdot a} = \sqrt{a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2}}$$

• 이 정의를 표본 분산을 구하는 데 사용해 보겠습니다.

• $\sqrt{E[(X - \overline{X})^{2}]}$ = $\sqrt{\frac{1}{n-1}\sum_{i=1}^{n-1}(X_{i} - \overline{X})^{2}} = \sqrt{\text{VAR}(X)}$

• 따라서 Pearson Correlation의 분모는 $\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}$ 로 정의되 Cauchy-Schwarz Inequality에서는 우변의 요소로 정의될 수 있습니다.
• 앞에서 다룬 Cauchy-Schwarz Inequality에 따른 식을 전개해 보도록 하겠습니다.

• $$\vert \langle a, b \rangle \vert \le \Vert a \Vert \cdot \Vert b \Vert$$
• $$\Rightarrow \vert \text{COV}(X, Y) \vert \le \sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}$$
• $$\frac{\vert \text{COV}(X, Y) \vert}{\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}} \le 1$$
• $$-1 \le \frac{\text{COV}(X, Y)}{\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}} \le 1$$

Pearson Correlation이 선형 관계만 설명 가능한 이유

• 아래 식에서 표본의 갯수는 $n$ 개이며 $\overline{X}, \overline{Y}$ 는 각각 $X, Y$ 변량에 대한 표본의 평균을 의미합니다. $s_{x}, s_{y}$ 는 표본 표준편차를 의미합니다.
• 아래 식에서 사용된 $1/(n-1)$ 은 표분분산의 평균이 모분산과 같아져야 하기 때문에 적용한 것이며 상세 내용은 아래 링크에서 확인가능합니다.
  • 링크 : 표본분산에서 n-1로 나누어 주는 이유

• $$\begin{align} \rho_{(X, Y)} = \frac{\text{COV}(X, Y)}{\sqrt{\text{VAR}(X)}\sqrt{\text{VAR}(Y)}} &= \frac{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}} \\ &= \frac{\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{s_{x}s_{y}} \\ &= \frac{1}{n-1}\sum_{i=1}^{n} \frac{(X_{i}-\overline{X})}{s_{x}}\frac{(Y_{i}-\overline{Y})}{s_{y}} \\ &= \frac{1}{n-1}\sum_{i=1}^{n} Z_{X_{i}}Z_{Y_{i}} \end{align}$$

• 위 식에서 $Z_{X_{i}}, Z_{Y_{i}}$ 각각은 Standardization이 적용된 상태의 변량이 됩니다. 각 변량은 표준 정규 분포를 따르도록 Standardization가 적용된 것이기 때문에 각 변량의 스케일에 상관없이 모두 평균이 0, 표준편차는 $s_{x}, s_{y}$ 를 따르도록 형성됩니다.
• 이 때, $Z_{X_{i}}, Z_{Y_{i}}$ 가 같이 양의 값 방향으로 증가하거나 음의값 방향으로 감소해야 두 값을 곱하였을 때, 큰 양수 값이 되며 평균을 내었을 때, 1에 가까운 값이 됩니다.
• 반면 $Z_{X_{i}}, Z_{Y_{i}}$ 값 중 한 값이 증가할 때, 나머지 값은 감소하게 되면 두 값을 곱하였을 때, 큰 음수 값이 되며 평균을 내었을 때, -1에 가까운 값이 됩니다.
• 만약 한 값이 증가하더라도 나머지 한 값이 뚜렷한 증감 없이 평균에 가까운 0에 머물게 되는 경우가 많이 생기게 된다면 평균을 내었을 때, 0에 가까운 값이 됩니다. 이러한 이유로 Pearson Correlation에서는 두 변수의 증감에 대한 상관관계가 없으면 0에 가까운 값을 얻게 됩니다.
• 앞에서 설명한 이유로 두 변량의 양의 상관관계가 클수록 1에 가까운 값을 얻게 되고 음의 상관관계가 클수록 -1에 가까운 값을 얻게 됩니다.

• Pearson Correlation은 두 변량 간의 선형관계를 나타내는 특성을 가지고 있습니다. 앞에서 Standardization을 하는 과정에서 각 변량에 평균을 빼고 표본 표준편차를 나누어 주는 과정을 통해 두 변량의 스케일을 맞춰준 후 곱하게 됩니다. 이 Standardization이 선형 변환을 적용하기 때문에 Pearson Correlation은 두 변량의 선형 관계만 설명할 수 있습니다. 비선형적인 관계라면 관계성이 있다고 하더라도 낮은 correlation 수치를 얻을 수도 있습니다. 이러한 점이 Pearson Correlation의 특징이면서 단점으로 작용하기도 합니다.
• 뿐만 아니라 몇 개의 데이터 쌍이 이상치가 되어 노이즈 처럼 작용된다면 비록 대부분의 데이터가 선형 관계를 가지더라도 Pearson Correlation을 계산할 때, 악영향을 끼칠 수 있습니다. 즉, Pearson Correlation은 노이즈에 취약하다는 단점이 있습니다. 관련 내용은 아래 예시를 살펴보면서 확인해 보도록 하겠습니다.
• 상세 내용 및 추가 해석등은 다음 위키피디아에서 참조할 수 있습니다.
  • 링크 : https://en.wikipedia.org/wiki/Pearson_correlation_coefficient#Interpretation

Pearson Correlation의 예시

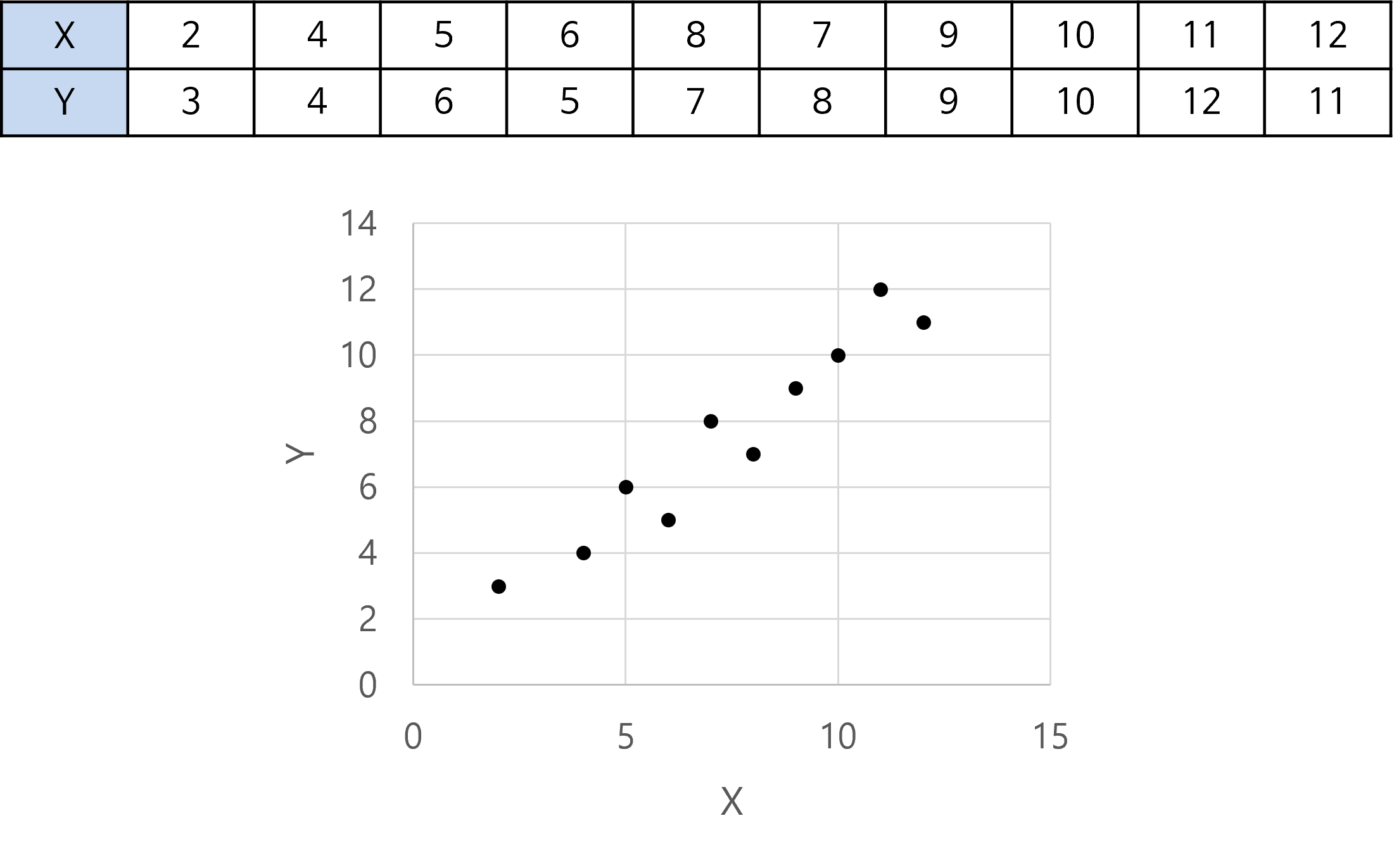
• 아래는 강한 선형 관계를 가지는 표본의 갯수가 10개인 데이터 셋 입니다.

import numpy as np

# Given data for X and Y
X = np.array([2, 4, 5, 6, 8, 7, 9, 10, 11, 12])
Y = np.array([3, 4, 6, 5, 7, 8, 9, 10, 12, 11])

# Calculate means of X and Y
mean_X = np.mean(X)
mean_Y = np.mean(Y)

# Calculate Pearson Correlation Coefficient
numerator = np.sum((X - mean_X) * (Y - mean_Y))
denominator = np.sqrt(np.sum((X - mean_X)**2) * np.sum((Y - mean_Y)**2))
r = numerator / denominator
print(r)
# 0.9620913858416693

• 계산 결과 0.96의 매우 강한 선형 관계임을 확인할 수 있습니다.

• 이번에는 아래와 같이 선형 관계가 없는 데이터 셋으로 상관 관계를 구해보도록 하겠습니다.

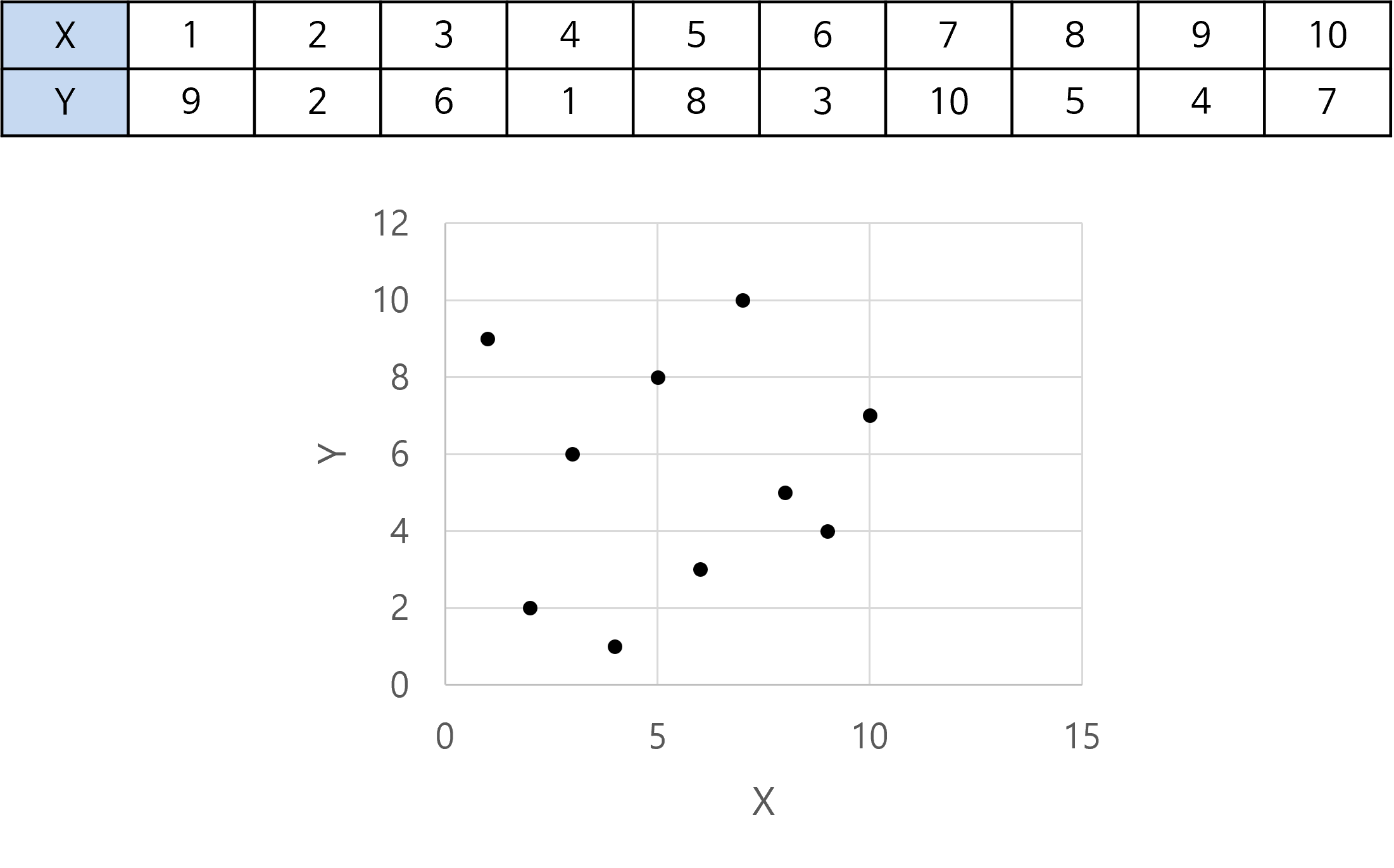
• 위 코드를 이용하여 동일한 방식으로 구하면 0.078 이라는 매우 낮은 값을 얻을 수 있습니다.

Spearman Correlation의 정의와 예제

• 앞에서 살펴본 Pearson Correlation의 경우 두 변량의 선형 관계 정도를 -1에서 1 사이의 범위로 나타냄을 확인할 수 있었습니다. 그리고 Pearson Correlation의 정의에 따라서 오직 선형 관계만 설명할 수 있다는 단점과 소수의 노이즈 데이터 쌍에도 상관계수가 영향을 받을 수 있음을 확인하였습니다.
• 이러한 문제점을 개선하기 위하여 데이터의 분산을 이용하는 방법이 아닌 rank를 이용하는 방법에 대하여 살펴보도록 하겠습니다.

Spearman Correlation의 정의

• 먼저 Spearman Correlation의 정의는 다음과 같습니다.

• $$r_{(X, Y)} = 1 - \frac{6 \sum_{i=1}^{n}(d_{i}^{2})}{n(n^{2}-1)}$$
• $$d_{i} = R(X_{i}) - R(Y_{i})$$
• $$R(X_{i}) : \text{Ranking order of X_i among all X data}$$
• $$R(Y_{i}) : \text{Ranking order of Y_i among all Y data}$$

• 위 식에서 $r_{(X, Y)}$ 의 값의 범위는 Pearson Correlation과 동일하게 -1 에서 1의 범위를 가지게 되고 그 의미 또한 1에 가까울 수록 양의 상관관계가 높고 -1에 가까울수록 음의 상관관계가 높습니다.
• Pearson Correlation과의 차이점에 대하여 살펴보면 $d_{i} = R(X_{i}) - R(Y_{i})$ 에 있습니다. Pearson Correlation은 Standardization 과정으로 전처리한 값을 사용하는 반면에 Spearman Correlation은 ranking을 이용합니다. 즉, 가지고 있는 데이터 셋에서 크기 순서의 인덱스 번호를 값으로 대체합니다. 예를 들어 $X_{1} = 100, X_{2} = -10, X_{3} = 3$ 이면 $R(X_{1}) = 1, R(X_{2}) = 3, R(X_{3}) = 2$ 가 됩니다.
• 이와 같은 방법으로 ranking을 이용하면 Pearson Correlation에서 발생한 노이즈에 대한 영향을 줄일 수 있습니다. 뿐만 아니라 Pearson Correlation에서는 선형 관계만 설명 가능하였지만 Spearman Correlation는 ranking으로 표현 가능한 단조 증가 관계 (monotonic relationship)는 모두 설명 가능합니다. 단조 증가 관계는

Spearman Correlation 식 유도 과정

• 아래와 같이 두 변수 $X, Y$ 의 원소가 $n$ 개라고 가정해 보겠습니다.

• $$X = \{X_{1}, X_{2}, \cdots , X_{n}\}$$
• $$Y = \{Y_{1}, Y_{2}, \cdots , Y_{n}\}$$

• 만약 $X, Y$ 에서 각 변수의 크기 순서를 $R(X_{i}), R(Y_{i})$ 라고 가정하겠습니다. 즉, 서수 (order)를 의미합니다. 이것을 랭킹으로 부르겠습니다.
• 두 변수의 랭킹의 차이가 없을 수록 두 변수가 모두 단조 증가 관계를 가진다고 말할 수 있습니다. 따라서 두 변수의 랭킹 차이가 없을수록 두 변수의 상관관계가 크다라고 말할 수 있으며 이와 같은 상관관계가 정의될 수 있도록 식을 세을 필요가 있습니다.
• 먼저 두 변수 간의 랭킹 차이를 Sum of Square방식으로 나타내 보겠습니다.

• $$\sum_{i=1}^{n} d_{i}^{2} = \sum_{i=1}^{n}(R(X_{i}) - R(Y_{i}))^{2}$$

• 앞에서 다룬 Pearson Correaltion은 강한 양의 상관관계는 1, 강한 음의 상관관계는 -1, 그리고 상관관계가 없으면 0에 가까워 지도록 설계되었습니다.
• Spearman Correlation 또한 같은 상관관계 지수를 가지도록 값을 설계해보도록 하겠습니다.
• Pearson Correlation은 값의 범위는 Cauchy–Schwarz inequality로 인하여 -1 ~ 1 사이 값으로 Normalization된 것을 앞에서 확인하였습니다. Spearman Correlation 또한 Normalization 과정을 통하여 범위를 -1 ~ 1 사이 범위로 만들어 보겠습니다.
• Normalization을 위해서 $\sum_{i=1}^{n} d_{i}$ 가 가장 커지는 경우를 분모로 나누어 주어야 합니다. $\sum_{i=1}^{n} d_{i}$ 값이 가장 커지는 경우는 두 변수의 랭킹 순서가 반대로 되어 있는 경우입니다.

• $$R(X_{1}) = 1, R(X_{2}) = 2, R(X_{3}) = 3, ... , R(X_{n-1}) = n-1, R(X_{n}) = n$$
• $$R(Y_{1}) = n, R(Y_{2}) = n-1, R(Y_{3}) = n-2, ... , R(Y_{n-1}) = 2, R(Y_{n}) = 1$$
• $$\begin{align} \sum_{i=1}^{n} d_{i} &= \sum_{i=1}^{n}(R(X_{i}) - R(Y_{i}))^{2} \\ &= (R(X_{1}) - R(Y_{1}))^{2} + (R(X_{2}) - R(Y_{2}))^{2} + (R(X_{3}) - R(Y_{3}))^{2} + ... + (R(X_{n-1}) - R(Y_{n-1}))^{2} + (R(X_{n}) - R(Y_{n}))^{2} \\ &= (n - 1)^{2} + (n - 3)^{2} + (n - 5)^{2} + ... + (3 - n)^{2} + (1 - n)^{2} \\ &= (n - 1)^{2} + (n - 3)^{2} + (n - 5)^{2} + ... + (n - 3)^{2} + (n - 1)^{2} = \frac{n(n^{2} - 1)}{3} \end{align}$$

• 위 식의 전개 과정을 sympy를 이용하여 풀면 다음과 같습니다.

from sympy import Sum
from sympy import symbols, solve

# Define symbols
n, k = symbols('n k')

# Calculate the number of terms for odd and even n
# For odd n, solve n - (2k-1) = 1
middle_term_odd = solve(n - (2*k - 1) - 1, k)

# For even n, solve n - (2k-1) = 0
middle_term_even = solve(n - (2*k - 1), k)

# Total number of terms for odd and even n (since the series is symmetric)
total_terms_odd = 2 * middle_term_odd[0] - 1
total_terms_even = 2 * middle_term_even[0]

total_terms_odd, total_terms_even

# Define the general term of the series
general_term = (n - (2*k - 1))**2

# Summation for odd n (from k=1 to (n-1)/2, double it, and add the middle term 0)
sum_odd_n = 2 * Sum(general_term, (k, 1, (n - 1)/2)).doit()

# Summation for even n (from k=1 to n/2, double it)
sum_even_n = 2 * Sum(general_term, (k, 1, n/2)).doit()

print(sum_odd_n.simplify())
# n*(n**2 - 1)/3
print(sum_even_n.simplify())
# n*(n**2 - 1)/3

• 따라서 $\sum_{i=1}^{n} d_{i}^{2}$ 을 Normalize 하면 다음과 같습니다.

• $$0 \le \frac{\sum_{i=1}^{n} d_{i}^{2}}{\frac{n(n^{2}-1)}{3}} \le 1$$

• 위 식은 0일 때, 가장 큰 양의 상관관계를 가지고 1일 때 가장 큰 음의 상관관계를 가집니다. Pearson Correlation과 같이 -1 ~ 1 사이의 범위를 가지고 -1을 가질 때, 가장 큰 음의 상관관계, 1일 때 가장 큰 양의 상관관계를 가지도록 식을 수정해 보도록 하겠습니다.

• $$0 \le \frac{\sum_{i=1}^{n} d_{i}^{2}}{\frac{n(n^{2}-1)}{3}} \le 1$$
• $$0 \le \frac{3\sum_{i=1}^{n} d_{i}^{2}}{n(n^{2}-1)} \le 1$$
• $$0 \le \frac{6\sum_{i=1}^{n} d_{i}^{2}}{n(n^{2}-1)} \le 2$$
• $$-2 \le -\frac{6\sum_{i=1}^{n} d_{i}^{2}}{n(n^{2}-1)} \le 0$$
• $$-1 \le 1 -\frac{6\sum_{i=1}^{n} d_{i}^{2}}{n(n^{2}-1)} \le 1$$

• 따라서 처음에 정의한 Spearman correlation의 식인 $r_{(X, Y)} = 1 - \frac{6 \sum_{i=1}^{n}(d_{i}^{2})}{n(n^{2}-1)}$ 를 유도할 수 있습니다.
• 위 식의 결과 $\sum d_{i}^{2}$ 이 작아질수록 양의 상관관계가 커지게 되고 $\sum d_{i}^{2}$ 이 커질수록 음의 상관관계가 커지게 됩니다. 반면 $\sum d_{i}^{2}$ 가 $n(n^{2}-1)/6$ 에 가까워질수록 상관관계가 없어짐을 알 수 있습니다.

• Spearman Correlation 식 유도 과정을 통해 Spearman Correlation의 의미와 값의 범위 그리고 단조 증가를 가지는 다양한 관계를 설명할 수 있다는 장점을 이해할 수 있었습니다.

Spearman Correlation의 예시

• 이번에는 앞의 Pearson Correlation 예시를 살펴본 바와 동일하게 Spearman Correlation에 대하여 살펴보도록 하겠습니다.
• 살펴볼 예시는 2가지 입니다. ① 선형 관계가 아니지만 단조 증가하는 관계와 ② 노이즈가 섞여있는 예제입니다.

• 먼저 아래는 ① 선형 관계가 아니지만 단조 증가하는 관계 예시입니다. 데이터는 9차 방정식을 가정하였습니다.

# Function to calculate ranks
def rank_data(data):
    sorted_data = sorted(enumerate(data), key=lambda x: x[1])
    ranks = [0] * len(data)
    for rank, (index, _) in enumerate(sorted_data, start=1):
        ranks[index] = rank
    return ranks

# Define the data for the 9th-degree polynomial relationship
X_data = np.array(range(1, 21))
Y_data = X_data ** 9  # 9th-degree relationship
n = len(X_data)

# Calculate ranks for X and Y
X_ranks = rank_data(X_data)
Y_ranks = rank_data(Y_data)

# Calculate Spearman's rank correlation coefficient manually
differences = [x - y for x, y in zip(X_ranks, Y_ranks)]
squared_differences = [d**2 for d in differences]
rho_spearman = 1 - (6 * sum(squared_differences)) / (n * (n**2 - 1))

# Calculate Pearson correlation coefficient manually
mean_Y_data = np.mean(Y_data)
covariance_data = np.sum((X_data - mean_X_data_cubic) * (Y_data - mean_Y_data))
variance_Y_data = np.sum((Y_data - mean_Y_data)**2)
r_pearson = covariance_data / np.sqrt(variance_X_data_cubic * variance_Y_data)

print(rho_spearman)
# 1.0,

print(r_pearson)
# 0.6976735795972945

• Spearman Correlation은 1.0인 반면에 Pearson Correlation은 0.69인 것을 확인할 수 있습니다.

• 이번에는 ② 노이즈가 섞여있는 예제를 살펴보도록 하겠습니다.

# Set up the base linear relationship with noise
np.random.seed(0)
X_data = np.linspace(-10, 10, 47)
Y_data = 2 * X_data + np.random.normal(0, 3, 47)

# Adding outliers that disrupt the ranks but not the overall linear trend
x_outliers = np.array([-9, 0, 9])
y_outliers = np.array([-30, 100, -25])
X_data = np.append(X_data, x_outliers)
Y_data = np.append(Y_data, y_outliers)

# Calculate Spearman's rank correlation coefficient manually
x_ranks = rank_data(X_data)
y_ranks = rank_data(Y_data)
differences = [x - y for x, y in zip(x_ranks, y_ranks)]
squared_differences = [d**2 for d in differences]
rho_spearman = 1 - (6 * sum(squared_differences)) / (len(X_data) * (len(X_data)**2 - 1))

# Calculate Pearson correlation coefficient manually
mean_x = np.mean(X_data)
mean_y = np.mean(Y_data)
covariance = np.sum((X_data - mean_x) * (Y_data - mean_y))
variance_x = np.sum((X_data - mean_x)**2)
variance_y = np.sum((Y_data - mean_y)**2)
rho_pearson = covariance / np.sqrt(variance_x * variance_y)

print(rho_spearman)
# 0.8436494597839136

print(rho_pearson)
# 0.5354899275518871

• 이번 예제에서는 꽤 큰 차이를 확인할 수 있습니다. Spearman Correlation을 이용 시, 약 0.84의 상관관계를 얻을 수 있는 반면에 Pearson Correlation은 0.53으로 상대적으로 낮은 상관관계를 얻은 것을 볼 수 있습니다.

통계학 관련 글 목록