기초 정보 이론 (Entropy, Cross Entropy, KL divergence 등)

머신 러닝 관련 글 목록

참조 : https://gaussian37.github.io/ml-concept-infomation_theory/

이번 글에서는 머신 러닝을 공부할 때 중요한 개념 중 하나인 정보 이론에 대하여 다루어 보도록 하겠습니다. 이번 글에서 다루게 될 키워드는 Entropy, Cross Entropy, KL divergence, Jensen's inqeuality, Mutual Information이 있습니다.
① 정보 이론 (Information Theory) : 확률 분포 $P(X)$ 의 불확실 정도를 평가하는 방법
② 정보량 (information) : 불확실함을 해소하기 위해 필요한 질문(정보)의 수, 또는 어떤 Event가 발생하기 까지 필요한 시행의 수
③ 엔트로피 (Entropy) : 확률분포 $P(X)$ 에 대한 정보량의 기댓값 (평균)
④ 크로스 엔트로피 (Cross Entropy) : 실제 데이터는 $P(X)$ 분포로부터 생성되지만 $Q(X)$ 분포를 사용하여 정보량을 축정해서 계산판 정보량의 기댓값
⑤ KL divergence : 크로스 엔트로피 - 엔트로피로 두 분포 $P(X)$ 와 $Q(X)$ 의 차이를 의미
⑥ Jensen's inequality : 아래로 볼록한 그래프에서 함수값의 평균 > 평균의 함수값을 만족함
⑦ Gibb's inqeuality : $H(P, Q) \ge H(P)$
⑧ Mutual Information : 두 확률 변수들이 얼마나 서로 dependent지 측정하는 방법으로 KL divergence로 측정할 수 있음

정보이론의 의미

먼저 정보이론 (Information Theory)의 의미에 대하여 살펴보도록 하겠습니다. 머신 러닝을 다루다 보면 나오는 개념인 Probability Theory와 Decision Theory와 비교하여 설명하면 다음과 같습니다.

① Probability Theory : 불확실성 (Evnet, 변수 등)에 대한 일어날 가능성을 모델링 하는 것을 의미합니다. 아래는 확률 모형 중 하나인 베이즈 모델의 예시 입니다.

\[P(Y \vert X) = \frac{P(X \vert Y)P(Y)}{P(X)} \tag{1}\]

② Decision Theory : 불확실한 상황에서 추론에 근거해 결정을 내리는 방식입니다.

\[Y = 1 \text{if } \frac{P(x \vert y = 1)p(y = 1)}{P(x \vert y = 0)p(y = 0)} > 1 \tag{2}\]

③ Information Theory : 확률 분포 $P(X)$ 의 불확실 정도를 평가하는 방법입니다.

\[H(X) = -\sum_{x}P(X) \log{P(X)} \tag{3}\]

이번 글에서 집중적으로 다룰 내용은 ③ Information Theory 이며 식 (3)의 의미를 이해하는 것이 글의 목표가 되겠습니다.

정보량의 의미

정보량의 의미를 이해하기 위하여 1 ~ 16 까지의 숫자 중 상대방이 선택한 하나의 숫자를 알아 맞추는 게임을 진행한다고 해보겠습니다.
상대방은 나의 질문에 Yes / No 2가지 답변만 가능합니다. 이와 같은 문제는 binary search 방식을 이용하여 어떤 수 $X$ 보다 큰 지 질문하고 그 질문에 Yes / No 답변을 이용하여 찾으면 $\log_{2}{16} = 4$ 만큼의 질문을 통해 찾을 수 있음이 알려져 있습니다.
이 때, 4를 정보량이라고 합니다. 여기서 log의 밑인 2는 Yes/No 2가지 질문의 경우의 수를 의미합니다.

위 예제에서 주목할 점은 처음에는 상대방이 생각한 숫자를 전혀 알 지 못해서 불확실성이 굉장히 큰 상황에서 질의를 통해 점점 불확실성을 줄일 수 있었고 최종적으로 불확실성이 완전히 줄어들어서 정답을 찾게 될 때까지 4번이라는 질의가 필요하다는 것입니다.
이와 같이 불확실함을 해소하기 위해 필요한 질문(정보)의 수, 또는 어떤 Event가 발생하기 까지 필요한 시행의 수를 정보량 (information)이라고 합니다.
특히, 위 예제와 같이 2가지의 질문 (Yes / No)를 사용한 경우 bit가 정보량의 단위가 됩니다.

이 문제에서 암묵적으로 가정한 것은 어떤 숫자를 선택할 지를 모두 동등한 확률인 $ p = 1/16 $$ 로 가정한 점이 있습니다.
선택한 숫자를 맞추귀 위한 정보량을 확률 $p = 1/16$ 를 이용하여 표현하면 다음과 같습니다.

\[n = -\log{2}{(p)} \tag{4}\]
\[n = \log{2}{(1/p)} \tag{5}\]
\[4 = -\log{2}{(16)} \tag{6}\]

이와 같이 일반적으로 어떤 event의 확률이 $p$ 라고 하였을 떄, 그 event에 대한 정보량 $I$ 는 다음과 같이 계산합니다.

\[I = \log_{2}{(\frac{1}{p})} = -log_{2}{(p)} \tag{7}\]

식 (7)과 같이 정보량을 계산할 때, 다음 3가지 예시에 대하여 정보량을 각각 구해보도록 하겠습니다.
① 주사위를 던져서 짝수의 눈이 나타날 event $E_{1}$ 의 정보량

\[P(E_{1}) = \frac{1}{2}\]
\[I = -\log_{2}{\frac{1}{2}} = 1 \text{(bit)} \tag{8}\]

② 주사위를 던져서 2의 눈이 나타날 event $E_{2}$ 의 정보량

\[P(E_{2}) = \frac{1}{6}\]
\[I = -\log_{2}{\frac{1}{6}} = 2.58492... \text{(bit)} \tag{9}\]

③ 주사위를 던져서 1 ~ 6의 눈이 나타날 event $E_{1}$ 의 정보량

\[P(E_{3}) = 1\]
\[I = -\log_{2}{1} = 0 \text{(bit)} \tag{10}\]

Entropy

앞의 예제를 통해 정보량의 의미에 대하여 살펴보았습니다. 결론적으로 정보량의 기댓값을 엔트로피 (Entropy)라고 합니다.
앞에서 16개의 수 각각에 대하여 정보량을 구하고 그 정보량의 평균을 구한다면 다음과 같이 계산할 수 있습니다.

\[H(X) = -\sum_{i=1}^{16} P(X = i)\log_{2}P(X = i) \tag{11}\]
\[= \sum_{i=1}^{16} \frac{1}{16} \log_{2}{(\frac{1}{16})} = 4 (\text{(bit)} \tag{12}\]

이는 불확실성을 해소하기 위해서 평균적으로 4번의 질의가 필요하다는 의미입니다.
즉, Entropy란 확률 분포 $P(X)$ 에 대한 정보량의 기댓값을 의미 합니다.

\[H(X) = -\sum_{X} \color{blue}{P(X)} \color{red}{\log_{2}{({P(X)})}} \tag{13}\]

식 (13)에서 파란색 항은 확률을 의미하고 빨간색 항은 정보량을 의미하므로 식 (13)은 기댓값으로 정의됩니다.

위에서 살펴본 예시에서는 각 event가 발생할 확률이 모두 같은 uniform distribution이었습니다.
이번에는 동전 던지기를 이용하여 uniform distribution과 non-uniform distribution에 대하여 엔트로피를 계산해 보도록 하겠습니다.

먼저 동전 던지기를 하여 앞면, 뒷면의 발생 확률이 각각 1/2일 때, 앞면 뒷면을 맞추기 위한 엔트로피 즉, 정보량의 평균을 계산해 보겠습니다.

\[H(P) = P(X = H) \times -\log{P(X = H)} + P(X = T) \times -\log{P(X = T)} = \frac{1}{2} \times -\log_{2}{(\frac{1}{2})} + \frac{1}{2} \times -\log_{2}{(\frac{1}{2})} = 1 \text{(bit)} \tag{14}\]

만약 동전이 굽어져서 앞면이 나올 확률이 1/4, 뒷면이 나올 확률일 3/4라고 가정해 보겠습니다. 이 때, 앞면 또는 뒷면을 맞추기 위한 엔트로피를 계산해 보면 다음과 같습니다.

\[H(P) = P(X = H) \times -\log{P(X = H)} + P(X = T) \times -\log{P(X = T)} = \frac{1}{4} \times -\log_{2}{(\frac{1}{4})} + \frac{3}{4} \times -\log_{2}{(\frac{3}{4})} = 0.81127... \text{(bit)} \tag{15}\]

여기서 주목할만한 점은 확률 분포 $P(X)$ 의 변화에 따라 엔트로피 값이 달라진다는 것입니다. 식 (15)의 경우에 엔트로피가 줄어든 것을 알 수 있습니다.

\[P(X = H) = p\]
\[P(X = T) = 1 - p\]
\[H(P) = -p\log_{2}{p} -(1-p)\log_{2}{(1-p)} \tag{16}\]

식 (16)을 이용하여 $p$ 값에 따른 그래프를 그려보면 다음과 같습니다.

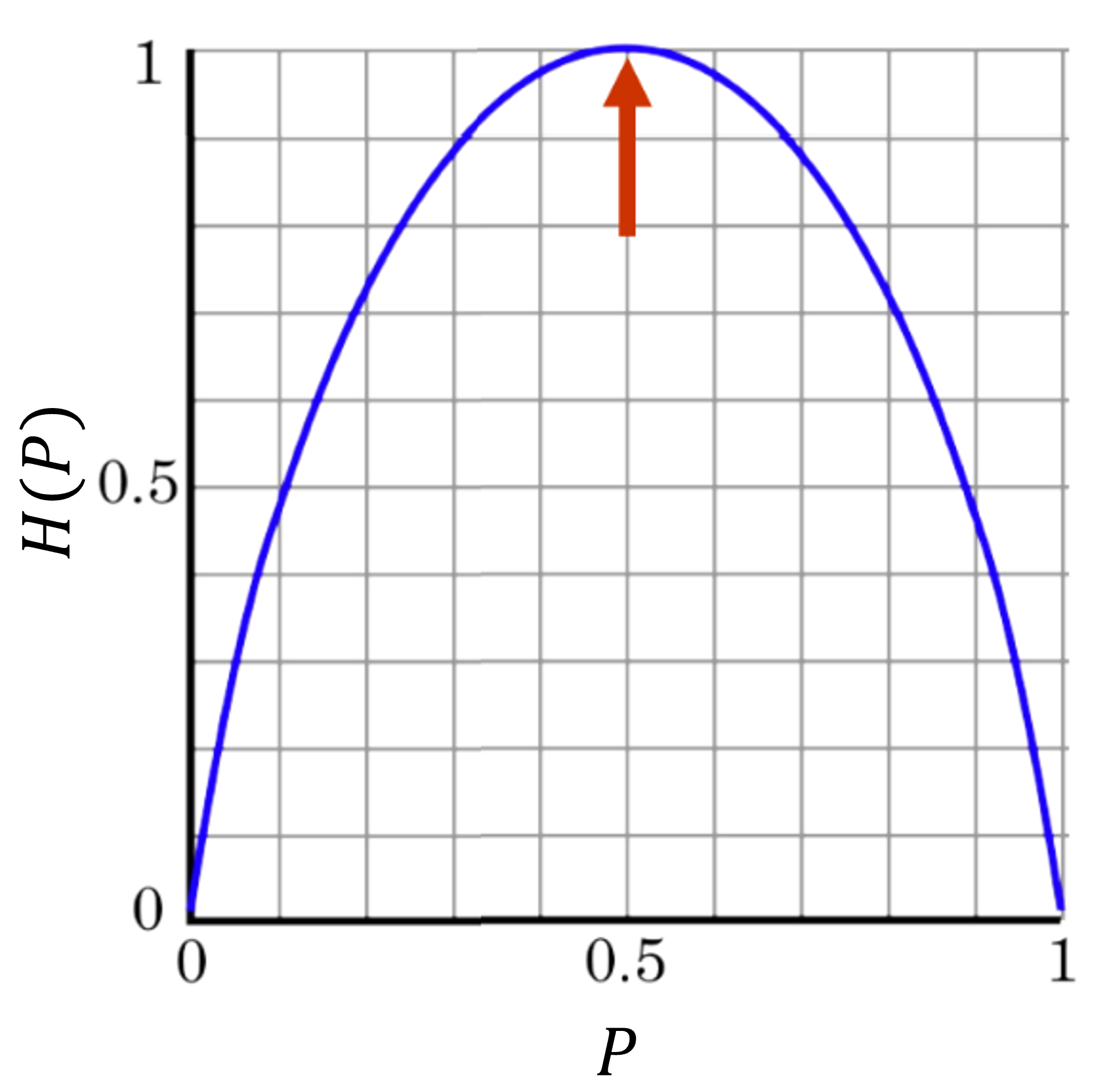
즉, uniform distribution일 때, 가장 엔트로피가 높고 한쪽으로 확률이 기울수록 엔트로피는 낮아집니다. 엔트로피의 의미를 곰곰히 생각해 볼 때, 위 그래프와 같은 결과가 나오는 것을 알 수 있습니다.

정리하면, 왼쪽 그래프와 같이 불균형한 분포 $P(X)$의 불확실성이 더 적으므로 엔트로피 $H(X)$ 가 더 낮고 오른쪽 그래프와 같이 균등한 분포 $P(X)$ 의 불확실성이 높으므로 엔트로피 $H(X)$ 가 높습니다.
엔트로피가 낮을 경우의 확률 분포에서는 표본을 샘플링하였을 때, 그 샘플링된 결과를 맞추기 쉽다고 생각하면 됩니다. 텍스트에 비유를 하자면 어떤 글에서 단어의 출현 빈도를 확률 분포라고 나타내었을 때, 분포가 균등한 것은 특정 주제가 없는 글이라서 단어의 출현 빈도가 균등하다고 보면되고 분포가 편향되어 있는 것은 특정 주제가 있는 글이라서 특정 단어가 자주 나온다고 생각할 수 있습니다.

지금까지 살펴본 엔트로피를 정리하면 다음과 같습니다.

엔트로피 : 확률 분포 $P(X)$ 에서 일어날 수 있는 모든 사건들의 정보량의 기대값으로 $P(X)$의 불확실 정도를 평가합니다.

\[H_{P} = -\sum_{x}P(X)\log_{2}{P(X)} \tag{17}\]
\[\text{discrete : } H_{P} = -\sum_{x}P(X)\log_{2}{P(X)} \tag{18}\]
\[\text{continuous : } H_{P} = -\int P(X)\log_{2}{P(X)}dX \tag{19}\]

엔트로피에 대하여 추가적으로 몇가지 살펴보면 다음과 같습니다.
① 머신 러닝 문제에서 Entropy를 계산할 때, log의 밑을 e로 사용하는 자연 로그를 많이 사용합니다. e를 사용하여도 앞에서 살펴 보았던 예제에서 엔트로피 크기를 비교할 때는 전혀 문제가 없으며 미분 등의 연산을 할 때에도 계산에 유리하기 때문입니다.
② 엔트로피 $H(X)$ 는 확률 분포 $P(X)$의 불확실 정도를 축정할 때 사용할 수 있습니다.
③ 엔트로피는 확률 분포 $P(X)$ 가 constatnt 또는 uniform distribution일 때 최대화가 됩니다.
④ 엔트로피는 확률 분포 $P(X)$ 가 delta function일 때 최소화가 됩니다.
⑤ 엔트로피는 항상 양수입니다.

엔트로피라는 개념을 이용하여 인코딩을 할 때에도 많이 사용됩니다. 이 방법을 엔트로피 인코딩이라고 합니다. 엔트로피 인코딩은 심볼이 나올 확률에 따라 심볼을 나타내는 코드의 길이를 달리하는 방법으로 좋은 인코딩 방식은 실제 데이터 분포 $P(X)$ 를 알고 있을 때 (ex, 어떤 문자가 출현할 갯수 및 확률) 이에 반비례하게 코딩 길이를 정하는 것입니다. 즉, 높은 확률로 등장하는 심볼 및 데이터는 짧은 길이로 정한다고 보시면 됩니다.
이와 같이 엔트로피 인코딩을 이용한 유명한 사례가 모스 부호입니다.

위 그림과 같이 E, I 같은 알파벳은 빈도수가 많기 때문에 그만큼 정보량이 작으므로 짧은 심볼에 매칭하였습니다.
반면 X, Y, Z 와 같은 알파벳은 빈도수가 작기 때문에 그만큼 정보량이 크므로 긴 심볼에 매칭하였습니다.
과거 모스 부호를 작성할 때에는 실제 데이터 즉, 알파벳이 발생하는 확률 분포 $P(X)$ 를 알 수 없기 떄문에 도서관에 있는 책, 문서들을 보고 대략적으로 추정한 확률 분포 $Q(X)$ 를 사용하였다고 알려져 있습니다.

Cross Entropy

현재 가지고 있는 데이터 분포가 $P(X)$ 일 때, 이 $P(X)$ 를 근사화 할 수 있는 새로운 분포 $Q(X)$ 를 이용하여 엔트로피를 구해볼 수 있을까요?
앞에서 배운 엔트로피의 정의가 정보량의 기댓값이었기 때문에, 정보량은 $Q(X)$ 를 사용하고 이 때 사용되는 확률 분포는 $P(X)$ 를 사용하여 다음과 같이 표현해 보겠습니다.

\[H(P, Q) = \sum_{X} P(X) \log{\frac{1}{Q(X)}} = -\sum_{X} P(X) \log{Q(X)} \tag{20}\]

크로스 엔트로피란 실제 데이터는 $P(X)$ 분포로부터 생성되지만 $Q(X)$ 분포를 사용하여 정보량을 축정해서 계산판 정보량의 기댓값을 의미합니다.
일반적으로 $H(P, Q) \ge H(P)$ 를 만족합니다. 즉, 새롭게 가정한 데이터 분포 $Q(X)$ 를 이용하여 엔트로피 인코딩을 하면 실제의 분포 $P(X)$ 를 가정한 최적의 코딩방식보다 엔트로피가 더 커지게 됩니다.

KL divergence

크로스 엔트로피 $H(P, Q)$ 엔트로피 $H(P)$ 보다 항승 크고 $P(X) = Q(X)$ 일때만 같음으로 두 항의 차이를 분포 사이의 거리처럼 사용할 수 있습니다.

\[D_{\text{KL}}(P \Vert Q) = H(P, Q) - H(P) \tag{21}\]
\[= \sum_{x} P(X) \log{\frac{1}{Q(X)}} - P(X)\log{\frac{1}{P(X)}} \tag{22}\]
\[= \sum_{x} P(X) \log{\frac{P(X)}{Q(X)}} \tag{23}\]

식 (23)을 KL divergence 라고 하며 데이터 인코딩 관점에서 보면 KL divergence는 데이터 소스의 분포인 $P(X)$ 대신 다른 분포 $Q(X)$ 를 사용해서 심볼을 인코딩하면 추가로 몇 bit의 낭비가 발생하는 지 나타낼 수 있다고 해석할 수 있습니다.
이와 같은 방식으로 KL divergence는 두 확률 분포 P와 Q의 차이를 측정할 수 있습니다.

추가적으로 KL divergence의 몇가지 성질에 대하여 살펴보겠습니다.

① $D_{\text{KL}}(P \Vert Q) = 0 \text{iff} P = Q$

② $D_{\text{KL}}(P \Vert Q) \ge 0$

③ $D_{\text{KL}}(P \Vert Q) \ne D_{\text{KL}}(Q \Vert P) \text{(reverse KL)}$

④ $P$ 를 고정하고 $Q_{\theta}$ 를 움직일 때, $D_{\text{KL}}(P \Vert Q_{\theta})$ 의 변화는 $H(P, Q_{\theta})$ 와 같습니다.

위 4가지 성질 중에서 ① 내용은 앞에서 다루었고, ④는 식을 살펴보면 알 수 있습니다.
② 내용 즉, KL divergence는 항상 0보다 크거나 같다라는 내용에 대하여 알아보겠습니다. 이 식을 유도하기 위하여 Jensen's inequality를 사용하겠습니다.

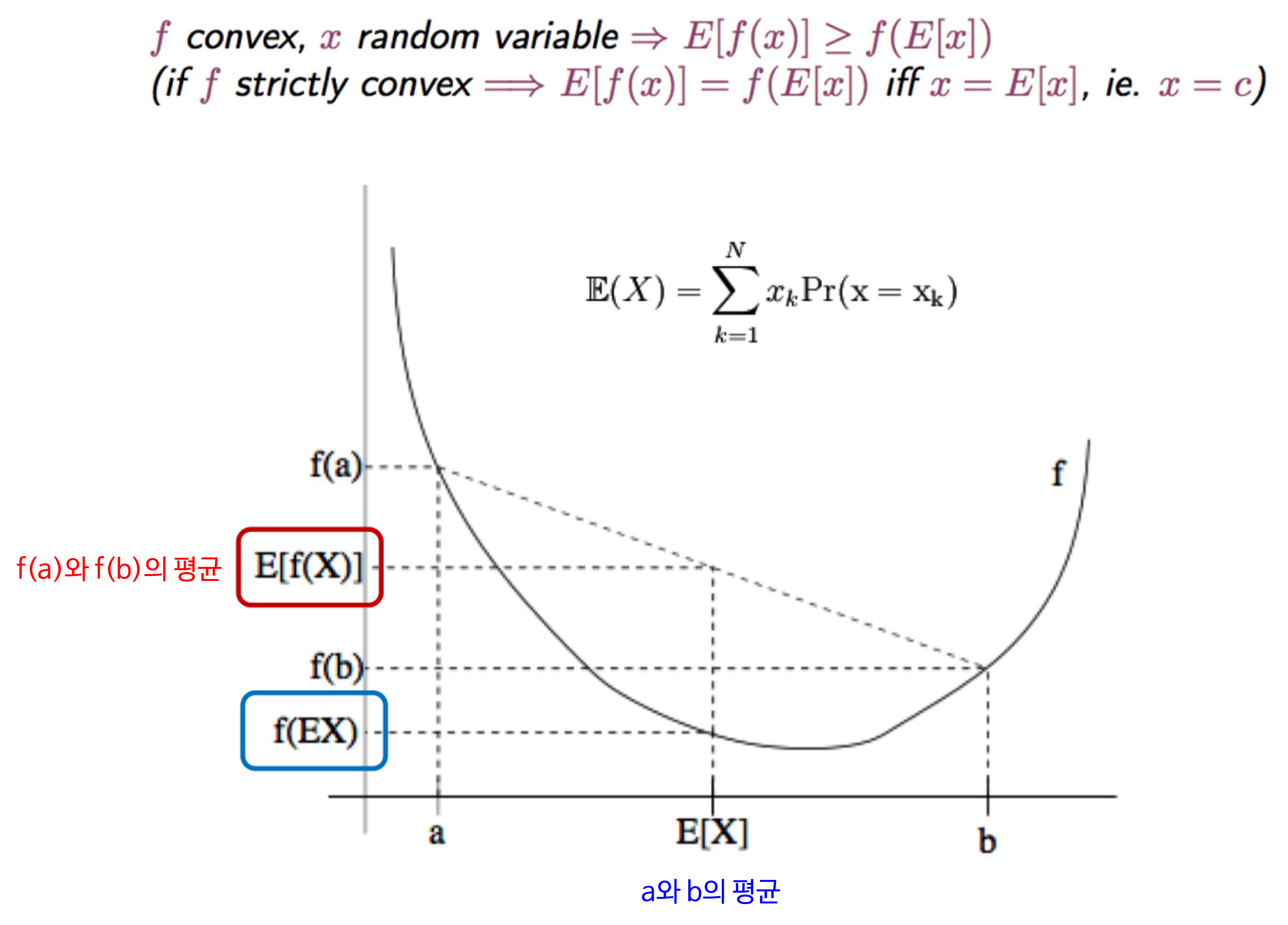
Jensen's inequality는 위 그래프와 같이 아래로 볼록한 그래프에서 함수값의 평균 > 평균의 함수값 보다 크다는 것을 의미합니다.
예를 들어 아래로 볼록한 Convex 함수로 지금까지 살펴본 -log를 대입하여 살펴보면 다음과 같습니다.

\[E[-\log{x}] \ge -\log{(E[x])} \tag{24}\]
\[\sum_{x}P(x)\log{x} \ge -\log{(\sum_{x}P(x) \times x)} \tag{25}\]

Jensen's inequality를 이용하여 아래 식을 유도해 보겠습니다.

\[D_{\text{KL}}(P \Vert Q) = H(P, Q) - H(P) \tag{26}\]
\[= \sum P(X) \log{\frac{P(X)}{Q(X)}} \tag{27}\]
\[= \sum P(X) -\log{\frac{Q(X)}{P(X)}} \tag{28}\]
\[\ge -\log{ \sum P(X){\frac{Q(X)}{P(X)}} } \tag{29}\]
\[= -\log{ \sum Q(X) } = 0 \tag{30}\]

식 (28) → 식 (29)로 전개할 때, Jensen's inequality가 사용이 되어 lower bound 값이 생겼고 이를 이용하여 $D_{\text{KL}}(P \Vert Q) \ge 0$ 을 만족할 수 있었습니다.
식 (26)과 같이 $H(P, Q) \ge H(P)$ 를 Gibbs' inequality라고 합니다.

KL divergence의 ③ 특성은 KL divergence에는 교환 법칙이 성립하지 않는다는 점입니다.
교환 법칙이 성립되지 않기 떄문에 정확히는 거리함수라고 말할 수 없습니다. 하지만 두 분포가 다를수록 큰값을 가지며 둘이 일치할 때에만 0이 된다는 성질을 이용하여 거리 함수와 비슷한 용도로 사용할 수 있습니다.

KL divergence와 Log likelihood

만약 $P$ 가 실제 데이터 분포이고 $Q_{\theta}$ 가 우리가 설계하는 확률 모델이라고 하면 $D_{\text{KL}}(P \Vert Q_{\theta})$ 를 최소화 하는 것은, 우리 모형의 log-likelihood를 최대화 하는 것과 같아지게 됩니다.

\[P(x \vert \theta^{*}) : \text{Data distribution with True parameter} \theta^{*} \tag{31}\]
\[P(x \vert \theta) : \text{Our Model with tunable parameter} \theta \tag{32}\]

\[D_{\text{KL}}[P(x \vert \theta^{*}) \Vert P(x \vert \theta)] \tag{33}\]
\[\mathbb{E}_{x \sim P(x \vert \theta^{*})} \left[\log{\frac{P(x \vert \theta^{*})}{P(x \vert \theta)}} \right] \tag{34}\]
\[\mathbb{E}_{x \sim P(x \vert \theta^{*})} \left[\log{P(x \vert \theta^{*})} - \log{P(x \vert \theta)} \right] \tag{35}\]
\[\color{blue}{\mathbb{E}_{x \sim P(x \vert \theta^{*})} \left[\log{P(x \vert \theta^{*})} \right]} - \color{red}{\mathbb{E}_{x \sim P(x \vert \theta^{*})} \left[\log{P(x \vert \theta)} \right]} \tag{36}\]
\[-\color{blue}{H[P(x \vert \theta^{*})]} + \color{red}{H[P(x \vert \theta^{*}), P(x \vert \theta)]} \tag{37}\]

식 (36), (37) 에서 파란색에 해당하는 부분이 엔트로피이고 빨간색에 해당하는 부분이 크로스 엔트로피입니다. 엔트로피 부분은 $\theta$ 를 학습하는 것과 무관하므로 고정값으로 두면 실제 모델을 학습 시 영향을 끼치는 것은 크로스 엔트로피가 됩니다.

식 (36) 에서 크로스 엔트로피 부분만 이용하여 큰 수의 법칙 (Law of Large Numbers)를 적용하면 크로스 엔트로피 부분을 다음과 같이 적을 수 있습니다.

\[\text{Cross Entropy : } \mathbb{E}_{x \sim P(x \vert \theta^{*})} \left[\log{P(x \vert \theta)} \right] = \color{red}{-\frac{1}{N}\sum_{i}^{N} \log{P(x_{i} \vert \theta)}} \tag{38}\]

식 (38)에서 빨간색 부분인 크로스 엔트로피는 Negative log-likelihood가 됩니다.
우리의 목적은 크로스 엔트로피를 최소화 하여 $P(x \vert \theta^{*})$ 와 $P(x \vert \theta)$ 의 분포 차이를 최소화 하는 것입니다. 이 과정은 결국 Negative log-likelihood를 최소화 하는 것과 같고 이는 Log-likelihood를 최대화 하는 것과 같으므로 Maximum Likelihood Estimation 이라고 할 수 있습니다.

Mutual Information

임의의 두 확률 변수 $X$ 와 $Y$ 가 독립적이라면 결합(Joint)확률 분포는 확률 곱으로 표현 가능합니다.

\[P(X, Y) = P(X)P(Y)\]

만약 $X, Y$ 가 서로 독립적이지 않다면 확률 곱과 결합 확률 분포간의 차이를 KL divergence로 측정할 수 있습니다.

\[I(X; Y) = \sum_{y \in Y}\sum_{x \in X} p(x, y) \log{ \left( \frac{p(x, y)}{p(x)p(y)} \right) } \tag{39}\]
\[I(X; y) = D_{\text{KL}}(p(x, y) \Vert p(x)p(y)) \tag{40}\]

이와 같이 Mutual Information은 두 확률 변수들이 얼마나 서로 dependent 한 지 측정하며 서로 independent한 경우 Mutual Information = 0을 만족하고 서로 dependent할 수록 값이 커집니다. (즉, divergnece가 크다고 해석할 수 있습니다.)

이번 글에서 다룬 핵심 내용을 정리하면 다음 4가지로 정리할 수 있습니다.
① 엔트로피는 확률 분포 $P(X)$ 에서 일어날 수 있는 모든 사건들의 정보량의 기대값으로 $P(X)$ 의 불확실 정도를 평가합니다.
② 크로스 엔트로피의 의미는 실제 데이터는 분포 $P(X)$ 로부터 생성되지만, 분포 $Q(X)$ 를 사용하여 정보량을 측정해서 나타낸 정보량의 기대값을 의미합니다.
③ KL divergence는 두 확률 분포 $P(X)$ 와 $Q(X)$ 의 차이를 측정합니다.
④ Mutual Information 은 두 확률 변수들이 얼마나 서로 dependent한 지 측정합니다.

머신 러닝 관련 글 목록

목차

정보이론의 의미

정보량의 의미

Entropy

Cross Entropy

KL divergence

KL divergence와 Log likelihood

Mutual Information

정보이론의 의미

정보량의 의미

Entropy

Cross Entropy

KL divergence

KL divergence와 Log likelihood

Mutual Information