ML(Maximum Likelihood)와 MAP(maximum a posterior)

머신 러닝 관련 글 목록

• 참조 : 패턴인식(오일석)
• 이번 글에서는 MLE(Maximum Likelihood Estimation)와 MAP(maximum a posterior)에 대하여 알아보도록 하겠습니다.

목차

• ML(Maximum Likelihood)에 대한 개념적 설명

• MAP(Maximum a posterior)에 대한 개념적 설명

ML(Maximum Likelihood)에 대한 개념적 설명

• 먼저 ML(Maximum Likelihood)은 개념적으로 어떠한 형태의 분포에도 적용 가능합니다. 현실적으로는 정규 분포와 같이 매개 변수로 표현되는 경우에만 적용 가능한 데 매개 변수로 표시 된 경우만 계산이 가능하기 때문입니다. 이 매개 변수 집합을 \(\theta\) 라고 보통 표시합니다.
• 이 때, 문제를 다음과 같이 정의 할 수 있습니다.
  • 데이터 \(X\) 를 발생시켰을 가능성이 가장 높은 \(\theta\)를 찾아라
  • 데이터 \(X\) 에 대하여 가장 큰 likelihood를 갖는 \(\theta\)를 찾아라

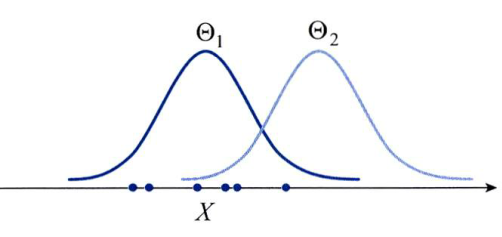
• 위 그래프에서 \(X\) 는 6개의 샘플을 갖습니다.
• 이 \(X\) 를 발생시킬 가능성은 \(\theta_{1}\) 이 \(\theta_{2}\) 보다 높습니다. 왜냐하면 각 \(X = (x_{1}, x_{2}, ... , x_{6})\) 에 해당하는 그래프 상의 함수값을 살펴보면 \(\theta_{1}\) 에 해당하는 그래프에서 더 큰 값을 가지기 때문입니다.
• likelihood를 이용하여 다시 표현하면 \(p(X \vert \theta_{1}) \gt p(X \vert \theta_{2})\) 라고 할 수 있습니다.
• 이 때 우리가 풀어야 할 문제는 어떤 \(\theta\)가 maximum likelihood를 가질까 입니다.

• Maximum likelihood를 이해하기 위해 다음과 같은 예제를 살펴보겠습니다.
• 3가지의 동전이 있습니다. 동전의 앞이 나올 확률이 \(p\), 뒤가 나올 확률이 \(1-p\)라고 하고 각각의 \(p\)는 1/4, 1/3, 1/2 입니다.
• 임의의 동전을 하나 집어서 50번 던졌을 때 관찰 결과 22번이 나왔습니다. 이 때, 과연 어떤 동전을 던졌을지 맞추는 것이 문제입니다.
• 이 문제의 해결법은 각 동전의 likelihood를 구한 다음에 그 값이 최대가 되는 것을 구하는 것입니다. 즉, maximum likelihood를 취하는 것입니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta \ P(X \vert \theta=p) \tag{1}\]
• \[P(\text{head} = 22 \vert p = \frac{1}{4}) = \begin{pmatrix} 50 \\ 22 \\ \end{pmatrix} (\frac{1}{4})^{22}(\frac{3}{4})^{28} = 0.0016 \tag{2}\]
• \[P(\text{head} = 22 \vert p = \frac{1}{3}) = \begin{pmatrix} 50 \\ 22 \\ \end{pmatrix} (\frac{1}{3})^{22}(\frac{2}{3})^{28} = 0.0332 \tag{3}\]
• \[P(\text{head} = 22 \vert p = \frac{1}{2}) = \begin{pmatrix} 50 \\ 22 \\ \end{pmatrix} (\frac{1}{2})^{22}(\frac{1}{2})^{28} = 0.0788 \tag{4}\]

• 따라서 p = 1/2 일 때, likelihood가 가장 크므로 위 3가지 케이스에 대해서는 p = 1/2 일 때 maximum likelihood라고 말할 수 있습니다.

• 문제를 좀 더 형식적으로 쓰면 다음과 같이 쓸 수 있습니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta \ p(X \vert \theta) \tag{5}\]

• 확률 분포 추정 문제를 위와 같이 maximum likelihood를 갖는 매개 변수를 찾는 것으로 규정하고 해를 구하는 방법을 Maximum Likelihood method 라고 합니다.
• 모든 샘플은 독립적으로 추출되었다고 가정할 수 있으므로, 즉 i.i.d (independent and identically distributed random variable)조건으로 가정하면 likelihood는 다음과 같이 쓸 수 있습니다.

• \[X = \{x_{1}, x_{2}, ... , x_{N} \} \tag{6}\]
• \[p(X \vert \theta) = p(x_{1} \vert \theta)p(x_{2} \vert \theta)...p(x_{N} \vert \theta) = \prod_{i=1}^{N}p(x_{i} \vert \theta) \tag{7}\]

• 식 (7)의 곱으로 표현된 식이 복잡하고 계산하기가 어려우므로 좀 더 단순한 형태로 식을 변경해 보겠습니다.
• 예를 들어 함수 \(f\) 가 단조 증가 함수라면 \(\operatorname*{argmax}_\theta p(X \vert \theta)\) 에서 \(P(X \vert \theta)\)를 최대화 하는 것과 \(f(p(X \vert \theta))\)를 최대화 하는 것은 같습니다.
• 따라서 likelihood에 단조 증가 함수인 log (ln)를 취한 것을 log likelihood 라고 하며 다음과 같습니다.

• \[\hat{\theta} = \operatorname*{argmax}_\theta \sum_{i=1}^{N} \ln{p(x_{i} \vert \theta)} \tag{8}\]

• 위 식은 최적화 문제에 해당합니다. 최적화 문제를 풀기 위해서는 미분을 한 결과가 0이 되는 것을 이용하겠습니다.

• \[\frac{\partial \ L(\theta)}{\partial\theta} = \frac{\partial\sum_{i=1}^{N} \ln{p(x_{i} \vert \theta)}}{\partial\theta} = 0 \tag{9}\]

• 만약 여기서 추정하고자 하는 확률 분포가 정규 분포를 따른다고 가정하면 풀이는 쉬워 집니다. 이 가정에 따르면 \(\operatorname*{argmax}_\theta = {\mu, \Sigma}\) (평균, 공분산) 이고 정규 분포에 대한 Maximum Likelihood를 하면 그 결과는 흔히 아는 평균과 분산을 구한 것이 됩니다. (풀이는 글 아래에서 진행하겠습니다.)
• 정리하면 정규 분포를 따른다고 가정하면 ML 방법에서 어떤 데이터 \(X\) 가 나오도록 하는 가장 가능성 높은 선택지는 평균 입니다. 그래프를 보았을 떄에도 정규 분포의 확률 분포 곡선을 보면 평균에서 가장 높은 확률값을 가지기 때문입니다.

• 그러면 좀 더 구체적으로 정규 분포를 위한 ML을 추정하는 과정입니다.
• 여기서 \(X\) 가 정규 분포에서 추정되었다고 가정하겠습니다. 수식 유도를 쉽게 하기 위하여 공분산 행렬 \(\Sigma\)는 이미 알고 있다고 가정하겠습니다. 즉, 추정해야 하는 것은 평균 벡터 \(\mu\) 뿐입니다. 따라서 아래 식 (10)에 정규 분포 식을 대입하고 정리해 보겠습니다.

• \[\frac{\partial\sum_{i=1}^{N}ln\ p(x_{i} \vert \theta)}{\partial\theta} \tag{10}\]

• 아래 식에서 \(d\) 는 특징 벡터 \(x_{i}\) 의 차원 입니다.

• \[p(x_{i} \vert \theta) = p(x_{i} \vert \mu) = \frac{1}{ (2\pi)^{d/2} \vert \Sigma \vert^{1/2} } \exp{ (-\frac{1}{2}(x_{i} - \mu)^{T} \Sigma^{-1} (x_{i} - \mu)) } \tag{11}\]
• \[\ln{p(x_{i} \vert \mu)} = -\frac{1}{2}(x_{i} - \mu)^{T} \Sigma^{-1}(x_{i} - \mu) -\frac{d}{2}\ln{2\pi} -\frac{1}{2}\ln{\vert \Sigma \vert} \tag{12}\]
• \[L(\mu) = -\frac{1}{2}\sum_{i=1}^{N}(x_{i} - \mu)^{T}\Sigma^{-1}(x_{i} - \mu) -N(\frac{d}{2}ln2\pi -\frac{1}{2}\ln{\vert \Sigma \vert)} \tag{13}\]
• \[\frac{\partial L(\mu)}{\partial \mu} = \sum_{i=1}^{N} \Sigma^{-1}(x_{i} - \mu) \tag{14}\]

• 이제 식 (14) = 0 이 되도록 두고 정리해 보겠습니다.

• \[\sum_{i=1}^{N} \Sigma^{-1}(x_{i} - \mu) = 0 \tag{15}\]
• \[\sum_{i=1}^{N}x_{i} - N\mu = 0 \tag{16}\]
• \[\hat{\mu} = \frac{1}{N}\sum_{i=1}^{N}x_{i} \tag{17}\]

• 이 식으로 구한 평균 벡터는 최적 매개 변수 값이기 때문에 hat 씌워 표시합니다.

• 평균, 분산의 ML을 추정하는 자세한 풀이는 다음 링크를 참조해 주시기 바랍니다.

• 링크 : https://gaussian37.github.io/ml-concept-probability_model/#mle-with-gaussian-1

• 위 식은 두가지 정보가 제공된 상황에서 구해졌습니다.
  • ① 훈련 집합 X 라는 정보
  • ② 확률 분포가 정규 분포를 따른다는 정보
• 이 상황에서 샘플의 특징 벡터를 모두 더하고 그것을 \(N\) 으로 나누어준 값, 즉 샘플의 평균 벡터가 바로 찾고자 하는 최적의 매개 변수가 된다는 직관과 동일 합니다.

MAP(Maximum a posterior)에 대한 개념적 설명

• 앞에서 ML에 대하여 설명할 때에는 \(p(\theta)\)가 균일하다는 가정으로 식을 전개하였습니다.
• 만약 \(p(\theta)\) 가 균일하지 않다는 추가적인 정보 가 주어져서 사용 가능하다면 어떻게 사용할 수 있을까요? 이 경우에는 \(p(\theta)\) 를 고려하여 최적화 문제를 풀어야 합니다.
• 식에서 \(p(x_{i} \vert \theta)\) 를 likelihood 라고 하고 \(p(\theta)\) 를 사전 확률 이라고 합니다.
• 이 때, \(p(x_{i} \vert \theta)p(\theta)\) 를 사후 확률이라고 합니다.

• 따라서 이 수식을 풀어 최적의 매개변수를 찾는 과정을 MAP(Maximum a posterior) 라고 합니다.

• \[\operatorname*{argmax}_\theta \sum \ln{(p(x_{i} | \theta))} + \ln{(p(\theta))} \tag{18}\]

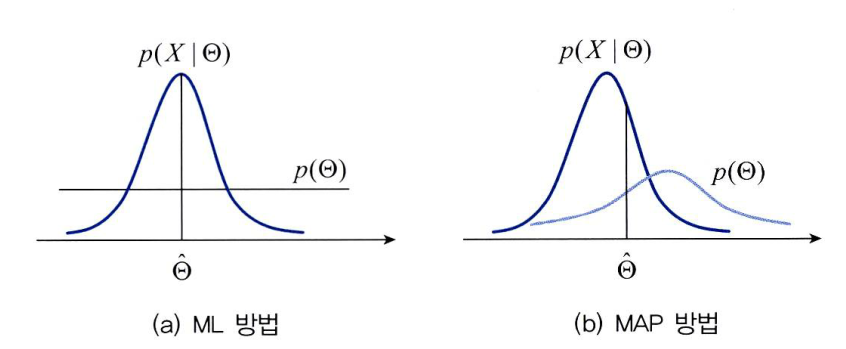
• 위 그림은 ML과 MAP를 비교합니다.
• ML에서는 사전확률이 균일하다고 가정합니다. 따라서 likelihood가 최고인 점을 찾으면 그것이 바로 최적해 \(\theta\)가 됩니다.
• 하지만 MAP 에서는 사전 확률이 균일하지 않습니다. 따라서 사전확률이 최적해에 영향을 미치게 됩니다. 이러한 차이점이 있습니다.

머신 러닝 관련 글 목록