Linear, Logistic Regression의 확률적 해석

2020, Aug 09    

머신 러닝 관련 글 목록

• 이번 글에서는 평소 익숙한 Linear Regression과 Logistic Regression을 확률 모형 (Probabilistic Model)로 표현하여 확률적인 해석을 해보도록 하겠습니다.

목차

• Linear Regression

• Linear Regression의 확률적 표현

• Logistic Regression

• Logistic Regression의 확률적 표현

• Summary

Linear Regression

• Linear Regression의 확률적 해석을 알아보기 이전에 간단히 Linear Regression의 개념을 리뷰하겠습니다.

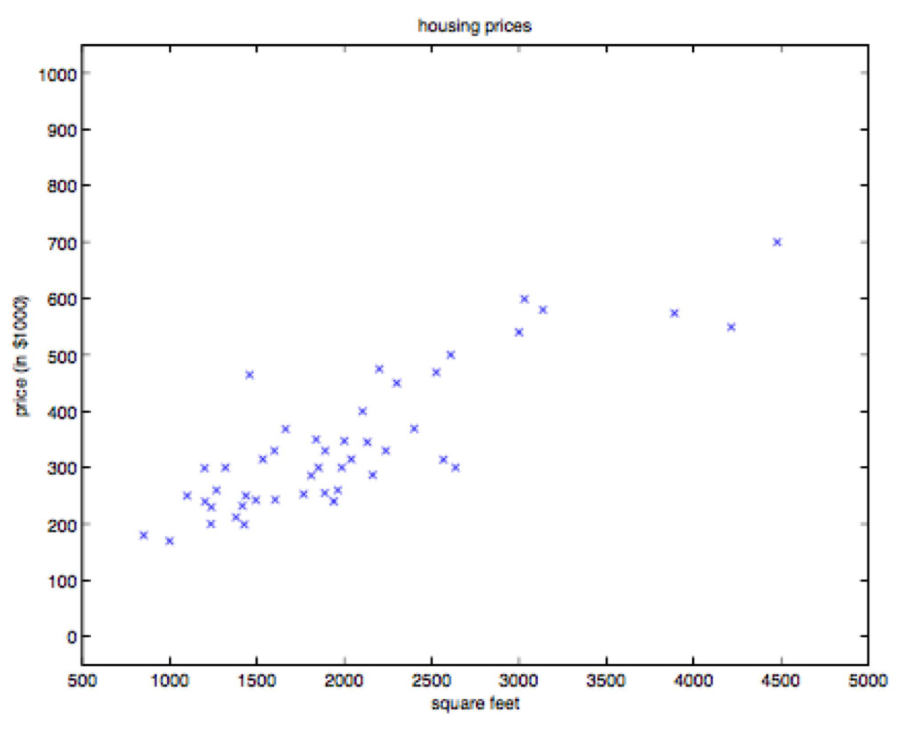
• 위 식은 집들의 면적과 그 면적에 따른 가격이 데이터로 주어졌을 떄, Linear Regression 모델로 표현하고자 하는 방식입니다.
• Linear Regression의 경우 위 그래프에서 직선을 하나 그어서 주어진 데이터를 가장 잘 표현하도록 만들고 주어지지 않은 입력값 (집의 면적)이 주어졌을 때, 그 집의 가격을 추정하는 방법이 됩니다.

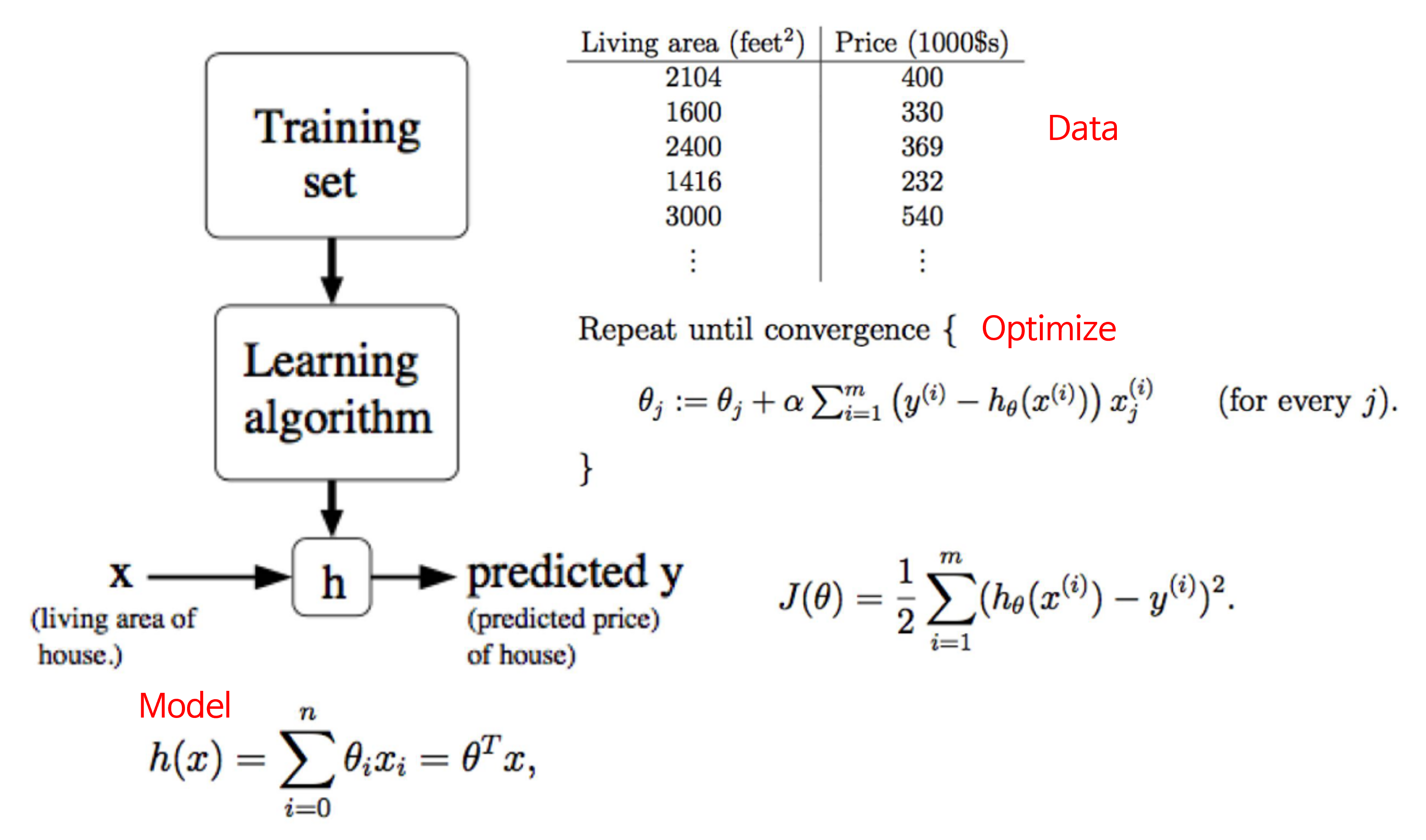
• Linear Regression 문제에서는 (집의 면적, 집의 가격) = ( $x$ , $y$ ) 가 되며 $x$ 는 모델에 입력이 되는 값이고 $y$ 는 정답값이 됩니다.
• 이 때, Linear Regression 모델을 $h_{\theta}(x)$ (hypothesis)로 표현하고 문제를 풀어가면서 최적화 (Optimize) 해야할 값은 $\theta$ 값이 됩니다.

• 이 $\theta$ 값을 최적화 하기 위하여 $J(\theta)$ 라는 Loss를 사용합니다.
• 머신 러닝 문제를 풀어갈 때, 이러한 Loss Function을 정의하는 것 또한 모델링의 일부분이며 학습을 하기 위하여 gradient가 필요하므로 미분이 가능한 Loss Function을 사용하는 것이 일반적입니다.

• 참조 사항으로 좀더 자세하게 Loss Function의 조건에 대하여 알아보면 다음 3가지 조건을 만족해야 합니다.
• ① Gradient를 계산할 수 있도록 미분이 가능해야 합니다.
• ② Loss 값에 음수가 없어야 합니다.
• ③ Loss Function이 Convexity 형태를 가져야 합니다.

Linear Regression의 확률적 표현

• 앞에서 알아본 Linear Regression을 확률적으로 어떻게 표현되는 지 한번 살펴보도록 하겠습니다.
• 정답 y와 입력 x의 관계를 Linear Model로 표현하면 다음과 같습니다.

• $$y^{(i)} = \theta^{T}x^{(i)} + \epsilon^{(i)} \tag{1}$$

• 식 (1)의 노이즈 $\epsilon$ 가 평균이 0인 zero mean gaussian 분포를 따른다고 가정하겠습니다. ( $\epsilon \sim N(0, \sigma)$ )
• 식 (1)을 $\epsilon$ 를 기준으로 정리하면 다음과 같습니다.

• $$p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi} \sigma}\exp{\biggl( -\frac{(\epsilon^{(i)} - 0)^{2}}{2\sigma^{2}} \biggr)} \tag{2}$$

• 이 때, $y$ 에 대한 확률 모형인 Discriminative Model $p(Y \vert X ; \theta)$ 는 다음과 같이 정의될 수 있습니다.

• $$\epsilon^{(i)} = y^{(i)} - \theta^{T}x^{(i)} \tag{3}$$
• $$p(y^{(i)} \vert x^{(i)}; \theta ) = \frac{1}{\sqrt{2\pi} \sigma}\exp{\biggl( -\frac{( y^{(i)} - \theta^{T}x^{(i)})^{2}}{2\sigma^{2}} \biggr)} \tag{4}$$
• $$y^{(i)} \vert x^{(i)}; \theta \sim N(\theta^{T}x^{(i)}, \sigma^{2}) \tag{5}$$

• 위 식 $p(y^{(i)} \vert x^{(i)}; \theta )$ 을 통하여 $\theta$ 에 대한 likelihood 함수를 구하면 다음과 같습니다.

• $$L(\theta) = \prod_{i=1}^{m} p(y^{(i)} \vert x^{(i)}; \theta ) \tag{5}$$
• $$= \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi} \sigma}\exp{\biggl( -\frac{( y^{(i)} - \theta^{T}x^{(i)})^{2}}{2\sigma^{2}} \biggr)} \tag{6}$$

• MLE(Maximum Likelihood Estimation)은 Likelihood를 최대화하는 $\theta$ 를 추정하는 것이며 곱 연산으로 인해 값이 굉장히 작아지는 문제를 개선하기 위하여 log를 적용하 log-likelihood를 사용하여 다음과 같이 표현합니다. 상세 내용은 다음 링크 https://gaussian37.github.io/ml-concept-probability_model/를 참조해 주시기 바랍니다. 식을 전개해 보겠습니다.

• $$l(\theta) = \log{L(\theta)} \tag{7}$$
• $$= \log{\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma} \exp{\biggl(-\frac{(y^{(i)} - \theta^{T}x^{(i)})^{2}}{2\sigma^{2}} \biggr)}} \tag{8}$$
• $$= \sum_{i=1}^{m} \log{ \frac{1}{\sqrt{2\pi}\sigma} \exp{\biggl(-\frac{(y^{(i)} - \theta^{T}x^{(i)})^{2}}{2\sigma^{2}} \biggr)}} \tag{9}$$
• $$= -m \log{\frac{1}{\sqrt{2\pi}\sigma} \frac{1}{\sigma^{2}} \cdot \frac{1}{2} \sum_{i=1}^{m}(y^{(i)} - \theta^{T}x^{(i)})^{2}} \tag{10}$$

• 식 (10)이 음수 식으로 정리됨에 따라 $l(\theta)$ 를 최대화 하기 위해서는 결론적으로 $\frac{1}{2} \sum_{i=1}^{m}(y^{(i)} - \theta^{T}x^{(i)})^{2}$ 을 최소화 해야 함을 알 수 있습니다. 따라서 MLE를 하기 위해서는 다음을 만족해야 합니다.

• $$\text{Minimize : } \frac{1}{2} \sum_{i=1}^{m}(y^{(i)} - \theta^{T}x^{(i)})^{2} \tag{11}$$

• 식 (11)은 앞에서 살펴 보았던 Loss Function에 해당하며 Loss Function의 사용 목적도 Loss를 최소화 하기 위함인 것을 상기하면 Linear Model $y^{(i)} = \theta^{T}x^{(i)} + \epsilon^{(i)}$ 에서 $\epsilon^{(i)}$ 가 zero-mean gaussian 분포를 따른다는 가정하에 MLE와 Loss를 최소화 하는 것은 같음을 알 수 있습니다.
• 참고로 $\epsilon$ 을 Laplacian으로 가정하면 Loss Function이 절대값으로 나오게 됩니다. 따라서 어떤 분포로 가정하느냐에 따라 다른 형태의 Loss Function으로 유도됩니다.

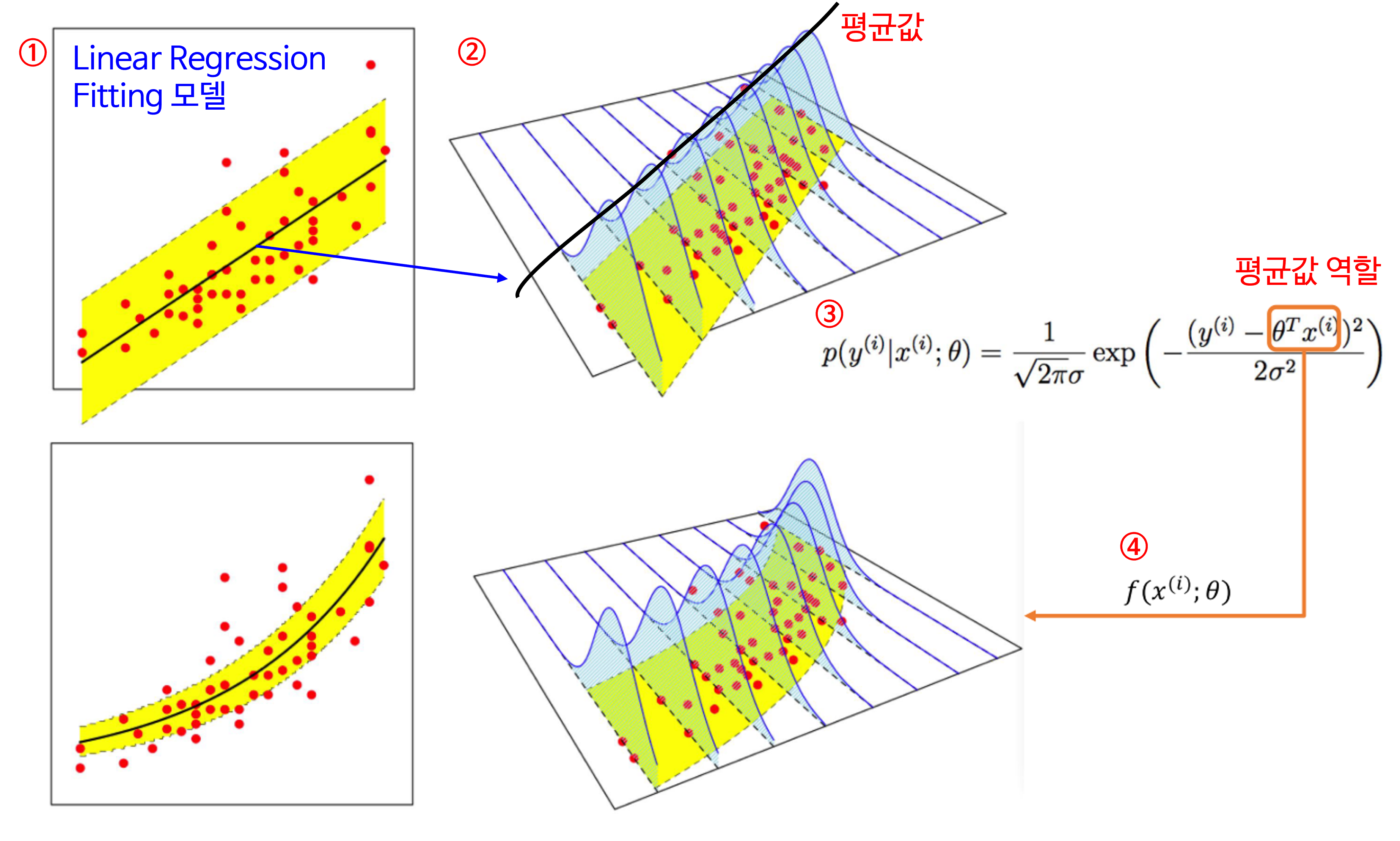
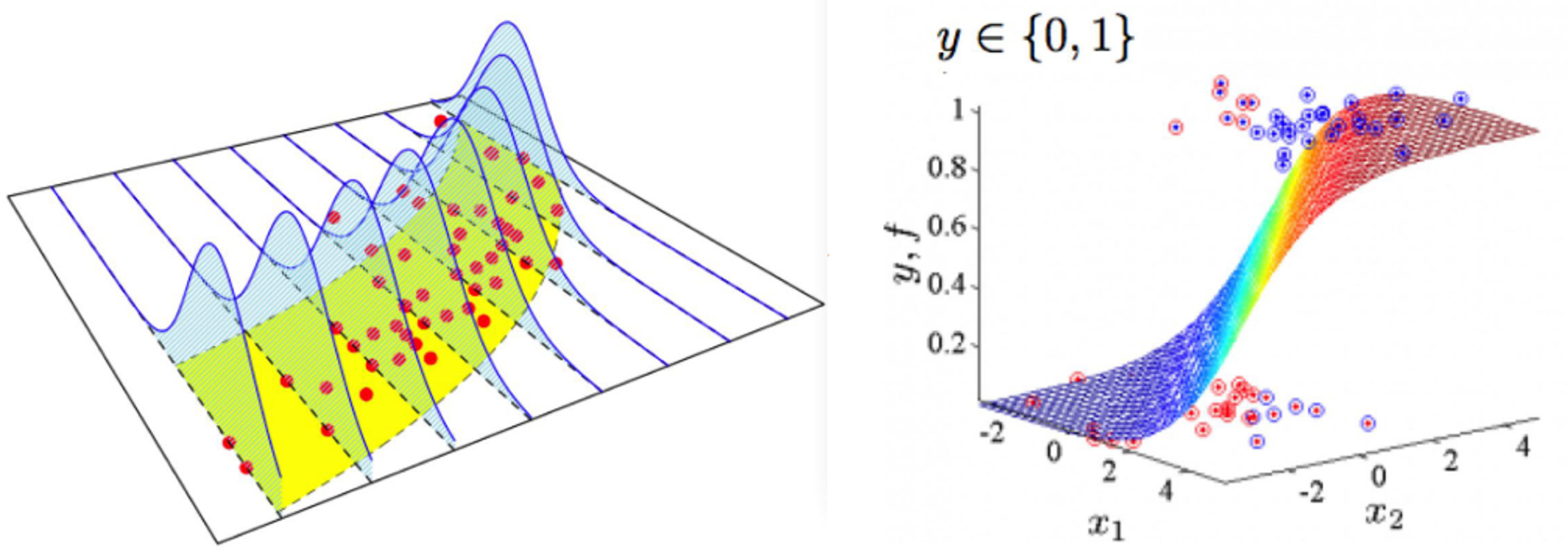
• 앞에서 수식으로 표현한 것을 그래프로 나타내면 위 그림과 같습니다.
• 먼저 ① 그림에서 검정색 선이 Linear Regression Fitting한 것이 됩니다. ② 그림에서 보면 이 Fitting한 선을 따라 데이터가 가우시안 분포를 가지게 되며 선에 해당하는 값이 평균값이 됩니다. 참조 링크를 통해 확인하면 가우시안 분포의 Maximum Likelihood는 평균값에서 만족합니다.
• 식 ③과 같은 확률 모형이 결정이 되면 이 식에 따라 데이터가 분포됩니다. 식 ③은 가우시안 분포를 가정하여 수립되었기 때문에 $x^{(i)}$ 가 입력값이고 그 함수값인 $\theta^{T}x^{(i)}$ 는 평균값의 역할을 하게 됩니다.
• 이 때, $f(x^{(i)}; \theta) = \theta^{T}x^{(i)}$ 라고 정의하면 이 함수값의 변형에 따라 평균과 분포가 바뀌게 되고 그 결과 fitting된 곡선이 바뀔 수 있습니다.

• 지금까지 과정을 정리하면 변수 $X, Y$ 들의 관계를 확률 모형 $p_{\theta}(Y \vert X)$ 로 정의하고, Likelihood $L(\theta)$ 를 정의하였을 때, MLE(Maximum Likelihood Estimation)을 통하여 최적의 해 $\theta$를 찾는 과정은 Least-square cost를 최소화 하는 것과 같음을 살펴 보았습니다. (몇가지 가우시안 가정을 전제로 하였습니다.)
• 이와 같이 확률 분포를 이용한 모형 해석을 통해 기존 Linear Regression에서 Least Square Loss를 사용하는 하나의 근거를 찾을 수 있었습니다.

Logistic Regression

• Logistic Regression 또한 많이 알려진 모델이며 Classification Model로써 사용되고 있습니다. 이번에는 앞의 Linear Regression과 유사하게 Logistic Regression을 이용한 확률적 해석을 해보도록 하겠습니다.

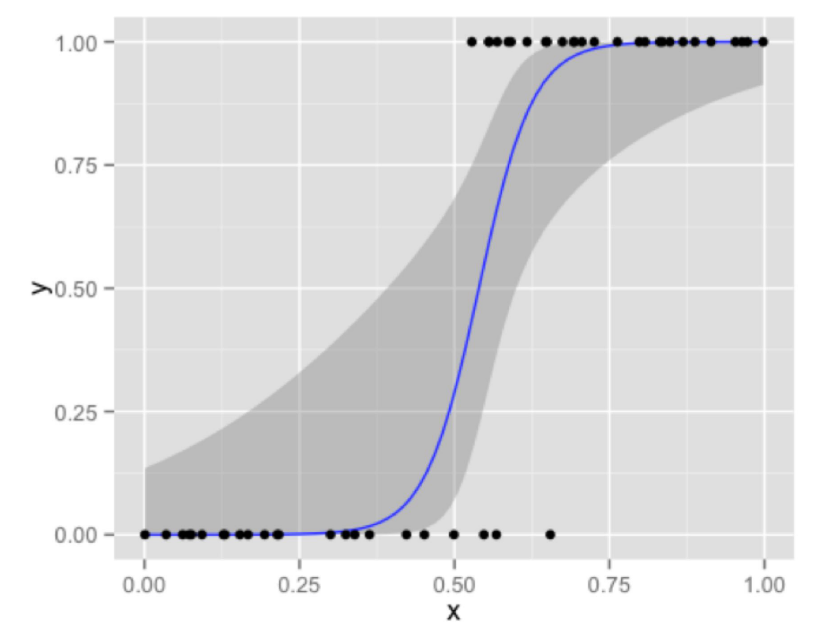
• 위 그림과 같이 입력값 $x$ 에 따라 출력값 $y$ 는 0 또는 1을 가지게 되므로 Logistric Regression의 경우 입력값 $x$ 를 받았을 때, 0 또는 1의 출력을 내야 합니다. 먼저 모델의 형태에 대하여 알아보도록 하겠습니다.

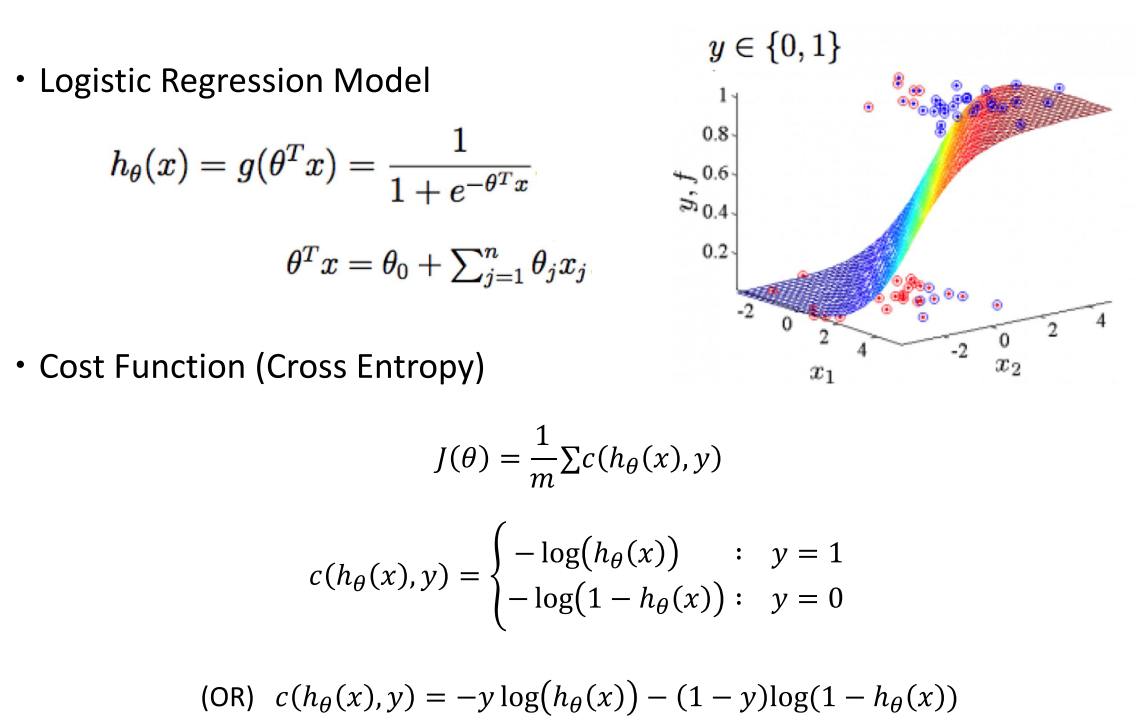
• $$h_{\theta}(x) = g(\theta^{T}x) = \frac{1}{1 + e^{-\theta^{T}x}} \tag{12}$$
• $$\theta^{T}x = \theta_{0} + \sum_{j=1}^{n}\theta_{j}x_{j} \tag{13}$$

• 앞에서 Linear Regression에서 기본적으로 사용하였던 Loss Function이 Squared Error를 소개하였었습니다. 일반적으로 Logistic Regression에서는 Cross Entropy를 Loss Function으로 사용합니다. 형태는 다음과 같습니다.ㄴ

• $$J(\theta) = \frac{1}{m} \sum c(h_{\theta}(x), y) \tag{14}$$
• $$c(h_{\theta}(x), y) = \begin{cases} -\log{(h_{\theta}(x))} & : y = 1 \\ -\log{(1 - h_{\theta}(x))} & : y= 0 \end{cases} \tag{15}$$
• $$\to c(h_{\theta}(x), y) = -y\log{(h_{\theta}(x))} -(1-y)\log{(1 - h_{\theta}(x))} \tag{16}$$

• Logistic Regression에서 사용되는 Cross Entropy 형식은 0/1을 선택하는 Binary Cross Entropy를 따릅니다. 보통 Softmax → Cross Entropy를 차례로 적용하거나 Sigmoid → Binary Cross Entropy를 적용합니다.
• 현재 다루고 있는 Logistic Regression의 경우 Sigmoid → Binary Cross Entropy에 해당합니다. 즉, Sigmoid를 거치기 때문에 0/1 사이의 값을 가지게 됩니다.

Logistic Regression의 확률적 표현

• 그러면 이 정보들을 이용하여 앞의 Linear Regression에서 다룬 바와 같이 확률 모델로 나타내 보겠습니다. $h_{\theta}(x)$ 즉, hypothesis를 인풋 변수 $x$ 가 주어졌을 때 아웃풋 변수 $y$ 에 대한 확률 모형 $p(Y \vert X)$ 로 가정하겠습니다.

• $$p(y = 1 \vert x; \theta) = h_{\theta}(x) \tag{17}$$
• $$p(y = 0 \vert x; \theta) = 1 - h_{\theta}(x) \tag{18}$$

• Sigmoid 함수의 출력을 이용하므로 Binary Cross Entropy를 적용하기 전 출력의 범위가 0 ~ 1 사이가 되고 식 (17 ), (18)의 확률 모형이 $x$ 가 주어졌을 때, 0 이나올 확률 또는 1이 나올 확률 2가지를 대상으로 확률을 얻는 문제가 되므로 Bernoulli Distribution으로 해석할 수 있습니다.

• $$p(y \vert x; \theta) = (h_{\theta}(x))^{y}(1 - h_{\theta}(x))^{1-y} \tag{19}$$
• $$y \vert x; \theta \sim \text{Bernoulli}(\phi) \tag{20}$$

• 식 (20) 에서 $\phi$ 에 해당하는 값은 $h_{\theta}(x)$ 입니다.
• 식 (19)의 확률 모델을 이용하여 MLE를 구하기 위해 likelihood 함수 식을 유도하면 다음과 같습니다.

• $$L(\theta) = p(Y \vert X; \theta) \tag{21}$$
• $$\prod_{i=1}^{m} p(y^{(i)} \vert x^{(i)}; \theta) \tag{22}$$
• $$\prod_{i=1}^{m} (h_{\theta}(x^{(i)}))^{y^{(i)}}(1 - h_{\theta}(x^{(i)}))^{1-y^{(i)}} \tag{23}$$

• $$l(\theta) = \log{L(\theta)} \tag{24}$$
• $$= \sum_{i=1}^{m} y^{(i)} \log{(h_{\theta}(x^{(i)}))} + (1-y^{(i)})\log{(1 - h_{\theta}(x^{(i)}))} \tag{25}$$
• $$= -\sum_{i=1}^{m} y^{(i)} -\log{(h_{\theta}(x^{(i)}))} - (1-y^{(i)})\log{(1 - h_{\theta}(x^{(i)}))} \tag{26}$$

• 식 (26)의 값을 최대화 하는 것은 식 (14)인 Logistic Regression의 Loss Function을 최소화 하는 것과 같은 의미를 가지게 됩니다. 따라서 Logistic Regression의 MLE를 구하는 것은 Binary Cross Entropy Loss Function을 최소화 하는 것과 같다라고 이해할 수 있습니다.

Summary

• 지금까지 평소 익숙한 Linear Regression과 Logistic Regression을 확률 모형 (Probabilistic Model)로 표현하였고 두 모형 다 input $X$ 와 output $Y$ 데이터 쌍이 활용되는 Supervised Learning 상황에서 학습하였습니다.
• 평소 익숙한 모형들의 학습에 사용되는 Loss Function이 확룔로 정의되는 모형에 의한 log-Likelihood 함수를 최적화 하는 것과 같은 것임을 확인하였습니다.
• 또한 용어를 정리하면 Discriminative Approach는 확률 모형 $p_{\theta}(Y \vert X)$ 를 가정하고 MLE를 만족시키는 최적의 파라미터 $\theta$ 를 학습하는 것임을 숙지하시면 도움이 됩니다.

머신 러닝 관련 글 목록